2. 中国科学院地质与地球物理研究所油气资源重点实验室, 北京 100029;;
3. 中国国土资源航空物探遥感中心, 北京 100083
2. Key Laboratory of Petroleum Resource Research, Chinese Academy of Sciences, Beijing 100029, China;;
3. China Aero Geophysical Survey & Remote Sensing Center for Land and Resources, Beijing 100083, China
目前,油气资源地震勘探正面临西部高陡山地、山前带、盐下等复杂构造的精确成像问题.在过去的几十年里,叠前深度偏移技术得到了快速的发展,基于波动方程的深度偏移,诸如单程波偏移[1-2]、逆时偏移[3-4],逐渐取代基于高频近似的射线类方法,有效地提高了高陡构造、山前带、盐下等复杂地质体的成像效果.波动方程类深度偏移有效实施的一个前提是需提供一个高分辨率的速度模型,但是目前广泛应用于速度分析的还是基于射线的走时层析技术[5-6],该类方法虽然计算效率高,但其高频近似的射线追踪正演计算导致只能反演得到一个光滑的速度模型.为了能够应用波动方程偏移获得一个更为精确的成像结果,对速度模型的精度和分辨率提出了更高的要求,因此需要基于求解波动方程的速度分析方法.
直接求解波动方程的速度分析方法总体可以分为两类,一类称之为波动方程偏移速度分析(MVA)[7-8],该类方法一般采用人机交互方式执行,需要计算机辅助质控来保证方法的有效实施,可获得一个光滑的速度模型;另外一类是波形反演方法[9-14],该类方法直接应用地震波形反演地下介质速度,更充分的利用反射折射等波形信息,能够得到精度和分辨率较高的速度模型,是目前国内外速度分析研究的重要方向.
波形反演方法最早由Tarantola 在1984 年提出,目前从计算方式上主要可以分为三类:一是时间空间域波形反演[9-10];二是频率域波形反演[11-12];三是Laplace域波形反演[13-14].相对比三种方法,频率域波形反演方法有如下的优点:(1)只需有限个频率便可以反演得到一个精度很高的速度模型,计算量相对另外两种方法大大减小;(2)频率域波形反演很容易通过复速度引进吸收系数,同时边界条件计算容易实施,减小了计算的复杂度;(3)频率域波形反演比时间域的计算更容易进行多尺度计算,避免了计算陷落于局部最小.
在国内,随着勘探复杂度的增加,许多专家学者开展了波形反演的研究及应用工作,其中包括高静怀,丁继才等[15-17]对井间地震的波形反演研究,石玉梅等[18]通过波形反演对密度和孔隙度的研究,宋海斌等[19]通过波形反演对天然气水合物BSR 反射的研究,王彦飞等[20]对反演中正则化问题的研究等.
频率域波形反演计算得以实施的要素中与频率相关的因素占据主要地位,这其中包括用频率域多尺度计算方式来解决初始模型选择不当而导致的反演过程陷落于局部最小问题,选择合适的频带来解决频带范围选择不当导致的不同尺度模型不均匀性反演效果差的问题,以及子波频带的选择对反演结果是否带来影响等.本文将着重就频率域波形反演中这几个方面的问题展开研究和实验分析.
2 频率域波形反演的基本理论根据Pratt的介绍[11-12],从二维(2D)声波方程出发的频率域波形反演计算可归纳为如下的过程:
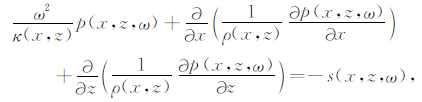
|
(1) |
其中,ρ(x,z)是介质密度,κ(x,z)为体积模量,p(x,z,ω)为频率域波场,s(x,z,ω)为频率域震源.
根据波场与震源的线性性质,方程(1)可表示为如下的矩阵形式:
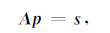
|
(2) |
A在频率域为一个复数矩阵,称为阻抗矩阵.
频率域波形反演加权最小二乘目标函数为C(m):
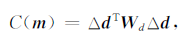
|
(3) |
其中,Δd为采集数据与模型为m时的正演结果的残差,ΔdT 是残差转置,Wd是一个与偏移距有关的加权函数,可调节Δd中不同部分对反演过程的贡献.应用梯度法求取模型第i个散射点的模型扰动量为
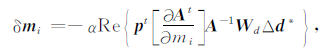
|
(4) |
α是一个步长加权系数,方程(4)可理解为一个正传的波场p和一个反传的波场残差A-1WdΔd* 的乘积.
为了增加反演过程的稳定性,(4)式引入正则化和光滑因子后变为
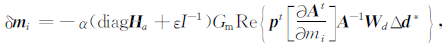
|
(5) |
diagHa是对角Hessian矩阵,Gm 是一个起平滑作用的二维高斯滤波器.(5)式是反演的单炮单频率形式,多炮多频率反演为(5)式对频率和震源的叠加,表达为
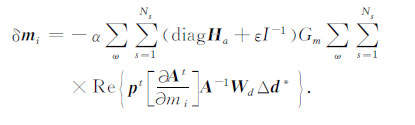
|
(6) |
频率域波形反演进行前,需要对采集的数据进行滤波,废道编辑,炮间能量均衡,计算时窗选择等.而在反演计算中,计算得以实施的要素中与频率相关的因素占据主要地位,本文将就其中的四个方面进行分析研究:一是反演数据频率范围的选定,以消除观测系统假频对反演结果的影响;二是频率域多尺度反演计算的实施,用以解决初始模型选择不当而易导致的反演过程陷落于局部最小,影响最终反演结果的问题;三是试验分析参加频率域波形反演计算的频带范围的选择,为因频带范围选择不当而导致的不同尺度的模型不均匀性反演效果差的问题提供参考;四是用频带范围不同的雷克子波和脉冲子波对波形反演结果的影响进行对比测试.
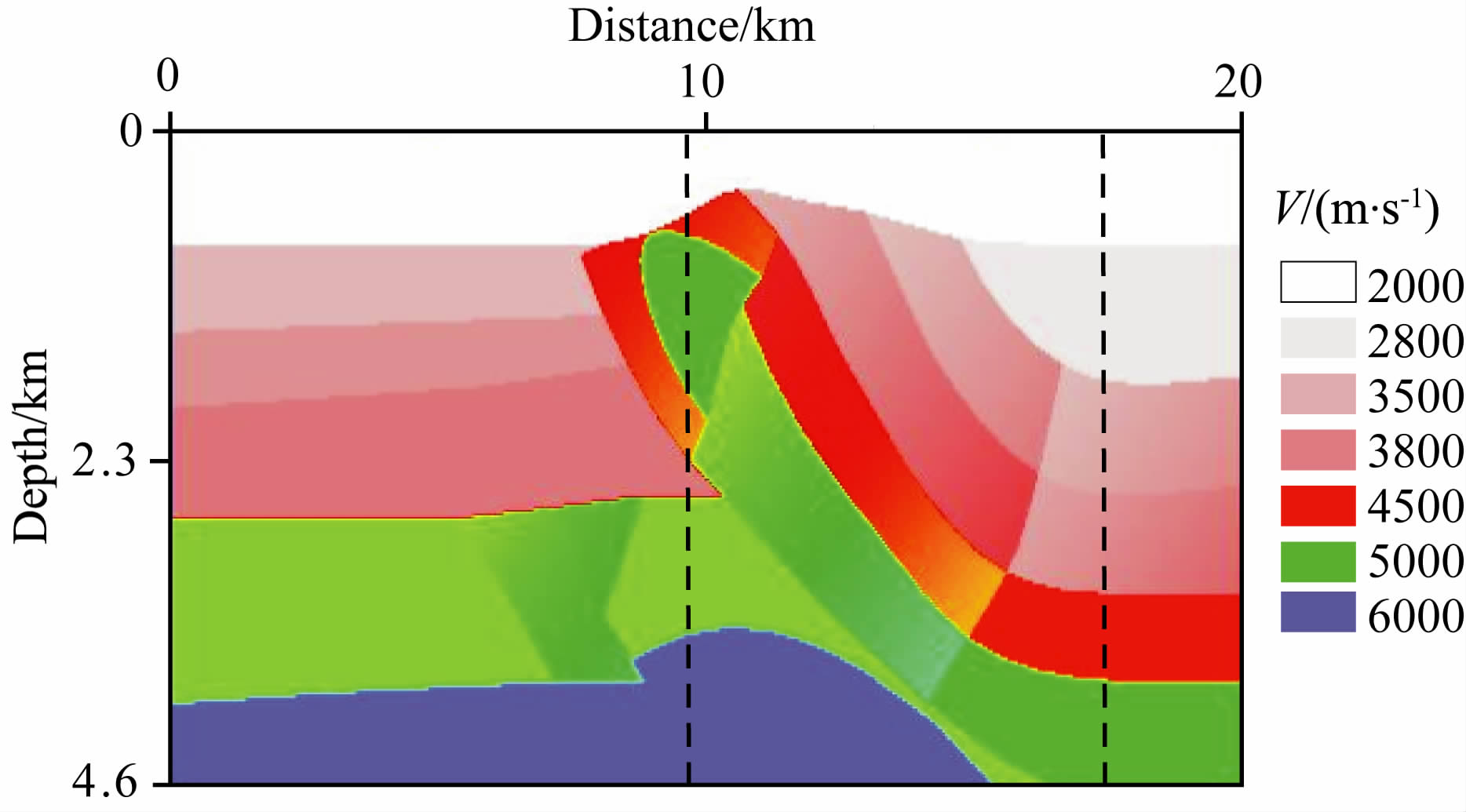
根据中国西部某山地构造设计了地质模型(如图 1),用于本文方法测试和对比.应用该模型共模拟400炮地震记录,其中炮间距为50m, 道间距50m, 最大偏移距为7000m, 采样间隔为4ms, 道长为6s.分别在水平方向10km 和17.5km 处选择两个CMP作为反演对比及质控点,如图 1中黑色点线所示.
|
图 1 根据西部某山地构造设计的速度模型 Fig. 1 A designed geology model based on Chinese western mountain structure |
同偏移成像一样,输入数据的空间分布是反演过程成功的保障,数据中的假频可能对反演结果造成假象,对于给定的观测系统,数据中无假频的条件为
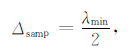
|
(7) |
其中,λmin 为单频波的最小波长,Δsamp为地震记录的采样间隔.
对于以频率为f,最小传播速度为cmin, 传播角度为θ 的地震波,波长可表示为
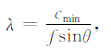
|
(8) |
当角度θ 趋于90°时,方程变(8)为
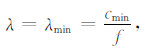
|
(9) |
将(9)式带入方程(7),得到对于道间距确定的输入数据,数据频率范围应该满足:
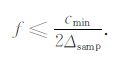
|
(10) |
虽然上述公式给定了数据频带范围的一个选择公式,但是,具体的输入数据假频与反演结果中的假象间的具体关系目前还没有明确的理论依据,需要更深入的研究[21].
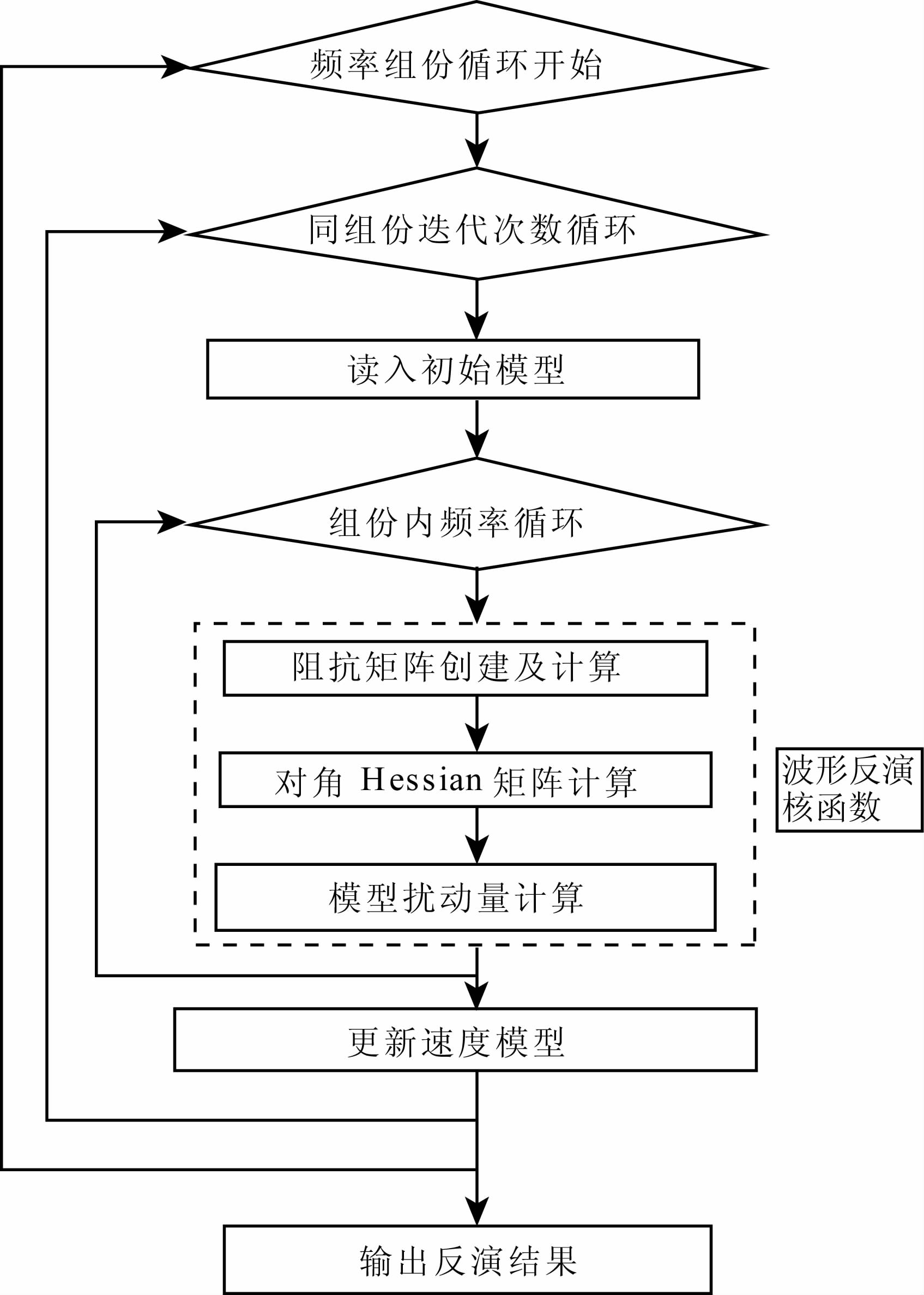
3.2 频率域波形反演计算方式分析波形反演过程是一个非线性反演问题,初始模型选择不当会导致目标函数陷落于局部最小[22].研究表明可通过多尺度的反演过程来使反演的结果达到全局最优.时间域波形反演的多尺度波形反演通过设计有效的通带滤波器来优化选择数据频带[23-25],先用低频数据反演出一个光滑的初始模型,然后用高频数据反演出模型的小尺度不均匀部分,最终得到一个高分辨率的反演结果.上述思路在频率域的执行更为方便简洁,在计算的过程中将参与反演的数据频率按从低到高分成不同组份,各组份内频率一起反演,不同组份间依次反演,即可实现多尺度计算,本文实现了频率域多尺度波形反演计算,计算流程如图 2所示,流程包括三重循环,即包含组份内的多频率计算组、不同迭代次数间反演计算和不同组份间反演计算.
|
图 2 频率域多尺度反演流程 Fig. 2 Flowchart of multi-scale frequency domain waveform inversion |
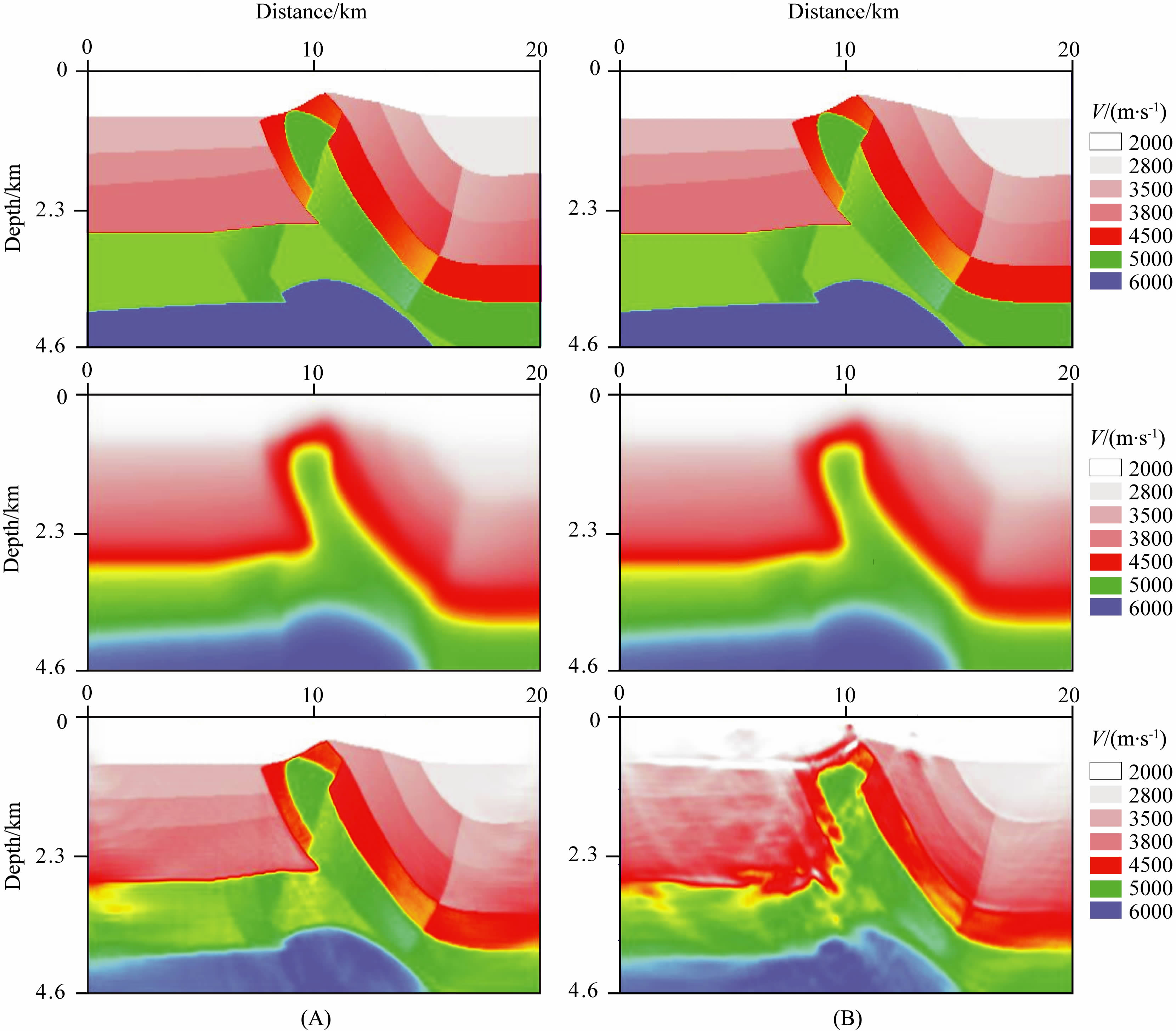
应用图 1模型模拟的地震记录对频率域多尺度反演流程进行对比测试,在0~20Hz之间平均选择7个频率的数据作为反演的输入数据,第一种方法是将这7个频率分成7 个组份(每个组份包含一个频率)进行依次反演,单组份迭代次数为20次,第二种方法是将7个频率分成2 个组份,前三个频率为第一组,后四个为第二组,各组迭代次数为70次.反演网格数为801×374,网格间距为25×12.5 m.图 3~5 是两者的反演结果,对比可以看出,在总的迭代次数一样的情况下,细化的多尺度计算效果明显优于粗化的多尺度反演结果.
|
图 3 第一种方法(A)及第二种方法(B)的反演结果 (A)、(B)中从上到下分别为正确模型,初始模型和反演结果(说明同图 6,9,12). Fig. 3 Inversion result with method one(A)and method two(B) In (A)and(B),the module from up to down are true velocity,initial velocity and inversion result |
|
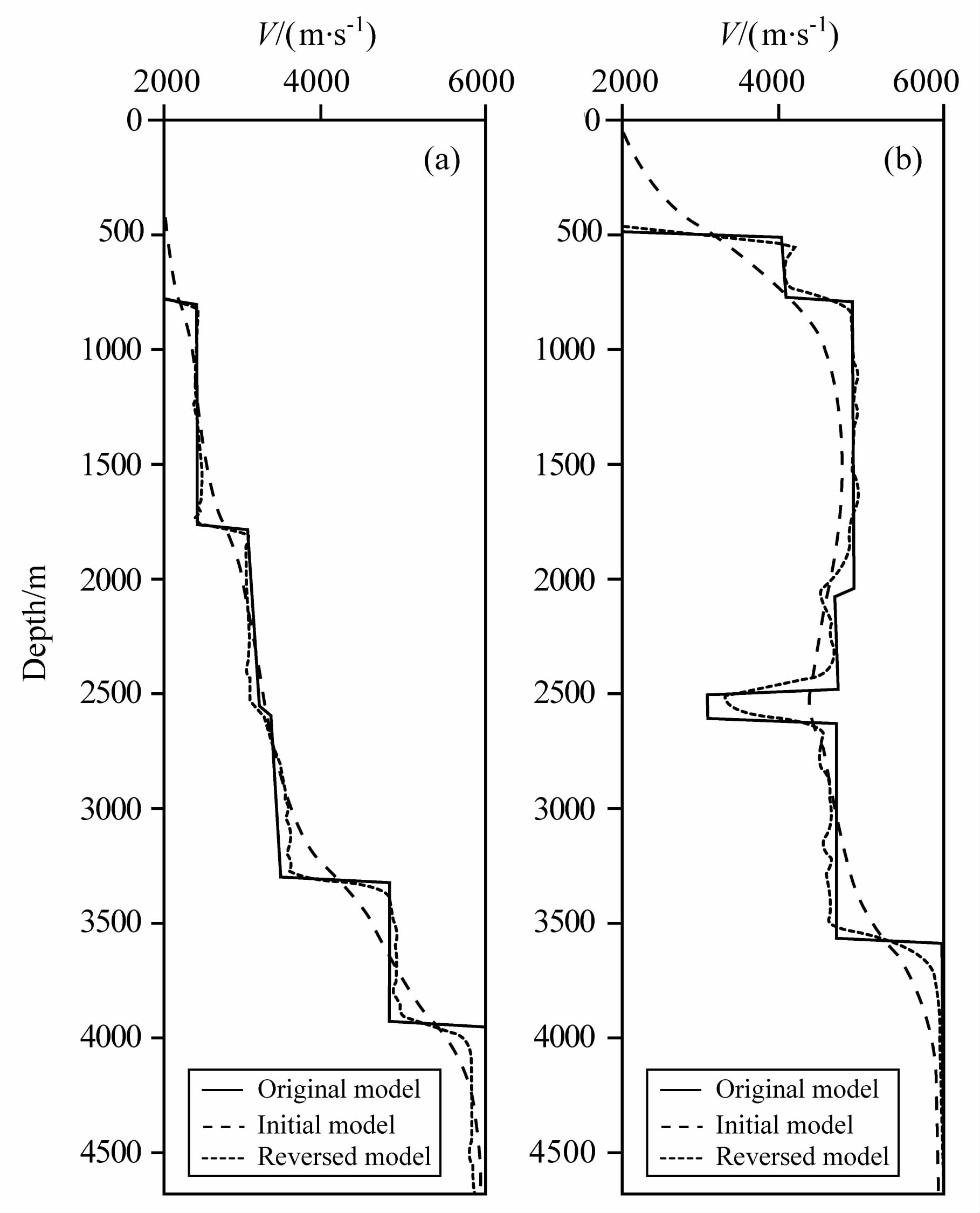
图 4 方法一中17.5km (a)和10km(b)处反演结果. Fig. 4 Inversion results with method one at 17.5km(a) and 10km(b) of the module |
|
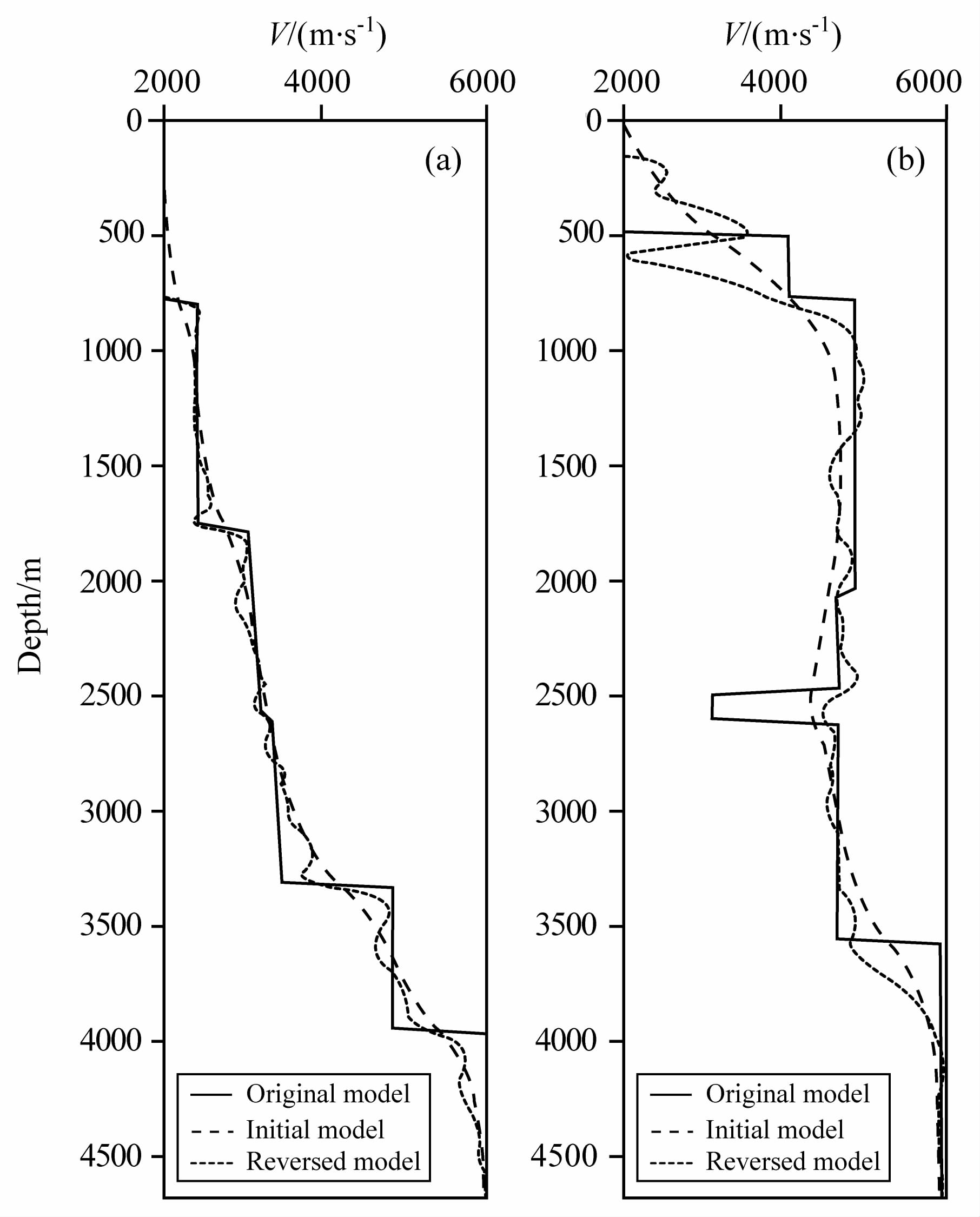
图 5 方法二中17.5km (a)和10km (b)处反演结果 Fig. 5 Inversion results with method one at 17.5km (a) and 10km (b) of the module |
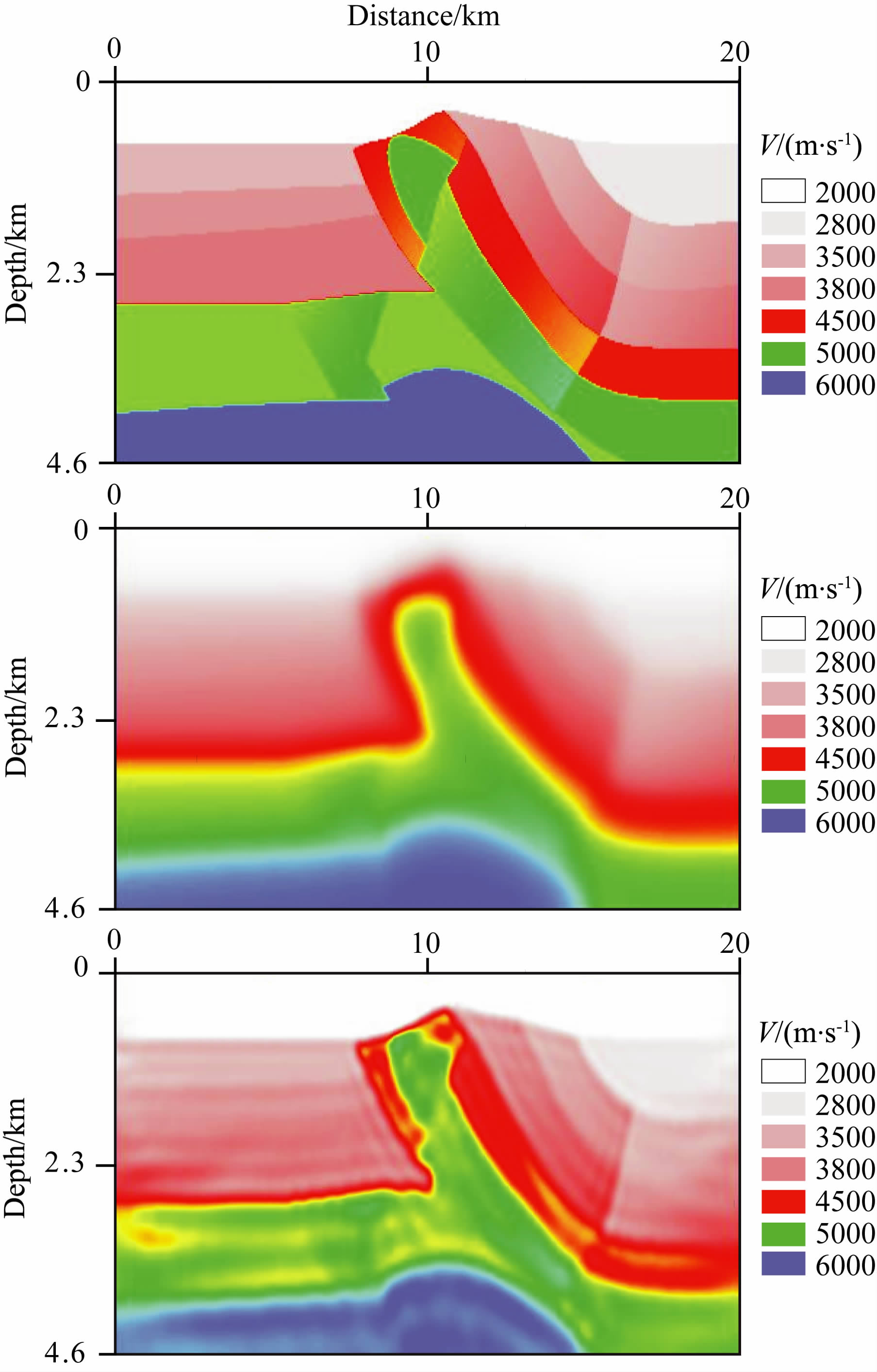
3.2节的测试应用0到20 Hz内平均分配的7个频率,反演得到了较为理想的速度模型,验证了频率域波形反演多尺度计算的有效性.同时也佐证了频率域波形反演的优点之一———应用有限个频率的信息就能够得到较为理想的反演结果.这一优点很大程度上推动了波形反演在勘探尺度上的应用.本节将测试不同频带范围对波形反演结果的影响,采用3.2节中的第一种计算方法,将0到20 Hz之间的7个频率更换为0到10Hz之间均匀分布的7个频率,其他反演参数均不变.图 6 和图 7 为反演结果.对比图 3a和图 6,从窄带频率数据获得的模型相对平滑,高频变化的速度不均匀性没有得到很好的反演.因此,在频率域波形反演中,合理地选择数据频带是保证反演结果精度的重要因素.
|
图 6 0到10 Hz间7个频率第一种方法反演结果 Fig. 6 Inversion result of method one with 7 frequency point at 0~10 Hz |
|
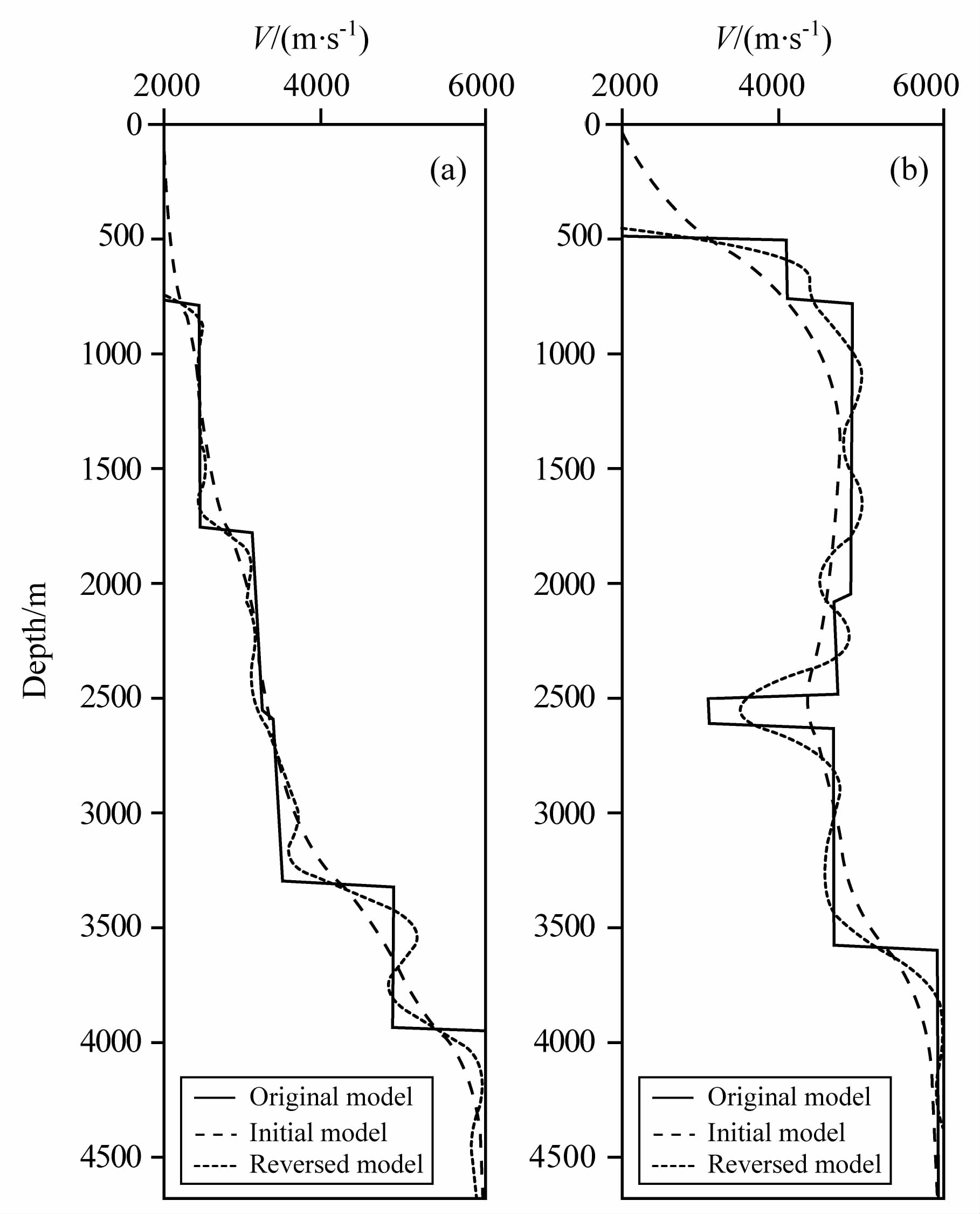
图 7 图 6中17.5km (a)和10km (b)处反演结果 Fig. 7 Inversion results of Fig.6 at 17.5km(a) and 10km(b) of the module |
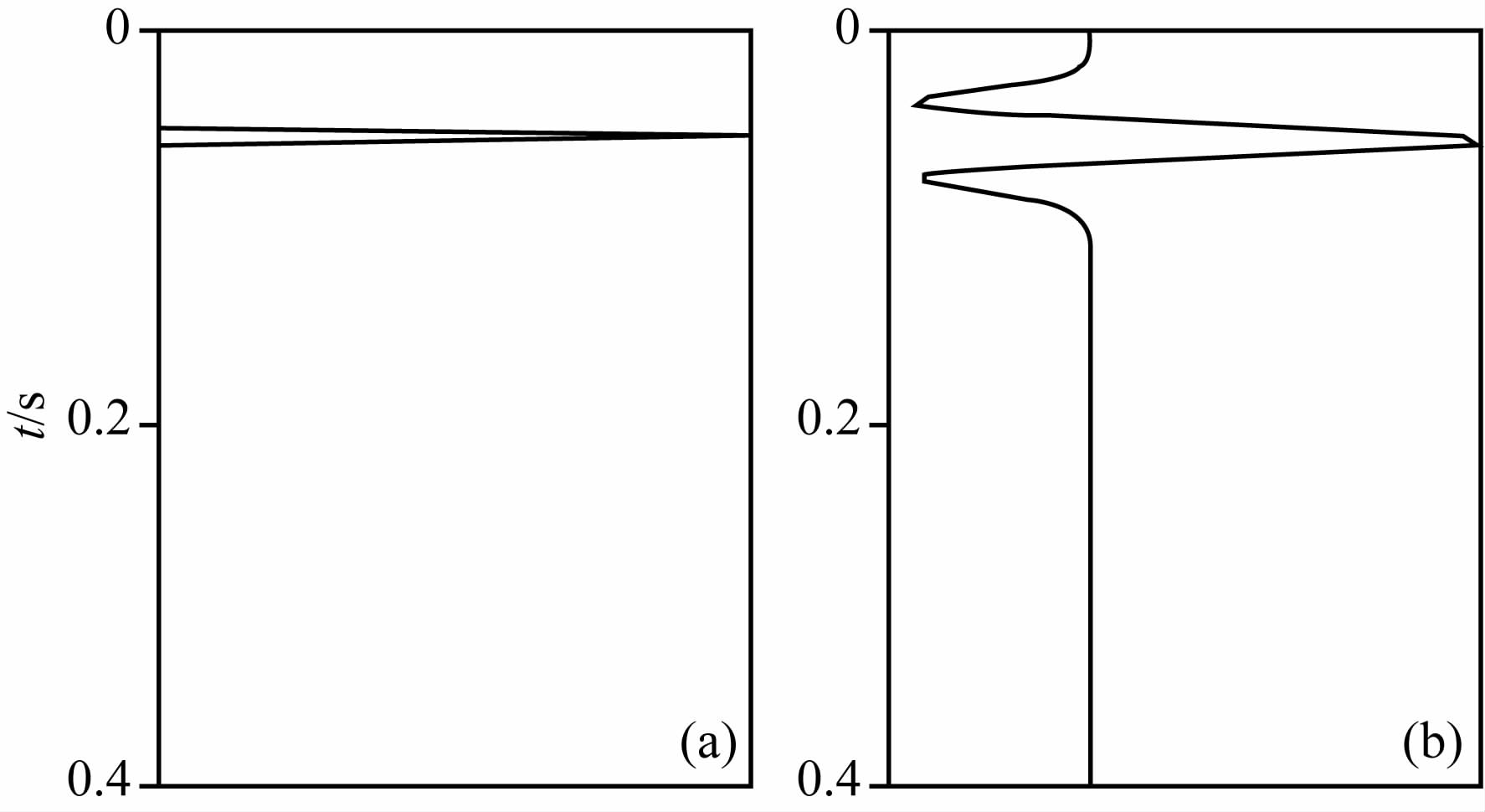
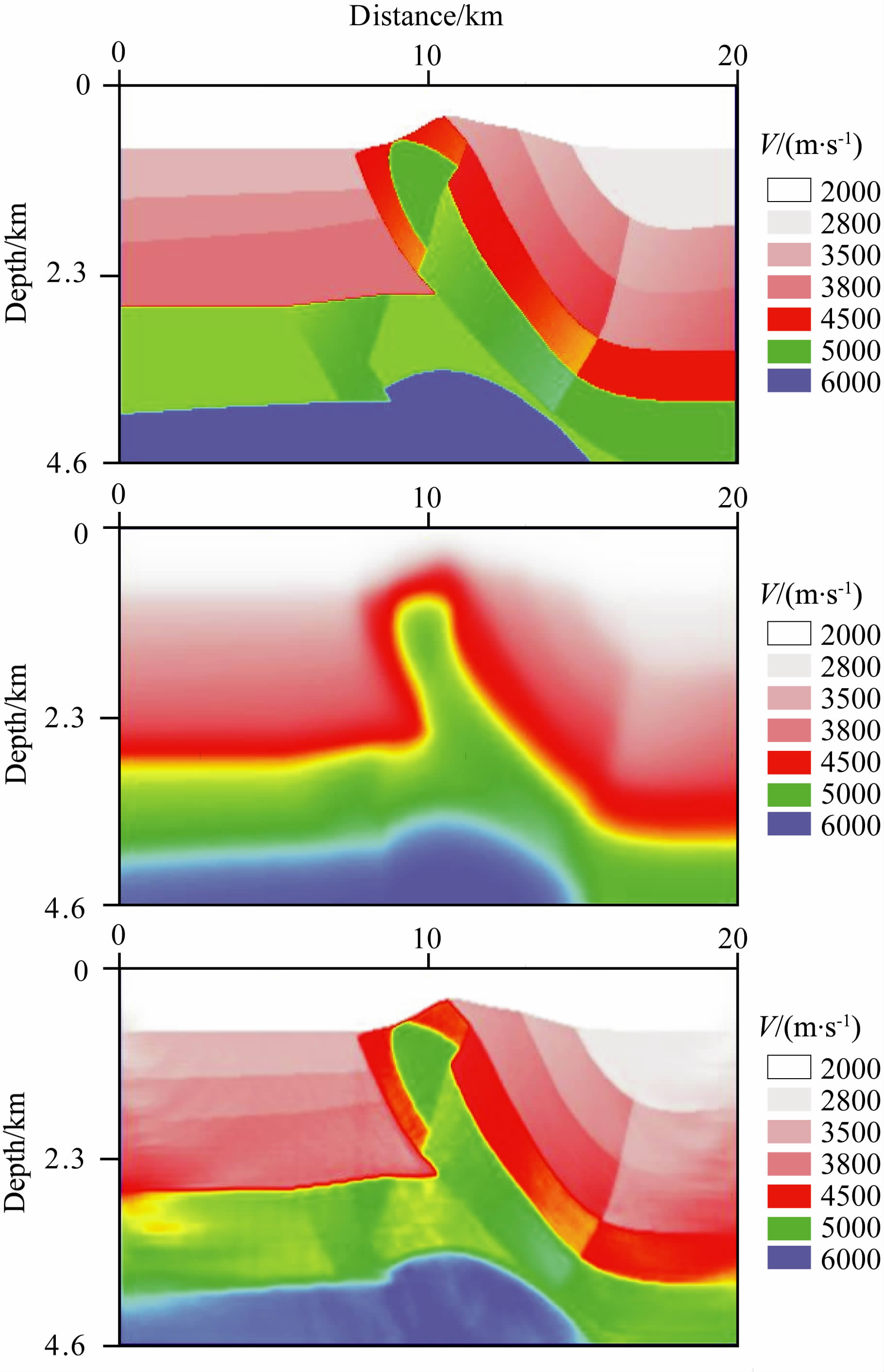
频率域波形反演中另外一个与频率有关的参数就是子波的频带范围,在3.2节和3.3节的计算中,选择的子波主频为7Hz的Ricker子波,如图 8b所示.为了测试子波的频带范围对波形反演的影响,选择了一个脉冲子波与之对比,如图 8a.除子波改变成脉冲子波外,其他的参数都与3.2 节中第一种计算方法相同、测试首先在没有噪声加入的数据上进行(图 11a),反演的结果如图 9和图 10.对比图 3a和图 9,可以看出,在没有噪声频率的影响下,应用脉冲子波反演的结果除深部稍有改善外,其他无明显变化.
|
图 8 脉冲子波(a)和主频为7 Hz的Ricker子波(b) Fig. 8 Pulse (a) and 7 Hz ricer wavelet (b) |
|
图 9 应用脉冲子波,第一种计算方法和参数时的反演结果 Fig. 9 Inversion result of method one with pulse wavelet |
|
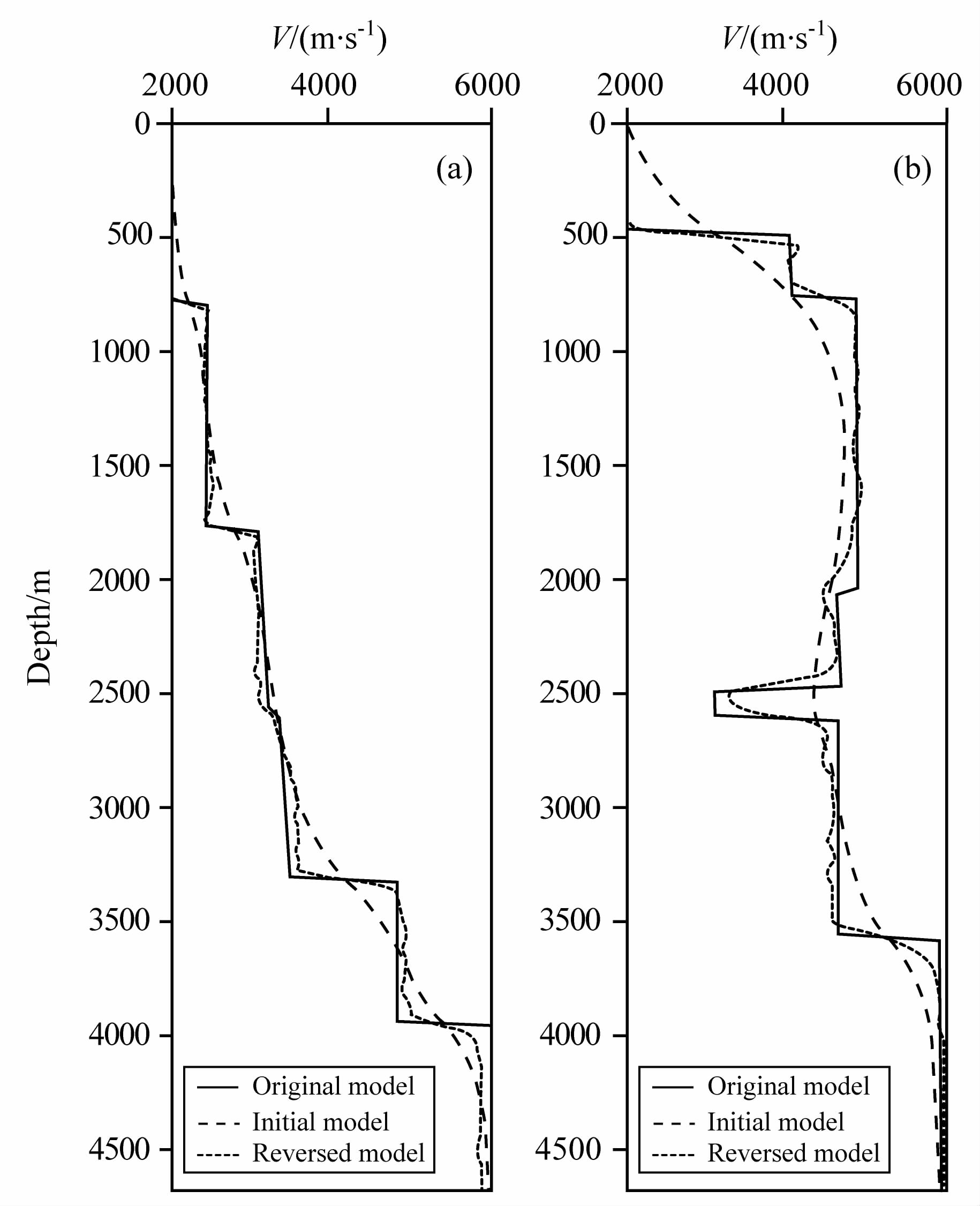
图 10 图 9中17.5km (a)和10km (b)处反演结果 Fig. 10 Inversion results in Fig.9 at 17.5km(a) and 10km(b) of the module |
|
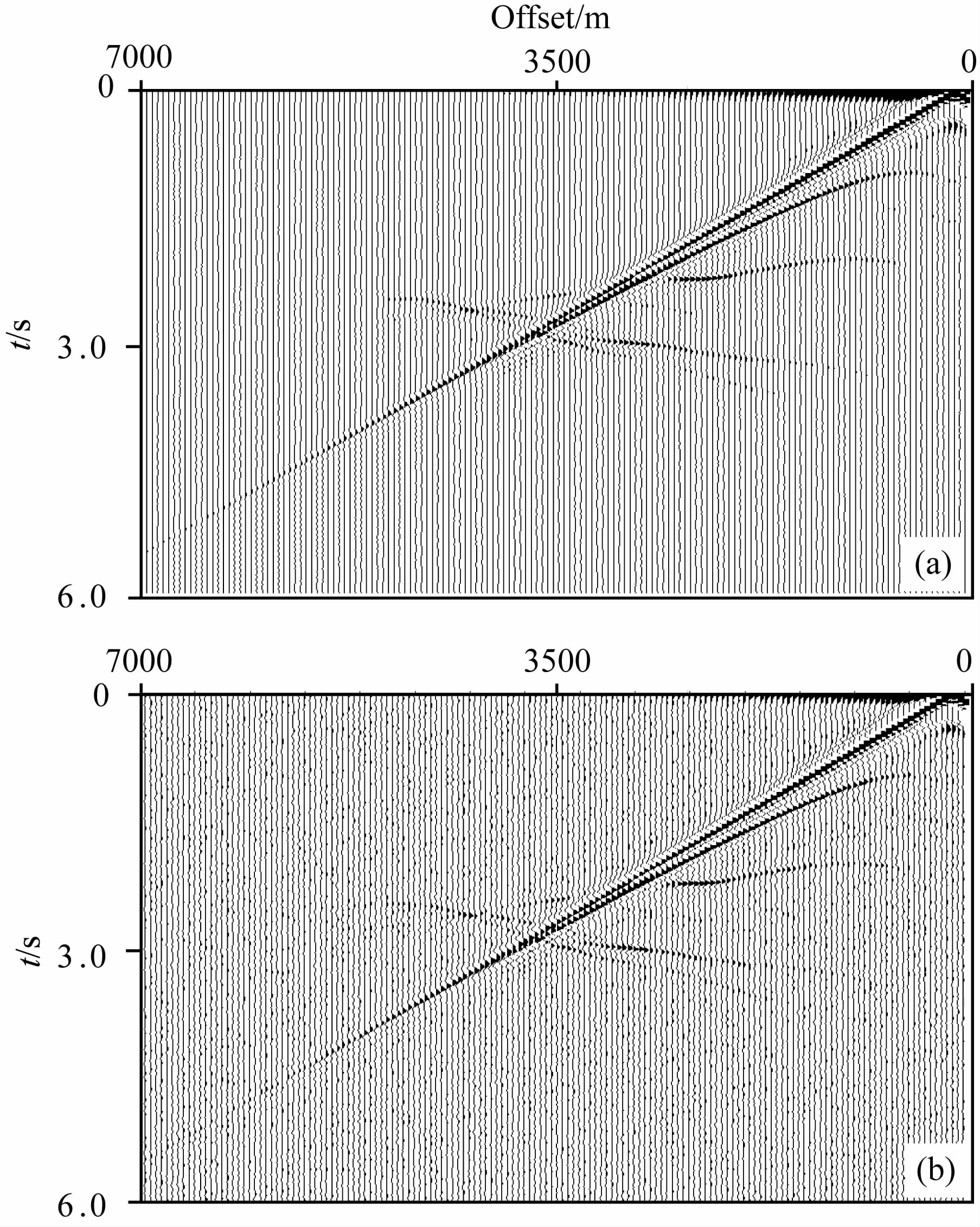
图 11 单炮数据:(a)无噪声;(b)有噪声 Fig. 11 One shot gather data with (b)and without noise(a) |
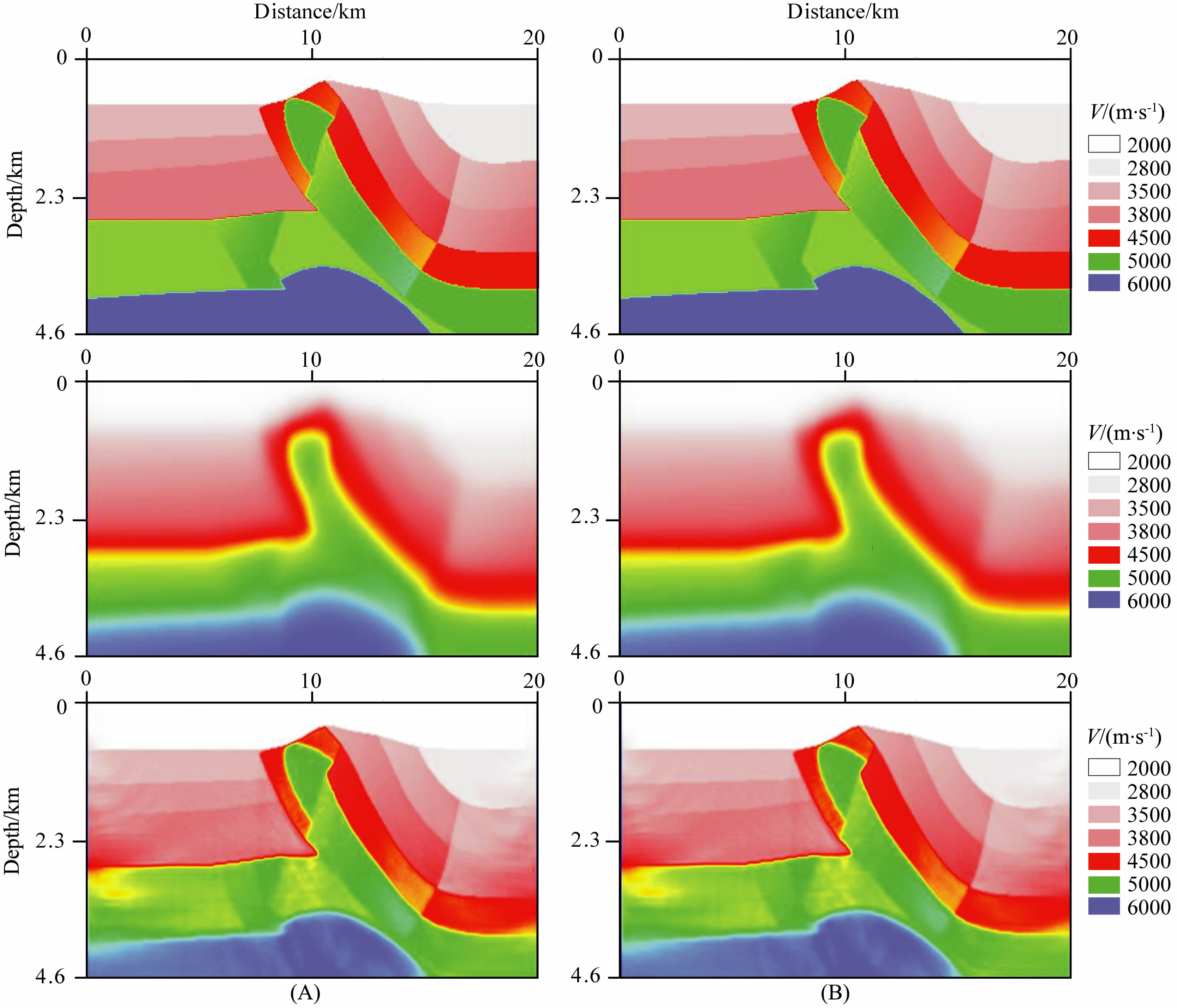
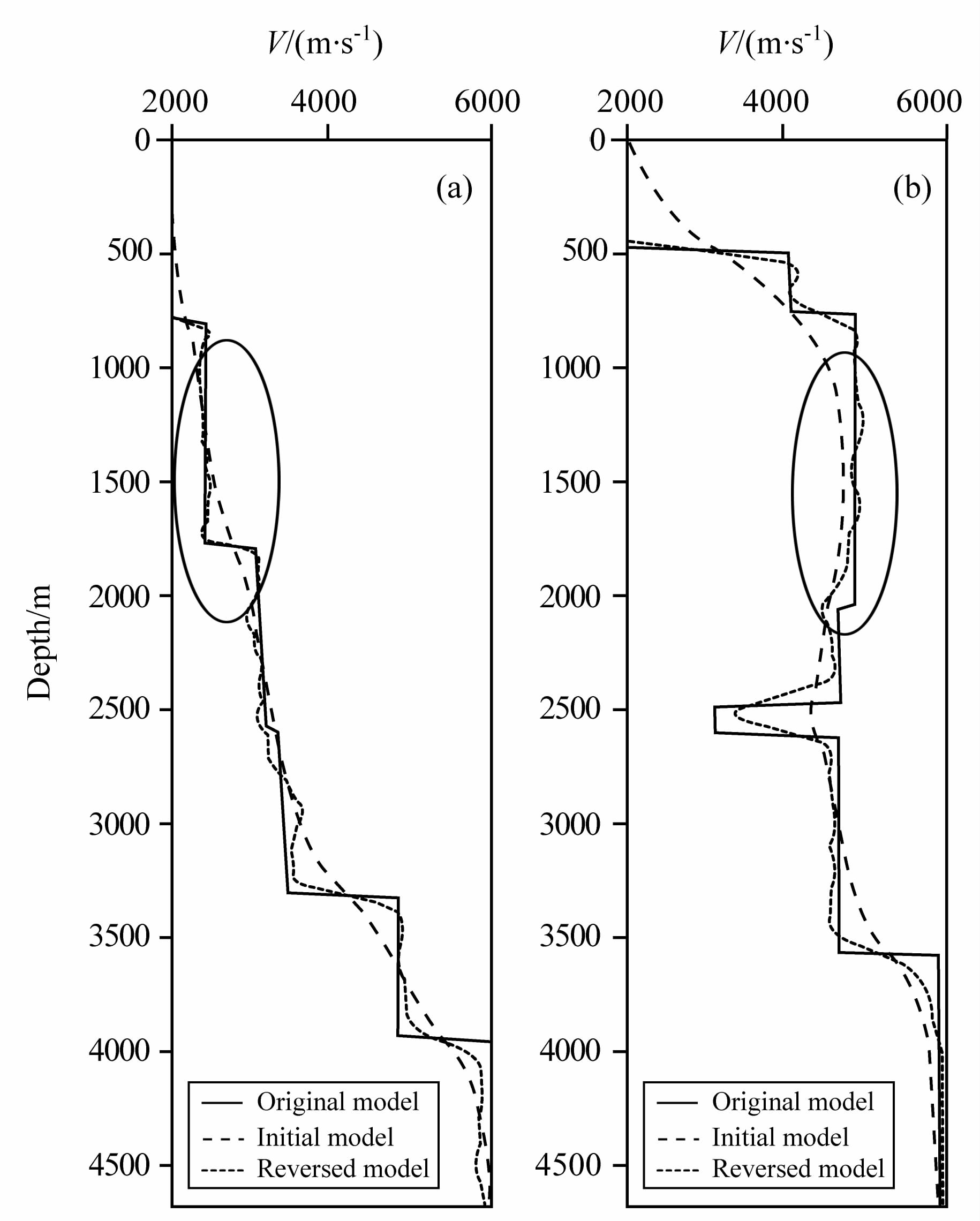
试验的第二部在数据中加入高斯噪声,信噪比为100(根据CWP软件suaddnoise程序),其中单炮数据如图 11b所示,应用与图 9相同参数进行反演,反演结果如图 12,13,14所示,因为高斯噪声的引入,使信号的频带升高,此时,相比应用7 Hz的Ricker子波,应用了脉冲子波的反演结果在相同的迭代次数时,模型反演结果得到了一定程度的改善,如图 13,14.
|
图 12 有噪声数据反演结果:(A)应用脉冲子波;(B)应用7 HzRicker子波 Fig. 12 Inversion result of the data with noise:(A)Using the pulse wavelet,(B)Using 7 Hz Ricker wavelet |

|
图 13 图12a中17.5km (a)和10km(b)处反演结果 Fig. 13 Inversion result in figure 12a at 17.5km (a) and 10km (b) |
|
图 14 图12b中17.5km (a)和10km (b)处反演结果 Fig. 14 Inversion result in figure 12b at 17.5km (a) and 10km (b) |
频率域波形反演推动了基于波形反演的速度建模在勘探尺度上的应用,本文实现了任意尺度条件的频率域波形反演计算,对频率域波形反演中与频率相关的影响因素进行了分析对比,得到如下的初步结论:
(1) 给出了数据频带范围选择公式,确保无数据假频给反演模型带来的假象.
(2) 将频率从低到高分成几个组份,然后从低到高依次反演,即可实现频率域波形反演的多尺度计算,该方法有效地解决了目标函数陷落于局部极值点问题,提高了反演的精度.
(3) 波形反演中输入数据频带太低可能导致只反演出低频的不均匀性,当输入数据的频点间隔和初始频带一定时,频带高则增加了计算量,因此选择合适的频带范围和计算尺度对反演效果也有很大的影响.
(4) 本文的模型测试中,在数据无噪声时,对0~20Hz数据的反演,应用主频为7 Hz的Ricker子波和脉冲子波反演的结果无太大差异.当数据加入高斯噪声后,使信号的频带升高,相比应用7 Hz的Ricker子波,应用了脉冲子波的反演结果在相同的迭代次数时,模型反演结果得到了一定程度的改善.
| [1] | Chen J B, Liu H. Two kinds of separable approximations for the one-way wave operator. Geophysics , 2006, 71(1): T1-T5. DOI:10.1190/1.2159059 |
| [2] | Liu L N, Zhang J F. 3D wavefield extrapolation with optimum split-step Fourier method. Geophysics , 2006, 71(3): T95-T108. DOI:10.1190/1.2197493 |
| [3] | Bayasl E, Kosloff D D, Sherwood J W C. Reverse time migration. Geophysics , 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [4] | 李博, 刘红伟, 刘国峰, 等. 地震叠前逆时偏移算法的CPU/GPU 实施对策. 地球物理学报 , 2010, 53(12): 2938–2943. Li B, Liu H W, Liu G F, et al. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU. Chinese J. Geophys. (in Chinese) , 2010, 53(12): 2938-2943. |
| [5] | Nemeth T, Normark E, Qin F. Dynamic smoothing in crosswell traveltime tomography. Geophysics , 1997, 62(1): 168-176. DOI:10.1190/1.1444115 |
| [6] | Min D, Shin C. Refraction tomography using a waveform-inversion back-propagation technique. Geophysics , 2006, 71(3): R21-R30. DOI:10.1190/1.2194522 |
| [7] | Sava P C, Biondi B, Etgen J. Wave-equation migration velocity analysis by focusing diffractions and reflections. Geophysics , 2005, 70(3): U19-U27. DOI:10.1190/1.1925749 |
| [8] | Sava P, Vlad I. Numeric implementation of wave-equation migration velocity analysis operators. Geophysics , 2008, 73(5): VE145-VE159. DOI:10.1190/1.2953337 |
| [9] | Tarantola A. Inversion of seismic reflection data in the acoustic approximation. Geophysics , 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [10] | Tarantola A. A strategy for nonlinear elastic inversion of seismic reflection data. Geophysics , 1986, 51(10): 1893-1903. DOI:10.1190/1.1442046 |
| [11] | Pratt R G. Seismic waveform inversion in the frequency domain, Part 1: Theory and verification in a physical scale model. Geophysics , 1999, 64(3): 888-901. DOI:10.1190/1.1444597 |
| [12] | Pratt R G, Worthington M H. Inverse theory applied to multi-source cross-hole tomography, Part I: Acoustic wave-equation method. Geophysical Prospecting , 1990, 38(3): 287-310. DOI:10.1111/gpr.1990.38.issue-3 |
| [13] | Shin C, Cha Y H. Waveform inversion in the Laplace domain. Geophysical Journal International , 2008, 173(3): 922-931. DOI:10.1111/gji.2008.173.issue-3 |
| [14] | Shin C, Cha Y H. Waveform inversion in the Laplace-Fourier domain. Geophysical Journal International , 2009, 177(3): 1067-1079. DOI:10.1111/gji.2009.177.issue-3 |
| [15] | 高静怀, 杨森林. 利用零偏移VSP资料估计介质品质因子方法研究. 地球物理学报 , 2007, 50(4): 1198–1209. Gao J H, Yang S L. On the method of quality factors estimation from zero-offset VSP data. Chinese J. Geophys. (in Chinese) , 2007, 50(4): 1198-1209. |
| [16] | 高静怀, 汪超, 赵伟. 用于零偏移距VSP资料的自适应波形反演方法研究. 地球物理学报 , 2009, 52(12): 3091–3100. Gao J H, Wang C, Zhao W. On the method of adaptive waveform inversion with zero-offset VSP data. Chinese Journal Geophysics (in Chinese) , 2009, 52(12): 3091-3100. |
| [17] | 丁继才, 常旭, 刘伊克, 等. 基于声波方程的井间地震数据快速WTW反演方法. 地球物理学报 , 2007, 50(5): 1527–1533. Ding J C, Chang X, Liu Y K, et al. Rapid method for acoustic wave-equation WTW inversion of crosshole seismic data. Chinese J. Geophys. (in Chinese) , 2007, 50(5): 1527-1533. |
| [18] | 石玉梅, 姚逢昌, 孙虎生, 等. 地震密度反演及地层孔隙度估计. 地球物理学报 , 2010, 53(1): 197–204. Shi Y M, Yao F C, Sun H S, et al. Density inversion and porosity estimation using seismic data. Chinese J. Geophys. (in Chinese) , 2010, 53(1): 197-204. |
| [19] | 宋海斌, MatsubayashiO, KuramotoS. 天然气水合物似海底反射层的全波形反演. 地球物理学报 , 2003, 46(1): 42–46. Song H B, Matsubayashi O, Kuramoto S. Full waveform inversion of gas hydrate-related bottom simulating reflectors. Chinese J. Geophys. (in Chinese) , 2003, 46(1): 42-46. |
| [20] | 王彦飞, 杨长春, 段秋梁. 地震偏移反演成像的迭代正则化方法研究. 地球物理学报 , 2009, 52(6): 1615–1624. Wang Y F, Yang C C, Duan Q L. On iterative regularization methods for migration deconvolution and inversion in seismic imaging. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1615-1624. |
| [21] | Takougang E M T, Calvert A J. Application of waveform tomography to marine seismic reflection data from the Queen Charlotte Basin of western Canada. Geophysics , 2011, 76(2): B55-B70. DOI:10.1190/1.3553478 |
| [22] | Gauthier O J, Virieux, A Tarantola. Two-dimensional nonlinear inversion of seismic waveforms: Numerical results. Geophysics , 1986, 51(7): 1387-1403. DOI:10.1190/1.1442188 |
| [23] | Bunks C, Saleck F M, Zaleski S, et al. Multiscale seismic waveform inversion. Geophysics , 1995, 60(5): 1457-1473. DOI:10.1190/1.1443880 |
| [24] | Boonyasiriwat C, Valasek P, Routh P, et al. An efficient multiscale method for time-domain waveform tomography. Geophysics , 2009, 74(6): WCC59-WCC68. DOI:10.1190/1.3151869 |
| [25] | Sirgue L, Pratt R G. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies. Geophysics , 2004, 69(1): 231-248. DOI:10.1190/1.1649391 |
 2012, Vol. 55
2012, Vol. 55


