2. 96165部队, 江西 乐平 333300
2. No 96165 Troops of PLA, Jiangxi Leping 333300, China
大气长波即Rossby波是旋转大气中一类重要的波动,由于其在天气和气候演变中起着重要作用,一直倍受气象学家的关注.关于大气长波的发展和演变问题也一直是大气动力学研究的重点,前人的研究已认识到波与流的相互作用、波与波的非线性作用是长波演变的重要机制.
关于波与流相互作用的研究有着悠久的研究历史和丰富的理论成果,主要表现在不稳定理论和E-P 通量理论.不稳定理论主要是研究基流在波动演变过程中的作用,有利的基流结构不仅为波动发展提供能量,同时也影响着波动的结构.如斜压不稳定[1-2]和正压不稳定[3]就是反映流对波作用的经典理论.Rossby[4]讨论了纬向平均流与驻波的关系,还研究了与波流作用有关的指数循环[5].曾庆存[6-10]利用波包近似和WKB 方法,讨论了基流与扰动的相互作用,对Rossby 波演变与发展作了开拓性研究.张立凤等[11]在研究南海夏季风爆发机制时,指出在季风爆发前的真实基流结构中,球面Rossby波是不稳定,而波动的不稳定发展是南海夏季风爆发的动力机制之一.
从能量学角度较早研究在切变基本流中波动动力学性质的工作是Eliassen 和Palm[12]提出的E-P通量,后来,Andrews等[13]、Edmon 等[14]、Hoskins等[15]开展了更深入研究,对E-P通量作了非常有意义推广.我国黄荣辉等[16]、吴国雄等[17]在E-P 通量方面也做了许多工作.除了用E-P 通量来研究波与流相互作用外,高士欣等[18]利用数值计算方法研究了基流对波的作用,何建中[19]、赵强等[20-21]通过研究揭示了不同基流下Rossby 波传播和演变特点,还有徐祥德和高守亭[22]系统介绍了波流相互作用的动力学原理.
以上关于波流相互作用的研究,基流大多是纬向平均流,其在纬向上不变化,而实际大气为非均匀介质,基流在经向上是变化的,在纬向上也不是常值.李崇银[23]详细说明了在时间平均基本流下扰动能量不但与基本流经向不均匀有关,还与基本流纬向分布密切相关.杨大升等[24]以气候态作为基本场研究了波动流场演变.
在长波的演变过程中,长波的调整与环流形势的变化、天气预报和气候预测有着密切关系,其调整的机制是值得研究的课题.我们的研究已发现在纬向均匀的基流中,波与波非线性作用是长波调整出现的关键[25-26],若基流是纬向非均匀时,线性Rossby波能否出现长波调整现象?为了揭示这个问题,本文利用非均匀基本场情形下准地转正压位涡方程,通过数值求解,分析基本场结构和初始场对Rossby波演变的影响,目的是揭示纬向非均匀基本场对大气长波调整的作用.
2 数学模型描述大气Rossby波运动的β 平面无量纲无摩擦、无黏性、无外源强迫的准地转正压位涡方程可写为[27]
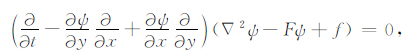
|
(1) |
其中:ψ 为地转流函数,f=f0+βy为地转参数,f0和β为常数,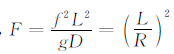
令ψ(x,y,t)=ψ(x,y)+ψ′(x,y,t),不难得到(1)式的扰动方程为
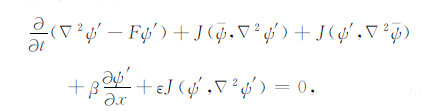
|
(2) |
其中ψ′ 为扰动流函数,ψ为基本场流函数,是x和y的函数,由于纬向基本流为U=-∂ψ/∂y,所以纬向基流也与x和y有关,当∂U/∂x≠0,基流为纬向非均匀基流.ε等于0或1,ε=0时,方程为线性位涡方程,反映线性Rossby波的运动;ε=1时,方程描述的是非线性Rossby波运动.
求解方程(2)时,须给定计算区域、基本流函数以及扰动流函数的初边值条件.为了方便计算,计算区域选择矩形通道即Ω = [0,Lx]× [0,Ly],且有:基本流函数[24]:
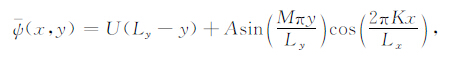
|
(3) |
初值条件:
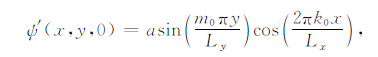
|
(4) |
纬向取周期边界条件:
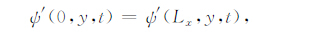
|
(5) |
经向取固壁边界条件:

|
(6) |
其中Lx和Ly分别代表计算区域的长度和宽度,U为常数,代表纬向平均西风基流的大小,K和M/2分别为基本流函数在纬向和经向上波的个数,A为其振幅,而初始时刻扰动流函数经向和纬向上波数分别为m0/2和k0,振幅为a.
为了揭示大气长波调整规律,设扰动流函数ψ′的经向平均值为ψ′y,即有:

|
(7) |
对线性正压位涡方程(2),由于解析解求解的困难性,数值求解成为一种可行的方法.对方程采用差分离散,空间采用蛙跳格式,时间采用一阶隐式格式,则方程(2)的差分形式可写为
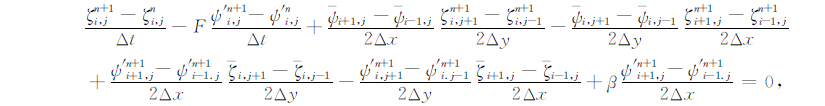
|
(8) |
其中ζ =Δ2ψ′ 为扰动涡度,ζ=Δ2ψ为基本场涡度,下标i和j分别表示在x和y方向网格点的序号,上标n和n+1表示积分时间层次,Δt、Δx和Δy分别表示时间步长和网格距.将差分方程(8)各项展开可得:
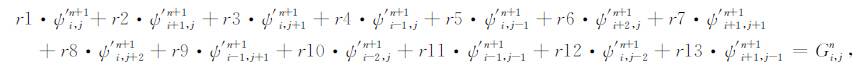
|
(9) |
其中r1~r13是一组由Δt、Δx、Δy和ψ 组成,且与ψ′ 无关又不随时间变化的系数,Gi,jn与第n时间层次的扰动流函数ψ′n有关.具体形式可参见附录.
由差分格式(9)可知,若计算第n+1时间层上(i,j)点的流函数,需用到该层上(i,j)点周围12个点的值,而这些值也是待计算的,故须迭代求解,本文利用Gauss-Seidel迭代方法[28]求解.
数值计算试验时,以45°N 无量纲纬圈长度作为计算区域的长度Lx,宽度Ly由y方向的网格距和网格数决定,将Lx作144等分,y方向有13个等距格点,且满足Δx= Δy,Δt=0.05Δx,每一积分时间层允许的迭代误差小于等于10-8,且环境参数F和β 取该纬度上的值,即F=0.19623,β=1.6125.以下分别对不同的初始场和背景场参数进行计算和分析.
4 结果分析 4.1 纬向非均匀基流对长波调整的作用前期的研究发现,当基流在纬向均匀,只随y变化时,波与波的非线性相互作用是出现长波调整的重要机制[26].但当基流在纬向非均匀时,非线性作用还是长波调整的唯一机制吗?为了研究纬向非均匀基流对长波调整的作用,计算时取ε=0,即不考虑波与波的非线性作用.图 1给出了纬向非均匀基流下线性波动流场结构随时间的演变,其中基本场参数为U=1.0,A=1.0,K=3,M=1,初始场参数取k0 =4,m0 =1,a=0.1.由图可看出,初始纬向波数为4的波动,在积分到80天后演变成2波,这说明基流纬向非均匀时,线性Rossby波也会出现长波调整现象,故基流随纬向变化是长波发生调整的又一个重要机制.
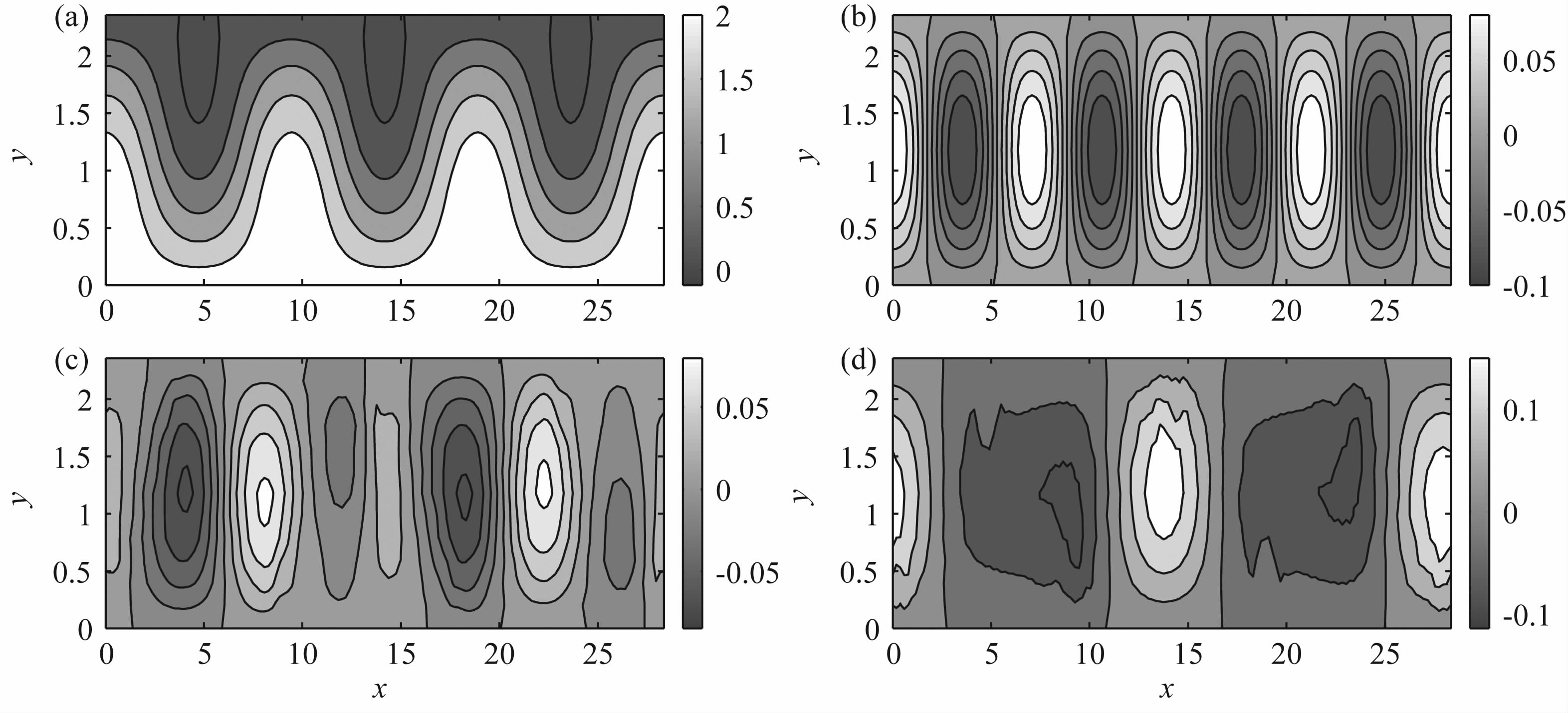
|
图 1 纬向非均匀基流下线性Rossby波流场结构演变 (a)基本流场ψ(x,y),(b—d)分别为初始时刻,积分20天和积分80天的线性Rossby波. Fig. 1 The linear Rossby wave on zonal non-uniform basic flow (a)The basic flow field ψ(x,y),(b—d) The linear Rossby wave at the initial time,20 days and 80 days. |
大气长波调整与基本场振幅A密切相关,其不但影响长波调整能否出现及出现的时间,还影响调整稳定后流场的结构.图 2是初始场参数取为k0 =5,m0 =1,a=0.1,基本场参数取为U=0,K=3,M=1,而A分别取为0.1、0.5、1.0、2.0时,经向平均流函数随时间的变化.图中左边的阴影图是流函数经向平均ψ′y随时间的变化,右边是相应流场纬向波数K(t)随时间演变,其中K(t)为ψ′y纬向上符号变化次数的半数.从图上可知,当A=0.1 时,基本场主要由U决定,而U为常数,所以线性波动的结构不会随时间改变,即在积分相当长的时间内都不会发生长波调整现象.当A增大,在积分一段时间后,波数K就会发生变化,有时增加,有时减少,但最终调整到稳定结构时,波动的尺度更大.长波调整现象出现的时间也与A有关,A越大,波动调整出现越早,如A=1.0比A=0.5时长波调整要早200多天出现,但A越大,长波调整最终状态出现时间不一定最早,如A=2.0 比A=1.0 时,调整达到稳定状态的时间还要晚100 多天;而且调整到稳定状态的波动结构也与基流振幅有关,当A=0.5和1.0时,最终流场调整为1 波,而当A=2.0,调整为2波.
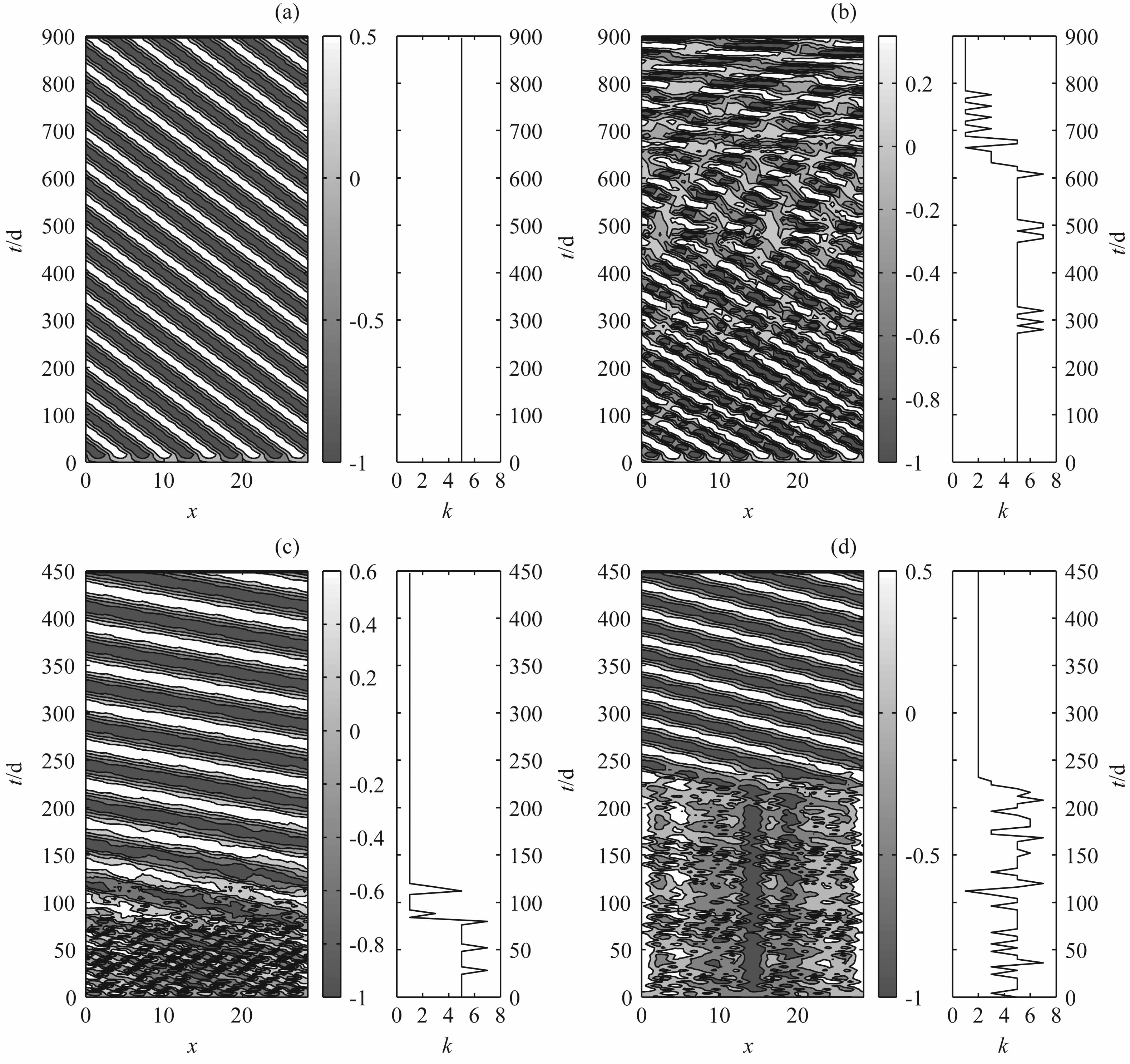
|
图 2 不同振幅的基本流场下Rossby波经向平均流场结构演变 (a)A=0.1;(b)A=0.5;(c)A=1.0;(d)A=2.0. Fig. 2 The evolution of Rossby in basic flow field with four different amplitudes |
图 3 给出了基本场参数为A=1.0,K=3,M=1,U分别为0.0、1.0、2.0,初始场参数取为m0=1,a=0.1,k0分别为2、3、4、5时,波动经向平均流场随时间的演变(具体说明同图 2).从图可见,纬向平均西风基流U决定了波的传播方向和速度,当U=0.0时,无论扰动初始结构如何,波动随时间都向西传,而当U≠0时,波动出现了东传,且传播速度与U的大小有关,U越大,速度越快.分析图 3 还可见,U的大小不仅影响波动传播的速度和方向,还影响长波调整出现的时间和规律,但无论U为何值,k0 ≤K的波动都不发生调整,k0 >K的波向更长的波动调整.随着U的增大,波动调整出现的时间越早,如对于k0 =4和k0 =5的波动,U=1.0时的波动调整要比U=0.0 时早几十天.值得注意的是当纬向平均西风基流U太大时,也会延迟长波调整的发生,如U=2.0时,波数出现变化的时间比相应U=1.0情形下要晚很多,这是由于U很大时,基流的纬向非均匀特征相对减小,而均匀基流下的线性波动是不发生长波调整的.

|
图 3 不同纬向平均西风基本场下,不同初始场的波动经向平均流场结构演变(a—d)分别表示k0=2,3,4,5时的情形;1—3分别表示U=0.0,1.0,2.0时的情形. Fig. 3 The evolution of ψ'y with four different initial fields in the three different zonal average of basic field (a—d) k0= 2 , 3 , 4, 5 ; 1—3:U=0, 1. 0, 2. 0. |
图 4是在基本流场参数为U=1.0,A=1.0,M=1,K分别为2,3,4,5,波动初始场参数为k0=4,m0=1,a=0.1时,波动纬向波数K随时间演变.从图上可见,长波调整的出现与基流纬向波数K密切相关,在不同基本场下,波动可不发生调整,也可向高波数或向低波数调整,调整的方向主要由基本场结构决定,如当K=2或4时,初始纬向结构为4波的波动在积分的150 天内保持纬向波数不变,没有发生长波调整,但在K=3时,4 波向低波数调整,而K=5时,初始波数为4的波动向高波数调整.

|
图 4 不同基本场下波动纬向波数K随时间演变 Fig. 4 The evolution of zonal wavenumber k in different basic fields |
图 5给出了不同初始振幅的线性波动流场结构随时间的演变,其中基本场参数为U=0.0,A=1.0,K=3,M=1,初始场参数取k0=4,m0=1,a=0.1、0.5、1.0、2.0.从图可看出,不同的波动初始振幅情况下,波动流场结构随时间演变特征都相同.这说明线性Rossby波的长波调整特征对波动的初始振幅不敏感,故在前面的数值计算中,a都取为0.1.
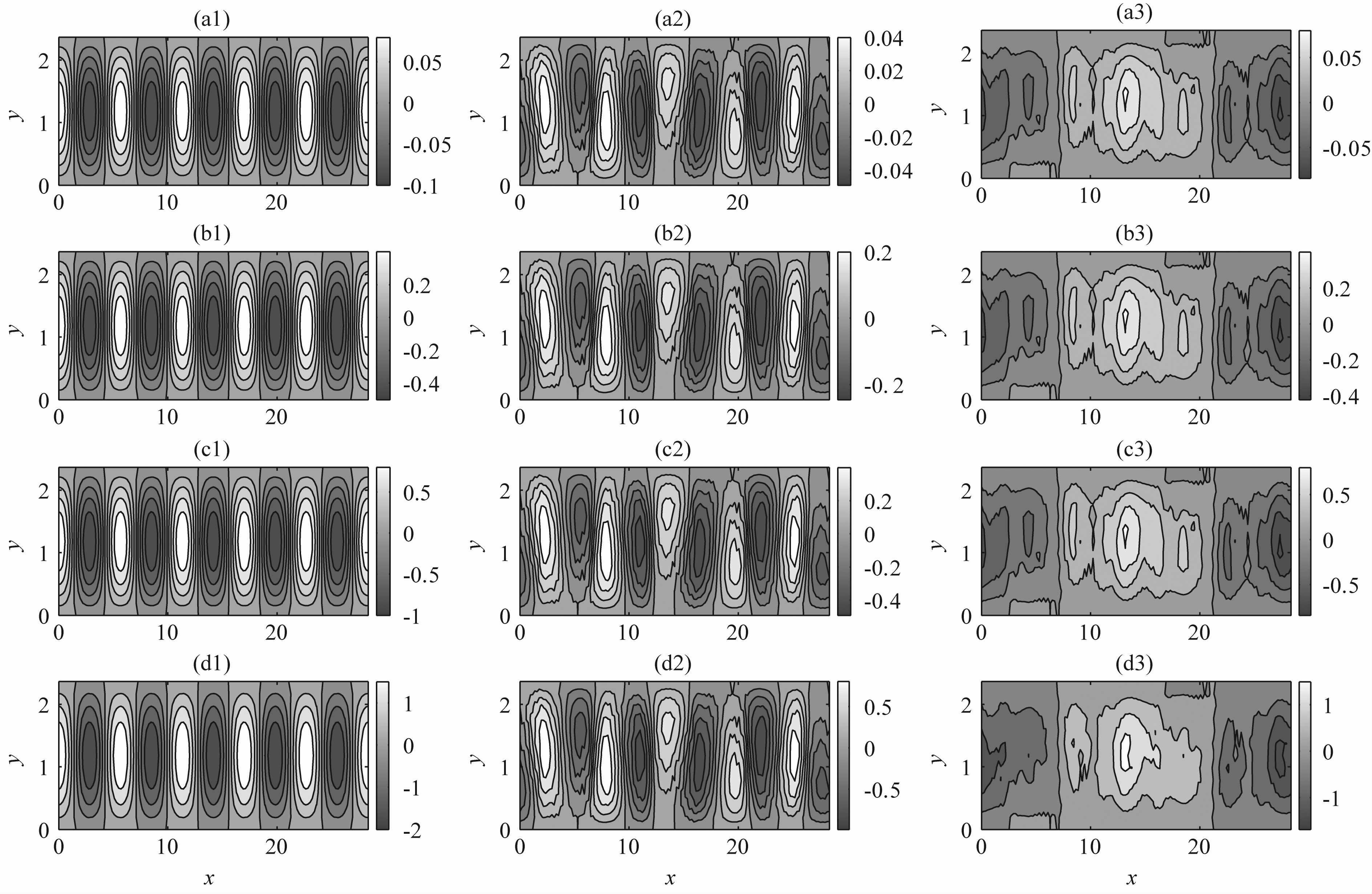
|
图 5 波动初始振幅不同时,线性波动流场结构随时间演变1—3分别表示初始时刻,积分40天和积分120天的线性Rossby波流函数.(a—d)分别表示初始波动振幅a=0.1,0.5,1.0和2.0时的情形. Fig. 5 The evolution of linear Rossby wave with the different amplitude of initial fluctuations 1—3: the initial time, 40 days and 120 days; (a—d)a= 0.1, 0.5 , 1.0 and 2.0. |
在非线性作用下大气长波调整与初始场结构有关[26],而线性Rossby波在基流非均匀下纬向波数的调整是否也与波动的初始结构有关呢?图 6给出了在基本场参数取U=0.0,A=1.0,K=3,M=1,初始场参数取m0=1,a=0.1,k0 为1、2、3、4、5时波动流函数随时间演变.分析图可见,在相同的基本环流下,波动的初始结构不同,其流场演变特征也不同.当波动的初始纬向波数k0 ≤ K时,波动在演变过程中,纬向波数不发生变化;当k0 >K时,波动在演变过程中,波数向减小的方向调整,且波动调整的最终状态与初始场的结构有关,当K=3 时,k0=4的波动,最终调整为2 波,k0=5 的波动,最终调整为1波.总之,不同初始结构的波动有着不同的演变过程,但演变到最后一般都达到一个稳定状态,且稳定状态与初始的纬向波数有关.
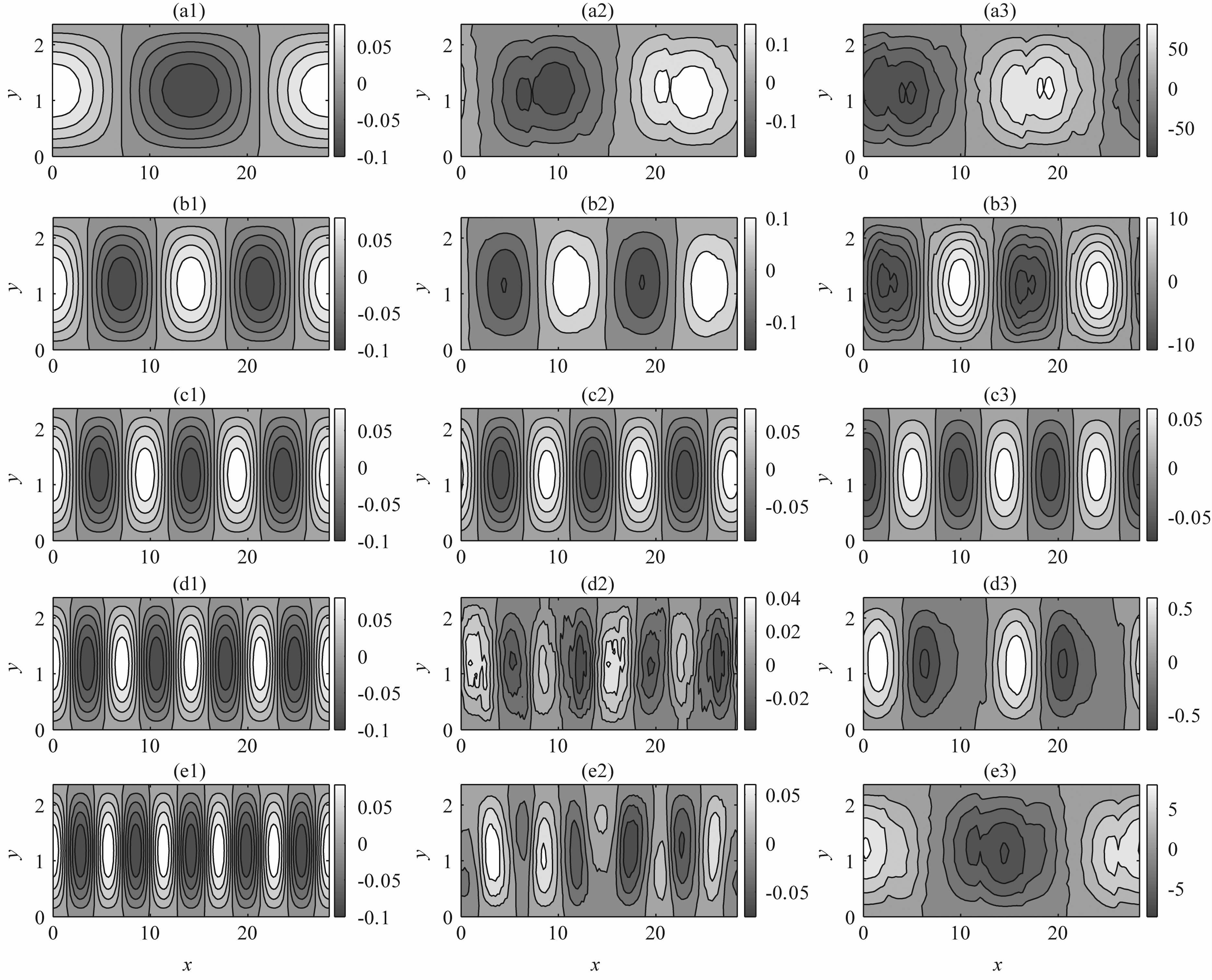
|
图 6 固定基本场下,五种不同初始结构的Rossby波流场演变1—3分别表示初始时刻,积分50天和积分350天的流场结构.(a—e)分别表示k0=1,2,3,4,5时情形. Fig. 6 The Rossby wave with the five different initial structures 1一3: the initial time,50 days and 350 days; (a—e)k0= 1,2,3,4,5. |
本文通过大量的数值试验分析了纬向非均匀基流对大气长波调整的作用及基流结构和波动初始场结构对Rossby波演变特征的影响,主要的结论有:
(1)基流纬向非均匀时,线性Rossby波也会出现长波调整现象,基流随纬向变化是长波发生调整的又一个重要机制.
(2)大气长波调整对波动的初始振幅不敏感,但与基本场振幅密切相关,基本场的振幅不但影响长波调整的能否出现和出现的时间,还影响最后稳定流场结构.
(3)大气长波调整与基本场的纬向平均西风基流的大小有关,其不但影响Rossby 波传播的速度和方向,还影响长波调整出现的时间和调整规律.
(4)长波调整的出现与基本场和初始场的结构有关.在不同基本场下,波动不仅可不发生调整,也可向高波数或向低波数调整,调整的方向主要由基本场结构决定;不同初始结构的波动有着不同的演变过程,但演变到最后一般都达到一个稳定状态,且稳定状态与初始的纬向波数有关.
本文虽然揭示了大气长波调整的一些规律,但研究的模型是理想模型,没有考虑非绝热加热和地形等作用,与实际大气还有很大的差别.在实际大气中除基流纬向非均匀和非线性作用引发长波调整外,还存在许多外源强迫作用,这些还有待进一步研究.
附录
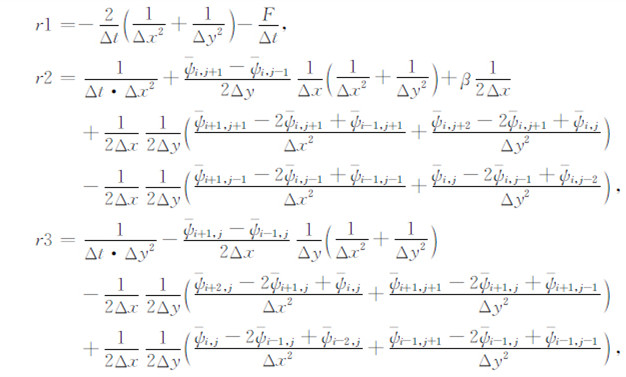
|
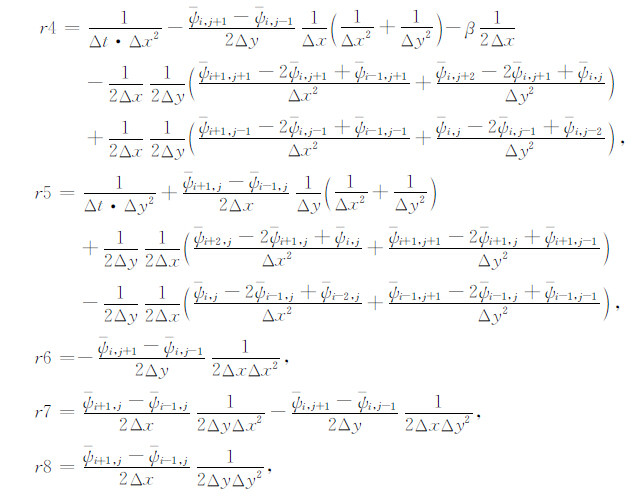
|
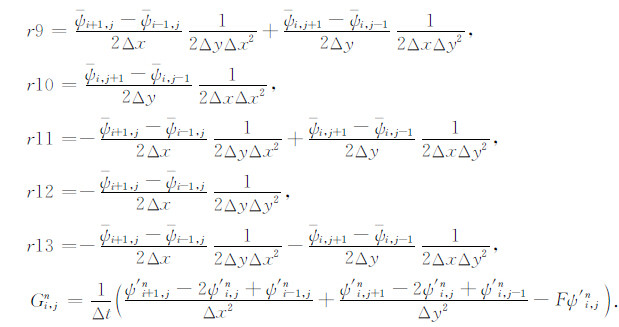
|
| [1] | Charney J G. The dynamics of long waves in a baroclinic westerly current. J. Meteor. , 1947, 4(5): 135-162. |
| [2] | Eady E T. Long waves and cyclone waves. Tellus , 1949, 1(3): 33-52. DOI:10.1111/tus.1949.1.issue-3 |
| [3] | Kuo H L. Dynamic instability of two-dimensional non-divergent flow in a barotropic atmosphere. J. Meteor. , 1949, 6(2): 105-122. DOI:10.1175/1520-0469(1949)006<0105:DIOTDN>2.0.CO;2 |
| [4] | Rossby C G, Collaborators. Relation between variations in the intensity of the zonal circulation of the atmosphere and the displacements of the semi-permanent centers of action. J. Marine Research , 1939, 2: 38-55. DOI:10.1357/002224039806649023 |
| [5] | Rossby C G, Willett H C. The circulation of the upper troposphere and lower stratosphere. Science , 1948, 108(2815): 643-652. DOI:10.1126/science.108.2815.643 |
| [6] | 曾庆存, 卢佩生. 非均匀基流上扰动的演变. 中国科学A辑:数学 , 1980, 23(12): 1193–1202. Zeng Q C, Lu P S. The evolution process of disturbances on non-uniform basic flow. Science in China, Series A (in Chinese) , 1980, 23(12): 1193-1202. |
| [7] | 卢佩生, 曾庆存. 正压大气中扰动的演变. 大气科学 , 1981, 5(1): 1–8. Lu P S, Zeng Q C. On the evolution process of disturbances in the barotropic atmosphere. Chin. J. Atmos. Sci. (in Chinese) , 1981, 5(1): 1-8. |
| [8] | Zeng Q C. On the evolution and interaction of disturbances and zonal flow in rotating barotropic atmosphere. J. Meteor. Soc. Japan , 1982, 60: 24-30. |
| [9] | Zeng Q C. The evolution of a Rossby-wave packet in a three-dimensional baroclinic atmosphere. J. Atmos. Sci. , 1983, 40(1): 73-84. DOI:10.1175/1520-0469(1983)040<0073:TEOARW>2.0.CO;2 |
| [10] | Zeng Q C. The development characteristics of quasi-geostrophic baroclinic disturbances. Tellus , 1983, 35: 337-349. |
| [11] | Zhang L F, Zhang Y C, Zhang M. Study on the dynamic process of the onset of South China Sea summer monsoon. Acta Meteor. Sinica , 2008, 22(4): 511-521. |
| [12] | Eliassen A, Palm E. On the transfer of energy in stationary mountain waves. Geophysics Publikasjoner , 1961, 22(3): 1-23. |
| [13] | Andrews D G, McIntyre M E. Planetary waves in horizontal and vertical shear: The generalized Eliassen-Palm relation and the mean zonal acceleration. J. Atmos. Sci. , 1976, 33(11): 2031-2048. DOI:10.1175/1520-0469(1976)033<2031:PWIHAV>2.0.CO;2 |
| [14] | Edmon H J, Hoskins B J, McIntyre M F. Eliassen-Palm cross-sections for the troposphere. J. Atmos. Sci. , 1980, 37(12): 2600-2616. DOI:10.1175/1520-0469(1980)037<2600:EPCSFT>2.0.CO;2 |
| [15] | Hoskins B J, James I N, White G H. The shape, propagation and mean-flow interaction of large-scale weather systems. J. Atmos. Sci. , 1983, 40(7): 1595-1612. DOI:10.1175/1520-0469(1983)040<1595:TSPAMF>2.0.CO;2 |
| [16] | Huang R H, Gambo K. The response of a hemispheric multi-level model atmosphere to forcing by topography and stationary heat sources in summer. J. Meteor. Soc. Japan , 1983, 61: 495-509. |
| [17] | |
| [18] | 高士欣, 张立凤, 高锋. 南海夏季风爆发前后扰动演变及其数值研究. 大气科学 , 2007, 31(5): 898–908. Gao S X, Zhang L F, Gao F. The numerical research on the disturbance evolution before and after the South China Sea summer. Chin. J. Atmos. Sci. (in Chinese) , 2007, 31(5): 898-908. |
| [19] | 何建中. 纬向切变基流中的非线性正压Rossby波. 气象学报 , 1994, 52(4): 433–441. He J Z. The effects of latitudinal shearing flow on nonlinear barotropic Rossby waves. Acta Meteor. Sinica (in Chinese) , 1994, 52(4): 433-441. |
| [20] | 赵强, 刘式达, 刘式适. 切变基本纬向流中非线性赤道Rossby长波. 地球物理学报 , 2000, 43(6): 746–753. Zhao Q, Liu S D, Liu S K. Nonlinear equatorial Rossby long waves in a shear flow. Chinese J. Geophys. (in Chinese) , 2000, 43(6): 746-753. |
| [21] | Zhao Q, Fu Z T, Liu S K. Equatorial envelope Rossby Solitons in a shear flow. Advances in Atmospheric Sciences , 2001, 18(3): 418-428. DOI:10.1007/BF02919321 |
| [22] | 徐祥德, 高守亭. 外源强迫与波流作用动力学原理. 北京: 海洋出版社, 2002 . Xu X D, Gao S T. Dynamics of External Force and Wave-Flow Interactions (in Chinese). Beijing: China Ocean Press, 2002 . |
| [23] | 李崇银. 气候动力学引论. 北京: 气象出版社, 2000 . Li C Y. Introduction to Climate Dynamics (in Chinese). Beijing: China Meteorological Press, 2000 . |
| [24] | 杨大升, 曹文忠. 中高纬大气30—60天低频振荡的一种动力学机制. 大气科学 , 1995, 19(2): 210–218. Yang D S, Cao W Z. A possible dynamic mechanism of the atmospheric 30—60 day period oscillation in the extratropical latitude. Chin. J. Atmos. Sci. (in Chinese) , 1995, 19(2): 210-218. |
| [25] | 张立凤, 张亮, 李崇银. 真实基流中非线性Rossby波演变特征(一):数值模式设计. 地球物理学报 , 2011, 54(3): 629–633. Zhang L F, Zhang L, Li C Y. The evolution characteristic of nonlinear Rossby wave in the real basic flow I: Numerical model design. Chinese J. Geophys. (in Chinese) , 2011, 54(3): 629-633. |
| [26] | 张立凤, 张亮, 李崇银. 真实基流中非线性Rossby波演变特征(二):能量、结构演变及初始场的影响. 地球物理学报 , 2011, 54(4): 886–895. Zhang L F, Zhang L, Li C Y. The evolution characteristic of nonlinear Rossby wave in the real basic flow II: The energy and structure evolution of Rossby wave and the effect of the initial field on it. Chinese J. Geophys. (in Chinese) , 2011, 54(4): 886-895. |
| [27] | 余志豪, 杨大升, 贺海晏, 等. 地球物理流体动力学. 北京: 气象出版社, 1995 . Yu Z H, Yang D S, He H Y, et al. Geophysics Hydrokinetics (in Chinese). Beijing: China Meteorological Press, 1995 . |
| [28] | Schoeberl M R, Lindzen R S. A numerical simulation of barotropic instability. Part I: wave-mean flow interaction. J. Atmos. Sci. , 1984, 41(8): 1368-1379. DOI:10.1175/1520-0469(1984)041<1368:ANSOBI>2.0.CO;2 |
 2012, Vol. 55
2012, Vol. 55

