2. 中国科学院力学研究所, 北京 100190;
3. 清华大学工程物理系, 北京 100084
2. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China;
3. Department of Engineering Physics, Tsinghua University, Beijing 100084, China
在过去几十年,人们多数都采用就地观测的方法对地球等离子体层进行探测研究,通过分析这些探测资料,得到了等离子体层的全球密度整体分布[1-3].其间,1972 年美国在STP-2 卫星上首次利用光度计测量到了来自等离子体层的30.4nm 极紫外(ExtremeUltravioletImaging,EUV )辐射[4],证实了利用EUV 成像可探测等离子体层.2000 年,美国的磁层-极光全球成像探测卫星(Imager for Magneto pause-to-Aurora Global Exploration,IMAGE)上的EUV 成像仪第一次拍摄到等离子体层He+ 的图像,由于He+ 是等离子体层的主要成分之一,因此能够反映全球等离子体层的动力学过程[5].2004年,Huang 等人结合IMAGE 卫星观测数据,提出了一个三维等离子体层的经验模式,该模式认为空间等离子体层的密度分布可表示为以磁纬度和离地心的距离为变量的函数[6].由于等离子体层内的He+ 辐射可近似为光学薄层,EUV 成像仪观测到的辐射强度正比于仪器视线方向He+ 的柱密度,即沿视线方向上单位立体角范围内所有He+ 密度的积分值,这与计算机断层成像(Computed Tomography,CT)的投影过程一致,所以可通过CT方法重建出He+ 的全球密度分布[7].从严格的数学角度出发,观测数据要能精确重建出原密度分布,需要满足数据完备性条件,即待重建物体的任意点,经过它的投影线必须覆盖至少180°角范围[8-10].而IMAGE 卫星的角度覆盖范围最多只达90°,这种情况属于CT 中的有限角度重建问题.另外,还存在地球遮挡问题,地球背面的He+ 无法被成像仪观测到,这就进一步造成了投影数据的缺失.2004 年,Santhanam 等人对等离子体层模型进行代数重建,得到了初步的数值模拟结果[11].2009年,李亮等人提出了等离子体层在CT 重建中的地球遮挡问题,并给出用滤波反投影(Filtered Back Projection,FBP)算法精确重建的条件[12].此后,黄娅等人对二维的等离子体层观测进行数值模拟,用代数迭代算法(Algebraic Reconstruction Techniques,ART)进行180°覆盖角的重建[13],进一步解决了利用FBP 算法重建出现的由地球遮挡引起的偏差问题.在此基础上,金鑫等人用ART 算法实现了三维等离子体层的数值模拟,并对地球遮挡效应做了进一步的研究[14].2006 年Sidky 等人[15]将图像总变差(Total Variation,TV)极小化与ART 算法相结合(以下简称为ART-TV),在少量视角和有限角度的CT 图像重建上取得了极佳的效果.本文将该方法应用到重建等离子体层的密度中,在上述所涉及的投影数据缺失的情况下,得到了较ART 更好的重建图像,这为今后利用实际EUV 成像图重建等离子体层全球密度分布提出了更为有效的方法.
2 地球等离子体层和电离层的建模在CT重建领域,普遍使用仿真模型(Phantom)来研究新的重建理论和算法.这些仿真模型一般采用一些替代材料(和研究目标具有相近的密度),按照研究目标的结构进行设计和加工而成,因此,在这些仿真模型的不同结构内部,通常假定密度是均匀分布的[16-19].利用这种仿真模型进行CT 研究的优点在于:新理论和算法的数值模拟重建结果和仿真模型的真实值便于比较,一些微小的差异能够通过调节重建图像的显示窗一目了然地表现出来;如果密度是渐变的,就很难设置一个显示的窗宽和窗位,对重建图像和原模型图像进行一个准确、全面的比较.另外,这种看似简单的仿真模型设计在进行算法可行性和准确性验证方面是足够的,也就是说算法的有效性并不会随模型的变化而发生本质的改变.
在重建地球等离子体层时,为了寻求一种最有效的CT 算法来解决投影数据缺失的问题,我们借鉴CT 重建领域中建立仿真模型的方法,在地心太阳磁层坐标系(Geocentric Solar Magnetospheric,GSM)中建立等离子体层模型[11-13].假定等离子体层的密度分布均匀,其边界由偶极磁场磁力线R=Lcos2φ 构成.其中,φ 为纬度,L为磁力线在赤道面上(φ=0°)离地心的距离.根据实际等离子体层分布,可设L=4Re,其中Re 为地球半径,即等离子体层模型的边界为4个地球半径.另外,在地球和等离子体层之间有个较薄的电离层,里面的部分离子也可以被EUV 成像仪观测到,且He+ 的密度远大于等离子体层.根据建模和计算的需求,假设电离层分布在1.1Re 和1.2Re 之间的球壳内,并设电离层和等离子体层的密度值分别为10 和1.此外,处在背阳面的He+ 不受太阳辐射,因此,EUV 成像仪不能观测到这些He+ ,这样就会在背阳面形成一个以X轴为对称轴,半径为Re 的圆柱阴影区.
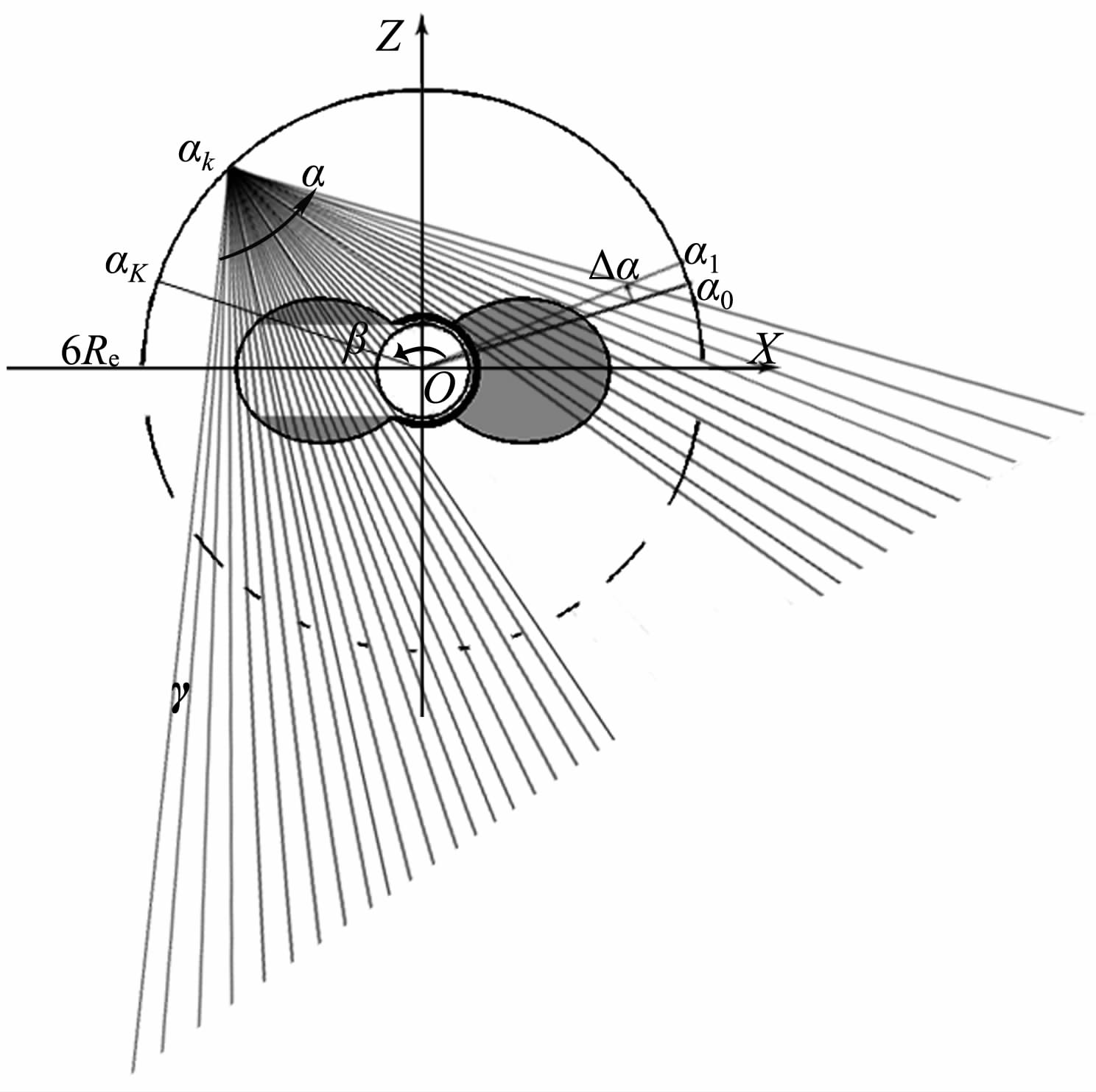
将模型沿垂直于Y轴的方向分成许多断层,断层Y=0(中心子午面)如图 1所示.其中,淡灰色和黑色分别表示等离子体层和电离层.由于地球遮挡的影响,该断层的投影数据缺失最为严重,因此本文仅针对该断层进行重建.
3 ART-TV 算法原理设成像仪由M1 个探测单元组成,共有M2 个投影角度.随着投影角度的变化,每一个探测单元的视线方向(也称为投影射线)也将不同.因此,投影射线总数M=M1×M2.将待重建物体划分为N个网格,xn表示第n个网格的密度值,其中,n=1,2,…,N.各投影射线对应的测量值p(或称投影值)与待重建物体可以用方程
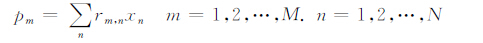
|
(1) |
来表示.其中,rm,n是权重因子,其值一般为第m条投影射线与第n个网格的交线长.rm,nxn表示待重建物体的第n个网格点对第m条投影射线的投影值pm所做的贡献.此外,地球遮挡对投影射线有截断作用,因此若投影射线经过地球,则投影射线的路径从探测器出发到地球结束,如图 1所示.
|
图 1 等离子体层模型在中心子午面上的扇束投影 Fig. 1 The fan-beam projections based on the noon-meridian plane of the plasmasphere phantom |
将式(1)简写为矩阵的形式:
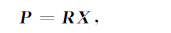
|
(2) |
P=RX,(2)其中,图像向量X= (x1,x2,…,xn,…,xM)T,投影向量P= (p1,p2,…,pm,…,pM)T,R= (rm,n)为M×M的投影矩阵.ART 算法的本质就是通过迭代的方法求解上述线性方程组.
Sidky等人将图像重建问题归结为:在投影方程为约束的条件下,求解图像总变差最小的优化问题,即
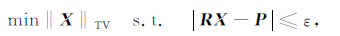
|
(3) |
其中,‖X‖TV = Σ▽x,▽ 是梯度算子.ε 是允许误差.
另外,在重建中利用先验知识能够有效地改善图像的质量.针对等离子体层成像问题,重建过程中可以增加如下的修正处理:(1)地球及阴影区不存在任何密度值,因此将重建结果中对应的区域置为零.(2)由于密度值不可能为负数,因此将重建结果中数值小于零的密度值修正为零.算法的具体步骤如下:
(a) 对图像赋初值;
(b) 利用ART 算法重建出一幅图像;
(c) 将地球内部和阴影区的值修正为0;
(d) 对图像进行非负校正;
(e) 利用TV 约束条件得到新的图像;
(f) 将新图像设为初值,进行下一次迭代.重复步骤(b)—(e),直到图像不再发生变化为止.
4 计算参数的选取IMAGE 卫星EUV 成像仪是锥体成像[5],二维情况即为扇束投影.另外,不同轨道之间可以相互转化[18],且轨道的具体形状对ART 算法的本质没有影响.因此本文采用圆轨道的扇束投影,如图 1 所示.圆轨道的中心为地心,半径为6.0Re.为了保证在轨道上的任意位置进行采样时,等离子体层除了被地球遮挡的区域外都可被观测到,扇角α 取75°.每个扇角的投影射线数为150,且采用等角射线形成的投影,因此相邻投影射线的夹角γ=0.5°(=75°/150).设从坐标原点出发,经过某一采样点的射线为LK.由于是圆轨道,采样点的位置可通过+X轴到射线LK的到角αK确定出.相邻采样点间的角度间隔Δα=1.0°.若α0 为第一个采样点的位置,则第K个采样点的位置αK=α0+(K-1)Δα,K=1,2,…,K.因此,角度覆盖范围β =αK-α0.计算中,采样点的中心取在+Z轴上,并分别向+Z轴的两边对称采样.因此,αK和α0 关于Z轴对称.例如,β=150°相当于采样点位于15°到165°之间;重建物体划分为150×150个网格点,网格点的间距为0.06Re.
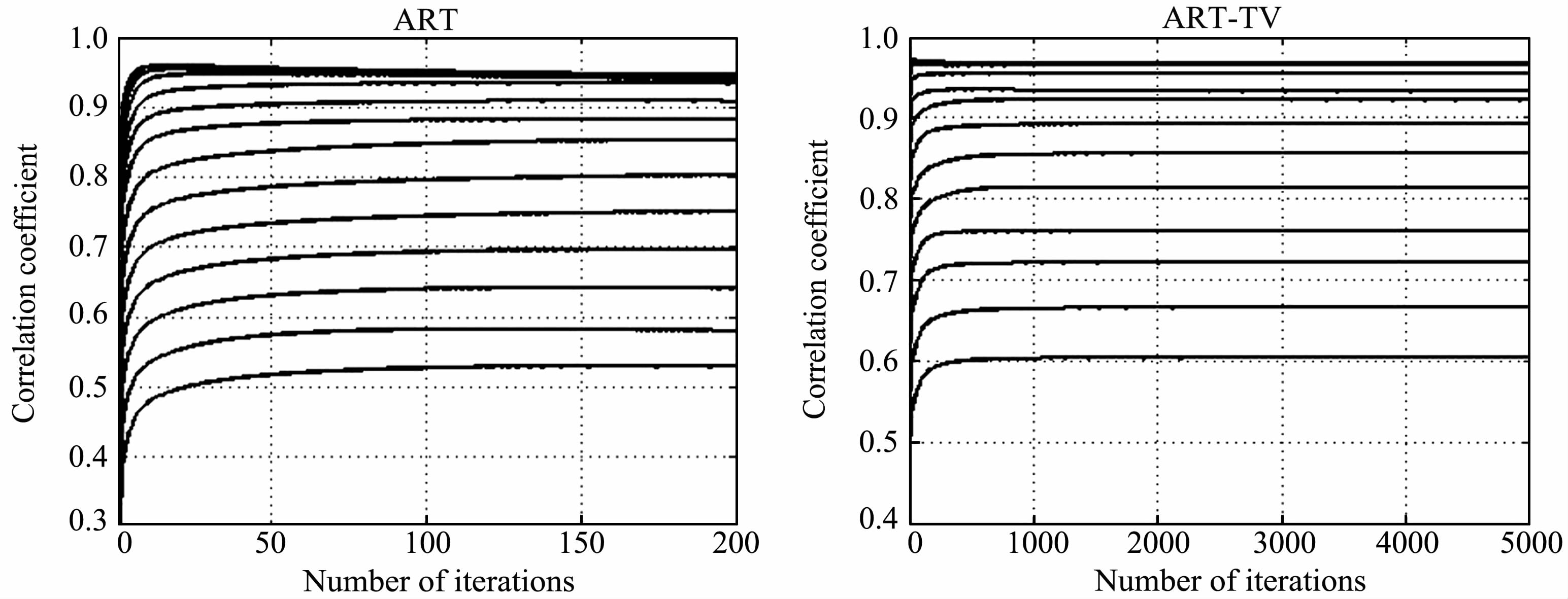
为了比较在不同β 时,分别用ART 和ART-TV 算法重建的效果,β 取45°,60°,75°,90°,105°,120°,135°,150°,165°,180°,195°,210°,225°,240°,270°,300°以及330°.此外,为了在提高计算速度的同时又不影响重建图像的质量,还需要确定两种算法的收敛速度.计算中,分别取不同迭代次数重建的结果与原模型做相关分析,并用相关系数[20]来衡量重建图像的质量,得到的结果如图 2所示.其中,曲线从下到上分别是β=45°,60°,…,330°.可以看出:对于相同的迭代次数,两种算法的相关系数起初都随β 的增加而增大,直到大于195°后曲线重合,相关系数几乎不再发生变化;并且,随着β 的增加,两者的收敛速度逐渐加快,但ART 算法的收敛速度始终比ART-TV 的快(当β=45°时,两者相关系数不再变化的迭代次数分别是90 和1000,当β=330°时则分别减少到10和50).对于前者,当迭代到100次后,所有β 的相关系数都不再发生变化,而后者则需要迭代到几百甚至上千次.因此,对于不同的角度覆盖范围,在计算中都统一选取了ART 算法的迭代次数为100,ART-TV 的为1000.
|
图 2 ART 和ART-TV 算法的收敛速度 Fig. 2 The convergence rates for the algorithms of ART and ART-TV |
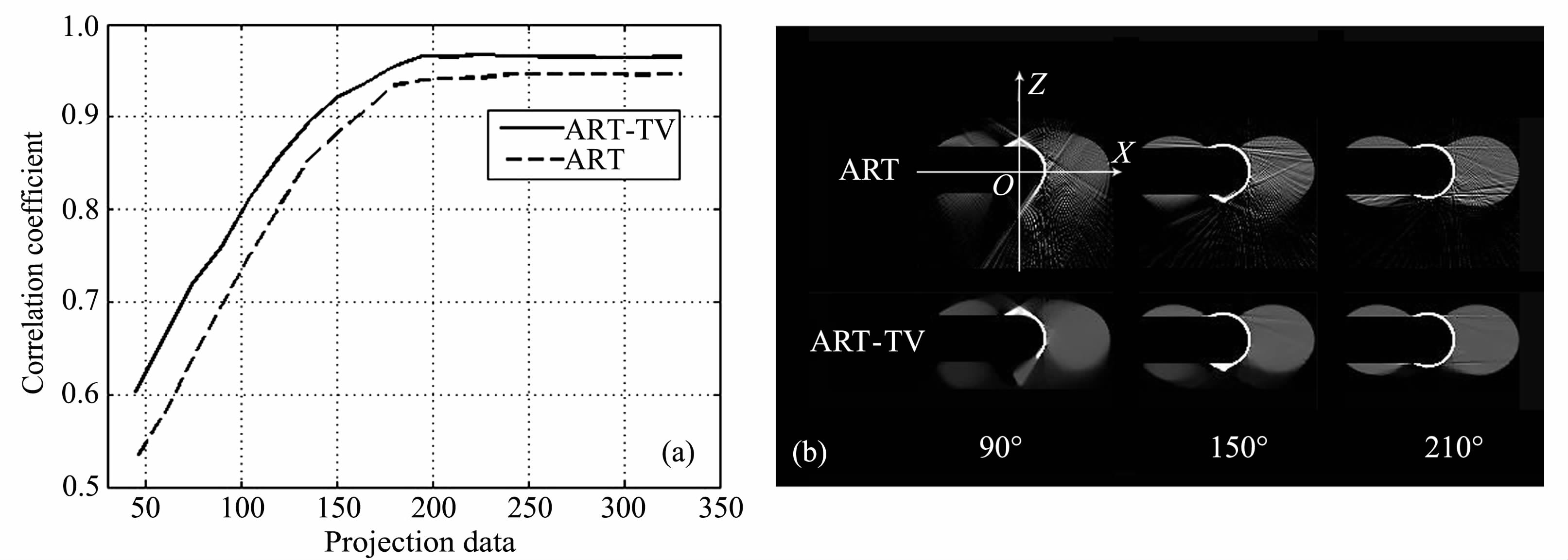
根据上面的计算参数,分别用ART 和ART-TV 两种算法进行重建,并将重建结果与原模型进行相关分析,其结果如图 3a所示.实线和虚线分别表示ART-TV 和ART 算法.其中,β=90°,150°和210°的计算结果显示在图 3b中,为了较为明显地比较重建等离子体层的图像质量,灰度图的显示窗口限制在0到3之间.从图 3a可以看出:(1)两种算法的相关系数都随着β 的增加而增加,直到β=195°,这与图 2的结果一致.这说明,当达到一定的角度覆盖范围时,投影数据已经完备,图像可以被完整地重建出来.(2)对于相同的β,ART-TV 的相关系数比ART 大.当β=45°时,两者的相关系数分别为0.603和0.529;当β=90°时,前者的为0.760,后者的仅为0.696;β=195°时则分别为0.966和0.940.这就是说,在拥有相同投影数据的前提下,ART-TV的重建结果会更好.
|
图 3 不同角度覆盖范围对重建图像的影响(a)不同角度覆盖范围的重建结果与原模型做相关分析;b)角度覆盖范围分别为90°150。和210。时,AR丁与ARTT-TTV重建的结果图. Fig. 3 Influence of image reconstruction from different projection data (a) The relationship between the phantom and the reconstruction results from different projectio data.(b) Reconstruction results for algorithms of ART and ART-TV,using 90,150,and 210 degree data. |
从图 3b可以看出:等离子体层基本上呈灰色,电离层呈白色;ART-TV 算法重建的图像比ART算法的噪声小,即图像更光滑;随着β 增大,两种算法重建出来的图都越接近图 1所示的原模型,且Z轴正半轴部分恢复得比Z轴负半轴部分快.对于电离层,在Z轴正半轴部分,β=90°时两种算法的结果都出现向上的凸起,该凸起随着β 的增大逐渐消失,当β=150°时,凸起几乎消失.在Z轴负半轴部分,β=90°时两种算法重建出来的电离层都有比较严重的变形,当β=150°时,变形演化为向下的凸起,且该凸起随着β 的增大逐渐减小,到β=210°时,凸起才基本上全部消失.可以看出,Z轴正半轴区域的电离层恢复得比Z轴负半轴区域的快.同样,对于等离子体层,当β=90°时,Z轴负半轴部分损失更为严重.β=150°时,上半轴部分已经基本接近体模,而下半轴部分仍存在较大的亏损.
从上面的参数设置可知,采样的中心在+Z轴上,且分别向+Z轴的两边对称采样.这样地球遮挡就会使得处在Z轴负半轴区域的点被观测到的几率减小,因此,只要角度覆盖范围还达不到投影数据完备的要求,重建出来的图像在+Z轴的部分总会比在-Z轴的部分偏好.同样,地球的遮挡会使得Z轴负半轴区域恢复得比Z轴正半轴区域的慢.
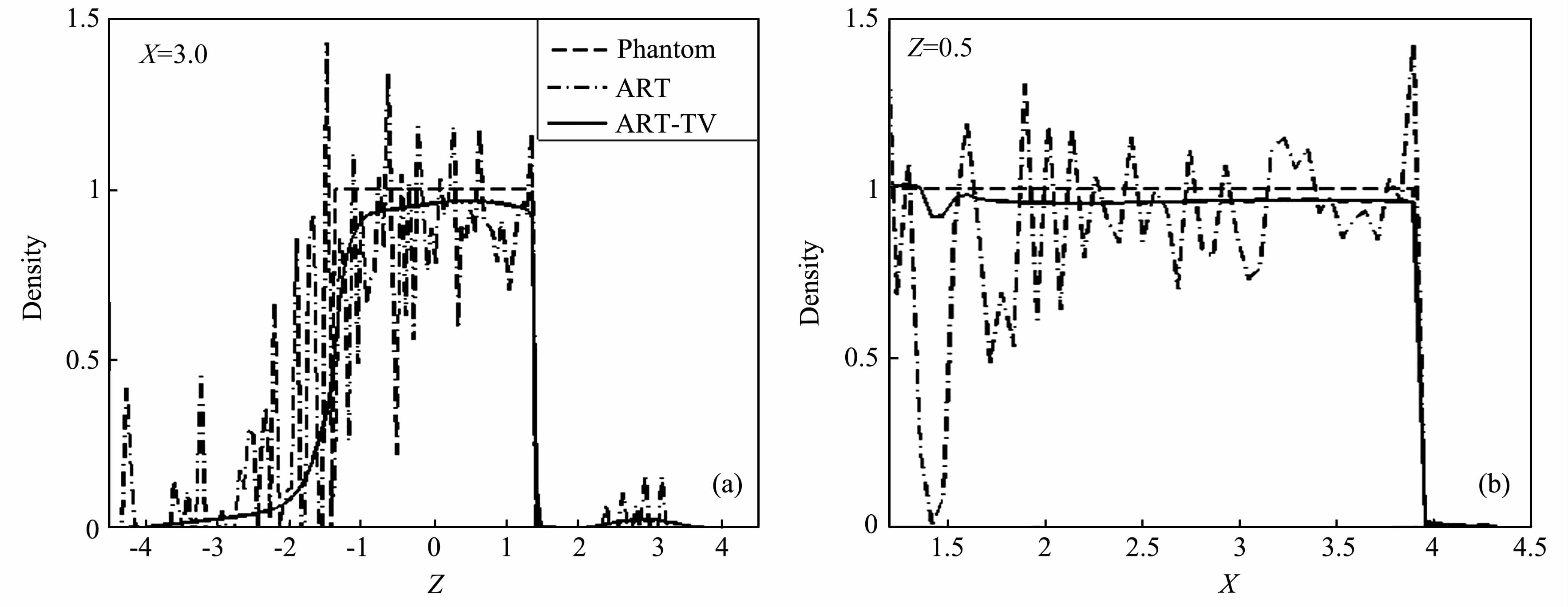
考虑到IMAGE 卫星轨道的角度覆盖范围最多只能达到90°,我们将进一步分析β=90°时两种算法得到的密度分布图.此时,投影数据是不完备的.重建区域的任意点,经过它的投影射线都不可能达到180°的角范围,尤其在Z轴负半轴地球边缘附近的点,几乎没有投影射线经过,因此这些点的密度值可信度最低.随着距离地球越远,遮挡效应逐渐减少,重建图像也逐渐接近原模型.为了更明显地看出这一特点,将图 3b中β=90°时的两条剖面线X=3.0和Z=0.5展现在图 4 中.其中,虚线、点划线和实线分别表示原模型、ART 和ART-TV 算法重建得到的密度.对于Z=0.5的剖面线,在X<1.2的部分处于电离层、地球内部和阴影区内,因此图中只显示X>1.2的部分.从图 4中可以看出,ART 算法重建图的剖面线振荡较大,即图像存在较大的噪声.产生噪声的一个原因是离散化的计算,另一个重要的原因就是重建区域的投影数据不完备.
|
图 4 90°角度覆盖范围时的重建图像沿X=3.0和Z=0.5的剖面线 Fig. 4 The profiles at X=3. 0 and Z=0. 5 respectively for 90-degree data |
图 4a的剖面线X=3.0显示了等离子体层密图 3 不同角度覆盖范围对重建图像的影响(a)不同角度覆盖范围的重建结果与原模型做相关分析;(b)角度覆盖范围分别为90°,150°和210°时,ART 与ART-TV 重建的结果图.度沿Z方向的变化.可以看出,两种算法重建得到的等离子体层在-Z侧都没有明显的边界,只有在+Z侧才有明显的边界.ART 算法重建的结果显示,等离子体层密度的振荡范围在0~1.5 之间,偏差较大.沿+Z轴方向,地球遮挡的影响逐渐较小,其振荡的幅度明显变小,当接近等离子体层边界时,振荡幅度已减小到0.5;对于ART-TV 算法,沿+Z轴方向,密度迅速增加.当Z= -1.2 时,密度已增加到0.95,并在此后保持偏差在0.05之内.
图 4b的剖面线Z=0.5 显示了等离子体层密度随X方向的变化.与剖面线X=3.0 相类似,ART 算法重建得到的等离子体层,其密度振荡幅度也几乎达到了1.5.在靠近Z轴X=1.4的附近,密度甚至为0.随着离Z轴距离的增大,振荡幅度逐渐变小,因此也就更接近原模型的密度;用ART-TV 算法重建的结果,其剖面线比较光滑.可以看出,除了在X=1.4附近密度稍微低一些(但此时与原模型的偏差也仅0.1),其他部分的密度都已经达到0.96,仅有0.04的偏差.由于重建图像的密度沿+Z方向逐渐接近原模型,不难想象与Z=0.5关于X轴对称的剖面线Z= -0.5 的情况:两种算法在等离子体层内部密度变化的趋势与剖面线Z=0.5的情况相类似,但ART 算法得到的密度振荡幅度高达2.2,ART-TV 算法得到的密度偏差也更大.
比较图 3和图 4中ART-TV 和ART 算法分别重建等离子体层模型在断层Y=0 上的密度分布,可知ART-TV 算法重建的图像更为光滑,偏差更小,因此重建效果也更为理想.
6 结论和讨论在用CT 方法根据IMAGE 卫星的EUV 图像重建地球等离子体层的离子空间密度分布时,会碰到很多与传统X 射线CT 不同的问题:投影数据不完备(地球遮挡、有限角度投影)及地磁扰动期间等离子体层形态发生变化等.因此,为了分析投影数据不完备对CT 重建结果的影响,以及寻找一种最佳的CT 方法来解决该问题,我们需要先建立等离子体层和电离层模型.类似CT 重建领域中常使用的建模方法———假定不同结构内部的密度均匀分布.模型中也假设了等离子体层和电离层的密度是均匀分布的.虽然模型与实际的等离子体层和电离层都有差异,但在探索算法的可行性方面有极其重要的作用.
本文采用ART-TV 和ART 两种算法对投影数据缺失最严重的中心子午面进行重建,结果表明:ART 算法重建出来的图像噪声较大(噪声幅度随着角度覆盖范围变化),而ART-TV 重建出来的图像则比较平滑;随着投影角度覆盖范围β 的增大,两种算法重建出来的图都越接近原模型,当β 达到195°以后,两种算法重建的结果与原模型的相关度达到最高,ART-TV 算法的相关系数为0.966,ART 的为0.940;投影数据缺失得越严重的区域,重建出来的图像质量越差.
IMAGE 卫星最多只能达到的投影角度覆盖范围为90°.在该投影角度范围的情况,ART 算法重建结果的相关系数为0.696,而ART-TV 算法的能达到0.760.因此,ART-TV 算法比ART 算法取得更好的重建结果.所以,今后利用实际EUV 成像图重建等离子体层全球密度分布时,我们将采用ART与TV 相结合的算法.
有关在重建实际等离子体层密度过程中出现的其他问题及如何利用实际IMAGE 卫星的EUV 成像图,目前我们正在研究之中[21].
致谢感谢中国科学院空间天气学国家重点实验室的所有成员对第一作者的指导和帮助.对审稿人提出的修改意见表示衷心的感谢.
| [1] | Angerami J J, Carpenter D L. Whistle studies of the plasmasphere in the magnetosphere-2. Electron density and total tube electron content near the knee in the magnetosphere ionization. J.Geophys. Rev. , 1966, 71: 711-725. DOI:10.1029/JZ071i003p00711 |
| [2] | Gallagher D L, Craven P D, Comfort R H. An empirical model of the Earth's plasmasphere. Adv. Space Res. , 1988, 8(8): 15-24. DOI:10.1016/0273-1177(88)90258-X |
| [3] | Carpenter D L, Anderson R R. A ISEE/whistle model of equatorial electron density in the magnetosphere. J. Geophys. Rev. , 1992, 97(A2): 1097-1108. DOI:10.1029/91JA01548 |
| [4] | Weller C S, Meier R R. First satellite observations of the He+ 304-Å radiation and its interpretation. J. Geophys. Res. , 1974, 79: 1572-1574. DOI:10.1029/JA079i010p01572 |
| [5] | Sandel B R, Broadfoot A L, Chen J, et al. The extreme ultraviolet investigation for the IMAGE mission. Space Sci. Rev. , 2000, 91(1-2): 197-242. |
| [6] | Huang X Q, Reinisch B W, Song P, et al. Developing an empirical density model of the plasmasphere using IMAGE/RPI observations. Adv. Space Res. , 2004, 33(6): 829-832. DOI:10.1016/j.asr.2003.07.007 |
| [7] | Xu R L, Huang Y, Li L, et al. Deduction of the Global Density of Earth Plasmasphere from the Model Column Density of the Plasmasphere using Computer Tomography Technique. Abstract, Program, 37th COSPAR Scientific Assembly, July 13-20, Juillet 2008, pp 298, Montreal, Canada, 2008. |
| [8] | Heang K T. An inversion formula for cone-beam reconstruction. SIAM J. Appl. Math. , 1983, 43(3): 546-552. DOI:10.1137/0143035 |
| [9] | Li L, Chen Z Q, Xing Y X, et al. A general exact method for synthesizing parallel-beam projections from cone-beam projections via filtered backprojection. Phys. Med. Biol. , 2006, 51: 5643-5654. DOI:10.1088/0031-9155/51/21/017 |
| [10] | Li L, Kang K J, Chen Z Q, et al. An alternative derivation and description of Smith's data sufficiency condition for exact cone-beam reconstruction. J. X-Ray Sci. Technol. , 2008, 16(1): 43-49. |
| [11] | Santhanam N, Newman T S, Gallagher D L. Exploiting known latitudinal variations for improved limited-angle tomographic reconstruction of the plasmasphere. //ITCC'04: Proceedings of the International Conference on Information Technology: Coding and Computing (ITCC'04). Washington, DC, USA, 2004, 2: 602. |
| [12] | Li L, Chen Z Q, Kang K J, et al. A study of the plasmasphere density distribution using computed tomography methods from the EUV radiation data. Adv. Space Res. , 2009, 43(7): 1143-1147. DOI:10.1016/j.asr.2008.10.013 |
| [13] | 黄娅, 徐荣栏, 李亮, 等. 利用计算机断层成像方法由观测图像重建等离子体层全球密度分布——地球遮挡问题. 地球物理学报 , 2009, 52(11): 2683–2688. Huang Y, Xu R L, Li L, et al. Deduction of the global density of the plasmasphere reconstructed from the observation images using Computed Tomography technique—The Earth's shelter. Chinese J. Geophys. (in Chinese) , 2009, 52(11): 2683-2688. |
| [14] | 金鑫, 李亮, 陈志强, 等. 利用EUV模拟观测和CT方法重建均匀等离子体层全球密度分布——三维ART重建和地球遮挡效应研究. 地球物理学报 , 2011, 54(7): 1691–1700. Jin X, Li L, Chen Z Q, et al. Deduction of the global density of the plasmasphere reconstructed from the EUV images using CT method. Chinese. J. Geophys. (in Chinese) , 2011, 54(7): 1691-1700. |
| [15] | Sidky E Y, Kao C M, Pan X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. J. X-Ray. Sci. Technol. , 2006, 14(2): 119-139. |
| [16] | 庄天戈. CT原理与算法. 上海交大出版社. 1992 . Zhuang T G. Computed Tomography Theory and Algorithm. Shanghai Jiaotong University Press (in Chinese). 1992 . |
| [17] | Kak A C, Slaney M. Principles of Computerized Tomographic Imaging. New York: IEEE Press. 1987 . |
| [18] | Hsieh J. Computed Tomography: Principles, Design, Artifacts, and Recent Advances. APIE Press Monograph , 2003. |
| [19] | Li L, Kang K J, Chen Z Q, et al. A general region-of-interest image reconstruction approach with truncated Hilbert transform. J. X-Ray. Sci. Technol. , 2009, 17(2): 135-152. |
| [20] | 王爱莲, 史晓燕. 统计学. 西安交通大学出版社. 2010 . Wang A L, Shi X Y. Statistics. Xi'an Jiaotong University Press (in Chinese). 2010 . |
| [21] | Huang Y, Xu R L, Shen C, et al. Rotation of the Earth's plasmasphere at different radial distances. Adv. Space. Res. , 2011, 48(7): 1167-1171. DOI:10.1016/j.asr.2011.05.028 |
 2012, Vol. 55
2012, Vol. 55

