2. 江苏省有色金属华东地质勘查局814队,镇江 212005;
3. 大庆油田有限责任公司勘探开发研究院,大庆163712;
4. 中国地质大学(武汉),武汉430074
2. Team 814, Eastern China Geological & Mining OrganizsLion for Non-ferrous Metals in Jiangsu Province, Zhenjiang 212005, China;
3. Daqing Oilfield Co., Led.Exploration and Development Institute, Daqing 163712,China;
4. Universiy of Geosciences (Wuhan),Wuhan 430074, China
利用高精度区域磁测资料解释居里等温面对大地构造研究、地球动力学、地震、能源、成矿热力学、确定深部磁体结构和对深部热状态、地热能的开发利用、热害防治、原生热液矿产勘查以及火山喷发的监测与预报、油气资源评价与勘探研究等具有重要意义[1-6].1985年,申宁华等[7]指出:构造较活动区,居里面埋深较浅;新生代地层含油气构造分布在居里面较浅的地区,由于地下热力作用,可促使油气形成.古、中生代地层的含油气构造分布在居里面埋深较大的地区,由于地下热力作用小,有利于油气的保存.2006年,胡旭芝等[8]通过对中国东北地区航磁特征及居里面分析认为:居里面起伏与软流圈起伏相关性较强体现了地幔传导热对磁性层下界面的影响,刻画了目前地壳热结构状态,反映了深部地球动力学过程对浅部地壳热状态的控制.1999 年,李燕等[9]提出了利用居里深度结合地表温度资料,通过有限单元法求解热传导方程进行盆地现今温度场模拟计算的方法,并指出盆地内的凹陷引起地温梯度在相应地带降低,因此利用地温梯度的计算结果,可以在区域上预测局部断裂凹陷,在松辽盆地东南某地区的实际应用中取得了较好的应用效果.通过区域航磁反演居里面并通过居里温度建立与地温场的关系,可以间接研究地温场的分布特征.为了探索应用居里面研究地温场新的方法并且为松辽盆地北部油气盆地模拟提供现今的区域地温场资料,本文尝试利用松辽盆地北部的区域航磁结合一定数量的井温资料进行地温场的计算,以弥补由于探井数量有限且井距较大以致仅利用探井所提供的井温资料不能很好的反应较大区域无探井控制的地温变化情况,以便满足盆地模拟中通常需要连续变化的地温及地温梯度.提出应用区域航磁在井温控制下的地温场计算新方法,该方法在一定程度上提高了应用居里面间接计算地温及地温梯度的可靠程度.
2 居里面的反演磁源物质的底界既然存在,它必然在大面积的区域航磁中有所反映,与居里面相关的深部磁场主要表现为长波磁异常的磁场特征.为此,需要对区域航磁异常进行适当的数据处理以便分离出与居里面相关的低频长波磁异常.高斯低通滤波、小波多尺度磁异常分解等方法可以提取相关的居里面磁异常[10-19].通过对区域航磁异常的多种处理进行对比分析认为把经过化极处理的松辽盆地北部区域航磁异常经过如下两种处理提取的与居里面有关的磁异常信息更加可靠:
(1) 对化极处理的松辽盆地北部航磁异常(图 1)求取二次趋势剩余场,以消除由于幔源电流系而产生的大陆磁异常的影响;

|
图 1 松辽盆地北部航磁异常平面等值图 Fig. 1 Contour map of aeromagnetic anomalies of northern part n Songliao Basin |
(2) 为消除浅源磁异常的干扰,对二次趋势剩余磁场进行补偿圆滑滤波,突出与居里面有关的中间区域磁性地质体所产生的磁异常.
应用磁测数据反演居里等温面深度可分为单体磁异常法和组合磁异常法,由于在不同的区域,不同场源及其所产生的磁异常都有各自的特征,因此,基于SpectorGrant统计模型的组合磁异常统计功率谱分析法,适应于对大区域磁异常组合的分析,用此方法计算居里面深度在世界上得到了广泛应用.国内外学者也相继提出了居里面反演的二维单一磁性界面深度的非线性反演的样条函数法、自相似和分形模型法、三维磁性层下界面的反演方法、磁场矩谱法、变磁化强度双界面反演法、似功率谱法、导数谱法等多种居里面反演方法[20-30].
数学理论表明:采用磁异常的矩谱具有增强底界面磁异常弱信息的能力.矩谱法对于反演磁性体的质心具有较高的精度.因此,在反演居里面时本文应用了矩谱法来反演磁性块体的质心,应用平均径向归一化对数功率谱的方法获取磁性块体的顶深,间接地计算居里面的深度.
在计算居里面时,将窗口内地下深处的磁性体视为具有统计意义上的垂直棱柱体,其磁异常的频谱为

|
(1) |
式中,I为磁化强度;L、M、N为地磁场方向余弦;l、m、n为磁化强度方向余弦.由于ΔT异常已化向地磁极,故L=M=I=m=0,N=n=1.a、b为棱柱体的水平宽;S= (u2+v2)1/2,u、v为沿x轴及y轴水平方向的波数/单位长度;x0、y0 为磁性体中心的水平坐标;zt 为磁性体的顶深;zb 为磁性体的底深;i为虚数单位.由磁性棱柱体的矩谱求出磁性棱柱体的水平坐标x0、y0 及中心深度z0.磁性棱柱体的矩谱为
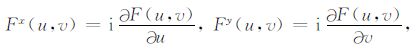
|
(2) |
经推导有:

|
(3) |
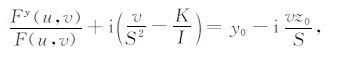
|
(4) |
式中,H、I、K为与磁化方向及地磁方向有关的常数;通过解给定不同的S的方程组可求得磁性棱柱体的x0、y0 及z0;磁性棱柱体的顶面埋深(zt)由磁性棱柱体异常频谱的高频端的平均径向归一化对数功率谱求得;最后居里面深度由Hc =2z0 -zt 计算得到.
松辽盆地北部的航磁异常划分为2.5km×2.5km的规则网格.因受松辽盆地高地温的影响,松辽盆地的居里深度不会很大,采用55km×55km的窗口可以近似反映17~30km 的居里深度.对松辽盆地北部经过以上处理的航磁资料进行了扫描计算,共计算了272个居里点深度,勾绘了松辽盆地北部居里面深度平面等值线图(图 2).在居里面的深度图上,不仅反映了松辽盆地北部由于受上地幔上隆引起的地热流升高而导致的居里面埋深浅(一般小于25km)的特点,而且从局部的居里面埋藏浅或深也较好地反映了基岩岩性在控制地温方面的作用.居里面埋藏浅的部位一般是规模较大的隐伏花岗岩所处的部位,花岗岩所产生的放射性热能是导致居里面局部偏浅的一个重要原因,古老巨厚的前震旦变质岩系是导致居里面局部偏深的主要原因,基岩岩性的变化产生了地温梯度以及地温差异性的变化.

|
图 2 松辽盆地北部居里面深度平面等值图 Fig. 2 Contour map of Curie point depth of northern part n Songliao Basin |
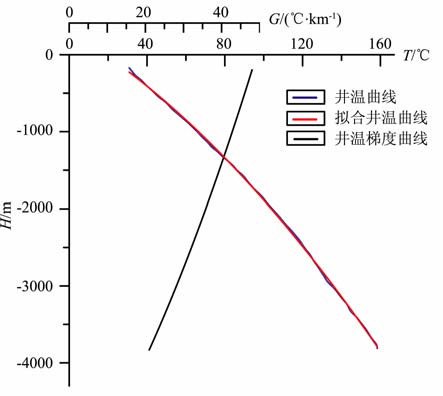
在分析了松辽盆地北部地区同深2、肇12等32口深探井的井温资料发现,松辽盆地北部的井温并不是都以一定的地温增加级随井深呈线性增加的.当把井温曲线转化为地温梯度曲线,发现该地区的地温梯度分三种情况变化:第一是地温梯度不变;第二是地温梯度随深度的加深而减小(图 3);第三是地温梯度随深度的加深而增加.这三种变化也正说明了松辽盆地北部地温梯度变化的复杂性.
|
图 3 同深1井井温曲线、地温梯度与拟合地温曲线对比图 Fig. 3 Comparison diagram between well temperature log, geothermal gradient and fitted geo temperature curve of tongshen-1 well in northern part in Songliao Basin |
通过对上述三种地温梯度曲线的分析发现,应用地温梯度随深度按
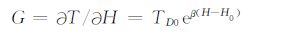
|
(5) |
的形式拟合实际的井温梯度曲线效果较好.其中,G=∂T/∂H是地温梯度;TD0 是近地表地温梯度;β 是地温梯度随深度变化的指数因子;H是深度;H0是常温层深度.
同时这种地温梯度形式的提出改变了以往应用
根据前面所提的求地温梯度的指数形式,通过对深度的积分得到某一深度的地温表达式为
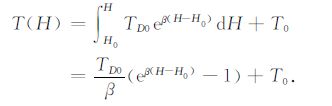
|
(6) |
式中,T(H)是H深度处的地温;T0 是常温层的温度;Tc 是居里温度;T0 一般为一个地区的年平均温度,松辽盆地北部地区取T0=15 ℃,H0=15m.常温层温度与深度对反演地温梯度影响不大
为了应用以上地温梯度、地温的公式计算出某一深度处的地温梯度及地温,必须知道计算点处的TD0、β.这两个参数均可以通过在已知探井的井温资料控制下应用插值的方法获得.
关于已知探井处的TD0,采用井温曲线前500m的平均地温梯度(图 4):
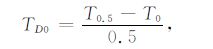
|
(7) |

|
图 4 松辽盆地北部近地表地温梯度平面等值图 Fig. 4 Contour map of geothermal gradient of near surface m northern part in Songliao Basin |
结合已知探井所处的居里面深度Hc 及常温层深度,在固定Tc=578 ℃就可以计算出β 的值.β 的计算方法如下:

|
(8) |
应用一定的数学变换手段,通过迭代的方法解此方程就可以获得β.应用同深2等32口井的β 勾绘出控制松辽盆地北部β 的平面分布(图 5),从β分布图可以看到,在松辽盆地北部大部分地区地温梯度随着深度的增加而降低.借此β 分布图可以查出未知区的β.既然采用地温梯度的指数变化形式,则地温梯度自常温层直到居里面也按同一规律变化.只有这样才有可能利用居里面来求出未知区的近地表地温梯度.当然也可以应用已知探井的井温资料得到控制全区的近地表地温梯度.如果采用居里面控制的方法,则:
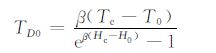
|
有了以上两种参数,就可以应用公式(5)、(6)来计算任何一点任何深度的地温梯度及地温.
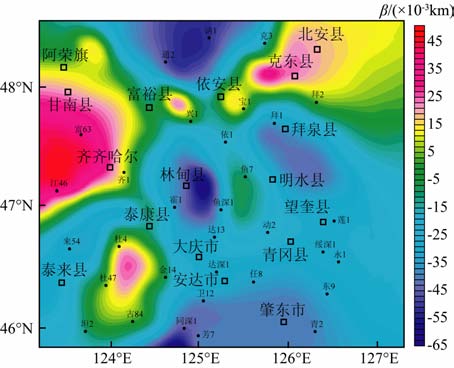
|
图 5 松辽盆地北部地温梯度随深度变化因子平面等值图 Fig. 5 Contour map of geothermal gradient variation factor with the depth of northern part in Songliao Basin |
图 6、图 7给出了应用上述方法得到的松辽盆地北部地下3km 处的地温梯度及地温.为了很好地评价盆地的地温场特征,应用一定深度范围内的平均地温梯度则更具有代表性.根据上述求地温及地温梯度的方法及公式经进一步推导,得到某一深度(H)范围内的平均地温梯度为
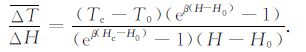
|
(9) |
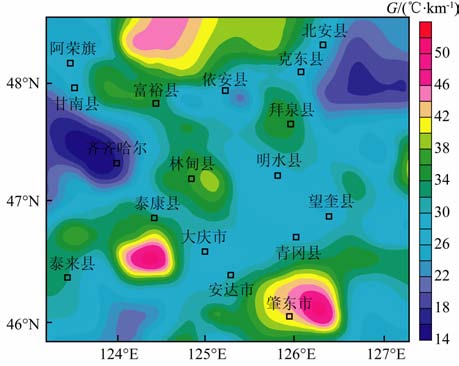
|
图 6 松辽盆地北部地下3 km地温梯度平面等值图 Fig. 6 Contour map of geothermal gradient in 3 km depth underground of northern part in Songliao Basin |

|
图 7 松辽盆地北部地下3 km地温平面等值图 Fig. 7 Contour map of geothermal temperature in 3 km depth underground of northern part in Songliao Basin |
根据上式计算了松辽盆地北部地下5km 以上的平均地温梯度(图 8).
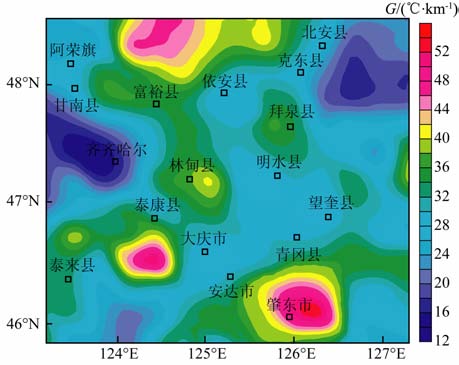
|
图 8 松辽盆地北部平均地温梯度平面等值图 Fig. 8 Contour map of average geothermal gradient of northern part m Songliao Basin |
依据传统的经典算法
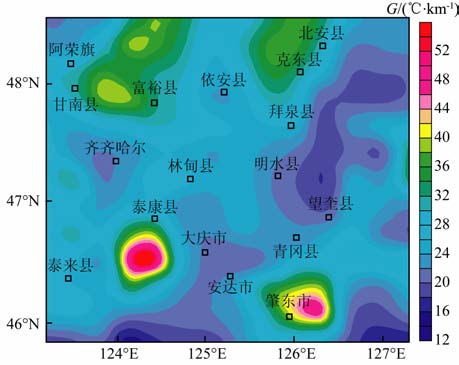
|
图 9 松辽盆地北部平均地温梯度平面等值图(按线性算法) Fig. 9 Contour map of average geothermal gradient of northern part n Songliao Basin (by linear algorithm) |
从大规律角度,应用居里面计算的地温梯度主要反映的是深部地温梯度的变化规律,经典算法与指数算法都能体现这一规律,甚至经典算法在反映深部地温场方面更具代表性,因为经典算法没有受井温资料的约束.虽然有时应用浅部的井温梯度作校正,但从总体上仍然反映深层的地温梯度变化规律,而这样作校正只是强行地把反映深层的地温梯度变化规律拉到盆地浅部作为盆地浅部的地温梯度指标来评价盆地的地温梯度的高低,这是不合适的,深层与浅层在地温梯度的变化上是不相同的,存在很大的差异,这已被苏联的科拉超深钻得到的温度资料所证实.
应用航磁资料研究地温场,不论是经典算法还是指数算法都具有一个共同的特点:两者都是借助于居里面和同一个固定的居里点温度.居里面计算的方法以及从区域航磁中提取有关居里面的异常信息的准确与否都会影响居里面深度计算的可靠性,间接地影响地温梯度计算的准确与否.居里温度选取的是否准确也是影响地温梯度精度的一个重要因素,居里温度是随着岩矿石类型不同而变化的,其主要的影响因素取决于岩矿石中钛的含量.业已证明,钛磁铁矿系列是岩石磁性主要矿物,两端分别为亚铁磁性的磁铁矿和顺磁性的钛尖晶石.钛磁铁矿具反尖晶石结构,随Fe2TiO4 比例增加居里点温度降低.此系列固溶体存在于高温条件,温度降低时成分不稳定,其TiO2 含量与结晶温度和氧的挥发度条件关系密切.当钛磁铁矿发生氧化时居里点温度升高;当铁氧化物及固溶体中铁离子被其他金属离子置换时,居里点下降.通常我们无法知道所研究地区的消磁界面是由什么样的磁性物质组成,因而也就无法选准居里温度,从而导致地温梯度计算的误差.
因无法确切的知道一个地区的居里温度,在松辽盆地北部地温场计算中,使用的居里温度是578℃,为铁磁性矿物的居里温度,利用这一温度结合居里面计算的地温梯度及地温与以实际的井所描绘的区域地温场基本上是吻合的.说明所选择的居里温度还是较合适的.
5 结论通过对松辽盆地北部平均地温梯度平面等值线图的分析可以看出,盆地内具有较高的地温梯度,5km以上地层的平均地温梯度为3.6 ℃/100m, 存在三个5km 以上地层平均地温梯度大于4.0 ℃/100m 的地区:一是林甸地区,二是泰康地区,三是肇东地区,其原因在于在这些地区的基岩岩性为大面积分布的花岗岩,花岗岩的放射性热能是产生地温梯度较高的主要原因.大庆、望奎、明水、依安一带的5km 以上的平均地温梯度较低,最低为2.2 ℃/100m, 这主要是由于基底岩性为前震旦古老结晶岩系所引起的.因而可以得出结论:基岩岩性与地温梯度之间是密切相关的,在一定程度上控制了局部地温场的分布.当然松辽盆地的地温场是由多方面制约控制的,松辽盆地上地幔的隆起则是对区域地温场控制的另一决定性因素.
| [1] | 王钧, 黄尚瑶, 黄歌山, 等. 中国地温分布的基本特征. 北京: 地震出版社, 1990 : 98 -130. Wang J, Huang S Y, Huang G S, et al. Basic Characteristics of the Geotemperature Distribution in China (in Chinese). Beijing: Seismological Press, 1990 : 98 -130. |
| [2] | Xiong S Q, Zhou F H, Yao Z X, et al. The Aeromagnetic Survey in the Central and Western Qinghai Tibet Plateau. Beijing: Geological Publishing House, 2001 : 111 -162. |
| [3] | 刘沈衡, 申宁华. 岩石圈居里等温面解释的若干问题. 长春科技大学学报 , 1999, 29(4): 373–376. |
| [4] | Tanaka A, Okubo Y, Matsubayashi O. Curie point depth based on spectrum analysis of the magnetic anomaly data in East and Southeast Asia. T ccLonophysics , 1999. |
| [5] | Chiozzi P, Matsushima J, Okubo Y, et al. Curie-point depth from spectral analysis of magnetic data in central-southern Europe. Physics of Lhc Earth and Planeiary InLeriors , 2005, 152(4): 267-276. DOI:10.1016/j.pepi.2005.04.005 |
| [6] | Hao S L, Gao H G, Wang C H. Isothermal surface of Curie temperature around the Beijing area and its relation to earthquakes. Chinese Journal of Geophysics , 1982, 25(3): 264-269. |
| [7] | 申宁华, 李春华, 张贵宾, 等. 用下扬子航磁资料计算居里等温面. 长春地质学院1985年科学研究报告年鉴 , 1985. Shen N H, Li CH, Zhang GB, et al. Using aeromagnetic data of lower Yangtze region calculate Curie point isotherm . Science Study Report (1985) of Changchun Geology Institute (in Chinese) , 1985. |
| [8] | 胡旭芝, 徐鸣洁, 谢晓安, 等. 中国东北地区航磁特征及居里面分析. 地球物理学报 , 2006, 49(6): 1674–1681. Hu XZ, Xu MJ, XieXA, et al. A characteristic analysis of aeromagnetic anomalies and Curie point isotherms in Northeast China. Chinese J.Geophys. (in Chinese) , 2006, 49(6): 1674-1681. |
| [9] | 李燕, 张明华, 刘德芳. 松辽盆地东南某部的地温场计算及油气预测. 石油地球物理勘探 , 1999, 35(5): 577–583. Li Y, Zhang M H, Liu D F. Geotemperature field estimation and hydrocarbon reservoir prediction in an area of southeast Songliao basin. Oil Geophysical Prospeding (in Chinese) , 1999, 35(5): 577-583. |
| [10] | 杨文采, 施志群, 侯遵泽, 等. 离散小波变换与重力异常多重分解. 地球物理学报 , 2001, 44(4): 534–542.. Yang W C, Shi Z Q, Hou Z Z, et al. Discrete wavelet transform for multiple decomposition of gravity anomalies. Chinese J.Geophys.(inChinese) (in Chinese) , 2001, 44(4): 534-542.. |
| [11] | 侯遵泽, 杨文采. 中国重力异常的小波变换与多尺度分析. 地球物理学报 , 1997, 40(1): 85–95. Hou Z Z, Yang W C. Wavelet transform and multi-scale analysis on gravity anomalies of China. Chinese J.Geophys (inChinese) (in Chinese) , 1997, 40(1): 85-95. |
| [12] | 杨文采, 郭爰缨, 谢玉清, 等. 重磁异常频率域解释的理论与方法. 物化探研究报导 , 1978, 78(2): 134–178.. Yang W C, Guo A Y, Xie Y Q, et al. Theory and methodsfor interpret at ion of gravity and magnetic anomalies in thefrequency domain. BulleL in of Institute of Geophysical and Geochemical Prospecting (in Chinese) , 1978, 78(2): 134-178.. |
| [13] | Okubo Y, Matsushima J, Correia A. Magnetic spectral analysis in Portugal and its adjacent seas. Physics and Chemistry of the Earth , 2003, 28(9-11): 511-519. DOI:10.1016/S1474-7065(03)00070-6 |
| [14] | Blakely R J. Potential Theory in Gravity and Magnetic Applications. Cambridge: Cambridge University Press, 1995 . |
| [15] | Arkani-Ilamed J. Differential reduction to the pole: Revisited. Gophscs , 2007, 72(1): L13-L20. |
| [16] | Cooper G R J, Cowan D R. Differential reduction to the pole. Computs & Gocenes , 2005, 31(8): 989-999. |
| [17] | Rajaram M, AnandSP, IlemantK, et al. Curie isotherm map of Indian subcontinent from satellite and aeromagnetic data. Earth and Planetary Science Letter , 2009, 281(34): 147-158. |
| [18] | Bhimasankaram V L S, Nagendra R, Rao S V S. Interpretation of gravity anomalies due to finite inclined dikes using Fourier transformation. Geophysic , 1977, 42(1): 51-59. DOI:10.1190/1.1440713 |
| [19] | Daubechies I. The wavelet transform, time-frequency localization and signal analysis. IEEE TransacLions on infrmation Theory , 1990, 36(5): 961-1006. DOI:10.1109/18.57199 |
| [20] | 韶丹, 髙国明, 罗开奇, 等. 功率谱法反演青藏髙原居里等温面. 云南大学学报(自然科学版) , 2010, 32(S2): 165–169. Shao D, Gao G M, Luo K Q, et al. Invert the curie isotherm of Tibetan Plateau by using of power spectrum method. Journal of Yunnan University (Natural Sciencss Edition') (in Chinese) , 2010, 32(S2): 165-169. |
| [21] | Spector A, Grant F S. Statistical models for interpreting aeromagnetic data. Geophysics , 1970, 35(2): 293-302. DOI:10.1190/1.1440092 |
| [22] | Bhattacharyya BK, Leu L K. Analysis of magnetic anomalies over Yellowstone National Park: mapping of Curie point isothermal surface for geothermal reconnaissance. J.Geophys.Res. , 1975, 80(32): 4461-4465. DOI:10.1029/JB080i032p04461 |
| [23] | Mayhew M A. Curie isotherm surfaces inferred from high-altitude magnetic anomaly data. J.Geophys.Res. , 1985, 90(B3): 2647-2654. DOI:10.1029/JB090iB03p02647 |
| [24] | Fedi M, Quarta T, Santis A D. Inherent power-law behavior of magnetic field power spectra from a Spector and Grant ensemble. Geophysics , 1997, 62(4): 1143-1150. DOI:10.1190/1.1444215 |
| [25] | 汪炳柱, 徐世浙, 陈培善. 利用AT异常反演居里面深度的一种新方法. 石油地球物理勘探 , 1999, 34(2): 137–147. Wang B Z, Xu S Z, Chen P S. A new method for Curie interface depth inversion using AT anomaly. Oil Geophysical Prospecting (in Chinese) , 1999, 34(2): 137-147. |
| [26] | 李春峰. 居里等温面深度的探测方法. 地球物理学进展 , 2005, 20(2): 550–557. Li CF. Methods of mapping the depth to the Curie isotherm. Progress in Geophysics (in Chinese) , 2005, 20(2): 550-557. |
| [27] | Bhattacharyya B K, Leu L K. Spectral analysis of gravity andmagnetic anomalies due to two-dimensional structures. Geophysics , 1975, 40(6): 993-1013. DOI:10.1190/1.1440593 |
| [28] | IlaoSJ, Wang C II. On the analysis of Curie isothermal surface over the Bohai sea Water Area. Seismology andGeology , 1982, 4(1): 39-42. |
| [29] | Shen N II. Introduction to principle and methods of Curie point calculation by aeromagnetic data. Computing Techniquss for Geophysical and Geochemical Exploration , 1985, 7(2): 89-98. |
| [30] | Blakely R J. Curie temperature isotherm analysis and tectonic implications of aeromagnetic data from Nevada. Journal ofGeophysical Research , 1988, 93(B10): 11817-11832. DOI:10.1029/JB093iB10p11817 |
 2012, Vol. 55
2012, Vol. 55

