大量的研究与观察证实了地球介质各向异性的普遍存在,主要表现为地震波的弹性参数随波传播方向的变化而变化.除各向异性矿物颗粒本身的原因外,各向同性地层中旋回性的薄互层或裂缝的定向排列同样会诱发各向异性.在地震勘探数据处理中,介质速度的各向异性影响地震波传播的走时与振幅信息.忽略各向异性带来的运动学上的误差会引起反射波归位不准,绕射波收敛不彻底,能量不聚焦,这种情况对于大偏移距、宽方位数据尤为明显.大量观察与总结表明,代表水平薄互层及页岩沉积层的垂直横向各向同性(VTI)介质是最为典型的各向异性模型,其特点是对称轴是垂直的,各向异性只取决于与对称轴的夹角.更一般地,当对称轴具有一定的倾角时,就使用倾斜横向各向同性(TTI)介质来描述.
处理各向异性介质中地震波的传播与成像问题最直接的方法即求解该介质下的弹性波方程.然而这样带来了两个问题:第一,复杂的各向异性弹性波计算成本很高;第二,针对纵波的成像需要对弹性波场进行分离,而复杂介质各向异性波场分离仍然存在许多的问题.我们知道,各向异性介质不可能只传递纵波,通常由于偏振方向不平行于传播方向而将其称为拟声波,因此我们力求得到近似描述拟声波的波动方程.从VTI介质出发,许多学者尝试用近似的方法来达到这个目的,如椭圆近似[1],反椭圆近似[2],弱各向异性近似[3],小倾角近似[4].然而这些近似在实际应用中都受到各自前提假设的限制.Alkhalifah[5]提出了声波近似,人为地设定横波速度为零仍然可以从运动学上很好地近似描述纵波,节省了计算量的同时还压制了横波的影响.然而,声波近似带来了横波的稳定性问题,在非均匀TTI介质中尤为明显.在声波近似方程中加入横波的处理可以很好地解决稳定性问题[6-7].保留横波的声波近似方程本质上描述的就是弹性波方程中耦合的qP、qSV 波分量.
随着勘探地质体复杂程度的增加,叠前深度偏移(PSDM)成为最精确的成像工具.其中,逆时偏移[8-10]在陡倾界面以及复杂构造成像方面相对于单程波偏移和Kirchhoff偏移具有明显的优势.逆时偏移通过求解双程波动方程进行波场延拓,通常将计算区域离散化,用数值方法求解双程波微分方程,目前较为常用的为有限差分法[11]、有限元法[12]、伪谱法[13]和谱元法[14-15].成像条件主要有激发时间成像条件[16]和互相关成像条件[17],其中互相关成像条件应用的更加广泛.
近年来在微机群(PC-Cluster)和图形处理单元(GPU)的支持下迅速发展[18-20].时至今日,各向同性逆时偏移已经步入工业化应用的阶段.随着宽方位、大偏移距采集技术的发展,各向异性的影响逐渐突出,针对TI介质的逆时偏移成为研究热点.目前国内各向异性单程波偏移技术有较多研究[21-22],而各向异性双程波逆时偏移仍限于VTI介质以及弹性波方程[23-24].
本文首先针对VTI介质,从弹性波方程的角度推导正应力表达的拟声波方程,讨论由频散关系分裂得到的拟声波方程的物理意义,并将拟声波方程扩展到更一般的倾斜横向各向同性(TTI)情况.而后根据是否应用声学近似将拟声波方程分为声波近似方程以及qP-qSV 波方程.在此基础上,将这两类拟声波方程应用在逆时偏移中,讨论了计算效率、稳定性等实际问题.数值试验表明合适地选择拟声波方程可以实现高效率、稳定的TI介质逆时偏移.
2 TI介质qP-qSV 波方程 2.1 VTI介质qP-qSV 波方程VTI介质中的波动方程揭示了TI介质中地震波的传播规律,是TI介质地震波正演模拟、偏移成像的基础.要得到TI介质下的拟声波方程,仍然需要从VTI介质的应力-应变关系出发.对于TTI情况,只需要在VTI介质的基础上进行坐标旋转,其传播规律并没有物理上的不同.VTI介质应力-应变关系为

|
(1) |
其中,σij为应力张量的分量,εij为应变张量的分量,ρ为密度.代入应力-位移方程(2式),以及应变和位移的关系(3式),在假定常密度的情况下,可以得到由位移表达的三维弹性波方程(4式):
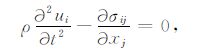
|
(2) |
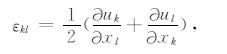
|
(3) |
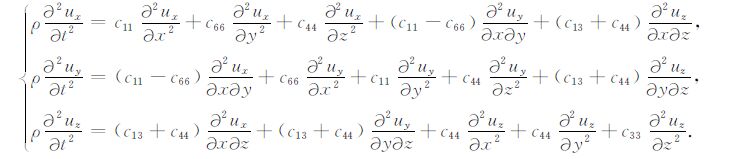
|
(4) |
由Christoffel方程的解可以知道,qSH 波的偏振垂直于qP、qSV 波所在平面[25].在其二维三分量的表达式(xoz平面)中,y方向的位移uy即为qSH 波,且与ux、uz无关.也就是说,(4)式在二维情况下即为仅描述qP-qSV 波的方程:
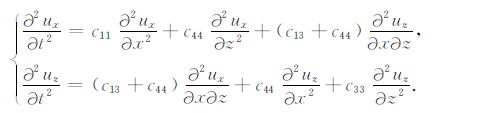
|
(5) |
(5) 式即为位移表达的qP-qSV 方程,本质上讲,(5)式可以作为拟声波方程进行VTI介质的正演与偏移.但该式存在混合偏导数,实现起来并不方便;并且其同时刻画了qP 和qSV 两种波的传播,在进行qP 的传播时,会带来很强的qSV 波的假象.由应力-应变关系,及应变-位移关系可以得到应力和位移偏导数的表达式:
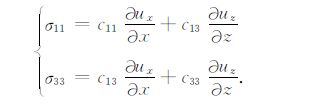
|
(6) |
σ11,σ33 分别为x,z方向上的正应力.将∂ux/∂x,∂uz/∂z代入(5)式中可以得到正应力表达的二维qP-qSV 波方程:
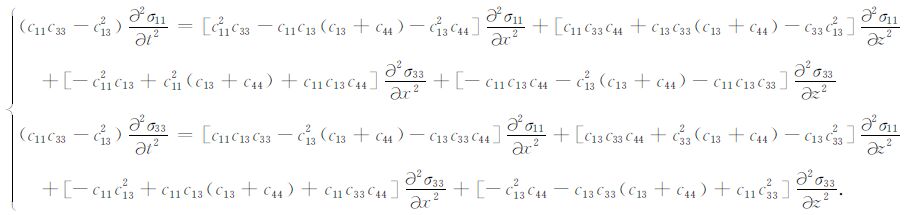
|
(7) |
进一步地,针对纵波正演或成像,可以通过对波场求取散度的方法来近似得到纵波波场.根据(6)式,可以利用正应力σ11,σ33 近似地表达对波场ux、uz的散度:
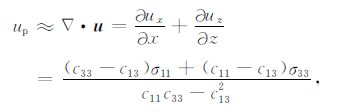
|
(8) |
由刚度矩阵的正定性可以得到c132>c33(c11-c66)[26].
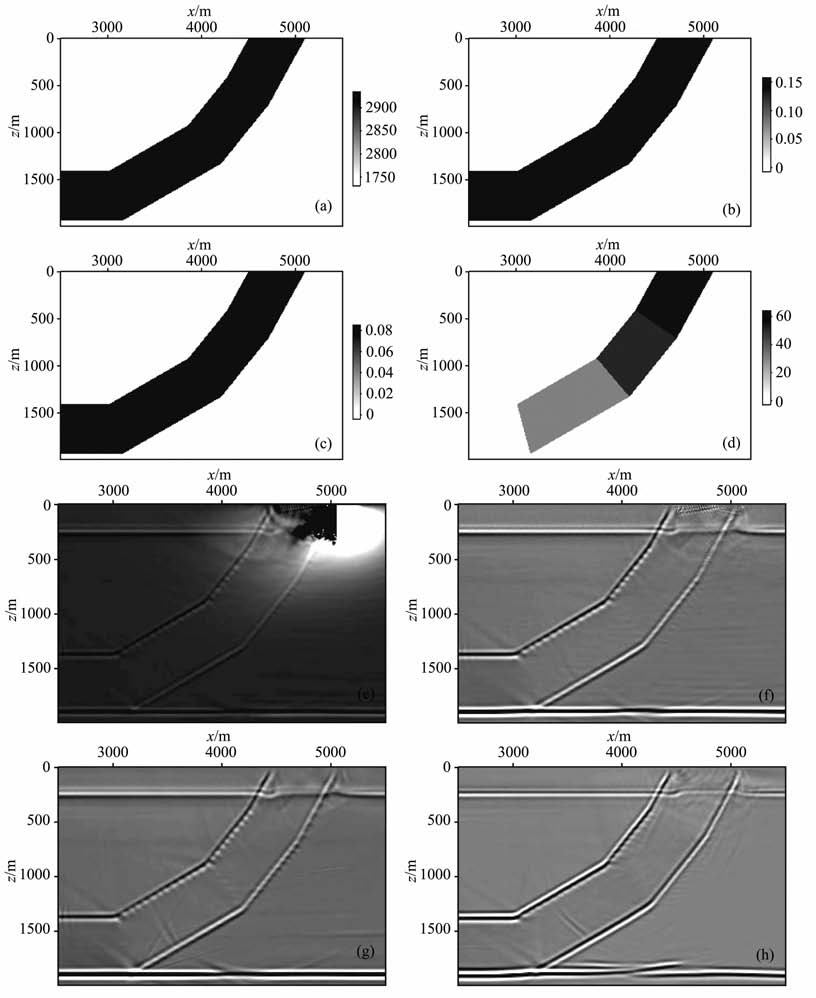
由于c66 对qP波没有影响,因此可以保证(7)式左端c213≠c33c11.相对于(5)式而言,(7)式的求解几乎不增加计算成本,因为二阶导数的系数是时不变的.利用x、y方向的对称性将∂2/∂x2 替换为∂2/∂x2 +∂2/∂y2,就得到(7)式的三维形式.图 1展示了二维情况下求解(7)式得到的σ11,σ33 以及两者的线性组合up, 图 1d为相应的VTI介质qP 波群速度平面.波前快照与群速度平面相吻合验证了其运动学的正确性.

|
图 1 均匀介质正应力qP-qSV 波方程波前快照(a)σ11;(b)σ33;(c)up;(d)qP波群速度平面. Fig. 1 Snapshots of qP-qSV wave-equation expressed by stress in homogenous media (a)σ11;(b)σ33;(c)up;(d Group velocity surface of qP wave. |
在其他文献[26-28]中,VTI介质的标量波方程多从四阶的频散关系的角度来推导.TI介质地震波的传播涉及qP、qSV 和qSH 波,其中前两者是耦合的.VTI介质中耦合的qP-qSV 频散关系为[23]
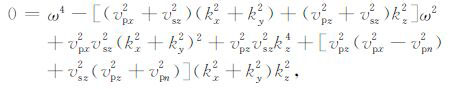
|
(9) |
其中,ω为频率;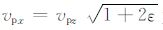
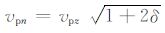

|
(10) |
对应的时空域的方程为
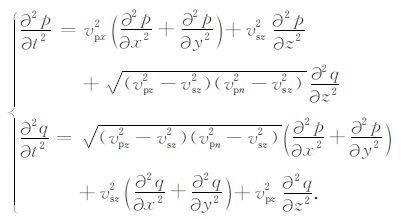
|
(11) |
容易验证(5)式和(7)式同样满足二维qP-qSV 波频散关系.也就是说,四阶频散关系的的分裂形式在运动学上等价.原则上任何一个分裂方式都可以作为VTI介质拟声波方程,只是用两个分量的不同线性组合来表达qP 波.但在所有的二阶分裂形式中,(5)式和(7)式具有明确的物理意义.而实际的应用中,可以选择任何一种形式,其计算效率、计算精度差别不大.
2.2 从VTI到TTIVTI介质与TTI介质并没有物理上的本质区别,如果在沿倾斜对称轴的坐标系下考查TTI介质波的传播则与VTI介质完全等价.对qP-qSV 波方程进行坐标旋转.假设x为垂直坐标系,对称轴倾角θ、方位角φ 的旋转后得到倾斜坐标系x′.顺时针旋转为正.由三维坐标旋转的关系:

|
(12) |
其中,
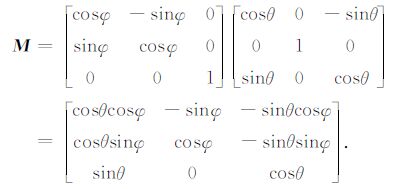
|
由(12)式可以得到旋转坐标系下一阶和二阶导数与坐标系的关系:
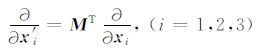
|
(13) |
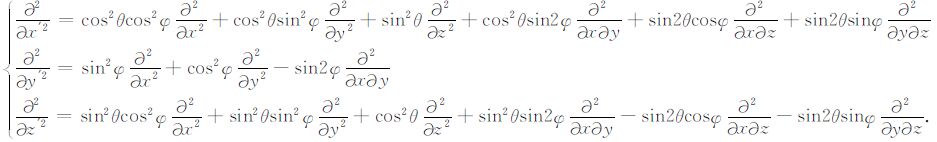
|
(14) |
其中,MT 为旋转矩阵M的转置.拟声波方程从VTI到TTI的过渡只需要将二阶偏导数替换为(14)式的形式.
2.3 qP-qSV 方程模拟实验这里在均匀介质下qP-qSV 波方程进行正演模拟来验证qP波和qSV 波的运动学信息的正确性.选择较为典型的砂岩(TaylorSand),各向异性参数ε=0.11、δ=-0.035[25],垂直P波速度vpz=3000m/s.采用十阶有限差分法求解(11)式来进行模拟.图 2(a、b)和(c、d)分别为VTI和TTI(θ=45°)情况下,vsz=0.1vpz及vsz=0.5vpz时300ms波前快照.图 3(a、b)为相应的以均匀相角间隔得到的群速度平面.可以看出,由于各向异性的影响,均匀介质中qP 和qSV 波波前已不再是正圆.波前快照与群速度平面的对比表明该方程能够对qP波和qSV 波进行精确的描述.

|
图 2 均勻介质qP-qSV波方程数值模拟波前快照 (a)VTI介质,vsz=0.1vpz;(b)VTI介质,vsz=0.5vpz;(c)TTI介质(θ=45°),vsz=0.1vpz;(d)TTI介质(θ=45°),vsz=0.5vpz. Fig. 2 Snapshots of qP-qSV wave-equation in homogenous media (a)VTI media, vsz=0.1vpz;(b)VTI media, vsz=0.5vpz;(c)TTI media(θ=45°),vsz=0.1vpz;(d)TTI media(θ=45°),vsz=0.5vpz. |

|
图 3 qP-qSV 波群速度平面 (a)VTI介质,vsz=0.1vpz;(b)VTI介质,vsz=0.5vpz;(c)TTI介质(θ=45°),vsz=0.1vpz;(d)TTI介质(θ=45°),vsz=0.5vpz. Fig. 3 Group velocity surfaces of qP-qSV wave (a)VTI media, vsz=0.1vpz;(b)VTI media, vsz=0.5vpz;(c)TTI media(θ=45°),vsz=0.1vpz;(d)TTI media(θ=45°),vsz=0.5vpz. |
在利用qP-qSV 方程对qP 波进行正演模拟和成像时,我们并不关心qSV 波.图 4为qP 波相速度和参数vsz的变化关系,可以看出在任何一个角度上横向变化很小,表明了vsz的变化对qP 的相速度影响很小.由于qSV 波的速度对qP 波运动学特征影响很小,因此不需要采用准确的qSV 波的速度.Alkhalifah[27]指出,人为地规定垂直横波速度vsz为零,可以简化qP-qSV 波方程,并且仍然能够很好地描述qP波.在声波近似意义下,qP-qSV 波频散关系退化为
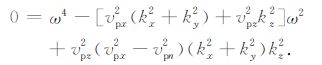
|
(15) |
同样地,四阶的频散关系不便于直接求解,为方便实现与提高计算效率,许多学者给出了不同的分裂形式[28-30].
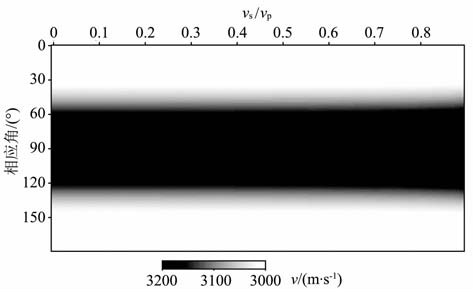
|
图 4 qP波相速度与vsz变化关系 纵轴为相角,横轴为vs0/vp0,灰度值为qP波相速度 Fig. 4 Variation of qP wave phase velocity withvsz The vertical axis is phase angle, and the horizontal axisisvs0/vp0.The value is phase velocity qP wave. |
由于声波近似中vsz=0等价于c44 =0(c66 对qP波没有影响),也就是说可以利用声波近似意义下的刚度矩阵来得到相应的应力或位移表达的声波近似方程.其推导过程与本文(7)式相同,因此在(7)式中代入c44=0,并将刚度矩阵系数代换为Thomsen参数,可以得到应力表达的声波近似方程:
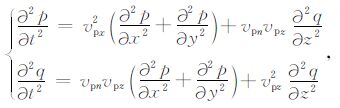
|
(16) |
(16) 式即与文献[30]所展示的方程相同.
采用与上节相同模型参数和方法利用声波近似方程(16)式进行数值模拟.图 5 为波前快照及其对应的群速度平面.由于人为的设定vsz为零,qSV 波会产生畸变,表现为波前快照中菱形的部分.从模拟结果看出,声波近似可以对qP 波运动学特征进行准确的刻画,同时qSV 波能量要小于qP-qSV 波方程.
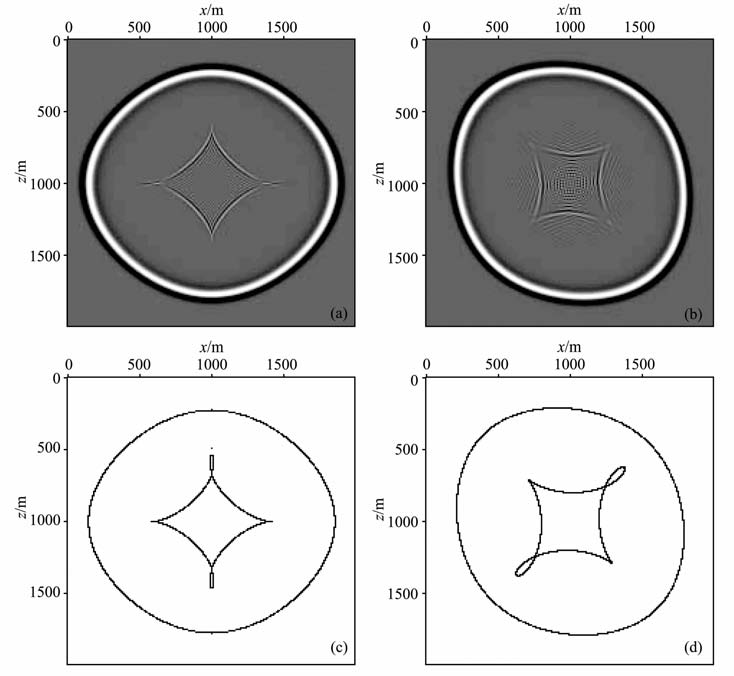
|
图 5 声波近似方程数值模拟波前快照及其群速度平面 (a)VTI介质波前快照;(b)TTI介质(θ=45°)波前快照;(c)VTI介质群速度平面;(d)TTI介质(θ=45°)群速度平面. Fig. 5 Snapshots and group velocity surfaces of wave-equation under acoustic approximation (a) Snapshots in VTI media; (b) Snapshots in TTI media(θ=45°) ; (c) Group velocity surface in VTI media;(d) Group velocity surface m TTI media(θ=45°). |
在逆时偏移中,通过求解双程的波动方程来进行波场延拓.具体来讲,从源点将波场自初始时刻t=0正向延拓至最大时刻t=tmax 得到顺时波场S(x,t);然后从检波点将地表炮记录作为边值条件自t=tmax 反向延拓至t=0得到逆时波场R(x,t),进而对两个波场施加成像条件.由于稳定性的原因,互相关成像条件是最常使用的成像条件.顺时延拓、逆时延拓及成像条件方程如下:
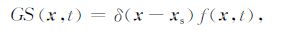
|
(17a) |
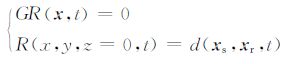
|
(17b) |
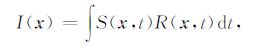
|
(17c) |
其中G表示双程波延拓算子,f(x,t)与d(xs, xr, t)分别为震源子波和地表炮记录,I(x)为成像结果.具体到TI介质逆时偏移,需要用描述TI介质地震波传播的算子替换式(17a)、(17b)中的算子G.前文讨论了两个标量波方程,即qP-qSV 波方程和声波近似方程,下面就方程的稳定性,计算效率问题将两者进行比较,并以脉冲响应对TI介质逆时偏移加以检验.
4.1 方程的稳定性由于波动方程要求刚度矩阵是对称正定的[31],那么Christoffel方程特征值(三种波的相速度)为正实数.声波近似中vsz=0(c44 =0)会引起qSV 波的不稳定,并由此可以导出其稳定性条件[32]:

|
(18) |
这个条件对于实际应用并不苛刻,因为大多数的沉积地层能够满足该条件.
除此以外,在TTI介质中,对称轴倾角θ、方位角φ 快速变化的区域声波近似也会带来数值的不稳定.许多学者在实际应用中观察到了这一现象[33-34].对模型进行平滑可以一定程度上减小这种不稳定性,但这种做法一定程度上牺牲了运动学的精确性,并且对模型的平滑缺乏定量的标准.
上述两个稳定性问题对于vsz≠0的qP-qSV 波方程并不存在,采用粘土页岩(Mesa Clay Shale)的各向异性参数(ε=0.189,δ=0.204)[25]对比其稳定性.图 6(a、b)展示了ε <δ 情况下声波近似方程和qP-qSV 波方程的模拟结果.图 6a中qSV 波表现出数值不稳定;而加入qSV波后的图 6b则不存在这种不稳定性.并且qP-qSV 波方程还可以应对TTI介质对称轴角度的快速变化,这一点在数值算例部分可以得到进一步的验证(图 9e).

|
图 6 VTI介质声波近似方程与qP-qSV 波方程(vsz=0.6vp0)稳定性对比,均匀介质vp0=3000m/s, ε=0.189,δ=0.204 (a)声波近似方程;(b)qP-qSV 波方程. Fig. 6 Stability comparison of acoustic approximation equation and qP-qSV wave-equation in homogenous VTI media with vp0=3000m/s, ε=0.189,δ=0.204 (a) Acoustic approximation equation; (b) qP-qSV wave-equation. |
在正演模拟和逆时偏移中,计算效率一直是我们非常关心的问题,而波动方程的选择对其有着直接的影响.就二维情况下qP-qSV 方程(11 式)和声波近似方程(16式)的计算效率进行对比.表 1展示了二维情况下两个方程每个时间、空间点所需的计算量以及下文脉冲响应的计算时间.虽然硬件的不同会导致所需的计算时间有所差别,但两个方程相对的所需时间具有一定的参考价值.可以看出在VTI情况中,qP-qSV 波所需计算量明显大于声波近似方程(约1.4 倍);而TTI情况下,两者近似相等.
|
|
表 1 qP-qSV波方程与声波近似方程计算效率对比 Table 1 Computational cost comparison of qP-qSV and acoustic approximation wave-equation |
利用qP-qSV 波方程和声波近似方程进行逆时偏移叠前脉冲响应试验,模型水平距离4km, 深度2km, 炮点坐标(1300 m, 0),检波点坐标(2700 m, 0),脉冲采用Ricker子波,设置在900ms.均匀介质vpz=3000m/s, ε=0.2,δ=0.1,vsz=0.33vpz.图 7(a、b)和(c、b)分别为VTI和TTI介质声波近似方程、qP-qSV 方程的脉冲响应.可以看出两个方程都可以很好地描述TI介质地震波的传播,将脉冲偏移到正确的位置上.在脉冲响应中,除qP波成像的响应外,还有并不明显的qSV 波对成像的干扰.在炮点和检波点附近设置ε=δ 是简单有效的压制方法[30].
|
图 7 TI介质逆时偏移脉冲相应试验 (a)VTI介质声波近似方程;(b)VTI介质qP-qSV 波方程;(c)TTI介质声波近似方程;(d)TTI介质qP-qSV 波方程. Fig. 7 Impulse response of RTM tn TI media (a) Using acoustic approximation equation in VTI media; (b) Using qP-qSV wave-equation in VTI media; (c) Using acoustic approximation equation rn TTI media; (d) Using qP-qSV wave-equation rn TTI media. |
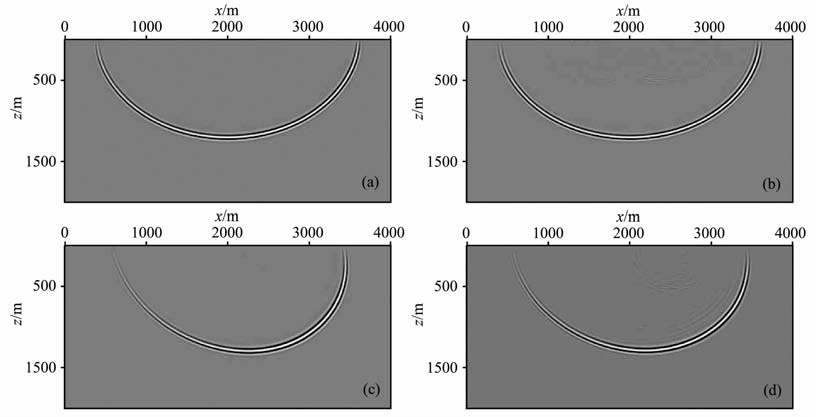
首先在SEG/HESS模型上测试VTI介质声波近似方程正演及逆时偏移.图 8(a、b、c)分别为vp0、ε、δ 模型,模型中满足ε≥δ.首先使用声波近似算子对模型进行正演,炮点坐标0~17950,炮间距50,共360炮.采用中间激发,两端接收的观测方式.震源采用Ricker子波,每炮1001道,道间距10 m, 采样8000ms得到合成炮记录.进而对该数据进行逆时偏移,采用十阶有限差分法求解(16)式进行波场延拓,施加互相关成像条件以及Laplace滤波去噪[35].图 8d为偏移结果,其中左半部分盐丘侧翼以及右半部分的陡倾断层都可以很好地聚焦成像;而对应地各向同性声波方程对该模型偏移结果(图 8e)表现出归位错误以及严重的不聚焦.
|
图 8 SEG/HESSVTI模型数值算例 (a)vp0模型;(b)ε模型;(c)δ 模型;(d)声波近似方程逆时偏移结果;(e)各向同性声波方程偏移结果. Fig. 8 Numerical example on SEG/HESS VTI model (a)vp0 model; (b)ε model; (c)δ model; (d)RTMimage using acoustic approximation; (e)RTM image using isotropic acoustic equation. |
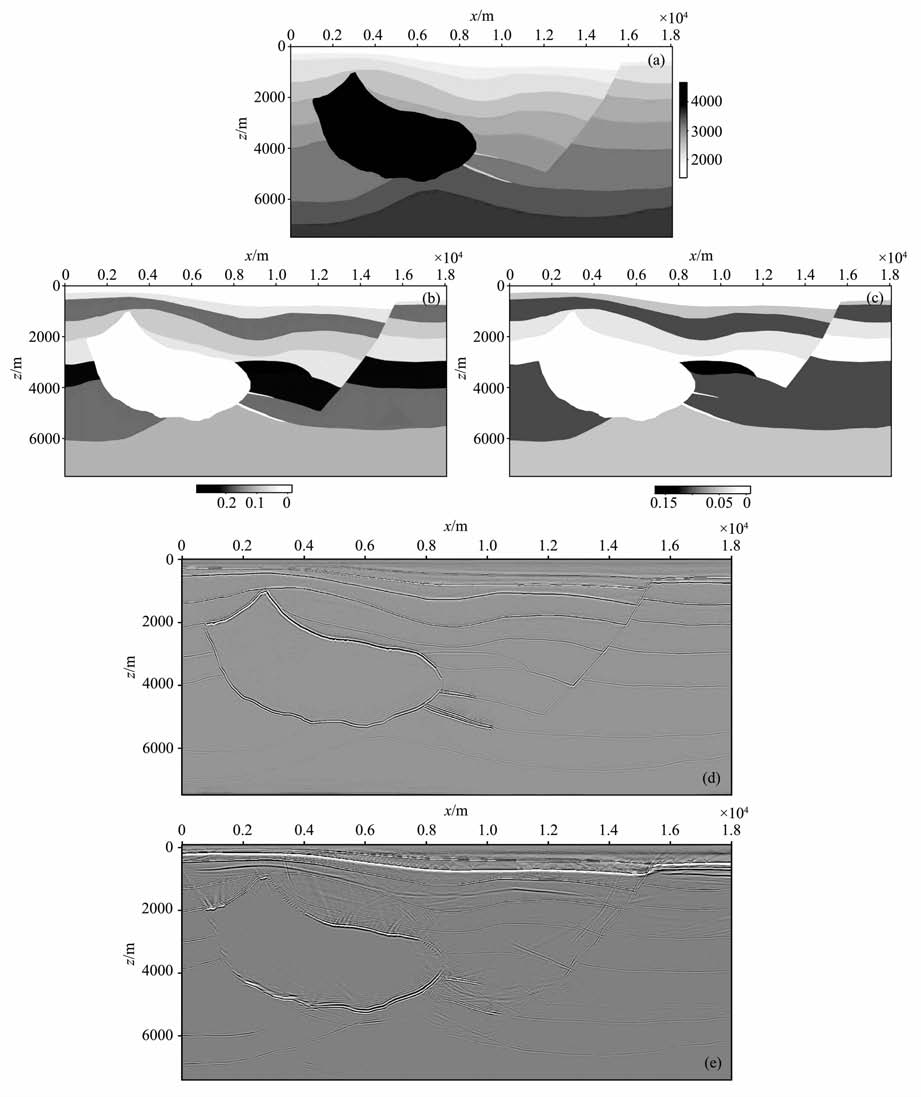
下面以逆冲模型[36]为例来测试TTI介质qP波的成像结果.其vp0、ε、δ、θ 模型分别如图 9(a、b、c、d)所示.该模型数据正演时底部有一平层用于测试上覆TTI介质中地震波传播走时的准确性.采用10m×10m×1ms的采样间隔进行逆时偏移.图 9e为直接使用声波近似方程的偏移结果,图中在参数快速变化的区域显示了严重的不稳定性,而对模型的平滑很大程度上消除了不稳定,得到了正确的成像结果(图 9f).图 9g为使用qP-qSV 波方程进行偏移.可以看到,该算子并不需要对模型进行平滑就能够保证稳定性.但注意到由于加入了对qSV 波的模拟,qSV 波与qP波的成像给偏移结果带来了少量的噪音,这种SV 波的干扰可以通过在正向延拓中使用涨缩震源很容易地压制掉.图 9h为使用VTI声波近似方程对该模型数据进行偏移,对图 9f对比看出,底部的平层由于走时的误差导致不能完全收敛.
|
图 9 逆冲模型数值算例 (a)vp0模型;(b)ε模型;(c)δ模型;(d)θ模型;(e)TTI声波近似方程偏移结果;(f)对模型平滑后声波近似方程偏移结果;(g)TTIqP-qSV 波方程偏移结果(模型未平滑);(h)使用VTI声波近似方程偏移结果. Fig. 9 Numerical example on overthrust model (a)vp0 model; (b) ε model (c)δ model; (d) θ model; (e) RTM image using acoustic approximation equation ; (f) RTM image of smoothed model using acoustic approximation ; (g) RTM image of unsmoothed model using qP-qSV wave-equation ; (h) RTM image using VTI acoustic approximation equation. |
不同于各向同性介质,TI介质中的地震波由qP,qSV,qSH 三类波进行描述.使用qP-qSV 波方程来近似描述qP波的传播可以简化弹性波方程的求解以及避免复杂的各向异性介质波场分离.从四阶qP-qSV 波频散关系得到的一系列分裂形式中,位移、正应力表达的方程具有明确的物理意义.本文推导了从VTI介质到TTI介质位移、正应力表达的波动方程的一般方法,并且用数值模拟加以验证.正演的波前面与群速度平面的对比表明qP-qSV 波方程可以精确描述两种地震波的传播,并且qSV 波速度的选取对qP 波影响很小.在VTI介质情况下采用声波近似可以大幅度降低计算成本并且较好地压制qSV 波的影响,但因破坏了刚度矩阵的正定性带来了稳定性问题,尤其是非均匀TTI介质下表现的更为明显,HESSVTI模型和逆冲TTI模型验证了这种认识.综合比较两类方程,建议VTI介质情况下采用声波近似方程以提高计算效率,而在TTI介质情况下qP-qSV 波方程则是较好的选择,因为其在效率相当的情况下可以保证稳定性.
致谢感谢国家自然科学基金(41074083)的资助.感谢SEG 提供文中使用的模型,以及Colorado School of Mines提供的Seismic Unix(SU)平台.
| [1] | Helbig K. Elliptical anisotropy-Its significance and meaning. Geophysics , 1983, 48(7): 825-832. DOI:10.1190/1.1441514 |
| [2] | Muir F, Dellinger J. A practical anisotropic system. SEP , 1985, 44: 55-58. |
| [3] | Thomsen L. Weak elastic anisotropy. Geophysics , 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [4] | Cohen J K. Analytic study of the effective parameters for determination of the NMO velocity function in transversely isotropic media. Colorado School of Mines Center for Wave Phenomena, 1996: CWP-191. |
| [5] | Alkhalifah T. Acoustic approximations for processing in transversely isotropic media. Geophysics , 1998, 60(2): 1550-1566. |
| [6] | Fletcher R P, Du X, Fowler P J. Reverse time migration in tilted transversely isotropic (TTI) media. Geophysics , 2009, 74(6): WCA179-WCA187. DOI:10.1190/1.3269902 |
| [7] | Fowler P J, Du X, Fletcher R P. Coupled equations for reverse time migration in transversely isotropic media. Geophysics , 2010, 75(1): S11-S22. DOI:10.1190/1.3294572 |
| [8] | McMechan G A. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting , 1983, 31(3): 413-420. DOI:10.1111/gpr.1983.31.issue-3 |
| [9] | Whitmore D N. Iterative Depth imaging by back time propagation. 53rd Annual International Meeting, SEG Expanded Abstracts , 1983: 827-830. |
| [10] | Baysal E, Kosloff D D, Sherwood J W C. Reverse time migration. Geophysics , 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [11] | 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报 , 2000, 43(3): 411–419. Dong L G, Ma Z T, Cao J Z, et al. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese) , 2000, 43(3): 411-419. |
| [12] | 张美根, 王妙月, 李小凡, 等. 各向异性弹性波场的有限元数值模拟. 地球物理学进展 , 2002, 17(3): 384–389. Zhang M G, Wang M Y, Li X F, et al. Finite element forward modeling of anisotropic elastic waves. Progress in Geophysics (in Chinese) , 2002, 17(3): 384-389. |
| [13] | 孙文博, 孙赞东. 基于伪谱法的VSP逆时偏移及其应用研究. 地球物理学报 , 2010, 53(9): 2196–2203. Sun W B, Sun Z D. VSP reverse time migration based on the pseudo-spectral method and its applications. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2196-2203. |
| [14] | 王童奎, 李瑞华, 李小凡, 等. 横向各向同性介质中地震波场谱元法数值模拟. 地球物理学进展 , 2007, 22(3): 778–784. Wang T K, Li R H, Li X F, et al. Numerical spectral element modeling for seismic wave propagation in transversely isotropic medium. Progress in Geophysics (in Chinese) , 2007, 22(3): 778-784. |
| [15] | 王童奎, 付兴深, 朱德献, 等. 谱元法叠前逆时偏移研究. 地球物理学进展 , 2008, 23(3): 681–685. Wang T K, Fu X S, Zhu D X, et al. Spectral-element method for prestack reverse-time migration. Progress in Geophysics (in Chinese) , 2008, 23(3): 681-685. |
| [16] | Chang W F, McMechan G A. Reverse-time migration of offset vertical seismic profiling data using thr excitation-time imaging condition. Geophysics , 1986, 51(1): 67-84. DOI:10.1190/1.1442041 |
| [17] | Claerbout J F. Toward a unified theory of reflector mapping. Geophysics , 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [18] | 李博, 刘红伟, 刘国峰, 等. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报 , 2010, 53(12): 2938–2943. Li B, Liu H W, Liu G F, et al. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU. Chinese J. Geophys. (in Chinese) , 2010, 53(12): 2938-2943. |
| [19] | 刘红伟, 刘洪, 邹振, 等. 地震叠前逆时偏移中的去噪与存储. 地球物理学报 , 2010, 53(9): 2171–2180. Liu H W, Liu H, Zou Z, et al. The problems of denoise and storage in seismic reverse time migration. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2171-2180. |
| [20] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1725-1733. |
| [21] | 吴国忱. TI介质qP波地震深度偏移成像方法研究. 上海: 同济大学, 2006. Wu G C. Seismic depth-migration imaging method of qP wave in TI media (in Chinese). Shanghai: Tongji University, 2006. |
| [22] | 朱兆林. 倾斜横向各向同性介质中P-S波处理方法研究.上海: 同济大学, 2008. Zhu Z L. The processing method of P-S wave in titled transversely isotropic media (in Chinese). Shanghai: Tongji University, 2008. |
| [23] | 杜启振, 秦童. 横向各向同性介质弹性波多分量叠前逆时偏移. 地球物理学报 , 2009, 52(3): 801–807. Du Q Z, Qin T. Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 801-807. |
| [24] | 陈沫. 横向各向同性介质地震波场逆时偏移. 岩性油气藏 , 2009, 21(4): 78–81. Chen M. The seismic wave field reverse-time migration in transversely isotropic media. Lithologic Reservoirs (in Chinese) , 2009, 21(4): 78-81. |
| [25] | Tsvankin I. Seismic Signatures and Analysis of Reflection Data in Anisotropic Media. Elsevier Science , 2001. |
| [26] | Dellinger J. Anisotropic seismic wave propagation. Stanford University , 1991. |
| [27] | Alkhalifah T. An acoustic wave equation for anisotropic media. Geophysics , 2000, 65(4): 1239-1250. DOI:10.1190/1.1444815 |
| [28] | Zhou H B, Zhang G Q, Bloor R. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media. 76th Annual International Meeting, SEG, Expanded Abstracts , 2006: 194-198. |
| [29] | Fletcher R, Du X, Fowler P J. A new pseudo-acoustic wave equation for TI media. 78th Annual International Meeting, SEG, Expanded Abstracts , 2008: 2082-2086. |
| [30] | Duveneck E, Milcik P, Bakker P M. Acoustic VTI wave equations and their application for anisotropic reverse-time migration. 78th Annual International Meeting, SEG, Expanded Abstracts , 2008: 2186-2190. |
| [31] | Cerveny V. Seismic Ray Theory. Cambridge: Cambridge University Press, 2001 . |
| [32] | Grechka V, Zhang L, Rector J W. Shear waves in acoustic anisotropic media. Geophysics , 2004, 69(2): 576-582. DOI:10.1190/1.1707077 |
| [33] | Zhang Y, Zhang H. A stable TTI reverse time migration and its implementation. 79th Annual International Meeting, SEG Expanded Abstracts , 2009: 2794-2798. |
| [34] | Jin S W, Jiang F, Ren Y Q. Comparison of isotropic, VTI and TTI reverse time migration: an experiment on BP anisotropic benchmark dataset. 80th Annual International Meeting, SEG Expanded Abstracts , 2010: 3198-3202. |
| [35] | Youn O K, Zhou H W. Depth imaging with multiples. Geophysics , 2001, 66(1): 246-255. DOI:10.1190/1.1444901 |
| [36] | Fei T, Dellinger J A, Murphy G E, et al. Anisotropic true-amplitude migration. 68th Annual International Meeting, SEG Expanded Abstracts , 1998: 1677-1679. |
 2012, Vol. 55
2012, Vol. 55



