1984年Ostrander[1]提出AVO 技术后,作为一种重要的油气检测和地震岩性分析工具,得到了迅速的普及和应用[2-4].AVO(amplitudeversusoffset)技术是一种研究地震反射振幅随炮检距(或入射角)变化的技术.振幅随偏移距的变化是地下岩石及其孔隙流体的弹性参数的函数[5],因此,根据振幅随炮检距的变化规律所反应出来的地下岩性及其孔隙流体的性质可以用来直接预测油气和估计地壳岩性参数[6-7].
AVO 反演就是采用Zoeppritz方程[8]或其近似方程由实际地震道集记录估算岩石的地震参数[9-11],例如密度、纵波速度、横波速度或泊松比,进行岩性分析或烃类直接检测.最初基于纵波资料的AVO 反演是Smith 等[12]提出的线性反演模型,即加权叠加反演,而后Stewart[13]于1990年首次提出了多分量数据的纵、横波联合反演,继而Xu, Larsen等[14-15]深入研究了AVO 联合反演方法,并提出了非线性反演模型和方法.地震道反演引入贝叶斯(Bayes)[16]理论为反问题求解提供了新的途径,但Bayes反演[17]理论在处理非线性问题时将局部线性化简化,使解的稳定性受到局部模型的影响,而AVO 反演本质上属于典型的非线性问题,非线性反演则可得到较好的反演效果,但其反演速度较慢.反演的另一种普遍采用的方法是神经网络法[18],如RBF神经网络方法[19],但此种方法受网络结构复杂性和样本复杂性的影响较大,有时会出现过学习或低泛化,因此,要尽可能的提高解的稳定性与反演速度,需寻求一种新的解决非线性问题的方法.
本文提出一种新的AVO 非线性反演方法,即利用支持向量机求解AVO 非线性反演问题.文中首先对基于支持向量机的原理进行了阐述,然后建立了适合AVO 反演的支持向量机模型.最后利用该方法对模型数据和实际资料进行了反演计算,反演结果表明,该方法在没有牺牲反演效果的情况下较好的解决了传统反演方法所具有的局限性,可以直接从合成记录中提取地层的弹性参数,反演速度快、稳定性好.
2 支持向量机支持向量机(SupportVector Machine, SVM)是一种新的机器学习算法,它的基础是Vapnik[20]的统计学习理论,是统计学习理论中最年轻的分支.统计学习理论和支持向量机建立了一套较好的有限样本下机器学习的理论框架和通用方法,既有严格的理论基础,又能较好地解决小样本、非线性、高维数和局部极小点等实际问题,支持向量机的最优求解基于结构风险最小化思想,因此比其它非线性函数逼近方法具有更强的泛化能力[21].
2.1 非线性支持向量机用于非线性回归估计的支持向量机(Support Vector for Regression, SVR)的基本思想是通过用内积函数定义的非线性变换将输入空间变换到一个高维空间(Hilbert空间),然后在这个高维空间中寻找输入变量和输出变量之间的一种线性关系[21-22],其基本结构如图 1所示.
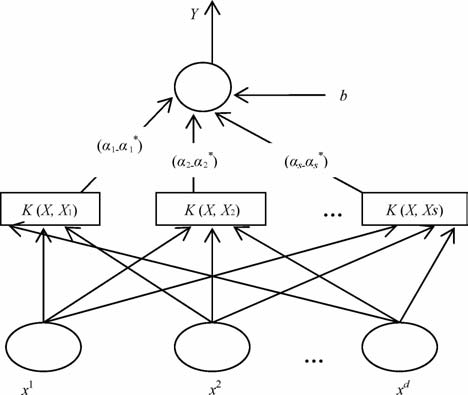
|
图 1 支持向量机结构示意图 Fig. 1 Structure of the SVM |
支持向量机算法是一个凸二次优化问题,可以保证找到的解是全局最优解并能较好的解决小样本、非线性、高维数等实际问题,特别是其小样本学习能力要远远优于传统的神经网络[19].
设训练样本集为 {(xi,yi),i=1,2,…,l},其中xi∈RN为N维测量模型样本输入值,yi∈R为样本输出值,l为样本数.
对上述训练样本集,通过非线性映射Φ(·)将训练集中的样本数据x映射到一个高维线性特征空间,在这个维数可能无穷大的线性空间中构造线性回归估计函数.设估计函数f的形式如下:
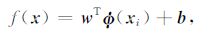
|
(1) |
其中w∈RNH,b∈R,Φ(·):RN→RNH是非线性映射,将输入空间映射到高维特征空间;b为偏置量.求解目的是寻求参数wT,b,使得对样本以外的输入x,有
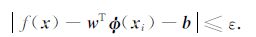
|
(1)式对应的最优化问题为
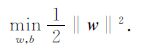
|
约束条件:

|
(2) |
引入松弛变量ζ,ζ* ,目的为确保上式有解,则(2)转化为
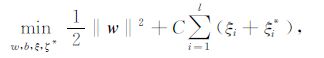
|
约束条件:
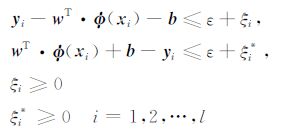
|
(3) |
这里C>0为惩罚系数,C越大表示对超出误差ε的数据点的惩罚越大,ε 为不敏感损失函数,其形式为
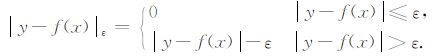
|
(4) |
显然(4)式为一个约束二次规划.下面采用拉格朗日乘子法求解这个具有线性不等式约束条件的二次规划,即
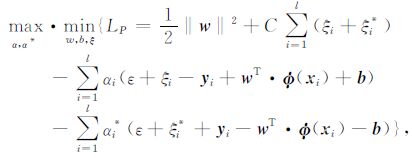
|
(5) |
其中,αi,αi*≥0,i=1,2,…,l为拉格朗日乘子.
引入核函数K(xi,xj)代替非线性映射Φ(·),核函数为满足Mercer条件[23]的任意对称函数.
由此可得到(5)式的对偶优化问题[16]:
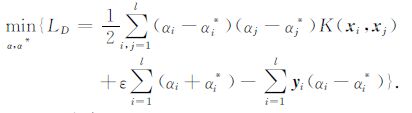
|
(6) |
约束条件:
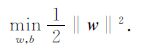
|
求解式(6),可得到最终的估计函数:
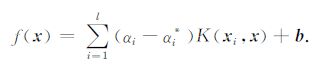
|
(7) |
式中,(αi-αi*)≠0对应的xi为支持向量,偏置量b可通过KKT 条件[23]求解.
2.2 支持向量机的回归性能用支持向量机进行线性回归,当样本数很多时,学习速度比较慢,而当样本数比较缺乏时,泛化能力却非常的好[24],也就是说支持向量机具有很强的小样本学习能力.
3 基于支持向量机的非线性AVO 反演叠后地震资料缺乏叠前资料所包含的丰富的振幅和旅行时信息,而且,叠后地震反演只能提供种类很少的纵波波阻抗等参数,不能给出纵横波速度比、泊松比等反映物性、流体特征的参数,在研究储层物性、流体方面受到了限制.叠前非线性AVO 反演与叠后地震反演相比,具有良好的保真性和多信息性,可以更可靠地揭示地下储层的展布情况、物性及含油气性.
3.1 正演模拟正演模拟是计算纵波入射到具有不同弹性参数的地层分界面上的响应.Zoeppritz方程是以平面波入射为基础描述反射界面的反射系数、投射系数与界面上下物性参数、入射和折射角之间关系的基本方程,完全形式的Zoeppritz方程全面考虑了平面纵波和横波入射在平界面两侧产生的纵横波和透射能量之间的关系:
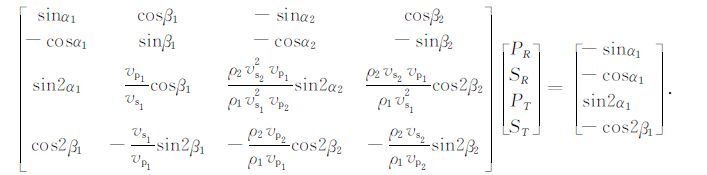
|
(8) |
其中,α1,β1 和α2,β2 分别为纵横波反射角与透射角,PR为纵波反射系数,SR为横波反射系数,PT为纵波透射系数,ST为横波透射系数,vp1,vs1,ρ1 和vp2,vs2,ρ2 分别为分界面两侧的纵波速度、横波速度以及介质密度.以下分别给出层状介质和连续介质情况下的AVO 正演模型.
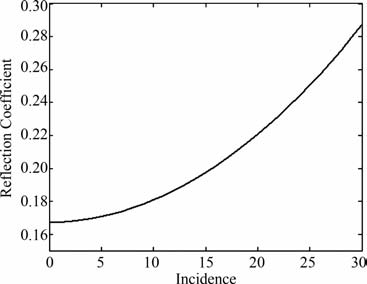
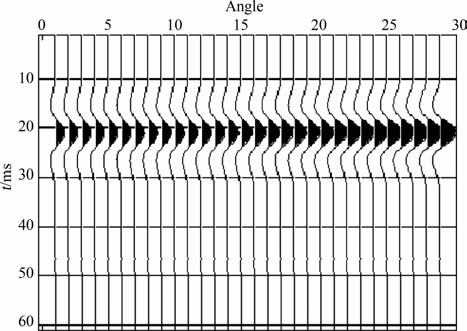
3.1.1 两层介质情况下的AVO 正演模型设有如表 1 所示的两层介质1 和2.利用Zoeppritz方程计算出反射系数与入射角的关系曲线,如图 2所示;然后利用反射系数与子波褶积得到CMP道集地震记录,如图 3所示;其中,子波采用30Hz的雷克子波,总道数为30 道,道集上反射振幅随入射角增加而增加.
|
图 2 反射系数与人射角的关系曲线 Fig. 2 Relation curve of reflection coefficient |
|
图 3 两层介质的合成地震记录 Fig. 3 Synthetic seismogram of two-layered mediumand incidence |
|
|
表 1 两层介质的弹性参数 Table 1 Elastic parameters of two-layered medium |
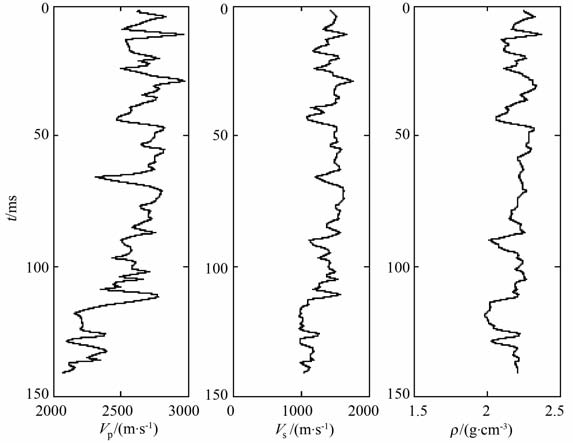
实际地层参数如图 4所示,包括纵波速度、横波速度及密度数据,图 5 是由该连续地层介质正演生成的角道集剖面.
|
图 4 连续地层介质模型 Fig. 4 Continuous layered medium model |

|
图 5 连续介质的合成地震记录 Fig. 5 Synthetic seismogram of continuous medium |
AVO 反演的目的是获得各种弹性参数,目前许多AVO 反演都是基于Shuey近似方程,而支持向量机较适合采用Zoeppritz方程直接进行反演.
3.2.1 支持向量机AVO 反演的数学模型用于训练SVM 的数据来自正演的过程,输入数据是P 波反射振幅,由角道集中提取,输出数据是介质分界面处的ΔVP,ΔVS 和Δρ[25, 26].
已知:P波反射振幅、界面P 波速度、S 波速度和ρ的N次样品取值为:(xi,yi)(i=1,2,…,l).支持向量机AVO 反演模型的建立,就是寻求xi和yi之间的关系:

|
(9) |
式中Rn为输入数据,R为输出数据.
根据支持向量机理论,AVO 反演模型的建立,也即寻求上节中式(7)的表达式,即:

|
式中:xi为第i个训练样本,αi,αi*,b可通过前面的优化算法求解.
采用如下形式的核函数:
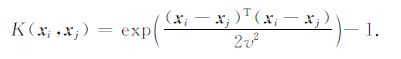
|
(10) |
其中v2 可由直线交叉验证法求得[13].
样本集和核函数确定后,求解式(7),即可得到支持向量机的AVO 非线性反演模型,根据得到的反演模型,对层状介质和连续介质做AVO 反演.
3.2.2 层状介质AVO 反演单界面AVO 反演中,观测资料是单一反射同相轴的振幅随偏移距、射线参数或入射角的相对变化.对上节的二层介质参数模型进行反演试验,首先通过正演生成角道集,对CMP 资料进行速度分析和正常时差校正(NMO),然后对每个CMP 道集内作切除和部分叠加,角度选在0~30°之间,每1度一道,共有30道,最后提取角道集的振幅和入射角信息,应用训练好的SVM 结果即可进行非线性AVO反演,反演结果见表 2所示.
|
|
表 2 层状介质AVO反演误差对比 Table 2 Performance analysis of AVO inversion error on layered medium |
从上表可看出,通过SVM 反演出的值与真实值较接近,绝对误差小,反演效果较好.
3.2.3 连续介质AVO 反演图 6是反演的结果,其中(a)中的灰色细线是实际垂直入射的ΔVP 曲线,黑色粗线是反演得到的垂直入射的ΔVP 曲线,(b)中的灰色细线是实际垂直入射的ΔVS 曲线,黑色粗线是反演得到的垂直入射的ΔVS 曲线,(c)中的灰色细线是实际垂直入射的Δρ 曲线,黑色粗线是反演得到的垂直入射的Δρ 曲线,从图中可以看出,反演得到的垂直入射ΔVP 曲线和ΔVS 曲线与实际垂直入射ΔVP、ΔVS 曲线几乎重合,Δρ 的反演效果也很好.
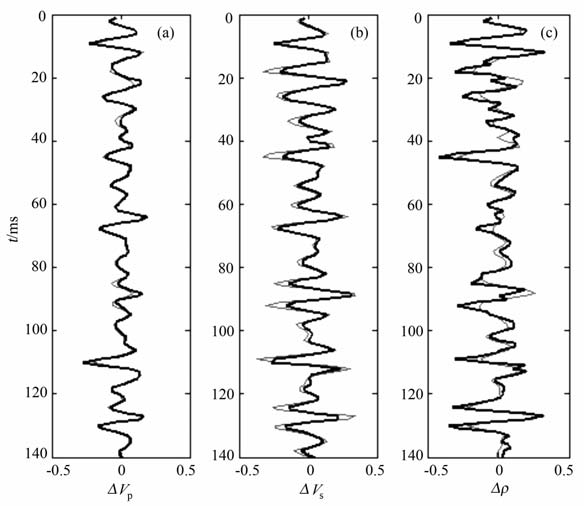
|
图 6 连续地层介质非线性AVO 反演 Fig. 6 Non-linear AVO inversion of continuous layered medium |
图 7所示为一实际CMP道集数据,长度为0.5s, 采样间隔4ms, 共有10道,图 8为此道集对应的密度和纵波速度曲线,第一条是密度曲线,第二条是纵波速度曲线,气层的位置如图中两直线所标.抽取0.48s至0.74s左右的数据进行非线性AVO 反演,图 9为抽取的角道集,图 10 为用SVM 方法进行反演的结果,图中第1 条为ΔVP 曲线,第2 条为ΔVS 曲线,第3 条为Δρ 曲线,从图中可以看出,在大约0.145s处(相对时间),ΔVP 曲线和Δρ 曲线数值减小,ΔVS 曲线数值增大,在大约0.155s处,ΔVP和Δρ 曲线数值增大,ΔVS 曲线数值减小,它们分别对应气层的顶部和底部,见图中两直线间所标部分.
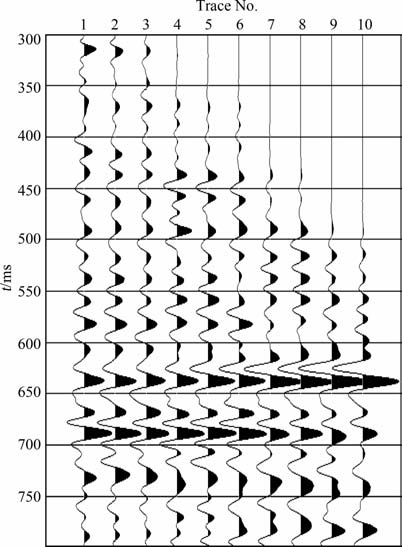
|
图 7 实际CMP道集 Fig. 7 Actual CMP gathers |
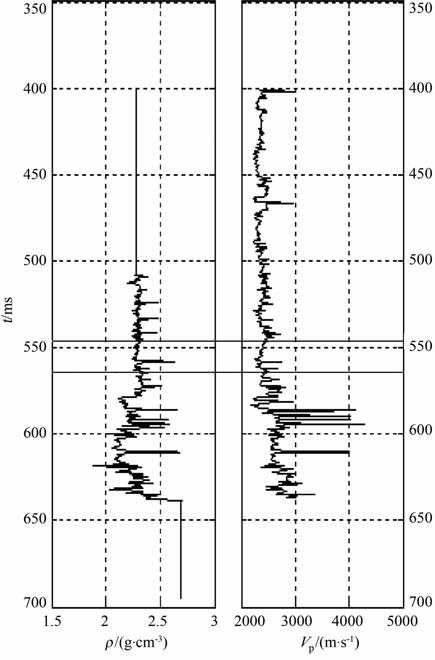
|
图 8 密度和纵波速度曲线 Fig. 8 Curves of density and P-wave velocities |
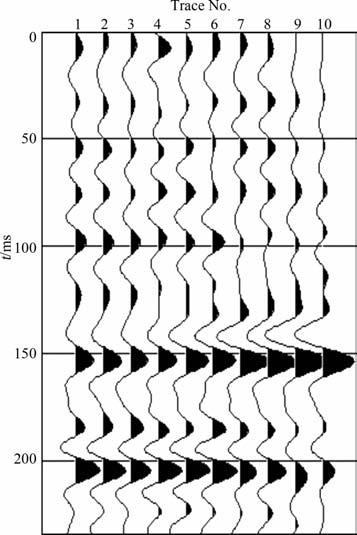
|
图 9 部分CMP道集 Fig. 9 Part of CMP gathers |
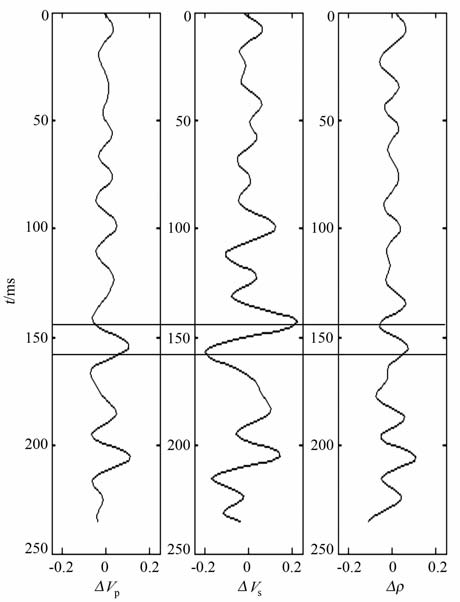
|
图 10 反演结果 Fig. 10 Results of inversion |
本文提出了一种基于支持向量机的AVO 非线性反演方法,支持向量机用于复杂非线性系统的参数估计还是一种较新的方法,通过正演计算得到的模型/数据对用来训练SVM,以完成非线性AVO反演;基于支持向量机的非线性AVO 反演速度快,只需训练一次,就可以解决反演问题,而其它的反演方法则需要多次迭代;该方法可以直接从合成记录中提取地层的弹性参数,不需要对Zoeppritz方程进行简化以及对弹性参数的任何假设,为AVO 非线性反演提供了一种全新的思路.通过对模型数据和实际资料的反演,证实了该方法的可行性与有效性.
| [1] | Ostrander W J. Plane-wave reflection coefficients for gas sands at nonnormal angles of incidence. Geophysics , 1984, 49(10): 1637-1648. DOI:10.1190/1.1441571 |
| [2] | Fatti J L, Smith G C, Vail P J, et al. Detection of gas in sandstone reservoirs using AVO analysis: A 3-D seismic case history using the Geostack technique. Geophysics , 1994, 59(9): 1362-1376. DOI:10.1190/1.1443695 |
| [3] | 李景叶, 陈小宏, 郝振江. 多波时移地震AVO反演研究. 地球物理学报 , 2005, 48(4): 902–908. Li J Y, Chen X H, Hao Z J. A study on multiple time-lapse seismic AVO inversion. Chinese J. Geophys. (in Chinese) , 2005, 48(4): 902-908. |
| [4] | 蒋鸿亮, 陈湛文, 陈小宏. 高分辨率AVO反演技术研究. 地球物理学进展 , 2006, 21(2): 478–482. Jiang H L, Chen Z W, Chen X H. High resolution research of AVO inversion technique. Progress in Geophysics (in Chinese) , 2006, 21(2): 478-482. |
| [5] | 殷八斤, 曾灏, 杨在岩. AVO技术的理论与实践. 北京: 石油工业出版社, 1995 . Yin B J, Zeng H, Yang Z Y. Theory and Practice of AVO Methods (in Chinese). Beijing: Petroleum Industry Press, 1995 . |
| [6] | Downton J E. Seismic parameter estimation from AVO inversion. Calgary: The University of Calgary, 2005 . |
| [7] | Downton J E, Lines L R. Three term AVO waveform inversion. // The 74th SEG Meeting. 2004, 215-218. |
| [8] | Shuey R T. A simplification of the Zoeppritz equations. Geophysics , 1985, 50(4): 609-614. DOI:10.1190/1.1441936 |
| [9] | Roden R, Latimer R. An introduction-Rock geophysics/AVO. The Leading Edge , 2003, 22(10): 987. DOI:10.1190/1.1623638 |
| [10] | Riedel M, Dosso S E, Beran L. Uncertainty estimation for amplitude variation with offset (AVO) inversion. Geophysics , 2003, 68(5): 1485-1496. DOI:10.1190/1.1620621 |
| [11] | Ursenbach C P. A non-linear, three parameter AVO method that can be solved non-iteratively. // The 74th SEG Meeting. 2004, 243-246. |
| [12] | Smith G C, Gidlow P M. Weighted stacking for rock property estimation and detection of gas. Geophysical Prospecting , 1987, 35(9): 993-1014. DOI:10.1111/gpr.1987.35.issue-9 |
| [13] | Stewart R R. Joint P and P-SV inversion. The CREWES Project Research Report , 1990, 2: 112-115. |
| [14] | Larsen J A. AVO inversion by simultaneous P-P and P-S inversion. Calgary: The University of Calgary, 1999 . |
| [15] | Margrave G F, Stewart R R, Larsen J A. Joint PP and PS seismic inversion. The Leading Edge , 2001, 20(9): 1048-1052. DOI:10.1190/1.1487311 |
| [16] | Duijindam A J W. Bayesian estimation in seismic inversion. Part I: Principles. Geophysical Prospecting , 1988, 36(8): 878-898. DOI:10.1111/gpr.1988.36.issue-8 |
| [17] | Buland A, Omre H. Bayesian linearized AVO inversion. Geophysics , 2003, 68(1): 185-198. DOI:10.1190/1.1543206 |
| [18] | 顾汉明, 江涛. 改进快速模拟退火方法进行AVO岩性参数反演. 地球科学 , 1999, 24(4): 418–422. Gu H M, Jiang T. Improvement of fast simulation annealing algorithm and its application on inversion of AVO lithological parameters. Earth Science (in Chinese) , 1999, 24(4): 418-422. |
| [19] | 冯瑞, 宋春林, 张艳珠, 等. 基于支持向量机与RBF神经网络的软测量模型比较研究. 上海交通大学学报 , 2003, 37(S1): 122–125. Feng R, Song C L, Zhang Y Z, et al. Comparative study of soft sensor models based on support vector machines and RBF neural networks. Journal of Shanghai Jiaotong University (in Chinese) , 2003, 37(S1): 122-125. |
| [20] | Vapnik V N. Estimation of Dependencies Based on Empirical Data. Berlin: Springer-Verlag, 1982 . |
| [21] | 张学工. 关于统计学习理论与支持向量机. 自动化学报 , 2000, 26(1): 32–42. Zhang X G. Introduction to statistical learning theory and support vector machines. Acta Automatic Sinica (in Chinese) , 2000, 26(1): 32-42. |
| [22] | 克里斯蒂亚尼尼. 支持向量机导论. 李国正, 王猛, 译. 北京: 电子工业出版社, 2004. Nello C. Introduction to Support Vector Machine (in Chinese). Li G Z, Wang M, translator. Beijing: Electronic Industry Press, 2004. |
| [23] | Vapnik V N. The Nature of Statistical Learning Theory. New York: Springer Verlag, 1995 . |
| [24] | Karl K, Kuzma H A, Rector J W. A comparison of standard inversion, neural networks and support vector machines. SEG/Houston 2005 Annual Meeting , 2005: 1725-1728. |
| [25] | Kuzma H A. A Support Vector Machine for AVO Interpretation. 73th Annual International Meeting SEG, Expanded Abstracts , 2003: 181-184. |
| [26] | Kuzma H A, Rector J W. Non-linear AVO inversion using support vector machines. 74th Annual International Meeting SEG, Expanded Abstracts , 2004: 203-206. |
 2012, Vol. 55
2012, Vol. 55



