2. 清华大学自动化系智能技术与系统国家重点实验室 清华信息科学与技术国家实验室(筹),北京 100084
2. State Key Laboratory of Intelligent Technology and Systems, Tsinghua National Laboratory for Information Science and Technology, Department of Automation, Tsinghua University, Beijing 100084, China
在地震勘探过程中,由于工作量的限制及施工条件的影响,使得地震数据沿空间方向不规则或出现稀疏采样现象,造成地震数据的道缺失、坏道或空间假频.地震数据的插值重建已成为地震勘探资料处理中最重要的问题之一.
目前,人们已提出多种地震数据的重建方法,如:基于非均匀Fourier变换的数据重建方法[1-3],是基于数学变换理论实现对不规则带限地震数据的规则化重建,不抗假频,不适合处理含有空间假频的地震数据;基于预测滤波的插值重建法[4-6],是根据地震道的低频信息提取高频数据的插值算子,能消除空间假频现象,但只能处理均匀采样的地震数据,不能用于不规则采样的地震数据的重建;基于多步自回归预测滤波的不规则地震数据抗假频重建方法[7-8],在实现不规则地震数据重建的同时,还能抗假频;还有基于数据变换的地震数据重建,如:Fourier变换[9-16],Radon 变换[17-18],曲波变换[19],SVD 分解法[20]等.
上述的地震数据重建方法主要考虑存有假频的数据或是不规则的采样数据的重建,对存有断层的地震数据在重建时如何保持其边缘特性考虑得较少.本文将边缘保持滤波方法[21]进行推广,提出一种边缘保持的插值重建方法.文章首先给出了地震数据边缘保持插值方法的理论;其次,通过对理论模型和实际资料的处理结果进行分析比较,说明该方法的优点;最后,给出了相关结论.
2 基本原理 2.1 一维信号的边缘保持插值假定y(i),i=1,…,N为待插值的一维信号,对应的空间坐标为x(i),i= 1,…,N.对于某一个待恢复的缺失采样点,存在多个包含(或邻近)它的信号片段用以估计.在本文提出的边缘保持插值算法中,首先采用多项式来拟合这些信号片段,然后选取拟合误差最小的信号片段来估计此缺失采样点,达到边缘保持的目的.设处理窗口长度为L,即每个信号片段包含L个已知信号采样点.对某待插值的采样点,其空间坐标为z,设其后边最近的已知采样点为第I个,共有L-1个信号片段包含采样点,并且,其前、后各有一个邻近的信号片段.在这L+1个信号片段中,第l个信号片段所包含的信号数据为
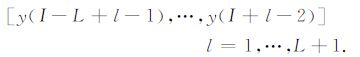
|
(1) |
对于第l个信号片段,通过m阶多项式来实现该信号片段的数据拟合,公式如下:
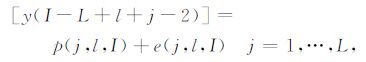
|
(2) |
其中,p(j,l,I)为m阶多项式(m<L),e(j,l,I)为拟合误差信号.p(j,l,I)定义如下:
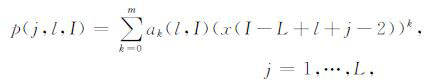
|
(3) |
式中,ak(l,I),k=0,…,m为m阶多项式系数.
公式(3)可以写为如下的向量矩阵形式:
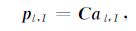
|
(4) |
式中,
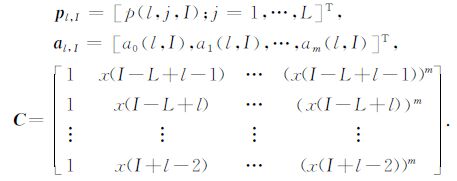
|
(5) |
为了求得多项式系数,需要优化如下目标函数,即最小化拟合误差:
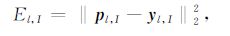
|
(6) |
式中,yl,I = [y(I-L+j+l-2);j=1,…,L]T.
采用最小二乘法,得到多项式系数如下:
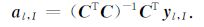
|
(7) |
根据式(7)获得的多项式系数,即可以得到对应第l个信号片段的拟合误差El,I.对所有的L+1个信号片段,可以获得L+1个拟合误差,其中对应最小拟合误差的信号片段被用来估计空间坐标为z的待插值采样点,估计值如下:
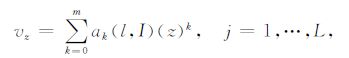
|
(8) |
重复上述处理过程,直到估计出所有待插值的缺失采样点.
2.2 二维信号的边缘保持插值对于一个N道,每道包含M个采样点的2D 地震数据u(i,j),(i=1,…,M,j=1,…,N),其每道对应的空间坐标为x(i),i= 1,…,N.对于空间坐标为z的缺失地震道上的第I个采样点,记为待插值点d,按照n=I+ (x(i)-z)/v(v为地震波的传播速度)线性抽取包含该点的1D 信号,抽取的1D信号可表示为
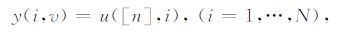
|
(9) |
式中,[n]为n 取整后的值.
通过式(9)获得1D 信号后,再通过上一节给出的一维信号的边缘保持插值方法对其进行处理,记待插值点d的1D 插值结果为s(d,v),其对应的拟合误差为E(d,v).通常,地震波的传播速度总是在一定范围之内,记传播速度的范围为V.以一定的速度步长,扫描速度范围V.对某一速度(即某一倾角方向),抽取对应的1D 信号,并利用一维信号边缘保持插值方法进行插值.完成所有倾角方向处理后,按照如下规则得到待插值点d的插值结果:
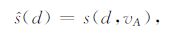
|
(10) |
式中的vA通过以下原则选取:
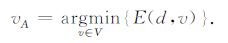
|
(11) |
为了检验本方法的有效性,将其用来处理了人工合成的1D 信号、2D 数据和实际地震数据.在2D数据处理实验中,为了说明本文方法具有保边缘、抗假频、不规则数据插值重建的特性,选择了规则空间采样的人工合成地震数据、实际地震数据及不规则空间采样的实际地震数据.并在规则空间采样数据的插值实验中与f-x预测滤波插值方法进行了分析比较.
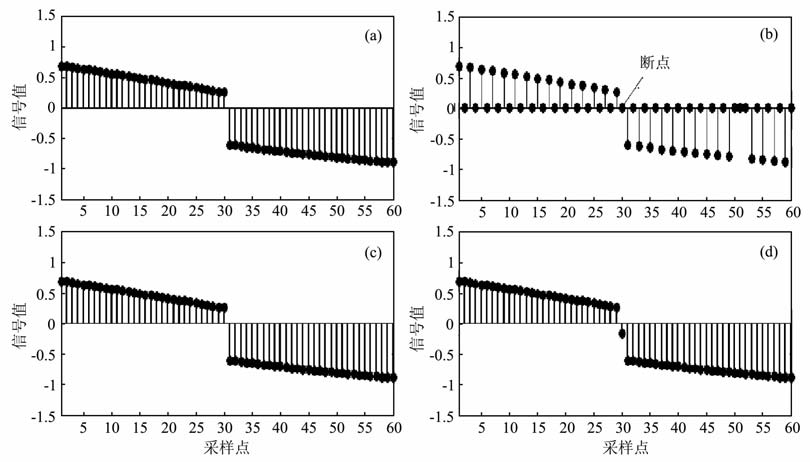
3.1 1D人工合成信号插值图 1给出了一个人工合成的1D 信号处理实例来说明基于边缘保持插值方法的优点.在这个实验中,边缘保持插值方法被用来从不规则数据中重建出原始信号.原始信号如图 1a所示;图 1b 为图 1a所示的信号剔除偶数点及第51和第53点后形成的不规则信号,用来实验所提出的插值方法;图 1c为利用边缘保持插值方法处理的结果,该方法中,取多项式的阶数为1,窗口长度为4;图 1d为利用线性插值处理的结果.根据实验结果来看,本文提出的方法比线性插值方法能更好的保持信号的边缘(断点)特性.
|
图 1 1D人工合成数据实验 (a)人工合成信号;(b)不规则抽取后信号;(c)本文方法处理结果;(d)线性插值处理结果. Fig. 1 A 1D synthetic signal test (a) Original signal; (b) Irregular signal extracted; (c) The result obtained by the proposed method;(d) The result obtained by linear interpolation method. |
需要指出的是,虽然本文提出的方法重建信号后能保持信号的边缘特性,但是如果待插值的采样点处于断点(如图 1b第30 个采样点)处,由于所提出方法不能判断该点是位于断点的前边还是后边,其插值结果可能会有误.如果这种插值错误存在,则断点的空间位置会发生一个空间采样点的位移,但不会模糊断层.如果断层有一定的宽度,则这个断层由两个边缘组成,在这种情况下,每个边缘的空间位置可能会发生一个空间采样点的位移.
3.2 2D人工合成数据插值为验证本文方法对2D 数据处理的有效性,首先对人工合成的二维数据进行实验.采用扫描直线在相邻两道的时差定义扫描方向,设扫描直线在左边道的时间采样点为K,扫描方向为Q,则扫描直线在右边道的时间采样点为K+Q.在实验中,选取了7个扫描方向为:[-3 -2 -10123],其单位是时间采样点,边缘保持处理窗口长度为5,多项式拟合阶数为1.
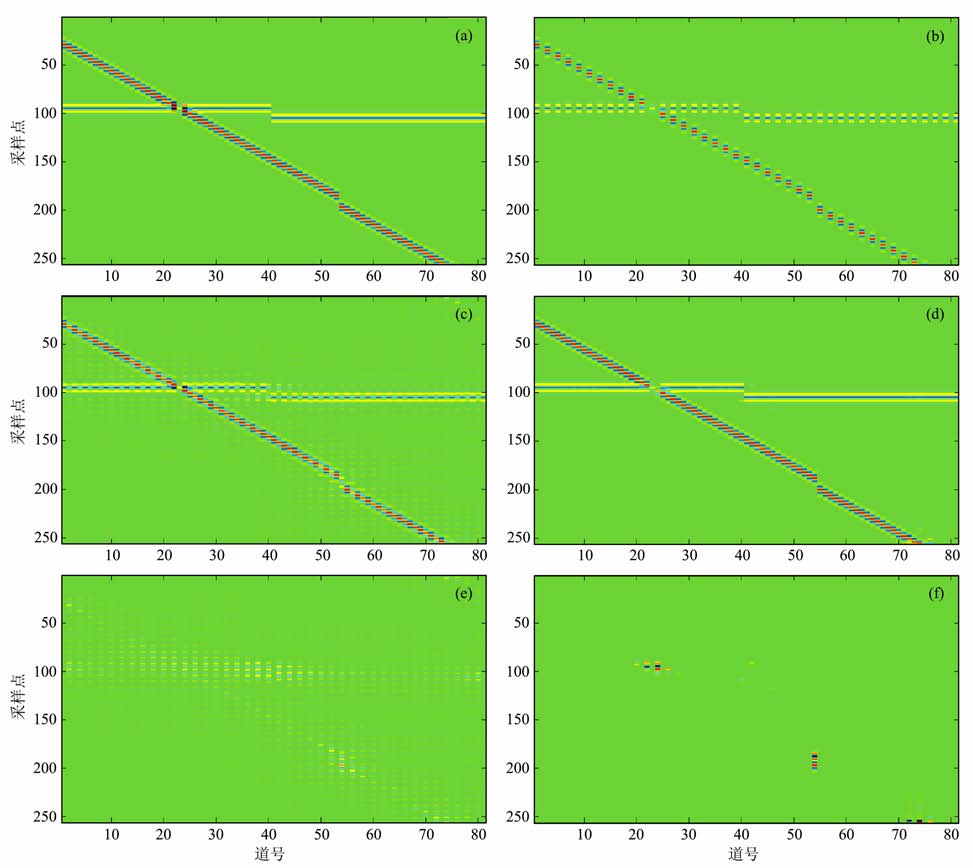
人工合成的2D 数据如图 2a所示,共合成80道地震记录,道间距为12.5 m, 每道包含256 个采样点,时间采样间隔为4ms.数据包含2个同相轴,且存在断层.图 2b为去掉偶数道后形成的规则降采样的地震数据,用来实验所提出的插值方法.图 2c给出了f-x方法插值结果.本文所提方法插值结果显示在图 2d中.f-x方法处理结果与真实数据的差如图 2e所示,而本文所提方法处理结果与原始数据的差如图 2f所示.
|
图 2 人工合成2D数据实验 (a)人工合成数据;(b)规则降采样后数据;(c)f-x方法插值结果;(d)本文方法插值结果;(e)f-x方法结果与真实数据之差;(f)本文方法结果与真实数据之差. Fig. 2 2D synthetic data test (a) Original data; (b) Regular down-sampled data; (c) The result obtained by method; (d)The result obtained by the proposed method; (e) The error between the true data and the result obtained by method; (f) The error between the true data and the result obtained by the proposed method. |
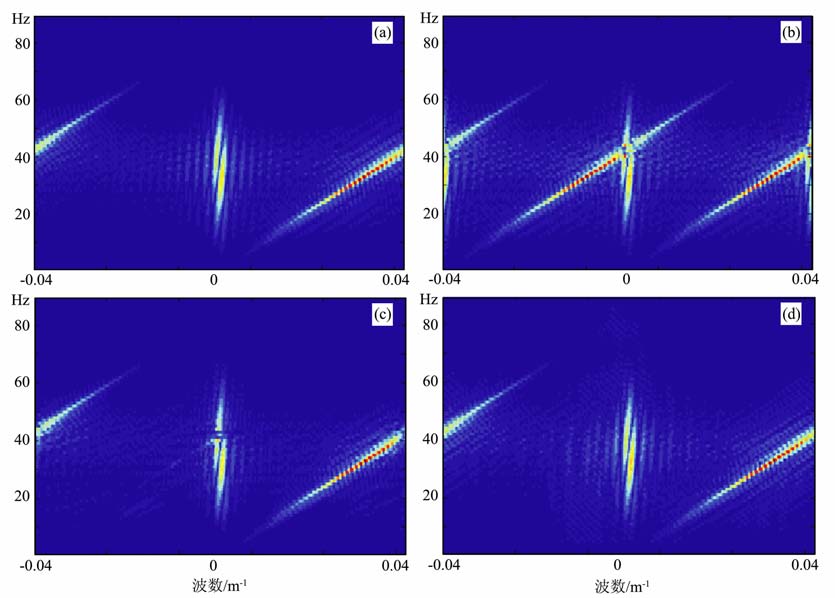
图 3(a-d)分别对应显示了对应图 2 (a-d)中数据的f-k谱.
|
图 3 对应图 2(a-d)中数据的f-k谱 (a)人工合成数据;(b)规则降采样后数据;(c)f-x方法插值结果;(d)本文方法插值结果. Fig. 3 The f-k spectra of the data shown in Figs, 2(a-d). (a) Original data; (b) Regular down-sampled data; (c) The result obtained by method;(d)The result obtained by the proposed method. |
对于规则数据的插值恢复,通过本文提出的方法和f-x方法处理结果的对比,可以看出:
(1) 本文提出的方法首先沿不同方向扫描抽取1D 信号,采用上述1D 边缘保持插值算法分别进行处理,得到沿不同方向的插值结果.对于任一待插值采样点,选取对应拟合误差最小的方向的插值结果作为最后输出的2D 数据的插值结果.与f-x预测滤波插值方法相比,能更好的保持信号的边缘特性.
(2) 比较图 3a、3c、3d, 可以发现,f-x预测滤波插值方法与本文提出的方法都可以有效地消除空间假象,但本文提出的方法所恢复的数据效果更好.
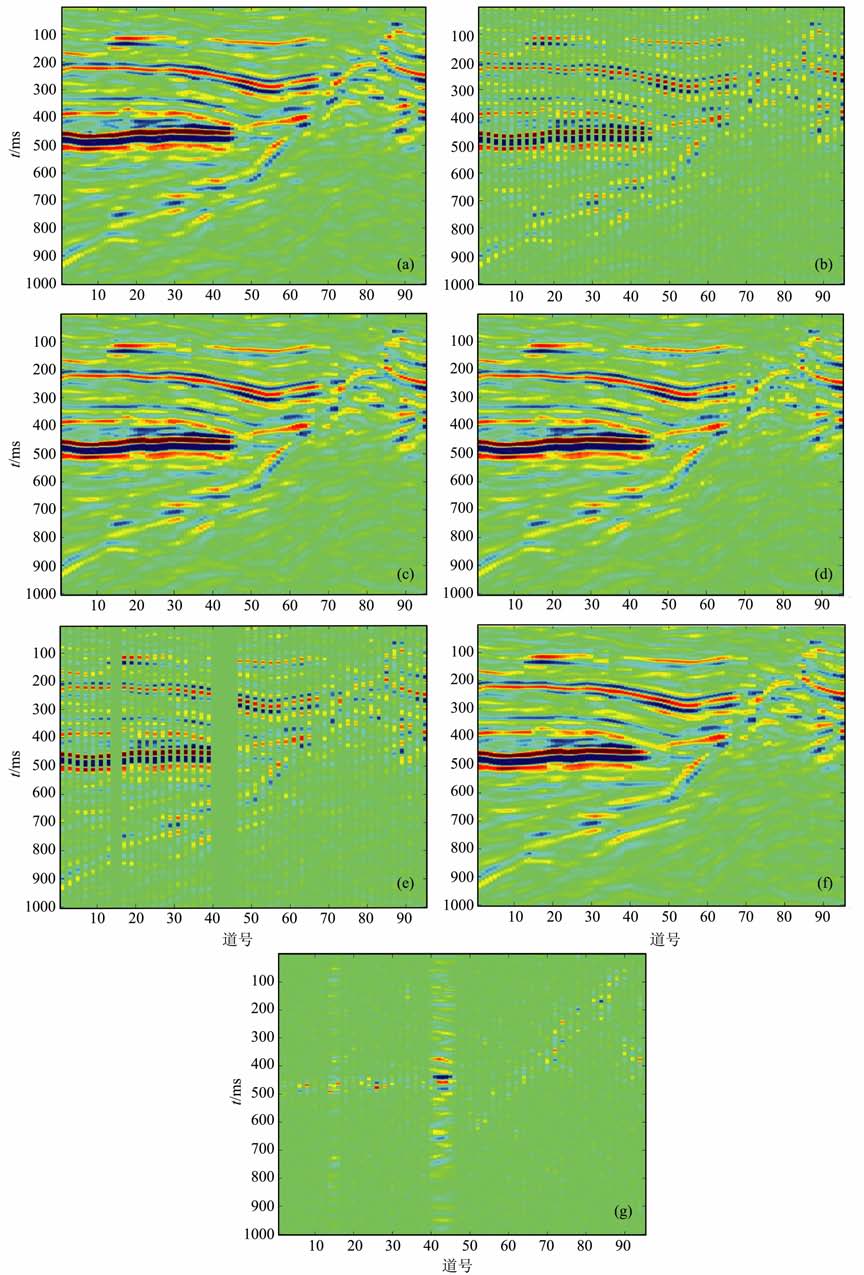
3.3 实际资料数据处理结果分析在理论分析的基础上,将该方法应用于二维的实际地震数据插值.用于处理的实际资料信号如图 4a所示,该信号的地震道数为95,道间距为12.5m, 每道的采样点数为500,时间采样间隔为2ms.图 4b 为图 4a所示的数据剔除偶数道后形成的规则地震数据,本文所提方法对规则地震数据插值处理后的结果如图 4c所示,f-x预测滤波插值方法对规则地震数据插值处理后的结果如图 4d所示.
|
图 4 实际资料处理实验 (a)真实数据;(b)规则抽取后数据;(c)本文所提方法处理结果;(d)f-x规则数据插值结果;(e)不规则抽取后数据;(f)本文所提方法不规则数据插值结果;(g)插值结果与真实数据之差. Fig. 4 A real-field data test (a) True data; (b) Regular data extracted; (c) The result of regular data obtained by the proposed method; (d) The result of regular data obtained hy f-xmethod; (e) Irregular data extracted; (f) The result obtained by the proposed method; (g) The error between the true data and the result obtained by the proposed method. |
图 4e为图 4a 所示的数据剔除偶数道、第15道、第40~46道后形成的不规则地震数据.本文所提方法对不规则地震数据插值处理后的结果如图 4f所示,本文所提方法对不规则地震数据插值与真实数据差如图 4g所示.
在实验中,我们选取了14 个扫描方向为[-9-8 -7-6-5-4-3-2-101234],单位是时间采样点,边缘保持处理窗口长度为5,多项式拟合阶数为1.
从图 4中可以看出,本文所提的方法可以实现不规则地震数据的插值,在对规则地震数据的插值重建时,本文所提的方法比f-x插值后能更好的保持数据的边缘特性.
4 结论本文提出了一种基于边缘保持的不规则地震数据的插值方法.对于1D 信号中的某一个待恢复的采样点,采用多个包含(或邻近)该点的信号片段,通过多项式拟合的方法来估计它,并选择拟合误差最小的信号片段的估计值作为其插值结果,达到边缘保持的目的.对于2D 地震数据,首先通过不同方向扫描,抽取1D 信号进行边缘保持插值处理,然后选取对应拟合误差最小的方向的插值结果作为最后输出的2D 数据的插值结果.相较f-x插值方法而言,所提不仅能实现不规则地震数据的抗假频重建,尤其对于具有断层的地震数据,插值重建后的数据依然能很好的保持其边缘特性.
| [1] | Zwartjes P M, Sacchi M D. Fourier reconstruction of non-uniformly sampled, aliased seismic data. Geophysics , 2007, 72(1): V21-V32. DOI:10.1190/1.2399442 |
| [2] | Liu B, Sacchi M D. Minimum weighted norm interpolation of seismic records. Geophysics , 2004, 69(6): 1560-1568. DOI:10.1190/1.1836829 |
| [3] | 孟小红, 郭良辉, 张致付, 等. 基于非均匀快速傅立叶变换的最小二乘反演地震数据重建. 地球物理学报 , 2008, 51(1): 235–241. Meng X H, Guo L H, Zhang Z F, et al. Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform. Chinese J. Geophys. (in Chinese) , 2008, 51(1): 235-241. |
| [4] | Spitz S. Seismic trace interpolation in the f-x domain. Geophysics , 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [5] | Naghizadeh M, Sacchi M D. Multistep autoregressive reconstruction of seismic records. Geophysics , 2007, 72(6): V111-V118. DOI:10.1190/1.2771685 |
| [6] | Naghizadeh M, Sacchi M. F-x adaptive seismic-trace interpolation. Geophysics , 2009, 74(1): V9-V16. DOI:10.1190/1.3008547 |
| [7] | 高建军, 陈小宏, 李景叶, 等. 不规则地震数据的抗假频重建方法. 石油地球物理勘探 , 2010, 45(3): 326–331. Gao J J, Chen X H, Li J Y, et al. Studies on anti-aliasing reconstruction method for irregular seismic data. Oil Geophysical Prospecting (in Chinese) , 2010, 45(3): 326-331. |
| [8] | 刘喜武, 刘洪, 刘彬. 反假频非均匀地震数据重建方法研究. 地球物理学报 , 2004, 47(2): 299–305. Liu X W, Liu H, Liu B. A study on algorithm for reconstruct of de-alias uneven seismic data. Chinese J. Geophys. (in Chinese) , 2004, 47(2): 299-305. |
| [9] | Duijindam A J W, Schonewille M A, Hindriks C O H. Reconstruction of band-limited signals, irregularly sampled along one spatial direction. Geophysics , 1999, 64(2): 524-538. DOI:10.1190/1.1444559 |
| [10] | Naghizadeh M, Sacchi M. On sampling functions and Fourier reconstruction methods. Geophysics , 2010, 75(6): WB137-WB151. DOI:10.1190/1.3503577 |
| [11] | 国九英, 周兴元. F-K域等道距内插. 石油地球物理勘探,1996,31(2):211-218. Guo J Y, Zhou X Y, Yu S P. Iso-interval trace interpolation in F-K domain. Oil Geophysical Propecting (in Chinese), 1996, 31(2):211-218. |
| [12] | Abma R, Kabir N. Comparisons of interpolation methods. The Leading Edge , 2005, 24(10): 984-989. DOI:10.1190/1.2112371 |
| [13] | Naghizadeh M, Innanen K. Seismic data interpolation using a fast generalized Fourier transform. Geophysics , 2011, 76(1): V1-V10. DOI:10.1190/1.3511525 |
| [14] | Dev A, McMechan G. Spatial antialias filtering in the slowness-frequency domain. Geophysics , 2009, 74(2): V35-V42. DOI:10.1190/1.3052115 |
| [15] | Gulunay N. Seismic trace interpolation in the Fourier transform domain. Geophysics , 2003, 68(1): 355-369. DOI:10.1190/1.1543221 |
| [16] | Abma R, Kabir N. 3D interpolation of irregular data with a POCS algorithm. Geophysics , 2006, 71(6): E91-E97. DOI:10.1190/1.2356088 |
| [17] | Trad D, Ulrych T, Sacchi M. Accurate interpolation with high-resolution time-variant Radon transforms. Geophysics , 2002, 67(2): 644-656. DOI:10.1190/1.1468626 |
| [18] | Darche G. Spatial interpolation using a fast parabolic transform. 60th SEG, Expanded Abstracts , 1990: 1647-1650. |
| [19] | Hennenfent G., Herrmann F. Simply denoise: Wavefield reconstruct via jittered undersampling. Geophysics , 2008, 73(3): V19-V28. DOI:10.1190/1.2841038 |
| [20] | 陆文凯, 李衍达. 利用SVD分解法对任意道距道内插. 石油地球物理勘探 , 1997, 32(4): 582–588. Lu W K, Li Y D. Any-interval trace interpolation using SVD method. Oil Geophysical Propecting (in Chinese) , 1997, 32(4): 582-588. |
| [21] | Lu Y H, Lu W K. Edge-preserving polynomial fitting method to suppress random seismic noise. Geophysics , 2009, 74(4): V69-V73. DOI:10.1190/1.3129907 |
 2012, Vol. 55
2012, Vol. 55


