2. 中国科学院地质与地球物理研究所, 北京 100029
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
太阳静日变化Sq是一种规则的地磁场日变化,由分布在向日面电离层南北半球中纬度区的两个电流涡产生[1-4].Sq主要起源于电离层E 区发电机电流[5],热层风和磁层电磁过程也有一定的贡献[6, 2, 7, 8].Sq的强度、相位和焦点存在明显的逐日变化[9-11],它们主要来源于电离层电导率、潮汐风场和太阳辐射条件等因素的影响[12, 13].另外,Sq还具有明显的季节变化和太阳活动周变化[1].
Sq的定义最早由Chapman用每月五天国际磁静日的平均值给出.他通过分析全球大量地磁台站的资料,得到了Sq的基本特征和规律.然而这种定义仅仅局限于给出每个月Sq场的平均状态,不能反映出Sq的逐日变化[1].为了能定量地描述Sq发电机电流强度及其逐日变化,徐文耀根据Hibberd(1981)[14]利用两个台站提取Sq变化的方法,提出了一种专门用来描述Sq发电机电流强度大小及逐日变化的活动指数.并且对1973年的资料进行了分析,结果表明Sq的逐日变化主要表现在强度上,并且具有2日、120 日和15 日等主要周期成分.与其他地磁活动指数不同,如Dst、AE/AU/AL 指数可以监测全天不同时段的环电流、极光电集流的强度及变化,由于Sq主要由白天电离层电流体系决定,因此由每天两个台站计算得到的Sq指数只能描述白天Sq电流体系的强度[15].
受电离层电磁环境、潮汐风场和太阳辐射条件等因素的影响和控制,许多研究表明Sq具有明显的季节变化和太阳活动周变化特征[16, 3, 17].本文的目的在于,计算分析Sq指数的长周期变化特征,考察其是否存在季节变化和太阳活动周变化的周期成分.使用的数据来源于INTERMAGNET 提供的1960-1980年中国广州(地理坐标23.1°N,113.3°E,简称GZH)和北京(40.0°N,116.2°E,简称BJI)两个地磁台站的地磁场X分量资料,计算1960-1980年的Sq指数,并研究其长周期成分的基本特征.
2 Sq指数的计算方法在地磁活动平静时期,地面上中低纬度区地磁场H/X分量的扰动主要来源于电离层发电机电流.当地磁场发生剧烈扰动时,磁层环电流是产生H/X分量扰动的主要来源,此时Sq场通常被淹没在剧烈的暴时变化中.为了能不仅仅局限于对地磁活动平静期间Sq场的研究,Hibberd(1981)提出,利用同一子午链中分别位于Sq焦点南北两侧的两个地磁台站的地磁场X或H分量的差值,不仅能够很好地提取Sq场,而且可以进行连续Sq场的研究.他指出,Sq焦点两侧台站的Sq场具有相反的时变结构,而其他来自磁层的扰动成分的时变结构和强度非常相似,因此将这两个地磁台站的地磁场分量相减,其差值就可以很好地反映Sq变化,有效地消除其他扰动成分的贡献[14].
基于Hibberd的这种方法,徐文耀(1992)利用中国广州和北京台1973 年的地磁场X分量记录,提出了一种新的地磁活动指数---Sq指数,用以描述Sq场的强度变化[15].
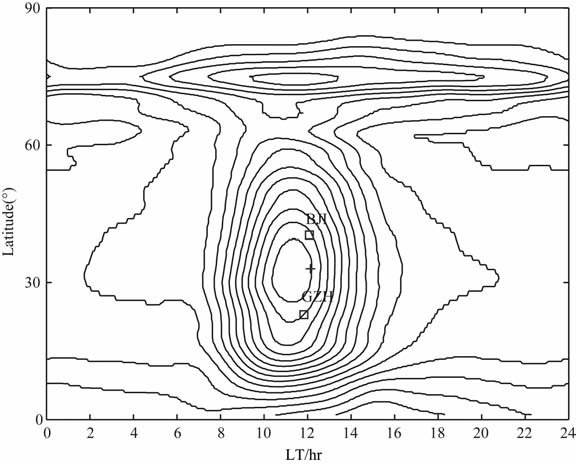
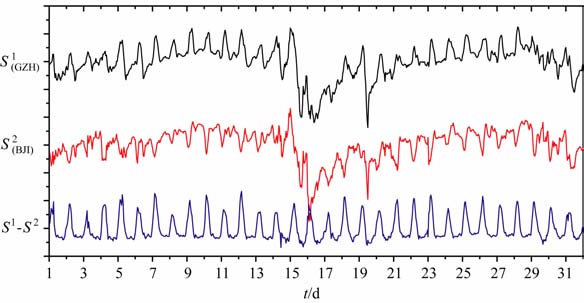
中国广州和北京地磁台位于同一子午链,其地理纬度分别为40.0°N 和23.1°N.图 1以2005年10月为例(由于1960-1980年期间INTERMAGNET公布的全球台站数量较少,且这里仅作示意图),给出Sq等效电流的空间分布,以便能更加清楚地认识Sq电流及台站的分布特点.可以看到,广州和北京台分别位于Sq焦点两侧,即Sq的焦点从两台站中间穿过.图 2 给出1960年7月广州和北京台的地磁场X分量曲线S1(GZH)和S2(BJI),以及二者的差值ΔS=S1-S2.显而易见,两个台站Sq场的时间变化形态相反.尽管单个台站日变化的形态和幅度变化很大,但是二者的差值曲线却显示出规则的变化形态,而只是在幅度上具有明显的逐日变化.即便在地磁活动剧烈时期,整个月份的夜间地磁场分量没有明显的逐日变化.这表明来自磁层电流的磁场成分得到了很好的消除,差值ΔS主要反映了电离层发电机电流在两个台站产生的磁场差异.同时ΔS的规则形态表明发电机电流的空间分布结构逐日变化不大,而强度具有明显的逐日变化.
|
图 1 2005年10月Sq等效电流分布 Fig. 1 Equivalent current of Sq on Oct.2005 |
地球磁场由地球内部的和外部的各种不同来源的磁场成分叠加而成.按照不同场源的时间变化特点,一般将地球磁场分为两部分:一是由地核发电机电流产生的主磁场和由地壳磁性岩石产生的局部异常场合称为稳定磁场;二是由分布在磁层-电离层空间电流体系及其在地球内部的感应电流所产生的磁场称为变化磁场.稳定磁场一般作为背景场扣除从而得到变化磁场,通常由年均值或月均值计算得到.
一个地磁台站的变化磁场可以写为
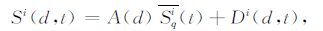
|
(1) |
式中,变量d和t分别表示日期和小时,上标i表示台站编号,Sqi(t)是台站i的平均Sq变化,由每月五天国际磁静日平均得到.A(d)表示每天Sq变化的相对强度,将其定义为“Sq强度指数",这里记作Asq指数.Di(d,t)表示除Sq场以外的其他磁扰变化.
同一子午线上两个台站的磁场变化差可以写为:
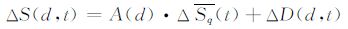
|
(2) |
其中
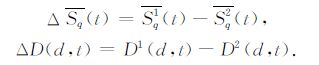
|
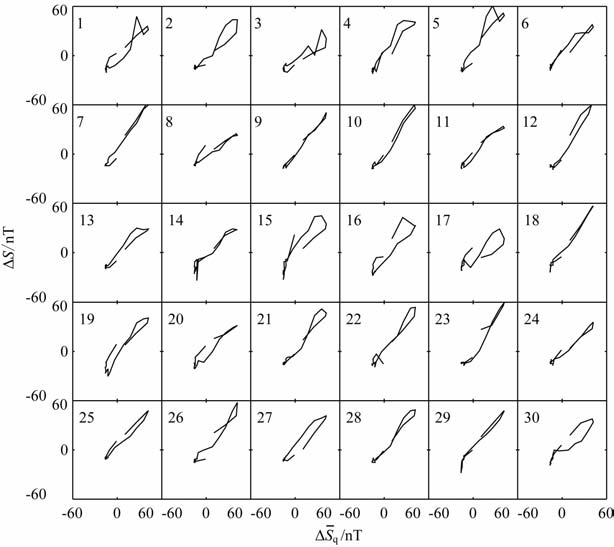
由图 2 可知,ΔD(d,t)$\ll $ A(d)ΔSq(t),因此ΔD(d,t)可以略去.用每月5个国际磁静日的资料可以求出该月的Sq1(t),Sq2(t)和ΔSq(t).ΔSq(t)与该月每天的ΔS(d,t)非常相似,其相似性可以从图 3中清楚看到.图 3 所示为平均ΔSq(t)与每日ΔS的变化关系,显而易见二者具有非常显著的线性关系.由(2)式求解ΔS与ΔSq(t)的拟和直线斜率就可以得到A(d),即Asq指数.
|
图 2 北京和广州地磁台1960年7月地磁场X分量以及二者的差值 Fig. 2 Geomagnetic X component in BJI and GZH observatories and its deviation on July 1960 |
|
图 3 1960年7月每日ΔS与ΔSq(t)的变化关系 Fig. 3 Variation of ΔS and ΔSq(t) on July 1960 |
以上阐明了Asq指数的计算方法,关于背景场的扣除需要指出的是,一方面由于背景场是稳定场,在短时间内几乎不变可以看作等于某一常数,因此其在线性拟合计算中只跟拟合直线的截距有关,对线性拟合斜率没有影响.也就是说,是否从地磁记录中消除背景场对于Asq指数的计算结果影响不大;另一方面,Sq指数的计算是利用两个子午台站X分量数据进行差值,差值过程自然也可以同时消除二台站的大部分背景场贡献,而未净部分在线性拟合计算中也只对截距产生贡献.
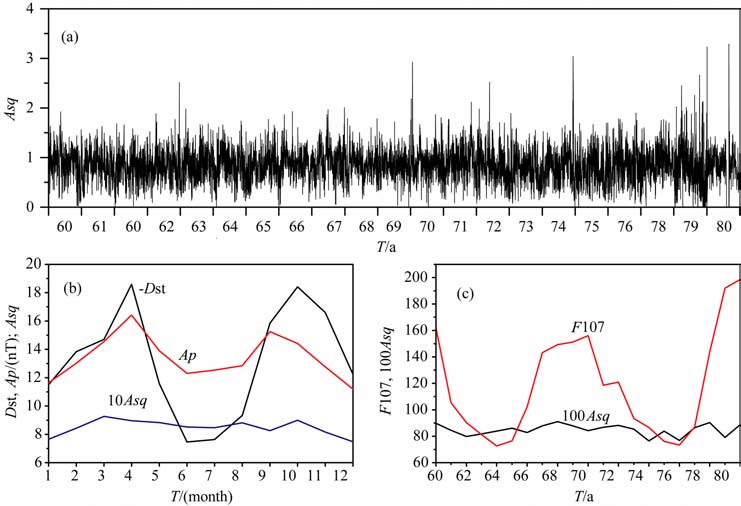
3 Sq指数及周期分析利用中国广州和北京地磁台1960-1980 年的地磁场X分量资料,计算得到相应的Asq指数.图 4给出Asq指数,Dst、Ap和Asq指数月均值,F107和Asq年均值变化曲线.从图 4a的Asq指数变化曲线可以看出,Sq的逐日变化非常显著,有时相邻两天Sq强度可能相差1倍以上.这表明利用每月五天国际磁静日平均值来消除Sq变化可能会产生很大的误差.
|
图 4 1960-1980年Asq指数曲线(a),Dst、Ap和Asq指数月均值曲线(b),F107和Asq均值曲线(c) Fig. 4 Asq curve (a) ,monthly value curves of Dst、Ap and Asq index (b),yearly vaule curves of F107 and Asq index in 1960 to 1980 |
从图 4b中Dst、Ap和Asq月均值曲线可以看出,Asq指数存在一定的春秋强夏冬弱的季节变化,但其变化幅度比Dst和Ap指数要弱得多.如图 4c所示,与F107年均值曲线相比,Asq年均值曲线也具有一定的11年太阳活动周变化,但是变化幅度要弱得多.
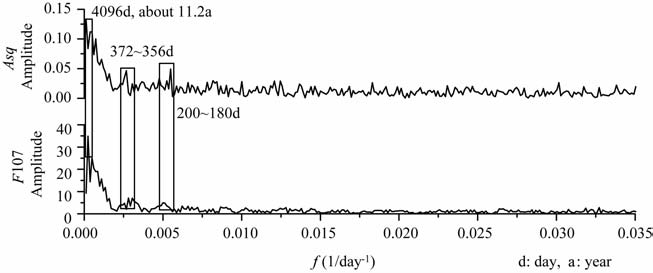
对Asq指数作傅立叶谱分析,结果如图 5 所示(本文只关注长周期变化,故只给出低频段部分),为了比较,图中同时给出了F107的傅里叶谱分析结果.可以看到,两条谱线具有相应的主要周期成分,包括有11年、年和半年等周期成分.对二者进行互相关分析,得到Asq和F107 的傅里叶频谱的相关系数约为0.78,呈显著的相关关系.这表明Asq指数与F107密切相关,其周期成分主要受到太阳辐射的影响.
|
图 5 F107和Asq指数的傅立叶频谱分布 Fig. 5 Fourier harmonics of F107 and Asq index |
Sq的日变幅和相位具有明显的逐日变化[18-20],这主要是由于受太阳辐射影响的电离层电导率和潮汐风电离层发电机电流的强度发生变化而产生的[12-13].Sq起源于太阳潮汐风的发电机效应.潮汐风的成分很多,其中对Sq贡献最大的潮汐风分量是(1,-2)模.其他一些潮汐风分量如(2,3),(2,4)和(2,2)模也会对Sq的日变幅和形态产生一定的影响[21-24].实际上,Sq还受其他一些磁扰成分的干扰,特别是在磁暴和亚暴发生时期.利用每月五天国际磁静日平均得到的Sq变化总是包含着其他一些非Sq成分的贡献,如电离层扰日发电机电流[25]、磁层顶查普曼-法拉罗电流[26]、场向电流及伴随的高纬电流体系等所产生的磁场[27-28].大量研究表明Sq具有非常复杂的逐日变化[27, 29-31].此外Sq的逐日变化还与太阳风之间存在着密切的关系[21, 24, 32-33].
Sq存在显著的季节变化和太阳活动周变化.由(2)式可知,ΔS(d,t)=A(d)·ΔSq(t)+ΔD(d,t).Hibberd利用ΔS每日极差值来研究Sq场的周期变化,其结果表明ΔS具有显著的季节变化和年变化.图 6 给出dSq、Asq和mSq的傅里叶频谱分布(这里dSq相当于ΔS,mSq定义为(2)式中每月ΔSq(t)的极差值).可以看出dSq具有显著的11年、年和半年变化的周期成分,此外还有周期为122天、91天和73天的主要周期成分.与之相比,Asq指数也存在11年、年和半年的周期成分,但是幅度较弱.对dSq和F107的傅里叶频谱进行互相关分析可得二者的相关系数约为0.82,的确好于Asq(上文已给出约为0.78).但是总体而言Asq和dSq与F107指数的频谱均呈显著的相关关系,表明Asq指数可以极大程度地反映出Sq的大部分周期变化信息.下面考察由每月平均ΔSq(t)的极差值(每日极大值与极小值之差)变化,其傅氏谱分布如图 6 中mSq所示.可以看到,与dSq类似,mSq具有显著的11年、年、半年的周期成分,此外还存在4个月的主要周期成分,这与dSq的122 天的周期成分相对应.将F107月均值与mSq的傅里叶频谱进行互相关分析可得,二者的相关系数为0.67,这表明ΔSq(t)也携带了Sq场的部分周期变化信息.
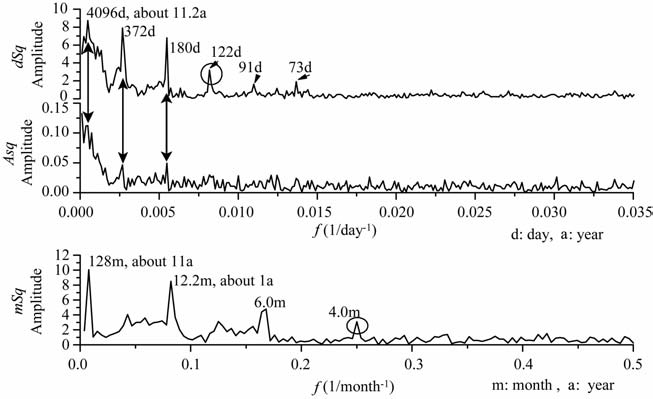
|
图 6 和mSg的傅里叶频谱分布 Fig. 6 Fourier harmonics of dSq^Asq and mSg |
以上分析表明,利用1960-1980年北京和广州的地磁场X分量资料计算得到的Asq指数具有11年、年和半年变化的主要周期成分,通过傅里叶分析表明其与F107 指数存在显著的相关关系,揭示了Asq指数与太阳辐射之间存在密切的相关关系.然而互相关分析表明,日变幅dSq与F107 的相关关系略强,这主要是由于在计算Asq指数的(2)式中,dSq与每月静日平均ΔSq(t)进行相关计算,ΔSq(t)也携带了部分Sq场的周期变化信息.
| [1] | Chapman S, Bartels J. Geomagnetism. London: Oxford University Press, 1940 . |
| [2] | Matsushita S. Solar quiet and lunar daily variation fields //Matsushita S, Campbell W eds. Physics of Geomagnetic Phenomena. New York: Elsevier, 1967: 301-424. |
| [3] | Campbell W H. The regular geomagnetic-field variations during quiet solar conditions //Jacobs J A ed. Geomagnetism. New York: Elsevier, 1989, 3: 385-460. |
| [4] | Campbell W. Introduction to Geomagnetic Fields. New York: Cambridge University Press, 1997 . |
| [5] | Tarpley J D. The ionospheric wind dynamo—II: solar tides. Planet. Space Sci. , 1970, 18(7): 1091-1103. DOI:10.1016/0032-0633(70)90110-8 |
| [6] | Hasegawa M. On the position of the focus of the geomagnetic Sq current system. J. Geophys. Res. , 1960, 65(5): 1437-1447. DOI:10.1029/JZ065i005p01437 |
| [7] | Matsushita S, Xu W Y. Equivalent ionospheric current systems representing solar daily variations of the polar geomagnetic field. J. Geophys. Res. , 1982, 87(A10): 8241-8254. DOI:10.1029/JA087iA10p08241 |
| [8] | Richmond A D. Modeling the ionosphere wind dynamo: a review. Pure Appl. Geophys. , 1989, 131(3): 413-435. DOI:10.1007/BF00876837 |
| [9] | Stening R, Reztsova T, Minh L H. Day-to-day changes in the latitudes of the foci of the Sq current system and their relation to equatorial electrojet strength. J. Geophys. Res. , 2005, 110: A10308. DOI:10.1029/2005JA011219 |
| [10] | Stening R, Reztsova T, Minh L H. Variation of Sq focus latitudes in the Australian/Pacific region during a quiet sun year. J. Atmospheric and Solar-Terres. Phys. , 2007, 69(6): 734-740. DOI:10.1016/j.jastp.2006.12.002 |
| [11] | Chen G X, Xu W Y, Du A M, et al. Statistical characteristics of the day-to-day variability in the geomagnetic Sq field. J. Geophys. Res. , 2007, 112: A06320. DOI:10.1029/2006JA012059 |
| [12] | Kirchhoff V W J H, Carpenter L A. The day-to-day variability in ionospheric electric fields and currents. J. Geophys. Res. , 1976, 81(16): 2737-2742. DOI:10.1029/JA081i016p02737 |
| [13] | Torta J M, Curto J J, Bencze P. Behavior of the quiet day ionospheric current system in the European region. J. Geophys. Res. , 1997, 102(A2): 2483-2494. DOI:10.1029/96JA03463 |
| [14] | Hibberd F H. Day-to-day variability of the Sq geomagnetic field variation. Aust. J. Phys. , 1981, 34: 81-90. DOI:10.1071/PH810081 |
| [15] | 徐文耀. Sq发电机电流的逐日变化和Sq指数. 地球物理学报 , 1992, 35(6): 676–684. Xu W Y. Day-to-day variability of the Sq dynamo currents and Sq index. Chinese J. Geophys. (in Chinese) , 1992, 35(6): 676-684. |
| [16] | Hibberd F H. The geomagnetic Sq variation-annual, semi-annual and solar cycle variations and ring current effects. J. Atmos. Terr. Phys. , 1985, 47(4): 341-352. DOI:10.1016/0021-9169(85)90014-5 |
| [17] | Nowoz·yński K. On regularities in long-term solar quiet geomagnetic variations. Earth and Planetary Science Letters , 2006, 241(3-4): 648-654. DOI:10.1016/j.epsl.2005.11.018 |
| [18] | Mayaud P N. Analyse morphologique de la variabilité jour-à-jour de la variation joumalière "régulière" Sr du champ magnétique terrestre, 2. Le système de courants CM (Régions non-polaires). Ann. Geophys. , 1965, 21: 514-544. |
| [19] | Butcher E C, Brown G M. The variability of Sq(H) normal quiet days. Geophys. J. R. Astron. Soc. , 1981, 64(2): 527-537. DOI:10.1111/j.1365-246X.1981.tb02681.x |
| [20] | Palumbo A. Lunar and solar daily variations of the geomagnetic field at Italian stations. J. Atmos. Terr. Phys. , 1981, 43(7): 633-642. DOI:10.1016/0021-9169(81)90135-5 |
| [21] | Brown G M, Williams W R. Some properties of the day-to-day variability of Sq(H). Planet. Space Sci. , 1969, 17(3): 455-470. DOI:10.1016/0032-0633(69)90076-2 |
| [22] | Malin S R C. Worldwide distribution of geomagnetic tides. Phil. Trans. R. Soc. London , 1973, 274(1243): 551-594. DOI:10.1098/rsta.1973.0076 |
| [23] | Winch D E. Spherical harmonic analysis of geomagnetic tides, 1964~1965. Phil. Trans. R. Soc. London, Ser. A , 1981, 303(1473): 1-104. DOI:10.1098/rsta.1981.0193 |
| [24] | Miyahara S, Ooishi M. Variation of Sq induced by atmospheric tides simulated by a middle atmosphere general circulation model. J. Geomagn. Geoelectr. , 1997, 49(1): 77-87. DOI:10.5636/jgg.49.77 |
| [25] | Blanc M, Richmond A D. The ionospheric disturbance dynamo. J. Geophys. Res. , 1980, 85(A4): 1669-1686. DOI:10.1029/JA085iA04p01669 |
| [26] | Olson W P. Introduction to the topology of magnetospheric current systems. Geophysical Monograph Series , 1984, 28: 49-62. |
| [27] | Takeda M. Day-to-day variation of equivalent Sq current system during March 11-16, 1970. J. Geomagn. Geoelec. , 1984, 36(5): 215-228. DOI:10.5636/jgg.36.215 |
| [28] | Xu W Y. Effects of the magnetospheric currents on the Sq field and a new magnetic index characterizing Sq dynamo current intensity. J. Geomagn. Geoelec. , 1992, 44(3): 449-458. |
| [30] | Suzuki A, Maeda H. Equivalent current systems of the daily geomagnetic variations in December 1964 //Data Book No. 1, World Data Center C2 for Geomagnetism. Kyoto: Kyoto University, 1978. |
| [30] | Stening R, Reztsova T, Ivers D, et al. A critique of methods of determining the position of the focus of the Sq current system. J. Geophys. Res. , 2005a, 110: A04305. DOI:10.1029/2005JA011219 |
| [31] | Takeda M. Time variation of geomagnetic Sq field in 1964 and 1980. J. Atmos. Sol.-Terr. Phys., , 199, 61(17): 1321-1322. |
| [32] | Matsushita M, Tarpley J D, Campbell W H. IMF sector structure effects on the quiet geomagnetic field. Radio Sci. , 1973, 8(11): 963-972. DOI:10.1029/RS008i011p00963 |
| [33] | Matsushita S. IMF polarity effects on the Sq current focus location. J. Geophys. Res. , 1975, 80(34): 4751-4754. DOI:10.1029/JA080i034p04751 |
 2012, Vol. 55
2012, Vol. 55

