2. 中国科学技术大学 蒙城地球物理国家野外观测站 地球和空间科学学院,合肥 230026;
3. 浙江华东工程安全技术有限公司,杭州 310014
2. Mengcheng National Geophysical Observatory,School of Earth and Space Science,University of Science and Technology of China,Hefei 230026,China;
3. Zhejiang East China Engineering Safety Technology Co. Ltd, Hangzhou 310014, China
岩体是一种复杂介质,宏观上含有大量的节理、裂隙;细观上含有微裂纹、微孔洞等缺陷,使得弹性波在岩体中的传播与衰减规律的研究非常困难.弹性波在地球物理探测、地震安全分析等领域具有广泛而重要的应用[1-2]:(1)地震波测试,频率范围约30~280Hz;(2)井间测试,频率范围约200~2300Hz;(3)声波测井,频率范围约8~24kHz;(4)实验室岩芯声波测试,频率范围约500~900kHz.以上四类实验技术在矿产勘探、石油勘探、无损检测等领域中已具有非常重要的地位.这些技术的核心就是不同频率的弹性波与岩体中各种尺度的特征“缺陷"发生相互作用,以及相应的波传播与衰减规律,以此来揭示岩体的物理力学特性.
过去的工作主要集中于弹性波与异质体的相互作用问题:如早期的弹性波与球状[3-4]、椭球状[5]、圆柱状[6-7]等规则异质体的相互作用,而后在Gurtin变分原理[8]的基础上发展到分析弹性波与多个不规则异质体的相互作用[9-11].相应的分析方法也得到了发展,从波特征函数展开法、积分方程法,发展到积分方程的Born近似、T 矩阵法、微扰法等,以及数值分析方法.这些理论方法促进了地球物理正演和反演分析理论和实验技术的迅速发展.
弹性波与裂纹的相互作用研究相对而言发展较慢.Hudson[12-13]研究了低裂纹密度下弹性波与币形裂纹的相互作用,分析了裂纹形状和分布对弹性波散射的影响;Achenbach[14-15]和Zhang[16]等采用射线理论,在Kramers-Kronig[17]关系的基础上研究了弹性固体中表面波与随机分布裂纹的相互作用.这些工作基本由弹性波与单裂纹的作用分析出发,裂纹基本假定为扁平或者币状,得到了一些有益的结论.但隧道、水利等工程中所涉及的岩体,是埋深比较浅的岩体,其内部所含裂纹形态复杂,裂纹内部经常含有泥土、碎屑、液体等其他介质,裂纹的分布呈现一些特殊的形式,如岩桥以及由岩桥组合成的雁型裂纹分布等,而且,随着时间的推移有些裂纹会逐渐张开.岩体中的弹性波表现出强频散和强耗散的特性,现场测试结果表明:无卸荷区域岩体的声波地震波波速比值在1.3 以内,而强卸荷区域岩体的声波和地震波波速的比值可以达到2.0 以上.对于浅埋岩体中弹性波的这种特性现有理论尚无法有效解决,本文将采用双裂纹模型对此进行研究.考虑多裂纹组成的复合体与弹性波的相互作用,在数学上是一个多连通域的问题,此处Gurtin变分原理存在理论分析的困难,已不能应用,需探索新的方法.为了克服此困难,本文提出一种新的分析思想,该方法将基于波动方程的Green基本解,应用边界积分方法,探讨由两个裂纹组成的体系与弹性波的相互作用的分析方法.
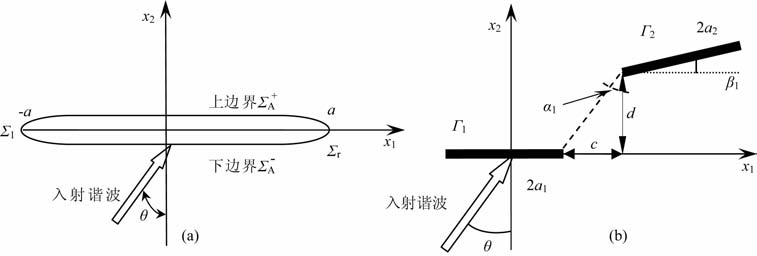
2 弹性波与岩体中双裂纹体系相互作用的频散效应分析图 1为弹性波与岩体中特征“缺陷"相互作用分析模型.一般情况,采用图 1a的简化构型[18],分析弹性波与单裂纹相互作用的情况,单裂纹的半长为a,具有上下表面ΣA+ 、ΣA- 和左右表面Σl、Σr, 对无厚度裂纹,Σl、Σr 可忽略,但当考虑裂纹内含夹杂物时,须考虑Σl、Σr.以裂纹中点为坐标原点,沿裂纹法向和切向建立正交直角坐标系.由于单裂纹模型产生的散射耗散较大,考虑到岩体多裂纹的特性,为考虑裂纹间弹性波散射效应的相互影响,本文采用图 1b的几何模型:岩体内部裂纹可简化为双裂纹体系来进行分析.
|
图 1 弹性波与裂纹相互作用的简化构型 (a)单裂纹模型;(b)双裂纹模型. Fig. 1 Simplitied configuration of interaction between elastic wave and cracks (a) Single crack model; (b) Double-crack model. |
双裂纹模型的两个裂纹长度分别为2a1 和2a2,两个裂纹方向夹角为β1,图中所示裂纹间距为d,两个裂纹尖端点相对角度为α1,Γ1、Γ2 分别为两个裂纹的边界面,以其中一个裂纹中心为参考点,建立如图 1b所示的坐标系.裂纹周边基体岩石为各向同性、线弹性体的.考虑一般情况,即弹性谐波P 波入射角为任意角度θ.
2.1 控制方程
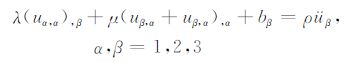
|
(1) |
岩石基体为弹性,一般采用虎克定律:
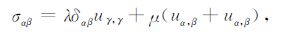
|
(2) |
其中,λ,μ 为拉梅常数,ρ、b分别为密度和体积力,δ为克罗内克符号.
当弹性波入射到裂纹面处时将产生散射,岩体内每一点总位移场u和总应力场σ 均为入射场和散射场的线性叠加,即:
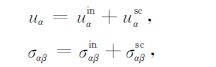
|
(3) |
其中uαin 为入射位移场,uαsc 为散射位移场,σαβin为入射应力场,σαβsc为散射应力场.
弹性谐波P波入射时,其位移场可表示为
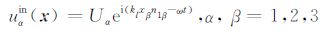
|
(4) |
其中kl为波数,ω 为圆频率,Uα 为入射位移幅值在α 方向的分量,n1β为入射波的方向,x为观测点与坐标原点的位移矢量,下标α 和β 分别表示沿不同坐标方向的分量.
入射位移场、散射位移场和总的位移场均满足波动方程,将其分别代入式(1)、(2),并忽略体积力,则有

|
(5) |
若考虑在裂纹面上为自由边界,则裂纹面上的边界条件为
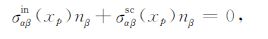
|
(6) |
其中,nβ为裂纹面的单位法线向量在β 方向的分量.单裂纹模型时:xp∈ (ΣA+ +ΣA-);若考虑双裂纹模型,则xp∈ (Γ1+Γ2).每一个Γ1 或Γ2 均包含上下表面ΣA+ 、ΣA- 和左右表面Σl、Σr.
若考虑裂纹内部含有流体时,裂纹界面可能承受一定的孔隙压力.裂纹面上的应力边界条件可表示为
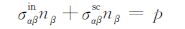
|
(7) |
式中p为裂纹面压力,裂隙内所含流体的孔隙压力,是其来源之一.
上述分析给出了弹性波作用与非均匀岩体问题的数学描述.最终问题归结为在满足裂纹面边界条件(6)或(7)下,求解波动方程(5),得到散射位移场的解,从而根据公式(3)和(1)得到问题的解.
2.2 Green函数解及频散方程采用Green函数解法,控制方程(5)的散射位移场为[14-15, 19]
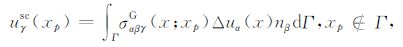
|
(8) |
其中,Δuα 为裂纹面张开位移,σαβγG 为应力Green 函数.同时,位移Green函数应满足:
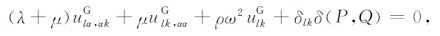
|
(9) |
式中,ulkG为在无限大平面弹性体内某一点P的xl方向有单位集中力作用时,在任意一点Q的xk方向上的位移分量解,其解为[19]
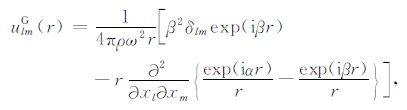
|
(10) |
式中,α2 =ρω2/(λ+2μ),β2=ρω2/μ,
r= (δlmxlxm)1/2,l,m=1,2,3.
联立式(8)和式(2),可得到散射应力场与应力Green函数的关系:
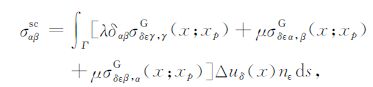
|
(11) |
式中,Γ 为裂纹边界,若为单裂纹:Γ =ΣA+ +ΣA-,对双裂纹模型:Γ =Γ1 +Γ2.
由以上分析,入射的位移场和应力场已知,当入射波为弹性谐波时,产生的散射场可由式(8)和式(11)确定.分析此二式,要得到散射位移场和应力场,必须先确定弹性谐波入射下的裂纹位移场.裂纹位移的求解则须结合裂纹面上的边界条件式(6)(裂纹内空)或式(7)(裂纹内含有液体等),采用数值积分的方法求解.由此,此问题可解.
将求解得到的裂纹位移Δu代入到散射位移场方程,并改用极坐标系,有:
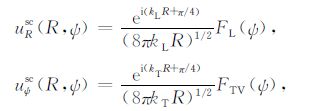
|
(12) |
式中,(R,ψ)为极坐标系,kL、kT 分别为纵波和横波的波数,FL、FTV分别为散射纵波和散射横波对应的散射幅度
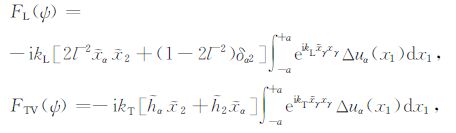
|
(13) |
其中
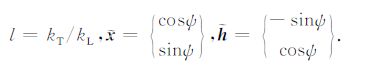
|
根据Foldy[20]理论,波数k对于裂纹密度进行复数域展开,则有效波数
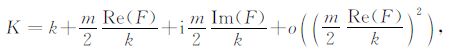
|
(14) |
式中,波数k和圆频率ω 满足关系

|
(15) |
有效波数定义为
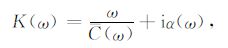
|
(16) |
其中C(ω)、α 分别为圆频率ω 对应的等效相速度和衰减系数.将式(15)、(16)代入式(14),可得圆频率ω 相对应的等效相速度的表达式:
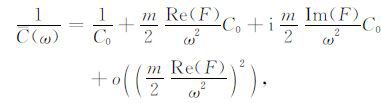
|
(17) |
式(17)中,m为双裂纹的密度,F为纵波或横波的散射幅度.等式左边C(ω)为考虑弹性波与岩体缺陷相互作用时的等效波速,等式右边第一项C0 为不含裂纹岩体中纵波或横波的波速,第二项反映了弹性波的频散效应,第三项反映了弹性波的衰减效应.这也表明:弹性波的频散效应和衰减效应之间是有紧密联系的,在线性黏弹性介质中速度频散和衰减是成对出现的[21],较大的衰减通常与较大的频散相关.
2.3 计算分析首先,求解弹性谐波作用下裂纹上各点的位移.当裂纹内部为自由边界时,由式(3)确定裂纹位移:
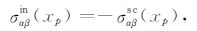
|
将式(11)代入得:
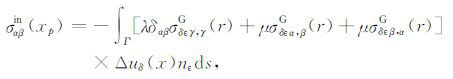
|
(18) |
其中,r= |x-xp|,xp为观测点.
如果观测点xp和边界上的点x重合,则
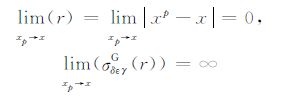
|
将会出现奇异性.为解决奇异性的问题,相关有意义的探讨已经很多.Sladak等[22]对积分变量采用优化变换,以提高计算精度;牛忠荣等[23]则引入接近度的概念,得到了一种精度更高的正则化计算方法.由此,本文采用边界元分析思想,沿双裂纹边界Γ1 +Γ2 离散单元,同时将式(18)离散为
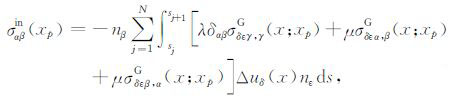
|
(19) |
其中,sj,sj+1 分别为第j个单元的两个节点在裂纹面上的局部坐标,N为单元总数.
3 含双裂纹岩体中频散效应分析 3.1 强相互作用下的频散分析双裂纹模型中裂纹间的相互作用对弹性波在岩体中的传播有一定的影响.弹性波与裂纹体系的相互作用,可通过式(19)求解裂纹位移.在求解过程中,认为任一裂纹面上点的位移不仅受该裂纹面上其他点的作用,而且还受其他裂纹面上点的位移的影响.这种考虑裂纹间相互影响的处理方式,我们称之为“强相互作用".基于此,对于平面应力状态,式(19)可化为
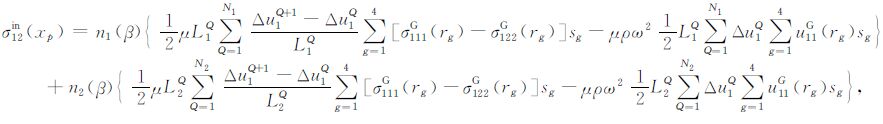
|
(20) |
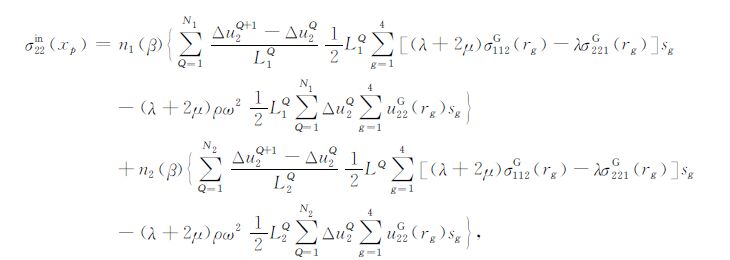
|
(21) |
其中,N1,N2 分别为裂纹1和2所划分的单元数,L1,L2 分别为裂纹1和2单元的长度,满足关系
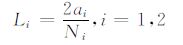
|
rg为高斯四点积分中积分点的整体坐标,满足关系
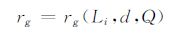
|
(22) |
具体表达式与坐标的选择、xp与x的相对位置有关,反映了组成双裂纹模型的两裂纹间的相互影响.
强相互作用下,根据式(20)、(21)求得裂纹的张开位移,将之依次代入式(14)、(17),就得到此条件下的频散关系.
3.2 线性叠加作用下的频散分析上述模型考虑两个裂纹的强相互作用,在理论上比较合理.但是考虑到现场岩体中,每一个裂纹的影响区域是有限的,实际上影响区域只在约3 倍裂纹长度范围以内[24],破碎岩体中这个区域更小.因此,对这种相互作用进行弱化,本文采用一种简单的“线性叠加"模式.
在线性叠加模式下,双裂纹模型区域每一点的散射位移场均为每条裂纹单独散射的线性叠加,一条裂纹上的张开位移不受另外一条裂纹的影响,即

|
(23) |
这种假定对于相隔较远的裂纹比较合适,但对于相隔较近的裂纹,裂纹中的相互影响不能忽略.为解决此矛盾,本文采用双裂纹模型,在模型内部裂纹采用强相互作用计算,以考虑局部裂纹的相互影响,而在双裂纹体系之间采用线性叠加模式分析,以考虑裂纹影响的局部性.
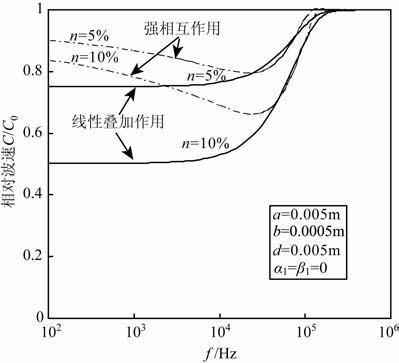
4 计算分析 4.1 强相互作用和线性叠加作用模型的比较图 2给出了“强相互作用"和“线性叠加"两种算法得到的弹性波与双裂纹模型相互作用的频散结果.在高频区域,采用线性叠加作用模型的计算结果与采用强相互作用模型计算结果基本一致.但是,在频率低于50kHz范围,两者差异很大.根本原因在于:“线性叠加法"只考虑裂纹对弹性波的单次散射,能量损耗大,而“相互作用法"在双裂纹模型内部对两个裂纹考虑了相互间的多次散射,虽然在模型之间仍采用“线性叠加法",但其散射损耗的能量已经大为降低.由于现场岩体情况差别较大,采用何种方法为好,尚需视具体情况进行分析.对于具一定裂隙分布强度的岩体而言,可采用双裂纹模型,但在模型内部采用强相互作用计算,在双裂纹体系之间采用线性叠加模式分析.
|
图 2 强相互作用对频散结果的影响 Fig. 2 Effects of strong interaction between cracks on the dispersion of rocks |
图 1b中双裂纹模型的几何参数很多,有裂纹间距d、模型中两个裂纹的长度、两裂纹的夹角等,一一进行分析篇幅很大,这里仅就部分参数进行分析,见图 3.
|
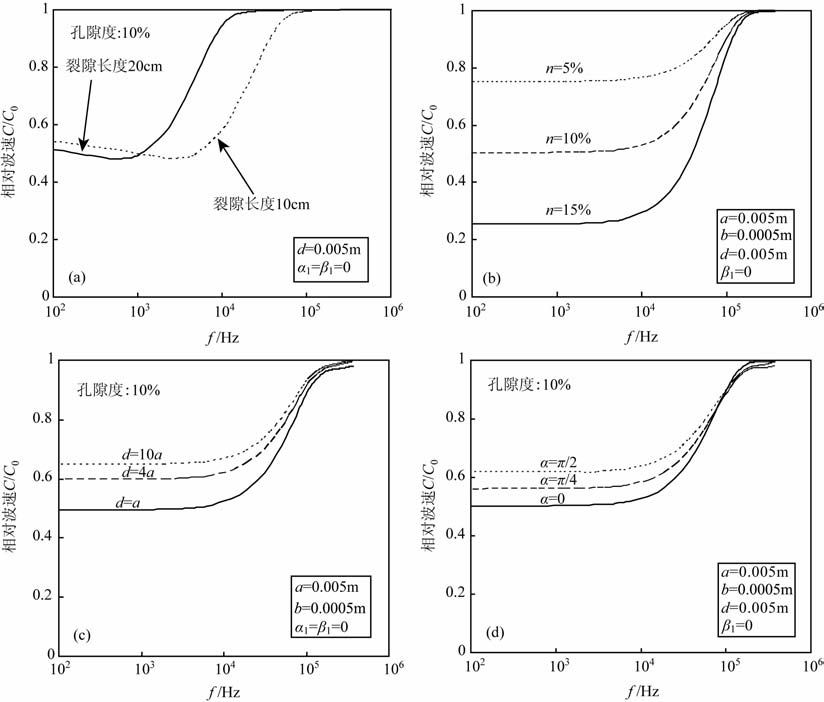
图 3 双裂纹模型参数对频散效应的影响 (a)裂隙长度对频散结果的影响;(b)孔隙度对频散结果的影响;(c)裂纹间距对频散结果的影响;(d)裂纹倾角对频散结果的影响. Fig. 3 Effects of parameters of the double-crack model on the dispersion of rocks (a) Effects of crack length on dispersion;(b) Effects of porosity on dispersion;(c) Effects of cracks distance on dispersion; (d) Effects of crack inclination angle on dispersion. |
图 3a反映了模型中裂隙长度对频散效应的影响,当裂隙长度从10cm 增至20cm, 其相应的相对速度最小和最大值两者几乎相同,但随着裂隙长度的增大,其相对波速剧烈变化的频率范围向低频移动,该范围的中心频率与fc =C0/D相近,其中:C0为完整岩石弹性波速,D为岩体中缺陷的特征长度,可取为裂纹平均长度.这同时也说明产生相对波速随频率剧烈变化的机制为共振散射.
图 3b给出了三种孔隙度(5%、10%和15%)的频散关系:随着孔隙度的增大,其频散效应显著增加.这同时也说明:随着双裂纹体系数量的增加,波传播过程中,裂纹系统产生的频散效应增强的同时,散射波的相互作用也愈来愈重要.当孔隙度较大时,裂纹间的相互作用不可忽略,线性叠加模式将不再合适,而须采用强相互作用的分析方法.
图 3c表明,改变模型中裂纹间距,从1cm 增加到10cm, 其相应的相对波速的最小值从0.49增加到0.65,即当裂纹间距较小时,裂纹间相互作用比较强,随着裂纹间距的增大,这种相互作用减弱,当裂纹间距很大时,其结果与单裂纹的一致.以上所用的倾斜角均为0°,即为垂直入射的情况.
图 3d 为固定裂纹间距为1cm, 使裂纹倾角(α 与图 1b中β1 对应)从0°增加到90°时频散关系的变化.随着角度的增加,相应的相对波速提高,频散效应减弱.事实上,当两个裂纹有一定夹角时,两个裂纹产生的散射波相互有影响,当夹角为0°时,这种影响最大.
总之,弹性波在岩体中的传播过程,其本质上是一个弹性波与岩体中双裂纹体系相互作用的过程,是一个双裂纹体系对弹性波能量吸收和转化的过程,在这个过程中,裂纹间距、裂隙倾角、孔隙度、相对入射角度等各种因素都会在不同条件下不同程度地影响其对能量的吸收,从而改变其频散程度.从图 3中分析结果来看,选择合适的参数,本模型可以分析强频散和强耗散的问题.
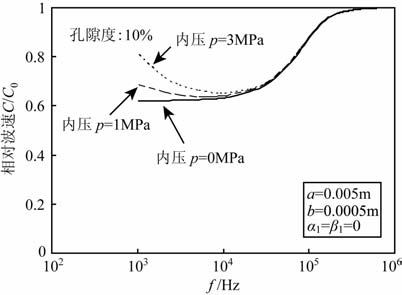
4.3 裂隙表面流体压力的影响岩体存在于各种压力环境中,多数岩体中存在有孔隙流体压力.针对孔隙度为10%的柱状节理玄武岩,图 4给出了其内双裂纹模型中裂纹受0MPa、1 MPa和3 MPa不同液体压力时的频散曲线.结果表明,孔隙流体压力在低频率范围内对频散特性影响很大,且随着孔隙流体压力的增大,其频散变化程度越强,但对高频率范围影响很小.
|
图 4 内压力对岩体频散效应的影响 Fig. 4 Effects of internal pressure on the dispersion of rocks |
这与岩体中等效介质理论和射线理论的适用性条件有些类似.低频时,等效介质理论比较合适;但高频时,射线理论比较合适.在计算的液体压力范围,内压力对于岩体的力学性能具有一定的影响.等效介质理论中岩体的性能与岩体骨架、孔隙、液体等都有关系,而射线理论中岩体的性能主要与岩体骨架有关,内压力对于等效介质简化的影响比较大,而对射线理论简化的影响较小,内压作用下弹性波与双裂纹体系的相互作用也与此相关.
4.4 现场岩体卸荷过程的分析卸荷是水利工程等工程领域关心的重要问题.作为初步探讨,假定岩体裂隙在卸荷过程中逐渐张开,从而通过组成岩桥的裂纹的张开位移和张开裂纹在总裂纹数中所占的比例来量化卸荷程度.下面进行了两种分析方法的探讨.
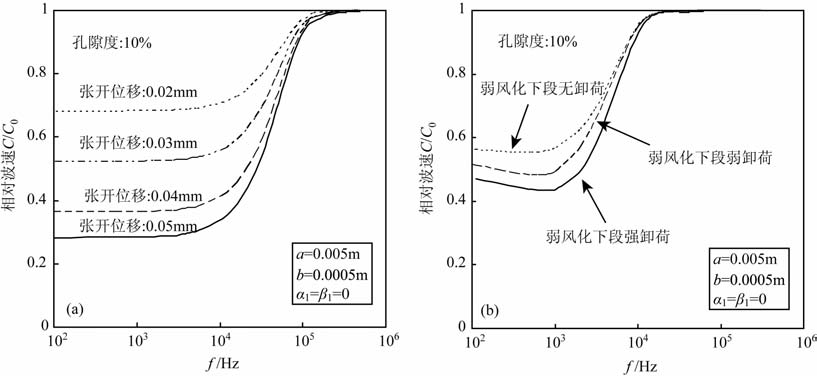
方法一,模型分析时,首先计算出入射波在裂隙表面产生的张开位移,然后统一叠加上由于卸荷产生的张开位移,进行频散效应的分析.图 5a为孔隙度10%时,不同张开位移对含随机分布单裂纹岩体弹性波波速的影响.裂纹张开位移分别为0.02、0.03和0.04mm 时,在地震波频率范围,相对波速分别为0.6814、0.5223和0.3628;对应主频25kHz声波,相对波速分别为0.7692、0.6487 和0.5251.随着裂纹张开位移的增大,岩体的频散特性愈加强烈.同时,随着卸荷程度的加强,岩体地震波波速明显降低,频散效应增强.
|
图 5 卸荷对岩体频散特性的影响 (a)方法一;(b)方法二. Fig. 5 Effects of unloading on the dispersion of rocks (a) Method a;(b) Method b. |
方法二,模型分析时,对某一岩性岩体调查其裂隙密度,对无卸荷、弱卸荷、强卸荷等不同卸荷程度的岩体调查裂隙的张开位移、张开裂隙占总裂隙条数的比例,由此采用第2 节中的方法进行频散效应的分析.图 5b为微风化柱状节理玄武岩不同卸荷程度的频散计算结果.裂隙密度为256 条/m2,无卸荷、弱卸荷和强卸荷情况对应的裂隙张开位移和裂隙张开率分别为:1mm 和10%、2mm 和30%,以及4mm和50%.三种卸荷状态,与主频25kHz声波和主频1kHz地震波对应的相对波速分别为0.7989、0.5626、0.7795和0.5179、0.7070、0.4556.同时随着卸荷时间的推移,波速也逐渐减小,但声波波速的减小幅度要比地震波减小的幅度小.合理地应用双裂纹模型进行卸荷岩体频散分析可以得到岩体波速随开挖卸荷时间的关系.
方法一是无差别的在所有双裂纹模型上叠加一张开位移,叠加位移的大小反映了卸荷的程度.方法二不仅考虑裂隙因卸荷产生的张开位移,而且统计不同卸荷程度的双裂纹模型中裂隙在总裂隙中的比例.同方法一相比,方法二在计算上要复杂得多,但其结果更符合工程实际.
5 结论为解决实际岩土工程中,由于开挖卸载、风化等原因造成的弹性波强频散和强耗散的问题,现有的理论模型都无法解释这一强频散和强耗散的实际问题,本文针对这一实际问题基于双裂纹体系模型,引入合适的裂纹面自由边界条件,采用基本奇异格林函数,通过傅里叶变换得到了整个频率域上的频散方程,计算了弹性波速随频率的变化关系.主要结论如下:
(1) 弹性波在含一定裂隙分布强度的岩体中传播时,当岩体孔隙度较小时,不考虑弹性波在裂隙间的多次散射作用,可采用单裂纹模型进行分析.但当孔隙度超过一定值时,可采用双裂纹模型进行分析.在模型内部考虑裂纹间的强相互作用,以分析弹性波在裂纹间的多次散射,在双裂纹体系之间采用线性叠加模式分析,不考虑双裂纹体系间的相互作用对弹性波传播的影响.
(2) 组成双裂纹模型的细微观特征对岩体频散特性具有重要影响.在一定范围内,随着孔隙率的增大,频散效应越显著;改变裂隙长度,其频散度亦随之变化.随着双裂纹模型中裂纹间距的增大,裂隙间相互作用减弱,岩体频散特性随之减弱,当裂隙间距超过一定值时,弹性波在裂隙间的多次散射作用可忽略,与单裂纹模型结果一致;改变模型中裂纹的相对倾角,当两裂隙平行时,频散效应最显著,垂直时,频散特性最弱.分析结果表明:双裂纹模型可以模拟岩体强频散和强耗散的问题.
(3) 孔隙流体压力的存在改变了岩体的力学性质,从而影响了岩体的频散特性.在低频率范围内对岩体频散特性影响很大,且随着孔隙流体压力的增大,其频散变化程度越强,但对高频率范围影响很小.
(4) 通过双裂纹模型中裂纹的张开位移和张开裂纹在总裂纹数中所占的比例两种方法来量化卸荷程度.随着裂隙张开位移的增大,岩体的频散特性愈加强烈;随着卸荷过程的推移,波速逐渐减小,但比较而言,高频对应的岩体波速(如主频25kHz的声波)的减小幅度要比低频对应的岩体波速(如主频500~1000Hz的地震波)减小的幅度小.
| [1] | 吴如山, 安艺敬一. 地震波的散射与衰减. 北京: 地震出版社, 1993 . Wu R S, A ki. Scattering and Attenuation of Seismic Wave (in Chinese). Beijing: Seismological Press, 1993 . |
| [2] | 楚泽涵. 声波测井原理. 北京: 石油工业出版社, 1987 . Chu Z H. Principle of Acoustic Logging (in Chinese). Beijing: Petroleum Industry Press, 1987 . |
| [3] | Ying C F, Truell R. Scattering of a plane longitudinal wave by a spherical obstacle in an isotropically elastic solid. J. Appl. Phys. , 1956, 27(9): 1086-1097. DOI:10.1063/1.1722545 |
| [4] | Nagase M. Diffraction of elastic waves by a spherical surface. J. Phys. Soc. Jpn. , 1956, 11(3): 279-301. DOI:10.1143/JPSJ.11.279 |
| [5] | Knopoff L. Scattering of compression waves by spherical obstacles. Geophysics , 1959, 24(1): 30. DOI:10.1190/1.1438562 |
| [6] | Tan T H. Diffraction of time-harmonic elastic waves by a cylindrical obstacle. Appl. Sci. Res. , 1976, 32(2): 97-144. DOI:10.1007/BF00383709 |
| [7] | Wang X M, Ying C F, Li M X. Scattering of antiplane shear waves by a circular cylinder in a traction-free plate. J. Acoust. Soc. Am. , 2000, 108(3): 913-923. DOI:10.1121/1.1287028 |
| [8] | Bhutani O P, Gupta N. Variational principle for linear initial value problems. International Journal of Engineering Science , 1982, 20(12): 1303-1309. DOI:10.1016/0020-7225(82)90056-8 |
| [9] | Sandhu R S, Pister K S. Variational principles for boundary value and initial-boundary value problems in continuum mechanics. Int. J. Solids Struct. , 1971, 7(7): 639-654. DOI:10.1016/0020-7683(71)90085-0 |
| [10] | 钟伟芳, 聂国华. 弹性波的散射理论. 武汉: 华中理工大学出版社, 1997 . Zhong W F, Nie G H. Scattering of Elastic Wave Theory (in Chinese). Wuhan: Publishing House of Huazhong University of Science and Technology, 1997 . |
| [11] | Datta S K, Shah A H. Scattering of SH waves by embedded cavities. Wave Motion , 1982, 4(3): 265-283. DOI:10.1016/0165-2125(82)90023-3 |
| [12] | Hudson J A. Wave speeds and attenuation of elastic waves in material containing cracks. Geophysics. J. R Astr. Soc. , 1981, 64(1): 133-150. DOI:10.1111/j.1365-246X.1981.tb02662.x |
| [13] | Hudson J A. Overall elastic properties of isotropic materials with arbitrary distribution of circular cracks. Geophys. J. Int. , 1990, 102(2): 465-469. DOI:10.1111/gji.1990.102.issue-2 |
| [14] | Achenbach J D. Wave Propagation in Elastic Solids. New York: North Holland, Amesterdam, 1973 . |
| [15] | Achenbach J D, Gautesen A K, McMaken H. Ray Methods for Waves in Elastic Solids. Boston: Pitman Press, 1982 . |
| [16] | Zhang C H, Gross D. Wave attenuation and dispersion in randomly cracked solids-I slit cracks and II penny-shaped cracks. Int. J. Eng. Sci. , 1993, 31(6): 841-858. DOI:10.1016/0020-7225(93)90097-E |
| [17] | Mavko, Ga ry, Mukerji. The Rock Physics Handbook: Tools for Seismic Analysis in Porous Media . Hefei: Publishing House of University of Science and Technology of China, 2008 . |
| [18] | 刘永贵, 徐松林, 席道瑛, 等. 节理玄武岩体弹性波频散效应研究. 岩石力学与工程学报 , 2010, 29(S1): 3314–3320. Liu Y G, Xu S L, Xi D Y, et al. Dispersion effect of elastic wave in jointed basalts. Chinese Journal of Rock Mechanics and Engineering (in Chinese) , 2010, 29(S1): 3314-3320. |
| [19] | Mura T. Mechanics of Elastic and Inelastic Solids 3: Micromechanics of Defects in Solids. Martinus Nijhoff Publishers , 1982. |
| [20] | Foldy L L. The multiple scattering of waves. Physical Review , 1945, 67(34): 107-119. |
| [21] | Batzle M L, Han D H, Hofmann R. Fluid mobility and frequency-dependent seismic velocity direct measurements. Geophysics , 2006, 71(1): N1-N9. |
| [22] | Sládak V Sládek J. On a new BEM formulation for 3D problems in linear elasticity. Engineering Analysis with Boundary Elements , 1992, 9(3): 273-275. DOI:10.1016/0955-7997(92)90101-C |
| [23] | 牛忠荣, 王秀喜, 周焕林. 三维边界元法中几乎奇异积分的正则化算法. 力学学报 , 2004, 36(1): 49–55. Niu Z R, Wang X X, Zhou H L. A regularization algorithm for the nearly singular integrals in 3-D BEM. Chinese Journal of Theoretical and Applied Mechanics (in Chinese) , 2004, 36(1): 49-55. |
| [24] | 杜善义, 王彪. 复合材料细观力学. 北京: 科学出版社, 1998 . Du S Y, Wang B. Micromechanics of Composites (in Chinese). Beijing: Science Press, 1998 . |
 2012, Vol. 55
2012, Vol. 55

