2. 清华大学计算机科学与技术系,北京 100084
2. Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China
弹性波方程是弹性介质中波传播所满足的偏微分方程.为了更好地指导地震勘探,我们需要求解这类方程.SH 波方程是波动方程中较为简单的一种,找出其解析解,尤其是找出层状介质中SH 波方程的解析解,有着重要意义.一方面,它可以反映SH 波的传播性质,如各种波的到时、振幅等;另一方面,可以用它来检验用于地震波传播模拟的各种数值方法(如差分方法[1-3]、有限元方法[4-6]等)的正确性,比较各种数值方法的优劣,指导我们更好地研究新的数值方法.用于检验数值方法正确性的传统办法是和精细网格下的数值结果进行比较[7-8],但是由于每一次迭代都会存在舍入误差,所以即便在网格很精细的情况下,得到的数值结果的误差也有可能较大,从而影响对新数值方法检验结果的正确评价.而且通常情况下,获得精细网格下数值结果所需要的计算量较大,而使用解析解方法可以直接计算在某一接收点处的解析解,其计算量相对很小,且计算结果更加精确,可以更好地检验数值方法的有效性.
SH 波方程的解析解问题既是研究地震波传播规律的基础问题,也是到目前为止尚未完全解决的重要理论问题.自20世纪50年代以来,许多著名学者在这方面已做了很多研究,并取得了不少研究成果.Ewing[9]研究了弹性波在层状介质中的传播规律.Hoop[10]利用Cagniard-de Hoop方法推导了均匀介质中声波方程的解析解.Bhattacharya[11-12]推导了弹性参数仅关于纵向有变化的介质中SH 波的解析解,但是他的推导中要求弹性参数关于深度z连续且至少一阶可导,而实际介质却存在明显的速度变化,这时弹性参数存在跳跃,既不连续也不可导,因此无法应用Bhattacharya的结果.Aki和Richards[13]使用Cagniard-de Hoop 方法推导了二维双层介质中反射波的解析解,但没有详细计算透射波的解析解.本文以波动理论为基础,使用Cagniard-de Hoop方法详细推导了比较常用的SH波方程的解析解,并和离散求解波动方程的经典数值算法修正的Lax-Wendroff方法(LWC)[1]以及最优近似解析离散化方法(ONADM)[3]模拟得到的结果进行比较,以验证解析解的正确性.
由于地球介质按其物性变化是分层的,具有明显的层状结构,而两层结构是研究多层结构的基础,所以研究波在具有一定速度反差的双层介质中的传播具有十分重要的意义.为此,本文针对双层介质中SH 波传播所满足的波动方程,利用Cagniard-de Hoop 方法[10]推导了其解析解.具体地说,我们选取震源为作用在z<0半空间的脉冲线震源,该半空间沿z=0与z>0的另一半空间紧密接触,在这样的双层介质中,我们使用Cagniard-de Hoop 方法,对SH 波方程关于时间t进行Laplace变换(t→s)、关于x进行Fourier变换(x→kx),再结合反射系数、透射系数,推导了SH 波在(kx,z,s)域的数学表达式,之后再对其进行Fourier逆变换,找出一条比较合适的积分路径,使得积分能够表达为关于t的Laplace变换的形式,最终给出双层介质中脉冲线震源情况下二维SH 波方程的解析解.在此基础上,推导了震源为一般线震源情况下双层介质中SH 波方程的解析解,并给出了直达波的到时、反射波的到时、出现首波的条件、首波的到时,以及在波场中直达波、反射波和首波的响应特征.
需要指出的是,通常情况下,我们得到的解析解是广义积分形式的,无法直接得到显式的表达式,需要使用数值积分方法计算接收点处的准确解.
2 二维SH 波方程的解析解 2.1 二维均匀介质中SH波方程的解析解二维均匀各项同性介质中SH 波方程为
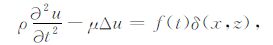
|
(1) |
其中,ρ 是介质的密度,u是位移,μ 是Lamé常数,μ =ρβ2,β 是波速,f(t)是震源强度随时间变化的函数,且满足当t<0时,f(t)=0.震源是线震源.
为了求解二维声波方程(1)的解析解,可以首先给出三维均匀介质情况下方程(1)的解析解,再利用降维法求解方程(1)的解析解[14].当然也可以直接利用Cagniard-de Hoop方法求出(1)式的解析解[10]:
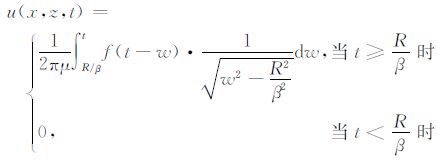
|
(2) |
其中,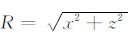
公式(2)给出了均匀各向同性介质中波动方程的解析解.但是实际地球介质却并非是均匀各向同性的,事实上,地球介质是具有明显的圈层结构的,所以研究波在多层介质中的传播更具实际意义.而两层结构是研究多层结构的基础,下面研究波在存在速度反差,且下层介质速度大于上层介质速度双层介质中的传播规律.
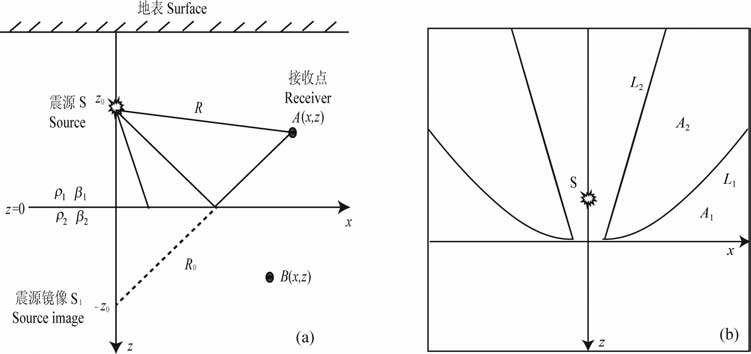
2.2 二维双层介质中SH波方程的解析解以下利用Cagniard-de Hoop 方法给出二维双层介质中SH 波方程的解析解.图 1a给出了震源、接收点和间断面等在x-z直角坐标系下双层介质模型的示意图.其中上、下两层介质沿分界面z=0密切接触,分界面两侧都是均匀各向同性介质,上层介质的密度和波速分别为ρ1 和β1,下层介质的密度和波速分别为ρ2 和β2,且β1 <β2,震源S位于上半空间,其坐标为(0,z0),且z0<0,接收点放在点(x,z).那么,当z<0时,接受点接收到的波包括直达波和反射波;当z>0时,接收点接收到的是透射波.下面分别就接收点位于上层和下层介质中这两种情况给出方程(1)的解析解.
2.2.1 直达波和反射波的解析解如果接收点在上层介质中(z<0),记为点A,此时接收点接收到的波包括直达波和反射波.下面首先给出震源为脉冲线震源时的解析解,再由格林函数法,给出震源为一般线震源时的解析解.具体推导过程见附录.
首先,当震源为脉冲线震源f(t)= (0,δ(t)δ(x)δ(z-z0),0),(z0 <0)时,得到的解析解如下:
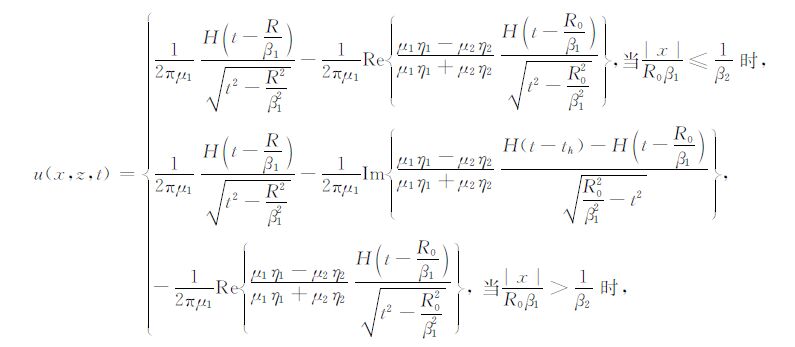
|
(3) |
其中,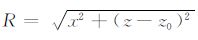
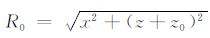
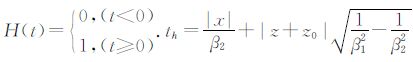
|
图 1 (a)双层介质模型;(b)波传播分析 Fig. 1 (a)八 two-layermediummodel; (b) Analysis of the wave propagation |
从(3)式可以看到,SH 波的解析解包括两种情况.当接收点A 与震源位置以及波速之间满足关系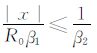
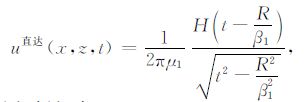
|
(4) |
反射波的解析解为

|
(5) |
从直达波解析解(4)和反射波解析解(5)可以看出,直达波的到时为R/β1,反射波的到时为R0/β1,这与实际地球介质中SH 波传播的走时完全一致.
当接收点、震源以及波速之间满足关系|x|/R0β1>1/β2时,从解析解(3)的表达式可看出,解析解中包含三项,分别表示直达波、首波[15-16]和反射波.换句话说,此时在接收点处能接收到三种波:直达波、首波和反射波.具体地,直达波和反射波的解析解表达式分别与方程(4)和(5)相同,而首波的解析解表达式为:
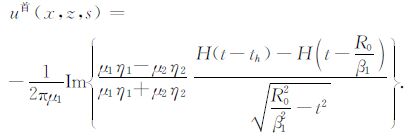
|
(6) |
从(3)式可以看出,直达波的到时为R/β1,反射波的到时为R0/β1,首波的到时为
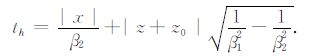
|
由于首波出现的条件是

|
所以只有在下层介质的速度β2 大于上层介质的速度β1 时才会出现首波.在上层介质中,显然有R/β1<R0/β1,这说明直达波要早于反射波到达上层介质中的接收点.另一方面,比较th和R0/β1,有th<R0/β1,所以在上层介质中的接收点处,首波也先于反射波被接收到.但是首波到时th可能大于也可能等于或小于直达波到时R/β1,这取决于两层介质的波速、接收点和震源的位置.图 1b是各种波传播分析的示意图,由于对称性,这里只对x> 0 一侧的情况加以说明,直线L2 和坐标轴x之间的区域是出现首波的区域(A1 和A2 部分),即满足条件|x|/R0β1>1/β2的区域,在该域中,位于曲线L1 以上的区域A2 中直达波早于首波到达,位于曲线L1 以下的区域A1 中直达波晚于首波到达.因此,在上层介质中任意一点,最先接收到的波是首波或直达波,最后接收到的波是反射波.
当震源为一般线震源f(t)= (0,f(t)δ(x)δ(z-z0),0)(z0 <0)时,可以用震源为单位脉冲震源时得到的解析解(3)式与函数f(t)关于时间t做卷积,从而得到震源为一般震源时的解析解.此时,在z< 0 一侧任一接收点(x,z)接收到的波解析解为
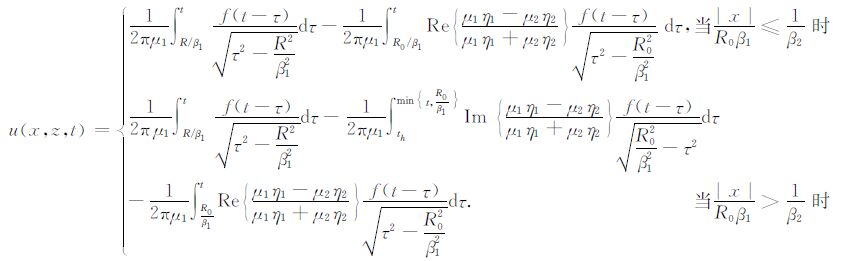
|
(7) |
在图 1a所示的坐标系下,若接收点位于z>0一侧,而震源位于z0 <0一侧,则在任一接收点(x,z)接收到的波为透射波.下面给出计算透射波解析解的具体推导过程.
当震源为单位脉冲线震源时,关于x做Fourier变换,关于时间t做Laplace变换后,可以得到波数域透射波的解析解为[13]
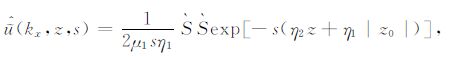
|
(8) |
其中,透射系数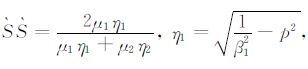
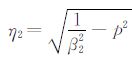
在本研究中,我们将通过使用Fourier逆变换和Laplace逆变换来推导波动方程(1)的时间-空间域的解析解.为此,首先将(8)式关于波数kx做Fourier逆变换,可得
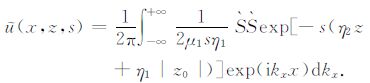
|
(9) |
由于被积函数的实部是关于kx的偶函数,被积函数的虚部是关于kx的奇函数,所以(9)式可写为
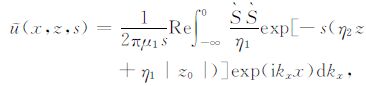
|
(10) |
将kx=isp代入方程(10),可得
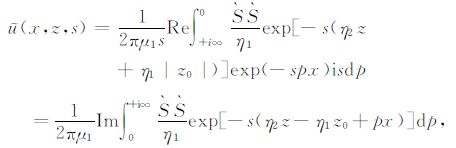
|
(11) |
令
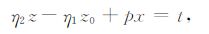
|
(12) |
且t为实数,则对任意t可由(12)式解出p=p(t),这就得到一条积分路径,根据对称性假设x≥0.且当p=0时,t=zβ2-z0β1.将(12)代入(11)得
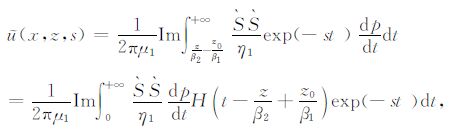
|
(13) |
根据Laplace变换的定义,由(13)可得
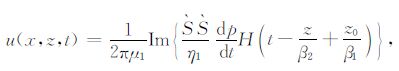
|
(14) |
其中,(14)式中需要的dp/dt可由表达式(12)得到:
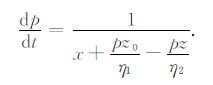
|
将dp/dt代入(14),则公式(14)即是单位脉冲线震源对应的透射波解析解.需要指出的是,在双层介质中,由于波速β1 ≠β2,因此难以从方程(12)得到p=p(t)的简单解析表达式,所以在实际计算时,我们建议利用数值方法来计算每一个时刻的p值.在本文的数值试验中,计算时刻t的p值时,我们将(12)式展开为包含p4,p3,p2,p的方程,使用Matlab命令求出关于p的四次方程的根,之后代入(12)式中验证,选取符合(12)式的根.当然也可以直接使用Matlab命令计算(12)式的零点.
当震源为一般的线震源(0,f(t)δ(x)δ(z-z0),0)时,只需将(14)式和震源函数f(t)做卷积,便可得到一般震源时的透射波解析解:
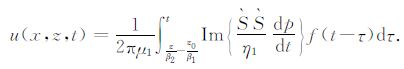
|
(15) |
下面通过与数值方法计算结果的比较来进一步说明本文所获得结果的正确性.由于本文给出的解析解是积分形式的,故在实际应用时,可以通过计算量很小、数值计算稳定、且计算误差可以通过积分步长控制的中矩形积分公式进行计算[17].为此,我们选取上下层速度反差较大的双层介质模型.具体地说,上层介质波速为β1=2.4km/s, 密度为ρ1=2.1kg/m3,下层介质的波速为β2=5.0km/s, 密度为ρ2=2.6kg/m3.数值计算的模型区域为0≤x≤25km, 0≤z≤25km, 双层介质的分界面位于地表下15km 处.空间步长为Δx=Δz=20 m, 时间步长为Δt=1 ms.震源位于地表下(12.5km, 14km)处.震源主频为f0=16 Hz.随时间变化的震源函数为
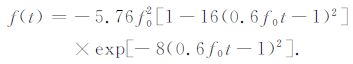
|
(16) |
为了验证解析解的正确性,我们给出了解析解与优化的近似解析离散化方法(ONADM)[3]和4阶Lax-Wendroff修正(LWC)[1]方法数值计算结果的比较.
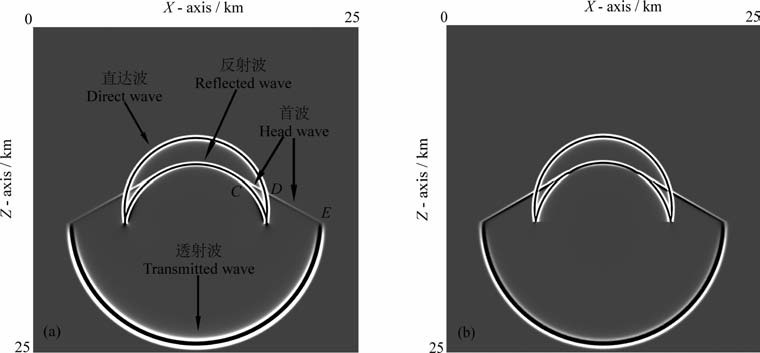
图 2a和2b分别是用ONADM 方法和本文给出的解析解得到的T=2.4s时刻的波场快照.为了便于理解,我们在图 2a中标出了各种波,可以看到在上层介质中存在直达波、反射波和首波,在下层介质中有透射波.可以看出图 2a中CE段出现了首波,CD段首波的到时晚于直达波但早于反射波,DE段首波的到时早于直达波和反射波,这与本文前面的理论分析得到的结果一致.比较图 2a和2b可以看到,利用本文解析解得到的波场快照与ONADM 数值方法所得到的波场快照一致,且各种波均比较清晰,这证明了解析解的正确性,同时也说明了ONADM 方法的正确性.
|
图 2 T=2.4 s时刻的波场快照 (a)ONADM方法得到的波场快照;(b)解析解得到的波场快照. Fig. 2 Snapshots of wave fields at T=2.4 s, generated by (a) the ONADM; (b) the analytical solution |
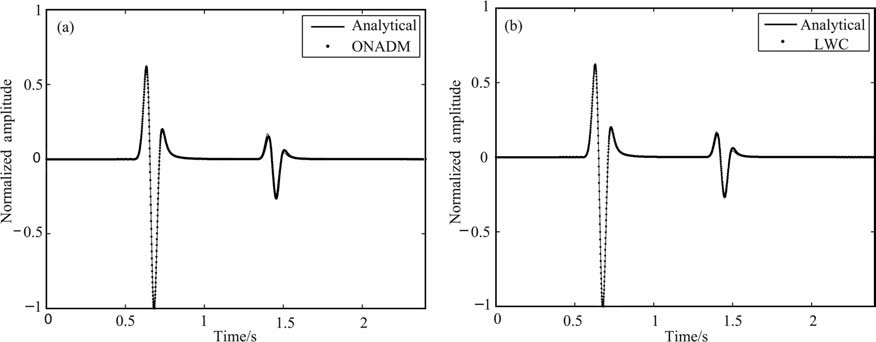
图 3给出了在接收点(13.3km, 12.9km)处接收到的波解析解与ONADM 方法[3]和4阶LWC方法[1]计算结果的比较.其中,图 3a和3b中的实线均为解析解,点画线是相应的数值方法计算得到的结果.可以看到,ONADM、LWC 两种数值方法计算得到的结果和解析解完全一致,即直达波和反射波的数值解和解析解完全一致,这进一步说明了本文所给解析解的正确性,也相互验证了数值方法(ONADM 方法和LWC 方法)的正确性.
|
图 3 接收点(13.3 km, 12.9 km)处接收到的直达波和反射波波形图 (a)解析解与ONADM方法数值结果的比较;(b)解析解与4阶LWC方法数值解的比较.图中实线表示解析解,点画线表示数值解. Fig. 3 Waveforms received at the receiver (13.3 km, 12.9 km) (a) The comparison between analytical solution and the numerical solution computed by the ONADM; (b) The comparison between analytical solution and the numerical solution computed by the fourth-order LWC.The solid line denotes the analytical solution, and the dot line denotes the numerical solution. |
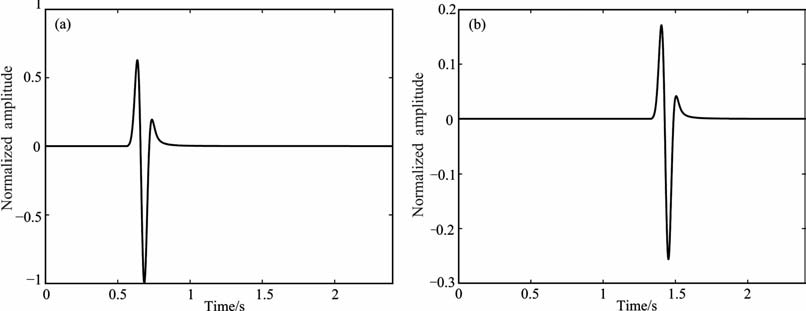
另一方面,此时接收点、震源、波速之间的关系(见图 1a)满足|x|/R0β1<1/β2,根据解析解(7)中首波出现的条件|x|/R0β1>1/β2,可以知道在接收点(13.3km, 12.9km)处不会接收到首波,解析结果和数值结果的比较(图 3)也证实了这一点.图 4给出了将接收点(13.3km, 12.9km)处接收到的解析解波响应分开显示的波形图.其中,图 4a和4b分别是直达波响应和反射波响应波形图.直达波到时是0.568s, 反射波到时是1.334s.这与利用速度、距离和时间之间的关系直接计算得到的结果一致.
|
图 4 在接收点(13.3km, 12.9 km)处接收到的直达波(a)和反射波(b) Fig. 4 The direct wave (a) and reflected wave (b) received at the receiver (13.3 km, 12.9 km) |
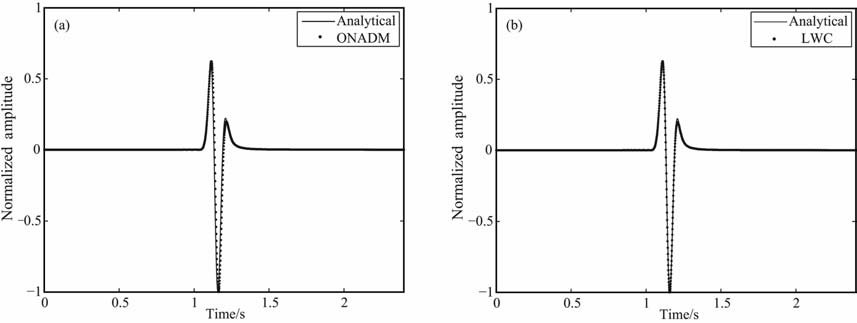
图 5是位于下层介质中接收点(13.5km, 18km)处接收到的透射波的解析解与ONADM 和4 阶LWC两种数值方法计算结果的比较.其中,图 5a和5b中的实线为解析解,点画线是数值方法计算的结果.图 5 表明,在精细网格条件下,ONADM和LWC 方法计算的数值结果与解析解一致,这说明本文获得的透射波解析解正确.
|
图 5 接收点(13.5 km, 18 km)处接收到的透射波波形图 (a)解析解与ONADM方法的比较;(b)解析解与4阶LWC方法的比较.其中,实线是解析解,点画线是数值结果. Fig. 5 The transmitted wave received at the receiver (13.5 km, 18 km) (a) The comparison between the analyticaf solution and the numericaf solution computed by the ONADM; (b) The comparison between the analyticaf solution and the numericaf solution computed by the fourth-order LWC.The solid line denotes the analytical solution, and the dot line denotes the numerical solution. |
本文结合波动理论和Cagniard-de Hoop方法,利用Fourier变换和Laplace变换等数学理论详细推导了二维双层介质中SH 波方程的解析解,给出了震源为脉冲线震源时的反射波解析解和透射波解析解,同时也给出了震源为一般线震源时SH 波方程解析解.在此基础上,我们研究了首波出现的条件,以及直达波、反射波、首波的到时.并利用本文给出的结果与精细网格条件下数值模拟方法(ONADM 和4阶LWC)计算得到的波场和波形图进行了比较.结果表明,我们给出的解析解与数值解结果一致,这说明本文给出的解析解是正确的.这些结果有望在检验各种数值新方法的正确性、评判数值方法的优劣、以及地震波传播理论分析等方面得到应用.
附录 SH 波方程解析解的推导过程在本附录中,我们将采用Cagniard-de Hoop方法[10]的基本思想,通过严格的数学推导给出双层均匀各向同性介质中,震源和接收点同时位于上层介质时(如图 1a所示),单位脉冲线震源激发条件下,在上层介质中任一接收点A(x,z)所能接收到的直达波和反射波解析解表达式.此时入射SH 波满足方程:
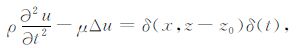
|
(A1) |
其中z0 <0.
通过对方程(A1)关于空间x做Fourier变换,关于时间t做Laplace变换,将空间-时间域(x,z,t)变到(kx,z,s)域,于是在z< 0 一侧的入射波经变换后可表示为[13]
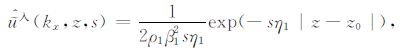
|
(A2) |
其中,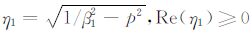
当波传播到z=0的间断面时,波的反射和透射系数分别为:
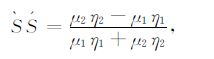
|
(A3) |
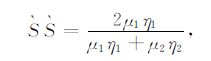
|
(A4) |
其中,
同样地,通过Fourier变换和Laplace变换,我们可得在z<0一侧所接收到的直达波和反射波,在(kx,z,s)域内的解析表达式为
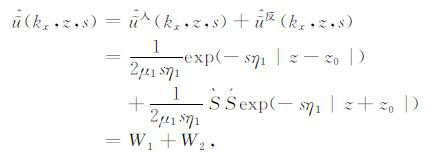
|
(A5) |
其中,W1 和W2 分别表示(A5)式中的第一项和第二项.第一项为直达波,第二项为反射波.
对(A5)式中所表示的直达波W1 进行逆变换得到直达波的解析解为
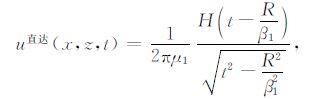
|
(A6) |
其中,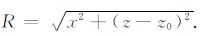
下面对(A5)式中表示反射波的项W2 进行逆变换.这里计算接收点(x,z)满足x≥0的情况,根据对称性,可以得到x<0时的解析解.
首先对反射波项W2 进行Fourier逆变换,得到
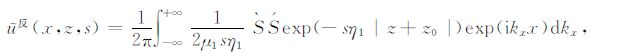
|
(A7) |
再将(A3)代入(A7),可得
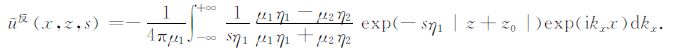
|
(A8) |
由于kx=isp,η1 和η2 是关于p的偶函数,从而η1 和η2 也是kx的偶函数,所以(A8)中被积函数的实部为kx的偶函数,虚部为kx的奇函数,因此,有
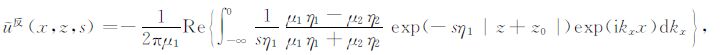
|
(A9) |
将kx=isp代入方程(A9)的右端,得
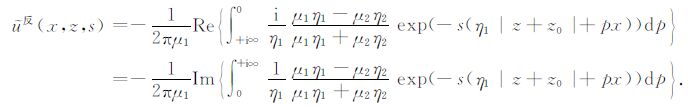
|
(A10) |
在方程(A10)中,令
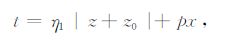
|
(A11) |
求解(A11)得到Cagniard路径[13]如下:
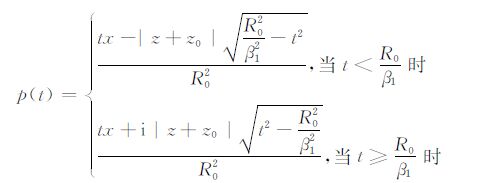
|
(A12) |
将(A12)代入(A11)中,得到

|
(A13) |
方程(A12)两边对t求导,并结合(A13)式可得
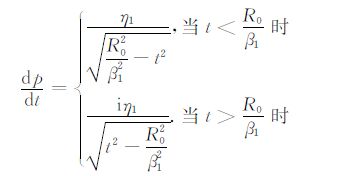
|
(A14) |
由方程(A11)可得,当p=0时,t=|z+z0|/β1.下面对(A10)中被积函数的虚实情况进行讨论.因为β1<β2,所以1/β1>1/β2.于是由方程(A13)知,当t<R0/β1时,η1 =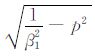
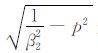
(1) 当|x|/R0β1≤1/β2时
在这种情况下,如果t<R0/β1,则η2 是实数.此时,将(A11)代入(A10)可得
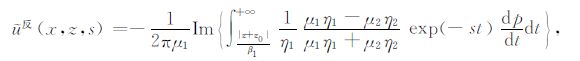
|
(A15) |
再将(A12)-(A14)代入方程(A15)中,并通过整理得到
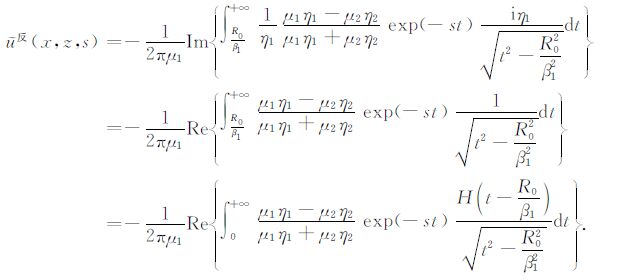
|
(A16) |
根据Laplace变换,由(A16)式可得,当|x|/R0β1≤1/β2时,反射波在时间-空间域的解析解为

|
(A17) |
(2) 当|x|/R0β1>1/β2时
在这种情况下,当0≤p<1/β2时,η1 和η2 均为实数;当1/β2<p<|x|/R0β1时,η2 为纯虚数,η1 为实数.当p=1/β2时,将其代入(A11)可得[13]
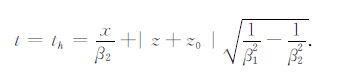
|
(A18) |
另外,将(A11)代入(A10)可得
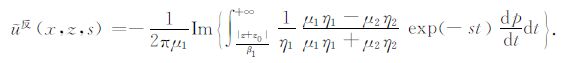
|
(A19) |
首先证明|z+z0|/β1<th.由于沿着由(A12)式所确定的路径进行积分,当0≤t≤R0/β1时,p为实数,且p(t)随t单调递增,当t=0时,p=-|z+z0|/R0β1,当t=R0/β1时,p=x/R0β1.所以在此段路径上t也是随p单调递增的,且根据(A11),p=0时,t=|z+z0|/β1,当p=1/β2时,t=th=x/β2+|z+z0|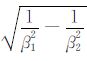
由(A19)和(A12)-(A14)可得到
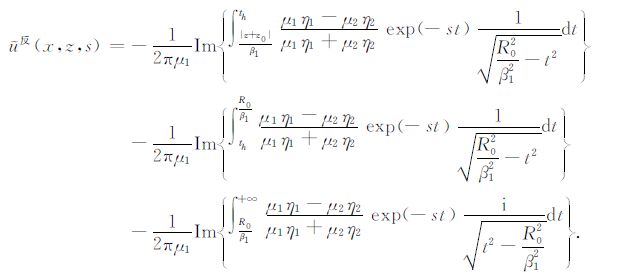
|
(A20) |
根据前述对被积函数虚实情况的讨论和(A20)中第一项的被积函数为实值函数,所以取虚部为0.由此方程(A20)右端实际只包含后面两项,再对其进行整理可得
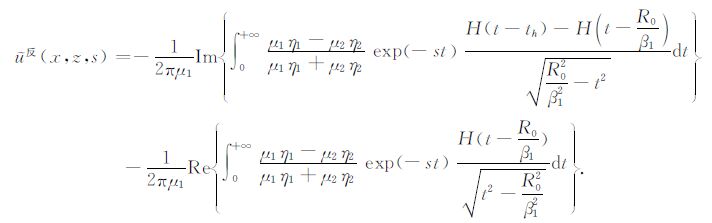
|
(A21) |
利用Laplace变换,由(A21)式可得反射波在时间-空间域的解析解为:
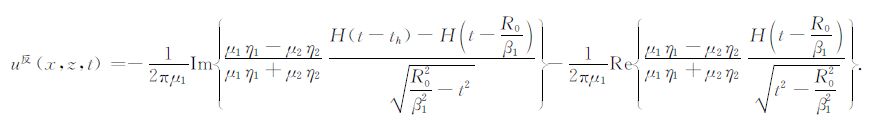
|
(A22) |
所以,综合表达式(A6)、(A17)、(A22),可以得到当震源为脉冲线震源时,在z<0一侧,接收点(x,z)接收到的波解析解表达式为(3)式.
| [1] | Dablain M A. The application of high-order differencing to the scalar wave equation. Geophysics , 1986, 51(1): 54-56. DOI:10.1190/1.1442040 |
| [2] | Yang D H, Teng J W, Zhang Z J, et al. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bull. Seism. Soc. Am. , 2003, 93(2): 882-890. DOI:10.1785/0120020125 |
| [3] | Yang D H, Peng J M, Lu M, et al. Optimal nearly analytic discrete approximation to the scalar wave equation. Bull. Seism. Soc. Am. , 2006, 96(3): 1114-1130. DOI:10.1785/0120050080 |
| [4] | 杨顶辉. 双相各向异性介质中弹性波方程的有限元解法及波场模拟. 地球物理学报 , 2002, 45(4): 575–583. Yang D H. Finite element method of the elastic wave equation and wavefield simulation in two-phase anisotropic media. Chinese J. Geophys. (in Chinese) , 2002, 45(4): 575-583. |
| [5] | 王妙月, 郭亚曦, 底青云. 二维线性流变体波的有限元模拟. 地球物理学报 , 1995, 38(4): 494–506. Wang M Y, Guo Y X, Di Q Y. 2-D finite element modelling for seismic wave in media with linear rheological property. Chinese J. Geophys. (in Chinese) , 1995, 38(4): 494-506. |
| [6] | 邓玉琼, 张之立. 弹性波的三维有限元模拟. 地球物理学报 , 1990, 33(1): 44–53. Deng Y Q, Zhang Z L. Three-dimensional finite element modelling of elastic waves. Chinese J. Geophys. (in Chinese) , 1990, 33(1): 44-53. |
| [7] | Levander A R. Fourth-order finite-difference P-SV seismograms. Geophysics , 1988, 53(11): 1425-1436. DOI:10.1190/1.1442422 |
| [8] | Komatitsch D, Barnes C, Tromp J. Simulation of anisotropic wave propagation based upon a spectral element method. Geophysics , 2000, 65(4): 1251-1260. DOI:10.1190/1.1444816 |
| [9] | Ewing W M, Jardetzky W S, Press F. Elastic Waves in Layered Media. New York: McGraw-Hill Book Company Inc., 1957 . |
| [10] | de Hoop A T. A modification of Cagniard’s method for solving seismic pulse problems. Appl. sci. Res. (section B) , 1960, 8(1): 349-356. DOI:10.1007/BF02920068 |
| [11] | Bhattacharya S N. Exact solutions of SH wave equation for inhomogeneous media. Bull. Seism. Soc. Am. , 1970, 60(6): 1847-1859. |
| [12] | Bhattacharya S N. Exact solutions of SH wave equation in transversely isotropic inhomogeneous elastic media. Pure and Appl. Geophys. , 1972, 93(1): 19-35. DOI:10.1007/BF00875218 |
| [13] | Aki K, Richards P G. Quantitative Seismology. Sausalito, Calif.: University Science Books, 2002 . |
| [14] | 杨桂通, 张善元. 弹性动力学. 北京: 中国铁道出版社, 1988 . Yang G T, Zhang S Y. Elastodynamics (in Chinese). Beijing: China Railway Press, 1988 . |
| [15] | Zhou H, Chen X F. Ray path of head waves with irregular interfaces. Applied Geophysics , 2010, 7(1): 66-73. DOI:10.1007/s11770-010-0007-0 |
| [16] | Cerveny V, Ravindra R. Theory of Seismic Head Waves. Toronto: University of Toronto Press, 1971 . |
| [17] | 李庆扬, 王能超, 易大义. 数值分析. 北京: 清华大学出版社, 2001 . Li Q Y, Wang N C, Yi D Y. Numerical Analysis (in Chinese). Beijing: Tsinghua University Press, 2001 . |
 2012, Vol. 55
2012, Vol. 55


