随着卫星定位技术的快速发展,用户对导航定位服务的质量(包括精确性、实时性、连续性、完好性等)及导航增值服务的内容提出了更高的要求.作为第三代GNSS定位技术的典型代表,网络RTK 与精密单点定位技术(PPP)优势互补,很好地应用于测绘、国土、物探、精细农业、监控及其他所有与位置信息相关的服务系统[1-2].基于差分模式的网络RTK 技术是目前使用最为广泛的高精度定位技术,其发展已较成熟,定位结果相对可靠,但其依赖区域内建立的高密度连续运行参考站生成的综合差分改正信息,有效作用距离有限,只能满足小范围内的区域性定位服务[3-4].而基于非差模式的精密单点定位技术,无需高密度的基站支持,作业机动灵活,数据处理简单,单机即可实现广域甚至全球范围内的精密定位与定轨,目前已经成为国际卫星导航领域的研究热点,已在低轨卫星精密定轨、航空摄影测量、海平面监测、GPS 气象、地球物理勘探以及精密授时等领域广泛应用[5-7].
然而,由于传统的PPP 采用浮点解,即整周模糊度参数实数化,其定位结果的精度及可靠性不及差分定位模式.此外,要实现毫米至厘米级的定位精度,通常需要较长的初始化时间(1~2h),从而限制了PPP技术在快速精密定位与定轨等领域中的应用[1].快速准确固定非差整周模糊度是解决这一问题的关键,也是当前国际GNSS领域的研究热点和难点.Ge和Gabor等提出了星间单差模糊度固定的方法,将星间单差相位未检验小数偏差(UFOs)从模糊度中分离出来[8-9];Laurichesse和Collins分别提出了固定非差模糊度的“整数钟"方法和钟差去耦模型,利用卫星和接收机钟差分别吸收卫星端和接收端的小数部分[10-11].笔者从GPS观测方程的基本数学模型出发,分析传统PPP 模型中非差模糊度无法固定为整数的根本原因,并在此基础上给出并推导了一种新的分离相位小数偏差(FractionalBiasIsolating, FBI)恢复相位模糊度的整数特性,从而实现非差模糊度整数解的PPP数学模型和算法.引入LAMBDA 模糊度搜索方法[12],最终实现PPP 固定解.笔者提出的方法与Ge等提出的估计所有卫星对的单差UFOs不同,新方法基于最小二乘整体平差解估计单星的非差UFOs, 方法更简单,实现更方便,效率更高.该方法中所用到的浮点模糊度来自于单站模式的PPP解,处理效率要远高于Laurichesse网解模式的“整数钟"方法.
2 非差模糊度整数解模型与方法 2.1 基本观测模型非差载波相位L和测码伪距P的基本数学模型分别可以表示为[13]
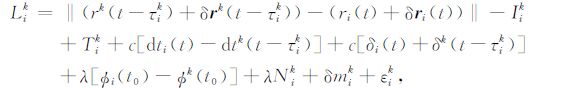
|
(1) |
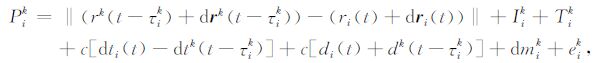
|
(2) |
式中,t为信号接收时刻;τik为卫星k到接收机i之间的信号传播时间;rk(t-τik)为卫星信号离开发射天线时刻的位置;δrk(t-τik)为卫星发射天线相位中心偏差向量;ri(t)为接收机天线接收信号时刻的位置;δri(t)为接收机天线相位中心偏差向量;Iik为卫星k到接收机i之间的电离层延迟;Tik为卫星k到接收机i之间的对流层延迟;dti(t)为接收机i在信号接收时刻的接收机钟差;dtk(t-τik)为卫星k在信号发射时刻的卫星钟差;δi(t)为接收机端信号从天线到信号处理器之间的载波相位信号延迟;δk(t-τik)为卫星端信号从产生到卫星发射天线之间的载波相位信号延迟;Φi(t0)为接收机i在参考时刻t0 的初始相位;Φk(t0)为卫星k在参考时刻t0的初始相位;Nik为卫星k与接收机i之间的整周模糊度;δmik为卫星k到接收机i之间的载波相位观测值多路径误差;εik为卫星k到接收机i之间的载波相位观测值测量噪声;drk(t-τik)为卫星发射天线的伪距观测值偏心向量;dri(t)为接收机天线的伪距观测值偏心向量;di(t)为接收机端信号从天线到信号处理器之间的伪距信号延迟;dk(t-τik)为卫星端从信号产生到信号发射之间的伪距信号延迟;dmik为卫星k到接收机i之间的伪距多路径误差;eik为卫星k到接收机i之间伪距测量误差.
2.2 FBI模型由于式(1)中的初始相位和载波相位硬件延迟不易分离,可将其合为一项,式中与频率无关的项合并,用ρg 表示.
方程(1)、(2)可简写为
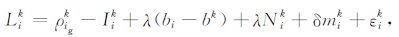
|
(3) |
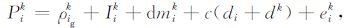
|
(4) |
其中:
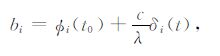
|
(5) |
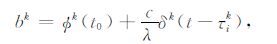
|
(6) |
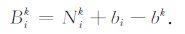
|
(7) |
B为非差相位模糊度.从式(7)可看出,bi与bk使得非差模糊度失去了整数特性.事实上,B中的整数部分与相位观测值中原始的整数模糊度难以分离,但其不会破坏模糊度的整数特性.因此(7)式中破坏非差模糊度整数特性的是B中的小数部分,也就是本文所谓的未检校的相位小数偏差UFOs.如果我们能够准确估计出卫星端和接收机端的UFOs, 并从B中分离出来,就能恢复出非差载波相位模糊度的整数特性,从而能够使用经典的LAMBDA 等方法将其固定为整数.其基本表达式为[14]
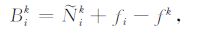
|
(8) |
其中,B为非差实数模糊度,$\tilde{N}$ 为式(7)中的N与b的整数部分之和,fi为接收机端bi的小数部分(接收机端的UFOs),fk为卫星端bk的小数部分(卫星端的UFOs).
2.3 FBI算法具体估计fi和fk的方法如下:
第1 步,基于Melbourne-Wübbena (MW)组合观测值计算宽巷实数模糊度,利用实数宽巷模糊度建立如式(8)的方程联立求解即可得到宽巷的$\tilde{N}$、fi、fk.
第2步,按照传统PPP 观测模型对服务端跟踪网的观测数据进行解算(基准站的坐标已知,可以强约束测站坐标)得到无电离层组合的实数模糊度参数B.
第3步,将第2步计算得到无电离层组合实数模糊度重构为宽巷模糊度和窄巷模糊度的线性组合,将第1步计算得到的宽巷模糊度代入该线性组合方程,求出实数窄巷模糊度,对其建立如式(8)的方程联立求解即可得到窄巷观测值的$\tilde{N}$、fi、fk.
这里需要指出的是,在上述计算宽巷和窄巷模糊度及其UFOs时,按(8)式建立的法方程是秩亏的,必须在法方程中引入整数模糊度基准且选取某颗卫星或某个接收机作为基准UFOs.这样,便可解决法方程的秩亏问题,实现整数模糊度与UFOs的分离,恢复非差模糊度的整数特性.
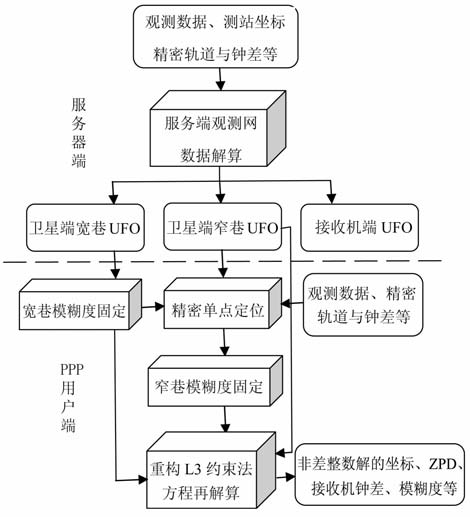
具体算法流程为:任意选取一个测站,将该测站上的模糊度定义为整数基准模糊度,并定义该站上的UFO 为基准UFO.然后选择与其相邻的一个测站作为第二个测站,并引入一个新的整数基准,依次类推,当所有测站上的基准定义好后,法方程不再病态,就可以求解得到N并将其固定为整数.得到整数后回代法方程即可以得到所有卫星端UFO 和接收机端UFO 的整体最小二乘平差解.最后将该UFO 解作为初始解代入原先的法方程重新求解,并固定模糊度,得到新的UFO 解.迭代处理,直到没有更多的整数模糊度固定为止.将服务端跟踪网解算得到的卫星端UFOs与IGS 轨道和钟差产品一起提供给PPP 用户即可在用户端实现模糊度固定成整数的PPP 解.算法流程(包括服务端和PPP 用户端)如图 1所示.
|
图 1 PPP整数固定解流程图 Fig. 1 PPP integer ambiguity solution flow chat |
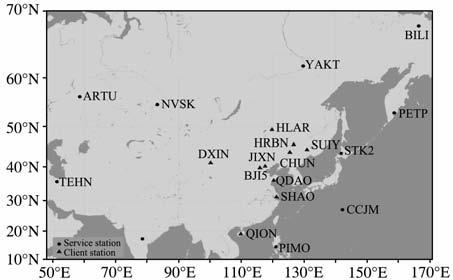
为了验证本文所提出的非差模糊度整数解FBI算法在快速精密定位应用中的可行性与有效性,笔者利用中国境外10个IGS跟踪站组成模拟的服务端观测网络,为整个中国区域的用户端提供快速PPP固定解所需的相应产品.然后在中国境内选择10个分布较均匀的用户站进行PPP 固定解实验以检验其精度及可靠性.该方案无需在中国境内单独建网布站,可直接免费使用IGS跟踪站的数据及产品,节约了大量建设成本.此外,面对重大自然灾害,如5·12汶川大地震使得中国境内大部分测站受到不同程度的影响,此时选用离震区较远的境外IGS跟踪站组网仍然能够有效地提供精密定位服务.这对研究整个中国区域的地壳形变和运动具有重要意义.服务站及用户站的分布如图 2所示,其中圆点标记的测站为服务站,10个服务站较好地覆盖了整个中国区域,测站间距大约为2500km 左右;三角形标记的测站为用户站,均位于服务网内,测站距离最近的基准站800~2500km 不等.
|
图 2 服务站与用户站分布图 Fig. 2 The distribution of reference stations and user stations used for the experimental validation |
使用GPS 时间第1477 周的观测数据进行实验,精密星历和钟差使用IGS 的产品.服务端估计UFOs时,宽巷为每天一组,而窄巷则每10min一组.用户端定位利用30min的观测数据,在动态(静态模拟动态,估计每个历元的坐标且历元间不加任何坐标约束)和静态模式下分别进行PPP 固定解和浮点解.PPP固定解采用LAMBDA 方法搜索整数模糊度,在不能全部固定的情况下,使用部分模糊度固定技术固定尽可能多的模糊度参数.精度评价时,静态PPP将每个时段解算得到的测站坐标及对流层延迟ZPD(ZenithPathDelay)与IGS提供的参考真值(或PPP静态周解)进行比较,统计每个测站所有时段(固定解取所有固定成功的时段)解算结果的偏差绝对值的均值.动态PPP 将每个时段所有历元的定位结果与参考真值作差,并统计其偏差均值及标准差.
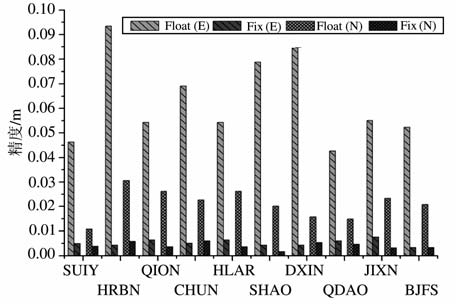
3.2 静态实验结果与分析用户端利用30min的数据进行静态PPP固定解和浮点解的N(北)、E(东)、U(高)方向的定位精度与ZPD 精度分别如图 3、图 4所示.
|
图 3 方案一用户站水平方向定位精度 Fig. 3 The horizontal positioning accuracy of user station tn static experiment |
|
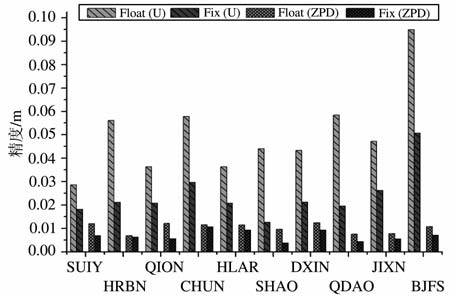
图 4 方案一用户站高程方向和ZPD解算精度 Fig. 4 The vertical positioning and ZPD accuracy of user station in static experiment |
从图中可以看出,对于30 min 的静态观测数据,浮点解定位精度N 方向为1~3cm, E 方向为4~10cm, U 方向为3~10cm.而固定解定位精度水平方向为毫米级,且大多在5mm 以内,高程方向为2~5cm.固定解水平方向定位精度相对浮点解提高了近一个量级,高程方向也有明显改善,固定解在E 方向改善最为明显.固定解与浮点解估计ZPD的精度一般都在1cm 以内,固定解的ZPD 与浮点解的ZPD 相比也有约10% ~30% 的改善,有的测站(如LHAS、HLAR 站)甚至可以达到约50%的改善效果.从模糊度固定成功率的统计结果来看,部分测站的成功率高于95%,HRBN、HLAR、SHAO 三个站成功率略低(这可能与观测数据的质量有关),但也在90%以上.该实验中,用户站距服务端观测网的距离从几百公里到二千多公里,这说明只需要利用分布稀疏的少量中国境外的IGS 跟踪站即可为整个中国区域提供可靠的高精度快速定位及GPS气象服务.
3.3 动态实验结果与分析与静态PPP 不同,动态PPP 的精度统计综合了所有测站所有时段的动态定位结果.动态PPP 固定解与浮点解的平均偏差和标准差分别如图 5、图 6所示.
|
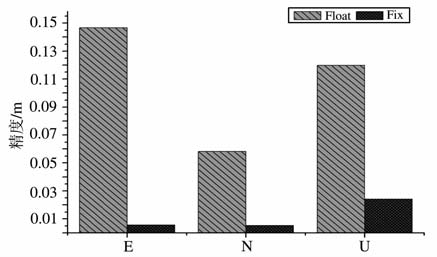
图 5 动态PPP固定解与浮点解平均偏差 Fig. 5 The average positioning bias of float and fix solution in kinematic PPP |
|
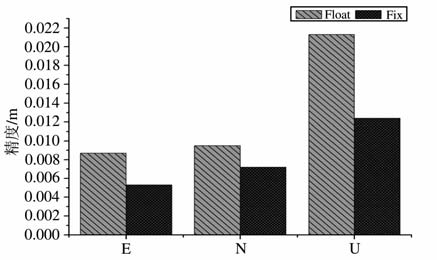
图 6 动态PPP固定解与浮点解标准差 Fig. 6 The standard deviation of positioning of float and fix solution in kinematic PPP |
从图 5中可以看出,利用30 min的观测数据,动态PPP浮点解的定位偏差N 方向为5cm 左右,E 方向达到15cm, U 方向达到12cm;而固定解水平方向的定位偏差均为几毫米,高程方向的约为2cm.很显然,固定解相对于浮点解的动态定位精度在水平方向提高了一个量级,高程方向上也有很明显的改善.结合图 3和图 4可以看出,PPP固定解模式下动态定位的精度改善程度较静态更为明显.尤其在E 方向上的精度改善最为明显.从图 6中可以看出,动态PPP浮点解水平方向标准差约为1cm, 高程方向约为2cm;而固定解水平方向的标准差为6mm 左右,高程方向约为1cm.固定解在三个方向上的定位标准差都有较为明显的改善,在高程方向上改善最为明显.对比图 5、图 6 可以看出,动态PPP浮点解的定位误差主要体现在有较大的系统性偏差,标准差则相对较小.而固定解对系统偏差的改善十分显著,对标准差也有一定的改善.固定解的平均偏差和标准差均为水平方向几毫米,高程方向1~2cm.
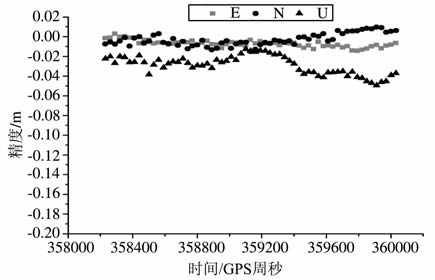
为了更加清晰地反映固定解相对浮点解的精度改善,本文代表性地给出其中一个测站(BJFS)某个时段(DOY1220∶00-0∶30)的动态定位结果,浮点解和固定解分别如图 7、图 8所示,其他测站的结果基本类似.
|
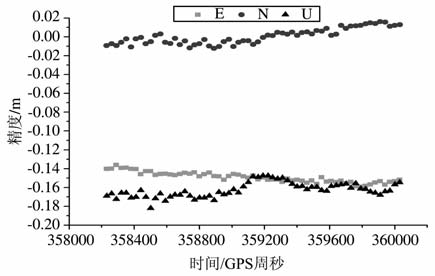
图 7 动态PPP浮点解定位结果偏差 Fig. 7 The positioning bias of float solution in kinematic PPP (BJFS DOY122) |
|
图 8 动态PPP固定解定位结果偏差 Fig. 8 The positioning bias of fix solution in kinematic PPP (BJFS DOY122) |
对比图 7、8可以看出,浮点解在N 方向没有明显的系统偏差,但在E、U 方向上均有较大的系统误差,达到15~20cm 左右.而固定解在E、U 方向上改善明显,在水平方向上的系统偏差优于1cm, 而高程方向为2cm 左右.这说明了固定解相对浮点解明显地提高了定位精度,而且改善主要是在E、U 方向,其中E 方向最为显著.另外,固定解对动态结果历元间的离散程度(即标准差)改善没有对系统偏差的改善显著,但还是可以看出具有一定程度的改善.这与前面的标准差统计结果分析是一致的.另外,动态PPP固定成功率的情况与静态情况基本类似,只是相对而言固定的成功率要略低一些.其原因可能是由于动态解算时历元间的坐标没有任何约束,浮点解的结果以及方差协方差信息比静态的略差,导致成功率略低.但总体而言一般可以保证90%以上的成功率.
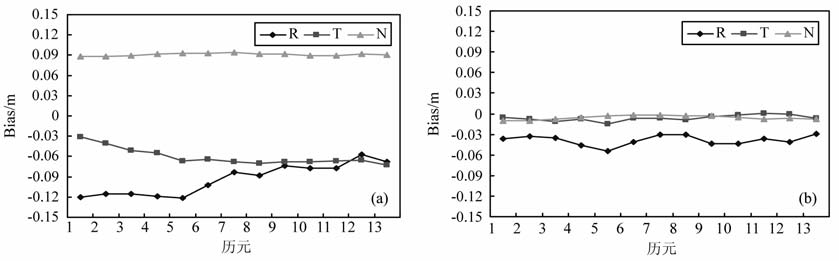
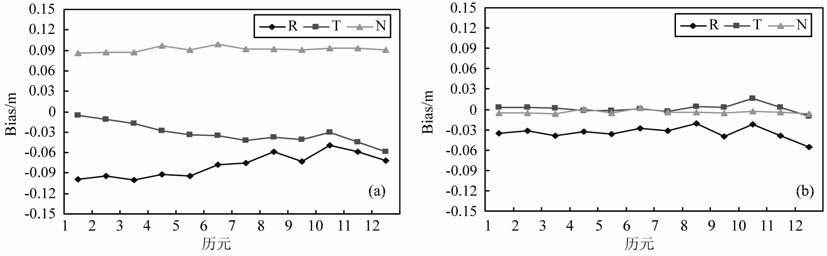
4 快速精密定轨近年来,低轨卫星LEO(Low Earth Orbiter)计划对于大地测量学、地球物理学、气象学等地球科学产生了广泛而深远的影响.精确确定低轨卫星的轨道对于研究地球重力场、海平面变化、大气探测等领域具有重要的意义.GPS技术以其高精度、全天候、实时、连续跟踪等优点,逐渐成为低轨卫星运动学精密定轨的主要技术手段.GRACE(Gravity Recovery and Climate Experiment)卫星是由美、德两国合作于2002年3月发射入轨的低轨卫星,其实验目的旨在改进地球重力场模型的精度.两颗GRACE(GRACE-A和GRACE-B)卫星运行在大约500km 高度的同一个准极轨道平面内,星间相距200km 左右.本文以GRACE 卫星为例,分析PPP 非差整数解在快速精密定轨中的应用.一颗GRACE 卫星每天大约有十次左右经过中国区域上空,每次对应的飞行弧段持续时间大约为15 min 左右.选取2010 年2 月5日的星载观测数据,对两颗GRACE 卫星所有经过中国区域上空的弧段分别进行浮点解与固定解PPP定轨.将定轨结果与JPL 中心提供的参考轨道进行比较,并将其互差转换至星固坐标系RTN(R、T、N 依次代表轨道径向、切向和法向).图 9、图 10分别为GRACE-A 和GRACE-B卫星某一弧段的定轨结果,其中(a)图为浮点解PPP 对应的定轨结果,(b)图为固定解PPP对应的定轨结果.横轴代表历元个数,每个历元间隔为1min, 整个弧段为15min;纵轴代表RTN 方向的定轨误差.
|
图 9 GRACE-A卫星浮点解PPP(a)与固定解PPP(b)定轨偏差 Fig. 9 The orbit determination bias of float solution (a) and fix solution (b) for GRACE-A |
|
图 10 GRACE-B卫星浮点解PPP()与固定解PPP(b)定轨偏差 Fig. 10 The orbit determination bias of float solution (a) and fix solution (b) for GRACE |
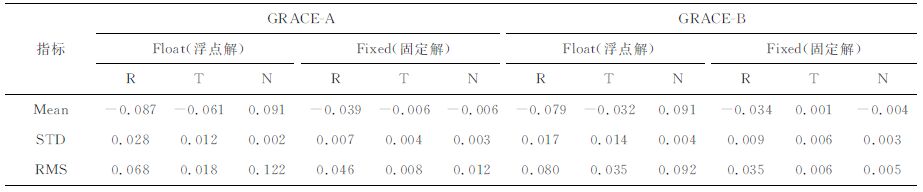
对所有弧段的定轨结果进行均值(Mean)、标准差(STD)及均方根误差(RMS)统计,得到相应的精度统计指标如表 1所示.
|
|
表 1 GRACE卫星浮点解PPP与固定解PPP定轨精度统计(单位:m) Table 1 The statistical accuracy of PPP float and fix solution for GRACE orbit determination (Unit : m) |
图 9、10和表 1 均表明,仅利用15 min 的观测数据对GRACE 卫星进行运动学定轨,浮点解PPP定轨结果存在一定的系统性偏差(1dm 左右).固定解的PPP 定轨结果较浮点解PPP 定轨结果有明显改善,尤其是切向与法向的定轨精度得到了显著提高,系统性偏差基本得到消除,定轨精度达到1cm左右;径向方向由于受到各种残余误差的影响更大(类似于地面定位时的高程方向),其定轨精度略低,为3~5cm 左右,但相对于浮点解的定轨结果也改善了50%~70%.总体而言,固定解PPP 显著改善了低轨卫星短弧段的定轨精度.传统的基于浮点解的精密定轨通常依赖长时间(譬如单天解)的连续观测数据以增强解的强度,其定轨精度一般为3~6cm左右[15-16].
5 结论本文给出了一种新的分离相位小数偏差(FBI)以实现非差模糊度整数解的模型和算法.设计了相应的实验方案验证该算法在快速动态定位与快速(准)实时定轨应用中的可行性与有效性,取得了令人满意的结果.使用LAMBDA 方法搜索整数模糊度可以在PPP用户端实现非差模糊度快速确定.在不能全部固定的条件下,使用部分模糊度固定技术固定尽可能多的模糊度,也能明显改善PPP 定位的精度和可靠性.
利用30min的观测数据进行动态PPP 和静态PPP解算,固定解PPP较浮点解PPP 而言,其水平方向的定位精度提高了近一个量级,达到毫米级或1cm 左右的精度;高程方向与ZPD 精度也改善了20%~60%.使用15 min 的低轨卫星数据进行定轨,基于固定解的PPP 显著改善了定轨精度,尤其是切向与法向的定轨精度得到了显著提高,系统性偏差得到消除,定轨精度达到1cm 左右;径向方向定轨精度略低,为3~5cm 左右,但与浮点解PPP定轨相比也改善了50%~70%.传统的基于浮点解的精密定轨通常采用一整天的观测数据,其定轨精度一般为3~6cm 左右.本文采用固定解PPP 仅用15min的短弧段观测数据即可获得高精度的定轨结果,而无需依赖长时间的连续观测来提高定轨精度,能够实现区域几何快速精密定轨.这改变了以前为了提高定轨精度而需要连续较长时间甚至一整天观测数据的局限性.因此,固定解PPP 可利用短弧段的观测数据实现厘米级的定轨精度,不需要全球布设定轨跟踪站,特别适用于对地观测的遥感卫星实现快速或准实时精密定轨.
| [1] | Bisnath S, Gao Y. Current state of precise point positioning and future prospects and limitations. Observing our changing Earth. International Association of Geodesy Symposia. Berlin Heidelberg: Springer-Verlag, 2007 : 133 . |
| [2] | 张小红, 李星星, 郭斐, 等. 基于服务系统的实时精密单点定位技术及应用研究. 地球物理学报 , 2010, 53(6): 1308–1314. Zhang X H, Li X X, Guo F, et al. Server-Based real-time precise point positioning and its application. Chinese J. Geophys. (in Chinese) , 2010, 53(6): 1308-1314. |
| [3] | Rizos C. Network RTK research and implementation: a geodetic perspective. Journal of Global Positioning Systems , 2002, 1(2): 144-150. DOI:10.5081/jgps |
| [4] | Dai L, Wang J, Rizos C, et al. Predicting atmospheric biases for real-time ambiguity resolution in GPS/GLONASS reference station networks. J. Geod. , 2003, 76(11-12): 617-628. DOI:10.1007/s00190-002-0286-1 |
| [5] | Zumberge J F, Heflin M B, Jefferson D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. , 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [6] | Kouba J, Hérous P. Precise point positioning using IGS orbit and clock products. GPS. Solut. , 2001, 5(2): 12-28. DOI:10.1007/PL00012883 |
| [7] | Zhang X H, Forsberg R. Assessment of long-range kinematic GPS positioning errors by comparison with airborne laser altimetry and satellite altimetry. J. Geod. , 2007, 81(3): 201-211. DOI:10.1007/s00190-006-0100-6 |
| [8] | Ge M, Gendt G, Rothacher M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. , 2008, 82(7): 389-399. DOI:10.1007/s00190-007-0187-4 |
| [9] | Gabor M J, Nerem R S. GPS carrier phase ambiguity resolution using satellite-satellite single difference. Proceedings of 12th Int Tech Meet Satellite Div Inst Navigation GPS 99. 14-17 September, Nashville, TN, USA, 1999. |
| [10] | Laurichesse D, Mercier F. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP. Proceedings of 20th Int Tech Meet Satellite Div Inst Navigation GNSS. 25-28 September, Fort Worth, TX, USA, 2007. |
| [11] | Collins P, Lahaye F, Hérous P, et al. Precise point positioning with ambiguity resolution using the decoupled clock model. Proceedings of ION GNSS . 16-19 September, GA, USA, 2008. |
| [12] | Teunissen P J G. A new method for fast carrier phase ambiguity estimation. Proceedings IEEE Position, Location and Navigation Symposium PLANS'94. Las Vegas, NV, 1994, 11-15: 562-573. |
| [13] | Teunissen P J G, Kleusberg A. GPS for geodesy //Volume 60 of Lecture Notes in Earth Sciences. Springer-Verlag , 1996: 175-217. |
| [14] | 张小红, 李星星. 非差模糊度整数固定解PPP新方法及实验. 武汉大学学报 (信息科学版) , 2010, 35(6): 657–660. Zhang X H, Li X X. A new method for zero-differenced integer ambiguity resolution and its application to PPP. Geomatics and Information Science of Wuhan University (in Chinese) , 2010, 35(6): 657-660. |
| [15] | 李建成, 张守建, 邹贤才, 等. GRACE卫星非差运动学厘米级定轨. 科学通报 , 2009, 54(16): 2355–2362. Li J C, Zhang S J, Zou X C, et al. Precise orbit determination for GRACE with zero-difference kinematic method. Chinese Sci. Bull. (in Chinese) , 2009, 54(16): 2355-2362. |
| [16] | 赵齐乐, 施闯, 柳响林, 等. 重力卫星的星载GPS精密定轨. 武汉大学学报(信息科学版) , 2008, 33(8): 810–814. Zhao Q L, Shi C, Liu X L, et al. Determination of precise orbit using onboard GPS data for gravity modeling oriented satellites. Geomatics and Information Science of Wuhan University (in Chinese) , 2008, 33(8): 810-814. |
 2012, Vol. 55
2012, Vol. 55