2. 海军工程大学天津校区,天津 300450
2. Naval University of Engineering Tianjin Campus, Tianjin 300450, China
海平面对大气压变化的响应,一般假设为海平面对大气压变化的静态瞬时响应(反变气压计响应,以下简称IB),此响应接近均衡态海洋响应,且在这种响应下洋底压力保持不变.一般地讲,海平面变化与气压变化之间的关系可表述为
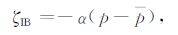
|
(1) |
式中,α 为响应系数,ζIB 为海平面高ζ 的IB 改正,单位为cm, p和p 分别为全球海洋网格点上的表面气压和全球海洋上的平均表面气压,单位为hPa.如果海平面对大气压变化的响应是理想IB,则系数α的值接近1.0,一般取为0.9984.更通俗地讲,理想的IB 是指海洋上的大气压每增加(减少)1hPa, 海平面相应地降低(升高)1cm 这一静态响应.但现实的海平面对大气压变化的响应中,系数α 是变化的,且α 与空间和频率相关.理想IB广泛应用于地球物理学、大地测量学等领域.例如,大气对重力的影响、章动、海平面改正、地球自转、地球动力学扁率的确定、地心变化、大气环流、甚长基线干涉测量(VLBI)改正、GPS改正等[1]以及多数与卫星测高数据相关的科学领域中都需要考虑IB 问题.由于IB 是卫星测高数据的一个常用改正,它的准确与否关系到卫星测高数据的有效应用,以及相关科学问题的合理解决.
海平面变化包含四个主要部分[2],一为气压变化引起的海平面变化,此变化在中高纬度尤为明显,可达到5~10cm;二为温盐变化(即海水热膨胀)引起的海平面变化,主要来自温跃层上部的温度和盐度变化,在低、中纬度区域可达到5~10cm;三为风压波动引起的海平面变化,应小于1cm;四为质量交换引起的海平面变化,它是由海洋上的降雨、蒸发、陆地径流、冰山融化等造成,考虑到海洋、大气和陆地水之间的水质量交换,其振幅大约为1cm.前期的研究工作中,主要考虑气压和风应力变化对全球海平面变化的影响,而较少考虑温盐变化和质量交换对海平面变化影响.
譬如,20世纪80年代初,Lambeck在研究地球自转变化时,较早地提出了利用理想IB假设来计算海洋上表面气压引起的大气角动量变化[2].在这个时期,大气、海洋观测数据比较缺乏,因此只能在海岸和海岛的部分验潮站对IB问题进行区域性研究,很难在全球海洋区域验证这一假设是否正确.Dickman在1988年则尝试从动态潮汐理论出发,研究IB 问题,指出IB 在研究海平面长期变化和地壳垂直运动中精度有所欠缺[3].
对于IB 的全球定量性研究主要始于20 世纪90年代初期,随着大气、海洋模式技术的发展,尤其是海洋模式和卫星测高技术的发展,使我们对海洋的认识和观测更加可靠.因此,对IB 的定量研究有了可能.在这一时期,一般根据简单的正压模式海洋数据、观测的海面高数据、验潮站数据、大气压变化数据以及风应力数据,主要通过线性回归方法来研究海平面对大气压变化的时域和空域响应,重点在北太平洋、南北大西洋等区域[4-5],以及全球区域[6-9].这些研究工作的主要结论是海平面变化方差的50%可以很好地被大气压变化解释[4],大气压与海平面变化之间存在非常强的相关性,且IB有纬度依赖特征.在高纬度区域,实测数据得到的IB 系数α 更接近于理想的IB,但在赤道区域则出现了明显的偏离.例如,Ponte研究了正压驱动下均匀海洋模式下的IB,指出IB与频率和地理位置紧密相关,且在中高纬度,海平面变化达到10~15cm, 但在赤道区域则非常小[6].
除了应用一元线性回归方法,只考虑大气压变化对海平面变化的影响外,上述研究工作中,还详细探讨了加入风应力因素,应用多元线性回归以及谱方法等研究IB[4, 9],并认为通过加入风应力来进行多元回归,可以更好地确定α.引入多元回归方法探讨海平面对大气压变化的响应,主要是因为Ponte证明了气压变化和风应力变化对海平面的影响在大部分海域是相互独立的,且在大于几天的周期上,气压的影响是主要和静态的(或接近IB),风的影响比较小,而且主要是动态信号[10].比较典型的研究工作是应用TOPEX/Poseidon(T/P)卫星测高数据,采用一元和多元线性回归方法研究IB.在应用多元线性回归方法,考虑了风应力影响后,海平面对大气压变化的响应基本符合静态均衡海洋响应[9, 11].
在应用多元回归分析进行IB研究的同时,许多研究工作还开展了IB 系数α 在不同频率上的特征研究.在周期小于几天的高频区间,IB 系数α 会明显偏离理想假设[5],因此在这个频段上应用理想的IB改正是不合适的.而在大于10 天到2 年左右的低频区间[7, 9],IB系数α 比较接近理想假设,可以应用IB改正.例如,Ponte等1991年应用一个正压的浅水海洋模式,研究了海洋盆地从1 天到1 年频段上的海平面对大气压变化的正压响应[12].其结果指出,在海洋盆地,在1周到1年频段上,IB 系数α 的偏离一般小于几个百分点;在2天到1周的频段上,此偏离增加到5% ~20%;小于1 天的频段,则IB不可信.
对于确定IB的各种误差,文献[7]做了深入分析,他们应用两年的T/P数据分析了全球海洋网格上的IB系数,认为在深海区域此假设近似成立,但由于海洋中各个信号相互之间的复杂关系,必需对此做深入研究.此外,Ponte和Gaspar则指出IB 系数在中高纬度区域一般为0.8~1.0cm/hPa, 在赤道区域为0.4~0.8cm/hPa, 且大气和海平面变化的误差不是IB系数偏离理论状态的主要原因,并从一个海洋模式验证了风的因素更大[8].近期,Ponte则指出从海平面变化(全球、验潮站等)数据中去除IB的长期变化趋势,可以使得验潮站和全球海平面的长期变化趋势更加准确;需要注意的是,在南大洋区域,应用不同的大气模式数据,对IB 影响显著[13].Wunsch和Stammer在1997年对IB 的研究现状和未来发展等做了详细综述[14].
从上述的研究工作可以看出,IB 研究主要集中在时频域,且所用到的海平面数据包含了海水温盐度变化和质量交换部分,因此不能客观准确地给出海平面对大气压变化的真实响应.随着海洋模式的逐渐成熟,为研究海平面变化提供了比较可靠的温盐度数据,可以使我们有机会首先扣除温盐度变化对海平面变化的影响,再来更好地研究海平面对大气压变化的响应.此外,对于IB 的大多数研究主要集中在时频域和地区响应,对于空间尺度的研究几乎没有,本文的主要目的是研究在多大空间尺度上,IB假设是合适的.
2 原理和数据 2.1 原理任一球面σ 上连续函数f(θ,λ)可以展开成空间二维缔合勒让德(Legendre)函数阶(degree)和次(order)的和:
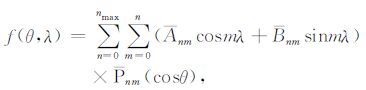
|
(2) |
其中,θ 和λ 分别是余纬和经度,n和m是标准化球谐系数的阶和次,nmax 是最高展开阶数,Anm和Bnm是标准化的球谐系数,Pnm(cosθ)是标准化的缔合勒让德函数,且满足
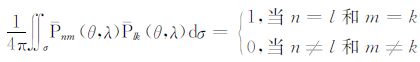
|
(3) |
则标准化的球谐系数可表示为
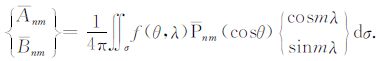
|
(4) |
大气压变化和海平面变化是地球表面的连续函数,因此可以通过公式(4)把相应时刻的大气压变化和海平面变化展开成对应的球谐系数.为了研究大气压和海平面变化的空间谱域特征,还需要用到阶振幅谱σn,它定义为
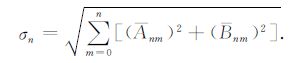
|
(5) |
在阶振幅谱公式(5)中,波长与球谐阶的物理性质只与距离有关而与方向无关,也对应于只与阶n有关而与次m无关.虽然球谐函数是二维的表面(球面),但在讨论等向性问题时,只应用一维波长无疑是方便的.由于球谐函数在π 区间有n个零点,所以波长λn定义为λn=2πRe/n,其中Re 为地球的平均半径.波长的等价定义为λn= 40000km/n.同时,由于半波长与球谐函数阶所对应的空间网格(π/nmax)是直接相关的,因此也是经常被采用的物理量,其量值为波长的一半.
为了计算温盐变化引起的热容海平面变化,需要对海洋模式数据中分层的温度和盐度进行积分,求得其密度变化,并根据(6)式得到热容海平面变化ζρ,
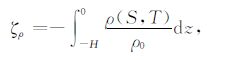
|
(6) |
其中,H为海洋模式的深度,S和T分别为海洋模式的盐度和温度数据,根据文献[15]可以从温度和盐度求出海水的密度变化ρ(S,T),并在全球海洋上进行平均,得到平均密度ρ0,z为深度积分变量.
2.2 数据本文用到了美国国家环境预报中心(NCEP)的再分析大气数据(http://www.cdc.noaa.gov/cdc/reanalysis/),参数为2.5°×2.5°×1 天的经纬度网格的表面气压.数据的时间跨度从1993年到2003年.
海洋模式数据来自Estimating the Circulation and Climate of the Ocean(ECCO)计划(http://www.ecco-group.org/),ECCO 模式源于麻省理工的环流模式,具有真实的海洋地形.其纬向范围为80°S—79°N,经向网格为1°,纬向网格从高纬度的1°到赤道附近的1°/3,垂直为46层,深度到5615m, 时间长度为1993—2003 年,数据时间间隔10 天.ECCO 海洋模式数据包括海平面高、海水各层的温度和盐度、海水各层的洋流(包括纬向洋流和经向洋流).对ECCO 海洋模式数据,我们利用公式(6),通过温盐度积分,得到了热容海平面变化.
卫星测高数据来源于喷气动力实验室(JPL)的T/P卫星观测数据(http://podaac.jpl.nasa.gov/).我们采用了T/P 数据的11—415 周沿轨数据,其中118周缺测,其他周的数据也有部分缺测.在每个观测点上,T/P 数据提供了海面高的变化(扣除了长期平均值)、反变气压计(IB)改正、测点时刻等信息.其中,海面高数据经过了电离层改正、干空气改正、湿空气改正、轨道偏差改正、海潮改正、极潮改正和IB改正等多项改正.为了研究海平面对大气压变化的空间响应,对已经进行IB 改正的T/P 数据加回了这一改正,也就相当于对T/P 数据不进行IB 改正.T/P观测数据的重复周期为10天.为了得到全球2.5°×2.5°×10天的时空网格化数据,我们采用高斯权函数法对T/P原始数据进行了网格化处理.同时,大气压和热容海平面数据也同样处理为与T/P相同的时空网格数据.对所有的大气压变化、海平面变化、热容海平面变化数据,我们根据公式(4)将其展开成了相应的球谐系数.
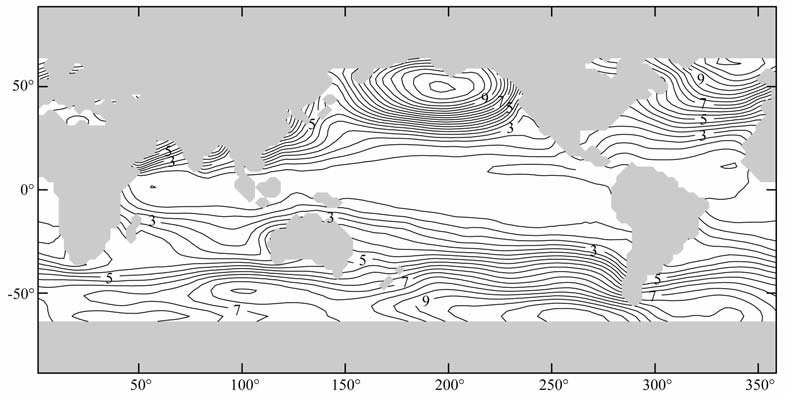
3 结果与讨论 3.1 海洋上表面气压和海平面变化的标准差为了给出海平面对大气压变化的空间响应尺度,首先需要了解驱动其变化的海洋上表面气压的变化情况.为此,图 1中给出了1993—2003年间,海洋上表面气压变化的标准差在全球海洋上的分布情况.海洋上表面气压变化的标准差与纬度具有密切相关性,其分布特点是气压变化的标准差随纬度的增加而增加,从赤道附近的0hPa一直增加到中高纬度的10hPa左右.说明海洋上表面气压变化与纬度带近似线性相关.在南海区域,则形成了几个气压变化的中心区域,说明在南海区域的气压变化相对复杂.
|
图 1 海洋上表面气压的标准差(993—2003年),等高线间隔为0.5hPa Fig. 1 Standard deviation of atmospheric sea surface pressure over ocean during 1993-2003.The contour interval is 0.5 hPa |
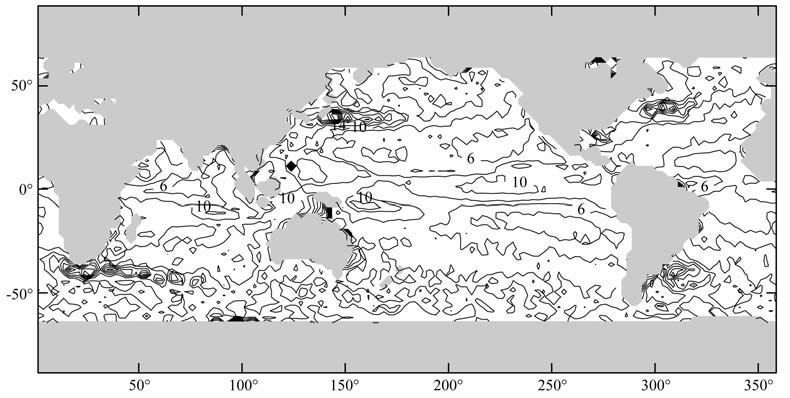
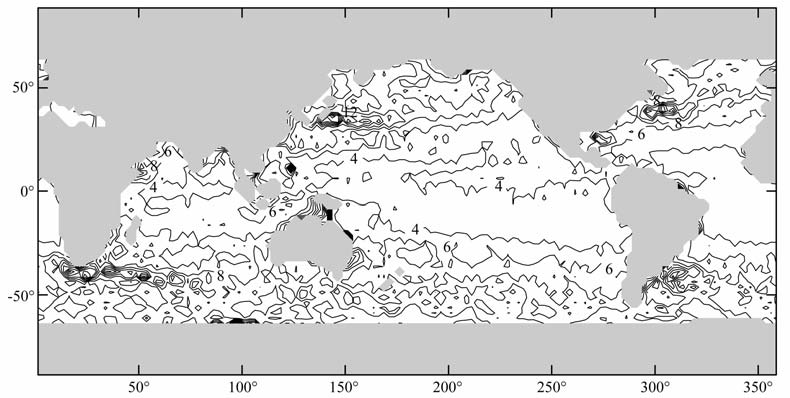
图 2则给出了海平面变化在1993—2003 年间的标准差在全球海洋上的分布.对T/P 海平面变化的标准差来讲,它的分布与纬度变化缺乏密切相关,没有呈现出海洋上表面气压变化标准差与纬度变化强相关的趋势.在赤道区域和西边界区域,海平面变化的标准差可以达到10cm, 在南海区域则呈现出了类似噪声的复杂分布.造成海平面变化全球标准差分布复杂,且与纬度相关性不大的一个主要原因是:海平面变化数据中包含热容海平面变化,这可以引起赤道及西边界区域存在较大的海平面变化标准差.为了消除热容海平面变化对海平面变化的影响,我们应用公式(6),将ECCO 模式的热容海平面变化从观测的海平面变化中扣除,得到质量海平面变化,再来看其标准差分布(图 3).此时,一个非常明显的变化是在赤道和西边界区域,海平面变化的标准差大大降低.同时,在印度洋和南太平洋区域,海平面变化的标准差有较小变化.这充分说明,在研究海平面变化时,必需考虑热容海平面变化.但是,除了赤道区域海平面变化的标准差显著降低外,海平面变化与纬度的相关性依旧不如大气压变化标准差那样明显.海平面变化与大气压变化的标准差在空间分布上,依旧缺乏相似性.对比图 1 和图 3,我们可以清楚地看到,海洋上表面气压变化的标准差主要包含长波长信号,而海平面变化的标准差中则包含了更多的短波长数据(即高频信号).
|
图 2 海平面变化标准差(1993—2003年),单位:cm Fig. 2 Standard deviation of sea surface height during 1993——2003,unit: cm |
|
图 3 质量海平面变化标准差(1993—2003年),单位:cm Fig. 3 Standard deviation of sea surface height with the steric sea surface height removed tirst from ECCO model during 1993—2003,unit: cm |
为了更好地了解表面气压和海平面变化的空间特征,首先对海洋上表面气压应用公式(5)来求解其阶振幅谱.我们可以将每一时刻的全球海洋上的表面气压按公式(4)展开成球谐系数的形式.由于T/P数据的范围是±66°(我们以后也将此范围的海洋称为全球海洋),所以,不在此区域范围的海洋上的表面气压与陆地上的表面气压一般被设为零.求得每一时刻表面气压的球谐系数后,我们就可以根据(5)式来求解每一时刻的阶振幅谱,然后将所有时刻的阶振幅谱进行平均,就可以得到平均阶振幅谱(图 4).NCEP海洋上表面气压的阶振幅谱主要集中在前24阶(阶振幅谱大于0.1hPa),其他阶振幅谱(小于0.1hPa)的贡献非常小.如果以这个标准来定义海平面对大气压变化的空间响应尺度,那么海洋上表面气压的空间半波长为180°/24=7.5°(约相当于空间800km).也就是说,海洋上表面气压的变化在空间上主要是长波长信息,其短波长信息可以忽略.从图 4还可以看到,海洋上表面气压变化的主要能量集中在第6阶振幅谱上(相当于半波长3000km),其阶振幅谱为13hPa.
|
图 4 海洋上表面气压变化的平均阶振幅谱(1993—2003年),单位:hPa Fig. 4 Average degree amplitude spectrum of sea surface pressure during 1993—2003,unit: hPa |
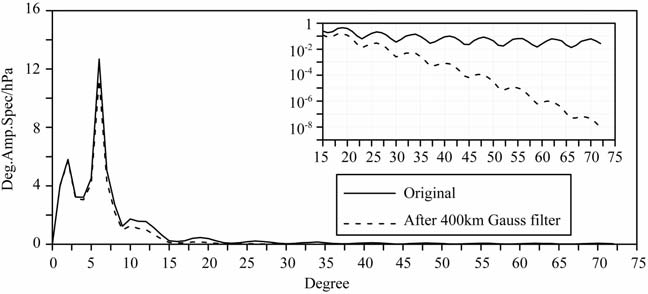
质量海平面变化的阶振幅谱如图 5所示.在扣除了ECCO海洋模式热容海平面变化的影响后,质量海平面变化的主要能量也集中在长波长区域,其阶振幅谱在能量上与海洋上表面气压的阶振幅谱存在一一对应的关系.但与海洋上表面气压阶振幅谱不同的是,质量海平面变化短波长的信息并没有随着阶数的增加而显著降低.相反,质量海平面变化短波长信号的能量维持在了一个固定的水平上,其阶振幅谱约为0.5cm, 是海洋上表面气压变化短波长能量的5倍,这与图 3 质量海平面变化标准差中高频信号较多的情况相符.据此,我们很自然地想到,由于海洋上表面气压变化主要是长波长的空间变化,所以海洋上表面气压变化引起的海平面变化也应该对应长波长变化.因此,研究海平面对大气压变化的空间响应时,有必要消除海平面变化中空间高频变化的影响.鉴于海洋上表面气压变化的空间尺度大约是800km, 我们按此空间尺度对海平面变化数据进行相应的空间滤波.在这里,我们选用了空间高斯滤波方法[16-17],且高斯平滑半窗宽选择为400km.通过400km 高斯空间滤波后,海平面变化的阶振幅谱在图 5中给出.可以看到,质量海平面变化短波长数据的阶振幅谱能量显著降低了,并在24阶左右达到了与海洋上表面气压变化相一致的阶振幅谱(约为0.1cm 和0.1hPa).对海洋上表面气压变化做同样的高斯空间滤波处理,则在20 阶左右,海洋上表面气压变化的阶振幅谱降到了0.1hPa(图 4).同时,我们发现400km 高斯空间滤波后的海洋上表面气压变化的标准差与滤波前差别非常小,也说明在阶振幅谱能量0.1hPa以下的短波能量对海洋上表面气压变化的标准差无显著贡献.这也是我们选择0.1hPa这个阶振幅谱能量作为海平面对大气压变化空间响应尺度标准的依据.

|
图 5 质量海平面变化的平均阶振幅谱(1993—2003年),单位:cm Fig. 5 Average degree amplitude spectrum of sea surface height with the steric sea surface height removed first from ECCO model during 1993—2003,unit: cm |
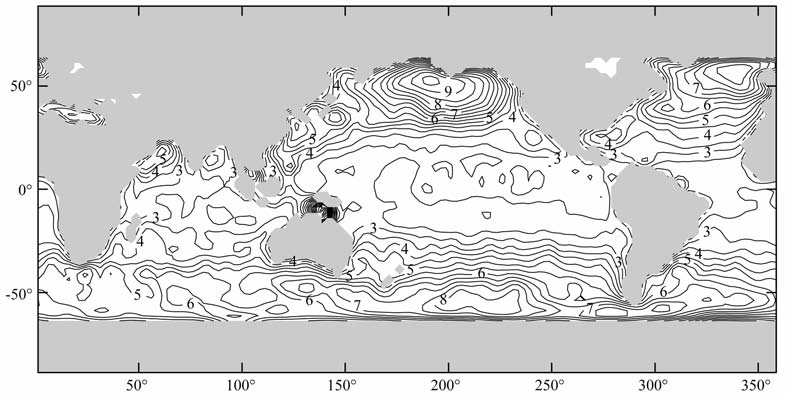
图 6给出了经过高斯空间滤波后的质量海平面变化的标准差在全球海洋上的分布.对比图 1 和图 6,可以看到,此时的质量海平面变化标准差与海洋上表面气压变化标准差有了实质性的相似.二者的空间分布在大部分区域出现了一一对应的关系,尤其是在赤道区域、大西洋区域和澳洲东部太平洋.但在南海区域,二者的差别还是明显存在.造成南海区域差异的原因,可能是这部分区域的海平面变化受到西风带和绕极洋流、热盐环流、南极冰川消融、海底地形等的影响,且在南海区域,海洋上的表面气压不确定性较大[13],我们目前不能很好地将这些因素的影响扣除.
|
图 6 400 km高斯空间滤波后质量海平面变化的标准差(1993—2003年),单位:cm Fig. 6 Standard deviation of 400km Gauss filtered sea surface height with the steric sea surface height removed first from ECCO model during 1993—2003,unit: cm |
在海平面变化的四个主要因素中,目前一般考虑到了其中三个,只有大气、海洋、陆地水之间的水质量交换还没有被很好地考虑.其原因主要在于,大气、海洋、陆地水之间的水质量交换非常复杂,目前还难以有合适的手段对其进行有效分离.虽然GRACE 重力卫星可以直接探测地表流体的质量变化[17-18],但其局限性是重力卫星给出的水质量变化是地表流体质量变化的总和.如果要分别给出大气、海洋和陆地水的质量变化,就必须采用相应的流体模式数据.譬如,在海洋和陆地上,需要分别扣除对应的大气质量变化,以期得到海水和陆地水质量变化.但研究海平面变化与大气压变化的关系又涉及到了大气压(相当于大气质量)的变化,因此,这两者是混在一起的.只有当某一地表流体模式(譬如,大气模式)能够准确确定后,才能准确分离得到另一地表流体模式的质量变化.此外,单独的地表流体模式或是地表流体模式的总和并不能保证全球质量守恒这一基本原则[19],这也对海平面质量变化造成相应的影响,这也是直接应用目前地表流体模式的一个问题.
虽然我们在本文中应用海洋模式数据,给出了热容海平面变化,但不同的海洋模式以及海洋观测数据等给出的各自热容海平面变化之间存在着比较明显的差别[20].同样,对于海水温度和盐度的观测数据,例如WOA 系列和Ishii系列,它们虽然源于同一观测数据源,但由于编辑和网格化数据时的处理技术不同,也会造成全球网格化的海水温度和盐度结果有明显不同[21-22].因此,热容海平面变化的不确定性,也最终会影响到准确确定海平面对大气压变化的响应过程.
此外,正如引言所指出的,海平面对大气压变化的响应是一个复杂的时空和频率响应问题.对于其应用,可以对应于时空和频率选择合适的模型.目前,还没有一个(或多个)模型,能够较好地适应各种不同的应用.因此,今后在这方面还需要进一步深入研究,建立一个(或多个)时频空相依的海平面对大气压变化的响应模型.
4 结论海平面对于大气压变化在空间上的响应主要分布在半波长为800km 的空间范围上(约为7.5°×7.5°经纬度网格),在小于此空间范围上,海平面变化表现出了更多高频变化,这部分变化可能与风应力变化密切相关.此外,通过GRACE 重力卫星等重力手段,结合更加准确的地表流体模式数据,有可能较好地给出大气、海洋、陆地水水质量交换引起的海平面变化部分,这将会促进海平面对大气压变化响应空间尺度的准确确定,并服务于卫星测高数据的处理与应用.
致谢感谢两位评审人提出的建设性修改意见.
| [1] | Dickman S R. Determination of oceanic dynamic barometer corrections to atmospheric excitation of Earth rotation. J. Geophys. Res. , 1998, 103(B7): 15127-15143. DOI:10.1029/98JB00614 |
| [2] | Lambeck K. The Earth's Variable Rotation: Geophysical Causes and Consequences. New York: Cambridge University Press, 1980 . |
| [3] | Dickman S R. Theoretical investigation of the oceanic inverted barometer response. J. Geophys. Res. , 1988, 93(B12): 14941-14946. DOI:10.1029/JB093iB12p14941 |
| [4] | Wunsch C. Large-scale response of the ocean to atmospheric forcing at low frequencies. J. Geophys. Res. , 1991, 96(C8): 15083-15092. DOI:10.1029/91JC01457 |
| [5] | Woodworth P L, Windle S A, Vassie J M. Departures from the local inverse barometer model at periods of 5 days in the central South Atlantic. J. Geophys. Res. , 1995, 100(C9): 18281-18290. DOI:10.1029/95JC01741 |
| [6] | Ponte R M. Variability in a homogeneous global ocean forced by barometric pressure. Dyn. Atmos. Ocean. , 1993, 18(3-4): 209-234. DOI:10.1016/0377-0265(93)90010-5 |
| [7] | Gaspar P, Ponte R M. Relation between sea level and barometric pressure determined from altimeter data and model simulations. J. Geophys. Res. , 1997, 102(C1): 961-971. DOI:10.1029/96JC02920 |
| [8] | Ponte R M, Gaspar P. Regional analysis of the inverted barometer effect over the global ocean using TOPEX/POSEIDON data and model results. J. Geophys. Res. , 1999, 104(C7): 15587-15601. DOI:10.1029/1999JC900113 |
| [9] | Fu L L, Pihos G. Determining the response of sea level to atmospheric pressure forcing using TOPEX/POSEIDON data. J. Geophys. Res. , 1994, 99(C12): 24633-24642. DOI:10.1029/94JC01647 |
| [10] | Ponte R M. Understanding the relation between wind- and pressure-driven sea level variability. J. Geophys. Res. , 1994, 99(C4): 8033-8039. DOI:10.1029/94JC00217 |
| [11] | 闫昊明, 朱耀仲. 全球海平面对大气压变化的响应. 地球物理学报 , 2001, 44(3): 320–326. Yan H M, Zhu Y Z. Response of sea level to variation of atmospheric pressure. Chinese J. Geophys. (in Chinese) , 2001, 44(3): 320-326. DOI:10.1002/cjg2.v44.3 |
| [12] | Ponte R M, Salstein D A, Rosen R D. Sea level response to pressure forcing in a barotropic numerical model. J. Phys. Oceanogr. , 1991, 21(7): 1043-1057. DOI:10.1175/1520-0485(1991)021<1043:SLRTPF>2.0.CO;2 |
| [13] | Ponte R M. Low-frequency sea level variability and the inverted barometer effect. J. Atmos. Oceanic Technol. , 2006, 23(4): 619-629. DOI:10.1175/JTECH1864.1 |
| [14] | Wunsch C, Stammer D. Atmospheric loading and the oceanic "inverted barometer" effect. Rev. Geophys. , 1997, 35(1): 79-107. DOI:10.1029/96RG03037 |
| [15] | Gill A E. Atmosphere-Ocean Dynamics. London: Academic Press, 1982 . |
| [16] | Jekeli C. Alternative Methods to Smooth the Earth's Gravity Field. Columbus: Report No. 327, Department of Geodetic Science. the Ohio State University , 1981. |
| [17] | Wahr J, Molenaar M, Bryan F. Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. , 1998, 103(B12): 30205-30229. DOI:10.1029/98JB02844 |
| [18] | Tapley B D, Bettadpur S, Ries J C, et al. GRACE measurements of mass variability in the Earth system. Science , 2004, 305(5683): 503-505. DOI:10.1126/science.1099192 |
| [19] | Yan H M, Chao B F. Effect of global mass conservation among geophysical fluids on the seasonal length of day variation. J. Geophys. Res. , 2012, 117. DOI:10.1029/2011JB008788 |
| [20] | 闫昊明. 海洋在地球自转和重力场变化中的作用. 武汉: 中国科学院测量与地球物理研究所, 2005 . Yan H M. Oceanic role in the variations of Earth's rotation and gravity field (in Chinese). Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2005 . |
| [21] | Ishii M, Kimoto M, Sakamoto K, et al. Steric sea level changes estimated from historical ocean subsurface temperature and salinity analyses. J. Oceanogr. , 2006, 62(2): 155-170. DOI:10.1007/s10872-006-0041-y |
| [22] | Levitus S, Antonov J I, Boyer T P. Warming of the world ocean, 1955—2003. Geophys. Res. Lett. , 2005, 32. DOI:10.1029/2004GL021592 |
 2012, Vol. 55
2012, Vol. 55

