2. 中国科学院空间天气学国家重点实验室, 北京 100190
2. State Key Laboratory of Space Weather, Chinese Academy of Sciences, Beijing 100190, China
电离层的地面人工加热就是利用大功率无线电波入射到电离层,引起局部电离层电子温度和电子密度的改变,继而造成电离层电导率、介电常数等相关物理量的变化,从而引起电离层特性的变化,也称为电离层的人工改变或人工变态.当电波通过变态区时,会发生很多的效应,如交叉调制、反常吸收、聚焦和散焦等,从而使信息传播的质量和电波传播的通道受到不同程度的影响.电离层的人工改变日益受到人们的重视.世界各地建立了许多电离层加热实验设备,也对实验现象进行了许多研究.Kero等[1]研究了D 层电离层加热的诊断方法;Vierinen等[2]对大范围的多普勒频移产生的雷达回波的振幅进行了分析;Blagoveshchenskaya等[3]研究了加热频率接近F 层临频时磁天顶产生的现象;Lofas等[4]研究了X波在欠密加热情况下电子温度的变化.
在电离层加热实验不断取得进展的同时,我们需要建立电离层加热的各种数值模型,对加热效应进行预测和评估,深入了解电离层加热的物理机制,从而在某些方面指导实验的进行.从1978年Gurevich[5]基于非磁化各向同性等离子体建立了较简单的加热模型以后,电离层加热模型的建立逐步兴起并日趋完善.Hansen等[6]对夜间HF泵波加热电离层作了深入的研究;Bernhardt[7]在电离层欠密加热情况下,用流体力学方程组描述了电离层F 区的加热,着重考虑了电波在加热过程中的自聚焦效应;Shoucri等[8]建立了极区F 区的加热模型,讨论了电子温度和密度的变化对其他电离层参量的影响,并讨论了波反射点密度谷的形成;石润[9]对高频加热电离层引起的IAR (Ionospheric AlfvenResonator, 电离层Alfven 谐振器)效应进行了研究,利用高频泵波加热电离层模型,建立了电波加热电离层改变电离层电导率激发Alfven波,进而形成Alfven谐振的物理模型;魏寒颖等[10]在均匀和平面分层背景下建立加热模型,解释了加热中不均匀体的生成是质动力和热压力共同作用的结果;邓峰等[11]在磁子午面内建立了中低纬地区泵波加热电离层中泵波反射高度处的二维模型,详细研究了反射高度处空洞及附近稠团的形成机制;黄文耿等[12-14]分别建立了较全面的低电离层和高电离层的加热模型,并考察了不同的加热参数对加热效应的影响;汪枫等[15]模拟采用ELF/VLF 调幅HF 电波加热电离层形成等效的ELF/VLF电离层虚拟天线.
本文中,我们忽略离子加热,由电子的连续性方程、动量方程和能量方程出发,考虑热传导、扩散和漂移等输运过程,在重力场中的偶极扩散假设下,给出了一维的电离层的加热模型,并与实验结果进行了比较.
2 电离层加热模型在电离层F区,主要离子成分是O+ ,由于O+不易与电子复合,而主要通过与双原子分子N2 和O2 的电荷交换后生成分子离子NO+ 和O2+ ,然后再与电子复合.主要的化学反应为

|
(1) |
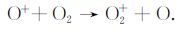
|
(2) |
以上两个反应的反应系数与电子温度无关,如果忽略加热过程中的O+ ,N2 和O2 密度的变化,则电子温度的变化对NO+ 和O2+ 的生成没有影响.随电离层高度的增加,O+ 逐渐占绝对优势,而β 复合与温度无关,因此加热引起的电子密度的变化主要由输运过程来决定.计算中,复合过程仅考虑NO+和O2+ 的离解性复合,即

|
(3) |

|
(4) |
NO+ 和O2+ 的密度由经验模式确定,此时电子的连续性方程为
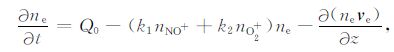
|
(5) |
其中复合系数k1 =4×10-9 (300/Te)cm3/s, k2 =1.89×10-9(300/Te)0.6cm3/s.Q0 是无外场作用时,平衡态(∂/∂t=0)的电子产生率.
主要考虑三种正离子(O+ ,NO+ 和O2+ )和电子,忽略黏滞和惯性项,并在最后考虑中性风的影响,这四种带电粒子的运动方程为

|
(6) |
其中α和β 为带电粒子种类,nα,mα,qα 和vα 分别为α类粒子的密度、质量、电量和速度.g为重力加速度,E为包括带电粒子的运动产生的极化场在内的自洽场,B为地磁场.Pα 为压力项,一般的Pα =nαkbTα,kb 为玻耳兹曼常量,Tα 为带电粒子温度,假设三种离子温度相同,设其为Ti.υαn和υαβ 分别为带电粒子与中性粒子和带电粒子之间的碰撞频率.将以上运动方程相加,由准中性条件和偶极扩散条件假设:
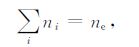
|
(7) |
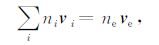
|
(8) |
其中下标i,e分别代表正离子和电子.则运动方程可以转化为

|
(9) |
一般地,离子和中性粒子的碰撞对电子流的贡献[16]:
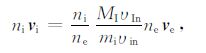
|
(10) |
MIυIn 是离子碰撞权重因子,由偶极扩散条件容易求出:
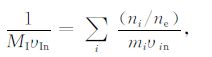
|
(11) |
则动量方程为

|
(12) |
其中vn 为中性风速度.
电子吸收电波能量后,能量方程为[17]
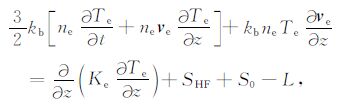
|
(13) |
其中方程左边第一项是由于HF外场加热引起的电子温度随时间的变化,第二项是对流项,第三项是压力流;右边第一项是热传导项,第二项为单位时间内吸收电波的能量密度,第三项为电子在平衡态没有电波作用下,吸收其他能量(主要是太阳能量)的能量密度,第四项为能量损失率.沿磁场方向的热传导系数为[18]
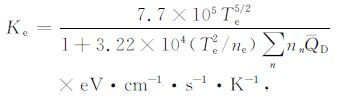
|
(14) |
其中分母中的求和项为中性粒子的作用,nn为中性粒子密度,QD 为相应中性粒子的平均动量传输截面[19]:

|
(15) |
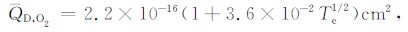
|
(16) |
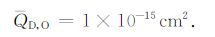
|
(17) |
一般地,在加热实验中,电波能量的吸收以反射点为中心呈近高斯分布[20-22].因此单位体积单位时间内吸收的电波能量可以写为
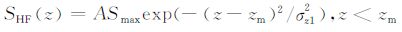
|
(18) |
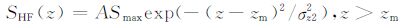
|
(19) |
其中zm 为反射点高度,A为比例常数.反射点处欧姆吸收为[23]
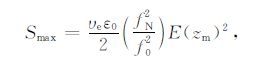
|
(20) |
其中ε0 为自由空间的介电常数,fN 为等离子体频率,E(z)= 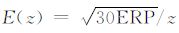
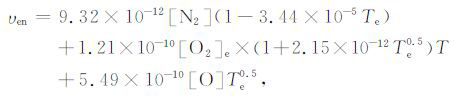
|
(21) |
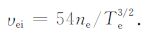
|
(22) |
电子能量的损失[24-25]主要包括以下过程:(1)和正离子及中性粒子的弹性碰撞;(2)分子N2 和O2 旋转能级的激发;(3)分子N2 和O2 振动能级的激发;(4)原子O 电子能级的激发;(5)原子O 精细结构的激发.
3 初始化和边界条件电离层加热仿真的背景电离层参数由IRI模型[26]给出,中性大气参数由MSIS 模型[27]给出.由于IRI模型对极区电离层状态的描述并不准确,我们需要对仿真初值进行修正,非相干散射雷达给出的可以在仿真中使用的3 个电离层参量为:电子温度、离子温度和电子密度.我们选取实验中满足电离层临频大于泵波频率的6 个O 波加热事件来做研究,分别为1月10日的10:40和10:56,1月11日的10:16、10:48、11:04 和11:52.对1 月10 日2个O 波加热时刻,及其两侧4 个未加热时刻,1 月11日4个O 波加热时刻,及其两侧8个未加热时刻分别作平均,如图 1[28]所示.从图中可以看到6个O波加热时刻前后的12个时刻的电子温度变化不大,电子密度也与此类似,因此我们使用这12个时刻的电子温度和密度的均值对电子温度和密度的仿真初值进行修正,离子温度由于几乎不受加热影响,因此我们使用6 个O 波加热时刻及其前后时刻,共18个时刻的离子温度均值进行修正.初始化的电离层参量如图 2所示.随高度的增加,电子温度、离子温度和中性粒子温度不再相等.加热地点为挪威Tromsø,仿真高度为120~600km, 空间分辨率为2km, 时间分辨率为5ms.泵波频率为4.04 MHz, 有效辐射功率ERP=90 MW,峰值高度为226km, 反射高度为218km.边界条件使用Hansen 边界条件,即加热过程中,上边界电子温度和密度梯度保持不变,下边界电子温度和电子密度保持不变.

|
图 1 6个O波加热事件加热期间的电子温度剖面[28] (a)10日,2个O 波加热时刻(10:40和10:56)的数据;(b)11日,4个O 波加热时刻(10:16、10:48、11:04和11:52)的数据. Fig. 1 Electron temperature profile ofthe six O mode heating cases[28] (a) Two O mode heating case sat 10:40 and 10:56 on January 10;(b) Four O mode heating cases at 10:16、 10:48、11:04 and 11:52 on January 11 |
|
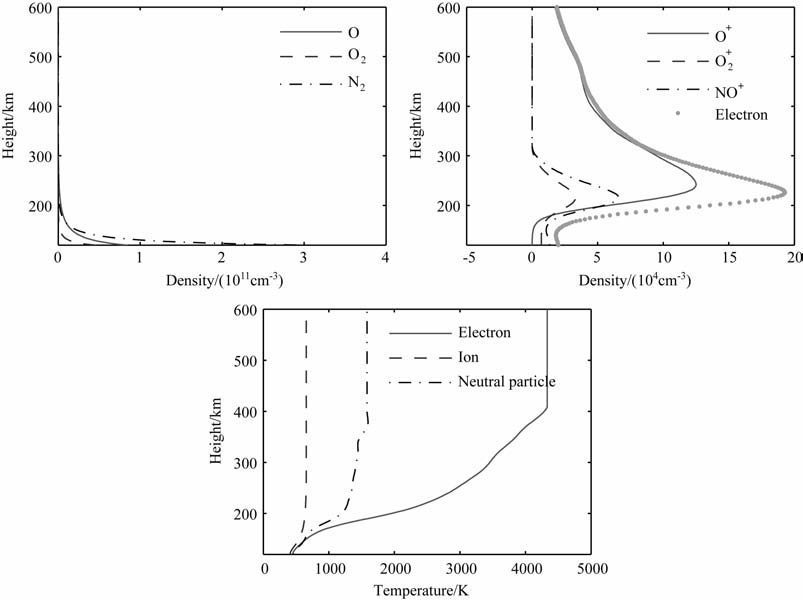
图 2 初始化电离层参数 Fig. 2 Initialized ionospheric parameters |
平静电离层条件下,从太阳吸收的能量与对流、压力流、热传导等输运过程传递的能量,以及各种碰撞和各种能级激发引起的能量损失达成动态平衡.大功率无线电波的注入,打破了平衡态,使得电离层等离子体中的电子在外加电场的作用下被加速,吸收泵波能量,然后在与重粒子的碰撞过程中失去一部分从电场获取的能量.连续加热条件下,电子吸收能量而温度升高,同时电子能量损失率也随之增大;另一方面,热压力导致电子向低温区扩散,在能量吸收和损失、电子的复合和扩散重新达到平衡状态时,电子温度和电子密度也达到稳定值.
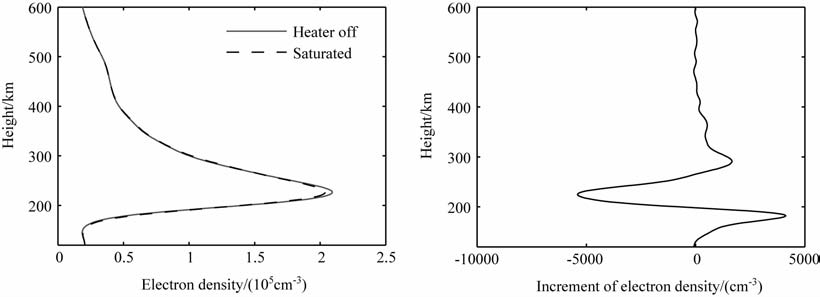
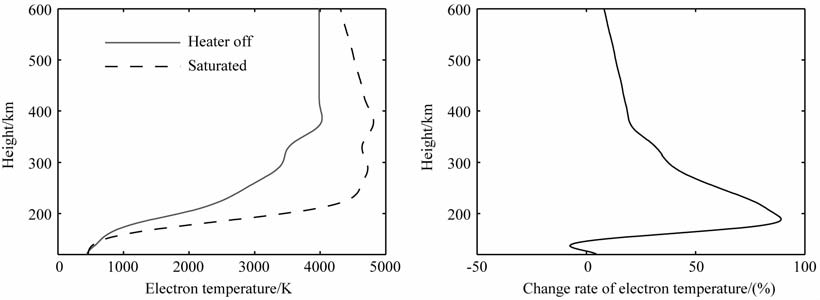
图 3和图 4分别给出了加热前后的电子密度和密度剖面以及温度和温度剖面的增量.由于热传导接近纵向,能量很容易沿磁力线传递到峰上高度,它具体的表现为:一直到600km 高度上都存在一致性的电子温度增强,在反射高度附近形成温度增强峰很平缓.电子密度在峰上高度224km 处形成密度谷,密度衰减百分比为2.69%.由于密度谷由热扩散形成,因此密度谷两侧182km 和292km 处存在小幅密度增强.电子温度增量峰值在188km, 增加百分比为89.16%.
|
图 3 加热饱和条件下电子密度和密度增量剖面 Fig. 3 Electron density and increment profiles in heating saturation conditions |
|
图 4 加热饱和条件下电子温度和温度增量剖面 Fig. 4 Electron temperature and increment profiles in heating saturation conditions |
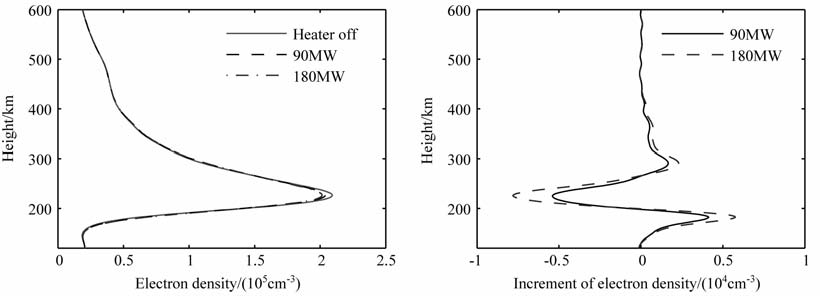
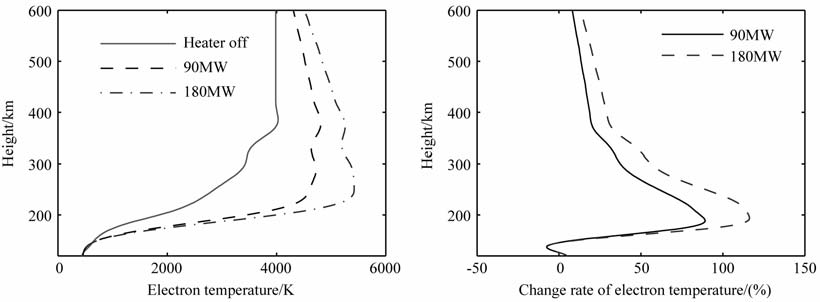
电离层的加热效应主要受到电波能量和加热频率这两个泵波参数控制,我们可以通过调整这两个参数改进电离层的加热效应.图 5和图 6分别给出了有效辐射功率为90 MW 和180 MW 时,电离层加热效应的对比.从图中可以看到,180 MW 的加热功率产生的加热效应比90 MW 产生的效应明显,密度谷处的衰减幅度更大,两侧的峰值也更明显,但加热效果与加热电场功率幅度之间不是简单的正比关系.180 MW 加热的密度衰减幅值约为90 MW的1.4倍左右,谷值两侧的峰值也有小幅增长,密度衰减结构的宽度基本没有变化.电子温度增量变化也比较显著,180 MW 加热的电子温度增量百分比为116.3%,约为90 MW 加热的1.3 倍,但增量的峰值位置也由188km 上升至194km.
|
图 5 有效辐射功率为90 MW,加热饱和条件下电子密度和密度增量剖面 Fig. 5 Electron density and increment profiles in heating saturation conditions when the heating power is 90 MW |
|
图 6 效辐射功率为180MW,加热饱和条件下电子温度和温度增量剖面 Fig. 6 Electron temperature and increment profiles in heating saturation conditions when the heating power is 180 MW |
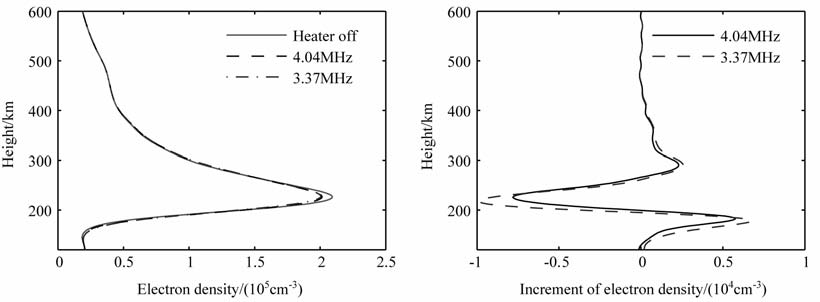
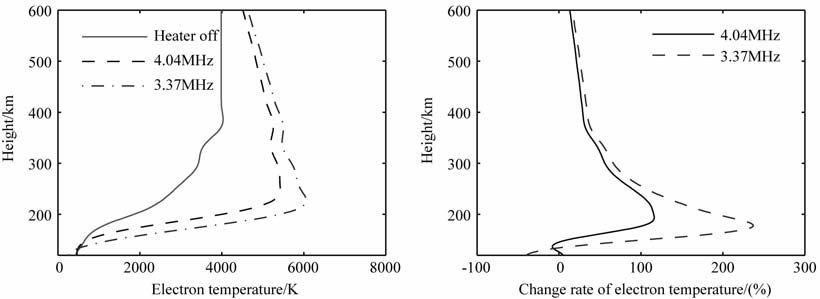
图 7和图 8分别给出了加热频率为4.04 MHz和3.37 MHz时,电离层加热效应的对比.从图中可以看到,加热效应随加热频率的减小而增大,且由于反射点位置下降,电离层参量变化的位形也发生了改变.3.37 MHz加热的电子密度衰减百分比约为4.04 MHz加热的1.3 倍,而且衰减的谷值位置下降了10km.电子温度的变化更为明显,3.37 MHz加热的饱和电子温度在228km 出现较为显著的尖峰,电子温度增量也呈现了同样的特征,在178km出现尖锐的峰值结构,幅度也增大到4.04 MHz加热的2倍.
|
图 7 加热频率为4.04 MHz加热饱和条件下电子密度和密度增量剖面 Fig. 7 Electron density and increment profiles in heating saturation |
|
图 8 加热频率为3. 37 MHz加热饱和条件下电子温度和温度增量剖面 Fig. 8 Electron temperature and increment profiles in heating saturation |
本次实验时间为2008年1月8—11日.由于极区冬季电离层临频相对较低,而EISCAT 加热设备当时可用加热频率最低为4.04 MHz, 根据当地测高仪对电离层探测数据决定实验开始和结束的时间,因此4天实验中实验时间不同.加热设备采用天线阵2,12 个发射机全部工作在85kW,总功率为85kW×12=1.02 MW,天线增益大约为22.5dB,加热有效辐射功率大约为180 MW.加热频率选择为4.04MHz.采用O 波X 波交替加热,4min开(O波)—4min关—4min 开(X 波)—4 min 关来循环加热.此加热周期满足加热机开启时,充分加热,电离层达到饱和;加热机关闭时,充分冷却,电离层恢复到未加热状态.采用UHF 雷达进行F 层电子密度和电子温度的探测.数据分析采用欧洲非相干散射科学联合会官方的非相干散射数据分析程序GUISDAP(Grand Unified Incoherent Scatter Design and Analysis Package)来处理.我们选取10日和11日的6个加热时间和仿真作对比.
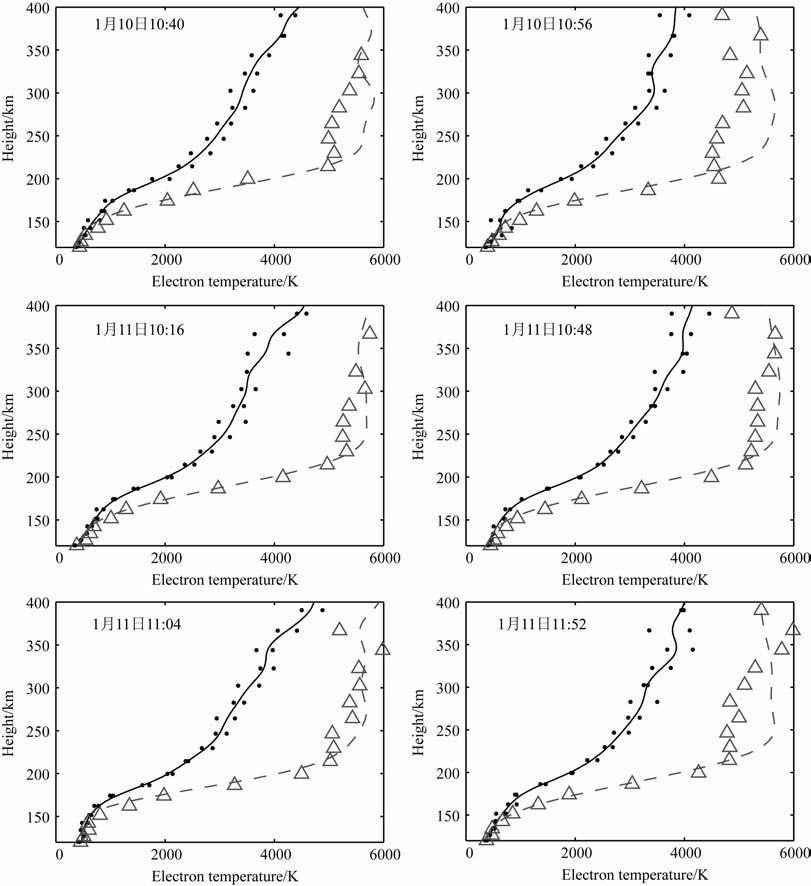
使用第4节给出的数值模型,我们对2008年1月10日10:40,10:56和2008年1月11日10:16,10:48,11:04,11:52的6个O 波加热时刻进行了电离层加热数值仿真.仿真所使用的电子密度和电子温度初值,由加热前后时刻的电子密度和电子温度均值给出,离子温度初值由加热时刻及其前后时刻的均值给出.图 9给出了6个O 波加热时刻仿真结果与由非相干散射雷达所测得的功率谱经过非相干散射数据分析程序GUISDAP处理得到的数据的对比[28].其中实线为仿真初始值,虚线为饱和电子温度,点为加热前后时刻的电子温度测量值,三角号为加热时刻的测量值.从图中可以看到,反射高度以下,全部6个O波加热事件的仿真结果都与实测数据十分符合,误差很小.反射高度以上,1月10日10:40,10:56时刻,11日11:52时刻3个加热事件250km附近,仿真结果要略大于实测值.1月11日10:16,10:48,11:04 时刻3 个加热事件350km 附近,仿真结果要略小于实测值.
|
图 9 6个O波加热事件电子温度剖面仿真与测量结果对比 Fig. 9 A comparison of numerical simulation and measurements of electron temperature profiles of the six O-mode heating cases |
一维数值仿真模型计算得到的电子温度的变化和大多数的实验结果是比较吻合的,但多种因素均导致了误差的存在.一方面,由于反射点附近高频电波与电离层等离子强烈的非线性相互作用,使得能量吸收率具有复杂的空间分布结构,对电波能量吸收率的准确描述仍存在困难,文中使用高斯分布函数对电波能量吸收率进行了描述,这与实际能量吸收的空间分布仍存在一定的差异,因此仿真结果存在一定误差.此外,受限于现有的非相干散射雷达数据分析程序(GUISDAP)的空间分辨率较差(仅为14km),电子温度、电子密度和离子温度也具有相同的空间分辨率,文中使用的反射高度事实上是由插值得到的,因此电波能量吸收率中心的位置也存在偏差,导致仿真结果也会存在误差.电波能量吸收率的计算需要使用加热前实测的电子温度、电子密度和离子温度值作为输入,而本身这些实测电离层参量即存在测量误差,这些因素都是造成电波能量吸收率产生误差,进而导致仿真结果产生误差的原因.另一方面,加热仿真需要的其他的背景电离层参数(正离子密度)和中性大气参数(中性大气密度和温度)是由IRI模型和MSIS模型给出的,不是实测值,这些因素都可能是误差产生的原因.
6 结 论依据我国2008 年1 月在挪威Tromsø进行的冬季电离层加热实验,通过电子的连续性方程、动量方程和能量方程,我们建立了人工大功率无线电波加热电离层的数值模型.文章考察了人工改变电离层引起的电子温度和密度的变化,以及泵波参数对加热效果的影响,并将仿真结果与实验数据进行了对比.主要结论如下:在泵波频率为4.04 MHz, 有效辐射功率ERP为180MW 的情况下,一直到600km高度上都存在一致性的电子温度增强,在反射高度(218km)附近形成温度增强峰很平缓.电子密度在峰上高度224km 处形成密度谷,密度衰减百分比为2.69%.由于密度谷由热扩散形成,因此密度谷两侧182km 和292km 处存在小幅密度增强.电子温度增量变化率峰值在188km, 增加百分比为89.16%.加热效应基本随加热功率的增大而增大,随加热频率的增大而减小,加热功率主要改变了电离层参量增量的幅度,频率还会影响到增量的位形.从仿真结果和实测数据的对比来看,基于近高斯分布电波能量吸收率的电离层数值仿真模型可以很好地描述电离层的加热特征,只是精细结构上略有差异.设计高分辨的电离层加热诊断实验,对上混杂谐振、磁旋谐振、参量不稳定性和欧姆碰撞吸收等不同的吸收机制进行区分,进而建立新的电波能量吸收率模型和电离层数值仿真模型,例如二维加热模型,并将其仿真结果与实验进行对比研究是我们进一步所要完成的工作.
致谢感谢欧洲非相干散射雷达协会(EISCAT)的数据提供.
| [1] | Kero A, Vierinen J, Enell C F, et al. New incoherent scatter diagnostic methods for the heated D-region ionosphere. Ann. Geophys. , 2008, 26: 2273-2279. DOI:10.5194/angeo-26-2273-2008 |
| [2] | Vierinen J, Lehtinen M S, Virtanen I I. Amplitude domain analysis of strong range and Doppler spread radar echos. Ann. Geophys. , 2008, 26: 2419-2426. DOI:10.5194/angeo-26-2419-2008 |
| [3] | Blagoveshchenskaya N F, Carlson H C, Kornienko V A, et al. Phenomena induced by powerful HF pumping towards magnetic zenith with a frequency near the F-region critical frequency and the third electron gyro harmonic frequency. Ann. Geophys. , 2009, 27: 131-145. DOI:10.5194/angeo-27-131-2009 |
| [4] | L?fs H, Ivchenko N, Gustavsson B, et al. F-region electron heating by X-mode radiowaves in underdense conditions. Ann. Geophys. , 2009, 27: 2585-2592. DOI:10.5194/angeo-27-2585-2009 |
| [5] | Gurevich A V. Nonlinear Phenomena in the Ionosphere. Springer-Verlag , 1978. |
| [6] | Hansen J D, Morales G J, Maggs J E. Large scale HF-induced ionospheric modification: theory and modeling. J. Geophys. Res. , 1992, 97(A11): 17019-17032. DOI:10.1029/92JA01603 |
| [7] | Bernhardt P A, Duncan L M. The feedback-diffraction theory of ionospheric heating. J. Atmos. Terr. Phys. , 1982, 44(12): 1061-1074. DOI:10.1016/0021-9169(82)90018-6 |
| [8] | Shoucri M M, Morales G J, Maggs J E. Ohmic heating of the polar F region by HF pulses. J. Geophys. Res. , 1984, 89(A5): 2907-2917. DOI:10.1029/JA089iA05p02907 |
| [9] | 石润. 电离层Alfven谐振器对ULF波传播影响的研究. 武汉: 武汉大学电子信息学院 , 2009. Shi R. Study of the effect of IAR on ULF wave propagation . Wuhan: School of Electronic Information of Wuhan University (in Chinese) , 2009. |
| [10] | 魏寒颖, 赵正予, 倪彬彬. 加热电离层生成不均匀体的理论及模拟研究. 电波科学学报 , 2006, 21(1): 84–93. Wei H Y, Zhao Z Y, Ni B B. Theoretical and numerical study on HF-induced ionospheric irregularities. Chinese Journal of Radio Science (in Chinese) , 2006, 21(1): 84-93. |
| [11] | 邓峰, 赵正予, 石润, 等. 中低纬电离层加热大尺度场向不均匀体的二维数值模拟. 物理学报 , 2009, 58(10): 7382–7391. Deng F, Zhao Z Y, Shi R, et al. Two-dimensional simulation of high-frequency-induced large-scale irregularities in F region. Acta Physica Sinica (in Chinese) , 2009, 58(10): 7382-7391. |
| [12] | 黄文耿, 古士芬. 大功率无线电波与低电离层的相互作用. 空间科学学报 , 2003, 23(3): 181–188. Huang W G, Gu S F. Interaction between the powerful high-frequency radio wave and the lower terrestrial ionosphere. Chinese Journal of Space Science (in Chinese) , 2003, 23(3): 181-188. |
| [13] | 黄文耿, 古士芬. 大功率无线电波对高电离层的加热. 空间科学学报 , 2003, 23(5): 343–351. Huang W G, Gu S F. The heating of upper ionosphere by powerful high-frequency radio waves. Chinese Journal of Space Science (in Chinese) , 2003, 23(5): 343-351. |
| [14] | 黄文耿, 古士芬, 龚建树. 大功率高频无线电波加热电离层. 电波科学学报 , 2004, 19(3): 296–301. Huang W G, Gu S F, Gong J S. Ionosphere heating by powerful high-frequency radio waves. Chinese Journal of Space Science (in Chinese) , 2004, 19(3): 296-301. |
| [15] | 汪枫, 赵正予, 张援农. 低纬地区电离层电流的人工调制数值模拟. 地球物理学报 , 2009, 52(4): 887–894. Wang F, Zhao Z Y, Zhang Y N. Numerical modeling of ionospheric current artificial modulation at low latitude. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 887-894. |
| [16] | Hinkel. Modeling of HF propagation and heating in the ionosphere. TRW Space and Technology Group, Final Technical Report , 1992. |
| [17] | Bernhardt P A, Duncan L M. The feedback-diffraction theory of ionospheric heating. J. Atmos. Terr. Phys. , 1982, 44(12): 1061-1074. DOI:10.1016/0021-9169(82)90018-6 |
| [18] | Banks P M, Kockarts G. Aeronomy, Part A and Part B. New York: Academic Press, 1973 . |
| [19] | Djuth F T, Sulzer M P, Elder J H. High resolution observation of HF-induced plasma waves in the ionosphere. Geophys. Res. Lett. , 1990, 17(11): 1893-1896. DOI:10.1029/GL017i011p01893 |
| [20] | Hansen J D, Morales G J, Maggs J E. Large scale HF-induced ionospheric modification: theory and modeling. J. Geophys. Res. , 1992, 97(A11): 17019-17032. DOI:10.1029/92JA01603 |
| [21] | Dubois D F, Rose H A, Russell D. Excitation of strong Langmuir turbulence in plasmas near critical density: application to HF heating of the ionosphere. J. Geophys. Res. , 1990, 95(A12): 21221-21272. DOI:10.1029/JA095iA12p21221 |
| [22] | Djuth F T, Sulzer M P, Elder J H. High resolution observation of HF-induced plasma waves in the ionosphere. Geophys. Res. Lett. , 1990, 17(11): 1893-1896. DOI:10.1029/GL017i011p01893 |
| [23] | Bernhardt P A, Duncan L M. The feedback-diffraction theory of ionospheric heating. J. Atmos. Solar-Terr. Phys. , 1982, 44(12): 1061-1074. DOI:10.1016/0021-9169(82)90018-6 |
| [24] | Stubbe P, Varnum W S. Electron energy transfer rates in the ionosphere. Planetary and Space Science , 1972, 20(8): 1121-1126. DOI:10.1016/0032-0633(72)90001-3 |
| [25] | Stubbe P. A new collisional relaxation model for small deviations from equilibrium. Journal of Plasma Physics , 1987, 38(1): 95-116. DOI:10.1017/S0022377800012435 |
| [26] | Bilitza D. International reference ionosphere-status. Advances in Space Research , 1997, 20(9): 1751-1754. DOI:10.1016/S0273-1177(97)00584-X |
| [27] | Hedin A E. Extension of the MSIS thermospheric model into the middle and lower atmosphere. J. Geophys. Res. , 1991, 96(A2): 1159-1172. DOI:10.1029/90JA02125 |
| [28] | 徐彬, 吴军, 吴健, 等. 我国极区冬季电离层加热实验研究. 地球物理学报 , 2009, 52(4): 1–8. Xu B, Wu J, Wu J, et al. Observations of the heating experiments in the polar winter ionosphere. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 1-8. |
 2012, Vol. 55
2012, Vol. 55

