2. 大庆钻探工程公司测井公司, 大庆 163412
2. Wireline Logging Company, Daqing Drilling Engineering Company, Daqing 163412, China
砂泥岩薄交互层是典型的低阻油气储层,其电导率存在非常明显的各向异性[1-2],如果能够同时测量出纵横向电阻率,对于该类储层的正确评价具有非常重要的意义.多分量感应是新一代测井技术,能够同时提供地层纵横向电阻率信息[3-4],与各种常规感应技术(双感应,阵列感应)相比,多分量感应不仅含有方向与井轴平行的发射和接收线圈(共轴线圈系),而且还增加了方向与井轴垂直的发射和接收线圈(共面线圈系),整个仪器由三个相互正交的发射线圈(TX、TY和TZ)和接收线圈(RX、RY和RZ)组成,利用这种三轴发射和接收系统,能够同时测量9个不同分量的感应磁场,提供地层纵横向电阻率、井眼相对倾角等有用信息.
由于共面线圈系的电磁场不再具有轴对称性,往往需要采用三维数值模拟技术研究多分量感应仪器的响应[5-8],其运算效率往往较低.因此,效率更高的解析法[9-11]与混合法[12-18]也得到了较广泛研究与应用.在文献[15-16]中,我们已经用模式匹配法研究建立了一套多分量感应测井的正演与反演算法,在不含井眼和侵入带的水平层状各向异性模型上取得了满意效果.然而,当地层模型存在井眼或侵入带时,由于共面线圈系产生的电场存在着径向分量,电流密度的连续性会在柱状电阻率分界面上产生积累面电荷.当用模式匹配算法对多分量感应测井响应进行数值模拟时,由于刚度矩阵是非对称的复矩阵,矩阵元素的微小变化往往对特征值和特征向量均产生较大影响,如果忽略这些积累面电荷对电磁场的影响将得不到正确的数值模拟结果.
本文将对文献[13-16]中的模式匹配算法进行改进,以便建立水平层状非均质各向异性地层(含有井眼和侵入带)中多分量感应测井响应快速数值模拟算法.首先利用电导率导数在柱状界面上的奇异性,引入两个附加奇异微分算子,用于描述井壁以及侵入带与原状地层分界面上的积累面电荷对电磁场的影响,然后再应用模式匹配算法求解含有附加奇异算子的偏微分方程,得到水平层状非均质各向异性地层中电磁场半解析解以及多分量感应响应有效算法.在此基础上,通过数值模拟结果研究考察井眼泥浆电阻率、侵入深度以及层厚等变化对阵列多分量感应测井响应的影响特征.
2 理论
图 1是水平层状各向异性非均质地层,地层总层数是N,其中,第n层原状地层(侵入带)横向和纵向电导率分别为σHT,n和σVT,n(σHX,n和σVX,n)(n=1,2,…,N),侵入半径和水平界面位置分别是rxo,n(n=1,2,…,N)和dn(n=2,3,…,N),井眼半径和井眼泥浆电导率分别为a和σmd.图中还建立了相应的直角坐标系xyz,其中,z轴与井轴重合,三轴单位发射线圈用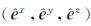
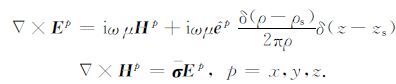
|
(1) |

|
图 1 地层模型与阵列多分量感应仪器结构示意图 Fig. 1 Formation model and the structure of array multicomponent induction logging tool |
方程(1)中,已假定三轴发射线圈${{\hat{e}}^{p}}$(p=x,y,z)具有单位磁矩,且均匀分布在半径为ρs 的小圆环上,其目的是保证井轴周围的电磁场仍然可解,δ 是Dirac-δ 函数.Ep和Hp表示发射线圈${{\hat{e}}^{p}}$产生的电磁场,珔σ 是电导率张量,μ 是磁导率,Ω 为发射信号的角频率,且忽略位移电流影响.
由于电导率是分片常数函数,第n层中的纵横向电导率函数可表示为[18]
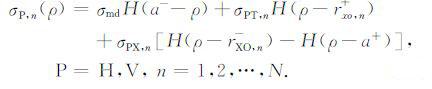
|
(2) |
其中,下标“P= H,V"分别表示横向与纵向方向,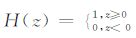
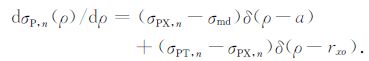
|
(3) |
(3) 式表明在井壁以及侵入带和原状地层交界面上,电导率导数是奇异的.
2.1 水平发射线圈的电磁场利用直角坐标系(xyz)中,单位正交向量${{\hat{e}}^{x}}$和${{\hat{e}}^{y}}$与柱坐标系(ρ,θ,z)中单位正交向量${{{\hat{e}}}_{\rho }}$和${{{\hat{e}}}_{\theta }}$的关系${{\hat{e}}^{x}}$=cosθ${{{\hat{e}}}_{\rho }}$ -sinθ${{{\hat{e}}}_{\theta }}$ 和${{\hat{e}}^{y}}$=sinθ${{{\hat{e}}}_{\rho }}$ +cosθ${{{\hat{e}}}_{\theta }}$,并与欧拉公式cosθ=0.5(eiθ+e-iθ)和sinθ=-0.5i(eiθ -e-iθ)结合,可以将直角坐标系中的两个单位向量${{\hat{e}}^{x}}$和${{\hat{e}}^{y}}$转换到柱坐标系中,并可展开成如下的Fourier级数:
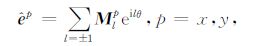
|
(4) |
其中,Mlx=0.5(1 il)T 和Mly=-0.5il(1 il)T分别是单位向量${{\hat{e}}^{x}}$和${{\hat{e}}^{y}}$在柱坐标系中的Fourier展开式系数(l阶谐变分量).
将(1)式中水平磁流源${{\hat{e}}^{x}}$和${{\hat{e}}^{y}}$产生的电磁场也转换到柱坐标系中,并将电磁场Ep= (Eρp,Eθp ,Ezp)T和Hp= (Hρp,Hθp ,Hzp)T(p=x,y)也展开成如下形式的Fourier级数:
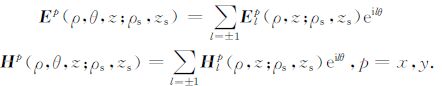
|
(5) |
将(4)式和(5)式代入(1)式,并对方程进行分解,得到水平电场的l阶谐变分量Es, lp= (σHEρ,lp,Eθ,lp)T 满足的方程(见附录):
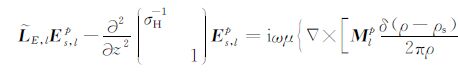
|
(6) |
其中${{{\tilde{L}}}_{E,L}}$是2×2阶的微分算子,定义为
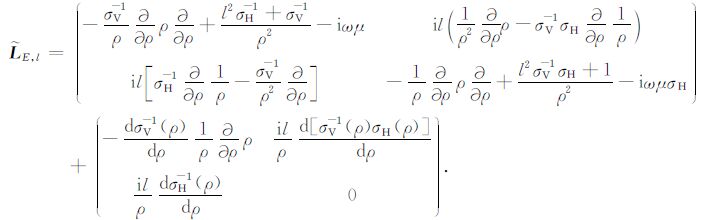
|
(7) |
(7) 式中的第二项为附加奇异算子,起因于(3)式中电导率导数的奇异性,主要反映柱状界面上积累面电荷对电场的影响.
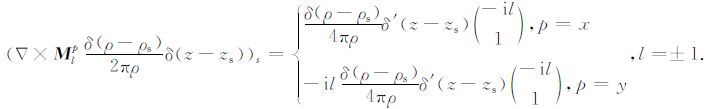
|
(8) |
为保证方程(6)在井轴附近仍然可解并保证其解存在和唯一,需要如下的边界条件[9, 15, 17]:
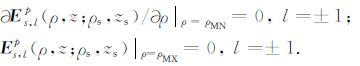
|
(9) |
其中,ρMN 是足够小的数(如10-6m),ρMX 是径向上的最大求解范围.
磁场强度水平方向和垂直方向的l阶谐变分量Hs,lp= (Hρ,lp,Hθ,lp)T 和Hz,lp与Es,lp= (σHEρ,lp,Eθ,lp)T间的关系方程[13-14]:
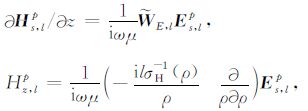
|
(10) |
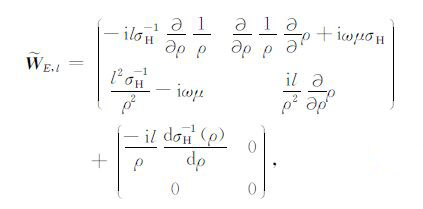
|
(11) |
是2×2阶的微分算子且右端的第二算子也是奇异微分算子.
2.2 垂向发射线圈的电磁场垂向单位发射线圈${{{\hat{e}}}^{z}}$是轴对称的,其产生的电场Ez中只有一个非零分量Eθ,0z、磁场Hz中仅有两个非零分量Hρ,0z,Hz,0z,用同样方法可以从(1)式中得到电场Eθ,0z 满足的方程:
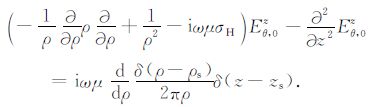
|
(12) |
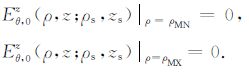
|
(13) |
磁场的两个非零分量Hρ,0z,Hz,0z与电场Eθ,0z的关系为[13-14]
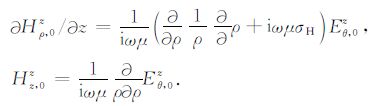
|
(14) |
由于(12)~(14)式的求解过程与(6)~(11)式完全类似且前者更为简单,因此下面仅给出(6)~(11)式的求解过程.
2.3 完全柱状介质中的电磁场为了研究(6)~(11)式的快速求解方法,首先假定模型中不含水平界面(即完全柱状介质),并用有限长区间[ρMN,ρMX]逼近半无限区间,并将其剖分成M(为偶数)个小区间、剖分节点位置为ρα,α=1,2,…,M+1.选用二次Newton插值函数作为径向节点ρα上的基函数φα(ρ),(α = 1,…,M),基函数定义如下[19]:
在内边界节点ρ=ρ1 =ρMN(α=1)上:φ1(ρ)=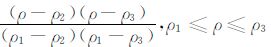
在其他奇数节点ρ =ρ2k-1(α =2k-1)上:
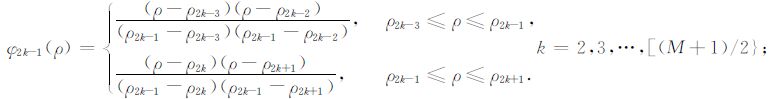
|
在偶数节点ρ =ρ2k(α =2k)上:
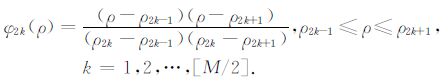
|
利用Galerkin法,将方程(6)中的水平电场的l阶谐变分量展开成如下形式[14-15]:
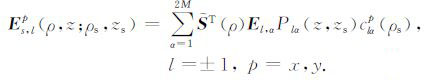
|
(15) |
这里的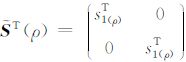
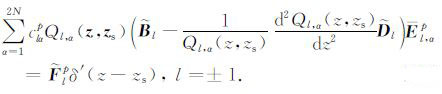
|
(16) |
其中,${{{\tilde{B}}}_{l}}$和${\tilde{D}}$分别是2M×2M阶刚度矩阵和质量矩阵,$\tilde{F}_{l}^{p}$是2M阶列向量,分别定义如下:
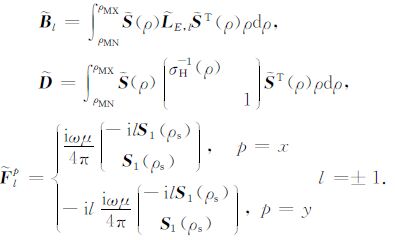
|
(17) |
通过分离变量,从(16)式可以得到如下三个独立方程:
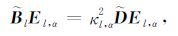
|
(18) |
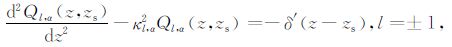
|
(19) |
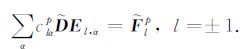
|
(20) |
求解(18)式,得到2M个本征值κl,α2和相应的本征向量El,α,(α =1,…,2M).方程(19)的解:
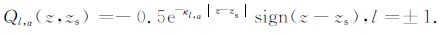
|
(21) |
进一步求解方程(20)确定向量Clp= (cl,1p,cl,2p,…,cl,2Mp)T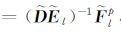
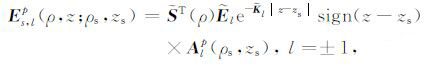
|
(22) |
其中,
利用文献[14-15]的结果,第n层非均质地层中的p-方向的磁偶极子产生的水平电场的l阶谐变分量可表示为如下形式:
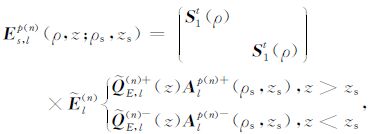
|
(23) |
其中,Alp(n)±(ρs, zs)是电场振幅,
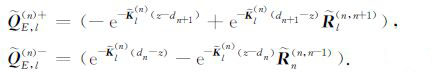
|
(24) |
(24) 式中符号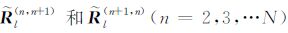
将(23)式代入(10)式中,经整理,得第n层中的水平和垂直磁场的l阶谐变分量(Hs,lp和Hz,lp):
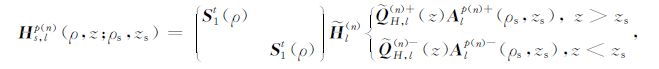
|
(25) |
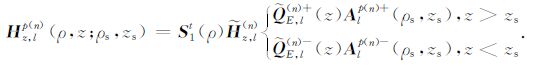
|
(26) |
其中,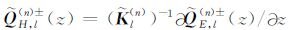
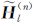

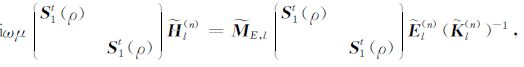
|
(27) |
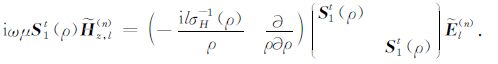
|
(28) |
最后,得到由x-方向的单位水平磁偶极子${{\hat{e}}^{x}}$产生的磁场强度:
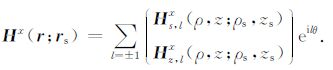
|
(29) |
y-方向水平磁偶极子${{\hat{e}}^{y}}$产生的磁场强度,由(17)式中的第三个公式得:
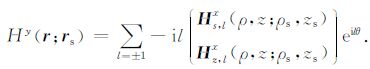
|
(30) |
设rR= (ρR,θR,zR)为接收线圈位置,将柱坐标系下的解(29)式转换到直角坐标系中,得磁场强度主分量Hxx和Hyy:Hxx=Hρx(rR;rs)cosθR-Hθx(rR;rs)sinθR和Hyy= Hρy(rR;rs)sinθR+Hθy(rR;rs)cosθR.
采用类似方法求解(12)~(14)式,可以确定垂直磁偶极子${{{\hat{e}}}^{z}}$产生的磁场强度Hz(rR;rs),其主分量记为Hzz= Hzz(rR;rs).
2.5 多分量感应视电导率
利用磁场的三个主分量Hxx、Hyy和Hzz,并按照公式[4]: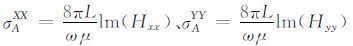

本节首先通过柱状介质模型中多分量感应响应的解析解[9]与本文的NMM 解的对比,检验NMM的有效性,然后,通过数值结果考察阵列多分量感应测井响应.假定阵列多分量感应仪由一个三分量的发射线圈和三个源距分别为0.8、1.2 m 和1.8 m三分量接收器组成(见图 1),发射线圈的工作频率为50kHz和200kHz.假定井眼半径a=0.1m, 由于在垂直井眼中σAXX=σAYY,所以本节中的数值结果仅包含两个主分量σAXX和σAZZ.在数值模拟过程中,方程(6)~(14)中的径向求解区间的范围为ρMN =10-6m 和ρMX =60m, 总节点数M+1=119,其中,节点ρα(α = 1,2,…,40)按等间距增加且间距为0.005m, 而节点ρα(α=40,42,…,M+1)按对数等间距增加.
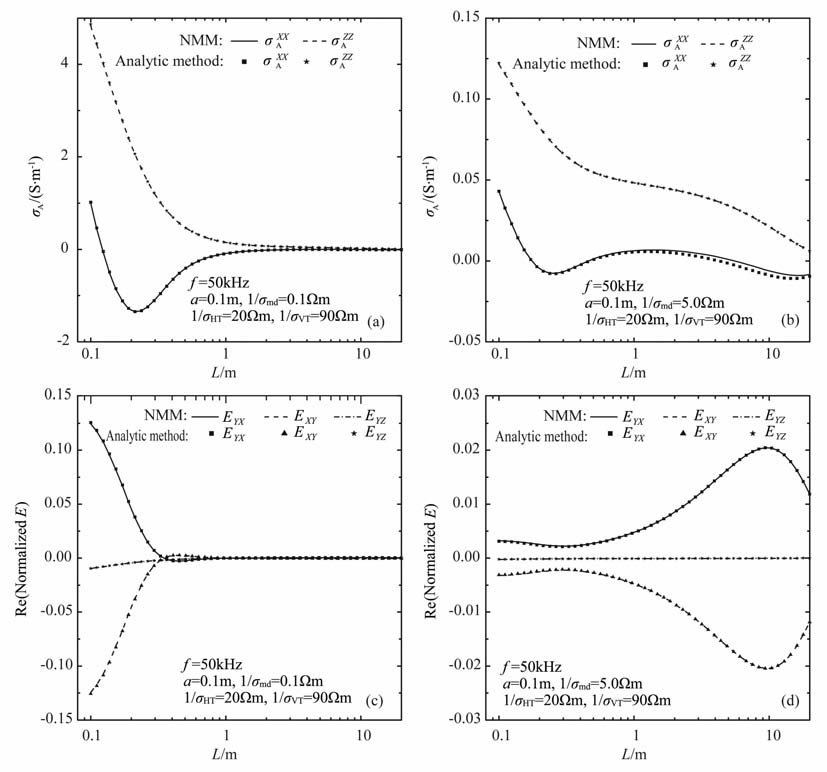
图 2 是一个完全柱状各向异性地层中,NMM和解析法[9]计算得到的不同源距条件下多分量感应的两个主分量σAXX 和σAZZ 以及归一化后的三个电场强度(EYX,EXY和EYZ)的实部对比结果.该模型的纵(横)向电阻率RVT(RHT)是90(20)Ωm, 泥浆电阻率RMD 分别为0.1和5Ωm, 且ρs=0.005m、接收线圈位置为(xR,yR)= (0.01m, 0).图 2a和图 2b分别是σAXX 和σAZZ 结果的对比,图 2c和图 2d是归一化的电场强度分量EYX、EXY和EYZ的实部对比情况,其中实线和虚线是NMM 数值结果而各个离散符号对应于解析法结果,结果清楚显示NMM 和解析法两种方法所得结果吻合得非常好.
|
图 2 两层完全柱状各向异性模型上NMM与解析法所得数值结果的对比 (a)导电率泥浆中的σAXX和σAZZ (b)电阻率泥浆中的σAXX和σAZZ;(c)导电率泥浆中的归一化电场强度实部;(d)电阻率泥浆中的归一化电场强度实部. Fig. 2 Comparison of the numerical results of EM fields in the 2-layercylindrical TI model by analytic method with that by NMM |
对于含有井眼和侵入带的水平层状非均质各向异性地层中NMM 算法的检验,在文献[8, 17]中已经与三维有限体积差分算法的数值结果进行了详细对比,故这里从略.
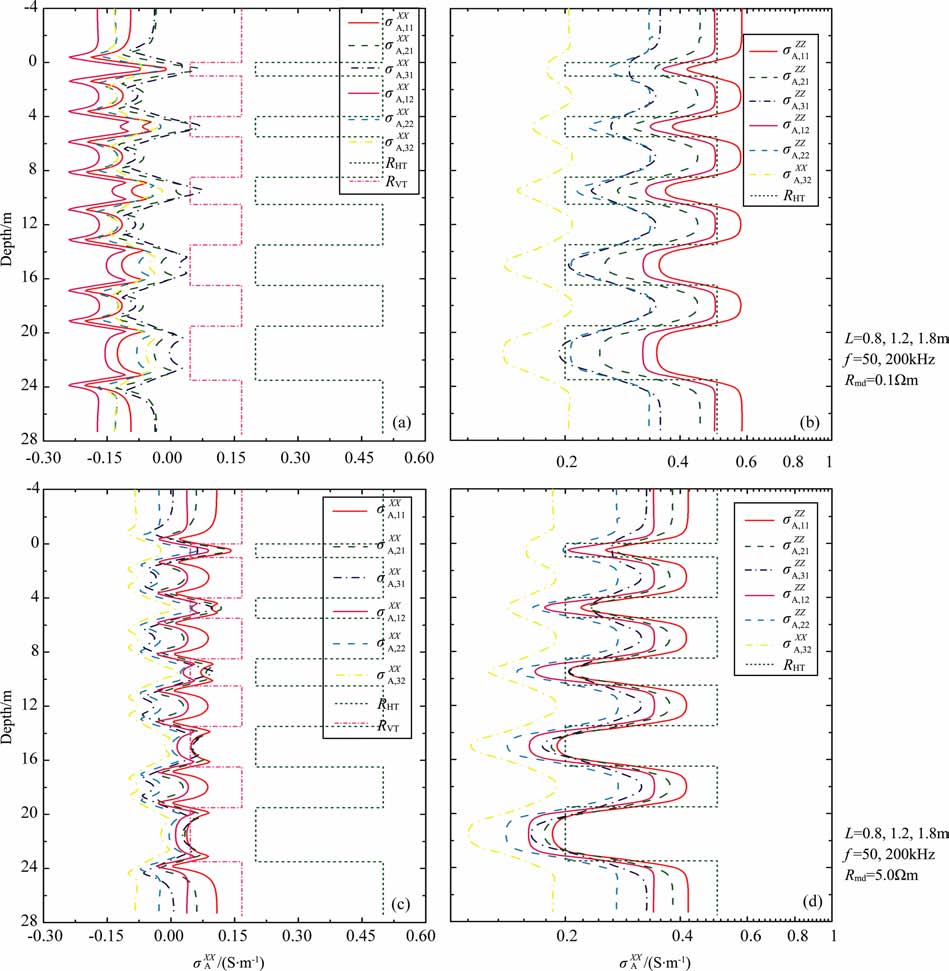
为考查层厚和泥浆电阻率变化对阵列多分量感应测井影响,并了解仪器的纵向分辨率大小,假定模型厚度分别为1、1.5、2、3m 和4m 的高阻层与厚度均为3m 的低阻层组成的交互层,上下围岩和低阻层的横向、纵向电阻率为1/(σHT,σVT)= (2,6)Ωm, 而高阻层横向、纵向电阻率为1/(σHT,σVT)= (25,85)Ωm.图 3是泥浆电阻率分别为Rmd=0.1、5.0Ωm时阵列多分量感应测井仪器的正演结果.数值结果清晰显示,源距、工作频率、层厚以及泥浆电阻率变化等,均对测井响应产生明显的影响.如果细心观测数值结果可以发现几个有趣的现象,首先分析图 3a中低阻泥浆情况下共面线圈系的主响应σAXX ,不难看出,源距增加会导致整个视电导率增大而频率增加导致视电导率减小,且在低阻层的层界面附件出现大量的负响应;σAXX 对不同厚度的高阻层均有明显反映,且在厚度2m 以下的薄层上,由于受围岩影响较大,其视电导率明显大于厚层上的视电导率,此外,高阻地层上几乎没有负响应.图 3c中高阻泥浆对应σAXX 响应,其变化规律与图 3a中低阻泥浆情况有很大不同,高阻泥浆对应的视电导率σAXX 明显大于低阻泥浆时的视电导率,并且源距增加会导致整个视电导率降低.特别需要指出的是,不论是在低阻还是在高阻泥浆情况下,其视电导率曲线σAXX 均难以直接指示出地层电导率的大小,且共面线圈系的纵向分辨率最多为1 m.图 3b和3d是低阻和高阻泥浆情况下共轴线圈系响应σAZZ ,共轴线圈系的响应特征要简单得多,从曲线的变化形态能够较易识别各个地层上电导率的相对大小,且源距(或频率)增加,会导致电导率地层上的视电导率减小、电阻率地层的视电导率增加,电导率泥浆和电阻率泥浆下的测井响应有一定的差别,但没有共面线圈系情况明显.图 3中含有314个深度点,在2.5GHz双核笔记本电脑上完成两个不同电阻率泥浆情况下的所有计算,使用的CPU 时间为4340.8+4472.4s.
|
图 3 无侵地层模型中阵列多分量感应测井响应(低阻和高阻率泥浆). (a)σAXX(Rmd = 0.1 nm); (b)σAZZ(Rmd = 0.1 nm);(c)σAXX(Rmd = 5.0 Dm) ; (d)σAZZ(Rmd = 5.0 Dm).上下围岩和低阻地层电阻率为1/(σHT,σVT) = (2,6)Ωm且地层厚度为3ra;髙阻地层电阻率为l/(σHT,σVT)=(25,85)Ωm且从上到下各个地层的厚度分别是1、1.5、2、3 ra和4 ra.井眼泥浆电阻率分别为Rmd = 0.1和5.0 Ωm, 图中电导率σA,βγXX,和σA,βγZZ办的下标β=1,2,3和γ= 1,分别对应于源距为0.8、1.2和1.8m和发射频率为50和200 kIIz的视电导率. Fig. 3 The MCIL responses in the inhoraogeneous TI raodel without invasion zone but the conductive raud or resistive mud |
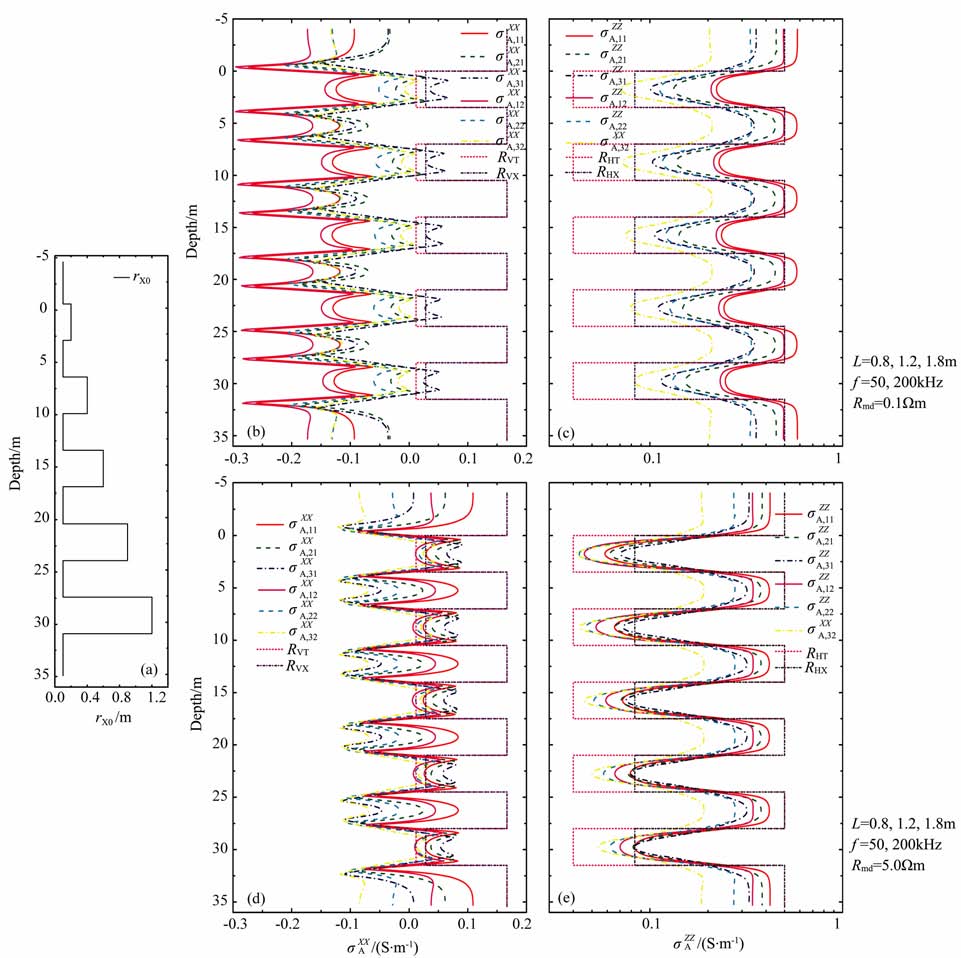
最后,为考查阵列多分量感应仪器的探测深度,假定上下围岩和导电率地层横向、纵向电阻率均为1/(σHT,σVT)= (2,6)Ωm, 导电率地层厚度均为3m, 5个电阻率地层厚度均3.5m, 其原状地层和侵入带横向、纵向电阻率均为1/(σHT,σVT)= (25,85)Ωm和1/(σXT,σVX)= (12,35)Ωm 且从上到下其各地层的侵入半径分别是0.2、0.4、0.6m、0.9m和1.2m.图 4是泥浆电阻率分别为Rmd=0.1和5.0Ωm时,阵列多分量感应测井响应的数值模拟结果.从图 4b中低阻泥浆情况下共面线圈系的主响应σAXX 曲线同样可以看出,源距增加会导致整个视电导率增大而频率增加导致视电导率减小,且在低阻层的层界面附件出现大量的负响应;高阻地层上负响应明显降少,且不同侵入深度地层上的视电导率曲线的差异也很小,从曲线形态差异和其视电导率的大小难以判断侵入深度变化对于测井响应的影响,不过,如果对视电导率采用对数表示,在侵入半径1.2m 的地层上,仍然可以看出侵入带影响.图 4d是高阻泥浆情况下共面线圈系的主响应σAXX 曲线,同样地,高阻泥浆对应的视电导率σAXX 明显大于低阻泥浆时的视电导率,并且源距增加会导致整个视电导率降低.图 4c和4e给出的低阻和高阻泥浆情况下的共轴线圈系响应σAZZ ,对侵入深度的变化有非常明显响应.图 4中含有394个深度点,在2.5GHz双核笔记本电脑上完成两个不同电阻率泥浆情况下的所有计算,使用的CPU 时间为6478.0+6597.6s.
|
图 4 不同侵人深度地层模型上阵列多分量感应测井响应(低阻和高阻泥浆) (a)侵人半径;(b)σAXX(Rmd = 0.lΩm); (c)σAXX(Rmd = 0.1Ωm).(d)σAXX(Rmd= 5.0 Ωm); (e)σAXX(Rmd= 5.0 Ωm).围岩和低阻地层不含侵人其电阻率为1/(σHT,σVT)= (2,6)Ωm;髙阻地层含义侵人、电阻率为1/(σHT,σVT) = (25,85)Ωm和1/(σXT,σVX) =(12,35)Ωm, 且从上到下其各地层的侵人半径分别是0.2、0.4、0.6、0.9 m和1.2m;各个地层厚度为3.5m.泥浆电阻率分别为只rad =0.1 和 5.0 Ωm. Fig. 4 The MCIL responses in the inhomogeneous TI model with variable invasion radii for the cases of the conductive raud or resistive raud |
本文用模式匹配算法建立了水平层状非均质各向异性地层中阵列多分量感应测井响应快速算法.利用电导率导数在柱状界面的奇异性,得到两个附加奇异微分算子,能够有效描述积累面电荷对电磁场的影响,使模式匹配算法能够快速准确地模拟非均质各向异性地层中阵列多分量感应的测井响应.
数值计算结果显示,源距、工作频率、地层厚度、侵入半径以及泥浆电阻率等变化,均对共面线圈系的主响应σAXX 产生明显影响.由于共面线圈系的空间响应函数与共轴线圈系的空间响应函数存在非常大的差别,共面线圈系主响应对泥浆电阻率的变化非常敏感,低阻泥浆情况下的视电导率σAXX 变化特征与高阻泥浆对应的视电导率σAXX 存在着很大差异;低阻泥浆视电导率明显小于高阻泥浆的视电导率;由于积累面电荷影响,在低阻层界面附件往往出现大量的负响应,而高阻层中的负响应明显较少;在不同侵入深度的高阻层上,由于共面线圈系的视电导率非常小,从曲线形态差异和视电导率大小难以判断侵入深度变化对于测井响应的影响.与共面线圈系响应相比,共轴线圈系响应σAZZ 要简单得多,从测井曲线的变化形态较易识别各个地层上电导率的相对大小,泥浆电阻率变化对共轴线圈系响应有一定影响,但没有共面线圈系明显.
附录
将l阶谐变电场强度的旋度公式Δ×El=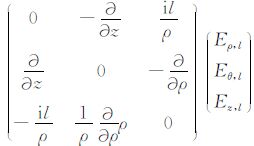

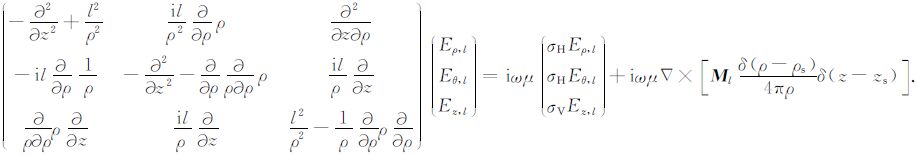
|
(A1) |
从(A1)中提取出柱坐标系中(ρ,θ)两个水平方向对应的偏微分方程:
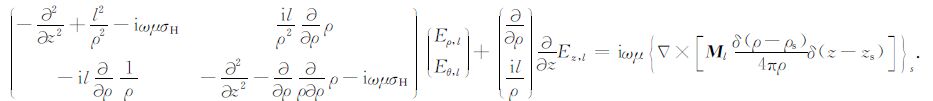
|
(A2) |
其中(A2)右端的下标“s"表示旋度的水平分量.进一步利用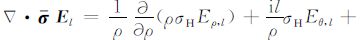
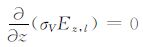
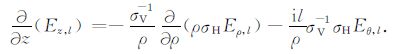
|
(A3) |
将(A3)代人(A2),并经整理得到方程(6)和(7).
| [1] | Moran J H, Gianzero S. Effects of formation anisotropy on resistivity-logging measurements. Geophysics , 1979, 44(7): 1266-1286. DOI:10.1190/1.1441006 |
| [2] | 汪宏年, 杨善德, 王艳. 各向异性地层中电阻率测井的响应特征. 石油地球物理勘探 , 1999, 34(6): 649–656. Wang H N, Yang S D, Wang Y. The response characteristic of resistivity log in anisotropic formations. Oil Geophys. Prospect. (in Chinese) , 1999, 34(6): 649-656. |
| [3] | Rabinovich M, Gonfalini M, Rocque T, et al. Multi-component induction logging: 10 years after. SPWLA 48th Annual Logging Symp., 2007, Paper CC. |
| [4] | Kennedy D, Peksen E, Zhdanov M. Foundations of tensor induction well-logging. Petrophysics , 2001, 42(6): 588-610. |
| [5] | 孙向阳, 聂在平, 赵延文, 等. 用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应. 地球物理学报 , 2008, 51(5): 1600–1607. Sun X Y, Nie Z P, Zhao Y W, et al. The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1600-1607. |
| [6] | Davydycheva S, Druskin V, Habashy T. An efficient finite-difference scheme for electromagnetic logging in 3D anisotropic inhomogeneous media. Geophysics , 2003, 68(5): 1525-1535. DOI:10.1190/1.1620626 |
| [7] | 杨守文, 汪宏年, 陈桂波, 等. 倾斜各向异性地层中多分量电磁波测井响应三维时域有限差分(FDTD)算法. 地球物理学报 , 2009, 52(3): 833–841. Yang S W, Wang H N, Chen G B, et al. The 3-D finite difference time domain (FDTD) algorithm of response of multi-component electromagnetic well logging in a deviated and layered anisotropic formation. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 833-841. |
| [8] | 张烨, 汪宏年, 陶宏根等. 用矢势和标势的三维有限体积法模拟非均匀各向异性地层的多分量感应仪器响应. 地球物理学报, (录用待刊). Zhang Y, Wang H N, Tao H G, et al. Finite volume algorithm of responses of multicomponent induction well logging tools in 3D inhomogeneous anisotropic formation using scalar-vector potentials, Chin. Journal of Geophy. (in Chinese), (accept). |
| [9] | Wang H N, So P, Yang S W, et al. Numerical modeling of multicomponent induction well logging tools in the cylindrically stratified anisotropic media. IEEE Trans on Geosci and Remote Sensing, IEEE Trans. On Geosci. and Remote Sensing , 2008, 46(4): 1134-1147. DOI:10.1109/TGRS.2008.915748 |
| [10] | 沈金松, 郭乃川. 各向异性层状介质中视电阻率与磁场响应研究. 地球物理学报 , 2008, 51(5): 1608–1619. Shen J S, Guo N C. Study on the apparent resistivity and magnetic field responses of a layered earth with arbitrary anisotropy. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1608-1619. |
| [11] | 姚东华, 汪宏年, 杨守文, 等. 用传播矩阵法研究层状正交各向异性地层中多分量感应测井响应. 地球物理学报 , 2010, 52(12): 3026–3037. Yao D H, Wang H N, Yang S W, et al. Study on the responses of multi-component induction logging tool in layered orthorhombic anisotropy formations by using propagator matrix method. Chinese J. Geophys. (in Chinese) , 2010, 52(12): 3026-3037. |
| [12] | Wang G L, Torres-Verdín C, Gianzero S. Fast simulation of triaxial borehole induction measurements acquired in axially symmetrical and transversely isotropic media. Geophysics , 2009, 74(6): E233-E249. DOI:10.1190/1.3261745 |
| [13] | Chew W C. Waves and fields in inhomogeneous media. New York: Van Nostrand Reinhold, 1990 . |
| [14] | Liu Q H, Chew W C. Diffraction of nonaxisymmetric waves in cylindrically layered media by horizontal discontinuities. Radio Sci. , 1992, 27(5): 569-581. DOI:10.1029/92RS00910 |
| [15] | 汪宏年, 陶宏根, 姚敬金, 等. 用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应. 地球物理学报 , 2008, 51(5): 1591–1599. Wang H N, Tao H G, Yao J J, et al. Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1591-1599. |
| [16] | Wang H N, Tao H G, Yao J J, et al. Fast multiparameter reconstruction of multicomponent induction well-logging datum in a deviated well in a horizontally stratified anisotropic formation. IEEE Trans. On Geosci. and Remote Sensing , 2008, 46(5): 1525-1534. DOI:10.1109/TGRS.2008.916080 |
| [17] | Wang H N, Tao H G, Yao J J, et al. An efficient and reliable simulation of multicomponent induction logging response in horizontally stratified inhomogeneous TI formations by numerical mode matching method. IEEE Trans. on Geosci. and Remote Sensing (accept). |
| [18] | Wang H N. Adaptive regularization iterative inversion of array multicomponent induction well logging datum in a horizontally stratified inhomogeneous TI formation. IEEE Trans. on Geosci. and Remote Sensing , 2011, 49(11): 4483-4492. DOI:10.1109/TGRS.2011.2142187 |
| [19] | 李荣华, 冯果忱. 微分方程数值解法. (版本). 北京: 高等教育出版社, 1996 . Li R H, Feng G C. Numerical Method of Differential Equation (in Chinese). Beijing: Higher Education Publication House, 1996 . |
 2012, Vol. 55
2012, Vol. 55

