2. 吉林大学电子科学与工程学院, 长春 130012
2. College of Electronic Science and Engineering, Jilin University, Changchun 130012, China
航空瞬变电磁法具有快速、灵活、高效等优点,目前已经成为较流行的矿产资源勘查手段[1],它广泛用于矿产资源勘探、水文地质调查、未爆炸物探测等领域[2-5].近几年,我国在863 计划资助下开展了吊舱式直升机航空TEM 系统的开发和集成工作,并取得一些阶段性理论成果[6-7],由于我国航空电磁法(AEM)相对薄弱,很多涉及系统级的关键理论问题亟待解决.
目前我国TEM 发射波形主要采用方波或梯形波,观测时间为无发射电流期间(发射电流I(t)=0),即所谓off-time观测,加拿大Geotech公司的VTEM旋翼系统即采用这种观测方式.但off-time观测的一个最大缺点是,由于高电导目标体的时间常数很大,涡流衰减很慢,感应的二次场很弱,而高电导目标又是最有开发价值的高品位富矿.虽然VTEM 系统具有通过dB/dt积分获得B的功能以提高灵敏度[8],但高电导率目标体响应弱的问题未从根本上解决.
目前很多国际先进的TEM 系统都具有on-time探测功能,即在有发射电流期间(I(t)≠0)采集,比如加拿大Fugro公司的GeoTEM 和MegaTEM固定翼系统,发射电流为半正弦[8];加拿大Aeroquest公司的AeroTEM 旋翼系统,发射电流为三角波等[9].因此,研究不同发射电流波形对on-time 和off-time瞬变电磁响应的规律,对于合理设计和系统优化并取得很好的应用效果意义重大.目前关于波形的影响规律多限于梯形波响应规律研究[10-12],但各种发射波形对响应的影响,尤其是on-time探测的问题国内还未见报道.
Liu[13]对阶跃波、方波、梯形波、三角波和半正弦波在off-time期间的响应做了报道,其响应模型为自由空间中按指数衰减的导体回线.本文在该模型下对off-time各种波形的响应进行了更为深入的讨论,且将自由空间回线模型推广至on-time响应进行研究,在此基础上揭示了on-time响应的许多重要规律,这些规律可为今后航空TEM 系统标定[14-16]以及设计具有on-time测量功能的系统提供理论指导.
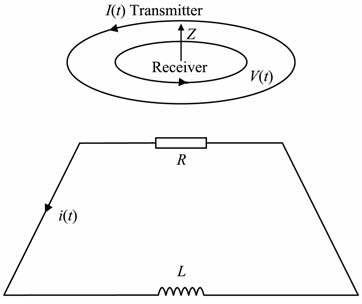
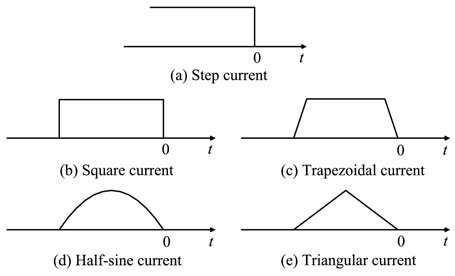
2 TEM 常用发射电流波形的响应图 1为自由空间中TEM 系统响应模型,其中I(t)为发射电流,i(t)为回线感应电流,V(t)为接收线圈响应电压,R和L分别为回线的电阻和电感.TEM 常用发射电流波形为矩形、梯形、三角形和半正弦.便于理论对比,对阶跃电流也一并讨论,各种电流波形如图 2所示.下面首先通过对阶跃电流响应的讨论,获得系统的冲激响应函数,通过该冲激响应函数与各种发射电流的卷积得到系统的响应.
|
图 1 TEM 系统响应模型 Fig. 1 Response model of TEM system |
|
图 2 典型TEM 发射电流波形示意图 Fig. 2 Schematic plot of typical transmitter current waveforms |
图 2a的阶跃电流可表示为

|
(1) |
其中I0 为电流峰值,u(t)为单位阶跃函数.由图 1模型可得阶跃电流的响应为
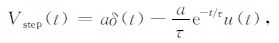
|
(2) |
其中a=-MTLMLRI0/L,MTL 为发射线圈与地回路的互感,MLR 为地回路与接收线圈的互感[14],τ =L/R为回线时间常数.图 1所示系统满足如下卷积关系:
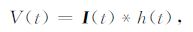
|
(3) |
将(1),(2)式代入(3)式并求导可得系统冲激响应为
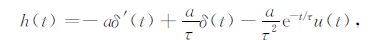
|
(4) |
当输入电流为I(t)时,得到系统的响应为
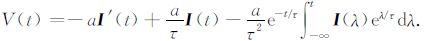
|
(5) |
由图 2可知各种电流的时域表达如下:
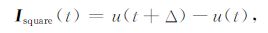
|
(6) |
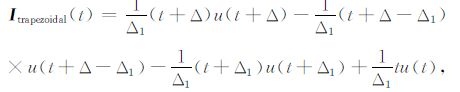
|
(7) |
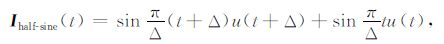
|
(8) |
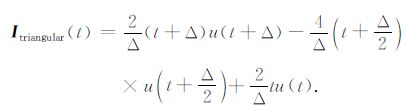
|
(9) |
将(6)~(9)式代入(5)式得各波形全时域响应如下:
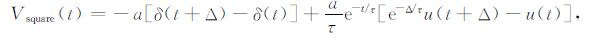
|
(10) |
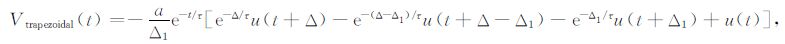
|
(11) |
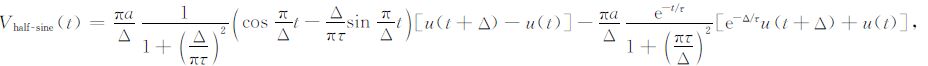
|
(12) |
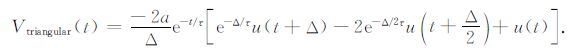
|
(13) |
由(2)、(10)~ (13)五式可获得在电流关断的off-time(t>0)期间激励响应分别为
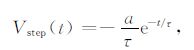
|
(14) |
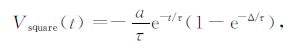
|
(15) |
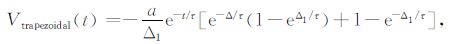
|
(16) |
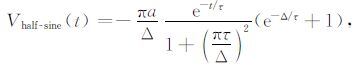
|
(17) |

|
(18) |
对(14)~(18)式分别取极限可求得off-time响应初值如下:
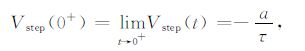
|
(19) |
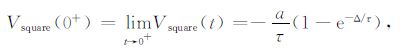
|
(20) |
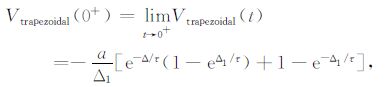
|
(21) |
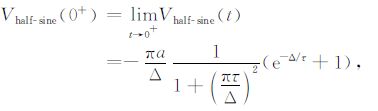
|
(22) |
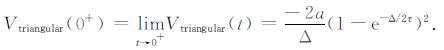
|
(23) |
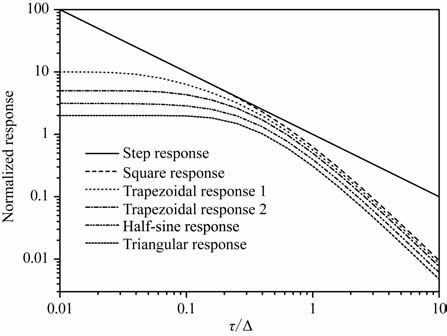
将(19)~(23)式对-a/Δ 归一化,得到响应初值幅度随τ/Δ变化的规律如图 3所示.其中Trapezoidal1和Trapezoidal2 的沿宽与脉宽的比值分别为0.1和0.2.
|
图 3 Off-time不同电流响应的初值与τ/Δ的关系 Fig. 3 Initial value of off-time response vs.τ/Δ |
由图 3可见off-time期间信号初值受τ/Δ 影响较大,下面分别讨论不同τ/Δ 对响应初值的影响规律.
当τ/Δ 较小时:
(1) 当τ/Δ<0.1 时,阶跃激励与方波激励的响应初值趋于一致,响应初值与τ/Δ 呈反比.因此,对于低电导率目标体,off-time期间方波激励与阶跃激励效果相同,且具有最强的响应初值.
(2) 梯形、半正弦和三角波电流激励的响应在τ/Δ 较小时都趋近各自的极限值,即τ/Δ 较小时,这三种电流响应初值与τ/Δ 无关.将(21)~(23)式对a/Δ 归一化取极限可得:
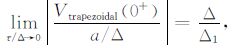
|
(24) |
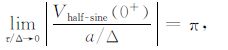
|
(25) |
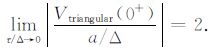
|
(26) |
由(24)式可见,当Δ 一定时,梯形波的沿时间Δ1 越小,信号越强.由(25)~(26)式可见,半正弦的响应初值为三角波的π/2倍,但都远远小于梯形波响应.
当τ/Δ 较大时:
(1) 当τ/Δ>1.0时,阶跃激励的响应幅度以一阶速率下降,其他脉冲激励的响应幅度则以二阶速率下降.该结果表明,无论梯形波还是三角波和半正弦波,在off-time期间探测高电导率目标体时,响应幅度都比较小.如果想提高信号幅度,就必须提高发射电流或者降低激励电流的基频,基频降低一半,信号幅度变为4倍.
(2) 当τ/Δ>1.0时,脉冲激励的响应曲线相互平行,即各种脉冲激励的响应在τ/Δ 较大的情况下比值不变.由(20)~(23)式可得以方波信号为基准时的各个信号的比值关系:
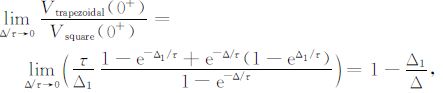
|
(27) |
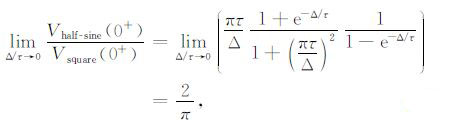
|
(28) |
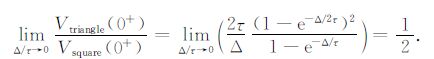
|
(29) |
下面进一步讨论这些比值的物理意义.当t>0,Δ/τ →0时,系统的响应(5)式简化为
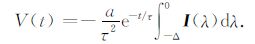
|
(30) |
其中的积分项即为发射电流与时间轴围成的面积.可见在τ/Δ 较大的情况下,off-time响应初值仅与电流与时间轴围成的面积成正比.式(27)~(29)正是这种规律的反映,该结果表明,通过提高发射波形与时间轴所围的面积,可以提高响应初值.从另一个方面证明:增加发射电流与降低基频可以使信号幅度增加.
(3) 当梯形波的沿变陡时,由于电流与时间轴所围的面积有所增加,所以信号会略有增加,但是一般情况下沿的时间与整个脉冲的时间相比可以忽略,即$1-\frac{{{\Delta }_{1}}}{\Delta }\approx 1$,所以即使沿非常陡,响应信号也不会有太大的变化.
(4)在τ/Δ=0.4时,半正弦与三角波都达到最佳激励效果(与阶跃响应最接近),因此探测不同电导率的目标体时应选择最佳的基频,梯形波的最佳激励脉宽与沿有关系,沿越陡,时间常数与最佳脉宽的比值越小.方波信号没有最佳值脉宽,脉宽越大响应信号幅度越接近阶跃信号.
4 On-time期间发射电流波形对TEM响应的影响由上面的讨论的结果可以看到,电导率增高引起目标体时间常数增加,off-time期间感应信号迅速衰减,所以这些电流脉冲对于测量低电导率目标体效率很高,但对高电导率目标体的探测不理想.主要原因在于如果地质体电导率较高,由脉冲激励前沿在地质体产生的涡流与脉冲后沿产生的涡流相互抵消,从而使off-time响应大大降低.所以需要研究on-time期间响应的特点.
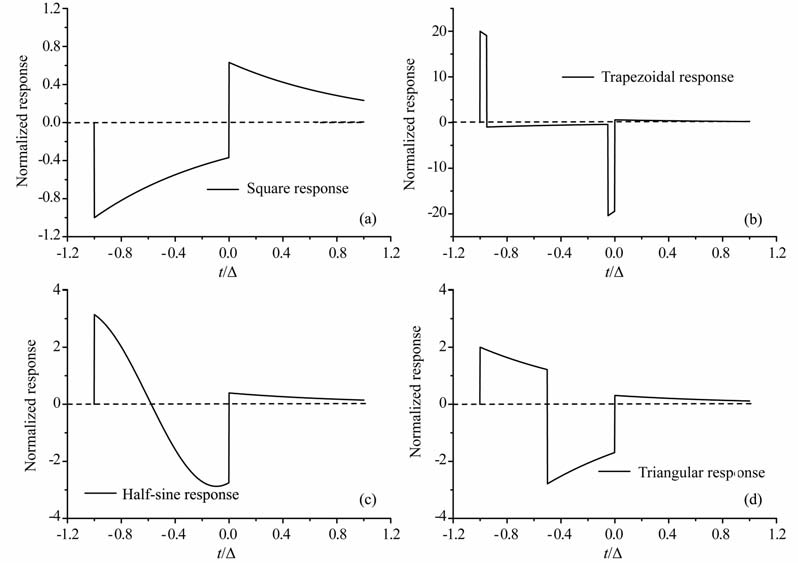
4.1 On-time采集区间的定义将公式(10)~(13)幅度对-a/Δ 归一化,时间对脉宽Δ 归一化,得到各种发射电流波形的时域响应如图 4 所示,其中回线时间常数τ = Δ,梯形波Δ1/Δ =0.05.
|
图 4 不同激励电流的时域响应 Fig. 4 Pulse response of different current in time domain |
如图 4所示,方波激励响应在整个on-time时间呈指数衰减,定义(-Δ,0)为方波激励响应的on-time信号采集区间;梯形波激励响应在上升沿与下降沿时间段内变化剧烈,一次场与二次场信号幅度非常高,并且由于梯形波沿时间很短,接收信号受线圈过渡过程的影响较大,实际无法得到精确的二次场信号,因此定义梯形波激励响应的on-time信号采集区为(-Δ+Δ1,-Δ1);半正弦波的激励响应在整个on-time期间不发生突变,因此定义半正弦激励响应的on-time信号采集区间为(-Δ,0);三角波激励在整个on-time区间内有一处突变,并且信号幅度变大,所以定义(-Δ/2,0)为三角波激励响应的on-time信号采集区间.
4.2 On-time期间不同激励电流响应的初值由(10)~(13)式,得到各个激励波形在on-time采集区间的响应如下:
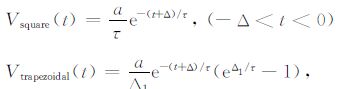
|
(31) |
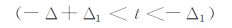
|
(32) |
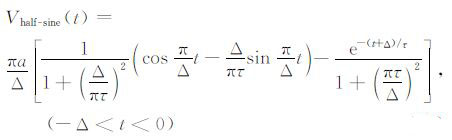
|
(33) |
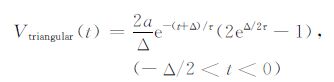
|
(34) |
由(31)~(34)式得到不同波形响应的初值分别为
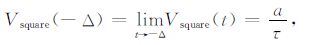
|
(35) |

|
(36) |
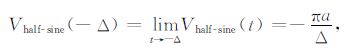
|
(37) |
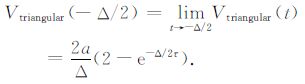
|
(38) |
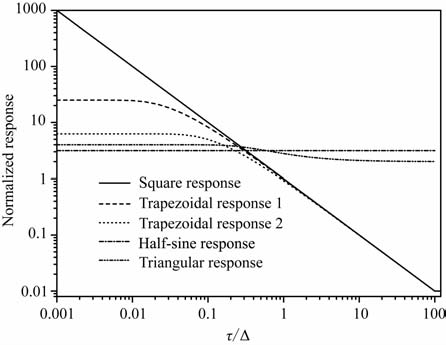
将(35)~(38)式对-a/Δ归一取幅度,如图 5所示.其中Trapezoidal1和Trapezoidal2的沿宽分别为Δ1/Δ =0.04和Δ2/Δ =0.16
|
图 5 On-time不同电流响应的初值与τ/Δ的归一化关系 Fig. 5 Initial value of on-time response vs.τ/Δ |
当τ/Δ 较小时:
(1) 当τ/Δ 较小时,方波激励响应的幅度最大,并且随着回线时间常数减小而增加,梯形波激励的响应幅度小于方波激励响应,但是大于三角波激励与半正弦激励响应.
(2) 当τ/Δ<0.1时,梯形波激励、三角波激励和半正弦激励的响应都趋于恒定,不随时间常数的变化而变化,梯形波激励的响应幅度随着上升沿的斜率增加而增加,(36)~(38)式对-a/Δ归一化,计算得到各种波形的激励响应在τ/Δ→0时极限分别为
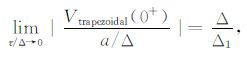
|
(39) |
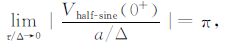
|
(40) |
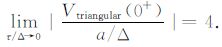
|
(41) |
对于梯形波的响应,当脉宽一定时,沿时间与响应成反比,沿越短,激励信号幅度越大,当Δ1 → 0时,梯形波的响应趋于方波响应.
(3) 对比(20),(21)式与(35),(36)式可以发现,在低电导率区域,梯形波激励响应的off-time信号与on-time信号幅度相同,但是on-time采集要求消除一次场的影响,并且on-time采集的噪声比off-time要大[9],所以方波激励与梯形波激励都不适用于on-time信号采集,在实际使用中,地面系统都采用方波或者梯形波激励采集off-time信号.
当τ/Δ 较大时:
(1) 梯形波与方波激励响应在τ/Δ >0.3时小于三角波与半正弦激励响应.方波激励响应与梯形波激励响应随回线时间常数的增加而一阶速率下降,不同上升沿时间的梯形波初值都趋于方波激励的初值.可见在on-time期间,梯形波和方波激励在探测高电导率目标体时会随着电导率的增加而下降,因此不适合探测高电导率目标体.
(2) 半正弦激励响应的幅度与时间常数无关保持恒定.当τ/Δ>1时,三角波信号幅度逐渐下降为低电导率时的一半,并保持恒定.所以利用三角波和半正弦的on-time 信号可以探测到低电导率目标体.三角波激励与半正弦激励是航空TEM 系统中最常用的波形.半正弦波的优点在于可以获得更大的峰值磁矩,进行深部探测,如固定翼航空TEM 的GeoTEM 与MegaTEM 都采用半正弦激励;三角波的优点在于一次场响应简单,适于浅部低阻体探测,以及早期信号的采集与处理,旋翼航空TEM,如AreoTEM 采用三角波激励.此外由于三角波与半正弦激励响应幅度与τ 值关系不大,可以适当地提高信号基频,以提高信号的叠加次数,从而提高信噪比和空间分辨率.
5 On-time与Off-time时间域全响应对比上面只是分别讨论了不同波形在on-time 和off-time响应初值的规律,还不能完整描述整个时间域信号在off-time和on-time的规律,下面以加拿大AeroTEM 使用的三角波为例,在不同的时间段进行抽道平均,给出各道在off-time 和on-time期间的响应结果并进行对比分析.图 6 为三角波在off-time期间的响应随τ/Δ 变化曲线(见公式(18));图 7为三角波在on-time期间的响应随τ/Δ 变化曲线(见公式(34)).off-time和on-time均取10 个抽道窗口.由图 6和图 7可见,三角波对高电导率矿体的on-time响应远大于off-time响应.三角波对低电导率矿体的on-time响应与off-time响应几乎相同,这与文献[9]在均匀半空间中板状矿体模型的结果完全吻合,故本文回线模型同样可以反映on-time期间的响应规律.由于通常航空TEM 的on-time期间噪声较大(1nT/s[9]),而off-time期间噪声较小(0.25nT/s[9]),低电导矿体利用三角波的off-time期间采集,可获得较高的信噪比.on-time采集既然对高τ/Δ 值的矿体敏感,这使得通过降低脉宽Δ 以获取高的响应信号成为可能.低的Δ 意味着高的基频,而高的基频又意味着信号叠加次数的增加,这对降低噪声提高信噪比和提高勘探深度是有益的[17].此外,基频的提高还可以显著改善系统的空间分辨率.AeroTEM 通常采用150Hz的基频.
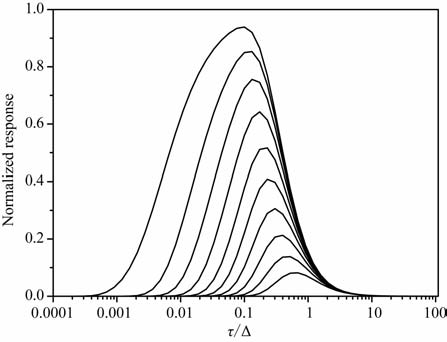
|
图 6 Off-time 10抽道响应随τ/Δ变化曲线 Fig. 6 Off-time normalized response for the 10 channels vs.τ/Δ |
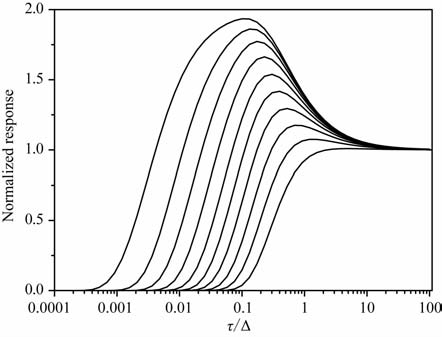
|
图 7 On-timelO抽道响应随τ/Δ变化曲线 Fig. 7 On-time normalized response for the 10 channels vs.τ/Δ |
由自由空间导电回线模型给出的响应规律具有简洁的数学表达,易于揭示不同发射电流波形在off-time和on-time响应的特点,且结论具有普遍的指导意义.
方波激励与梯形波激励适于off-time采集,而不适于on-time采集,在低电导率区域,方波与梯形波的on-time响应与off-time响应幅度相当,但是on-time采集时的噪声要大于off-time采集时的噪声,所以off-time采集可以获得更高的信噪比.地面系统通常使用方波或者是梯形波激励进行探测,但是在高电导率区域,on-time与off-time信号都会随电导率的增高而减小,所以系统对高电导率的探测能力以及分辨率都会下降.
半正弦激励与三角波激励适于航空TEM 探测,航空系统同时采集on-time信号和off-time信号.在高电导率区域进行on-time采集时,三角波激励与半正弦激励响应信号幅度几乎不随电导率的提高而下降,所以可以探测更高电导率的目标体,同时还能提高对高电导率目标体的分辨率.航空TEM通过提高发射磁矩来获得较强的off-time信号,以提高off-time信号的信噪比与探测深度.
在进行off-time测量时,梯形波、三角波与半正弦波激励都有最佳脉宽,即当τ/Δ = 0.4 时,系统可以获得最佳的响应信号,所以对于不同导电性的目标体需要选择最佳的基频信号进行测量.方波激励没有最佳脉冲宽度,脉宽越大信号幅度越大.在进行on-time测量时,由于半正弦激励和三角波激励的信号幅度与电导率关系不大,所以可以适当地提高基频信号以增加信号的叠加次数,提高系统的信噪比和空间分辨率.
| [1] | Stolz E M. Electromagnetic methods applied to exploration for deep nickel sulphides in the Leinster area, Western Australia. Exploration Geophysics , 2000, 31(2): 222-228. DOI:10.1071/EG00222 |
| [2] | Danielsen J E, Auken E, Jrgensen F, et al. The application of the transient electromagnetic method in hydrogeophysical surveys. Journal of Applied Geophysics , 2003, 53(4): 181-198. DOI:10.1016/j.jappgeo.2003.08.004 |
| [3] | Massoud U, Abbas A M, Mesbah H S A, et al. Mapping of subsoil water level and its impacts on Hawara archeological site by transient and multi-frequency electromagnetic survey. Chinese J. Geophys. , 2010, 53(3): 638-645. |
| [4] | Holladay J S, Doll W E, Beard L P, et al. UXO time-constant estimation from helicopter-borne TEM data. Journal of Environmental and Engineering Geophysics , 2006, 11(1): 43-52. DOI:10.2113/JEEG11.1.43 |
| [5] | Fountain D. Airborne electromagnetic systems-50 years of development. Exploration Geophysics , 1998, 29(2): 1-11. DOI:10.1071/EG998001 |
| [6] | 朱凯光, 林君, 韩悦慧, 等. 基于神经网络的时间域直升机电磁数据电导率深度成像. 地球物理学报 , 2010, 53(3): 743–750. Zhu K G, Lin J, Han Y H, et al. Research on conductivity depth imaging of time domain helicopter-borne electromagnetic data based on neural network. Chinese J. Geophys. (in Chinese) , 2010, 53(3): 743-750. |
| [7] | 嵇艳鞠, 林君, 关珊珊, 等. 直升机航空TEM中心回线线圈姿态校正的理论研究. 地球物理学报 , 2010, 53(1): 171–176. Ji Y J, Lin J, Guan S S, et al. Theoretical study of concentric loop coils attitude correction in helicopter-borne TEM. Chinese J. Geophys. (in Chinese) , 2010, 53(1): 171-176. |
| [8] | Smith R S, Annan A P. Using an induction coil sensor to indirectly measure the B-field response in the bandwidth of the transient electromagnetic method. Geophysics , 2000, 65(5): 1489-1494. DOI:10.1190/1.1444837 |
| [9] | Balch S J, Boyko W P, Paterson N R, et al. The AeroTEM airborne electromagnetic system. The Leading Edge , 2003, 7: 562-566. |
| [10] | Raiche A P. The effect of ramp function turn-off on the TEM response of layered earth. Exploration Geophysics , 1984, 15(1): 37-41. DOI:10.1071/EG984037 |
| [11] | Fitterman D V, Anderson W L. Effect of transmitter turn-off time on transient soundings. Geoexploration , 1987, 24(2): 131-146. DOI:10.1016/0016-7142(87)90087-1 |
| [12] | 嵇艳鞠, 林君, 于生宝, 等. ATTEM系统中电流关断期间瞬变电磁场响应求解的研究. 地球物理学报 , 2006, 49(6): 1884–1890. Ji Y J, Lin J, Yu S B, et al. A study on solution of transient electromagnetic response during transmitting current turn-off in the ATTEM system. Chinese J. Geophys. (in Chinese) , 2006, 49(6): 1884-1890. |
| [13] | Liu G M. Effect of transmitter current waveform on airborne TEM response. Exploration Geophysics , 1998, 29(2): 35-41. DOI:10.1071/EG998035 |
| [14] | Davis A C, Macnae J. Quantifying AEM system characteristics using a ground loop. Geophysics , 2008, 73(4): 179-188. DOI:10.1190/1.2943189 |
| [15] | Davis A C, Macnae J. Measuring AEM waveforms with a ground loop. Geophysics , 2008, 73(6): F213-F222. DOI:10.1190/1.2976791 |
| [16] | Yin C C, Hodges G. Wire-loop surface conductor for airborne EM system testing. Geophysics , 2009, 74(1): F1-F8. DOI:10.1190/1.3008055 |
| [17] | Spies B R. Depth of investigation in electromagnetic sounding methods. Geophysics , 1989, 54(7): 872-888. DOI:10.1190/1.1442716 |
 2012, Vol. 55
2012, Vol. 55


