2. 中国地质大学地球物理与信息技术学院, 北京 100083
2. Colledge of Geophysics and Information Technology of China University of Geosciences, Beijing 100083, China
核磁共振(NMR)测井[1, 2]具有多种烃类检测模式,能在一定条件下识别流体性质[3-8].但是,NMR测井在识别和定量评价油气水时却存在很大的局限性,原因在于现有的NMR 测井都是基于一维核磁共振(1D NMR)技术.该项技术只测量地层孔隙流体的横向弛豫时间T2,当地层孔隙中油气和水同时存在时,其T2 谱信号有时是重叠在一起的,运用通常的移谱法、差谱法和增强扩散法很难区分它们,这就促使发展二维核磁共振(2DNMR)测井方法[9-12].
所谓2D NMR 测井技术,就是在对横向弛豫时间观测的基础上对纵向弛豫时间(T1)、流体扩散系数(D)、内部磁场梯度(G)等参数进行观测[8].二维核磁共振测井技术对仪器和数据采集方式都有一定的要求,需要对其观测模式进行重新设计.目前,Schlumberger公司的MR-Scanner 和Baker Atlas公司的新核磁仪器MR-Explorer都可进行二维核磁测井.2002 年,美国Chevron 石油公司的Boqin Sun和Dunn[12-13]以及Schlumberger公司Doll研究中心的Hurlimann 和Venkatarama[14-15]等分别提出利用2个窗口改进自旋回波脉冲序列CPMG,实现了弛豫-扩散(T2,D)分析的2D NMR 测井,极大地提高了流体识别和饱和度计算的精度.国内,谢然红、肖立志等[18]对含有顺磁物质的人造砂岩和天然泥质砂岩饱和水,进行2D NMR 实验测量,给出了岩石横向弛豫时间-内部磁场梯度的(T2,G)二维分布图,研究结果对分析陆相沉积地层复杂岩性核磁共振测量结果具有重要指导意义.在反演方法方面,顾兆斌等[19-20]利用传统的奇异值分解(SVD)和改进的奇异值分解算法分别对核磁共振二维谱进行反演,实现了二维谱的连续反演,并讨论了信噪比对反演结果的影响,展示了2D NMR 技术测量扩散系数、弛豫时间、孔隙度、含油饱和度、可动流体体积等地层流体性质的广阔前景.谢然红、肖立志等[21-22]研究了(T2,D)二维核磁共振和(T2-T1)二维核磁共振在不同储层、不同测量信噪比以及不同外加磁场梯度条件下识别流体的效果.谭茂金等[23]针对核磁共振测井双等待时间(TW)观测数据提出了基于遗传算法和最小二乘分解(LSQR)的混合反演算法,并实现了流体的T1 和T2 参数反演,为勘探新区的流体识别和参数确定提供新方法.因此,在2DNMR 测井技术还未在油田勘探中取得广泛应用的情况下,作者在前人研究成果的基础上继续开展这方面的研究,对于解决目前勘探中的流体识别难题具有现实意义.
本文简述了2D NMR 测井的基本原理,针对梯度场条件下的NMR 测井弛豫机理和2D NMR 的数学模型,利用LSQR 算法和截断奇异值分解(TSVD)算法分别实现2D NMR 的反演.考虑到两种方法的效果和优点,提出了混合反演算法,即先用LSQR 进行反演,其结果作为初值再用TSVD 算法进行反演.理想模型合成的回波数据的反演结果表明,该混合算法较单一算法在计算精度和运算效率方面均具有较大改善.而且,利用此算法,分别实现了不同流体模型的二维谱反演,并系统考察了不同磁场梯度、不同回波间隔组合对反演效果的影响,为参数设计提供了参考依据.
2 (T2,D)二维核磁共振基本原理核磁共振测井的目的是通过对地层孔隙流体中氢核NMR 信号的观测,识别地层孔隙中的流体及其含量.对于地层岩石这类复杂的多孔介质,在梯度场条件下,核磁共振T2 弛豫包括表面弛豫、体积弛豫和扩散弛豫.设等待时间为TW ,回波间隔为TE,扩散系数为D,当TW 足够长时,CPMG 核磁共振信号可以写成

|
(1) |
式中,Aik是等待时间TW 、回波间隔TEk的第i个回波的幅度,εik为噪音.p为模型所设定的扩散系数的个数,m为模型所设定的横向弛豫时间的个数.flj为扩散系数为Dl、横向弛豫时间为T2j的信号幅度.(2)式也可以写成矩阵的形式:
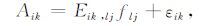
|
(2) |
式中,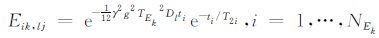
通过求取上述线性方程组,就可以得到扩散系数为Dl、横向弛豫时间为T2j的信号幅度flj,以(T2,D)图的形式表现出来,就可以进行流体评价.
3 反演算法 3.1 LSQR算法LSQR 方法是Paige和Sanders在1982年提出的一种利用Lanczos迭代法求解最小二乘问题的方法.该方法计算量小,且能很容易地利用矩阵的稀疏性简化计算,因而适合求解大型稀疏矩阵问题[24-25].
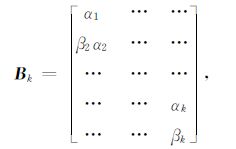
方程Ax=b的最小二乘问题min‖Ax-b‖2可以通过双对角化来求解.假定Uk= [u1,u2,…,uk]和Vk= [v1,v2,…,vk]是正交矩阵,且Bk为如下的(k+1)×k的下双角矩阵:
|
(3) |
用下列迭代方法可实现矩阵A的双对角分解:
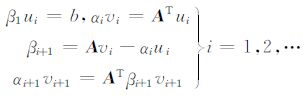
|
(4) |
其中,αi=0,βi=0.‖ui‖ ≡ ‖vi‖ =1.上式又可写成如下形式,
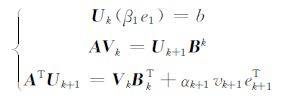
|
(5) |
其中,ek+1T表示n阶单位矩阵的第k+1行,再设

|
(6) |
可以确定

|
(7) |
由于我们希望‖rk‖ 尽量小,且Uk+1 理论上是正交矩阵,取yk使‖tk+1‖ 最小.解最小二乘问题min‖β1e1 -Bkyk‖,这就构成了LSQR算法的基础.
3.2 TSVD算法奇异值分解(Singular Value Decomposition, SVD)算法可用来求解大多数的线性最小二乘问题.奇异值分解算法给出是‖Ax-b‖2 最小意义下的一个最优解,但不满足非负约束条件.截断SVD(Truncated Singular Value Decomposition, TSVD)算法通过缩减A迭代求解,降低了解的维数,丢掉了振荡最厉害的那部分的解分量,提高了运算速度.
假设已知一个初始解x0,令b0 =Ax0,原方程可写为:A(x-x0)=b-b0,即AΔx= Δb.若求得‖AΔx-Δb‖2 最小意义下的最优解Δx,则x0 +Δx就是‖Ax-b‖2 最小意义下的最优解x.由于是求解Δx,因此在实现非负约束时,只将x小于零的分量改为零,再重新迭代计算Δx,直到x所有分量都满足非负约束.以计算Δx和Δb代替了A矩阵的奇异值分解过程.在求解的过程中,A矩阵只需进行一次奇异值分解过程,这样大大减少了计算量从而减少计算时间.
为了检验算法的效果,构造了一个具有多峰结构的二维流体模型,模拟的流体组分在二维图中均服从高斯分布形态,利用微机编制了相应的程序并对其进行相应的数值模拟实验.模拟过程中,在扩散系数(D),横向弛豫时间(T2)两个维度上进行网格剖分,剖分时均采用对数均匀布点[24].当模型建立好之后,根据观测参数及模型参数合成多组回波串,然后对这些回波串数据组合进行反演可得到二维谱图.设计模型参数如表 1.
|
|
表 1 气水流体模型及其性质 Table 1 Gas-water model and fluid properties |
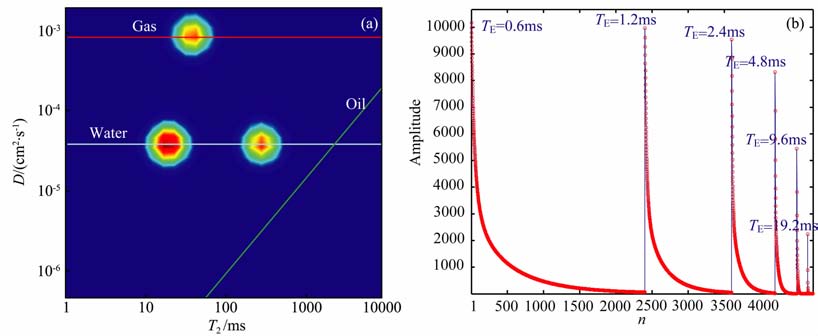
假设在完全极化的条件下,即等待时间(TW)足够长,磁场梯度为4.0×10-3T/cm, 在每个深度点设置6个回波间隔(TE)的回波串,为了确保采集周期的一致,其不同TE 组合取[0.6,1.2,2.4,4.8,9.6,19.2]ms, 对应每一个回波串,回波个数为INT(1440/TE)(其中INT 代表数值取整).正演模拟得到6组回波串如图 1所示.
|
图 1 流体模型和回波串数值模拟结果 (a)流体模型;(b)合成回波串. Fig. 1 Fluid model and numerical simulation results (a) Fluid model; (b) Synthetic echo trains. |
在数值模拟时,对模型进行30×30的网格剖分,计算得到系数矩阵A4725×900 的条件数为7.2908×10+24,此矩阵严重病态.利用合成的回波串数据,分别运用两种不同的反演算法对回波串数据进行二维反演.为了考察反演算法的效果与计算精度,记反演的相对误差为:
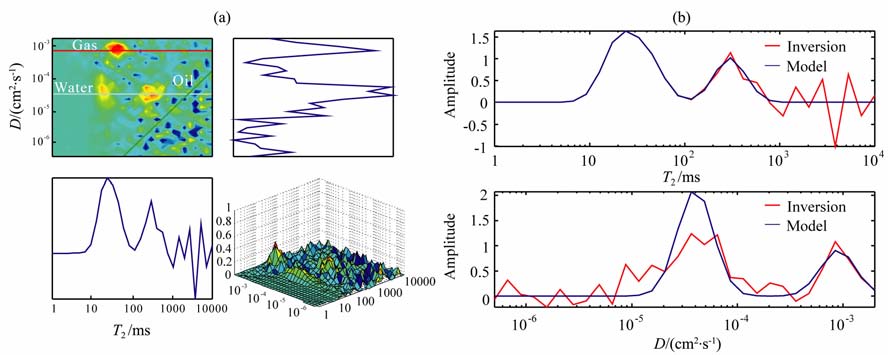
反演时,选定LSQR 和改进TSVD 算法的迭代次数均为800.图 2 和图 3 为分别利用LSQR 和改进TSVD 算法的反演结果.从图 2 和图 1 看出,反演得到的二维谱图中气信号识别较好(图 2a),在一维T2 分布上的短T2 部分(1~100 ms)重叠较好,但是在长T2 部分(100~10000 ms)重叠不好(图 2b,上);而且扩散系数与模型参数重复性差(图 2b,下),尚不能够实现流体的定性分析和流体的定量计算.
|
图 2 非负LSQR方法的反演结果 (a)反演结果;(b)反演结果与模型一维对比图. Fig. 2 Inversion results using LSQR method (a) Inversion results; (b) Inversion results comparison with model on 1D. |
|
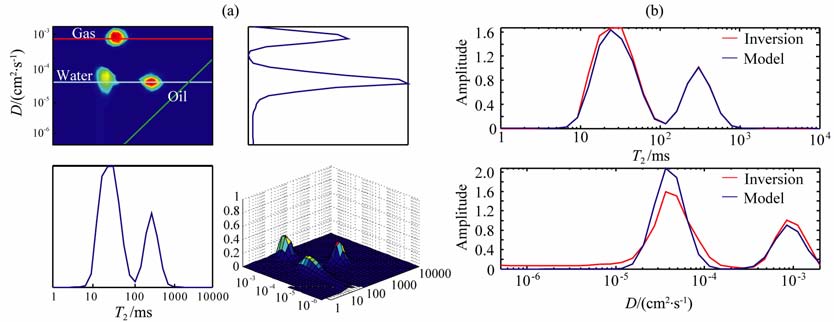
图 3 TSVD方法的反演结果 (a)反演结果;(b)反演结果与模型一维对比图. Fig. 3 Inversion results using TSVD method (a) Inversion results;b) Inversion results comparison with model on 1D. |
图 3为TSVD 方法的反演结果.与预设的流体模型(图 1)相比,该方法反演得到的二维谱图与模型匹配较好(图 3a),能基本能够实现流体的定性分析及定量计算要求,而且计算的T2 分布和扩散系数分布(简称D分布)与一维模型也具有较好的对应性,尤其是在一维T2 分布上的长T2 组分(100~10000ms)重叠较好(图 3b,上),但是短T2 组分(1~100ms)重叠较差;而且扩散系数与模型参数重复性比LSQR 算法效果要好(图 3b,下).
从计算精度和运行效率上看,LSQR 算法反演的相对误差为0.4869,计算时间为81.02s;TSVD算法反演的相对误差为0.2058,运行时间为59.64s.可以看出,TSVD 算法的反演精度比LSQR 高,而且速度快,但是其精度还有待改进.
3.3 LSQR与TSVD组合的混合反演算法反演精度高,分布连续,这对二维谱图的反演是至关重要的.改进的TSVD 降低了解的维数,使得解不完整,所以希望能把这部分解分量补上,以提高TSVD 算法的分辨率和精度.从图 2和图 3可以看出,LSQR 算法对短T2 组分的反演效果较好,且TSVD 方法对长T2 组分的反演效果较好.为此,本文采取TSVD 和LSQR 的混合算法,即先用LSQR进行反演,计算结果作为初值x0,然后再用TSVD算法进行反演.
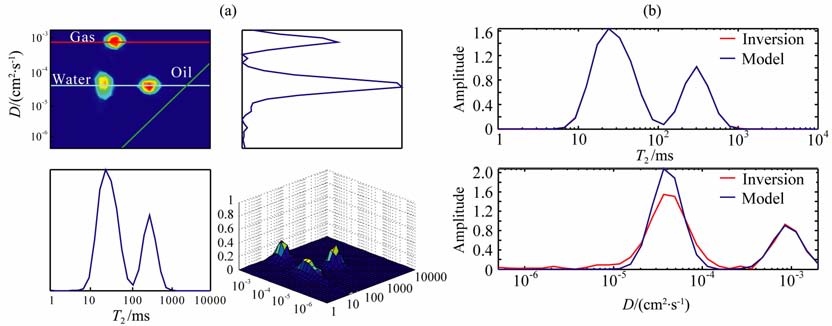
在实验中,选定LSQR 算法和TSVD 算法的迭代次数为400次.图 4为LSQR-TSVD 混合反演算法的反演结果,其束缚流体“峰"比图 3a更“聚焦",且与图 1所示的模型也很接近.此外,反演得到的T2 分布与模型几乎完全重合,反演的扩散系数也与模型更接近,尤其是慢扩散部分几乎完全重合.从运行效率和计算精度上看,混合反演算法的相对误差为0.1499,其运行时间为64.50s.当两算法的迭代次数均选为200时,计算相对误差为0.15613,计算时间为56.0156s.因此,LSQR-TSVD 方法比单一反演算法在精度和运算效率上均有明显改善.
|
图 4 LSQR-TSVD混合反演算法的反演结果 (a)反演结果;(b)反演结果与模型一维对比图. Fig. 4 Inversion results using LSQR-TSVD method (a) Inversion results; (b) Inversion results comparison with model on ID. |
此外,对于油水模型也做了类似的实验.其流体模型及其参数如图表 2所示.实验时,选定单一反演算法的迭代次数均为800次.单一LSQR 算法的反演的相对误差为0.558,单一TSVD 算法的反演的相对误差为0.2336.可以看出,TSVD 算法的反演精度比LSQR 高.从运行时间上看,LSQR 方法的运行时间为78.00s;用TSVD 算法反演时,其运行时间为56.08s.采用LSQR-TSVD 混合反演算法进行实验,当LSQR 算法和TSVD 算法迭代次数均选为400时,计算相对误差为0.1612,计算时间为67.52s;当两算法的迭代次数均选为200 时,计算相对误差为0.1563,计算时间为55.36s.因此,该混合算法同样适用于油水模型,其计算精度得到了改善,而且通过减少迭代次数也可以提高运算效率.
|
|
表 2 油水模型及其流体性质 Table 2 Oi--water model and fluid properties |
核磁共振测井测前参数设计对与识别流体是至关重要的.为了使得二维核磁共振测井能够应用于地层流体识别和参数计算中.数据核矩阵(A)和观测的回波串幅度(b)不仅受纵向弛豫时间和扩散系数的影响,而且受磁场梯度和回波间隔的影响.为此,设计了油水模型和气水模型并利用不同采集参数进行数值模拟研究,以考察不同的磁场梯度(G)和不同的回波间隔(TE)组合对反演结果的影响.表 1与表 2分别为实验的岩石物理模型及其流体性质参数.
4.1 不同磁场梯度(G)观测时,选取回波间隔组合[0.6,1.2,2.4,4.8,9.6,19.2]ms进行实验,回波个数采取上述类似的办法,设计不同的回波个数,以确保每个回波串的采集时间相同.采用不同的磁场梯度进行观测,观测磁场梯度分别为2.0×10-3T/cm、3.0×10-3T/cm 和4.0×10-3T/cm.
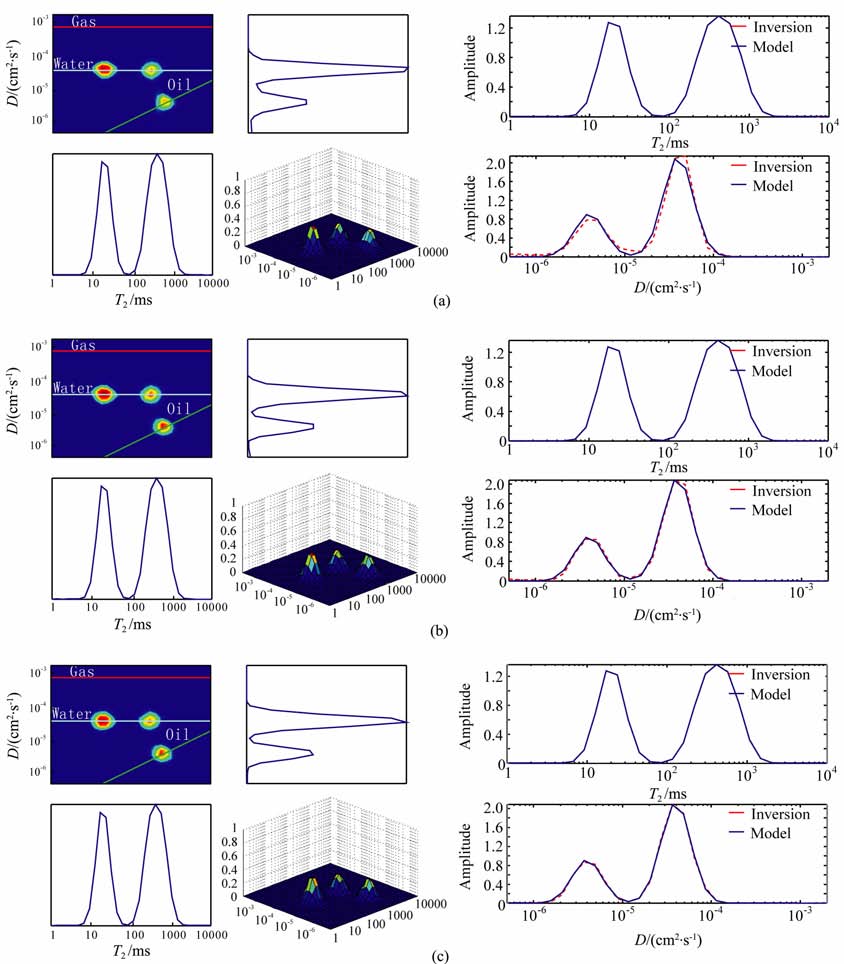
油水模型的不同磁场梯度的数值模拟和反演实验.从图 5所示的三个反演结果可以看出,磁场梯度为4.0×10-3T/cm 时的T2 分布和D分布(图 5c)均比小磁场梯度的实验结果(图 5a,b)好,并且与预设模型更接近.从计算的误差看,磁场梯度为2.0×10-3T/cm时计算的相对误差为0.1978,磁场梯度为3.0×10-3T/cm 时计算的相对误差为0.1393,磁场梯度为4.0×10-3T/cm 时计算的相对误差为0.1068.因此,在多TE 观测模式下,适当增大磁场梯度可以提高油层识别的精度.
|
图 5 不同磁场梯度下的油水模型反演结果 (a) G=2.0×10-3T/cm;(b) G=3.0×10-3T/cm;(c) G=4.0×10-3T/cm. Fig. 5 Inversion results of oil-water model under different magnetic field gradients |
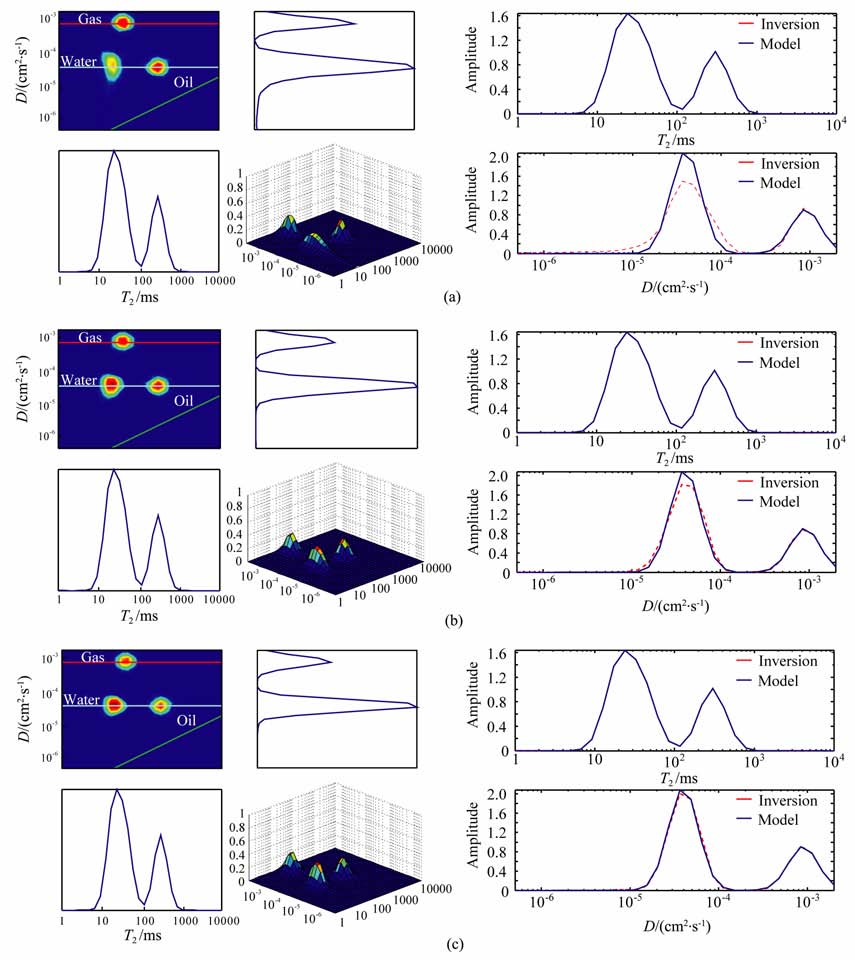
气水模型的不同磁场梯度时的正反演实验与结果对比.从图 6所示的三个反演结果可以看出,图 6(c)所示的T2 分布与扩散系数分布均与模型对比效果较好.从计算的相对误差看,在磁场梯度为2.0×10-3T/cm 下时计算的相对误差为0.3695,在磁场梯度为3.0×10-3 T/cm 下计算的相对误差为0.1931,磁场梯度为4.0×10-3T/cm 时计算的相对误差为0.1353.可以看出,增大磁场梯度可以提高气层识别的精度.
|
图 6 不同磁场梯度下的气水模型反演结果 (a) G=2.0×10-3T/cm;b) G=3.0×1×10-3T/cm;c) G=4.0××10-3T/cm. Fig. 6 Inversion results of gas-water model under different magnetic field gradient |
从油水层和气水层的适应性上说,在参数相同的情况下,油水层模型比气水层的计算误差小,计算精度高.
4.2 不同TE组合为了考察不同回波间隔组合对结果的影响,选取不同的回波间隔组合进行实验.实验中,分别选取短回波间隔组合[0.6,1.2,2.4,3.6,6.0,9.6]ms、长回波间隔组合[10.2,10.8,12.0,13.2,15.6,19.2]ms以及长短混合回波间隔组合[0.6,1.2,2.4,4.8,9.6,19.2]ms分别进行实验,相应的回波个数亦为INT(1440/TE)(其中INT 代表数值取整),设置观测磁场梯度为4.0×10-3T/cm.
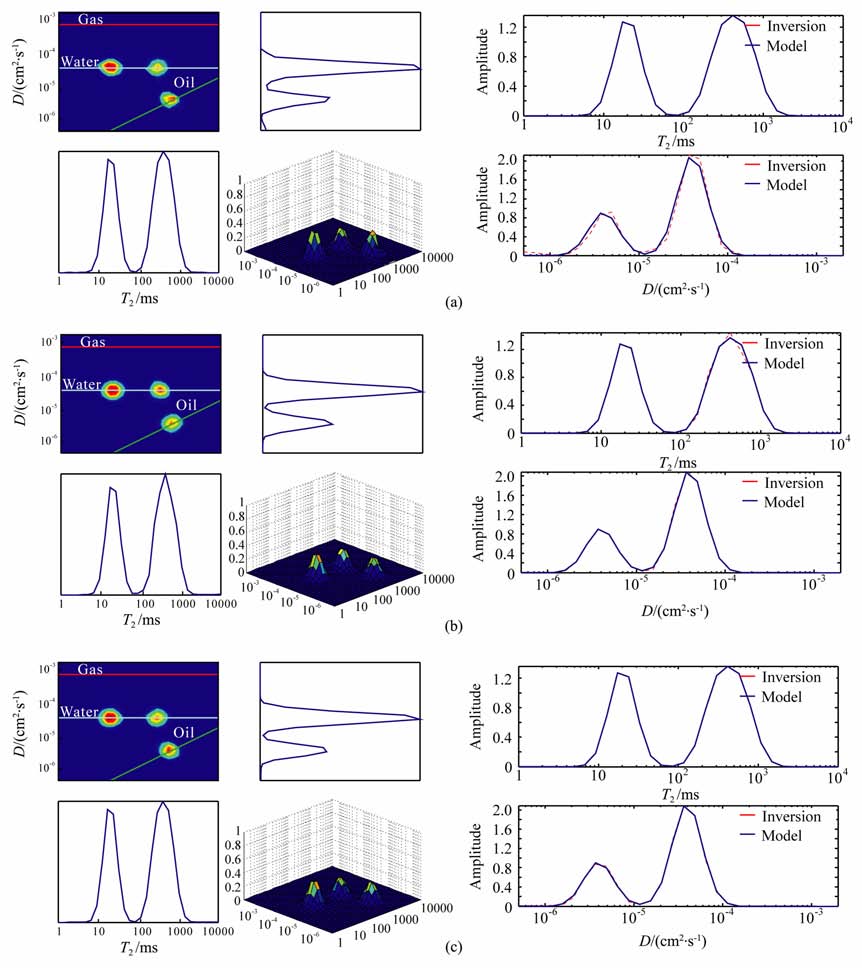
油水模型的不同回波间隔组合的数值模拟和反演实验.如图 7所示,采用短回波间隔组合时计算的相对误差为0.2159,采用长回波间隔组合时计算的相对误差为0.1068,采用长短混合回波间隔组合时计算的相对误差为0.1006.可以看出,在多TE 观测模式下,对于油水模型,采用长短混合回波间隔组合方案对流体识别效果较好.
|
图 7 不同回波间隔组合的油水模型反演结果 (a) TE = [0.6,1.2,2.4,3.6,6.0,9.6]ms; (b) TE = [10.2,10.8,12.0,13.2,15.6,19.2]ms; (c) TE = [0.6,1.2,2.4,4.8,9.6,19.2]ms. Fig. 7 Inversion results of oil-water model under different TE groups |
气水模型的不同TE 组合的数值模拟和反演实验,其结果如图 8所示.从图 8不同参数实验结果的对比可以看出,图 8c中的T2 分布与扩散系数分布均比图 8a和图 8b效果要好,而且与模型更接近.从计算的相对误差看,采用短回波间隔组合的相对误差为0.2012,采用长回波间隔组合时计算的相对误差为0.1875,采用长短混合回波间隔组合时计算的相对误差为0.1258.
可以看出,在多TE 观测模式下,对于油水模型和气水模型来说,长短混合回波间隔组合方案既能够反映弛豫快和扩散快的束缚流体组分,又能够分辨弛豫慢和和扩散慢的流体组分,反演精度最高.从油水层和气水层的适应性上说,在回波参数设置相同的情况下,油水层模型比气水层的计算误差小,计算精度高.
5 结论与讨论核磁共振多回波观测模式可以实现核磁共振二
维谱(T2,D)反演问题.本次研究针对这一问题研究了其数学原理,针对流体识别问题详细讨论了其反演问题.从计算精度和运算效率两个方面详细分析了非负LSQR 算法和TSVD 算法的计算结果,并据此提出了LSQR-TSVD混合反演算法.针对油水模型和气水模型,利用该反演算法可以实现(T2,D)二维核磁共振谱的高效和精确反演,并分析了流体识别的适应性.而且,利用该反演算法对采集参数进行研究,为采集参数设计提供了参考.通过分析研究可以得出以下结论:
(1) LSQR-TSVD混合反演算法结合了非负LQSR 和改进的TSVD 算法的优点,并且其存储空间小,通过设置较少的迭代次数就可以满足较高的计算精度,并提高了运算效率.相对于单一反演算法,该方法具有明显的优势.而且,该算法容易实现非负约束条件,能获得连续性好的高精度二维谱图.
(2) 在多TE 观测模式下,采用长短不同回波间隔组合进行观测时,反演结果既能反映弛豫快、扩散快的束缚流体,又能分辨反映弛豫慢、扩散慢的束缚流体可动流体,反演精度高,流体识别的效果好.
(3) 从设定的磁场梯度来说,磁场梯度愈大,反演的精度越好.
(4) 从油水层和气水层的适应性上说,在参数相同的情况下,油水层模型比气水层的计算误差小,计算精度高,即(T2,D)2D NMR 技术更适用于油水层的识别.
(5) 相对于一维核磁共振,通过增加观测次数和观测数据量就可以实现二维核磁共振测井.通过多回波核磁共振观测可以实现(T2,D)二维谱的反演,其反演精度的高低与观测参数设计有关.
在本文中,主要是基于设定的气水模型和轻质油模型讨论了提高反演精度的混合反演算法,对于不同粘度的稠油模型的(T2,D)二维核磁共振的测井响应特征尚需进一步讨论.
| [1] | 肖立志. 核磁共振成像测井与岩石核磁共振及其应用. 北京: 科学出版社, 1998 . Xiao L Z. NMR Imaging Logging Principle and NMR Petrophysics Experiment (in Chinese). Beijing: Science Press, 1998 . |
| [2] | 肖立志. 我国核磁共振测井应用中的若干重要问题. 测井技术 , 2007, 31(5): 401–407. Xiao L Z. Some Important Issues for NMR Logging Applications in China. Well Logging Technology (in Chinese) , 2007, 31(5): 401-407. |
| [3] | 赵文杰, 谭茂金. 胜利油田核磁共振测井技术应用回顾与展望. 地球物理学进展 , 2008, 23(3): 814–821. Zhao W J, Tan M J. Review and prospect on NMR logging application in Shengli oilefield. Progress in Geophysics (in Chinese) , 2008, 23(3): 814-821. |
| [4] | 王忠东, 汪浩, 向天德. 综合利用核磁谱差分与谱位移测井提高油层解释精度. 测井技术 , 2001, 25(5): 365–368. Wang Z D, Wang H, Xiang T D, et al. Integration of NMR DTW logs and DTE logs to improve the oilbed interpretation accuracy. WLT (in Chinese) , 2001, 25(5): 365-368. |
| [5] | 谭茂金, 赵文杰, 范宜仁. 用测井双TW 观测数据识别储层流体性质. 天然气工业 , 2006, 26(4): 38–40. Tan M J, Zhao W J, Fan Y R. Identification of fluid property with NMR dual-TW well logging data. Natural Gas Industry (in Chinese) , 2006, 26(4): 38-40. |
| [6] | 运华云, 谭茂金. 核磁共振测井双等待时间观测方式及分析方法. 油气地质与采收率 , 2006, 13(4): 96–98. Yun H Y, Tan M J. Observation way and analytical approach of dual waiting time by nuclear magnetic resonance logging. Petroleum Geology and Recovery (in Chinese) , 2006, 13(4): 96-98. |
| [7] | 程相志, 范宜仁, 周灿灿. 淡水储层中低阻油气层识别技术. 地学前缘 , 2008, 15(1): 146–153. Cheng X Z, Fan Y R, Zhou C C. Identification technology of low resistivity pays in fresh water reservoir. Earth Science Frontiers (in Chinese) , 2008, 15(1): 146-153. |
| [8] | 邵维志. 核磁共振测井移谱差谱法影响因素实验分析. 测井技术 , 2003, 27(6): 502–507. Shao W Z. On effect of NMR differential and shifted spectrum method in laboratory. WLT (in Chinese) , 2003, 27(6): 502-507. |
| [9] | Sun B Q, Dunn K J. A global inversion method for multi-dimensional NMR logging. Journal of Magnetic Resonance , 2005, 172(1): 152-160. DOI:10.1016/j.jmr.2004.10.003 |
| [10] | 毕林锐. 核磁共振测井技术的最新若干进展. 工程地球物理学报 , 2007, 4(4): 369–374. Bi L R. Latest advances in NMR logging technology. Chinese Journal of Engineering Geophysics (in Chinese) , 2007, 4(4): 369-374. |
| [11] | 林振洲, 潘和平. 核磁共振测井进展. 工程地球物理学报 , 2006, 3(4): 295–304. Lin Z Z, Pan H P. The progress of nuclear magnetic resonance logging. Chinese Journal of Engineering Geophysics (in Chinese) , 2006, 3(4): 295-304. |
| [12] | Sun B Q, Dunn K J. Multi-dimensional NMR logging. J Magnetic Resonance , 2005: 172-180. |
| [13] | Dunn K J, Bergman D J, Latorraca G A. Nuclear Magnetic Resonance Petrophysical and Logging Applications. Oxford: Pergamon Press, 2002. |
| [14] | Moody J B, Xia Y. Analysis of multi-exponential relaxation data with very short components using linear regularization. Journal of Magnetic Resonance , 2004, 167(1): 36-41. DOI:10.1016/j.jmr.2003.11.004 |
| [15] | Hurlimann M D, Venkataramanan L, Flaum C, et al. Diffusion-editing: New NMR Measurement of Saturation and Pore Geometry. Paper FFF in 43rd Annual Symposium of SPWLA, Oiso, Japan, June 3-6, 2002. |
| [16] | Dunn K J, Latorraca G A. The inversion of NMR log data sets with different measurement errors. Journal of Magnetic Resonance , 1999, 140(1): 153-161. DOI:10.1006/jmre.1999.1837 |
| [17] | 邓克俊, 谢然红. 核磁共振测井理论及应用. 山东: 中国石油大学出版社, 2010 . Dunn K J, Xie R H. NMR Logging Theory and Applications (in Chinese). Shandong: Press of China University of Petroleum, 2010 . |
| [18] | 谢然红, 肖立志, 邓克俊, 等. 二维核磁共振测井. 测井技术 , 2005, 29(5): 430–434. Xie R H, Xiao L Z, Dunn K J, et al. Two-dimensional NMR logging. Well Logging Technology (in Chinese) , 2005, 29(5): 430-434. |
| [19] | 顾兆斌, 刘卫. 核磁共振二维谱反演. 波谱学杂志 , 2007, 24(3): 311–319. Gu Z B, Liu W. The inversion of two-dimensional NMR map. Chinese Journal of Magnetic Resonance (in Chinese) , 2007, 24(3): 311-319. |
| [20] | 顾兆斌, 刘卫, 孙佃庆, 等. 2D NMR技术在石油测井中的应用. 波谱学杂志 , 2009, 26(4): 560–568. Gu Z B, Liu W, Sun D Q, et al. Application of 2D NMR techniques in petroleum logging. Chinese Journal of Magnetic Resonance (in Chinese) , 2009, 26(4): 560-568. |
| [21] | 谢然红, 肖立志, 陆大卫. 识别储层流体的(T2, T1)二维核磁共振方法. 测井技术 , 2009, 33(1): 10–20. Xie R H, Xiao L Z, Lu D W. (T2, T1) two-dimensional NMR method for fluid typing. Well Logging Technology (in Chinese) , 2009, 33(1): 10-20. |
| [22] | 谢然红, 肖立志. (T2, D)二维核磁共振测井识别储层流体的方法. 地球物理学报 , 2009, 52(9): 2410–2418. Xie R H, Xiao L Z. The (T2, D) NMR logging method for fluids characterization. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2410-2418. |
| [23] | 谭茂金, 石耀霖, 赵文杰, 等. 核磁共振双TW测井数据联合反演与流体识别. 地球物理学报 , 2008, 51(5): 1482–1490. Tan M J, Shi Y L, Zhao W J, et al. Joint inversion method for NMR dual-TW logging data and fluid typing. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1482-1490. |
| [24] | 刘劲松, 刘福田, 刘俊, 等. 地震层析成像LSQR 算法的并行化. 地球物理学报 , 2006, 49(2): 540–545. Liu J S, Liu F T, Liu J, et al. Parallel LSQR algorithms used in seismic tomography. Geophysics (in Chinese) , 2006, 49(2): 540-545. |
| [25] | 杨薇, 刘四新, 冯彦谦. 跨孔层析成像LSQR算法研究. 物探与化探 , 2008, 32(2): 199–202. Yang W, Liu S X, Feng Y Q. A study of the LSQR algorithm for cross-hole tomography. Geophysical and Geochemical Exploration (in Chinese) , 2008, 32(2): 199-202. |
 2012, Vol. 55
2012, Vol. 55



