2. 中国科学院寒区旱区环境与工程研究所, 兰州 730000
2. Cold and Arid Regions Environmental Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000,China
土壤的热力学特性影响着地表和大气之间的物质和能量交换,对地球大气边界层物理过程、大气环流和区域气候产生着重要影响,正确地模拟土壤温度和热通量是陆面物理过程模式、大气环流模式、区域气候模式数值模拟研究的重要环节,一直以来受到地球物理学家、大气科学家的重视[1-7],因此,对不同下垫面的土壤热扩散特性和湍流通量输送及其陆面过程参数化方面开展了一些研究工作[8-9].
计算土壤温度和热通量首先需要确定土壤的三个热力学参数:土壤热扩散率、土壤热传导率和土壤体积热容量.土壤体积热容量是由土壤的物质组成决定的,土壤热传导率可以通过体积热容量和热扩散率的乘积求得,因此在土壤热传输的研究中,通常只需考虑土壤热扩率.土壤热扩散率描述了土壤温度随边界条件变化的瞬时过程[10].假设所研究的土壤为常热扩散系数的半无界介质,在一维热传导方程[11]的基础上得出了很多求解土壤热扩散率的方法,主要有振幅法、相位法、反正切法、对数法、数值法和谐波法.Horton 等(1983),刘树华等(1991)和莫兴国等(2002)先后验证了这些方法的可靠性,认为谐波法可以精确地给出土壤热扩散率的近似值[12-14].Heusinkveld 等(2004)在地表能量平衡的研究中,利用谐波法很好地模拟了浅层土壤的温度和热通量[15].
实际上,土壤的热传输过程包含了热传导和多孔热对流两个过程[10, 16].Gao 等(2002,2003)指出土壤温度的日变化不仅受土壤热传导作用的影响,还与土壤中液态水热对流作用有关,给出了耦合热传导和热对流的一维热传导对流方程,并利用一阶谐波模型推导出了热传导对流方程的解析解和土壤热扩散率的计算公式[17-18].Gao 等(2005,2008,2009)利用青藏高原和黄土高原等地的土壤温度资料,验证了热传导对流法的可靠性,并与传统的热传导方法做了对比,认为新的热传导对流方程能更好地描述土壤中的热传输物理过程[19-23].
为了进一步了解绿洲系统的土壤温度分布特征和能量循环过程,中国科学院寒区旱区环境与工程研究所在甘肃金塔绿洲进行了绿洲系统能量与水分循环过程观测试验.本文将利用该试验中2005年6月11日至15日观测的土壤温度资料,分别使用谐波法、振幅法、相位法和热传导对流法,模拟计算该地区的土壤温度和热通量及其日变化特征,进一步验证热传导对流法的可靠性,并对计算方法的计算精度进行比较.研究结果可为正确选择计算土壤热力参数、模拟温度和热通量的方法提供参考.
2 计算方法若视分子传导是土壤热传输的主要传输过程,且在均一的土壤中,任意土壤深度上的热通量可用热传导傅里叶定律来描述为
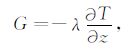
|
(1) |
其中,G为土壤热通量(W·m-2),T为土壤温度(℃),z为土壤深度(m),λ为土壤热传导率(W·m-1·℃-1).若只考虑垂直方向上的能量交换,则土壤中的热传导过程可以表示为
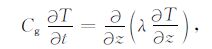
|
(2) |
其中,t为时间(s),Cg 为土壤的体积热容(J·cm-3·℃-1).假设土壤的体积热容Cg 和热传导率λ 不随深度变化,则可以得到经典的热传导方程[11]:
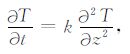
|
(3) |
其中,k为土壤热扩散率(m2·s-1),k=λ/Cg.
2.1 振幅法和相位法(Amplitude method and Phaee method)给定土壤温度的上边界条件:
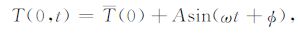
|
(4) |
其中,T(0)为地表的日平均温度,A是地表温度振幅,ω是地表温度相位,ω 是地球自转的角速度,ω =2π/p(rad·s-1),p为地表温度的日变化周期(p=24h).根据边界条件(4)式可以得到(3)式的解析解:
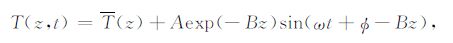
|
(5) |
其中,T(z)为土壤深度z处的日平均温度,$B=\sqrt{\omega /\left( 2k \right)}$用来表示深度对振幅和相位的影响.
由(4)和(5)式可知,任意深度的土壤温度都可以一个正弦函数来表示,则深度为z1 和z2 的土壤温度实测值可以表示为
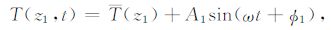
|
(6) |
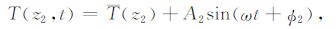
|
(7) |
其中,T(z1)和T(z2)分别是深度z1、z2 处土壤温度的日平均值,z1<z2,A1、A2、φ1 和φ2 是分别对应深度的温度振幅和温度相位.振幅A可以通过(8)式计算:
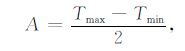
|
(8) |
其中,Tmax 为该深度土壤的日最高温,Tmin 为该深度土壤的日最低温.
相位φ1和φ2是由最小二乘法拟合(6)和(7)式得到.比较深度z1 和z2 的振幅和相位,由(5)~(7)式可以得到热扩散率k的振幅法和相位法计算公式[24]:
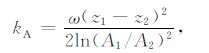
|
(9) |
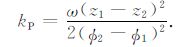
|
(10) |
若以深度z1 的土壤温度为上边界条件,可以用(11)式来计算任意深度(z1≤z≤z2)的土壤温度:

|
(11) |
当T(z)未知时,可以通过(12)式进行估算:
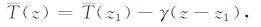
|
(12) |
其中,γ 为土壤平均温度随深度变化的递减率.
结合(1)、(11)和(12)式,可以得到土壤热通量的计算公式:
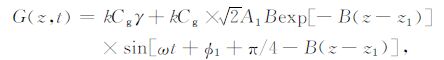
|
(13) |
其中,土壤体积热容Cg = (1-θs)ρdcd+θρwcw,(1-θs)ρdcd 为干土的土壤体积热容量,根据金塔绿洲土壤的特征[25],取值为1.09J·cm-3·℃-1;θ、ρw 和cw 分别为土壤的体积含水量、液态水密度、液态水的比热容.
2.2 谐波法(Har monicmethod)假设土壤温度的上边界条件是一个Fourier级数:
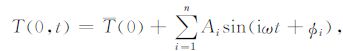
|
(14) |
其中,n为谐波阶数,Ai、φi分别表示第i阶谐波的振幅和相位.
假设初始相位i为常数,用变量分离法解可得出热传导方程即(3)式的解析解[26]:
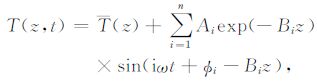
|
(15) |
其中,$B=\sqrt{\text{i}\omega /\left( 2k \right)}$用来表示深度对振幅和相位的影响.
在具体计算中,可以利用两层土壤温度的实测值,由最小二乘法算出(15)式中各参数的最优估计,得到土壤热扩散率的估计值[11].
若以深度z1 处的土壤温度为上边界条件,谐波法计算任意深度(z1≤z≤z2)土壤温度的公式为
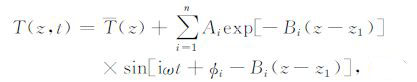
|
(16) |
其中,Ai、φi分别是深度z1 处的第i阶谐波的振幅和相位.
结合(1)、(12)和(16)式,可以得到谐波法的土壤热通量计算公式:
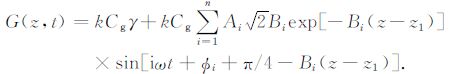
|
(17) |
在推导(2)式时,我们假设土壤热传导率λ 不随深度变化.实际上,土壤热传导率λ 随着深度会产生变化,这样(2)式可以变形为[23]
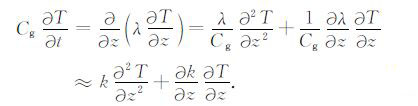
|
(18) |
Gao等耦合土壤热对流作用给出改进的土壤热传导方程[19]:
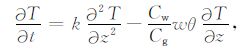
|
(19) |
其中,Cw 为液态水的体积热容(J·cm-3·℃-1),w为水的垂直速度(m·s-1),向上为正;θ为土壤体积含水量(cm3·cm-3),$-\frac{{{C}_{\text{w}}}}{{{C}_{\text{g}}}}\omega \theta $为土壤水通量密度(m·s-1).
合并(18)和(19)式,可以得到:

|
(20) |
其中,$W=\frac{\partial k}{\partial z}-\frac{{{C}_{\text{w}}}}{{{C}_{\text{g}}}}\omega \theta $,为土壤热扩散率的垂直梯度和液态水通量密度之和.
应用(4)式的上边界条件,可以推导出(20)式的解析解和土壤热扩散率的计算公式[19]:

|
(21) |

|
(22) |
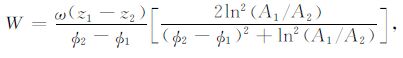
|
(23) |
其中,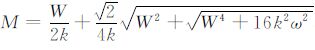
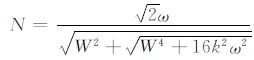
利用(22)和(23)式求得土壤热扩散率和液态水通量密度之后,以深度z1 处的土壤温度为上边界条件,可以利用(24)式计算任意深度(z1≤z≤z2)的土壤温度:
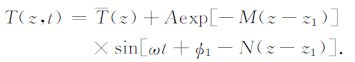
|
(24) |
结合(1)、(12)和(24)式,可以得到热传导对流法的土壤热通量计算公式:
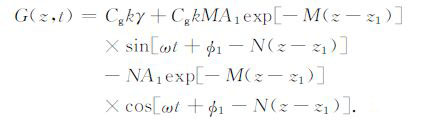
|
(25) |
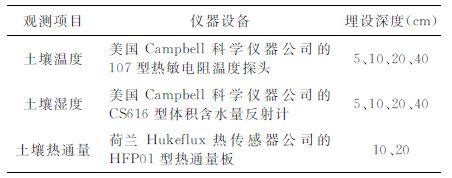
土壤温湿度资料来自中科院寒区旱区环境与工程研究所2005年在甘肃金塔绿洲进行的“绿洲系统能量与水分循环过程观测试验".本文所用资料是2005 年6 月11 日至15 日在绿洲中部的农田中(39°59.488′N,98°56.177′E)的观测数据,在此观测期间数据完整,天气晴好,可更好地应用于本文理论方法的分析比较研究.表 1 给出了本次试验的观测仪器和埋设深度,所有仪器均每10分钟记录一次数据.在实际应用中,我们将数据进一步平均为半小时平均数据.
|
|
表 1 试验仪器和埋设深度 Table 1 Instruments employed in the observation and their placements |
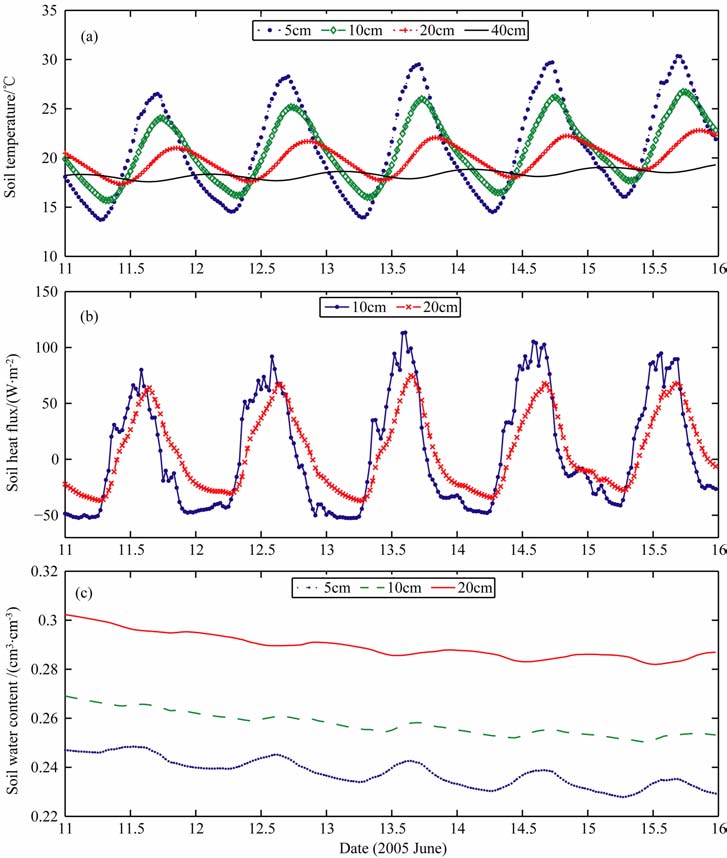
为了了解金塔绿洲农田不同深度的土壤温度、土壤热通量和土壤湿度观测资料的特性,图 1 给出了观测期间各观测要素的时间序列.图 1a显示了不同深度土壤温度的时间序列,可以看出随着土壤深度的增加,温度振幅明显减小,相位后移.图 1b是不同深度土壤热通量的时间序列,可以看出10cm 热通量存在不规则的振荡,20cm 热通量较10cm 要光滑许多.图 1c是不同深度土壤湿度的时间序列,可以看出土壤湿度随着深度的加深而增大;5cm 土壤湿度具有较明显的日变化,在每日的午后(14 时左右)达到最大;10cm 和20cm 土壤的湿度日变化幅度小于5cm.
|
图 1 各观测项目的时间序列 (a) 土壤温度,(b) 土壤热通量,(c) 土壤湿度. Fig. 1 The time series of the observed parameters (a)Soil temperature» (b)Soil heat flux,(c)Soil moisture. |
利用5cm 和20cm 的土壤温度实测值计算5~20cm土壤层的热扩散率,并以5cm 土壤层作为上边界条件,计算了不同深度的土壤温度和热通量特性.
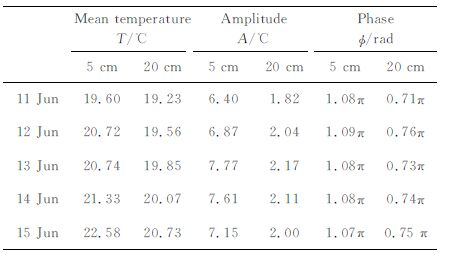
4.1 土壤热扩散率的计算首先利用(8)式计算出5cm 和20cm 的温度振幅,然后由最小二乘法拟合(6)式和(7)式,求得相位的最优估计值(见表 2).应用表 2的数据,计算出了振幅法、相位法和热传导对流法在5~20cm 土壤层的热扩散率(见表 3).
|
|
表 2 土壤温度拟合正弦曲线的各参数 Table 2 The parameters of the sine curves got from5 cmand 20 cmsoil temperature |
|
|
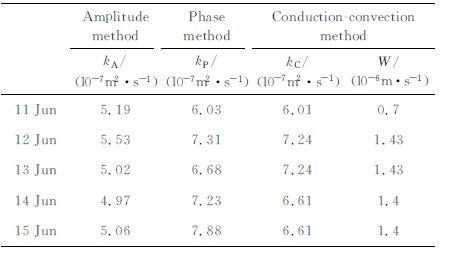
表 3 振幅法、相位法和热传导对流法计算土壤热扩散率 Table 3 The soii thermai difffusivity modeled by Amplitude method,Phase method and Conduction-convection method |
谐波法的上边界条件与上述三种方法有所不同,假设上边界为一个Fourier级数.利用6月12日5cm 的土壤温度实测值由最小二乘法拟合了不同阶数的谐波模型(见表 4),发现二阶谐波模型(n=2)已有很高的计算精度(相关系数r=0.998);考虑到模型的繁简和精度,本文选用二阶谐波模型作为谐波法的计算模型.首先利用5cm 的土壤温度实测值运用最小二乘法拟合二阶谐波函数${{T}_{1}}={{{\bar{T}}}_{1}}+\sum\limits_{i=1}^{2}{{{A}_{i}}\sin \left( \text{i}\omega t+{{\phi }_{i}} \right)}$,求得谐波模型的温度振幅和相位值;然后结合(14)式,利用20cm 土壤温度实测值迭代得到土壤热扩散率的最优估计值(见表 5).
|
|
表 4 不同阶数谐波模型对比 Table 4 The comparison of different order s Harmonic model |
|
|
表 5 二阶谐波模型的温度振幅、相位和热扩散率 Table 5 The soil temperature model parameters got from Harmonic method |
对比表 3和表 5,可以看出不同算法计算的土壤热扩散率存在差异,其值按大小排序,大致有:振幅法<谐波法<热传导对流法<相位法;由谐波法回归得到的第一阶谐波振幅小于应用(8)式计算的结果.
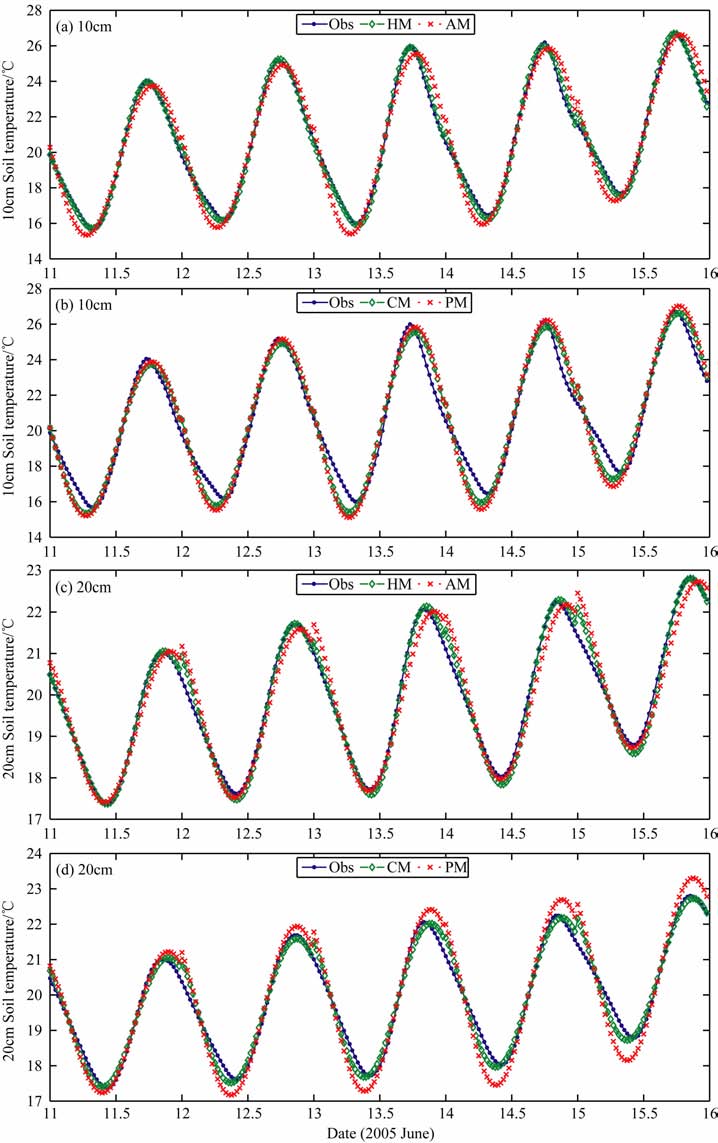
4.2 土壤温度的计算和误差分析假设5~20cm 土壤层的土壤热扩散率为一个常数,应用表 2、表 3和表 5的数据,利用(11)、(16)和(24)式,使用上述四种方法计算了10cm 和20cm的土壤温度,图 2给出10cm 和20cm 模拟值与实测温度的时间序列,可以看出由谐波法模拟的土壤温度与实测值基本吻合(见图 2a,2c),模拟效果最好.振幅法、相位法和热传导对流法在夜间的都会出现低估的现象(见图 2a,2b,2d),相位法计算20cm土壤温度误差较大,在日最大值附近出现了明显的高估现象(见图 2d).
|
图 2 土壤温度模拟值和实测值的时间序列 Obs:实测值,IIM:谐波法,CM:热传导对流法,AM:振幅法,PM:相位法,(a,b) 10 cm 土温,(c,d) 20 cm 土温. Fig. 2 The time series of modeled and observed 10 cm soil temperature Obs: Observed value,IIM: Harmonic method,CM: Conduction-convection method,AM: Amplitude method,PM: Phase method,(a,b) 10 cm soil temperature,(c,d) 20 cm soil temperature. |
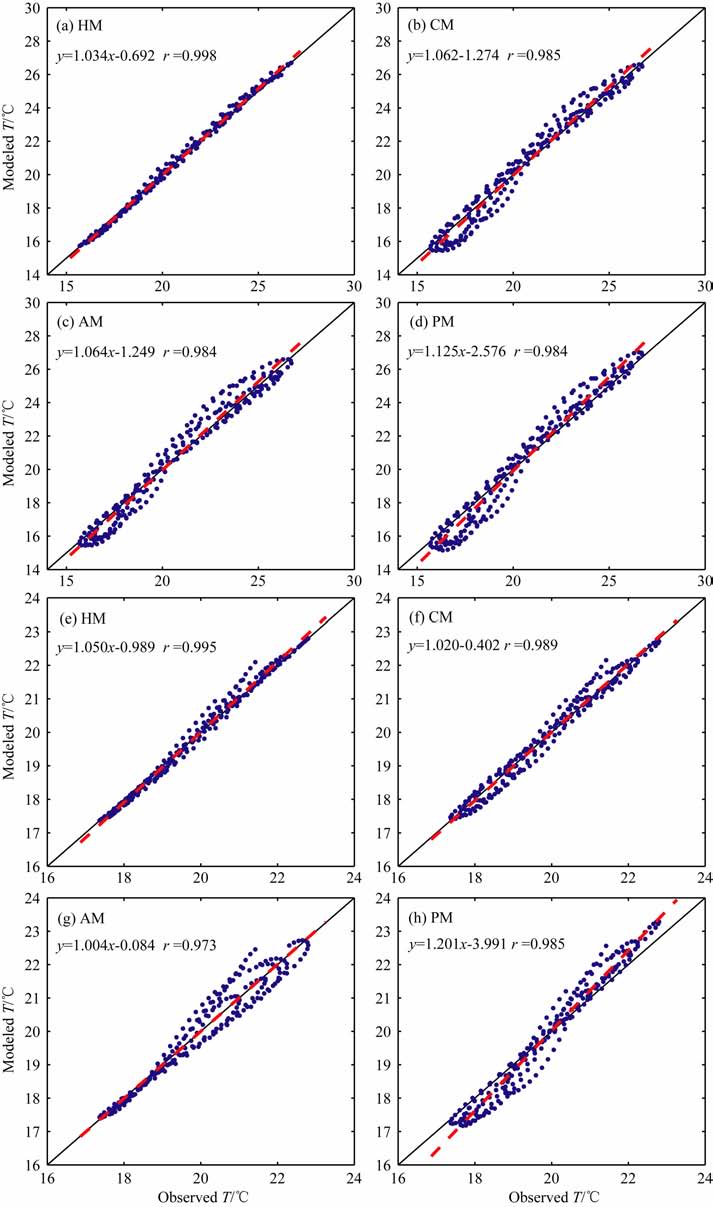
图 3 是不同算法模拟土壤温度值与实测值的1:1 散点图,可以看出所有算法的模拟值与实测值的比都接近于1.谐波法的模拟效果最好,散点的分布最密集(见图 3a,3e),10cm 和20cm 模拟值与实测值的相关系数分别达到0.998 和0.995;相位法在10cm 和20cm 处的散点回归直线斜率分别为1.125和1.201,其值大于其他计算方法,拟合效果差于振幅法和热传导对流法.
|
图 3 土壤温度模拟值与实测值的1:1散点图 (a-d) 10 cm 土壤温度,(e+h) 20 cm 土壤温度,(a,e)谐波法,(b,D热传导对流法,(c,g)振幅法,(d,h)相位法.r为模拟值与实测值的相关系数,:y =ax+b为散点的回归直线. Fig. 3 Scatter plots of the modeled soil temperature against observation (a-d) 10 cm soil temperature,(e一h) 20 cm soil temperature,(a,e) Harmonic method,(b,f) Conduction-convection method,(c,g) Amplitude method,(d,h) Phase method. r is the correlation coefficient,y=ax+b is the regress equation of the scatter. |
为了进一步了解上述算法模拟的土壤温度与实际观测值的离散程度,我们采用以下两种误差分析法[16, 18]进行了误差分析:

|
(26) |
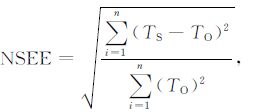
|
(27) |
其中,n是样本总数,TS、TO 分别是土壤温度的模拟值和实测值,SEE(Standard Error of the Estimate)和NSEE(Normalized Standard Error)分别是模拟值相对实测值的标准差、归一化标准差(见表 6).通过表 6,可以知道谐波法的计算误差最小,模拟效果最好;热传导对流法的拟合效果好于振幅法,相位法的计算误差最大.由于土壤温度日变化并不是一个纯正的正弦变化曲线,受到很多因素的影响;当使用二阶谐波模型时,第二阶谐波可以对第一阶谐波起到一定的校正作用,进而可以很好地模拟土壤温度.
|
|
表 6 土壤温度模拟值与实测值的标准差和归一化标准差 Table 6 SEE and NSEE of the modeled temperature against the observation |
热传导对流法的计算误差小于振幅法,可以很好地模拟出白天的土壤温度,但是在夜晚会出现低估的现象(见图 2b,2d),可能是由于假设一天中的土壤水分通量密度W为一个常数而引起的误差[26].通过图 1c我们可以知道浅层的土壤含水量存在明显的日变化,在每日的午后达到最大值,午夜时达到最小值.白天,特别是晴朗的天气状况下,由于受地表的蒸发作用,土壤水分向上运动,W>0;夜晚,随着地表温度的下降,地表蒸发作用减弱,土壤水分会由浅层向深层运动,W<0.因此,当忽略土壤水分通量密度W的日变化时,会出现土壤温度的计算误差.
热传导对流法定义的土壤热扩散率与其他三种方法有所不同[18].在经典的热传导方程((3)式)中,可以将热对流作用看成是热传导的一部分,由谐波法、振幅法和相位法所得到的土壤热扩散率同化了部分热对流的作用,而热传导对流法所得到的热扩散率只包含热传导作用.
谐波法在迭代计算土壤热扩散率的过程中,充分利用了土壤温度的实测信息;且由谐波法计算的土壤温度的误差最小(见表 6);因此,其结果可以作为热扩散率的最优估计.与振幅法和相位法对比,可以发现振幅法和相位法分别低估和高估了土壤热扩散率(见表 3和表 5).
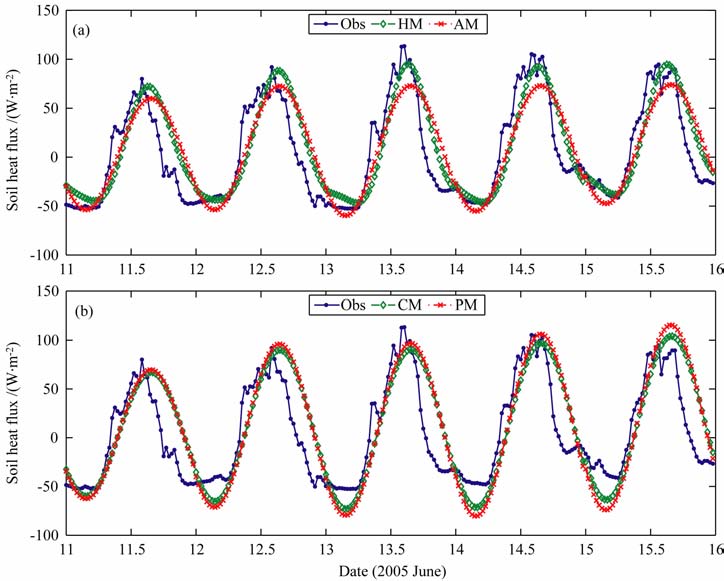
4.3 土壤热通量的计算结果应用表 2、表 3 和表 5 的数据,结合(12)、(17)和(25)式,计算了10cm 的土壤热通量;其中,土壤平均温度的递减率是由5cm、10cm 和20cm 的日平均温度逐日拟合得到.图 4 是土壤热通量的模拟值和实测值的时间序列,可以看出10cm 热通量存在不规则振荡;四种方法中,谐波法的拟合曲线与实测值最为吻合;振幅法在日最大值附近出现明显低估的现象,而热传导对流法和相位法在夜晚出现了低估的现象.这可能是由于振幅法和相位法在计算热扩散率时分别出现了低估和高估的现象,热传导对流法忽略了土壤水分通量密度的日变化.
|
图 4 土壤热通量的实测值与模拟时间序列 图注同图 2. Fig. 4 The time series of modeled and observed soil heat flux Please refer to Fig. 2 .for the description of the figures. |
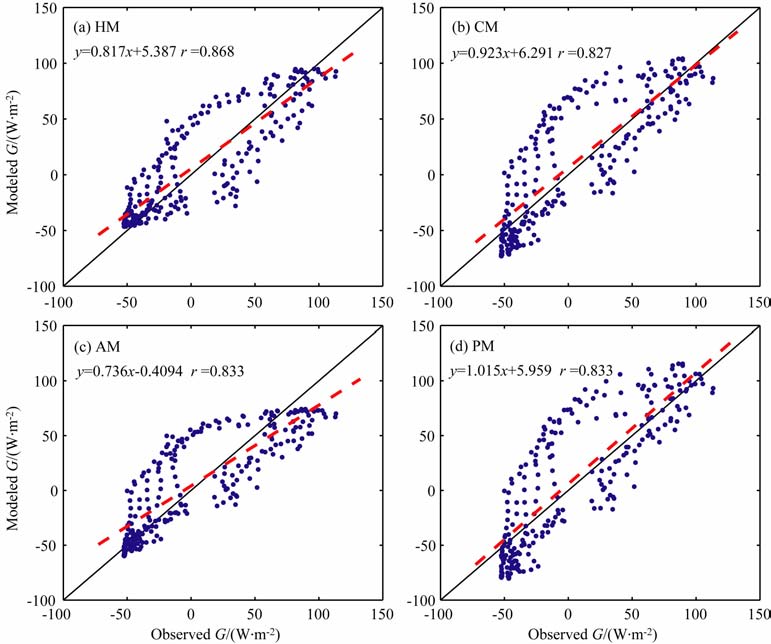
图 5给出了不同算法的模拟值与实测值的1∶1散点图,可以看出四种算法的散点分布都较为分散,其中谐波法的相关性最好(r=0.868).由于10cm热通量存在不规则的振荡,使得四种算法的计算误差都比较大(见表 7);其中谐波法计算的结果与实测值最为接近.
|
图 5
土壤热通量模拟值与实测值的1:1散点图
(a)谐波法,(b)热传导对流法,(c)振幅法,(d)相位法.其余图注同 |
|
|
表 7 土壤热通量模拟值与实测值的标准差 Table 7 SEE of the modeled soil heat flux against the observation |
本文利用2005年绿洲系统能量与水分循环过程观测试验中6月11 日至15 日期间的观测数据,运用谐波法、振幅法、相位法和热传导对流法计算了5~20cm 的土壤热扩散率,构建了土壤温度和热通量的计算模型,并计算了10cm、20cm 的土壤温度和10cm 的土壤热通量,得出以下结论:
(1) 由于土壤温度日变化并不是一个纯正的正弦变化曲线,谐波法使用高阶谐波模型来模拟土壤温度,与其他使用正弦函数模型的方法相比,可以更精确地模拟出土壤温度的日变化.谐波法在迭代计算土壤热扩率的过程中利用了大量的土壤温度信息,其结果比较可靠.
(2) 热传导对流法的拟合效果好于振幅法和相位法,它基于耦合了热对流作用的一维热传导对流方程,在理论上能够更好地反映土壤中的热传输过程.由于忽略了土壤水分通量密度W的日变化,该方法在模拟土壤含水量有明显日变化的浅层土壤温度和热通量时,会出现计算误差.与谐波法的高阶谐波模型相比,热传导对流法使用一个正弦函数来模拟土壤温度,局限了该方法的计算精度.在今后的研究中,可以考虑在热传导对流法中引入高阶谐波模型和土壤水分通量密度的日变化模型.
(3) 浅层土壤热通量存在着不规则的振荡,使得四种方法的计算结果都存在较大的误差;其中谐波法的计算结果与实测值最为接近,可以作为计算浅层土壤热通量的优选方法.
(4) 本文选用的是2005年绿洲系统能量与水分循环过程观测试验中6月11日至15日5天的观测数据,所得结果的代表性还有待于未来更多、更长资料的检验.
| [1] | 刘树华, 潘英, 胡非, 等. 沙漠绿洲地区夏季地表能量收支的数值模拟. 地球物理学报 , 2009, 52(5): 1197–1207. Liu S H, Pan Y, Hu F, et al. Numerical simulation of summer land surface energy budget in desert and oasis regions. Chinese J. Geophys. (in Chinese) , 2009, 52(5): 1197-1207. |
| [2] | 李婧, 刘树华, 茅宇豪, 等. 不同生态系统CO2通量和浓度特征分析研究. 地球物理学报 , 2006, 49(5): 1298–1307. Li J, Liu S H, Mao Y H, et al. Characteristics of CO2 flux and concentration in different ecosystems. Chinese J. Geophys. (in Chinese) , 2006, 49(5): 1298-1307. DOI:10.1002/cjg2.v49.5 |
| [3] | 薛彦广, 高志球, 沙文钰. 利用简单生物圈模式SiB2模拟青藏高原地表能量收支. 大气科学 , 2010, 34(1): 131–142. Xue Y G, Gao Z Q, Sha W Y. Modeling of surface energy budget in Tibetan prairie using the Simple Biosphere Model 2 (SiB2). Chinese Journal of Atmospheric Sciences (in Chinese) , 2010, 34(1): 131-142. |
| [4] | 刘树华, 胡予, 胡非, 等. 沙漠-绿洲陆-气相互作用和绿洲效应的数值模拟. 地球物理学报 , 2005, 48(5): 1019–1027. Liu S H, Hu Y, Hu F, et al. Numerical simulation of land-atmosphere interaction and oasis effect over oasis-desert. Chinese J. Geophys. (in Chinese) , 2005, 48(5): 1019-1027. |
| [5] | 王可丽, 程国栋, 江畅畅, 等. 青藏高原那曲地区非均质土壤导温率的变化及土壤温度数值模拟. 冰川冻土 , 2007, 29(3): 470–474. Wang K L, Cheng G D, Jiang C C, et al. Variation of thermal diffusivity and temperature simulation of soils of vertical heterogeneity in Nagqu prefecture in the Tibetan Plateau. Journal of Glaciology and Geocryology (in Chinese) , 2007, 29(3): 470-474. |
| [6] | 房云龙, 孙菽芬, 李倩, 等. 干旱区陆面过程模型参数优化和地气相互作用特征的模拟研究. 大气科学 , 2010, 34(2): 290–306. Fang Y L, Sun S F, Li J. The optimization of parameters of land surface model in arid region and the simulation of land-atmosphere interaction. Chinese Journal of Atmospheric Sciences (in Chinese) , 2010, 34(2): 290-306. |
| [7] | 王介民, 王维真, 刘绍民, 等. 近地层能量平衡闭合问题——综述及个例分析. 地球科学进展 , 2009, 24(7): 705–713. Wang J M, Wang W Z, Liu S M, et al. The problems of surface energy balance closure—An overview and case study. Advances in Earth Science (in Chinese) , 2009, 24(7): 705-713. |
| [8] | 刘树华, 茅宇豪, 胡非, 等. 不同下垫面湍流通量计算方法的比较研究. 地球物理学报 , 2009, 52(3): 616–629. Liu S H, Mao Y H, Hu F, et al. A comparative study of computing methods of turbulent fluxes on different underling surfaces. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 616-629. |
| [9] | 刘鹏飞, 刘树华, 胡非, 等. 湍流通量计算方法和误差的比较研究. 气象学报 , 2010, 68(4): 487–500. Liu P F, Liu S H, Hu F, et al. A comparison of the different methods for estimating turbulent fluxes and their errors. Acta Meteorologica Sinica (in Chinese) , 2010, 68(4): 487-500. |
| [10] | Passerat de Silans A M B, Monteny B A, Lhomme J P. Apparent soil thermal diffusivity, a case study: HAPEX-Sahel experiment. Agricultural and Forest Meteorology , 1996, 81(3-4): 201-216. DOI:10.1016/0168-1923(95)02323-2 |
| [11] | Bhumralkar C M. Numerical experiments on the computation of ground surface temperature in an atmospheric circulation model. Journal of Applied Meteorology , 1975, 14(7): 1246-1258. DOI:10.1175/1520-0450(1975)014<1246:NEOTCO>2.0.CO;2 |
| [12] | Horton R, Wierenga P J, Nielsen D R. Evaluation of methods for determining the apparent thermal diffusivity of soil near the surface. Soil Science Society of America Journal , 1983, 47(1): 25-32. DOI:10.2136/sssaj1983.03615995004700010005x |
| [13] | 刘树华, 崔艳, 刘和平. 土壤热扩散系数的确定及其应用. 应用气象学报 , 1991, 2(4): 337–345. Liu S H, Cui Y, Liu H P. Determination of thermal diffusivity of soil and its application. Quarterly Journal of Applied Meteorology (in Chinese) , 1991, 2(4): 337-345. |
| [14] | 莫兴国, 李宏轩, 刘苏峡, 等. 用土壤温度估算表层土壤导温率与热通量的研究. 中国生态农业学报 , 2002, 10(1): 62–64. Mo X G, Li H X, Liu S X, et al. Estimation of the soil thermal conductivity and heat flux in near surface layer from soil temperature. Chinese Journal of Eco-Agriculture (in Chinese) , 2002, 10(1): 62-64. |
| [15] | Heusinkveld B G, Jacobs A F G, Holtslag A A M, et al. Surface energy balance closure in an arid region: role of soil heat flux. Agricultural and Forest Meteorology , 2004, 122(1-2): 21-37. DOI:10.1016/j.agrformet.2003.09.005 |
| [16] | 范新岗, 汤懋苍. 土壤传导-对流通量计算的初步结果. 高原气象 , 1994, 13(1): 14–19. Fan X G, Tang M C. A preliminary study of conductive and convective soil heat flux. Plateau Meteorology (in Chinese) , 1994, 13(1): 14-19. |
| [17] | Gao Z Q, Fan X G, Bian L G. An analytical solution to one-dimensional thermal conduction-convection in soil. Soil Sci. , 2003, 168(2): 99-106. DOI:10.1097/00010694-200302000-00004 |
| [18] | 高志球, 卞林根, 张雅斌, 等. 土壤热传导方程解析解和那曲地区土壤热扩散率研究. 气象学报 , 2002, 60(3): 352–360. Gao Z Q, Bian L G, Zhang Y B, et al. Study on analytical resolution to soil thermal conductive equation and soil thermal diffusivity over Nagqu area. Acta Meteorologica Sinica (in Chinese) , 2002, 60(3): 352-360. |
| [19] | Gao Z Q. Determination of soil heat flux in a Tibetan short-grass prairie. Boundary-Layer Meteorology , 2005, 114(1): 165-178. DOI:10.1007/s10546-004-8661-5 |
| [20] | 王琳琳, 高志球, 沈新勇, 等. 土壤水分的垂直运动对黄土高原糜田土壤温度的影响. 南京气象学院学报 , 2008, 31(3): 363–368. Wang L L, Gao Z Q, Shen X Y, et al. Impact of soil water vertical movement on the soil temperature in a broomcorn millet field over the Loess Plateau. Journal of Nanjing Institute of Meteorology (in Chinese) , 2008, 31(3): 363-368. |
| [21] | 代成颖, 高志球, 王琳琳, 等. 两种土壤温度算法的对比分析. 大气科学 , 2009, 33(1): 135–144. Dai C Y, Gao Z Q, Wang L L, et al. Intercomparison between two soil temperature algorithms. Chinese Journal of Atmospheric Sciences (in Chinese) , 2009, 33(1): 135-144. |
| [22] | Gao Z Q, Lenschow D H, Horton R, et a1. Comparison of two soil temperature algorithms for a bare ground site on the Loess Plateau in China. Journal of Geophysical Research , 2008, 113: D18105. DOI:10.1029/2008JD010285 |
| [23] | Gao Z Q, Wang L L, Horton R. Comparison of six algorithms to determine the soil thermal diffusivity at a site in the Loess Plateau of China. Hydrology and Earth System Sciences , 2009, 6(2): 2247-2274. DOI:10.5194/hessd-6-2247-2009 |
| [24] | 刘树华. 环境物理学 , 2004: 93–127. Liu S H. Environmental Physics (in Chinese) , 2004: 93-127. |
| [25] | 李万莉, 吕世华, 傅慎明, 等. 金塔绿洲的辐射平衡特征和地表能量研究. 太阳能学报 , 2009, 30(12): 1614–1620. Li W L, Lü S H, Fu S M, et al. A study on radiation balance and surface energy in Jinta oasis. Acta Energiae Solaris Sinica (in Chinese) , 2009, 30(12): 1614-1620. |
| [26] | 王琳琳. 土壤水分的垂直运动对土壤温度的影响. 南京: 南京信息工程大学, 2007. Wang L L. The impact of soil water vertical movement on the soil temperature (in Chinese). Nanjing: Nanjing University of Information Science & Technology, 2007. |
 2012, Vol. 55
2012, Vol. 55