2. 安徽省地质调查院,合肥 230001
2. Geological Survey of Anhui Province, Hefei 230001, China
重力异常场是由地下不同规模、不同形态和不同埋深的不均匀地质体的重力作用叠加而成的,通过测量获取的重力资料存在着混叠效应,它既包括区域异常,又存在局部异常[1].在重力资料处理中,研究者根据研究目标的不同,力求从观测异常中提取由研究对象产生的异常,即进行异常分离.事实上,位场分离是一个出现很早但一直没有彻底解决的问题,几十年来人们一直在不断探求,提出了多种方法,包括趋势分析、插值切割、匹配滤波、解析延拓、圆周平均、垂向二阶导数以及小波分析等[2-10].并非每个方法对于所有的异常分离都有效,上述的这些方法由于数学原理不同,应用前提也不尽相同,因而都具有针对性和选择性,如何恰当地使用好现有这些方法对于重力数据的处理尤为关键.
目前,我国矿床勘探深度平均约400m,世界主要发达国家都超过了1000m,我国开辟第二找矿空间、寻找深部隐伏矿床的形势刻不容缓.作为长江中下游重要成矿区,安徽省庐江—枞阳(简称庐枞)地区大多数矿区具有重力异常高的特征,辖区内的泥河铁矿在区域重力异常图上表现为弱异常,钻孔资料显示该区600m 以下见厚层铁矿体.根据成矿条件及重力异常分析,泥河铁矿应该具有很好的找矿前景,因此有必要对该区重力资料开展位场分离工作,以获取反映矿体的局部异常.
针对位场的异常分离问题,Grant(1972),管志宁、张昌达、陈方道(1993),Nabighian(2005),宋景明(2007)等[11-14]对上述部分方法做了较好的总结.本文将从重力异常分离方法的理论基础和应用条件入手,通过模型试验对比,讨论趋势分析法、插值切割法、匹配滤波法、解析延拓法以及垂向二阶导数法,并将这些异常分离方法应用于庐枞盆地泥河铁矿区重力资料的处理实践中,以分离出矿体异常和背景场,为寻找深部隐伏铁矿提供直接依据和线索.
2 方法原理 2.1 趋势分析法趋势分析法是应用得最早的方法之一,其实质是用一个多项式拟合区域场.1951年Agocs详细地说明了如何在最小二乘意义下进行区域异常的多项式拟合[15].多项式系数的求解是趋势分析法的关键问题之一,围绕这个问题,后人做了很多努力.1954年Simpson将求解多项式的系数矩阵转化为稀疏矩阵,简化了矩阵求逆的过程[16];1955 年Oldham提出采用正交多项式拟合趋势面[17].关于趋势分析方法的应用和优化,总结和认识更是不少,Fajklewicz(1959)提出了系数矩阵对角化分解方法,即cracovian法[18];Skeels(1967)指出多项式拟合应尽量选择受局部异常影响小的数据点来计算,最好将异常图分成几个部分重叠的小区域单独计算[19];Abdelrahman等人(1991)采用连续两个阶次的趋势分析获得的剩余异常做相关,取相关性最好的两个阶次中的低阶作为最佳阶次[20].国内,张愉才(1980)基于对正交多项式的分析,提出用更高阶的趋势面来代表区域场[21];王四龙等(1993)考虑到趋势面在垂向上的变化,提出三维趋势面分析方法[5];李九亮(1998)提出变阶滑动趋势分析法[22];羊春华(2005)采用筛选的代表区域场的数据进行趋势面的拟合,以减少局部场的干扰[23].趋势分析方法的原理如下:
拟合区域场的多项式可以是任意n阶,设gi为拟合的区域重力异常,g0 为实际区域重力异常,g0 =C为常数,拟合的区域重力异常一般形式为:
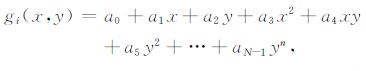
|
(1) |
式中a0,a1,…,aN-1 为N个待定系数,N=$\frac{1}{2}$(n+2)(n+1).
按照最小二乘法原理,得到最小二乘差值(SSR),
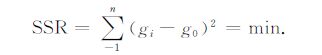
|
(2) |
显然,当n取1 时为一阶方程,代表一个平面;当n取2时为二阶方程,代表二次曲面;当n取3时为三阶方程,代表三次曲面;同理,高阶方程则代表高阶曲面.
可见趋势分析方法借鉴了最小二乘法原理,其实质与异常圆滑计算中的最小二乘圆滑是一样的,它们都属于函数拟合.但是趋势分析法的拟合计算与最小二乘圆滑计算又有不同:趋势分析要一次性地利用全测区(或整条测线)中所有测点的异常数据,异常圆滑则多次利用计算点附近一定范围内的数据;异常圆滑是局部拟合,圆滑计算时需要取计算点为坐标原点,计算点变化时,坐标原点和周围参与计算的已知点的异常值都随着变化,多次移动计算出多组多项式系数,趋势分析是整体拟合,趋势分析计算时坐标原点必须固定且一次性求解出多项式的全部系数.
2.2 插值切割法插值切割法是以当前计算点场值与四点圆周平均值的插值运算为切割算子,通过连续切割,得到重力异常的切割区域场,从重力异常中减去这个切割区域场后,就得到切割局部场,它包含了圆周平均的思想.插值切割法的原理如下:
设测区D内重力异常g(x,y)由区域场greg(x,y)和局部场gres(x,y)组成,局部场所在区域为D2,D2D,
用切割算子A作用于g(x,y),得第一次切割区域场
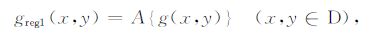
|
(3) |
对greg1(x,y)重复使用切割算子A得第二次切割区域场greg2(x,y),依次迭代下去,最终有
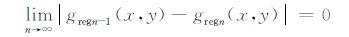
|
(4) |
以gregn(x,y)作为所求区域场的近似值,即
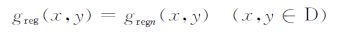
|
(5) |
再从观测场中减去切割区域场即得所求局部场的近似值
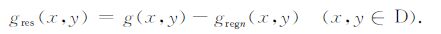
|
(6) |
插值切割法的关键点是切割算子,这个切割算子借鉴了四点圆周平均的思想,由于参与计算的点数有限,所以这个切割区域场难免会有偏差.文百红和程方道(1990)提出了在四点圆周平均法的基础上增加一项修正项,其改正值可随场的特点而自动调整[24],从而丰富和完善了插值切割方法.汪炳柱(1997)将研究区划分为浅、中、深三个层选择不同次数分别进行插值切割求解[25],得到了较好的异常分离效果.段本春(1998)由小到大选取一系列切割半径实验,他认为异常幅值是稳定极值时的切割半径数值与火成岩体的中心埋深相当[26].
2.3 匹配滤波法一般地,区域场和局部场的频率成分不同,区域场以低频成分为主,局部场以高频成分为主,因此可以通过提取不同波数成分的场进行位场的分离.在重力数据处理中匹配滤波法是分离局部与区域异常场的重要手段之一.1970年,Spector等根据磁异常的功率谱设计了匹配滤波器来分离不同深度的异常[27],后来Syberg(1972)、Jacobsen(1987)、Cowan(1993)等进一步改善和发展了这一方法[28-30].匹配滤波是最佳滤波的一种,当输入信号具有某一特殊波形时,其输出达到最大.原理如下:
设${{\left( {{{\tilde{V}}}_{zz}} \right)}_{1}}$、${{\left( {{{\tilde{V}}}_{zz}} \right)}_{2}}$ 分别为深部和浅部模型重力异常一阶垂直导数的波谱,则在不考虑水平尺寸因子影响的条件下,有
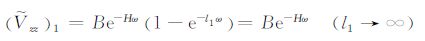
|
(7) |
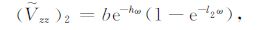
|
(8) |
其中B=2πGρ1(ρ1 为深部模型的剩余密度),b=2πGρ2(ρ2 为浅部模型的剩余密度),H、h分别为深部和浅部模型的顶面深度,l1、l2 分别为深部和浅部模型的厚度.
当波数较大时,${{\text{e}}^{-{{l}_{{{2}^{\omega }}}}}}\to 1$,于是有(9)
两模型的重力异常一阶垂直导数波谱应为
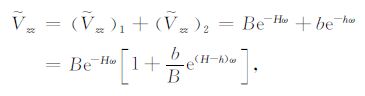
|
(10) |
或者
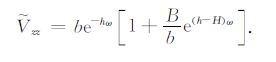
|
(11) |
令
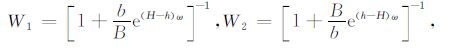
|
则有
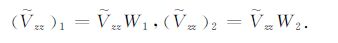
|
(12) |
因${{{\tilde{V}}}_{zz}}=\omega \vartriangle \tilde{g},{{\left( {{{\tilde{V}}}_{zz}} \right)}_{1}}=\omega \vartriangle {{{\tilde{g}}}_{1}},{{\left( {{{\tilde{V}}}_{zz}} \right)}_{2}}=\omega \vartriangle {{{\tilde{g}}}_{2}}$,所以有
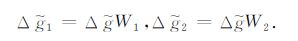
|
(13) |
可见若已知W1 和W2,则实际重力异常的波谱$\vartriangle \tilde{g}$乘以W1 为区域场的波谱$\vartriangle {{{\tilde{g}}}_{1}}$,而乘以W2 为局部场的波谱$\vartriangle {{{\tilde{g}}}_{2}}$,从而可将区域场或局部场分离出来.W1 、W2 为匹配滤波因子,而H、h和$\frac{b}{B}$( 或$\frac{B}{b}$)为滤波参数.
匹配滤波器要求某时刻t0 上有最大的信号瞬时功率与噪声平均功率的比值,此时输出达到最大.在形式上,一个匹配滤波器是由按时间反序排列的输入信号构成,滤波器的振幅特性与信号的振幅谱一致.因此,对信号的匹配滤波相当于对信号进行互相关运算.提取区域场的匹配滤波是一种低通滤波器,它与数学解析向上延拓不同之处在于它有一个较为复杂的类似于汉宁滤波器的窗函数.提取局部场的匹配滤波是一种高通滤波器.匹配滤波的波数响应以1为渐近线,它只能起到提取高频成分的作用,不会放大而产生振荡.
2.4 解析延拓法它是根据一个面上的一组位场数据确定另一个不同高度面上位场值的过程.解析延拓最早由Peters(1949)提出,他认为延拓可以对不同波长的信号进行增强或衰减,并推导出不同高度的加权系数[31].根据Stokes理论,如果已知地表某一点的重力值,那么任何更高一点的重力值能够通过这些值计算出来.计算公式如下:
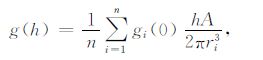
|
(14) |
其中g(h)是上延(或下延)高度h时的重力值,gi(0)是第i个原位置的重力异常值,A是异常体的表面积,ri是第i点上延(或下延)后和原位置之间的距离,见图 1.
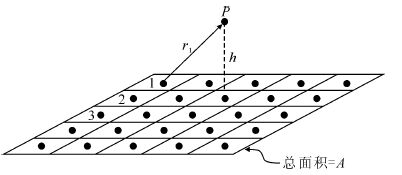
|
图 1 重力异常上延示意图 Fig. 1 Upward continuation map of gravity anomalies |
向上延拓方法在理论上是严密并且可以实现,其误差主要是积分范围有限所致,上延的另一个误差是取值点的密度以及插值的误差影响,当上延高度不太大时结果的误差并不大.曾华霖(2002)[32]指出通过计算两个相邻延拓高度结果的互相关系数对延拓高度的曲线的拐点高度,可确定最佳向上延拓高度.向下延拓从数学意义上讲是不适定的,因此实际应用就困难得多,可以串联低通滤波器以减少高频振荡[33],本文不作讨论.
2.5 垂向二阶导数法Darby和Davies(1967)对垂向二阶导数的计算做了详细的总结和对比[34];Clarke(1969)基于Wiener滤波理论,推导了新的空间域和波数域的优化二阶导数和向下延拓算子,可减少近地表噪声的干扰[35];Agarwal和Lal(1971)利用合理近似的Taylor级数提高了垂向二阶导数计算的精度[36].
这里基于四点圆周平均来说明垂向二阶导数法.设已知某点(i,j)的重力异常值gi,j,以及其周围四点的重力异常值gi-1,j,gi,j-1,gi+1,j,gi,j+1,则点(i,j)的局部场重力异常值(gi,j)reg 可由它周围的四个重力异常值求出(见图 2).
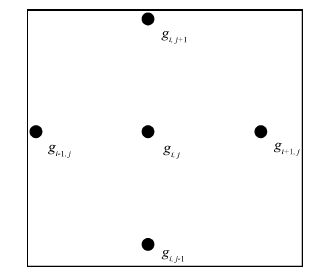
|
图 2 四点圆周平均各点位置示意图 Fig. 2 Point location of the four average circles |
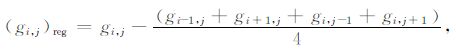
|
(15) |
设g为实际测量的重力异常值,根据拉普拉斯方程,有
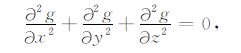
|
(16) |
定义gi-1,j和gi,j两点的水平距离为ΔX,gi+1,j和gi,j两点的水平距离也是ΔX(见图 3),则有
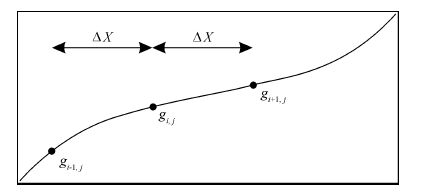
|
图 3 水平距离相等的相邻三点示意图 Fig. 3 djacent three points of equal horizontal distance |
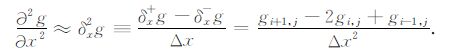
|
(17) |
类似地,
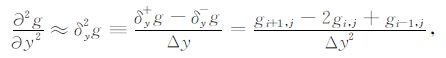
|
(18) |
假设Δx= Δy,因此垂向二阶导数
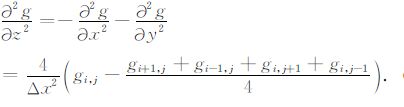
|
(19) |
(19)式说明,某点(i,j)处重力异常的垂向二阶导数与该点重力异常值gi,j同周围四点重力异常平均值的差值成正比,与相邻点距离平方成反比.事实上,由于计算误差,垂向二阶导数一般不能用来求解反问题;但是由于垂向二阶导数的零值点坐标X0的计算值与理论值偏差较小,可以利用改变它的计算半径(R/h<1情况下)来估算某些局部异常源的中心埋深.
3 模型试验对比为探讨位场分离各方法原则,结合实际设计一组由3个密度体两两垂向和两两水平叠加的模型体(见图 4a).其一椭球体S1,长轴长100 m,短轴长50m,密度为3.25×103 kg/m3,椭球体质点埋深200m.其二是在S1下方设计一板状长方体S2,长500m,宽50m,厚度100m,密度4.3×103 kg/m3,板状体质点埋深1000m,延伸2000m.其三椭球体S3,与S1 处于同一深度,质点埋深也为200 m,与S1水平距离为2000 m,S3 长轴长100 m,短轴长50m,密度为3.5×103 kg/m3.该模型体所处的观测区域为5000m×5000m 方格网,网格线距50m、点距50m,背景场密度为2.67×103 kg/m3.由此正演生成模型体的布格重力异常(见图 4b),再对该布格异常分别采取趋势分析、插值切割、匹配滤波、解析延拓以及垂向二阶导数方法,开展重力异常分离试验.考虑到边界效应,对该数据进行了20% 的扩边处理.

|
图 4 设计的叠加模型体 (a)三维立体图;(b)模型体的布格重力异常图. Fig. 4 Superposed model (a) 3D diagram; (b) Bouguer gravity anomaly map of model. |
如前所述,趋势分析的实质是最小二乘意义下的多项式拟合,做趋势分析我们选择1~3不同阶次的多项式实验,拟合时选取受局部异常影响小的数据点,采用正交多项式拟合趋势面,并对趋势分析获得的剩余异常做相关,取相关性最好的两个阶次中的低阶作为异常分离的最佳阶次.本次实验得到二阶趋势分析效果较好(见图 5),它反映出模型体的背景场(图 5a),同时从水平方向上清晰地描绘出异常体的边界,对于纵向叠加的S1 和S2 两个密度体,却没能区分开.
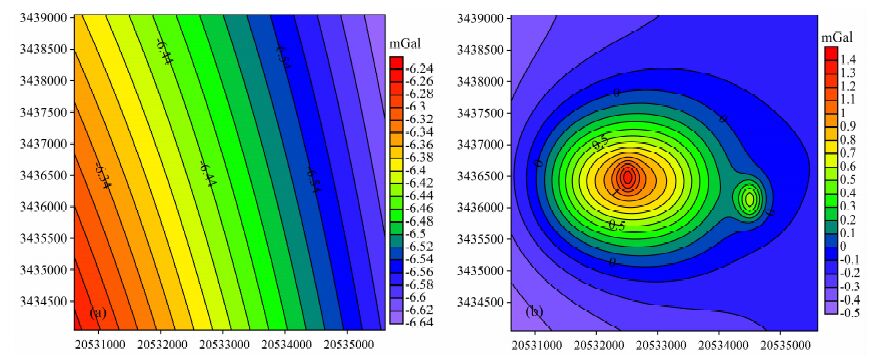
|
图 5 二阶趋势分析效果图 (a)背景场;(b)局部异常图. Fig. 5 2 order trend analysis map (a) Regional field; (b) Local anomalies. |
采用插值切割方法进行实验,发现当切割半径为5m(是线距50m 的1/10),切割次数为2时分离效果较好,见图 6.该局部异常在水平方向上反映了S1、S2 与S3 三个密度体的形态边界,同时显示出S1与S2的叠加状态,对于S1与S2的具体埋藏深度却无能为力,这囿于重力勘探纵向分辨率低的缘故.本次实验模型体置于小测区,单个异常的分离效果较好,对于大范围资料插值切割法则应具体分析.
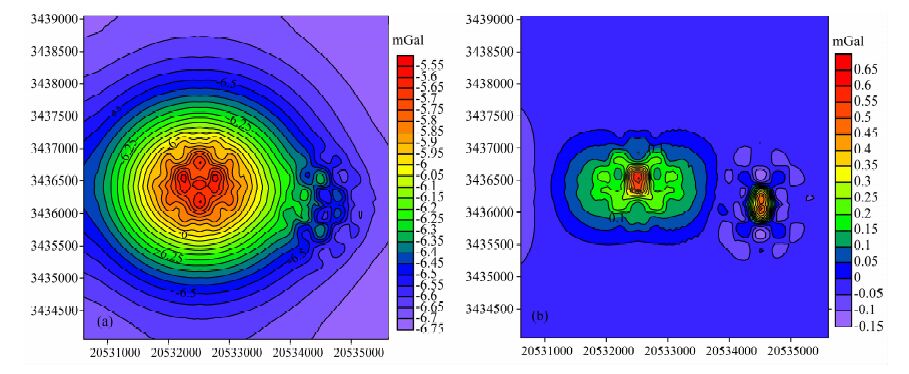
|
图 6 切割半径为5m,迭代次数为2时的插值切割效果图 (a)区域异常图;(b)局部异常图. Fig. 6 Interpolating cut map of 5 m cutting radius and 2-time iteration (a) Regional anomalies; (b) Local anomalies. |
利用滤波法进行位场分离,应分析实测异常功率谱曲线,选择合适的滤波段(一般取功率谱变化曲线的切线),建造适宜的低通、带通滤波器,对实测异常波谱进行滤波,来提取不同波数成分的异常场.图 7准确地划分出功率谱的低频段和中高频段非常关键,由此才能很好地分离出约200m 浅源和1000m深源的局部异常(见图 8),同时从平面上划分了异常体S1、S2与S3的形态边界.
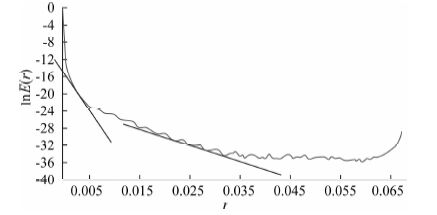
|
图 7 匹配滤波对数功率谱曲线图 (左切线为截断低频,右切线为截断中高频) Fig. 7 Logarithm power spectrum curves of matched filtering (Lett line is low-frequency truncation,right line is middle and high frequency truncation) |
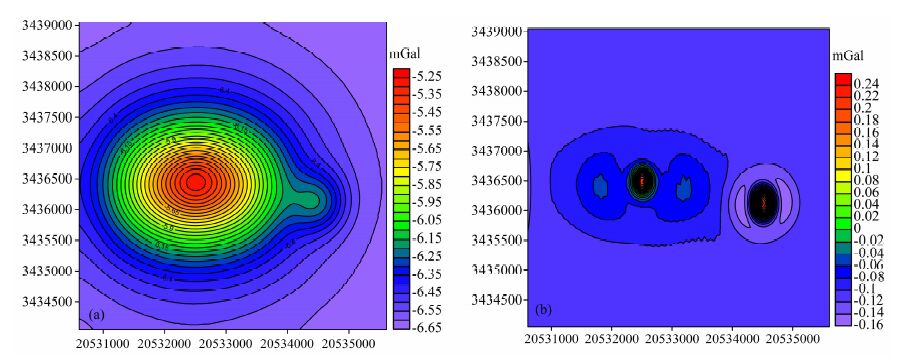
|
图 8 匹配滤波效果图 (a)区域异常图;(b)局部异常图. Fig. 8 Matched filtering map (a) Regional anomalies; (b) Local anomalies. |
由于向上延拓算子具有低通特性,因此向上延拓不同高度可反映不同深度的场源特征.本实验中,向上延拓高度达到800 m,延拓后的异常仅包含极少的浅部异常,当再次上延到1000m 时,异常形态几乎没有变化,可以把上延到800m 时的异常作为深部区域异常,用模型体原始异常减去上延800 m后的区域异常,就可得到浅部异常(见图 9).说明向上延拓可区分浅部和深部异常,但延拓高度和深度并不一一对应,由此亦可把水平方向上的异常体划分开来.图 10垂向二阶导数法很好地反映了S1 和S2的形态,背景场几乎完全被消除.
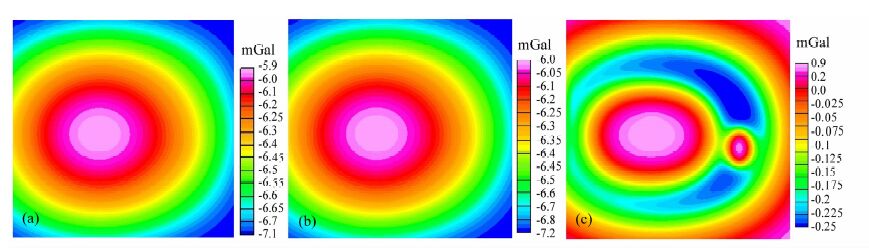
|
图 9 解析延拓效果图 (a)向上延拓800 m;(b)向上延拓1000 m;(c)模型体一向上延拓800 m=局部异常. Fig. 9 Analytic continuation maps (a) 800 m upward continuation; (b) 1000 m upward continuation; (c) Local anomalies. |
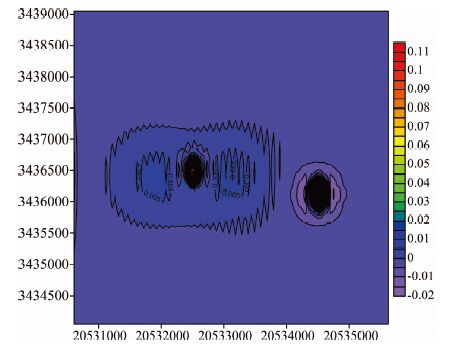
|
图 10 垂向二阶导数法效果图 Fig. 10 Second derivative map of vertical direction |
通过以上模型试验,结果表明:①趋势分析法是多项式整体拟合区域场,能够分离出背景场,可在平面上描绘异常体的边界,却无法区分纵向叠加的异常体.其计算过程很少利用已知的地质信息,分离效果受趋势函数多项式的选择和阶次影响较大.多项式次数的定性选择,原则上由区域异常的复杂程度决定,阶次太高,会造成趋势值包含过多的局部异常成分,使得计算出的局部异常偏小,趋势面也会畸变.对于范围大、地质情况复杂的测区则应分区,分别选用不同阶次的多项式进行计算.② 插值切割法对于小测区单个异常的分离效果较好,当测区范围不大,矿体叠加不太复杂时,取较小的切割半径(切割半径一般取线距的1/10、1/20等),迭代次数取1或2次即可.采用插值切割法进行场分离还应尽量多了解研究区的地质情况,可按深度分层次、选择不同的切割半径进行实验确定合适的参数.③ 匹配滤波将实测场看成由埋深大、延伸大、规模大的直角棱柱体和埋深小、延伸小、规模小的直角棱柱体这两个统计模型共同引起,它适用于随机场和非随机场的滤波.准确分析实测异常的功率谱曲线是匹配滤波取得成功的关键,对于埋深和尺寸相差很大的垂向叠加场源分离效果好,用匹配滤波提取局部场时最好进行低通滤波以压制高频干扰.④ 解析延拓是根据一个面上的位场数据确定另一个不同高度面上位场值,把握好延拓高度非常重要.⑤垂向二阶导数法可用来提取埋藏较浅的局部异常,同时可区分水平叠加异常,确定异常体的边界,还可消除或削弱背景场的作用.
4 安徽泥河铁矿重力场分离安徽省泥河铁矿是安徽省地质调查院在玢岩铁矿成矿模式和大型矿集区成矿理论指导下,利用钻探对重磁异常进行验证,于2007 年5 月首孔发现的.泥河铁矿床位于庐枞火山岩盆地西北边缘,处于罗河—黄屯北东向成矿带上.南西距罗河铁矿床3km,北东距龙桥铁矿床13km(图 11),与罗河铁矿有着相同的成矿地质条件.泥河矿区内地层主要为白垩统砖桥组(K1zh)和双庙组(K1sh)火山岩,杨湾组(K1y)砂岩以及第四系(Q).矿区构造较为简单,主要为火山岩地层的北西倾斜单斜构造和成矿期后的浅层断裂.地层产状平缓,褶皱不发育,往深部地层产状略有起伏变化[37-41].据前人研究资料[42],泥河铁矿主要赋存在闪长玢岩(次火山岩)体的顶部与砖桥组下段的火山碎屑岩中,砖桥组下段的火山碎屑岩是寻找铁矿的地层标志.赋矿的有利构造是闪长玢岩体的穹状隆起部位,矿床成因类型为广义玢岩型铁矿.
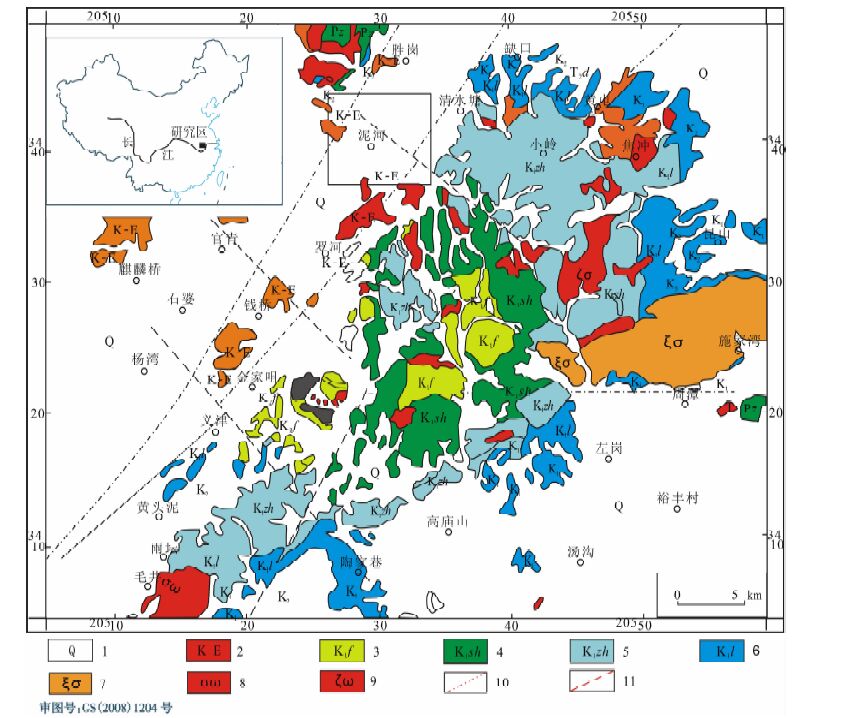
|
图 11 泥河铁矿区域地质简图 1 一第四系;2一白垩系一第三系(红层);2一白垩系浮山组;4一白垩系双庙组;5一白垩系砖桥组;6一白垩系龙门院组;7一燕山期侵入岩正长岩, 正长斑岩;8一燕山期早期侵入岩石英闪长玢岩;9一次火山岩粗安玢岩;10—推断的区域断裂;11 一推断的次级断裂. Fig. 11 Regional geological map of the Nihe iron deposit 1一Quaternary; 2 — Cretaceous-Tertiary (red layer) ; 3一Fushan group in Cretaceous; 4一Shuangmiao group in Cretaceous; 5一Zhuanqiao group in Cretaceous ; 6 一 Longmenyuan group in Cretaceous; 7 — Intrusive rock of syenite, syenite porphyry in Yanshan period; 8 — Intrusive rock of quartz diorite porphyrite in early Yanshan period; 9一Sub volcanic rock of trachyandesite porphyrite; 10 一Inferred region fracture; 11 一Inferred secondary fracture. |
泥河铁矿勘查现已累计完成钻探工作量8.33×104 m,74口钻孔,如此丰富的钻孔资料可以很好地控制矿体的形态,验证重力场分离效果.图 12 是泥河铁矿布格重力异常图.
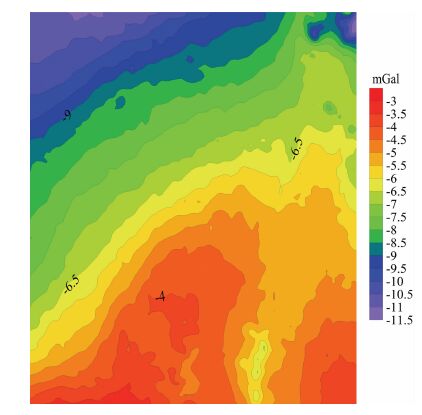
|
图 12 泥河铁矿布格重力异常图 Fig. 12 Bouguer gravity anomaly map of the Nihe iron deposit |
根据物性统计和分析,首先开展了趋势分析(见图 13).对比一阶、二阶、三阶趋势分析图,发现采用三阶趋势分析得到的局部重力异常高点更集中一些,与地质资料和钻井吻合很好.图 13a是拟合的趋势面,较为平缓光滑,反映的可能是深部大的区域构造,图 13b局部重力异常高点和钻井吻合(700~1000m深度是含铁矿层的高密度体).接着还开展了解析延拓工作,图 14反映的是泥河铁矿的重力异常解析延拓结果,当向上延拓到800m 后重力异常形态基本没有大变化,因此考虑将800 m 深度作为背景场.图 14b是原始异常减去上延800m 时的重力得到反映矿体的局部异常.
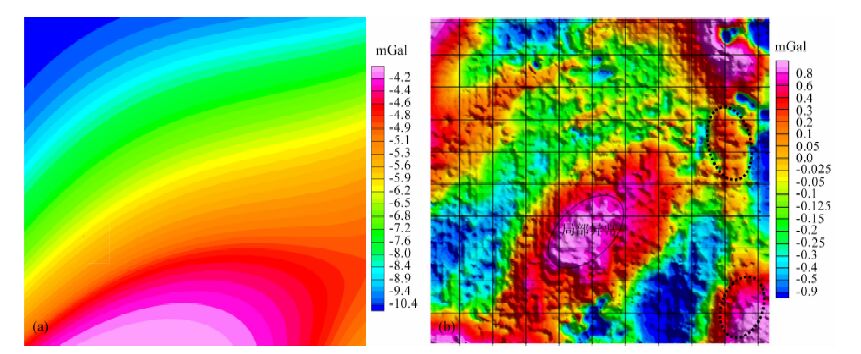
|
图 13 泥河铁矿重力异常三阶趋势分离结果 (a)为背景场;(b)为局部异常图. Fig. 13 3 order trend analysis map of the Nihe iron deposit (a) Regional field; (b) Local anomalies. |
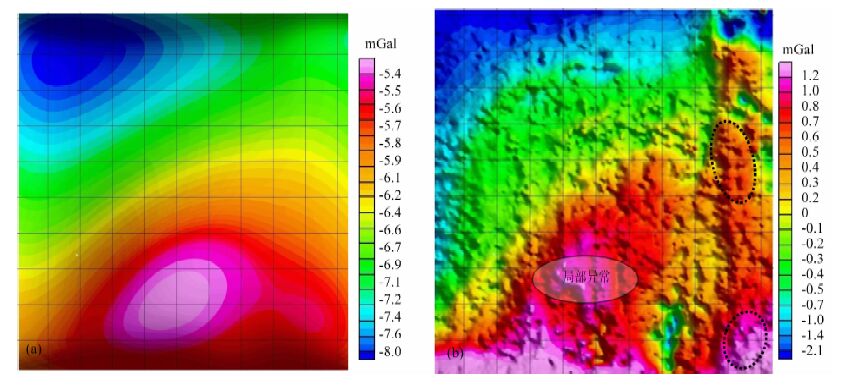
|
图 14 泥河铁矿重力异常解析延拓分离结果 (a)向上延拓800 m; (b)原始异常减去上延800 m的剩余异常. Fig. 14 Analytic continuation map of the Nihe iron deposit (a) 800 m upward continuation;(b) Original gravitational anomalies minus upward continuation 800 m gravitational anomalies. |
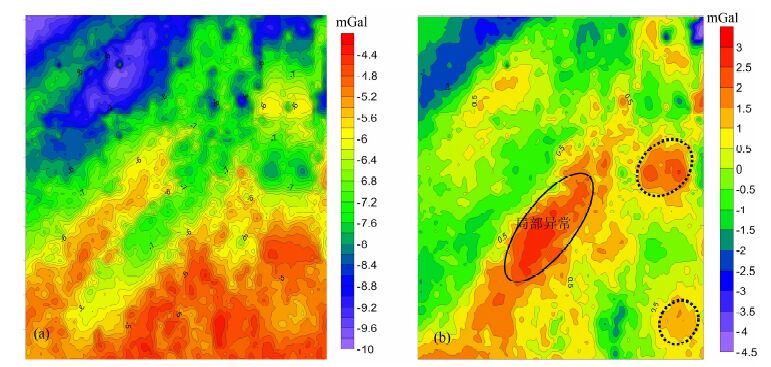
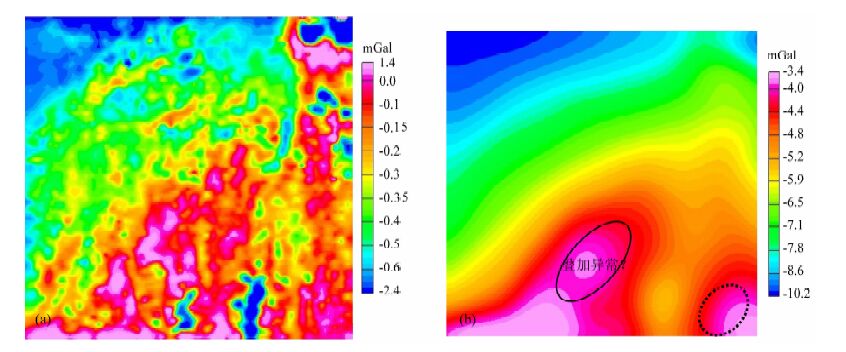
为进一步对比异常分离的效果,还采用了插值切割(见图 15)、匹配滤波(见图 16)等方法.对于插值切割法,难点在于切割半径的选择,根据测线和测点间距(100 m×50 m),选择适合的网格大小和切割半径.通过实验发现切割半径为20 m、迭代次数为2时效果较好(图 15),符合现有地质情况,尽管图 15a区域重力异常等值线也有小规模扭曲,说明浅部少量地质信息可能残留在区域异常图中,但局部重力异常图刻画得较好,其中重力高点和圈闭与之前进行分离的局部异常较为一致.匹配滤波的关键是对功率谱的分解和拟合,根据区域场功率谱以低频为主、局部场以高频为主原则,对实际测量的功率谱进行分解和拟合.由于泥河铁矿重力异常波谱重叠比较严重,功率谱呈现出不明显的线性段,因此只获得泥河铁矿约100m 以内的浅源场(图 16a)和深源场(图 16b).同之前分离的局部异常相比,图 16b并没有剥离掉深部背景场,仍是叠加重力场,并没完全反映出千米埋深的矿体异常.
|
图 15 泥河矿区切割半径为20,迭代次数为2的插值切割法分离效果图 (a)区域场;(b)局部场. Fig. 15 Interpolating cut map of 20 m cutting radius and 2-times iteration (a) Regional field; (b) Local field. |
|
图 16 泥河矿区匹配滤波异常分离效果图 (a) 浅源场;(b)深源场. Fig. 16 Matched filtering map of the Nihe iron deposit (a) Shallow-source field; (b) Deep-source field. |
垂向二阶导数法用来提取埋藏较浅的局部异常效果较好,由于研究区域泥河矿区范围较小,矿体埋藏较深(达千米),且水平方向异常体单一,经试验垂向二阶导数法不适宜于此处的矿体异常提取.
根据泥河矿区的地质和钻井资料得到矿区的物性密度值,与以上重力异常分离效果进行对照.泥河矿区岩石的密度值按大小可分成三类:第一类:主要为二长岩及潜火山岩,平均密度一般为2.62×103 kg/m3.第二类:主要为粗安质、安山质熔岩和次生石英岩、象山群砂页岩,以及正长岩和粗面斑岩,密度一般为(2.47~2.62)×103 kg/m3.第三类:主要为凝灰岩、粗面岩,以及K-E红层砂岩,平均密度一般为(2.43~2.44)×103 kg/m3.据泥河矿区资料查证铁矿石的密度值为(3.00~4.26)×103 kg/m3,矿化、蚀变岩石的密度值为(2.78~3.00)×103 kg/m3.说明泥河矿区含矿体与周围岩石之间存在明显的密度差异,这些密度差异在重力异常上必有反映,因此通过重力分离得到的局部异常应当是由矿体引起的异常.事实上通过钻孔验证,泥河矿区分离后的剩余重力异常,图 13b、图 14b 和图 15b 中标注“局部异常"处,于埋深700~1000m 处见含磁铁矿层.
对于深部隐伏矿床勘查,在地质构造有利地段,通常重磁联合解释是寻找隐伏铁矿的有效手段.由于泥河铁矿体埋藏深度接近1000m,地面磁异常显示非常零乱和微弱,而重力异常仍然较为明显,所以在泥河矿区重力异常是寻找铁矿的重要标志.仔细分析三阶趋势分析、向上延拓、插值切割以及匹配滤波分离出的局部异常,图 13b、图 14b、图 15b 和图 16b虚线圆圈标注处,发现存在另外的重力高值区,结合成矿条件和重力异常特征,推断在泥河矿区东南部和东北部区域具有较好的找矿远景,可能存在新的铁矿体.
5 结论与讨论(1) 本文对趋势分析、插值切割、匹配滤波、解析延拓、垂向二阶导数这些重力异常分离方法进行了较为系统的总结和比较,依据方法的理论基础和应用条件,通过模型试验检验对比,得到各方法的适用原则:趋势分析法多项式次数的定性选择,原则上由区域异常的复杂程度决定,对于范围大、地质情况复杂的测区则应分区,选用不同阶次的多项式进行计算;插值切割法对于小测区单个异常的分离效果较好,切割半径一般取线距的1/10或1/20,迭代次数取1或2次即可;匹配滤波法适用于随机场和非随机场的滤波,对于埋深和尺寸相差较大的垂向叠加场源分离效果好,准确分析实测异常的功率谱曲线是匹配滤波取得成功的关键;解析延拓法把握好延拓高度非常重要;垂向二阶导数法可用来提取埋藏较浅的局部异常,并可区分水平叠加异常.
(2) 将讨论成果应用于长江中下游安徽省泥河矿区寻找深部隐伏矿床实践,发现三阶趋势分析、向上延拓以及插值切割这些异常分离方法,可以较好地分离出矿体异常和背景场,与钻井吻合良好.匹配滤波没能把泥河矿区千米深的铁矿体从深部背景场中剥离,说明匹配滤波法更适宜于埋深和尺寸相差很大的垂向叠加场源的分离,当异常的波谱重叠比较严重,即功率谱表现为不明显的线性段时,分离效果并不理想.因此,匹配滤波方法对于埋深相差不很大的中深部完全定量的异常分离还要做深入的工作.垂向二阶导数法也不适宜于像泥河铁矿这样范围小、埋藏深的矿体异常提取.
(3) 通过以上模型试验和深部隐伏矿床实践,进一步说明各种重力异常分离方法都具有侧重点和局限性,进行位场分离前必须弄懂每种方法的数学依据和理论前提.否则,同样的方法参数选择不同,结果将大相径庭.此外,解释人员对研究区地质情况的熟悉和了解,也是准确分离出目标异常的前提条件.
(4) 根据成矿条件和分离后的局部重力异常特征,推断泥河矿区在主矿体东南部和东北部区域可能存在新的铁矿体,找矿远景较好.
致谢本文在构思和研究中得到中国地质科学院矿产资源研究所吕庆田研究员的大力支持和帮助,在此表示深深地谢意.还要感谢中国地质大学(北京)孟小红教授和魏文博教授的帮助和指导.同时,非常感谢审稿专家的宝贵意见.
| [1] | 曾华霖. 重力场与重力勘探. 北京: 地质出版社, 2005 : 189 -234. Zeng H L. Gravity Field and Gravity Exploration (in Chinese). Beijing: Geological Publishing House, 2005 : 189 -234. |
| [2] | 穆石敏, 申宁华, 孙运生. 区域地球物理数据处理方法及其应用. 长春: 吉林科学技术出版社, 1990 . Mu S M, Shen N H, Sun Y S. Regional Geophysical Data Processing Method and its Application (in Chinese). Changchun: Jilin Science &Technology Press, 1990 . |
| [3] | Pawlowski R S, Hansen R O. Gravity anomaly separation by Wiener filtering. Geophysics , 1990, 55(5): 539-548. DOI:10.1190/1.1442865 |
| [4] | Pawlowski R S. Preferential continuation for potential-field anomaly enhancement. Geophysics , 1995, 60(2): 390-398. DOI:10.1190/1.1443775 |
| [5] | 王四龙, 宁书年, 李郴, 等. 用三维趋势面分析分离位场异常. 煤田地质与勘探 , 1993, 21(5): 60–64. Wang S L, Ning S N, Li C, et al. 3D trend analysis application to the dissociation of potential field anomaly. Coal Geology and Exploration (in Chinese) , 1993, 21(5): 60-64. |
| [6] | 徐世浙, 张研, 文百红, 等. 切割法在陆东地区磁异常解释中的应用. 石油物探 , 2006, 45(3): 316–318. Xu S Z, Zhang Y, Wen B H, et al. The application of cutting method to interpretation of magnetic anomaly in region of Ludong. Geophysical Prospecting for Petroleum (in Chinese) , 2006, 45(3): 316-318. |
| [7] | 许德树, 曾华霖. 优选延拓技术及其在中国布格重力异常图处理上的应用. 现代地质 , 2000, 14(2): 215–222. Xu D S, Zeng H L. Preferential continuation and its application to Bouguer gravity anomaly in China. Geoscience (in Chinese) , 2000, 14(2): 215-222. |
| [8] | 侯遵泽, 杨文采. 中国重力异常的小波变换与多尺度分析. 地球物理学报 , 1997, 40(1): 85–95. Hou Z Z, Yang W C. Wavelet transform and multi-scale analysis on gravity anomalies of China. Chinese J| Geophys| (in Chinese) , 1997, 40(1): 85-95. |
| [9] | 杨文采, 施志群, 侯遵泽, 等. 离散小波变换与重力异常多重分解. 地球物理学报 , 2001, 44(4): 534–541. Yang W C, Shi Z Q, Hou Z Z, et al. Discrete wavelet transform for multiple decomposition of gravity anomalies. Chinese J| Geophys| (in Chinese) , 2001, 44(4): 534-541. |
| [10] | 邱宁, 何展翔, 昌彦君. 分析研究基于小波分析与谱分析提高重力异常的分辨能力. 地球物理学进展 , 2007, 22(1): 112–120. Qiu N, He Z X, Chang Y J. Ability of improving gravity anomaly resolution based on Multiresolution wavelet analysis and power spectrum analysis. Progress in Geophysics (in Chinese) , 2007, 22(1): 112-120. |
| [11] | Grant F S. Review of data processing and interpretation methods in gravity and magnetics, 1964-1971. Geophysics , 1972, 37: 647-661. DOI:10.1190/1.1440288 |
| [12] | 管志宁, 张昌达, 程方道. 磁法勘探重要问题理论分析与应用. 北京: 地质出版社, 1993 . Guan Z N, Zhang C D, Cheng F D. Theoretical Analysis and Application of Important Problems in Magnetic Prospecting (in Chinese). Beijing: Geological Publishing House, 1993 . |
| [13] | Nabighian M N, Grauch V J, Hansen R O, et al. The historical development of the magnetic method in exploration, 75th Anniversary. Geophysics , 2005, 70(6): 33-61. DOI:10.1190/1.2133784 |
| [14] | 宋景明. 基于对应分析的重力异常分离技术及应用. 天然气工业 , 2007, 27(Suppl.A): 318–319. Song J M. The technology and application of gravity anomaly separation based on correspondence analysis. Natural Gas Industry (in Chinese) , 2007, 27(Suppl.A): 318-319. |
| [15] | Agocs W B. Least-squares residual anomaly determination. Geophysics , 1951, 16(4): 686-696. DOI:10.1190/1.1437720 |
| [16] | Simpson S M Jr. Least squares polynomial fitting to gravitational data and density plotting by digital computers. Geophysics , 1954, 19(2): 255-269. DOI:10.1190/1.1437990 |
| [17] | Oldham C H G, Sutherland D B. Orthogonal polynomials: their use in estimating the regional effect. Geophysics , 1955, 20(2): 295-306. DOI:10.1190/1.1438143 |
| [18] | Fajklewicz Z. The use of cracovian computation in estimating the regional gravity. Geophysics , 1959, 24(3): 465-478. DOI:10.1190/1.1438615 |
| [19] | Skeels D C. What is residual gravity. Geophysics , 1967, 32(5): 872-876. DOI:10.1190/1.1439896 |
| [20] | Abdelrahman E M, Bayoumi A I, El-Araby H M. A least-squares minimization approach to invert gravity data. Geophysics , 1991, 56(1): 115-118. DOI:10.1190/1.1442946 |
| [21] | 张愉才. 正交多项式趋势面分析. 物探化探计算技术 , 1980(2): 84–97. Zhang Y C. Orthogonal polynomial trend surface analysis. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1980(2): 84-97. |
| [22] | 李九亮. 划分重力区域异常与局部异常的变阶滑动趋势分析法. 物探化探计算技术 , 1998, 20(1): 53–61. Li J L. Variable order sliding trend analysis method used in the division of regional and local gravity anomalies. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 1998, 20(1): 53-61. |
| [23] | 羊春华. 筛选—趋势分析法分离区域异常与局部异常. 物探与化探 , 2005, 29(2): 167–170. Yang C H. The application of the sieving-trend analysis method to separating regional anomaly from local anomaly. Geophysical and Geochemical Exploration (in Chinese) , 2005, 29(2): 167-170. |
| [24] | 文百红, 程方道. 用于划分磁异常的新方法——插值切割法. 中南矿冶学院学报 , 1990, 21(3): 229–235. Wen B H, Cheng F D. A new interpolating cut method for identifying regional and local fields of magnetic anomaly. Journal of Central South Mining and Metallurgy Institute (in Chinese) , 1990, 21(3): 229-235. |
| [25] | 汪炳柱, 徐世浙, 刘保华, 等. 多次插值切割法分场的一个实例. 石油地球物理勘探 , 1997, 32(3): 431–438. Wang B Z, Xu S Z, Liu B H, et al. An example of aeromagnetic anomaly separation using multi-interpolation division. Oil Geophysical Prospecting (in Chinese) , 1997, 32(3): 431-438. |
| [26] | 段本春, 徐世浙, 阎汉杰, 等. 划分磁异常场的插值切割法在研究火成岩体分布中的应用. 石油地球物理勘探 , 1998, 34(1): 125–131. Duan B C, Xu S Z, Yan H J, et al. Application of interpolation-cut method for magnetic anomaly division to igneous mass investigation. Oil Geophysical Prospecting (in Chinese) , 1998, 34(1): 125-131. |
| [27] | Spector A, Grant F S. Statistical models for interpreting aeromagnetic data. Geophysics , 1970, 35(2): 293-302. DOI:10.1190/1.1440092 |
| [28] | Syberg F J R. A Fourier method for the regional-residual problem of potential fields. Geophysical Prospecting , 1972, 20(1): 47-75. DOI:10.1111/gpr.1972.20.issue-1 |
| [29] | Jacobsen B H. A case for upward continuation as a standard separation filter for potential-field maps. Geophysics , 1987, 52(8): 1138-1148. DOI:10.1190/1.1442378 |
| [30] | Cowan D R, Cowan S. Separation filtering applied to aeromagnetic data. Exploration Geophysics , 1993, 24(4): 429-436. DOI:10.1071/EG993429 |
| [31] | Peters L J. The direct approach to magnetic interpretation and its practical application. Geophysics , 1949, 14(3): 290-320. DOI:10.1190/1.1437537 |
| [32] | 曾华霖, 许德树. 最佳向上延拓高度的估计. 地学前缘 , 2002, 9(2): 499–503. Zeng H L, Xu D S. Estimation of optimum upward continuation height. Earth Science Frontiers (in Chinese) , 2002, 9(2): 499-503. |
| [33] | 毛小平, 吴蓉元, 曲赞. 频率域位场下延的振荡机制及消除方法. 石油地球物理勘探 , 1998, 33(2): 230–237. Mao X P, Wu R Y, Qu Z. Oscillation mechanism of potential field downward continuation in frequency domain and its elimination. Oil Geophysical Prospecting (in Chinese) , 1998, 33(2): 230-237. |
| [34] | Darby E K, Davies E B. The analysis and design of two-dimensional filters for two-dimensional data. Geophysical Prospecting , 1967, 15(3): 383-406. DOI:10.1111/gpr.1967.15.issue-3 |
| [35] | Clarke G K C. Optimum second-derivative and downward-continuation filters. Geophysics , 1969, 34(3): 424-437. DOI:10.1190/1.1440020 |
| [36] | Agarwal B N P, Lal L. Application of rational approximation in calculation of the second derivative of the gravity field. Geophysics , 1971, 36(3): 571-581. DOI:10.1190/1.1440192 |
| [37] | 吕庆田, 韩立国, 严加永, 等. 庐枞矿集区火山气液型铁硫矿床及控矿构造的反射地震成像. 岩石学报 , 2010, 26(9): 2598–2612. Lü Q T, Han L G, Yan J Y, et al. Seismic imaging of volcanic hydrothermal iron-sulfur deposits and its hosting structure in Luzong ore district. Acta Petrologica Sinica (in Chinese) , 2010, 26(9): 2598-2612. |
| [38] | 董树文, 高锐, 吕庆田, 等. 庐江—枞阳矿集区深部结构与成矿. 地球学报 , 2009, 30(3): 279–284. Dong S W, Gao R, Lü Q T, et al. Deep structure and ore-forming in Lujiang-Zongyang ore concentrated area. Acta Geoscientica Sinica (in Chinese) , 2009, 30(3): 279-284. |
| [39] | 吕庆田, 史大年, 汤井田, 等. 长江中下游成矿带及典型矿集区深部结构探测-SinoProbe-03年度进展综述. 地球学报 , 2011, 32(3): 257–268. Lü Q T, Shi D N, Tang J T, et al. Probing on deep structure of middle and lower reaches of the Yangtze metallogenic belt and typical ore concentration area: A review of annual progress of SinoProbe-03. Acta Geoscientica Sinica (in Chinese) , 2011, 32(3): 257-268. |
| [40] | 赵文广, 吴明安, 张宜勇, 等. 安徽省庐江县泥河铁硫矿床地质特征及成因初步分析. 地质学报 , 2011, 85(5): 789–801. Zhao W G, Wu M A, Zhang Y Y, et al. Geological characteristics and genesis of the Nihe Fe-S deposit, Lujiang country, Anhui province. Acta Geologica Sinica (in Chinese) , 2011, 85(5): 789-801. |
| [41] | 刘彦, 吕庆田, 严加永, 等. 庐枞矿集区结构特征重磁研究及其成矿指示. 岩石学报 , 2012, 28(10): 3125–3138. Liu Y, Lü Q T, Yan J Y, et al. The structure of Luzong ore district and its metallogenic indication from gravity and magnetic information. Acta Petrologica Sinica (in Chinese) , 2012, 28(10): 3125-3138. |
| [42] | 吴明安, 汪青松, 郑光文, 等. 安徽庐江泥河铁矿的发现及意义. 地质学报 , 2011, 85(5): 802–809. Wu M A, Wang Q S, Zheng G W, et al. Discovery of the Nihe iron deposit in Lujiang, Anhui, and its exploration significance. Acta Geologica Sinica (in Chinese) , 2011, 85(5): 802-809. |
 2012, Vol. 55
2012, Vol. 55

