2. 地下信息探测技术与仪器教育部重点实验室, 中国地质大学, 北京 100083;
3. 地球物理与信息技术学院, 中国地质大学, 北京 100083
2. Key Laboratory of Geo-detection(China University of Geosciences, Beijing), Ministry of Education, Beijing 100083, China;
3. School of Geophysics and Information Technology, China University of Geosciences, Beijing 100083, China
随着重力测量设备的不断发展,重力勘探方法已经广泛应用于油气勘探、金属矿勘查、地球深部构造及地壳研究、划分大地构造单元及工程与环境地球物理勘探等领域[1-2].特别是近几年来,具有更高分辨率的航空、海洋重力梯度测量仪器与配套技术的快速发展,使得重力勘探方法也愈来愈引起地球物理学界的重视.相应地,重力(重力梯度)数据量也愈来愈成为海量级别.针对海量重力(重力梯度数据)实际资料快速估算解释的要求,国内外学者已经开展了很多工作,特别是带有不同约束条件的物性反演研究[3-21].物性反演是将观测区域对应的地下半空间离散化成规则的长方体单元,通过反演方法确定各离散单元的物性值,由物性的分布确定场源的实际分布情况.近几年来随着计算水平的提高,这种方法已逐渐成为国内外重力数据反演的主要方向[22].
在基于物性模型的重力(重力梯度)数据约束反演或者联合反演中,模型体的正演计算是反演过程的重要组成部分.不同规模模型体的正演计算效率是主要制约反演充分发挥作用的瓶颈问题.将网格观测单元与地半空间模型单元中心一一对应,采用等效格架技术,只需计算一遍模型正演,并且只计算每层的一个网格单元,使模型正演计算几乎消失[22-23].上述方法只适用于模型的剖分与网格采取某种对应关系时.基于小波变换,采用系数矩阵压缩与重构的方式,减少存储空间,提高了反演效率.但这种方法损失信号[8, 24].
另外一种思路是采用并行计算技术.以往大规模数据并行运算只局限于专业以及昂贵的并行计算机上.如今随着GPU 通用计算的实现,这一现状得到改变.GPU 在处理能力和存储器带宽相对CPU有明显优势,在成本和功耗上也不需要付出太大代价,从而为相同的大规模数据运算问题提供了新的解决方案[25-29].鉴于正演计算程序具有很好的并行改进能力,本文利用NIVIDIA CUDA 编程平台,详细分析了并行计算中的几个关键问题(代码设计、存储器优化、精度问题),从而实现了基于GPU 并行的重力、重力梯度三维快速正演计算方法.试验结果表明,该并行技术计算结果和单线程计算结果一致,可大大提高效率.最后讨论了基于GPU 并行计算的重力、重力梯度数据三维反演策略.
2 正演理论常规重力测量只观测到重力位的铅垂一次导数,即Δg或Uz,而重力梯度测量可以得到重力位的一次导数Gx,Gy,Gz在x,y,z方向上的变化率,即重力位的二次导数.重力梯度张量由9 个重力梯度分量构成:
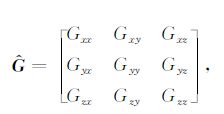
|
(1) |
即,重力梯度分量可写为
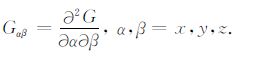
|
(2) |
根据场论可知,Gxy= Gyx,Gxz= Gzx,Gyz=Gzy,Gxx+Gyy+Gzz=0.因此,重力梯度张量的9个分量中仅有5个是独立的.
重力梯度异常反映了地下密度突变引起的重力异常的变化,突出场源体的细节,具有比重力异常本身高的分辨率,综合利用各梯度张量分量信息能够提高地质解释的准确性.
单个直立长方体模型的重力、重力梯度正演计算解析公式如下[30-32]:
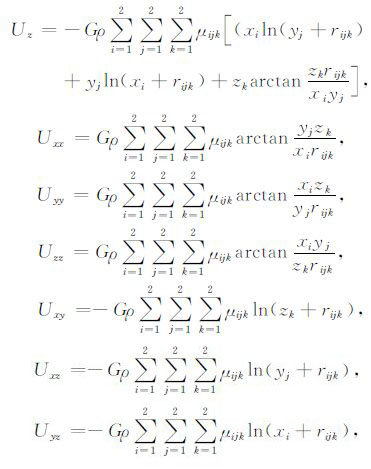
|
(3) |
其中,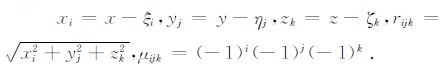
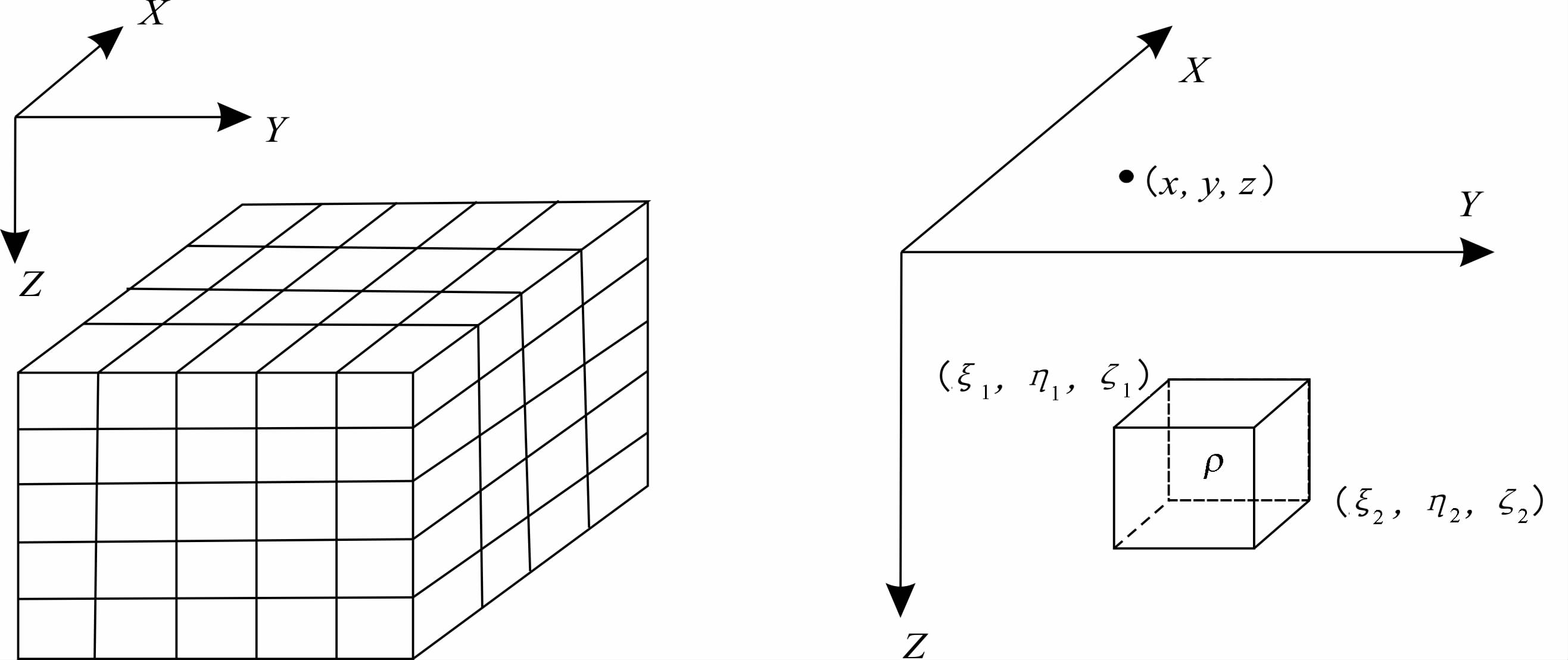
将所有直立长方体模型异常在地面某点的异常响应累加求和(图 1),就可以得出地下半空间在该点的异常响应值,可记为:

|
(4) |
|
图 1 地下剖分模型示意图 (a)地下剖分单元示意图;(b)单个直立长方体模型. Fig. 1 Interpretation models of the subsurface |
其中,Δgi为第i个观测点处的重力(重力梯度)异常值,Gij为第i个观测点处第j个模型单元所对应的核函数,ρj为第j个模型单元的密度值.
写成矩阵形式:
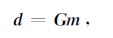
|
(5) |
其中,d为数据向量,G为核矩阵,m为模型向量.正演问题就是已知上述G和m,求d,而反演问题则是已知G和d,求m.
后文的基于物性模型的重力(重力梯度)数据三维正演,观测数据是二维的,而地下剖分网格单元是三维的.因此根据公式(5)计算观测面上的重力(重力梯度)异常需要五重循环.当测点数据量大,剖分网格单元个数多时,每次循环都要计算单个G以及G和m的乘积,计算量相当大.而在三维物性反演中,需要反复迭代进行正演计算,因此需要更多的计算时间,以致无法实现海量重磁数据的快速反演.为缩短计算时间,需寻求快速算法.因此本文首先采用GPU 并行算法进行正演计算加速试验研究.
3 正演计算GPU 并行策略 3.1 GPU简介新近发展的NVIDIA GPU(GraphicsProcessingUnit)通用计算技术,在处理能力和存储器带宽方面相对CPU 计算技术有明显优势,在成本和功耗上也不需要付出太大代价,已在诸多领域得到了广泛应用.GPU 以CUDA (Compute Unified DeviceArchitecture)作为新的并行计算设备的软硬件体系,其编程模型将CPU 作为主机(host),负责逻辑性强的事务和串行计算;GPU 作为设备(device),负责执行高度并行的线程化任务.运行在GPU 上的CUDA并行计算函数定义为kernelFunction〈〈〈dimGrid,dimBlock〉〉〉(Parameters).其中,dimGrid为并行计算所用的线程块(block)数目,dimBlock为每个block中所包含的线程(thread)数目.同一线程块内在线程执行过程中可以通过共享存储器(Sharedmemory)共享信息,为了便于并行控制,CUDA 提供了四个内建变量(blockIdx,gridDim,threadIdx,blockDim)来描述线程块和线程网格的维数及索引.这些内建变量可以有多维形式,我们使用一维线程和一维线程块,完成正演计算.
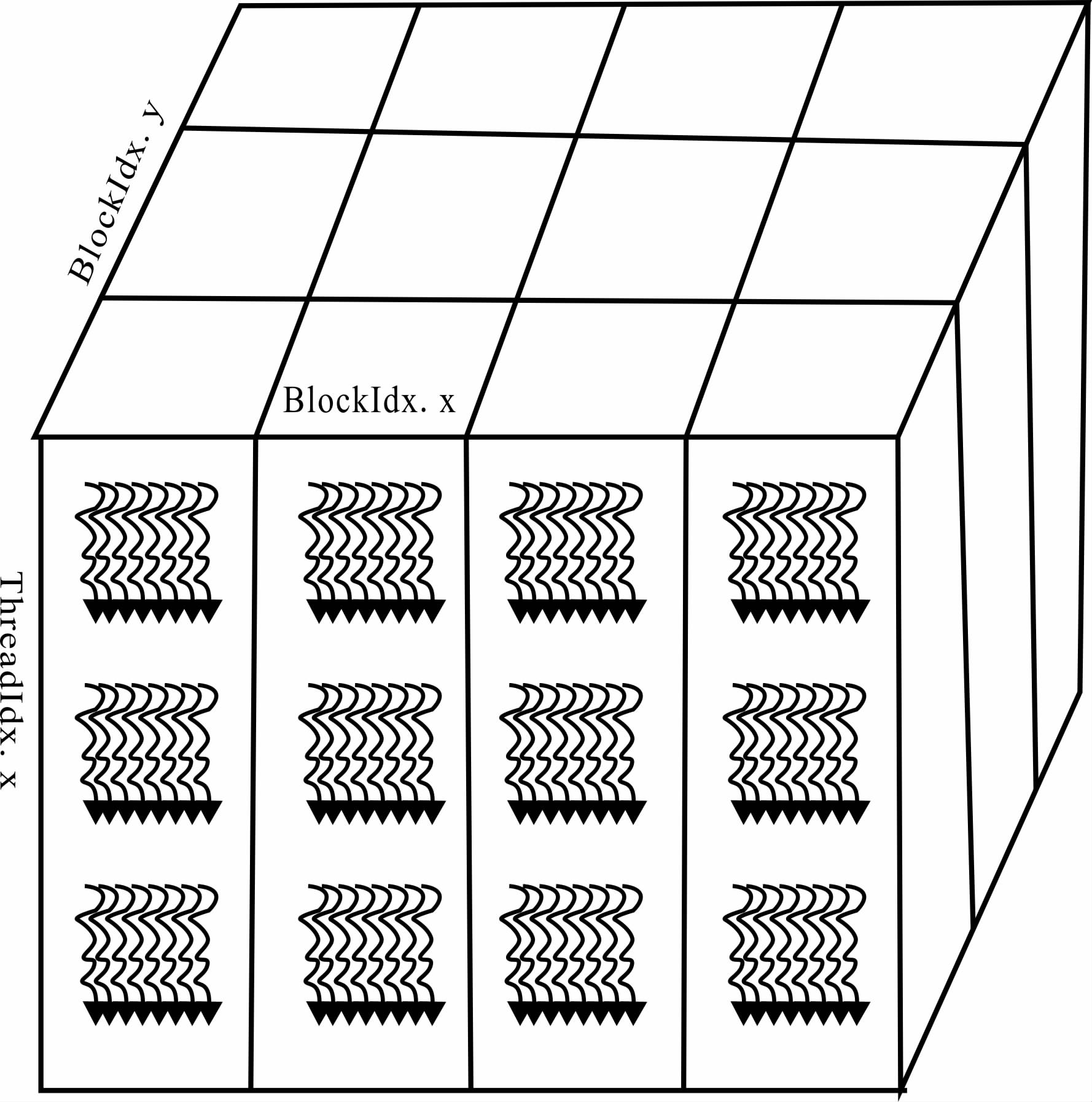
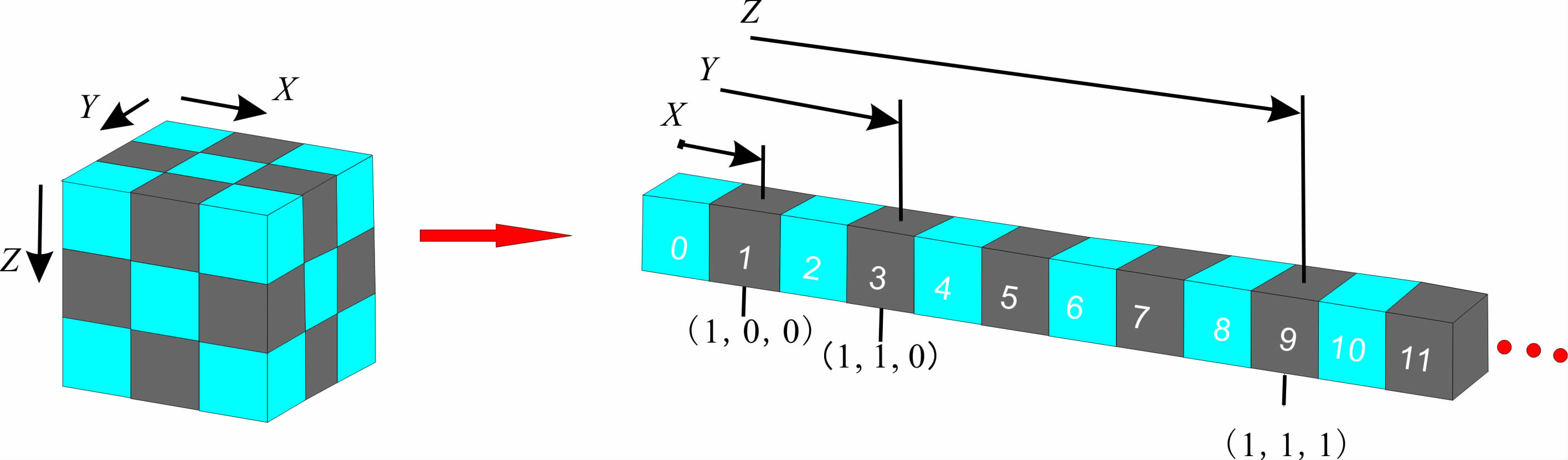
3.2 正演计算GPU并行策略地面上某一测点的重力(重力梯度)正演计算,需要对地下半空间所有的长方体单元异常响应值一一计算并进行叠加,即在地下半空间X方向、Y方向和Z方向完成三重模型域循环.对于面积性观测数据,还要包括在X、Y方向测点方向的两重数据域循环.鉴于该过程中计算每个点核矩阵(G)的独立性,可以将五重循环同时进行并行化.但当模型体数目变大时,如100×100×100,模型域循环数目就已达到百万,并且还会受到显存大小的限制.因此,这里只将三重模型域循环在GPU 设备上进行并行计算.一种的最直接方法是按照循环方式采用线程块和线程为多维的形式进行并行索引,将模型域三重循环(X、Y、Z方向循环)分别利用blockIdx.x 和blockIdx.y 和threadIdx.x 有效索引表示,如图 2所示.然而当模型数据体很大时,这种方法会在分配线程的过程中会产生很多的线程空闲,从而造成线程资源的巨大浪费.为了更有效地利用线程块内的每一个线程,我们将三维模型域循环利用一维线程块和线程进行有效索引.图 3 是三维数据体映射为一维数据体示意图,可以根据所对应的映射关系,根据内建变量blockDim.x,blockIdx.x和threadIdx.x完成X、Y和Z方向循环变量的有效索引.
|
图 2 二维线程块与一维线程有效索引表示 Fig. 2 The index representation for 2D blocks and ID threads |
|
图 3 三维数据映射一维数据体示意图 Fig. 3 The mapping relations between 3D data and ID data |
具体有效索引表示如下:
线程索引:index=blockIdx.x*blockDim.x+threadIdx.x;
Z方向循环索引表示:z index=index%nz;
临时变量:tmp=(index-z index)/nz;
Y方向循环索引表示:y index=tmp %ny;
X方向循环索引表示:x index=(tmp-y index)/ny.
这样,每个线程完成以后,需要对求得的异常响应值进行求和运算.为了充分利用共享存储器(sharedmemory)访问速度快等优势,采用经过优化的并行归约算法(reduction).优化的并行归约算法在编程技巧和存储器使用等方面做了优化改进(包括避免取模、分支要求,循环完全展开等),有关其算法进行优化的详细内容请参考CUDAprogrammingguide[25, 28].如图 4 所示,在第一层次(浅绿色),首先将每个block内的线程进行优化并行归约到第一个线程上;在第二层次(橘红色),将所有的block得到的值传递到一个或几个block内的线程进行优化并行归约,一直循环计算得到一个叠加值,从而完成并行计算.

|
图 4 优化的并行归约流程图 Fig. 4 The flow chart of optimized parallel reduction |
这里采用的数值试验硬件环境为:CPU 配置为IntelQ9550.主频2.83GHz,4G 内存.GPU 显卡型号为NVIDIAQuadro2000.192个处理核心,993MB显存.软件环境为:CUDA 驱动版本号为CUDA4.0Windows764 位操作系统,VisualStudio2008 集成开发编译环境.以下计算时间为计算循环十次取平均所得的统计时间.
以下计算中所用模型皆可视为三维复杂模型.因为,这里所用的观测地面下剖分而成的长方体单元模型物性值是随机的.因此,不同长方体单元随机物性值的组合可以代表不同形态的复杂模型.对于特殊的简单模型,由于剖分的长方体单元大部分值为零,在计算过程中可以忽略.这里只针对一般情况进行分析.
4.1 精度分析目前GPU 的单精度计算性能要远远超过双精度计算性能[25].具体对于重力异常正演计算来说,利用单精度数据类型进行计算要比双精度数据类型快四倍还要多,但是利用单精度数据计算并不能达到要求.这是由于重力、重力梯度正演公式中有反正切函数和对数函数的存在,在利用单精度数据计算过程中舍入误差会变得更加明显,通过误差传递从而影响最终结果.分别在GPU 设备上用单精度数据类型和双精度数据类型进行了计算,并与该程序在CPU 上的双精度数据类型计算结果进行对比(以重力正演计算32×32数据个数为例).从图 5中可以看出,当数据使用单精度数据类型时候,最大相对误差为1×10-4,并不能满足计算精度要求.正如M.Moorkamp所指出,当数据类型为双精度时候最大相对误差为1.5×10-12,基本满足计算要求[33].但是,随着计算设备的改进(如GTX500Series)和计算能力的提高(CUDA4.0),利用GPU 得到的结果与利用CPU 计算得到的结果是一致的.因此,在重力正演计算过程中必须采用双精度数据类型或者更高数据类型进行计算,并且对精度要求已经不成问题.

|
图 5 利用不同数据类型在GPU 上计算与CPU 上计算的得到的相对误差 (a)单精度数据类型;(b)双精度数据类型. Fig. 5 The relative difference between GPU and CPU results (a) Single-precision data type.(b)double-precision data type. |
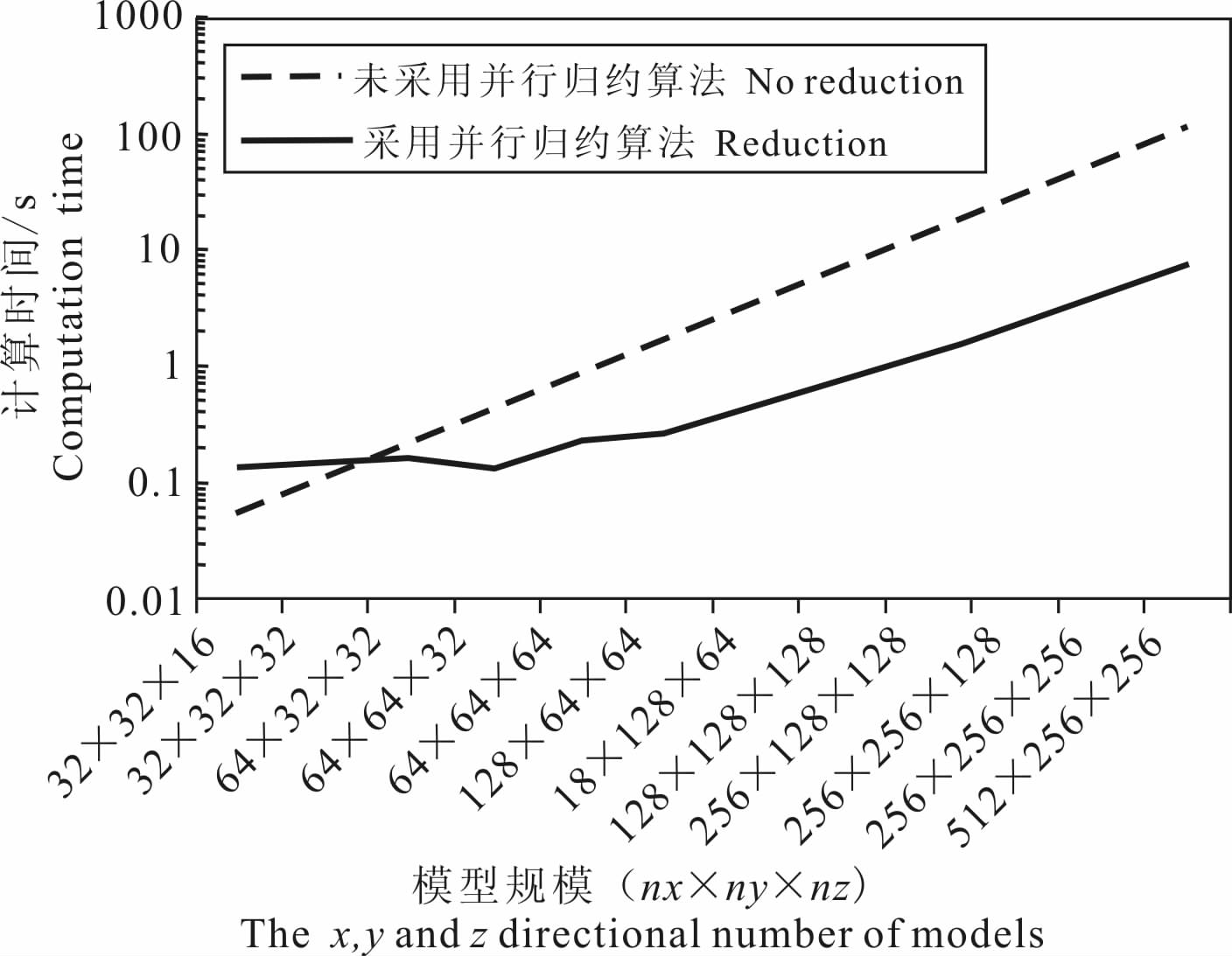
有效地采用共享存储器隐藏延迟,可以在一定程度上提高加速比.本文在异常值叠加过程中采用经过优化的并行归约算法.将地下剖分成不同规模的长方体单元,以计算地面上某一点的重力异常为例,对采用并行归约和未采用并行归约的算法进行了时间对比(去掉数据在CPU与GPU之间传输所消耗的时间影响).从图 6 中可以看出,当数据规模小于64×32×32时,采用并行归约算法比未采用并行归约算法的速度要慢,这时GPU 处理性能由于数据量小,性能并没有体现.当数据规模大于(64×64×32)时,GPU 处理明显加快,数据规模再进一步变大时,加速比基本上呈线性增长,其最高可达15倍左右.
|
图 6 异常值叠加过程中的优化效率对比 Fig. 6 Comparsion of reduction and non-reduction for anomaly summation |
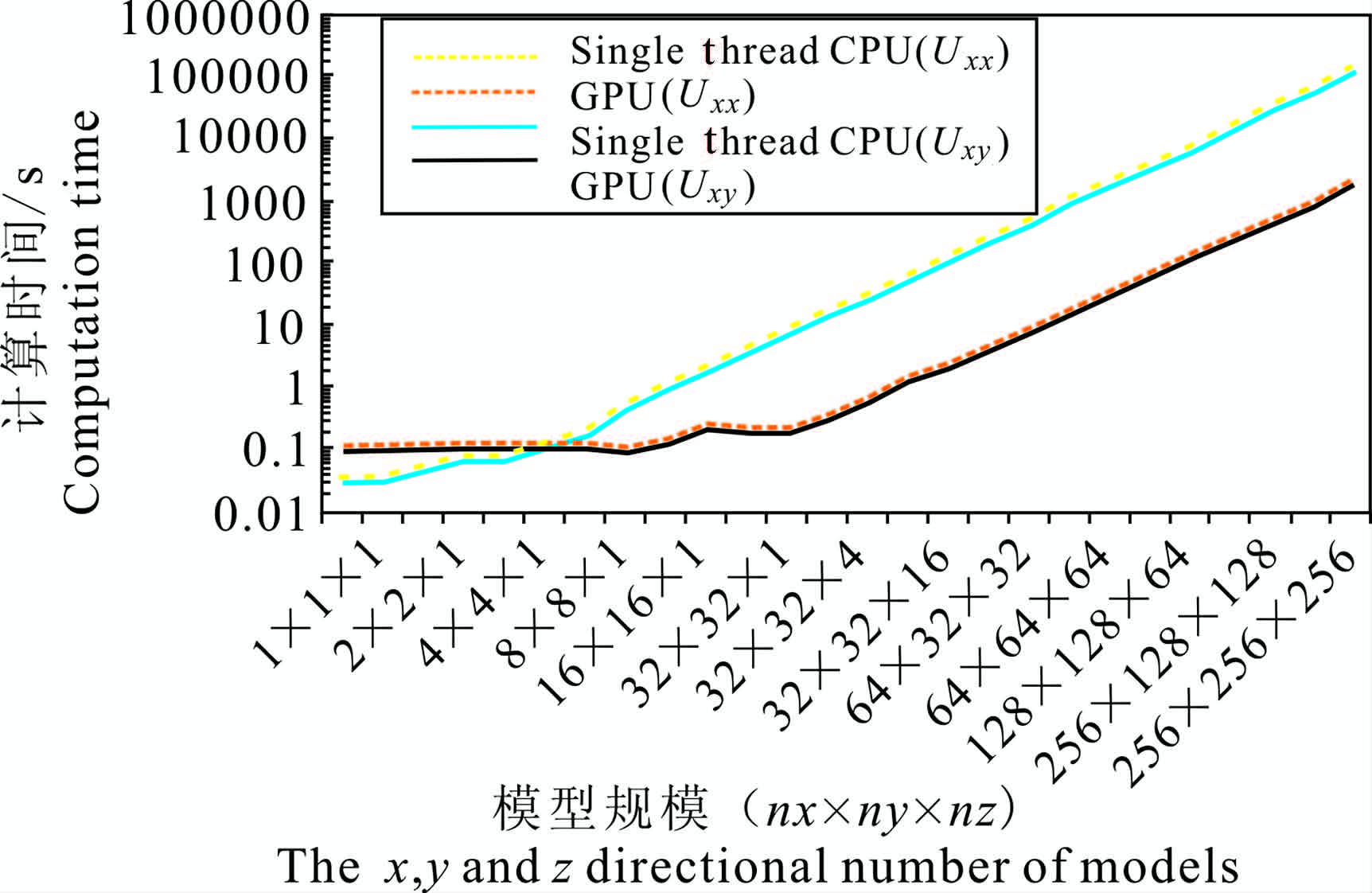
对比分析了32×32 个测点、不同模型规模重力、重力梯度数据正演计算的加速比.从图 7可以看出,和上述共享存储器优化中的加速比形态类似,当数据规模小于8×8×1 时,采用GPU 并行算法比单线程CPU 算法的速度要慢,这时GPU 处理性能由于数据量小,性能并没有体现出来.由于重力和重力梯度正演在计算过程中只有很少的系统开销,当数据规模大于8×8×1 时,GPU 计算速度明显加快,一直到32×32×4.由于计算能力达到饱和,加速比大体上呈线性增长,最高可达60倍.对比重力、重力梯度数据,由于并行计算中的大部分时间用在计算公式(4)中反正切函数和自然对数函数上,因此正演公式的复杂度决定着计算效率的快慢.由于重力正演公式比重力梯度正演公式复杂度高,因此前者的加速效果更明显.如图 8,对于Uxx和Uxy正演计算加速比可达50倍左右.

|
图 7 不同规模模型重力正演GPU 与单线程CPU 计算时间对比(测点数为32×32) Fig. 7 Comparison of GPU and CPU computing time for gravity modeling (32X 32 observational points) |
|
图 8 不同规模模型重力梯度(Uxx和Uxy)正演GPU 与单线程CPU 计算时间对比(测点数为32×2) Fig. 8 Comparison of GPU and CPU computing time for gravimetry modeling (32X32 observational points) |
基于上述GPU 正演快速算法的有效实现,本节首先讨论GPU 相关成像三维物性反演思路,然后探讨基于GPU 的重力(重力梯度)数据三维约束反演策略.
5.1 GPU相关成像三维物性反演策略根据测区范围将地下半空间剖分为大小相等、规则排列的长方体网格单元.首先,根据三维相关成像原理[5],利用实测重力(重力梯度)异常计算地下网格单元节点q的相关系数Cq,该相关系数在-1与1之间变化.其次,根据实测区域的密度范围,将相关系数线性加权转化后,作为该网格节点相邻的网格单元的初始密度值,利用直立长方体无奇点正演公式进行重力(重力梯度)正演计算.最后,利用实测重力(重力梯度)异常与正演计算结果的残差进行相关成像,将残差的相关成像的线性加权结果作为模型的修改量,再对模型进行正演计算.如此迭代反复,直到残差达到合理要求为止.通过分析不难发现,对于三维相关成像求取某一网格节点的相关系数值,不受其他网格节点的影响.对于正演计算求取某一观测点的异常值,同样不受其它观测点值的影响.可以采用GPU 并行计算技术提高计算效率.将三维相关成像和正演计算算法改造成GPU 并行程序,并将相关数据及参数传递到GPU 上,使得三维相关成像和正演计算在GPU 进行.最后将计算结果传回主机端内存中[34].
5.2 重力(重力梯度)数据三维约束物性反演GPU加速策略重力(重力梯度)异常三维约束物性反演是基于反演理论、在最小二乘意义下使目标函数达到极小的线性或非线性反演.在引入足够的、适当的约束条件下,使反演目标函数最小化,能够得到接近于实际地质情况的物性分布和几何形态.即:
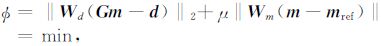
|
(6) |
其中,Φd= ‖Wd(Gm-d)‖2 为数据拟合函数,Φm= ‖Wm(m-mref)‖ 为模型目标函数.Wd为数据空间加权矩阵,Wm为模型空间加权矩阵.μ 为拉格朗日算子.
对(6)式,通过采用不同的加权因子Wd 和Wm以及不同的计算策略,可以得到不同种意义上的解.对于式(6),求解方式有很多种,首先为模型空间迭代法,给定初始Wd和Wm以及m0 采用公式:
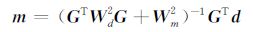
|
(7) |
进行迭代求解.同样,在数据空间可采用公式
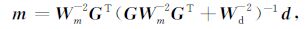
|
(8) |
进行迭代求解.上述两种直接求解法,需要构造显式矩阵,并且涉及到矩阵求逆.只是在最初的数据量很小的二维物性反演中适用.当数据量很大时,需要采取相应的计算技巧才能实现.Li和Oldenburg结合小波压缩算法存储核矩阵,对目标函数采用对数障碍法求解[11],实现了大数据重磁数据的三维反演计算.Pilkington[18]提出了利用预条件共轭梯度法进行三维磁化率成像.共轭梯度算法沿着由已知点处梯度构造的共轭方向搜索目标函数的极小值,理论上经过有限步迭代,算法就可以收敛.另外,非线性的广义随机算法模拟退火算法等,可使反演求解过程稳定,约束条件容易结合,但计算速度和维数困难同样制约其发挥作用,采取针对性措施(等效存储几何格架)后,使三维反演进入实用化阶段.采用预条件共轭梯度法对目标函数式(6)进行求解的思路如下:
加入约束因子后,目标函数(6)可写为
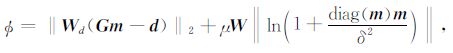
|
(9) |
对目标函数极小化,得到:(GTG+Q)x=CTd其中:Q= w(z)×diag(2/(x2 +δ2)).

|
(10) |

|
图 9 相关成像算法的三维物性反演流程图 Fig. 9 Flow chart of 3D property inversion based on correlation imaging algorithm |

|
图 10 GPU相关成像三维物性反演算法流程图 Fig. 10 Flow chart of 3D property inversion based on correlation imaging algorithm using GPU |
原问题可变成求解:

|
(11) |
令
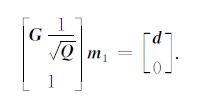
|
(12) |
利用预条件共轭梯度法对(11)式进行求解,结果再乘以
将重力(重力梯度)异常三维约束算法任务划分,确定程序中的并行部分.对于公式(7)和(8)涉及到矩阵与向量计算,矩阵求逆,矩阵与矩阵计算,在GPU 加速计算中,已经能够很好地实现,并能取得很高的加速比,关键在于如何合理地利用好计算机内存和显卡内存.当反演数据以及反演的模型空间规模变得很大时,虽然预条件共轭梯度法中的矢量运算在一定程度上减轻了内存使用量,但仍然耗费很长的时间.NVIDIA 的CUBLAS 是在CUDA 基础上实现的一种并行的BLAS,并且实现了对CUDA过程的封装.这样很容易将预条件共轭梯度移植到GPU 上进行计算.相关的共轭梯度GPU 加速的计算案例已证明了该方法的有效性.
6 结论与讨论利用GPU 能够很好地并行实现重力、重力梯度正演快速计算,并且可以获得很高的加速比.数值试验显示,利用双精度数据类型或者更高精度数据类型进行计算,可达到精度要求.文章还讨论了GPU 并行计算在两种反演方法中的策略,为快速三维反演技术提供了借鉴.本文取得的认识如下:
(1) 由于GPU 单元在传输上具有很高的带宽,所以在数据传输方面不会占有很长的时间.因此,真正能够对提高速度有效的是每个线程所处理的复杂度,复杂度越大,加速比就越高.由于重力正演公式比重力梯度正演公式复杂度高,因此前者的加速效果更明显.
(2) 利用共享存储器的存储特点以及线程设计,对每个线程计算出的响应值叠加采用经过优化过的并行归约算法,在相同条件下能够得到高达15倍的加速比.
(3) 由于GPU 在一定时间内还会受到显存的限制,因此在处理更大规模数据时,可以采用分块的方式进行.
(4) 在以往的基于物性模型的三维重力、重力梯度反演过程中,由于核矩阵(G)计算时间较长,须采用一次性计算完成并存储核矩阵(G).此加速算法策略可以无须一次性存储G,这为基于物性模型的三维重力、重力梯度快速反演奠定了基础.
(5) 本文GPU 加速计算是针对重力、重力梯度数据开展试验的.值得说明的是,此方法可以推广到其它位场数据的类似计算.
| [1] | Nabighain M N, Grauch V J S, Hansen R O, et al. 75th anniversary-The historical development of the magnetic method in exploration. Geophysics , 2005, 70(6): 33N-61ND. DOI:10.1190/1.2133784 |
| [2] | Nabighain M N, Ander M E, Grauch V J S, et al. 75th anniversary-Historical development of the gravity method in exploration. Geophysics , 2005, 70(6): 63N-89ND. DOI:10.1190/1.2133785 |
| [3] | Guspí F, Introcaso B. A sparse spectrum technique for gridding and separating potential field anomalies. Geophysics , 2000, 65(4): 1154-1161. DOI:10.1190/1.1444808 |
| [4] | Meng X H, Guo L H, Chen Z X, et al. A method for gravity anomaly separation based on preferential continuation and its application. Applied Geophysics , 2009, 6(3): 217-225. DOI:10.1007/s11770-009-0025-y |
| [5] | 郭良辉, 孟小红, 石磊, 等. 重力和重力梯度数据三维相关成像. 地球物理学报 , 2009, 52(4): 1098–1106. Guo L H, Meng X H, Shi L, et al. 3D correlation imaging for gravity and gravity gradiometry data. Chinese J.Geophys. (in Chinese) , 2009, 52(4): 1098-1106. |
| [6] | 郭良辉, 孟小红, 石磊. 磁异常ΔT三维相关成像. 地球物理学报 , 2010, 53(2): 435–441. Guo L H, Meng X H, Shi L. 3D correlation imaging for magnetic anomaly ΔT data. Chinese J.Geophys. (in Chinese) , 2010, 53(2): 435-441. |
| [7] | 刘天佑, 杨宇山, 李媛媛, 等. 大型积分方程降阶解法与重力资料曲面延拓. 地球物理学报 , 2007, 50(1): 290–296. Liu T Y, Yang Y S, Li Y Y, et al. The order-depression solution for large-scale integral equation and its application in the reduction of gravity data to a horizontal plane. Chinese J.Geophys (in Chinese) , 2007, 50(1): 290-296. |
| [8] | 刘天佑. 位场勘探数据处理新方法. 北京: 科学出版社, 2007 . Liu T Y. New Data Processing Methods for Potential Field Exploration (in Chinese). Beijing: Science Press, 2007 . |
| [9] | Fedu M, Quarta T. Wavelet analysis for the regional-residual and local separation of potential field anomalies. Geophysical Prospecting , 1998, 46(5): 507-525. DOI:10.1046/j.1365-2478.1998.00105.x |
| [10] | Last B J, Kubik K. Compact gravity inversion. Geophysics , 1983, 48(6): 713-721. DOI:10.1190/1.1441501 |
| [11] | Li Y G, Oldenburg D W. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method. Geophys.J.Int. , 2003, 152(2): 251-265. DOI:10.1046/j.1365-246X.2003.01766.x |
| [12] | Constable S C, Parker R L, Constable C G. Occam's inversion: A practical algorithm for generation smooth models from electromagnetic sounding data. Geophysics , 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |
| [13] | Li Y G, Oldenburg D W. 3D inversion of gravity data. Geophysics , 1998, 63(1): 109-119. DOI:10.1190/1.1444302 |
| [14] | Li Y G, Oldenburg D W. 3D inversion of magnetic data. Geophysics , 1996, 61(2): 394-408. DOI:10.1190/1.1443968 |
| [15] | Li Y G, Oldenburg D W. Joint inversion of surface and three-component borehole magnetic data. Geophysics , 1996, 65(2): 540-552. |
| [16] | Portniaguine O, Zhdanov M S. Focusing geophysical inversion images. Geophysics , 1999, 64(3): 874-887. DOI:10.1190/1.1444596 |
| [17] | Portniaguine O, Zhdanov M S. 3-D magnetic inversion with data compression and image focusing. Geophysics , 2002, 67(5): 1532-1541. DOI:10.1190/1.1512749 |
| [18] | Pilkington M. 3-D magnetic imaging using conjugate gradients. Geophysics , 1997, 62(4): 1132-1142. DOI:10.1190/1.1444214 |
| [19] | Nagihara S, Hall S A. Three-dimensional gravity inversion using simulated annealing: Constraints on the diapiric roots of allochthonous salt structures. Geophysics , 2001, 66(5): 1438-1449. DOI:10.1190/1.1487089 |
| [20] | Boulanger O, Chouteau M. Constraints in 3D gravity inversion. Geophysical Prospecting , 2001, 49(2): 265-280. DOI:10.1046/j.1365-2478.2001.00254.x |
| [21] | Fedi M, Rapolla A. 3D inversion of gravity and magnetic data with depth resolution. Geophysics , 1999, 64(2): 452-460. DOI:10.1190/1.1444550 |
| [22] | 姚长利, 郝天珧, 管志宁, 等. 重磁遗传算法三维反演中高速计算及有效存储方法技术. 地球物理学报 , 2003, 46(2): 252–258. Yao C L, Hao T Y, Guan Z N, et al. High-speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic algorithms. Chinese J.Geophys. (in Chinese) , 2003, 46(2): 252-258. |
| [23] | 姚长利, 郑元满, 张聿文. 重磁异常三维物性反演随机子域法方法技术. 地球物理学报 , 2007, 50(5): 1576–1583. Yao C L, Zheng Y M, Zhang Y W. 32D gravity and magnetic inversion for physical properties using stochastic subspaces. Chinese J.Geophys. (in Chinese) , 2007, 50(5): 1576-1583. |
| [24] | Li Y G, Oldenburg D W. Fast inversion of large-scale magnetic data using wavelet transform and a logarithmic barrier method. Geophys.J.Int. , 2003, 152(2): 251-265. DOI:10.1046/j.1365-246X.2003.01766.x |
| [25] | Zhang S, Chu Y L. GPU High-Performance Computing-CUDA. Beijing: China Water Power Press, 2009 . |
| [26] | 刘国峰, 刘洪, 李博, 等. 山地地震资料叠前时间偏移方法及其GPU实现. 地球物理学报 , 2009, 52(12): 3101–3108. Liu G F, Liu H, Li B, et al. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation. Chinese J.Geophys. (in Chinese) , 2009, 52(12): 3101-3108. |
| [27] | 李博, 刘国峰, 刘洪. 地震叠前时间偏移的一种图形处理器提速实现方法. 地球物理学报 , 2009, 52(1): 245–252. Li B, Liu G F, Liu H. A method of using GPU to accelerate seismic pre-stack time migration.Chinese J. Geophys (in Chinese) , 2009, 52(1): 245-252. |
| [28] | Sanders J, Kandrot E. CUDA by Example-An Introduction to General Purpose GPU Programming. Pearson Education Press, 2010 . |
| [29] | 刘国峰, 刘钦, 李博, 等. 油气勘探地震资料处理GPU/CPU协同并行计算. 地球物理学进展 , 2009, 24(5): 1671–1678. Liu G F, Liu Q, Li B, et al. GPU/CPU co-processing parallel computation for seismic data processing in oil and gas exploration. Progress in Geophys (in Chinese) , 2009, 24(5): 1671-1678. |
| [30] | Nagy D. The gravitational attraction of a right rectangular prism. Geophysics , 1966, 31(2): 361-371. |
| [31] | Li X, Chouteau M. Three-dimensional gravity modeling in all space. Surveys in Geophysics , 1998, 19(4): 339-368. DOI:10.1023/A:1006554408567 |
| [32] | 郭志宏, 管志宁, 熊盛青. 长方体ΔΤ场及其梯度场无解析奇点理论表达式. 地球物理学报 , 2004, 47(6): 1131–1138. Guo Z H, Guan Z N, Xiong S Q. Cuboid ΔΤ and its gradient forward theoretical expressions without analytic odd points. Chinese J.Geophys. (in Chinese) , 2004, 47(6): 1131-1138. |
| [33] | Moorkamp M, Jegen M, Roberts A, et al. Massively parallel forward modeling of scalar and tensor gravimetry data. Computers and Geosciences , 2010, 36(5): 680-686. DOI:10.1016/j.cageo.2009.09.018 |
| [34] | Chen Z X, Meng X H, Guo L H, et al. GICUDA: A parallel program for 3D correlation imaging of large scale gravity and gravity gradiometry data on graphics processing units with CUDA. Computers and Geosciences , 2012, 46: 119-128. DOI:10.1016/j.cageo.2012.04.017 |
 2012, Vol. 55
2012, Vol. 55

