2. 地下信息探测技术与仪器教育部重点实验室和地质过程与矿产资源国家重点实验室, 北京 100083
2. Key Laboratory of Geo-detection (China University of Geosciences, Beijing), Ministry of Education; State Key Laboratory of Geological Processes and Mineral Resources(China University of Geosciences, Beijing), Beijing 100083, China
目前,大地电磁测深法(MT)常采用短时傅里叶变换进行电、磁分量时间序列数据的频谱分析[1].众所周知,短时傅里叶变换建立在稳态信号基础之上,它仅能获得信号总体所包含的各种频率成分的频谱,对信号的时间定位能力差,给出的频谱响应易受噪声污染.为了提高大地电、磁分量数据的频谱分析精度,国内外学者利用小波变换[2-3]、希尔伯特-黄变换[4-6]等时频分析方法,开展了大地电磁测深数据处理的研究.但是,由于小波变换是时间-尺度分析,信息尺度与频率的关系依赖于小波函数的选取,有时会存在随着尺度增大,频谱局部性变差的缺陷;希尔伯特-黄变换中,固有模态函数的频率分辨力较差.这些不足影响了它们在大地电磁测深数据处理中的应用效果.天然电磁场信号弱,易受人文电磁噪声干扰.为了获得高品质的大地电磁阻抗张量资料,必须在时间序列频谱估计中引入先进的时频分析技术.
针对以往时频分析存在的问题,Stockwell等[7-8]对短时傅里叶变换和连续小波变换的思想进行延伸与推广,提出一种称为S变换的信号分析技术.随后,许多学者对S变换的相关技术进行了有益探讨.高静怀等[9]、Pinnegar等[10]先后发展了各种广义S变换的基本小波函数,使其在应用中更为灵活;Schimmel等[11]、Simon等[12]研究了S反变换方法;刘保童等[13]对比了利用S反变换重建信号的误差;Pei等[14]采用叠加窗函数消除S 变换边缘效应,提高了S变换的精度.这些研究成果使S变换具有更高的实用价值.
S变换克服了短时傅里叶变换时窗函数固定、对信号时间定位能力差的缺点,同时其基本小波不必满足容许性条件,是一种优于短时傅里叶变换和小波变换的时间-频率分析技术.利用S变换进行大地电磁场时间序列的频谱分析,一方面能够提高对电磁噪声成分的时间定位能力,便于实现电磁噪声的滤波处理;另一方面可以增加频谱系数的个数,从而改善大地电磁阻抗张量的统计特性.本文首先详细阐述了广义S变换原理,并通过理论信号,对S变换时频谱特点进行分析.在此基础上,对大地电磁测深数据频谱分析与离散广义S变换的相关技术问题展开讨论,并研究基于广义S变换的大地电磁测深资料处理方法.最后,通过实际大地电磁测深数据检验方法的应用效果.
2 采用叠加窗函数的离散广义S变换Stockwell等[7]将时域信号h(t)的S 变换定义为
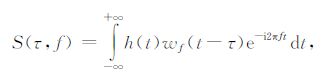
|
(1) |
其中,S(τ,f)为变换后得到的时频谱,以下简称S变换时频谱;wf(t)为高斯时窗函数;τ 表示时窗函数中心对应的时间;f表示频率(单位Hz).
(1) 式中S变换窗函数形态固定,使其在应用中受到限制.刘丽娟等[15]对高静怀等[9]提出的广义S变换的基本小波函数进行简化,得到(2)式:
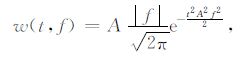
|
(2) |
式中,A为比例因子,用于调节窗口的宽度.S 变换还可以由h(t)的傅里叶谱H(f)表示为[7]
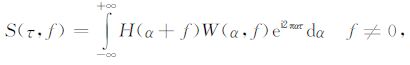
|
(3) |
W(α,f)为w(τ,f)的傅里叶变换,α 为与τ 对应的傅里叶变换频率,表达式为
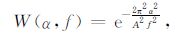
|
(4) |
在(3)、(4)式中,令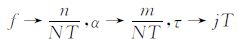

|
(5) |
这里,T为时间序列的采样周期,N为采样数.
由于对时域信号的采样和截断处理,利用(5)式计算的时频谱将受到边缘效应影响,从而使高频与低频频谱产生较大误差,此时可采用叠加窗函数削弱广义S变换边缘效应的影响[14].对于高斯窗函数(4)式,频率域叠加窗函数Wf(m,n)为
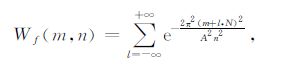
|
(6) |
由(5)式,采用叠加窗函数的离散广义S变换可以表示为
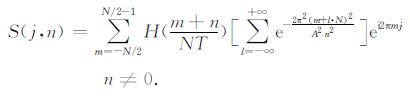
|
(7) |
对于一个时窗的信号,短时傅里叶变换仅仅能够给出单频的一个振幅和相位系数,而广义S变换则可以给出同一频率信号频谱随时间的变化特征.因此,通过S变换可以对信号中的噪声实现精确的时频滤波处理,同时可以改善随机信号频谱的统计特性[16].定义一个理论信号x(t):
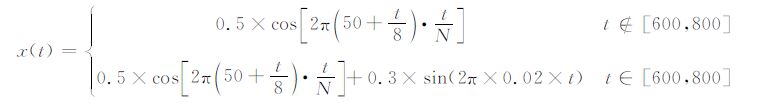
|
(8) |
该信号的采样率为1 Hz,时窗长度为1000s,采样点数N为1000.
方波噪声是大地电磁测深时间序列数据的常见噪声类型.这里以方波噪声为例,对S变换的时频分析特点加以说明.在式(8)理论信号的300~320s之间分别加上振幅为1 和4 的方波噪声(这里分别称为方波1和方波2,见图 1a.对这三个序列分别进行快速傅里叶变换,得到图 1b中各序列的振幅谱.由图可见,原始信号各个频点的振幅都不同程度的受到方波噪声的干扰,低频段受到的干扰最大,并且方波幅度越大,噪声对信号的影响越大.比如,在傅里叶变换频谱中,600~800s出现的0.02 Hz的正弦波信号,受到300~320s方波噪声谱的严重污染.当方波幅度变大时,信噪比迅速降低,甚至无法有效识别该正弦波信号.可见,当利用短时窗傅里叶变换进行时间序列频谱分析时,分析时窗内出现的较强方波噪声将对有用信号的频谱产生严重干扰.
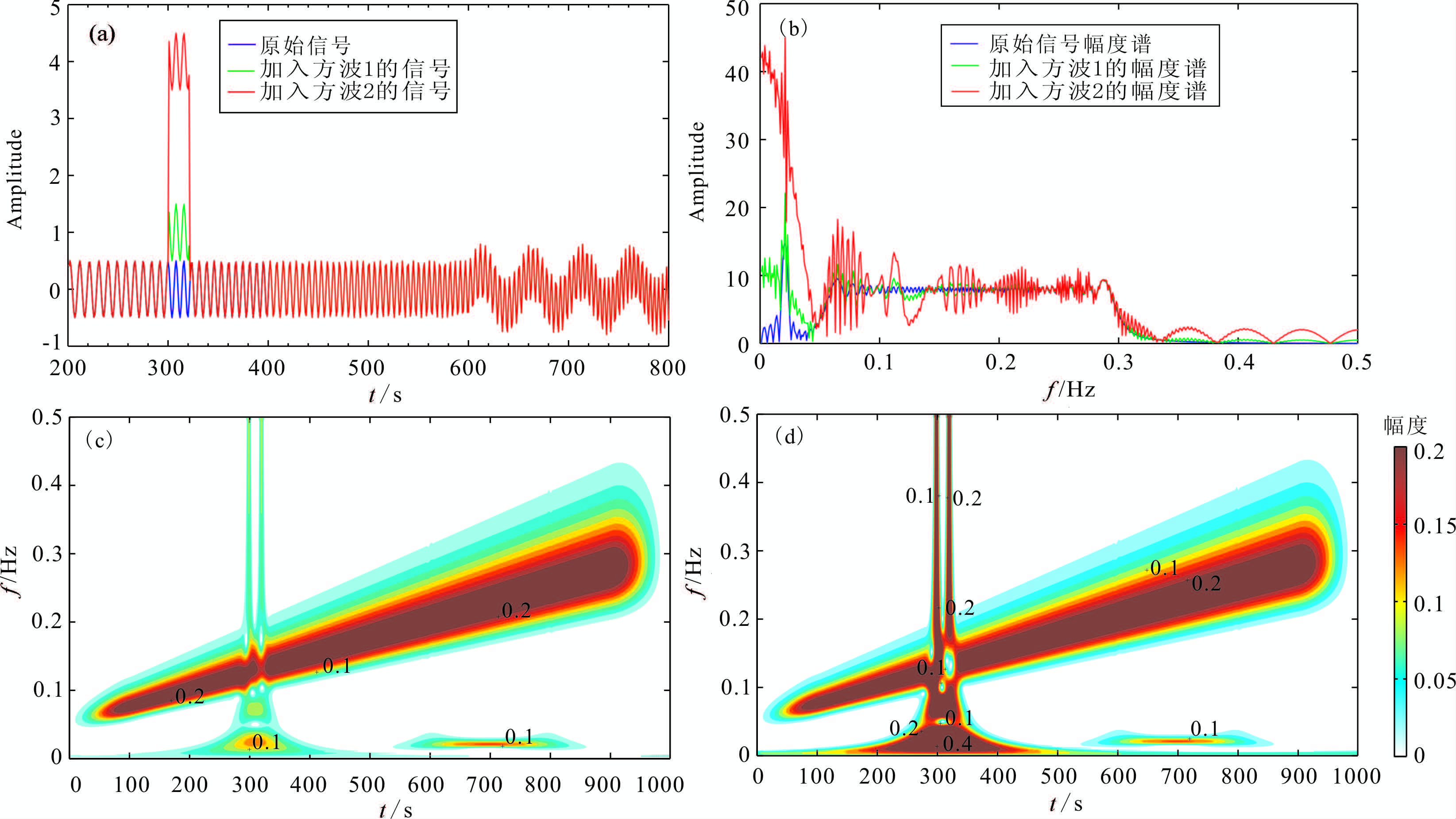
|
图 1 理论信号广义S变换的时频谱 Fig. 1 Time-frequency spectrum of theoretical signal by generalized S transform |
分别对含方波1、方波2的信号进行S变换,得到的时频谱示于图 1(c,d)中.图中,在300~320s时段,方波在上升沿和下降沿处对原始信号产生了通频带的干扰;具有一定时宽的方波对有用信号产生了不同程度的干扰,频率越低、方波的幅度越大,噪声在时间轴上波及的范围越大.尽管如此,从图 1(c,d)中,仍然能够从600~800s时段识别出0.02Hz的低频信号.因此,若选取600s以后的时频谱对信号进行分析,则可以避开方波噪声的干扰.在实际中,如果大地电磁场时间序列中这样的方波噪声过多,则基于短时窗傅里叶变换的处理方法就很难得到满意的阻抗数据.此时,用S变换取代傅里叶变换则更具优势.
4 基于广义S变换的大地电磁阻抗张量估计方法 4.1 大地电磁场信号广义S变换时频分辨率由离散广义S变换公式(7)可知,离散信号第n个频点的S变换谱实际上是以各频点傅里叶谱乘以频窗系数的积为振幅的周期函数按相位mj在时间轴上展开后叠加的结果.也就是说,频点n的频谱受到周边频谱的影响,同时也向周边频点泄漏.在大地电磁测深数据处理中,通常取以n为中心的某个频带功率谱的平均值作为频点n的功率谱.一方面,这个频带宽度应尽可能宽,这样可以增加功率谱的自由度,从而提高置信水平,减小数据误差;另一方面,这个频带又不能过宽,否则功率谱过于平滑,会降低探测地下电性结构的分辨率.因此,需要在功率谱置信水平与探测分辨率之间权衡,确定合适的频带宽度,保证相邻频点大地电磁阻抗元素具有较高的频率分辨率.
大地电磁阻抗元素的频点选择一般需满足两个条件:一是,频率对数呈均匀分布,以适应大地电磁探测的分辨率随频率减小而降低的特点;其次,在一个数量级中频点个数应不少于6 个,以达到对地下介质的最佳分辨与探测[17].目前,对频率的选择一般是在一个倍频程中选择四个频点,这样相邻两个频率的比例系数为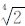
本文参考加拿大Pheonix 公司的频点选择方法,根据(4)式的频窗函数确定合适频带宽度.(4)式为一高斯函数,其标准偏差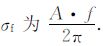
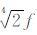
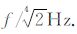
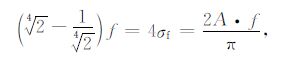
|
(9) |
由此得到A为0.55.
采用高斯窗函数广义S变换的时频谱具有最小的二次时频矩,即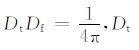
公式(1)离散后,对采样率为fs 的N个采样点数据进行S变换时,为避免产生较严重的边缘效应,一般取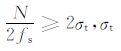
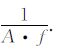
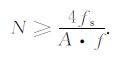
|
(10) |
在对大地电磁场时间序列数据进行S变换时,应根据(10)式选取序列长度.由此可知,频率f越低,离散序列数据的长度N就越大,因此应根据最低频率选取N.对于高频数据,可根据(11)式确定频谱系数个数Q:
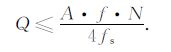
|
(11) |
频率为ω 的大地电磁场水平分量振幅谱满足如下关系:
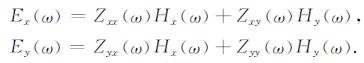
|
(12) |
理论上,求解阻抗张量元素只要两组非线性相关的振幅谱观测值.但是,由于电磁场观测值受噪声干扰影响,不能由(12)式精确求得阻抗张量元素.所以,只能利用多组实际观测资料计算其近似解.根据最小二乘原理,估计阻抗张量的公式为[1]
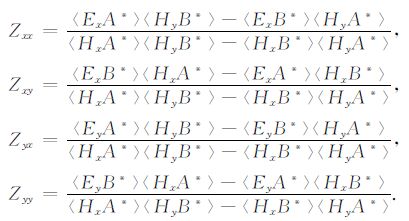
|
(13) |
式中(A* ,B*)取(Ex*,Hy*)和(Ey*,Hx*)之外的其它分量组合,〈·〉表示平均功率谱.若电磁场水平分量的广义S变换结果为Ex,l(j,n)和H
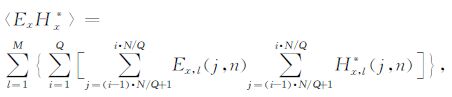
|
(14) |
其中,M为整个时间序列数据所开时窗的总个数;N为广义S变换中一个时窗内的采样数.Q用于控制一个时窗内可以得到的频谱个数,其最大值由(11)式确定.当Q=1时,S变换只得到一个频谱系数,计算结果与短时傅里叶变换的结果相同.
为消除少量“飞点"异常数据影响,大多采用Robust估计方法计算阻抗张量元素[18-21].Robust估计实际上是一种迭代计算方法.每次迭代只对两个电场分量进行修改.
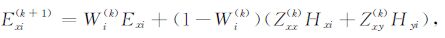
|
(15) |
W(k) 为第k次迭代的Huber权函数,定义为
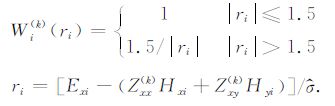
|
(16) |
$\hat{\sigma }$为残差标准偏差的估计值[18].利用迭代得到的电场分量与实测的磁场重新估算阻抗元素,然后进行电场分量的迭代修改,直到阻抗元素改变量收敛到一个很小的值为止.
5 实测资料处理效果与分析利用上文介绍的方法对实测MT 资料进行处理与分析,以检验方法的实际应用效果.
5.1 华北实测MT数据处理效果图 2为华北地区实际测点(点号为10437N30)大地电磁测深数据的视电阻率与相位曲线.图 2A为加拿大凤凰公司SSMT2000软件的处理结果;2B为基于S变换的处理结果.由图 2可知,对于高信噪比的大地电磁测深数据,基于S变换方法的处理结果与SSMT2000的结果相同,证明了本文方法的有效性和所编程序的正确性.同时,由于S变换能够给出更多的频谱系数,在低频端,S变换方法得到的视电阻率与相位曲线更为平滑.
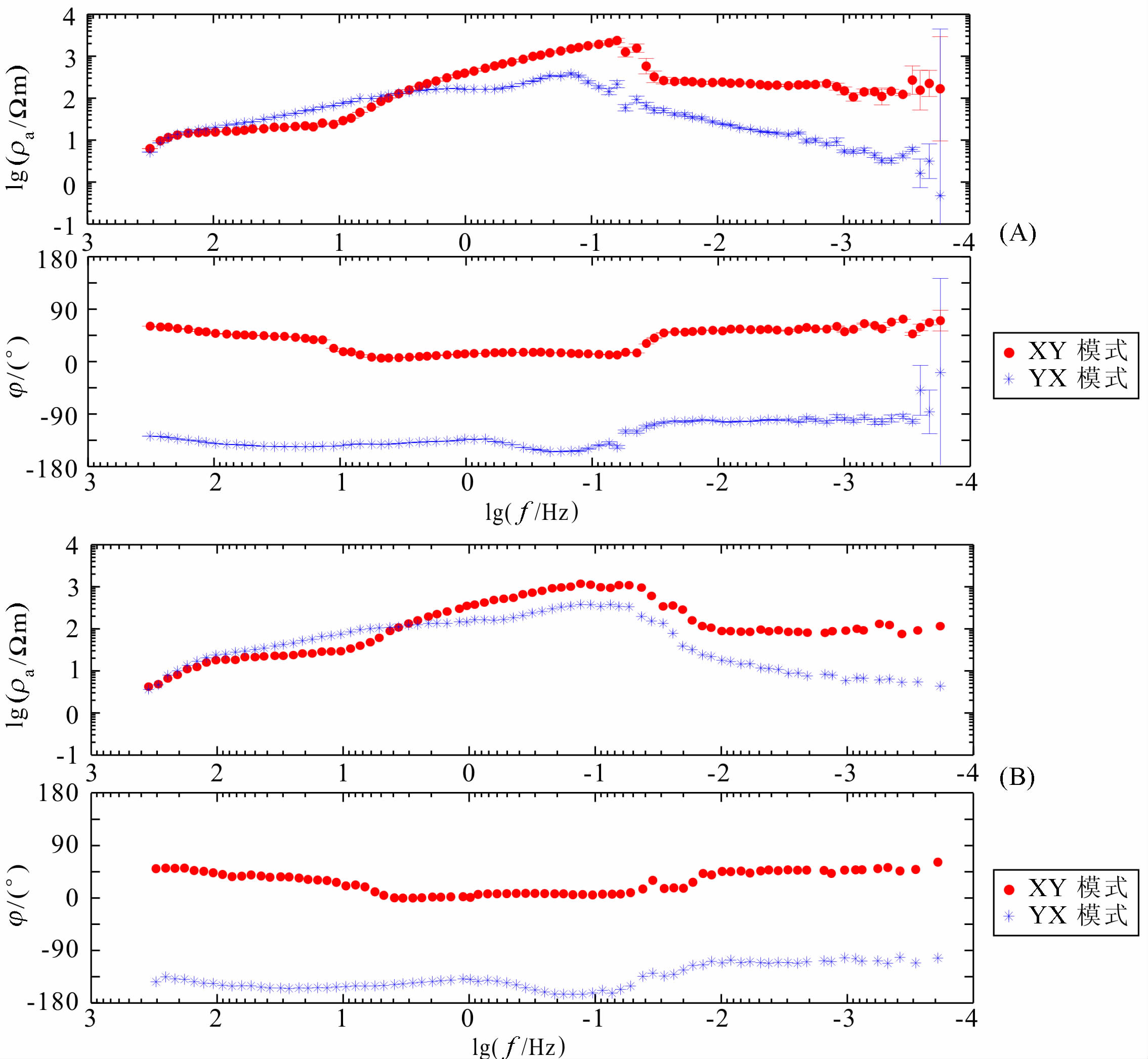
|
图 2 10437N30号大地电磁测深点视电阻率与相位曲线 (A)SSMT2000处理结果;(B)基于S变换的处理结果. Fig. 2 Curves of apparent resistivity and phase of MT site 10437N30 |
图 3为西北地区实际测点(点号为260)大地电磁测深数据的视电阻率与相位曲线.由图 3a可知,当频率低于0.1Hz时,SSMT2000软件处理的视电阻率与相位曲线极不光滑,且误差棒较大,几乎无法判断视电阻率曲线的变化规律,这表明原始数据中存在频率低于0.1Hz的强电磁噪声.为了分析这些噪声,在采样率为15 Hz的水平电磁场分量中提取4096个样点,利用广义S 变换进行时频分析.图 4给出了一段数据广义S变换的时频谱.由图 4可知,当频率大于0.1Hz时,两组正交电场与磁场水平分量的时频谱具有相当好的相关性.但是当频率小于0.1Hz时,它们的相关性变差,尤其是在230s之后,磁道出现严重的噪声干扰.这些噪声影响了SSMT2000的处理效果.
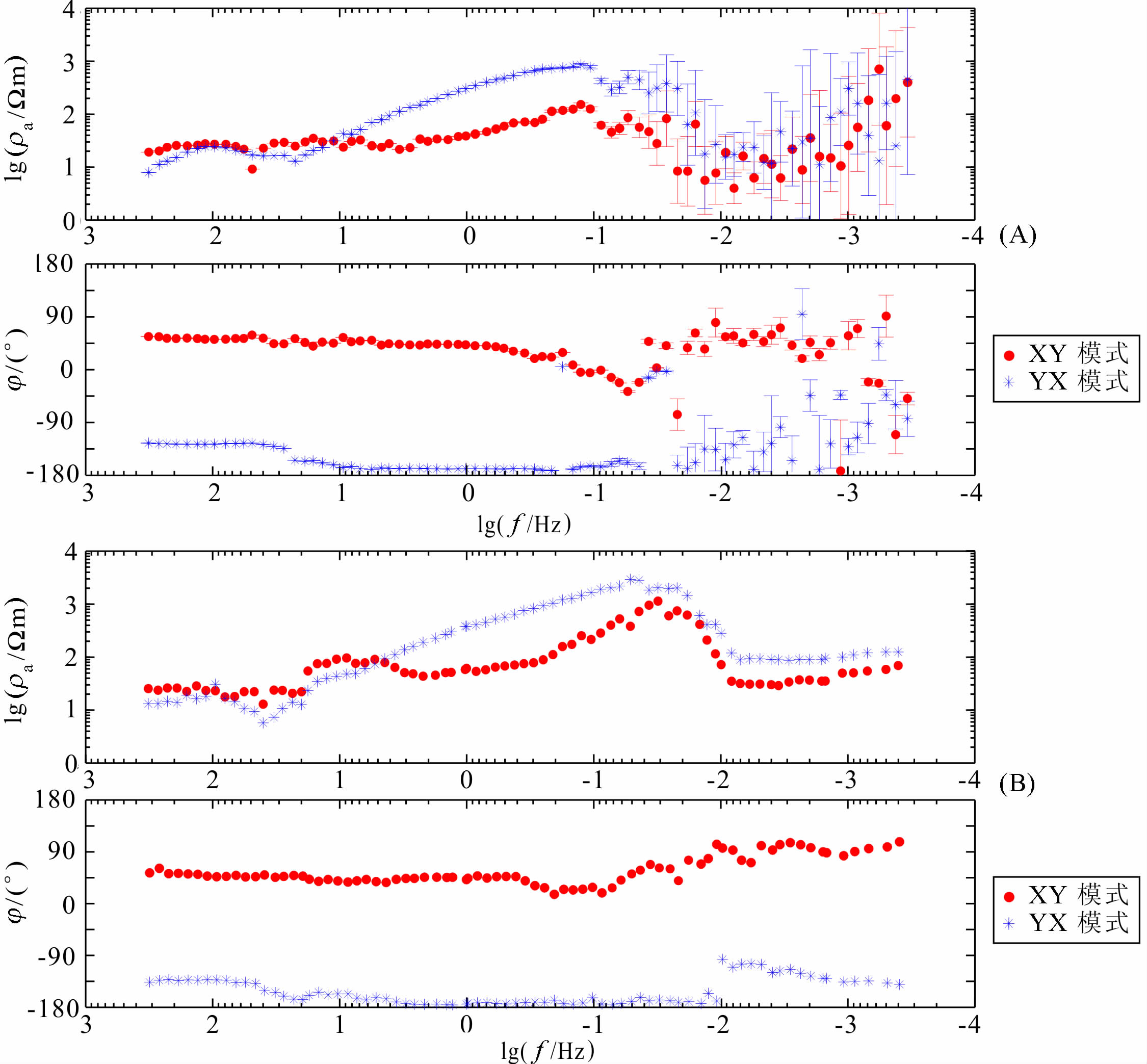
|
图 3 260号大地电磁测深点视电阻率与相位曲线 (A)SSMT2000处理结果;(B)基于S变换的处理结果. Fig. 3 Curves of apparent resistivity and phase of MT site 260 |
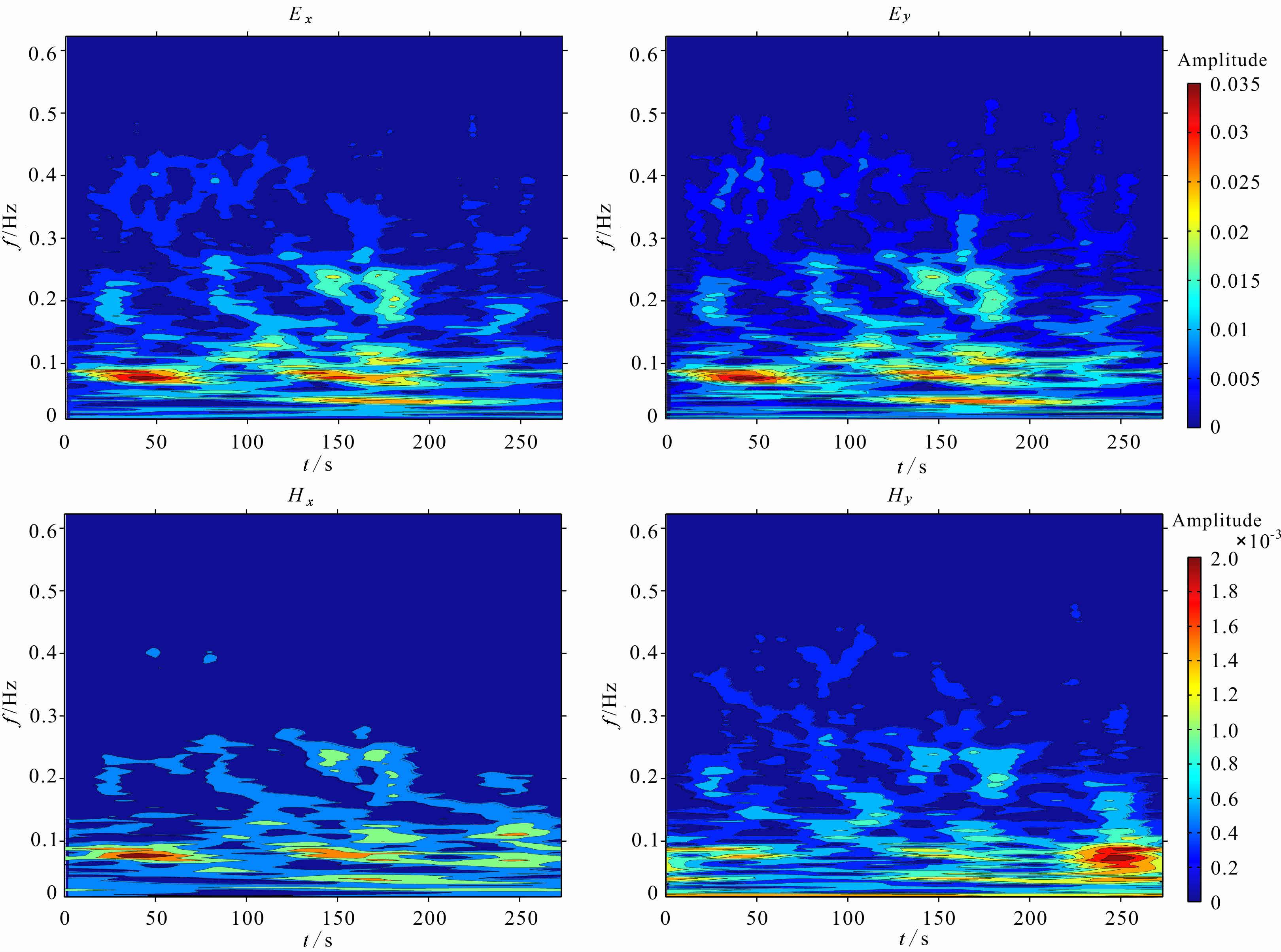
|
图 4 260号大地电磁测深点某段时间序列数据广义S变换时频谱 Fig. 4 Time-frequency spectrum of certain time series of MT site 260 by generalized S transform |
从图 4数据中,提取0.06 Hz和0.08 Hz的广义S变换时频谱数据,并利用不同时刻时频谱计算卡尼亚电阻率,结果见图 5.从图 5中可以看到,230s之后的视电阻率明显偏低,表现为磁道噪声的影响.另外,0.06HzXY 模式视电阻率曲线在80s和200s附近出现高值畸变,表现为电道噪声的干扰.但从图 4中,很难发现这两处存在的电道噪声.显然,通过计算图 5中的卡尼亚电阻率,更有利于判断电磁场分量中存在的电场和磁场噪声.这为电磁噪声的滤波处理提供了更为精确的时间与频率信息.
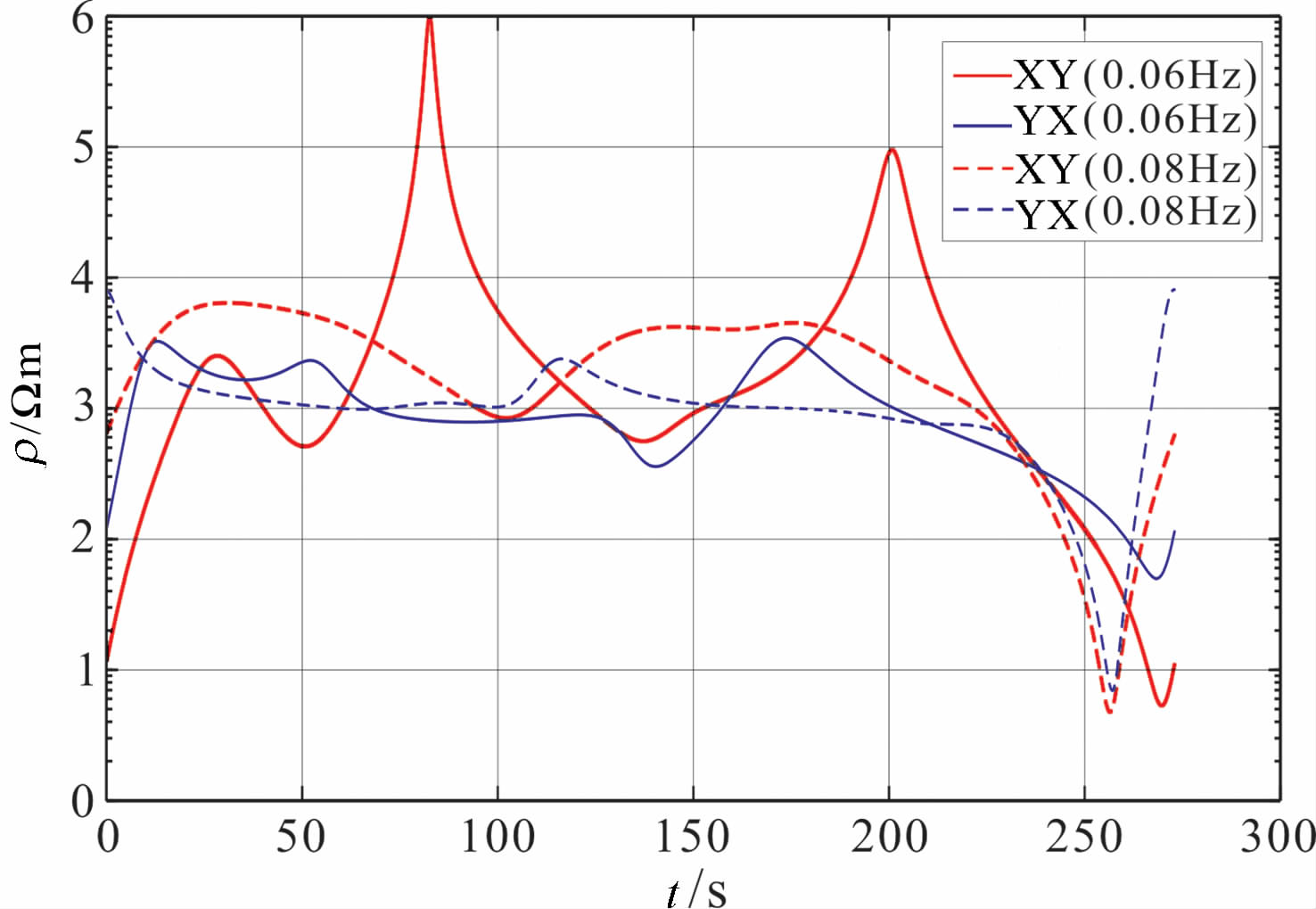
|
图 5 不同时刻广义S变换时频谱计算的卡尼亚电阻率 Fig. 5 Cagniard resistivity calculated by using generalized S transformspectrumat different time |
通过设计时频域滤波器,容易压制广义S 变换时频谱中的电磁噪声[22].图 3b 为噪声滤波处理后计算的视电阻率与相位曲线,与SSMT2000处理结果相比,频率小于0.1Hz的视电阻率与相位曲线的质量得到明显提高.
6 结论和讨论获得高质量大地电磁场信号频谱是提高阻抗张量元素求解精度的基础.广义S变换根据分析信号的频率自适应地调节分析窗口宽度,是一种较为先进的时频分析方法,适用于大地电磁场信号的时频分析.利用广义S变换对大地电磁场分量进行处理,不仅可以提供更多频谱系数,改善大地电磁测深阻抗张量元素的统计特性,使低频端视电阻率与相位曲线更平滑;而且能够根据广义S变换时频谱确定电磁噪声在时频平面上的分布特征,为压制干扰大地电磁场的电磁噪声提供了技术选择.
尽管广义S 变换在诸多领域中已得到广泛应用,但是关于窗函数调节参数的取值问题并没有得到深入的讨论.Pei等[14]研究表明,当时窗函数标准偏差为8时,广义S变换时频谱将受到较大的边缘效应影响.因此,在广义S 变换的应用中,需要讨论窗口参数的取值问题.本文根据大地电磁场信号分析的特点,利用广义S变换高斯窗函数,分析了窗口宽度比例因子A、采样数N与可提取频谱系数个数Q的关系,为实际信号分析中窗口宽度与比例因子的选取提供了依据.
理论信号分析表明,在大地电磁测深数据处理中,S变换较短时窗傅里叶变换具有更大的优势.本文研究了基于离散广义S变换的大地电磁测深数据ROBUST 处理方法.实际资料处理结果表明,本文方法比短时傅里叶变换处理效果更好,并且有利于识别和压制电磁噪声干扰.
| [1] | 陈乐寿, 刘任, 王天生. 大地电磁测深资料处理与解释. 北京: 石油工业出版社, 1989 . Chen L S, Liu R, Wang T S. Magnetotelluric Sounding Data Processing and Interpretation (in Chinese). Beijing: Petroleum Industry Press, 1989 . |
| [2] | 徐义贤, 王家映. 基于连续小波变换的大地电磁信号谱估计方法. 地球物理学报 , 2000, 43(5): 677–683. Xu Y X, Wang J Y. Power spectrum estimation for magnetotelluric signal based on continuous wavelet transform. Chinese J.Geophys. (in Chinese) , 2000, 43(5): 677-683. |
| [3] | Xavier G, Alan G J. Robust processing of magnetotelluric data in the AMT dead band using the continuous wavelet transform. Geophysics , 2008, 73(6): 223-234. DOI:10.1190/1.2987375 |
| [4] | 汤井田, 化希瑞, 曹哲民, 等. Hilbert-Huang变换与大地电磁噪声压制. 地球物理学报 , 2008, 51(2): 603–610. Tang J T, Hua X R, Cao Z M, et al. Hilbert-Huang transformation and noise suppression of Magnetotelluric sounding data. Chinese J.Geophys. (in Chinese) , 2008, 51(2): 603-610. |
| [5] | 汤井田, 蔡剑华, 任政勇, 等. Hilbert-Huang变换与大地电磁信号的时频分析. 中南大学学报(自然科学版) , 2009, 40(5): 1399–1405. Tang J T, Cai J H, Ren Z Y, et al. Hilbert-Huang transform and time-frequency analysis of magnetotelluric signal. Journal of Central South University (Science and Technology) (in Chinese) , 2009, 40(5): 1399-1405. |
| [6] | 蔡剑华, 龚玉蓉, 王先春. 基于Hilbert-Huang变换的大地电磁测深数据处理. 石油地球物理勘探 , 2009, 44(5): 617–621. Cai J H, Gong Y R, Wang X C. Magnetotelluric data processing based on Hilbert-Huang transform. Oil and Gas Exploration (in Chinese) , 2009, 44(5): 617-621. |
| [7] | Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform. IEEE Transactions on Signal Processing , 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [8] | Stockwell R G. A basis for efficient representation of the S-transform. Digital Signal Processing , 2007, 17(1): 371-393. DOI:10.1016/j.dsp.2006.04.006 |
| [9] | 高静怀, 陈文超, 李幼铭, 等. 广义S变换与薄互层地震响应分析. 地球物理学报 , 2003, 46(4): 526–532. Gao J H, Chen W C, Li Y M, et al. Generalized S transform and seismic response analysis of thin interbeds. Chinese J.Geophys. (in Chinese) , 2003, 46(4): 526-532. |
| [10] | Pinnegar C R, Manainha L. Time-local Fourier analysis with a scalable phase-modulated analyzing function: the S-transform with a complex window. Signal Processing , 2004, 84(7): 1167-1176. DOI:10.1016/j.sigpro.2004.03.015 |
| [11] | Schimmel M, Gallart J. The inverse S transform in filters with time-frequency localization. IEEE Transactions on Signal Processing , 2005, 53(11): 4417-4422. DOI:10.1109/TSP.2005.857065 |
| [12] | Simon C, Ventosa S, Schimmel M, et al. The S-transform and its inverses: side effects of discretizing and filtering. IEEE Transactions on Signal Processing , 2007, 55(10): 4928-4937. DOI:10.1109/TSP.2007.897893 |
| [13] | 刘保童, 刘启源, 吴玉林. S变换数值计算方法比较的实验研究. 湖南文理学院学报(自然科学版) , 2010, 22(3): 16–19. Liu B T, Liu Q Y, Wu Y L. Experimental researches on comparison of S transform numerical methods. Journal of Hunan University of Arts and Science (Natural Science Edition) (in Chinese) , 2010, 22(3): 16-19. |
| [14] | Pei S C, Wang P W, Ding J J, et al. Elimination of the discretization side-effect in the S transform using folded windows. Signal Processing , 2011, 91(6): 1466-1475. DOI:10.1016/j.sigpro.2010.11.005 |
| [15] | 刘丽娟, 王山山. 广义S变换窗函数的分析和改进. 岩性油气藏 , 2007, 19(2): 76–79. Liu L J, Wang S S. Analysis and improvement of window function of generalized S-transform. Lithologic Reservoirs (in Chinese) , 2007, 19(2): 76-79. |
| [16] | 高静怀, 满蔚仕, 陈树民. 广义S变换域有色噪声与信号识别方法. 地球物理学报 , 2004, 47(5): 869–875. Gao J H, Man W S, Chen S M. Recognition of signals from colored noise background in generalized S-transfromation domain. Chinese J.Geophys. (in Chinese) , 2004, 47(5): 869-875. |
| [17] | Fiona S, Karsten B. Practical Magnetotellurics. New York: Cambridge University Press, 2005 . |
| [18] | Egbert G D, Booker J R. Robust estimation of geomagnetic transfer functions. Geophys.J.R.Astr.Soc. , 1986, 87(1): 173-194. |
| [19] | Chave A D, Thomson D J, Ander M E. On the robust estimation of power spectra, coherences and transfer functions. J.Geophys.Res. , 1987, 92(B1): 633-648. |
| [20] | Egbert G D, Livelybrook D W. Single station Magnetiotelluric impedance estimation: Coherence weighting and the regression M-estimation. Geophysics , 1996, 61(4): 964-970. DOI:10.1190/1.1444045 |
| [21] | Larsen J C, Mackie R L, Manzella A, et al. Robust smooth Magneto tell uric transfer functions. Geophys.J.Int. , 1996, 124(3): 801-819. |
| [22] | 陈海燕, 景建恩, 魏文博. 广义S变换时频域滤波在MT数据处理中的应用. 现代地质 , 2012, 26(6): 1212–1217. Chen H Y, Jing J E, Wei W B. GST time-frequency filter application in MT data processing. Geoscience (in Chinese) , 2012, 26(6): 1212-1217. |
 2012, Vol. 55
2012, Vol. 55

