2. 地下信息探测技术与仪器教育部重点实验室和地质过程与矿产资源国家重点实验室, 北京 100083
2. Key Laboratory of Geo-detection of Ministry of Education, Beijing 100083, China
近年来,大地电磁测深(MT)资料的三维反演方法有了长足的发展,在MT 实际勘探工作中,三维反演、解释的案例也在逐渐增多[1-2].为深入了解地壳和上地幔的导电性结构,SinoProbe专项01 项目在华北布设了1°×1°网度的大地电磁测深(MT)阵列式示范观测网,其中包括约1400个宽频和长周期大地电磁测深站点的数据.考虑到真实地下介质的几何或导电性结构往往具有三维特征,在实际资料解释中采用三维反演方法当然是最合理的选择[3].然而,一方面,相对于传统的MT 一、二维反演方法,MT 三维反演计算需要耗费大量计算时间和计算机内存;而对于MT 阵列观测,其数据体过于庞大,即使运用计算机集群平台和最新的并行算法,所能计算的MT 三维模型数据密度以及剖分网度与二维反演相比仍相对有限,这可能导致三维反演模型的分辨率降低,达不到预期效果.另一方面,由于大地电磁测深资料的三维反演方法目前还远未成熟,对于欠定性很高的三维反演问题,多数反演算法的稳定性问题仍然难以解决.因此,当前大地电磁二维反演仍然是应用最为广泛的MT 反演方法.研究大地电磁测深二维反演在三维问题中的适应性,无疑对于SinoProbe-01项目的成功至关重要.
然而,用二维反演方法来近似解释地下三维结构,不可避免地会产生各种问题[4-5].在实测MT 资料解释工作中,进行MT 二维反演首要的问题是判定地下电性结构的维性和电性主轴方向;在此基础上确定计算剖面的方向.然而,在大区域的MT 阵列观测工作中,截取的MT 长剖面往往跨越多个地质构造单元,抑或遭遇地质构造复杂多变的研究区域,电性主轴方向的分析结果很难有比较一致的趋势,这给判定地下电性结构的维性和电性主轴方向带来很大的困难,从而影响了MT二维反演的效果.
其次,根据大地电磁测深方法理论,大地电磁场在二维介质中沿电性主轴方向传播时可以分解为互不相关的两组线性偏振波,即电场水平分量平行构造走向、磁场水平分量垂直构造走向的TE(transverse-electric)极化模式和电场水平分量垂直构造走向、磁场水平分量沿构造走向的TM(transverse-magnetic)极化模式;此外,还有同时使用水平磁场和垂直磁场的TP(tipper)模式.当对MT 实测数据进行二维反演时,单独使用上述几种模式的数据,其反演结果往往差别较大.因而,如何合理选择极化模式数据进行二维反演,以取得尽可能接近真实的地下电性结构模型,一直是人们关注的问题.
对于极化模式数据的选择,较早的研究者们在计算了三维体在层状模型中的响应之后认为,对于浅部的三维异常体,使用TE 模式容易产生虚假的低阻异常,而TM 模式可以得到较好的效果[6-7].Parker和Mackie在对印度河谷的实测数据进行分析之后则发现,TM 模式的反演无法反映某些三维异常[8].Ledo等先后研究实测三维数据和一系列复杂的二维/三维体模型响应的二维反演结果,认为很难判断某一个模式是否优于其他模式[9-10].胡祖志等研究了不同深度三维棱柱体的二维反演,认为TE+TM 模式的联合反演效果相对较好[11].Ogawa和Jones则分别通过对三维正演模型响应和实测三维数据的二维反演的研究指出,TM 模式的反演无法发现某些特殊产状的低阻异常体,只有TE 模式能够发现[12-13]某些特殊产状的低阻异常体.蔡军涛等研究了不同延伸长度三维棱柱体响应的二维反演,认为TM 模式对于二维假设的要求较低,其单独反演要优于其他模式的反演或多模式联合反演[14].传统的二维理论认为,应将大地电磁场的张量阻抗和磁倾子信息旋转到主轴方向进行反演;而陈小斌等研究了三维立方体响应的二维近似反演的剖面选择之后,得出了在三维条件下将其旋转到主轴方向并不一定最优,旋转到剖面方向进行反演有可能更好地还原地下的真实信息的结论[15].究竟如何运用二维反演方法才能更逼近真实的地下三维结构,研究者们的观点显得莫衷一是.
本文针对上述问题,利用大地电磁测深二维、三维建模及正反演技术,设计和分析了一系列正演模型,并对其进行了响应计算和数据分析,对不同模式反演和数据旋转方向对二维反演结果的影响进行了分析,并与三维反演结果做了对比研究.同时使用华北某地实测数据进行了二维和三维反演的分析对比试验,对MT 二维反演方法在解释三维结构问题中的适用性进行了深入探讨.
2 合成数据的计算及分析对于大地电磁测深方法,由于地下介质真实的电阻率始终是未知的,要探讨二维反演方法对于求解复杂结构问题的适应性,以及使用何种极化模式数据进行二维反演才能更好地还原地下电性信息等问题,都需要构建三维理论模型并对其正演响应进行分析和反演对比.而就目前而言,此类的研究仍有不足,多数的研究仍局限在较为简单的三维棱柱体或立方体的情况,难以模拟真实的地下复杂构造.因此,本研究中设计了一系列较为复杂的二维/三维模型并进行分析对比,由于篇幅限制,这里仅给出部分模型及其响应.
2.1 理论模型的设计及正演计算我们设计了一系列二维/三维混合模型来模拟实际工作中使用MT 二维反演方法研究复杂三维问题的情况.首先,假设地下半空间地层导电性总体上为两层结构.第一层厚度为30km,电阻率100Ωm;第二层为低阻基底,电阻率10Ωm.我们将两个近二维柱状异常体A 和B作为目标体置于第一层中,其顶部埋深均为10km;目标体沿 x , y , z 三方向的延伸分别为40km,10km 和10km,两目标体之间距离为15km;为了模拟三维异常体的畸变效应,在目标体上方的地表对应覆盖两个不规则形状(L 字形)的厚度为1km 的高/低阻的三维异常体.为模拟二维大地电磁测深工作,设计一条剖面(MN)穿过三维异常体的上方;模型的空间结构及电阻率分布如图 1所示.
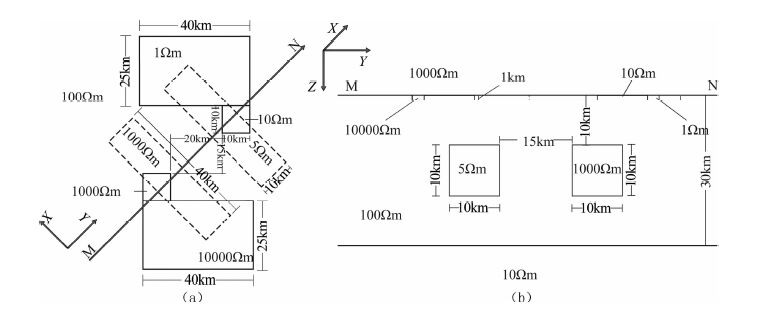
|
图 1 走向与剖面垂直的三维理论模型(a)俯视图;(b)剖面方向断面图.其中MN 为测线. Fig. 1 (a) Plan view of the 3D syntheticmodel; (b) Profile section of the syntheticmodel.MN: data profile. |
为了试验不同电阻率目标体模型的正/反演效果,研究中分别测试了A 为低阻(10Ωm),B为高阻(1000 Ωm)以及A 为高阻(1000 Ωm),B 为低阻(10Ωm)的两组模型,以模拟不同强度的三维畸变效应对正/反演结果的影响.
此外,为了实验异常体不同走向对模型响应数据与反演结果的影响,我们在保持前述两组模型中地表三维异常体位置以及测线位置不变的情况下,将两个近二维目标体的走向进行了调整,研究中测试了与垂直测线方向分别相差0°、15°、30°、45°的模型(模型L0-L45),其几何形状及电阻率分布如图 2所示.
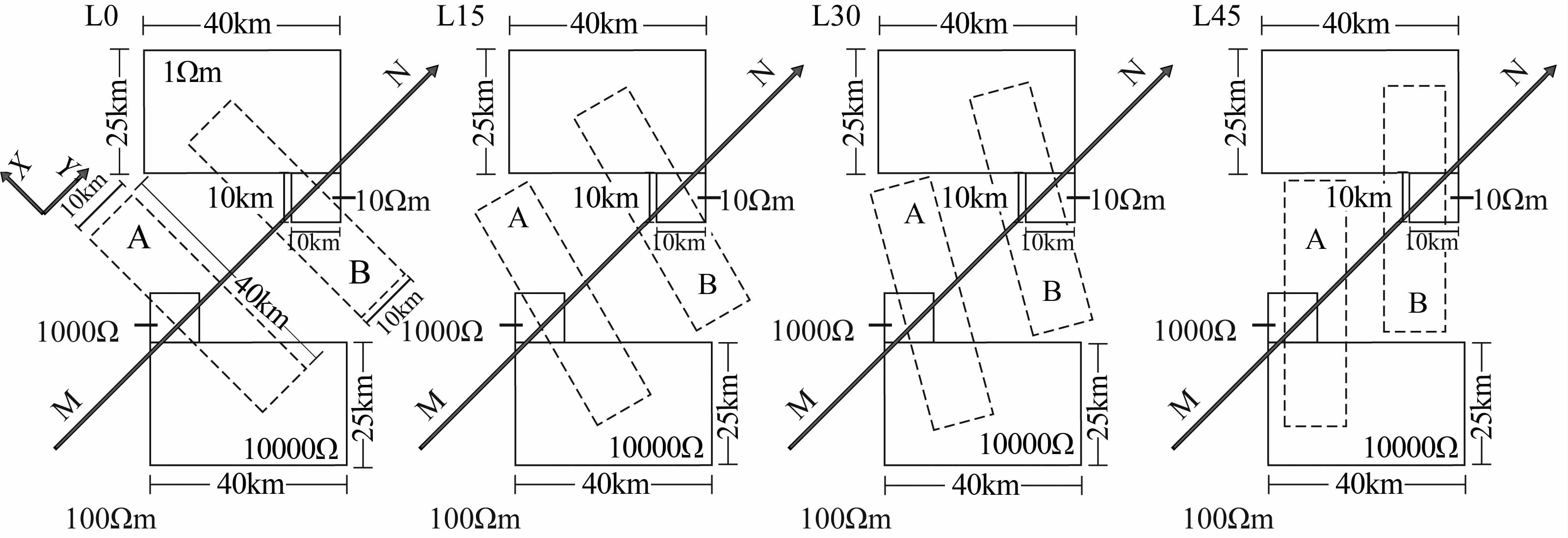
|
图 2 三维理论模型俯视图 从左至右分别为目标体走向与剖面正交方向相差0°、15°、30°、45°的模型.其中MN 为测线. Fig. 2 Plan view of the 3D synthetic model from the orthogonal direction of the profile.MN : data profile. |
本研究中三维模型的正演响应采用Mackie等开发的三维交错网格有限差分正演程序[16]进行计算;将上述三维模型进行离散化,得到单元数为65×65×55的三维网格;模型响应的频率范围从0.0001~100Hz共6个数量级,每数量级设计了7个在对数域上均匀分布的频点,共42 个频点;沿测线MN 方向共布置了站间距为约2km的模拟测站共40个;为了模拟真实数据中的噪声和测量中的误差,我们对合成数据的阻抗张量加入了2.5% 的高斯随机噪声.
2.2 低阻-高阻模型的合成数据响应对于模型中目标体A 为低阻(10Ωm),B 为高阻(1000Ωm)的低阻-高阻模型,从大地电磁反演的一般经验来看,由于低阻目标体受其上方的高阻的三维异常体影响,其所受畸变应较小,而高阻目标体受上方的低阻的三维异常体的影响,所受三维畸变影响一般较大.为了较为精确地检验合成数据体是否具有较为典型的三维特性,研究中采用了G-B(Groom-Bailey)阻抗张量分解[17-18]方法对合成数据进行维度分析.G-B 阻抗张量分解理论一般假设三维异常体对二维区域构造的阻抗张量有畸变作用,实测阻抗张量可以分解为:
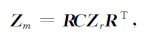
|
(1) |
其中, R 为旋转矩阵, C = g T S A 为局部畸变矩阵,其中, g 为常量, T 为扭转矩阵, S 为剪切矩阵, A 为分裂张量,而 Z r 为区域二维阻抗张量.将其分别展开有:
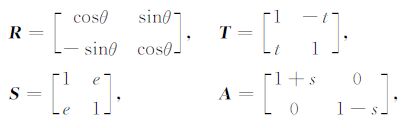
|
(2) |
其中θ 为旋转走向角, t 为扭曲(twist)因子, e 为剪切(shear)因子, s 为分裂比例因子.这几个畸变参数,尤其是其中的 T 和 S ,对于描述区域大地电磁场信号的三维畸变十分重要.
图 3为近二维目标体在走向角固定在垂直剖面(-45°)时(即L0模型)G-B分解计算得到的剪切角 S 和扭曲角 T 以及二维偏离度skew 沿不同站点及频率的分布.不难看出,正演响应的三维畸变量绝大部分存在于三维异常体的正下方,而低阻三维体对高阻目标体的影响要远高于高阻局部异常对低阻目标体的影响,其对于阻抗张量的畸变作用主要表现在扭曲作用上,剪切作用的影响相对较小.而地表的三维体的影响范围远不止于中高频率的大地电磁场,即使对于低频的大地电磁场也具有较强的影响;总体而言,响应数据的二维偏离度较小(<0.2),而在三维异常体的下方,尤其是低阻三维体的附近,模型响应表现出强烈的三维结构.
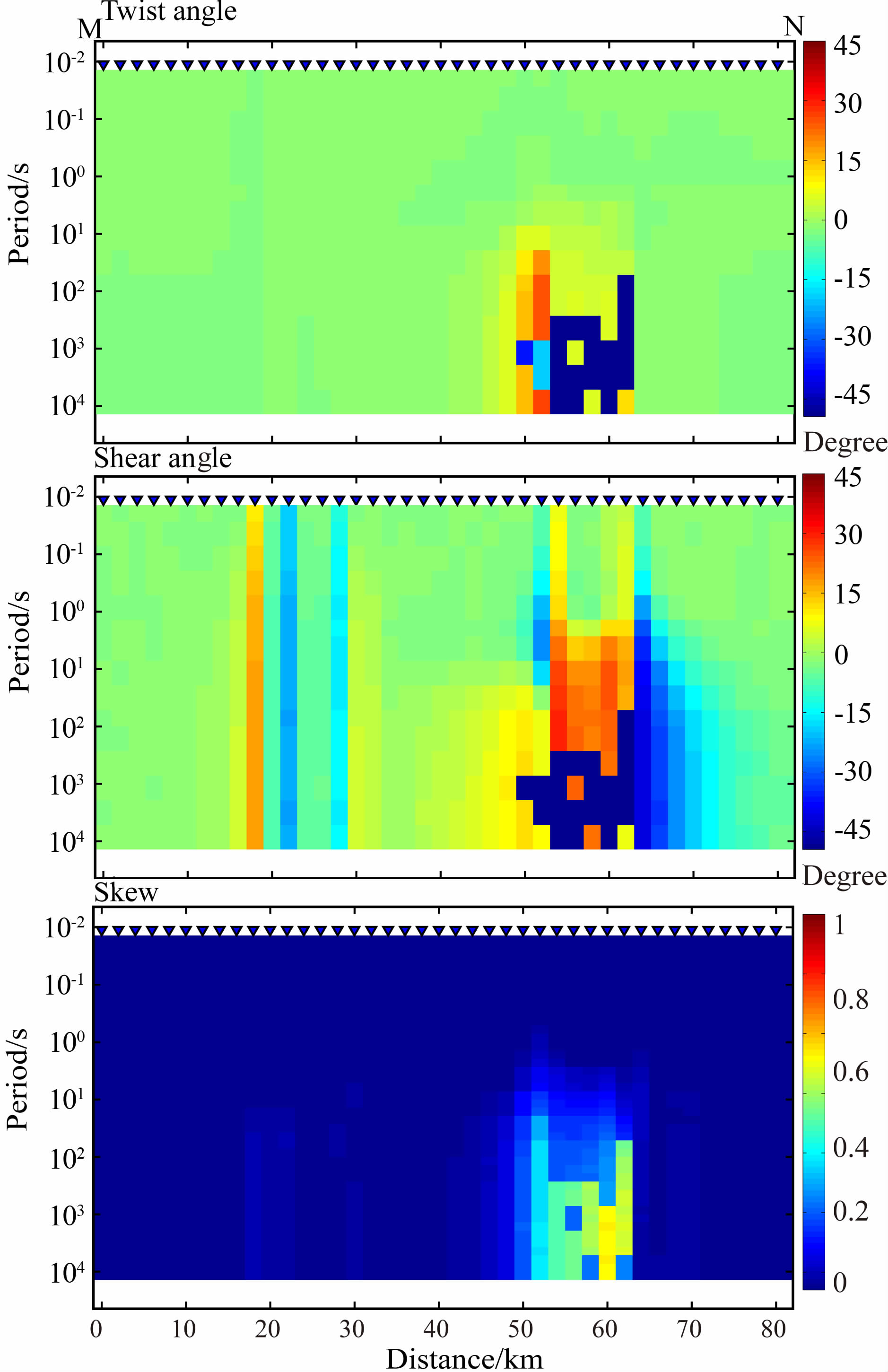
|
图 3 L0模型Groom-Bailey阻抗张量分解畸变参数拟断面图.从上到下分别为扭曲角、剪切角和二维偏离度 Fig. 3 Pseudo section of the distortion parameters of Groom-Bailey decomposition for model L0,from up to down: Twist,shear and skew |
图 4为近二维目标体与垂直测线方向分别相差0°、15°、30°、45°的模型(模型L0-L45)的响应拟断面图.对频率域的数据进行分析,可以得到一部分有用的电性信息.和之前维度分析的结果相似,对于不同的模式,响应的畸变都集中在三维异常体,尤其是低阻三维异常体的附近;XY,YX 模式的视电阻率拟断面低阻三维异常体的左右两侧均有较大的畸变异常,而在高阻三维异常体的附近畸变则较小.同时,相对于电阻率值的较大变化,不论是XY 还是YX的相位的变化都相对较小,异常较为平滑,且较少出现类似电阻率拟断面中突变的情况.这反映出相位信息相对于视电阻率可能更不易受三维畸变的影响.
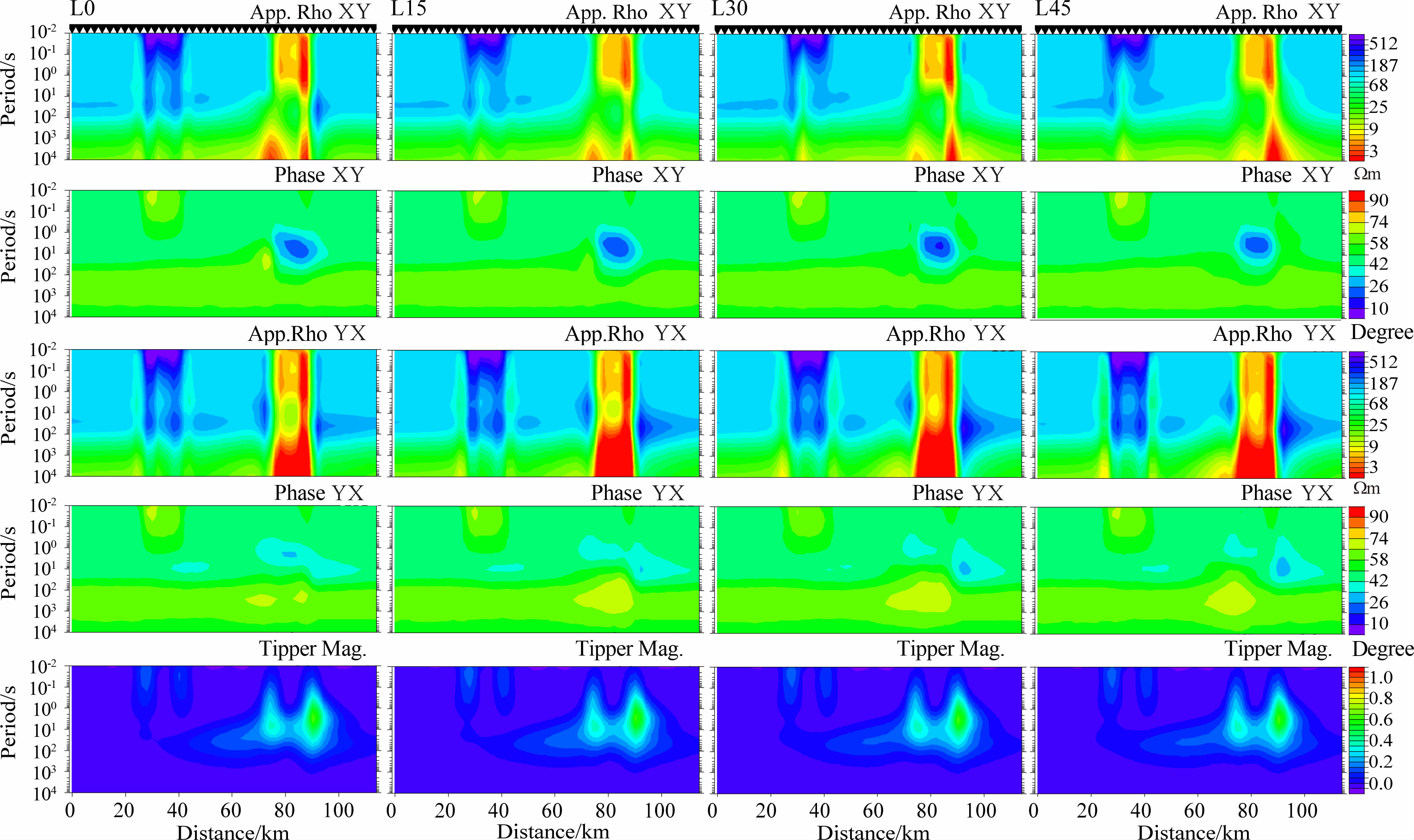
|
图 4 三维低阻-高阻模型响应拟断面图,从左至右分别为模型L0,L15,L30,L45的响应,从上至下分别为XY 模式视电阻率,XY 模式相位,YX 模式视电阻率,YX 模式相位,磁倾子模值 Fig. 4 Pseudo section of the responses for the L-H model,Left to right: responses from L0,L15,L30,L45.Up to down: XY apparent resistivity,XY phase,YX apparent resistivity,YX phase,Tipper magnitude |
对比模型L0,L15,L30 和L45 的响应,不难发现,随着近二维体的走向方向逐渐偏离垂直剖面方向,各个模式中的目标体的响应有着逐渐减小的趋势,而畸变的影响则有着逐渐增大的趋势.对于不同模式而言,随着走向方向的变化,XY 模式的响应变化相对较大,其次是YX 模式的响应,而磁倾子的模值响应则变化量最小.
2.3 高阻-低阻模型的合成数据响应与上述模型类似的,对于模型中目标体A 为高阻(1000Ωm),B 为低阻(10Ωm)的高阻-低阻模型的正演响应,研究中同样使用G-B 分解方法进行了维度分析.图 5为近二维目标体在走向角固定在垂直剖面(-45°)时(即L0模型)G-B分解计算得到的剪切角 S 和扭曲角 T 以及二维偏离度skew 沿不同站点及频率的分布.与前一组模型相似的是,模型的三维畸变量绝大部分存在于三维异常体的正下方,且畸变量主要存在于中低频的响应中;而低阻三维体对地下电性结构的影响同样要高于高阻体.整体而言,其二维偏离度相对于之前的低阻-高阻模型有所减小.从剪切角和扭曲角的分布状态来看,低阻三维异常体的畸变影响有所减小,而高阻三维异常体的畸变影响则有所增加.但实际上,模型的三维异常体的位置和电阻率相对前述的低阻-高阻模型并未有任何改变,这是由于相对高阻目标体,低阻目标体的二维性更强,对于同样的三维体干扰,更不易为三维畸变所影响,这两者的位置交换导致了相对畸变程度的变化.
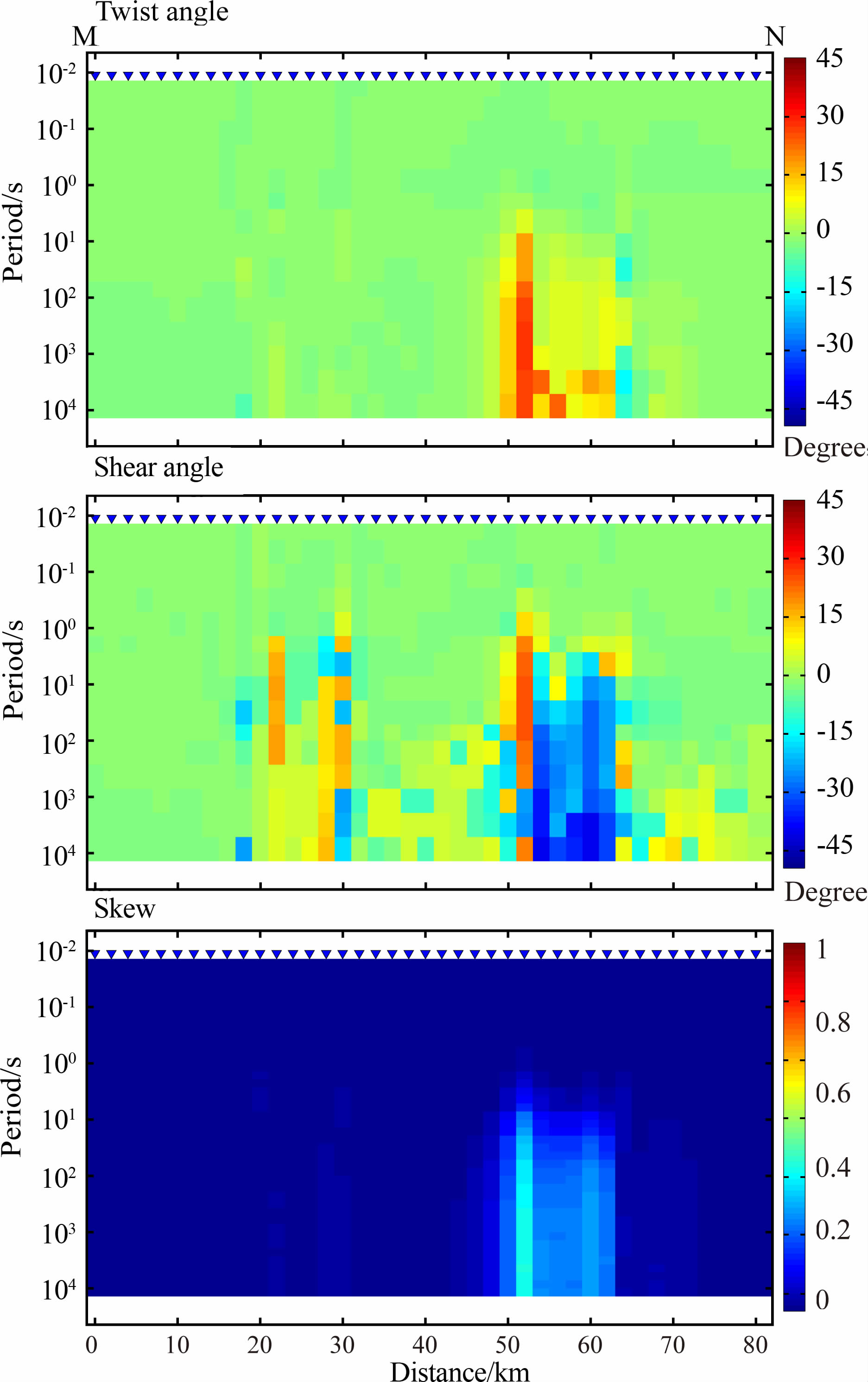
|
图 5 L0模型Groom-Bailey阻抗张量分解畸变参数拟断面图,从上到下分别为扭曲角,剪切角和二维偏离度 Fig. 5 Pseudo section of the distortion parameters of Groom-Bailey decomposition for model L0,from up to down: Twist,shear and skew |
图 6为近二维目标体与垂直测线方向分别相差0°、15°、30°、45°的模型(模型L0-L45)的响应拟断面图.和之前维度分析的结果相对应的,对于不同的模式响应的畸变相对之前的低阻-高阻模型的响应结果较低,同样;XY,YX 模式的视电阻率拟断面低阻三维异常体的左右两侧均有较大的畸变异常,而相对于电阻率值的较大变化,不论是XY 还是YX 的相位的变化都同样较小,异常较为平滑.

|
图 6 三维高阻-低阻模型响应拟断面图,从左至右分别为模型L0,L15,L30,L45的响应,从上至下分别为XY 模式视电阻率,XY 模式相位,YX 模式视电阻率,YX 模式相位,磁倾子模值 Fig. 6 Pseudo section of the responses for the H-L model,Left to right: responses from L0,L15,L30,L45.Up to down: XY apparent resistivity,XY phase,YX apparent resistivity,YX phase,Tipper magnitude |
和之前的模型相似的,对比模型L0,L15,L30和L45 的响应,不难发现,随着近二维体的走向方向逐渐偏离垂直剖面方向,各个模式中的目标体的响应有着逐渐减小的趋势,而畸变的影响则有着逐渐增大的趋势.对于不同模式而言,随着走向方向的变化,XY 模式的响应变化相对较大,其次是YX 模式的响应,而磁倾子的模值则同样并无太大变化.
3 对合成数据的反演研究在以前关于三维数据体的二维反演研究中,研究者们多关注TE,TM 或TE+TM 联合反演.对于倾子反演的涉及较少.实际上,当前使用比较广泛的二维反演方法如Occam 法[19],Rebocc法[20],非线性共轭梯度法(NLCG)[21]等都支持带倾子的独立反演或与其他模式的联合反演;在实际的勘探或深部结构研究中,多数大地电磁测深工作也都会测量垂直方向的磁场.为了解倾子反演在二维反演中的作用,本文中加入了对二维倾子反演模式的比较.二维反演方法采用的是非线性共轭梯度法,在此进行了TE、TM、TE+TM 以及TM+TP 四种模式的反演.
由于在前一节的数据分析中我们发现相位受到的畸变影响要小于视电阻率,因此,我们将相位的误差基设置的相对较小,使反演程序更多的拟合相位数据,从而相对地减少三维畸变的影响.具体的反演参数的设置如表 1所示.
|
|
表 1 二维非线性共轭梯度反演参数 Table 1 Parameters for 2D NLCG inversions |
为了测试剖面方向/电性主轴旋转方向对反演结果的影响,我们主要进行了两组反演旋转对比测试:一组将阻抗张量及磁倾子旋转到垂直剖面方向,另一组将其旋转到电性主轴方向,在这里,我们简单地将其旋转到近二维构造体的走向方向.对于这两组反演测试,XY 模式使用垂直于剖面/主轴方向的电场和平行于剖面/主轴方向的磁场,即为TE 模式,而YX 模式使用垂直于剖面/主轴方向的磁场和平行于剖面/主轴方向的电场,即为TM 模式.
3.1 低阻-高阻模型图 7为目标体A为低阻异常,B为高阻异常时将阻抗张量和磁倾子旋转到电性主轴方向之后L0-L45各模型响应的反演结果.此时,高阻目标体受上方的低阻三维异常影响,低阻目标体受其上方的高阻三维异常影响,总体而言,各反演结果对左侧低阻目标体的反应要好于右侧的高阻目标体,在所有的模式中,左侧的低阻目标体都有着一定的反映,而右侧的高阻目标体则基本没有正确的反映,这与之前数据分析中模型响应右侧的畸变程度远高于左侧的结果相吻合.
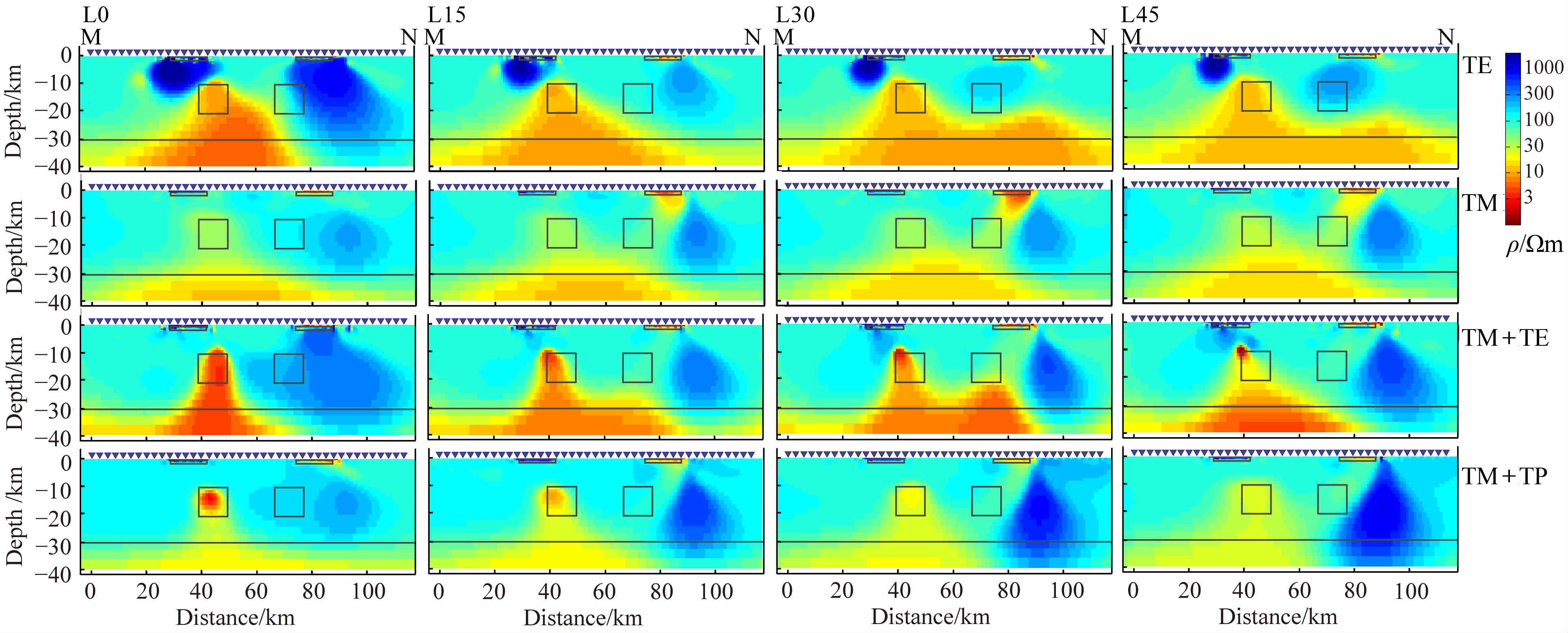
|
图 7 低阻-高阻理论模型响应旋转到电性主轴方向的二维NLCG 反演结果.从左至右:走向分别为与垂直剖面方向相差0°,15°,30°,45°;从上到下,反演模式分别为TE,TM,TM+TE,TM+TP,图中的方框标示了异常体的原始位置 Fig. 7 2D NLCG inversion result of the L-H models.Left to right: results of models with strikes of 0°,15°,30°,45° degree from the orthogonal direction of the profile.Up to down: results in TE,TM,TM+TE and TM+TP mode.Gray boxes indicate the location of the anomalies in the forward models |
对比不同的模式,不难发现单独TE 模式的反演结果较不稳定,受到电性主轴方向变化的影响很大,即使电性主轴方向仅仅与垂直剖面方向相差15°(L15模型),反演结果也有较大的变化,这体现出TE 模式对于二维假设的敏感性,其反演结果对于高导体的下界基本没有约束,甚至可能得到完全不同于地下结构的反演结果;TM 模式的反演结果较为稳定,并未受到电性主轴方向变化的影响,然而,其异常体的边界较不清晰,不但基本无法得到高阻二维目标体的位置,对于畸变较小的高导二维目标体的反映也极为模糊.TM+TE 模式的反演结果对异常体的边界判断较为清楚,尤其是在电性主轴与剖面方向垂直时(L0模型),对高导近二维目标体有着较好的反映,但随着电性主轴方向逐渐偏离垂直剖面方向,其反演结果逐渐不稳定,冗余构造较多,在某些情况下会得到错误的异常体位置或虚假异常;TM+TP模式的反演结果对于异常体边界的判断,尤其是底界的判断相对最佳,而和TM+TE模式类似的,随着电性主轴偏离垂直剖面方向角度的增加,异常体的轮廓越来越不明显,而虚假异常则逐渐增加.
图 8为将阻抗张量和磁倾子旋转到垂直剖面方向时L0-L45各模型响应的反演结果.需要注意的是,对于L0模型,其电性主轴方向就是垂直剖面方向,因此反演的结果是相同的;而对于L15-L45模型,其电性主轴方向与垂直剖面方向分别相差15°、30°、45°.和上一组反演结果相似,各反演结果对左侧高导目标体的反应要好于右侧的高阻目标体.对比图 7可以发现,旋转到垂直剖面方向之后,二维反演的结果可以分为两组:对于TE 和TM+TE 而言,由于TE 模式对二维假设要求较高,旋转到剖面方向之后,二维假设不再有效,因此反演的结果要差于旋转到主轴方向的结果;对于TM 和TM+TP模式,由于TM 模式对二维假设要求较低,因此旋转到剖面方向之后,反演的结果并无太大变化,甚至可能优于旋转到主轴方向的结果.
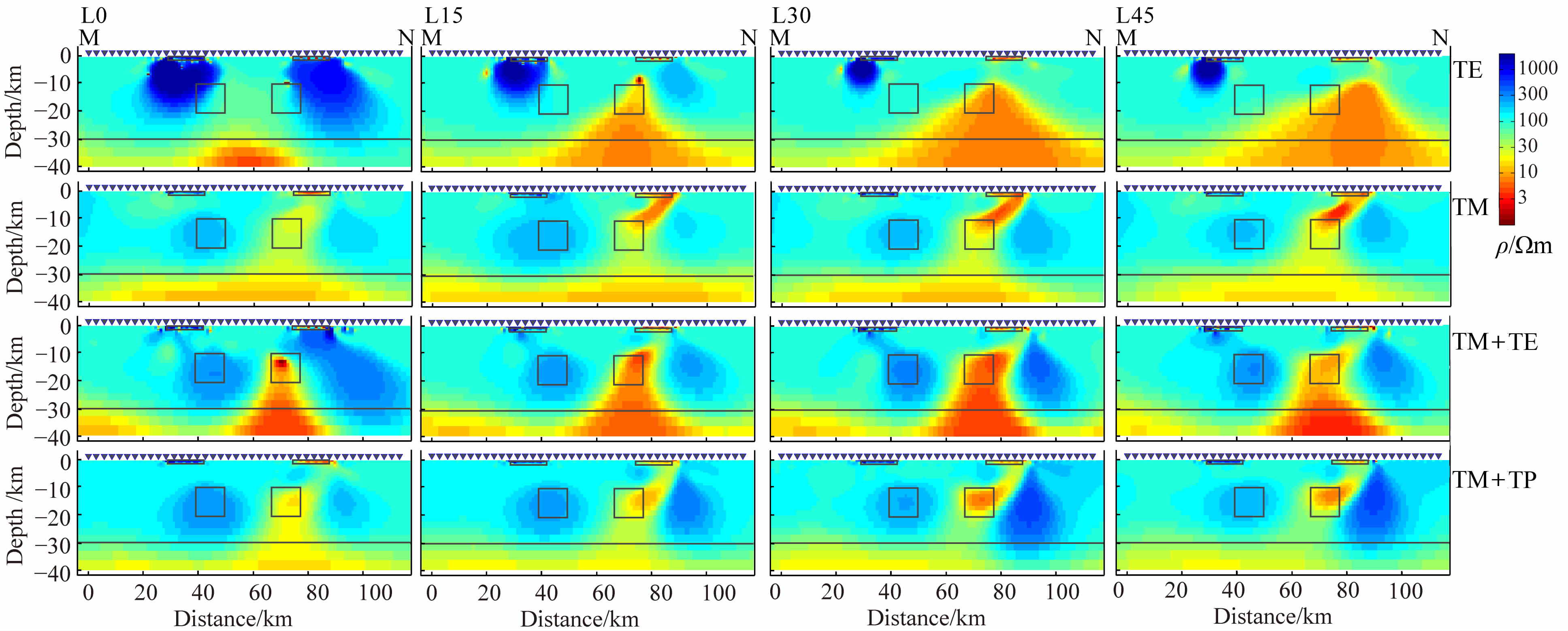
|
图 8 低阻-高阻理论模型响应旋转到垂直剖面方向的二维NLCG 反演结果.从左至右:走向分别为与垂直剖面方向相差0°,15°,30°,45°;从上到下,反演模式分别为TE,TM,TM+TE,TM+TP.图中的方框标示了异常体的原始位置 Fig. 8 2D NLCG inversion result of the L-H models.Left to right: results of models with strikes of 0°,15°,30°,45° degree from the orthogonal direction of the profile.Up to down: results in TE,TM,TM+TE and TM+TP mode.Gray boxes indicate the location of the anomalies in the forward models |
对于低阻-高阻模型,二维方法的各个模式的结果都不是十分理想;对于这一模型,三维反演是否能够得到较好的结果呢?由于目前三维反演相对耗费资源较大,计算时间较长,因此在本研究中仅仅对L0模型的响应进行了三维反演,三维反演是采用Siripunvaraporn等开发的三维数据空间Occam 算法代码WSINV3DMT[22],使用Zxy,Zyx,Zxx 和Zyy的全阻抗张量进行反演.在数据方面为了便于对比,采用与二维反演相同的站点与频点进行反演.图 9为L0模型三维反演测线方向的电阻率断面.由三维反演结果可见,三维反演对于低阻目标体的位置和电阻率的反映都相对较好,对于高阻体的反映虽然较差,但仍好于二维反演的结果.然而,三维反演的结果相对二维反演有较多的小尺度的冗余构造和虚假异常,也可能给实际的解释工作带来一定的问题.这一方面是由于三维反演的最优化问题的模型网格数要远高于二维方法,造成了其欠定性远远高于二维反演,反演的不确定性较多;另一方面也可能是由三维反演程序本身相对二维反演程序仍不成熟,反演的稳定性较差造成的.
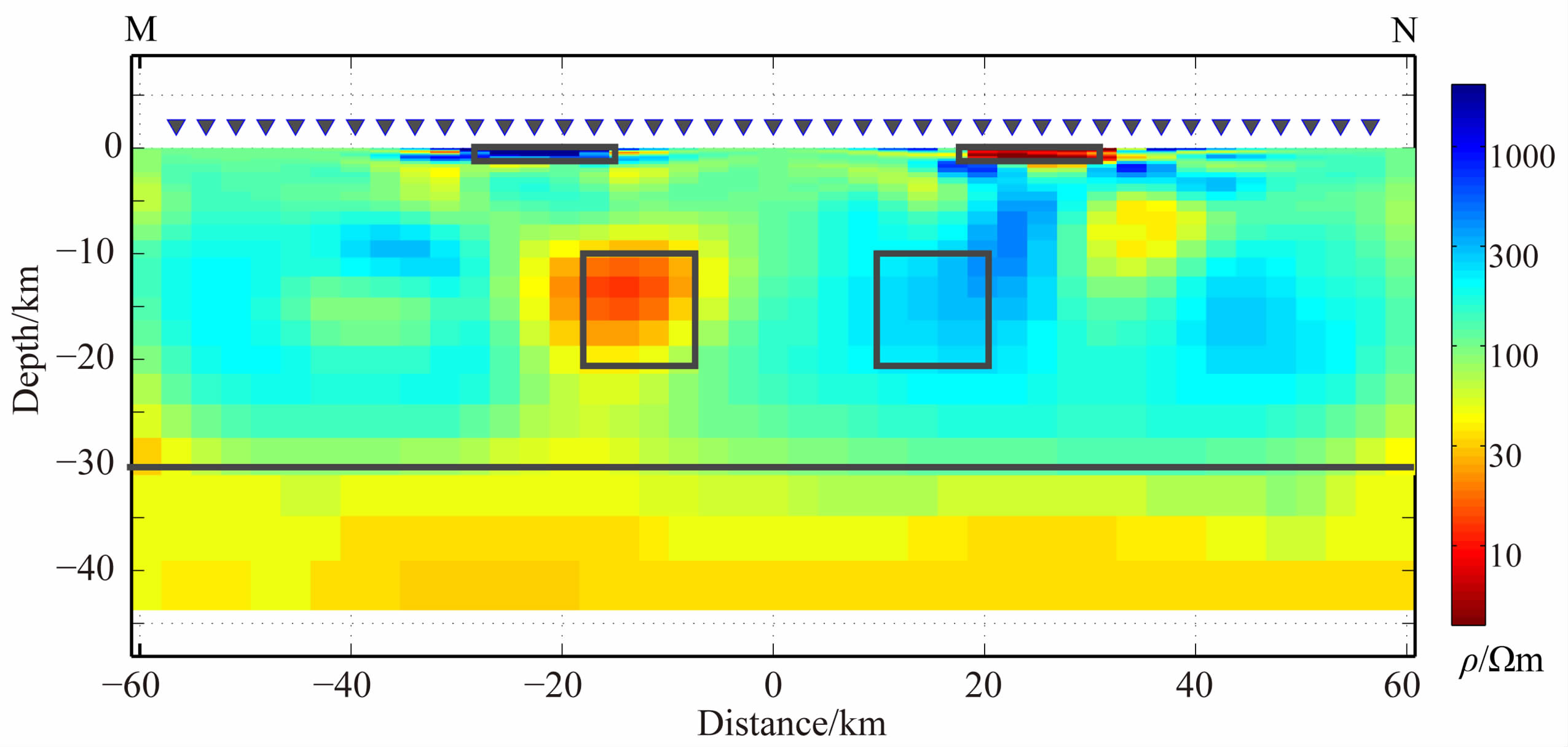
|
图 9 低阻-高阻理论模型L0响应的三维反演结果测线方向的电阻率剖面.图中的方框标示了异常体的原始位置 Fig. 9 Profile section of 3D WSINV3DMT inversion result for the L-H model L0.Gray boxes indicate the location of the anomalies in the forward models |
图 10为目标体A 为高阻异常、B 为低阻异常时,将阻抗张量和磁倾子旋转到电性主轴方向之后L0-L45模型响应的反演结果.此时,高阻目标体受上方的高阻三维异常影响,低阻目标体受其上方的低阻三维异常影响,相对于低阻-高阻模型,各模式反演结果对两个目标体的总体反应都较好,这与之前数据分析中模型响应的畸变较小的结果相吻合.
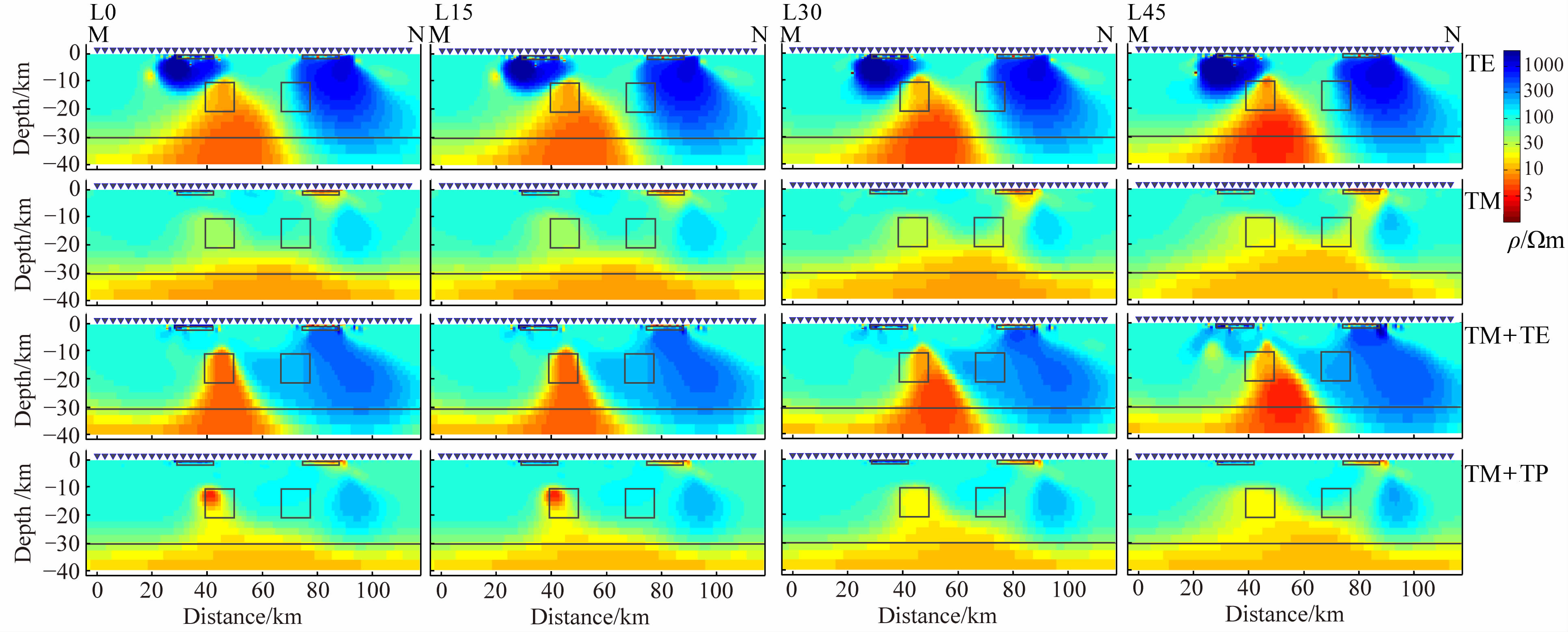
|
图 10 高阻-低阻理论模型响应旋转到电性主轴方向的二维NLCG 反演结果.从左至右:走向分别为与垂直剖面方向相差0°,15°,30°,45°;从上到下,反演模式分别为TE,TM,TM+TE,TM+TP,图中的方框标示了异常体的原始位置 Fig. 10 2D NLCG inversion result of the H-L models.Left to right: results of models with strikes of 0°,15°,30° 45° degree from the orthogonal direction of the profile.Up to down: results in TE,TM,TM+TE and TM+TP mode.Gray boxes indicate the location of the anomalies in the forward models |
对于反演结果对电性主轴的稳定性,总体而言,高阻-低阻模型要高于前述的模型.在模式选择方面,和之前的模型类似,单独TE 模式的反演结果较不稳定,受到电性主轴方向变化的影响很大,反演结果同样难以反映真实地下模型;TM 模式的反演结果较为稳定,其异常体的边界较不清晰,但已经可以较好地同时分辨出低阻和高阻二维体,但随着电性主轴方向逐渐偏离垂直剖面方向;TM 反演的结果也同样受到了三维局部异常体的影响,高导二维体的异常反映受到了畸变.TM+TE 模式的反演结果对异常体的边界判断较为清楚,但也伴随着较多的虚假异常和冗余构造;TM+TP 模式对于本模型的反演结果与TM 模式非常类似,但对异常体的边界有着更好的约束,受到畸变的扭曲作用也相对较小,但仍然有假异常出现.
图 11为将阻抗张量和磁倾子旋转到垂直剖面方向时L0-L45各模型响应的反演结果.除去TE 模式之外,旋转到垂直剖面方向的各模式的结果并无太大区别.具体而言,其反演的结果同样可以分为两组:对于TE 和TM+TE 联合模式,由于TE 模式对二维假设要求较高,旋转到剖面方向之后,二维假设不再有效,因此反演的结果要差于旋转到主轴方向的结果;对于TM 和TM+TP 联合模式,由于TM 模式对二维假设要求较低,因此旋转到剖面方向之后,反演的结果并无太大变化.实际上,对比上一组反演中TM 和TM+TP模式的结果,其异常体的畸变有所减小,但同时,其边界也变得更加模糊.这让TM 或TM+TP模式似乎成为了一种比较“保险"的反演方式,即不容易得到分辨率高的地下电性结构,但也不容易得到错误结论.
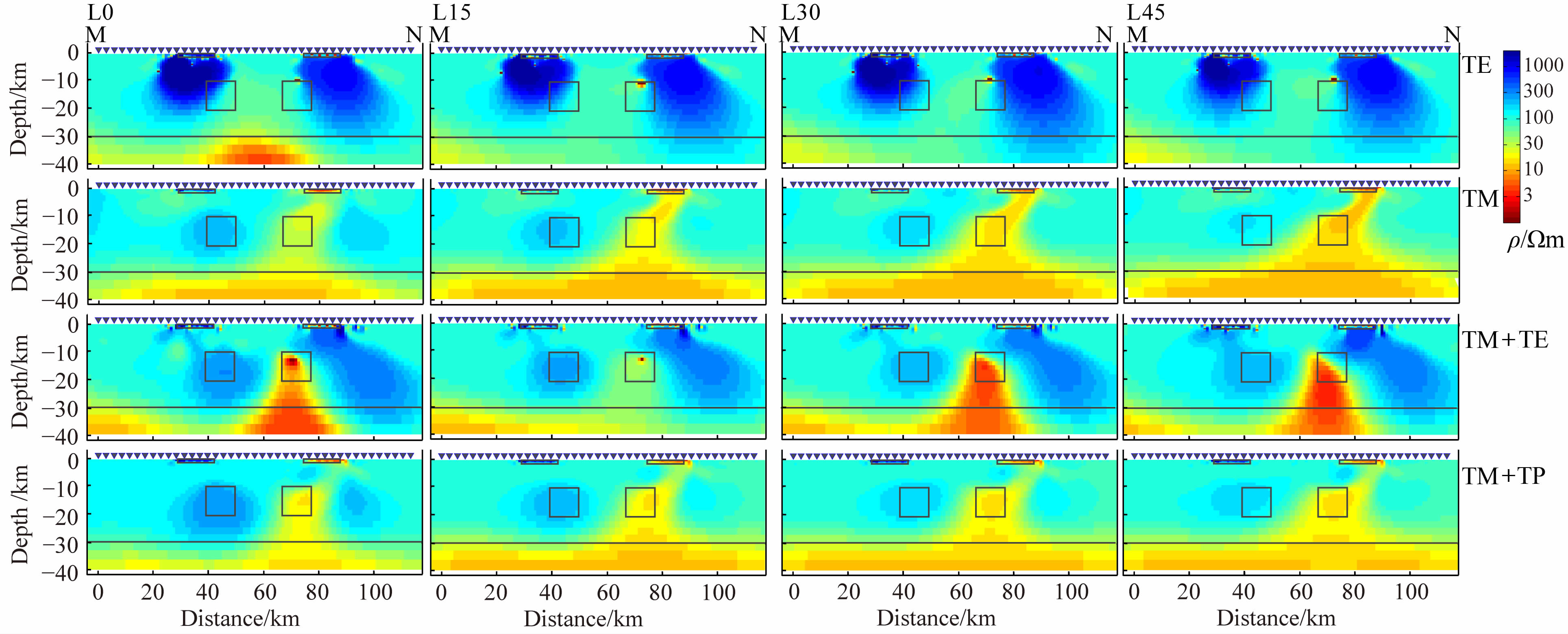
|
图 11 高阻-低阻理论模型响应旋转到垂直剖面方向的二维NLCG 反演结果.从左至右:走向分别为与垂直剖面方向相差0°,15°,30°,45°;从上到下,反演模式分别为TE,TM,TM+TE,TM+TP,图中的方框标示了异常体的原始位置 Fig. 11 2D NLCG inversion result of the H-L models.Left to right: results of models with strikes of 0°,15°,30° 45° degree from the orthogonal direction of the profile.Up to down: results in TE,TM? TM+TE and TM+TP mode.Gray boxes indicate the location of the anomalies in the forward models |
对于高阻-低阻模型,在本研究中同样针对L0模型的响应使用WSINV3DMT 方法进行了三维反演测试.其反演参数与之前的低阻-高阻模型中的参数相同.图 12为三维反演在L0模型测线方向的电阻率断面.由图可见,相对于二维反演的结果,三维反演的结果中高阻和低阻异常体的位置都有所偏差,相对的冗余构造也较多,主要的电性结构还是可以较为准确地反映出来.由于在此模型中,三维异常体对于区域的影响较小,响应相对于更接近二维,所以利用二维方法进行反演可能相对更为适合和准确.
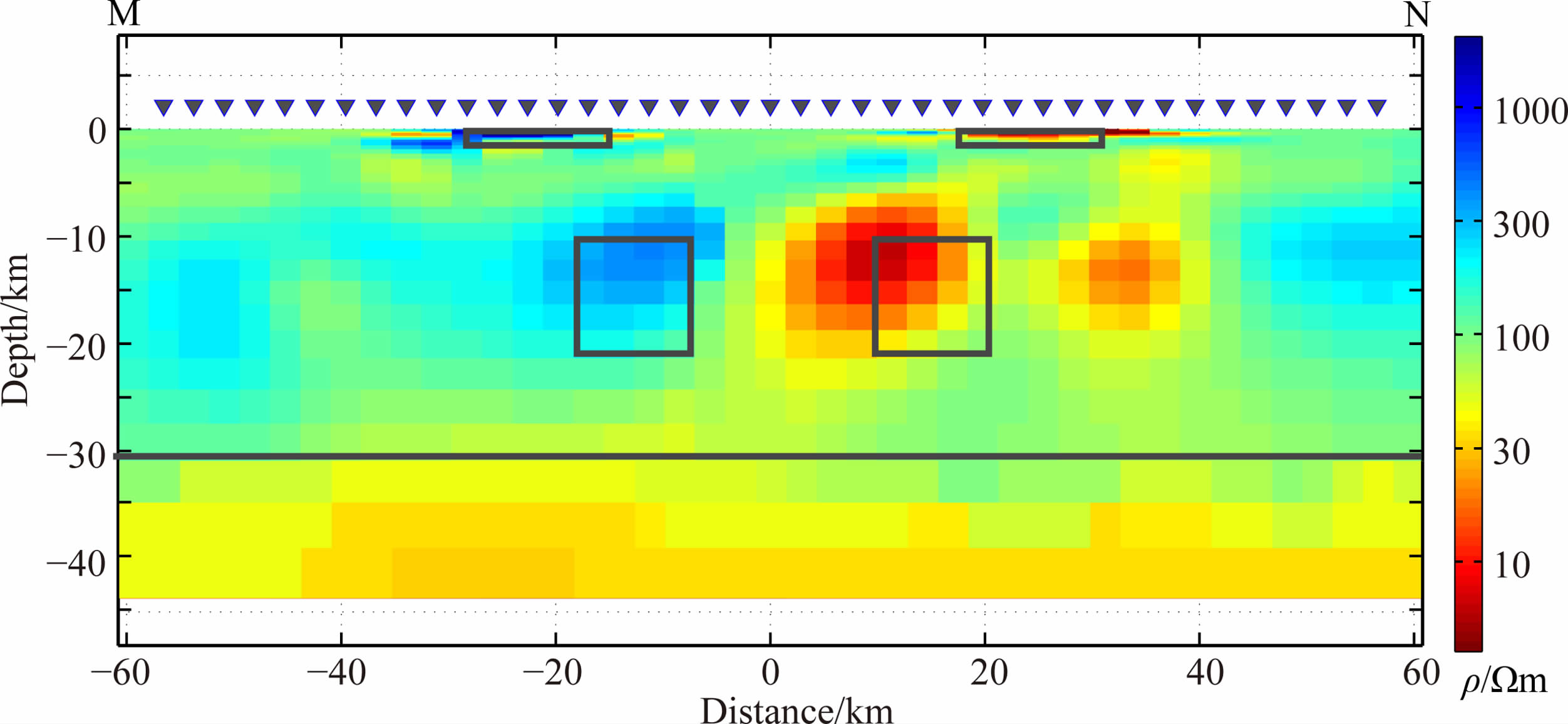
|
图 12 高阻-低阻理论模型L0响应的三维反演结果测线方向的电阻率剖面.图中的方框标示了异常体的原始位置 Fig. 12 Profile section of 3D WSINV3DMT inversion result for the H-L model L0.Gray boxes indicate the location of the anomalies in the forward models |
我们截取了华北西部某地的大地电磁测深标准网阵列的一部分测点进行了不同模式的二维对比反演实验,使用的参数与合成数据反演时的相同.由于实际地下的电性结构是未知的,无法像正演模拟中一样事先知道真实的电性分布,在此,我们使用三维反演的结果作为基准模型,进行了二维反演不同模式的对比(图 13).不难看出,和之前进行的合成数据的反演结果相似,TE 模式的反演结果对低阻反应较为明显,电阻率界面较为清晰,但冗余构造相对其他模式较多,容易出现不真实的电阻率突变;TM模式的反演结果对高阻体反应更为明显,且冗余结构较少,但反演过于平滑,是所有模式中最缺乏细节的;TM+TE 模式集合了TM 与TE 模式的特点,与三维反演的结果相近,但同样对异常体,尤其是低阻体的下界缺乏约束;TM+TP 模式的结果同样较为平滑,和三维反演的结果最为相似,但和三维反演相比,其对于垂向的分辨率仍然相对较低.

|
图 13 实测数据二维反演各个模式与三维反演结果测线方向的电阻率剖面的对比.从上到下分别为TE 模式,TM 模式,TM+TE 模式,TM+TP模式,WSINV3DMT 三维反演 Fig. 13 Comparison between profile sections from different 2D inversion modes and 3D inversion on field data.Up to down: inversion result from TE,TM,TM+TE,TM+TP,3D WSINV3DMT |
总体而言,对于三维模型的二维反演,TM 模式对地下结构的二维假设要求较低,不容易受到局部三维电性畸变的影响,反演结果一般比较符合真实情况,也较少出现冗余构造或虚假异常;然而在另一方面,TM 模式的反演模型断面通常较为平滑而分辨率较低,有时难以精确分辨异常体的尺度及位置,不太适合单独进行解释工作.TE 模式最容易受到三维结构体的影响而出现虚假异常,甚至可能反演出完全不同于地下真实电性构造的结果.但TE 模式在地下模型较为符合二维假设的情况下,其异常界面相对较为清楚,容易分辨构造位置.TM+TE模式同时具有TM 和TE 模式的特性,其分辨率通常高于TM 模式,受三维畸变的影响也通常低于TE 模式,但受到TE 模式数据的影响,仍然容易产生不真实的构造,因此进行解释时需要特别注意.由于磁倾子不易受电场畸变的影响,TM+TP模式的反演结果通常不易受局部三维结构的畸变,在多数情况下最为接近真实结构,并且其分辨率,尤其是垂向分辨率较单独的TM 模式为高,在多数情况下,尤其是电性主轴方向不易确定时应优先考虑.对于电性主轴旋转方向的问题,研究结果表明,当垂直剖面方向与主构造方向相差不大的情况下(<15°),将主轴旋转至垂直剖面方向的二维反演结果与主构造方向的反演结果都可以较好地还原理论模型,在大的构造的反映上并无太大差异.而当垂直剖面方向与主构造相差较大时,反演的结果则呈现两极分化的趋势.一方面,对于TE 和TM+TE 模式而言,旋转到主构造方向的反演效果要好于垂直剖面方向,且主轴方向与垂直剖面方向相差越大,其优势越明显.另一方面,对于TM 和TM+TP 模式而言,旋转到主构造方向的反演结果相对旋转到垂直剖面方向的结果并无明显优势,而在某些情况前者可能还会差于后者,这一点在三维畸变更强的情况中表现的尤为明显.
因此,综上所述,在研究区域三维性较强,电性主轴方向难以确定的情况下,将阻抗张量和倾子信息旋转到剖面方向,进行二维TM+TP或TM 模式的反演可以较好地还原地下电性结构信息;对于单独的TE 模式反演则应予以避免;而在二维性较为明显的情况下,适宜将阻抗张量和倾子信息旋转到电性主轴方向,使用TM+TE 模式得到分辨率更高的地下结构.然而,同时我们也应注意到,尽管本文中进行了大量的正反演工作,但相对千变万化的真实地下介质,本研究中提出的二维/三维模型体仍然较为简单,在实际工作中进行的实测资料处理解释时也难免挂一漏万,遇到特殊情况,需要在解释时特别注意以免得出错误结论.
致谢笔者在此感谢AlanJones教授提供研究中使用的阻抗张量分解程序以及WeerachaiSiripunvaraporn教授提供三维反演代码,并对审稿专家给予的意见与建议表示衷心感谢.
| [1] | Xiao Q B, Zhao G Z, Wang J J, et al. Deep electrical structure of the Sulu orogen and neighboring areas. Science in China Series D: Earth Sciences , 2009, 52(3): 420-430. DOI:10.1007/s11430-009-0013-3 |
| [2] | Zhdanov M, Wan L, Gribenko A. Large-scale 3D inversion of marine magnetotelluric data: Case study from the Gemini prospect, Gulf of Mexico. Geophysics , 2011, 76(1): 77-87. DOI:10.1190/1.3526299 |
| [3] | Jones A G. Three-dimensional galvanic distortion of three-dimensional regional conductivity structures: Comment on "Three-dimensional joint inversion for magnetotelluric resistivity and static shift distributions in complex media" by Yutaka Sasaki and Max A. Journal of Geophysical Research , 2011, 116: B12104. DOI:10.1029/2011JB008665 |
| [4] | Garcia X, Ledo J, Queralt P. 2D inversion of 3D magnetotelluric data: The Kayabe dataset. Earth Planets and Space , 1999, 51(10): 1135-1143. DOI:10.1186/BF03351587 |
| [5] | Roy K K, Dey S, Srivastava S, et al. What to trust in a Magnetotelluric Model?. J.Ind.Geophys.Union Jan., , 2014, 8(2): 157-171. |
| [6] | Jones A G. The problem of current channelling: a critical review. Geophysics Surveys , 1984, 6(1-2): 79-122. |
| [7] | Wannamaker P E, Hohmann G W. Magnetotelluric responses of three-dimensional bodies in layered earths. Geophysics , 1984, 49(9): 1517-1533. DOI:10.1190/1.1441777 |
| [8] | Park S K, Mackie R J. Crustal structure at Nanga Parbat, northern Pakistan, from magnetotelluric soundings. Geophysical Research Letters , 1997, 24(19): 2415-2418. DOI:10.1029/97GL02147 |
| [9] | Ledo J, Queralt P. Effects of galvanic distortion on magnetotelluric data over a three-dimensional regional structure. Geophysical Journal International , 1998, 132(2): 295-301. DOI:10.1046/j.1365-246x.1998.00417.x |
| [10] | Ledo J. 2-D Versus 3-D magnetotelluric data interpretation. Surveys in Geophysics , 2005, 26(5): 511-543. DOI:10.1007/s10712-005-1757-8 |
| [11] | 胡祖志, 胡祥云, 何展翔. 三维大地电磁数据的二维反演解释. 石油地球物理勘探 , 2005, 40(3): 353–359. Hu Z Z, Hu X Y, He Z X. Using 2-D interpretation of 3-D MT data. Oil Geophysical Prospecting (in Chinese) , 2005, 40(3): 353-359. |
| [12] | Jones A G. Electromagnetic interrogation of the anisotropic Earth: Looking into the Earth with polarized spectacles. Physics of the Earth and Planetary Interiors , 2006, 158(2-4): 281-291. DOI:10.1016/j.pepi.2006.03.026 |
| [13] | Ogawa Y. On two-dimensional modeling of magnetotelluric field data. Surveys in Geophysics , 2002, 23(2-3): 251-272. |
| [14] | 蔡军涛, 陈小斌. 大地电磁资料精细处理和二维反演解释技术研究(二)——反演数据极化模式选择. 地球物理学报 , 2010, 53(11): 2703–2714. Cai J T, Chen X B. Refined techniques for data processing and two-dimensional inversion in magnetotelluric Ⅱ: Which data polarization mode should be used in 2D inversion. Chinese J.Geophys. (in Chinese) , 2010, 53(11): 2703-2714. |
| [15] | 陈小斌, 赵国泽, 马霄. 关于MT二维反演中数据旋转方向的选择问题初探. 石油地球物理勘探 , 2008, 43(1): 113–118. Chen X B, Zhao G Z, Ma X. Preliminary discussion on selecting rotation direction in 2-D MT inversion. Oil Geophysical Prospecting (in Chinese) , 2008, 43(1): 113-118. |
| [16] | Mackie R L, Madden T R. Three-dimensional magnetotelluric inversion using conjugate gradients. Geophysical Journal International , 1993, 115(1): 215-229. DOI:10.1111/gji.1993.115.issue-1 |
| [17] | Groom R W, Bailey R C. Decomposition of magnetotelluric impedance tensors in the presence of local three-dimensional galvanic distortion. Journal of Geophlsical Research , 1989, 94(B2): 1913-1925. DOI:10.1029/JB094iB02p01913 |
| [18] | Mcneice G W, Jones A G. Multisite, multifrequency tensor decomposition of magnetotelluric data. Geophysics , 2001, 66(1): 158-173. DOI:10.1190/1.1444891 |
| [19] | De Groot-Hedlin C, Constable S. Occam's inversion to generate smooth, two-dimensional models from magnetotelluric data. Geophysics , 1990, 55(12): 1613-1624. DOI:10.1190/1.1442813 |
| [20] | Siripunvaraporn W, Egbert G. REBOCC: An Efficient data-subspace inversion method for 2-D magnetotelluric data-subspace inversion method for 2-D magnetotelluric data.. Geophysics , 200, 65(3): 791-803. |
| [21] | Rodi W, Mackie R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion. Geophysics , 2001, 66(1): 174-187. DOI:10.1190/1.1444893 |
| [22] | Siripunvaraporn W, Egbert G, Lenbury Y, et al. Three-dimensional magnetotelluric inversion: data-space method. Physics of the Earth and Planetary Interiors , 2005, 150(1-3): 3-14. DOI:10.1016/j.pepi.2004.08.023 |
 2012, Vol. 55
2012, Vol. 55


