2. 华中光电技术研究所—武汉光电国家实验室,武汉 430073;
3. 武汉大学地球空间环境与大地测量教育部重点实验室,武汉 430079;
4. 武汉大气遥感国家野外科学观测研究站,武汉 430079
2. Huazhong Institute of Electro-Optics-Wuhan National Laboratory for Optoelectronics, Wuhan 430073, China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan 430079, China;
4. State Observatory for Atmospheric Remote Sensing, Wuhan 430079, China
大气分子纯转动拉曼谱线的强度和温度的关系遵从Boltzmann 分布[1-4].在1972 年,Cooney 提出利用这个原理探测大气的温度[1].1983 年,Arshinov用一个双光栅单色仪探测纯转动拉曼谱,并反演出了温度[2].此后,世界各地陆续建立了多台纯转动测温激光雷达,探测的精度高于±1K[5-7].
除了测温外,纯转动拉曼激光雷达还可以探测大气气溶胶的消光系数.Whiteman和Miles报道了由于全部的转动拉曼谱线之和是与温度无关的,不需要假设气溶胶的消光与散射比值,就可得到大气气溶胶的后向散射比[8-9].但是,要提取全部的转动拉曼信号是十分困难的,这不仅需要分辨率很高的光谱仪,而且量子数较低的谱线(J=0 和J=1)与Rayleigh & Mie信号很接近(对532nm 的发射光,间隔仅有0.35nm),要把它们抑制掉也十分困难.还有,N2 和O2 的纯转动谱重叠在一起,信号的提取更加困难.Arshinov等人用F-P 干涉仪透过率曲线的梳状结构将空气中N2和O2 的纯转动谱分离开来[5, 10].用这种方法,每支谱线的透过率不相同,会导致提取的总的纯转动拉曼信号的扭曲.本文提出获取纯转动拉曼的单支谱,计算出不同温度下单支谱占全部拉曼谱的比重.然后根据纯转动反演的温度结果,可以得到大气各个高度上的全部拉曼谱的信号强度,进一步反演气溶胶的消光系数和后向散射系数.
2 氮分子和氧分子的纯转动谱的性质激光雷达方程一般可写为:$N\left( z \right)=PC\frac{\beta }{{{z}^{2}}}{{T}^{2}}_{r}\left( z \right)$,其中N(z)是回波光子数,P是激光发射的功率,C是激光雷达常数,z是探测目标的距离,Tr 是大气透过率,β 是后向散射系数.对于纯转动拉曼散射,βλJ(λJ表示转动量子数为J的纯转动拉曼散射的波长)有:

|
(1) |
n是氮分子或氧分子的数密度;σJ→J′ 是微分后向散射截面;FJ是分子的转动配分函数,其物理意义是在初始转动量子态J上的分子所占的百分比,因此,$\sum\limits_{J=0}^{\infty }{{{F}_{J}}=1}.$

|
(2) |
其中Q渐近等于$\frac{{{\left( 2I+1 \right)}^{2}}kT}{2hcB}$;gI是一个统计权重因子,由原子核的自旋决定;B0 是转动常数;I是核自旋量子数;它们的取值见表 1.
|
|
表 1 参数列表 Table 1 Parameters |
后向微分散射截面的表达式为:
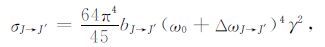
|
(3) |
其中,bJ→J′ 是对于线性分子的Placzeek-Teller系数;ω0 是激发光的波数(cm-1),ΔωJ→J′ 是转动拉曼的频移;γ 是分子极化率张量的各向异性部分[11].方程(1)的完整表达式为:
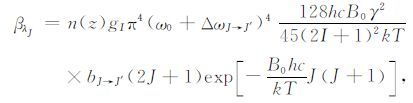
|
(4) |

|
(5) |
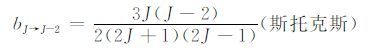
|
(6) |
至此,我们可以计算出N2 和O2 的纯转动拉曼谱散射相对强度廓线(图 1).

|
图 1 N2 和O2 的纯转动拉曼谱 Fig. 1 Pure rotational Raman spectra for N2 and 02 |
从图 1中,我们不难发现,相邻转动谱线的间距是非常小的,N2 大约有8cm-1,O2 大约有11.5cm-1,再加上它们之间相互交叠,对于单支谱的提取就更有难度了.以往的纯转动拉曼激光雷达,多是提取的N2 分子J=6和J=12的两支谱进行测温[5, 12],中国科学院安徽光机所也利用这个原理成功研制出对流层测温纯转动Raman 激光雷达(http://lidar.aiofm.ac.cn/AML.htm).但是通过图 1,可以清楚地看到,N2 分子J=6 和J=12 这两支谱都和O2分子的纯转动谱线距离很近,间距分别只有0.8cm-1和1.05cm-1.利用光栅等分光手段,是无法提取这两条单支谱的.因此,该方案并不是提取的单支纯转动谱,而是多条谱线的和,在后续的温度反演过程中,需要假设多支谱加权求和后对温度近似有相同的函数关系.
若提取两个转动拉曼单支谱J1 和J2,由激光雷达方程与后向散射系数的表达式(4),可得:
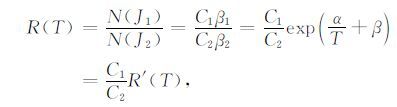
|
(7) |
其中
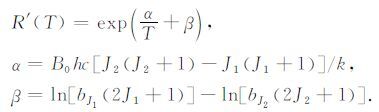
|
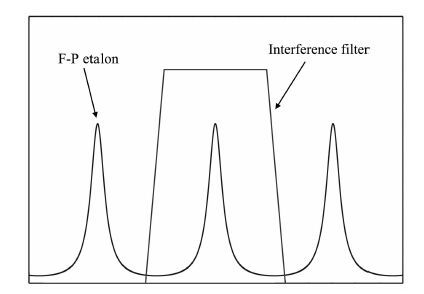
从图 1还可以看出,N2 的J=4和J=14这两支谱相对比较独立,两侧的谱线间隔相对比较大.其中J=4的这一支,两侧的O2 谱线与它的距离分别为6.4cm-1和5.1cm-1;J=14 的这一支,两侧的O2 谱线与它的距离分别为5.5cm-1和6.0cm-1.在532nm 波长附近,可以选用半高宽(FWHM)小于55pm 的F-P标准具,配合干涉滤光片提取这两支转动谱线(图 2).F-P 标准具的带外抑制有2~3个数量级,可以有效抑制附近的O2和N2的纯转动谱;干涉滤光片有7个数量级的带外抑制,加上F-P标准具一共有9 个数量级的带外抑制,能够对Rayleigh & Mie信号以及背景光有很好的抑制.需要注意的是,F-P的透过率曲线十分精细,因此需要对激光器进行稳频,或者激光器本身的频率足够稳定,在一天的时间里频率漂移不超过1pm.
|
图 2 F-P标准具和干涉滤光片叠加使用提取纯转动单支谱 Fig. 2 Superposition of the interference filter and F-P etalon to extract single pure rotational Raman branch |
到目前为止,已有的纯转动拉曼激光雷达,提取的都是纯转动的多支谱.利用多支谱反演大气温度,需要假设两个通道的比值仍然有公式(7)的关系[13-14],这在数学上不能严格成立.
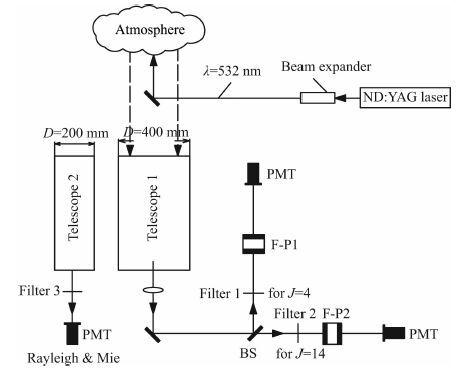
4 气溶胶的反演利用纯转动拉曼谱反演气溶胶,需要在普通的转动拉曼雷达上,增加一个Rayleigh & Mie通道,如图 3所示.本文选用的方式是增加一个由小口径望远镜(200 mm)构成的接收系统,形成一个Rayleigh & Mie通道,这样做的好处是不用改动已有雷达的后继光路,也不会损失纯转动通道的能量.
|
图 3 系统结构框图BS,分光镜;PMT,光电倍增管;F-P,法布里-珀罗标准具. Fig. 3 Schematic diagram of pure rotational Raman lidar setupBS,beam splitter; PMT,photomultiplier tubes; F-P, Fabry-Perot etalon. |
F-P透过率曲线随着环境温度和压强的变化,会有一定的改变,这对反演大气的温度有十分不利的影响.为了保证F-P 透过率曲线的稳定,需要对它经行温度[15]和压强的控制[16].
如图 3所示,有3个通道,它们的激光雷达方程分别为:
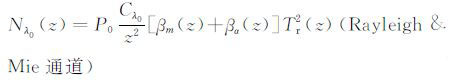
|
(8) |
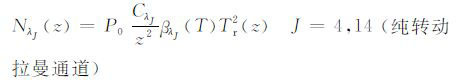
|
(9) |
βm是大气分子的后向散射系数,βα 是气溶胶的后向散射系数,βλJ是转动量子数为J的纯转动拉曼后向散射系数.
将方程(8)和(9)相除,整理可得:
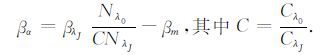
|
(10) |
对于βm,有βm=n(z)σm,其中σm是大气分子的后向微分散射截面,是一个固定的值;对于βλJ,因为大气中N2 占总含量的78%,有βλJ=0.78×n(z)FJ(T)σλJ,σλJ不依赖于温度,J确定的情况下,σλJ就是一个常数,FJ在第2部分已经叙述过.则βzλJ和βm的关系有:
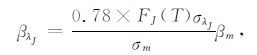
|
(11) |
将方程(11)代入(10),并整理有:
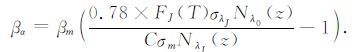
|
(12) |
要求解这个方程,要想办法将常数C消掉.我们找比较晴好的天气,选取一个比较高的高度z0,在这个高度上,要求没有气溶胶或者气溶胶含量极低,则βα$\cong $0,代入方程(12)求解C,有:
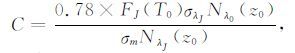
|
(13) |
将方程(13)代入方程(12),有:
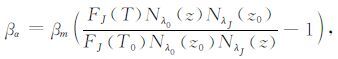
|
(14) |
将方程(2)代入方程(14),有:
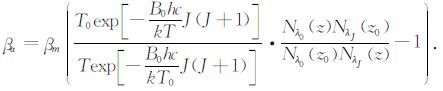
|
(15) |
方程(15)中,βm可以通过大气模式得到;J的取值可以为4或者14,一般选用4,因为J=4的这支谱散射强度更大一些,可以获得更高的信噪比;B0、h、c、k都是已知的常数,因此,只要事先反演出大气的温度来,就可以求出大气的后向散射系数.βα求出来以后,将结果代入方程(8)并将大气透过率Tr 展开可以求出气溶胶的消光系数,然后可以得到气溶胶的消光后向散射比.气溶胶的消光后向散射比可以分析气溶胶的成分和性质.
5 误差分析该方法对气溶胶的反演是以温度数据已知为前提的.温度反演的误差对于气溶胶反演的误差有着直接的影响,因此我们先计算温度反演的误差,然后再讨论气溶胶反演的误差.
5.1 信噪比由方程(7)出发,有:

|
(16) |
如果ΔR/R是很微小的变化,并且是由光子噪声的起伏决定的,则两个纯转动通道的噪声是相互独立的,即

|
由该式给出信噪比的表达式为:
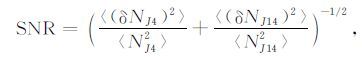
|
(17) |
〈(δR)2〉、〈(δNJ4)2〉和〈(δNJ14)2〉分别是R、NJ4 和NJ14 的方差.假设NJ4 和NJ14 服从泊松分布,则
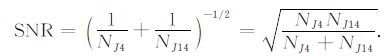
|
(18) |
假设两个纯转动通道F-P 的峰值透过率为33%,PMT 的量子效率100%.并且在10km 处纯转动量子数J=4 的回波信号经过望远镜后有12000个光子.分光镜(BS)对J=4通道的反射率为k,对J=14 通道的透过率为1-k,则CJ4/CJ14 =k/(k-1).对于方程(18),就有:
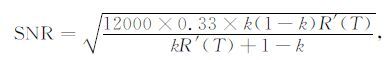
|
(19) |
其中,NJ4 =12000×0.33×k,NJ14 = (1-k)/R′(T)k.计算三个温度下的R′(T),R′(200)=4.258,R′(260)=2.910,R′(300)=2.201.从图 4 中可以看出,当k=0.4的时候有比较高的信噪比,信噪比可以有40.所以分光镜(BS)应选取40/60的.
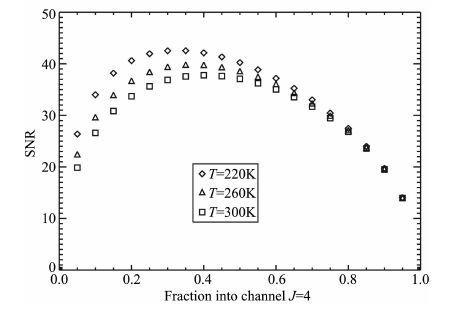
|
图 4 假设纯转动量子数J=4通道的回波信号经过望远镜后光子数为12000,分光镜(BS)的反射率k和信噪比的函数关系 Fig. 4 Assuming a total of 12000 photons, resultingfrom pure rotational Raman spectrum of J = 4 branch, pass through the telescope, the signal-to-noise ratio as afunction of the reflectivity of beamsplitter, 0<k<1 |
从公式(7)出发,有:
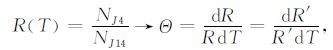
|
(20) |
计算结果如图 5,随着温度的升高,灵敏度有所下降.220K 时的灵敏度为0.0115K-1,300K 时的灵敏度为0.006K-1.
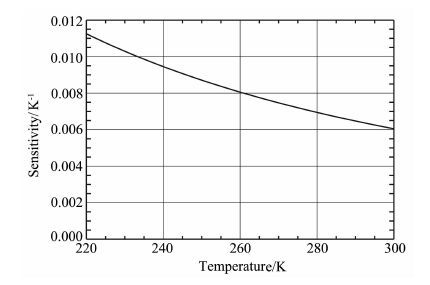
|
图 5 不同温度下反演的灵敏度 Fig. 5 Sensitivity from inversion withdifferent temperatures |
温度反演的误差由信噪比和灵敏度共同决定,用公式表达为:
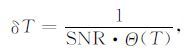
|
(21) |
这其中,信噪比(SNR)与回波光子数密切相关,在不同高度上,激光雷达探测到的光子数是不同的,与高度的平方成反比,与大气的密度成正比.根据5.1节的叙述,如果在10km 处,纯转动量子数J=4的回波信号经过望远镜后有12000 个光子,k的取值为0.4,F-P的峰值透过率为33%,PMT 的量子效率为100%,则PMT 探测到的光子数为NJ4 = 12000×0.33×0.4=1600个[5, 7].根据1976年美国标准大气模式的密度数据,可以模拟计算出其它高度上的回波光子数,如图 6a所示.由此可以计算其它高度上的信噪比(SNR),并根据温度的数据计算这些高度上的灵敏度Θ,将计算的结果代入公式(21)中计算出不同高度上温度反演的误差,结果如图 6b所示.模拟计算出的结果显示,在10km 以内的范围,温度的误差随着高度上升而增加,最大值为±2.3K,最小值为0,实际情况也大致如此[7, 17],在10km 以下,误差都是小于±2K 的.
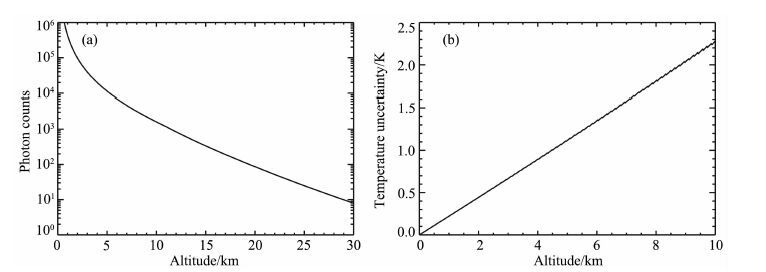
|
图 6 (a)假设10km 处,转动量子数为J=4的通道探测到的光子数为1600,根据美国标准大气模式计算的其它高度上的回波光子数.(b)根据信噪比和温度灵敏度计算的不同高度上温度反演的误差 Fig. 6 (a) Simulated photon counts of J = 4 channel by USSA1976 with assuming that there are 1600 photons detected byideal photodetecter at 10 km.(b) Temperature uncertainty based on signal-to-noise ratio and temperature sensitivity |
由公式(12)出发,将公式右边的βm移到左边,有:
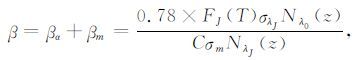
|
(22) |
其中,J的取值是4,σλJ4、σm和C都是常数,但是C是根据雷达实际测量的结果推导出来的,有误差,因此在计算时必须要考虑:
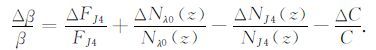
|
(23) |
根据方程(13),有:
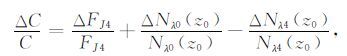
|
(24) |
将方程(24)代入方程(23)有:
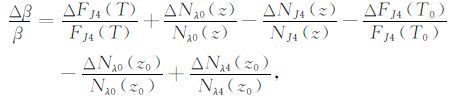
|
因此,误差的最大值可以有:
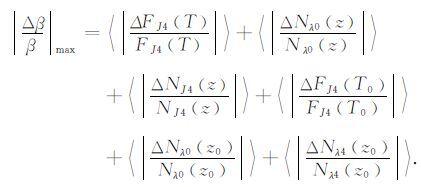
|
(25) |
对于〈|ΔFJ4/FJ4|〉项,可以通过方程(2)计算出来(图 7).本文计算了三个温度(220K,260K,300K)下,温度误差对于气溶胶反演误差的影响.从图 7可以看出,在温度为220K,温度误差为±3K 时,有最大的误差1%.假设参考高度z0 选在8km, 实际情况中[5, 7, 17],温度的反演误差都是小于±2K的,根据1976年美国标准大气模式,大气温度应该在236K 左右.因此,该项引入的误差在0.7% 以内.在8km 以下的高度,随着温度的升高,温度反演误差的下降,该项引入的误差会越来越小.因此〈|ΔFJ4(T)/FJ4(T)|〉+〈|ΔFJ4(T0)/FJ4(T0)|〉小于1.4%.
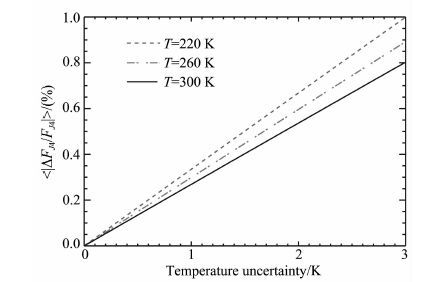
|
图 7 不同温度下(220K,260K,300K),温度误差对于气溶胶探测的影响 Fig. 7 Influence of temperature errors on aerosol detection at different temperatures (220 K,260 K,300 K) |
对于〈|ΔNλ0/Nλ0 〉项,假设Nλ0 服从泊松分布,有〈|ΔNλ0/Nλ0|〉=$\sqrt{1/{{N}_{\lambda 0}}}$.在8km 处,如果Nλ0 有1600个光子计数以上,则该项引入的误差在2.5%以内.在8km 以下,随着高度的下降,回波光子数增加,该项引入的误差也会越来越小.因此〈|ΔNλ0(z)/Nλ0(z)|〉+〈|ΔNλ0(z0)/Nλ0(z0)|〉小于5%.
对于〈|ΔNJ4/NJ4|〉项,对气溶胶反演误差的影响与〈|ΔNλ0/Nλ0|〉项相同,主要取决于回波光子数的多少.因此,〈|ΔNJ4(z)/NJ4(z)|〉+〈ΔNJ4(z0)/NJ4(z0)|〉也小于5%.
根据βα 和βm的关系βα =β-βm,若βα 比βm小,或者它们的值差不多,则βm的误差对βα 的影响很大,有可能求出负值.而且βα 值很小的区域,都在离地面比较高的高度上,8km 处β 的误差本身就有11.4%,再加上βm是根据大气模式计算出来的,与实际情况也有误差,求解出来的βα 就没有实际意义了.因此,该方法反演气溶胶,适用范围是在4km以下[18],气溶胶含量比较集中的区域(βα 比βm大一个数量级以上).在4km 以下,温度的测量精度也都高于±1 K[5-7],回波光子数大于20000 个(图 6a),〈|ΔFJ4/FJ4|〉就小于0.3%,〈|ΔNJ4/NJ4|〉就小于0.7%.综合以上的讨论,在8km 处,光子计数为1600 的情况下,β 的总误差应小于11.4%;4km以下探测气溶胶的误差小于6.7%.
另外,对β 的误差影响较大的,是雷达在参考高度z0 上探测到的回波信号的光子数$\left( \sqrt{1/{{N}_{\lambda 0}}\left( {{z}_{0}} \right)} \right.$和$\left. \sqrt{1/{{N}_{J4}}\left( {{z}_{0}} \right)} \right)$.所以,我们要选用高功率的激光器,Continuum 的9020在532nm 的单脉冲能量能稳定输出在500 mJ以上,重复频率20 Hz.还可以通过提高接收系统的效率获得更高的信噪比,比如在低空选用模拟信号计数,高空选用光子计数的方式[19],或者直接选用Licel的仪器[20-21].
6 结论用激光雷达数据反演气溶胶后向散射系数和消光系数通常需要引入某些假定(如在Fernald 方法中假定的雷达比,在常规Raman激光雷达中引入的Angstrom 关系).本文提出了一种利用纯转动单支谱(J=4和14)反演气溶胶后向散射系数的方法.整个激光雷达系统由基于F-P 标准具的二通道纯转动Raman激光雷达加上一个小口径望远镜构成的Rayleigh & Mie接收系统组成.在纯转动Raman温度测量结果的基础上,不需要附加任何假设,我们导出了气溶胶后向散射系数的数学表达式.而且计算纯转动谱用到的大部分常数都消掉了,这些常数有些难以确定,有些本身就存在较大误差.最后反演气溶胶的公式(15)中,仅剩下B0、h、c、k这四个.B0 是转动常量,主要决定了纯转动谱各支谱的位置,它的取值是确定而且精确的.h是普朗克常量,c是光速,k是玻耳兹曼常数,它们都是被各种实验确定的、取值十分精确的常数,不会引入误差.
误差估计表明,这种方法得到的气溶胶后向散射系数在4km 以下的相对误差在7%以内.获得了后向散射系数后,将其代入Rayleigh & Mie通道的雷达方程,便可获得气溶胶的消光系数剖面.这种方法得到的气溶胶参数可为当前普遍采用的激光雷达观测结果提供定量的数据比对.
| [1] | Cooney J A. Measurement of atmospheric temperature profiles by Raman backscatter. J. Appl. Meteor. , 1972, 11(1): 108-112. DOI:10.1175/1520-0450(1972)011<0108:MOATPB>2.0.CO;2 |
| [2] | Arshinov Y F, Bobrovnikov S M, Zuev V E, et al. Atmospheric temperature measurements using a pure rotational Raman Lidar. Appl. Opt. , 1983, 22(19): 2984-2990. DOI:10.1364/AO.22.002984 |
| [3] | Penney C M, Peters R T St, Lapp M. Absolute rotational Raman cross sections for N2, O2, and CO2. Journal of the Optical Society of America , 1974, 64(5): 712-715. DOI:10.1364/JOSA.64.000712 |
| [4] | BuP, YangJ G, HaY Q, 等. Chinese Journal of Light Scattering (in Chinese). 光散射学报 , 2002, 14(3): 183–185. |
| [5] | Arshinov Y, Bobrovnikov S, Serikov I, et al. Daytime operation of a pure rotational Raman Lidar by use of a Fabry-Perot interferometer. Appl. Opt. , 2005, 44(17): 3593-3603. DOI:10.1364/AO.44.003593 |
| [6] | Balin I, Serikov I, Bobrovnikov S, et al. Simultaneous measurement of atmospheric temperature, humidity, and aerosol extinction and backscatter coefficients by a combined vibrational-pure-rotational Raman Lidar. Appl. Phys. , 2004, 79: 775-782. |
| [7] | Behrendt A, Nakamura T, Onishi M, et al. Combined Raman Lidar for the measurement of atmospheric temperature, water vapor, particle extinction coefficient, and particle backscatter coefficient. Appl. Opt. , 2002, 44(36): 7657-7666. |
| [8] | Whiteman D N. Examination of the traditional Raman Lidar technique. Appl. Opt. , 2003, 42(15): 2571-2592. DOI:10.1364/AO.42.002571 |
| [9] | Miles R B, Lempert W R, Forkey J N. Laser Rayleigh scattering. Measarement Sci. Technol. , 2001, 12(5): R33-R51. DOI:10.1088/0957-0233/12/5/201 |
| [10] | Arshinov Y, Bobrovnikov S. Use of a Fabry-Perot interferometer to isolate pure rotational Raman spectra of diatomic molecules. Appl. Opt. , 1999, 38(21): 4635-4638. DOI:10.1364/AO.38.004635 |
| [11] | Buldakov M A, Matrosov I I, Papova T N. Determination of the anisotropy of the polarizability tensor of the O2 and N2 molecules. Opt. Spectrosc. (USSR) , 1979, 46(5): 488-489. |
| [12] | Chen S Y, Qiu Z J, Zhang Y C, et al. A pure rotational Raman Lidar using double-grating monochromator for temperature profile detection. Journal of Quantitative Spectroscopy & Radiative Transfer , 2011, 112(2): 304-309. |
| [13] | Vaughan G, Wareing D P, Pepler S J, et al. Atmospheric temperature measurements made by rotational Raman scattering. Appl. Opt. , 1993, 32(15): 2758-2764. DOI:10.1364/AO.32.002758 |
| [14] | Arshinov Y F, Bobrovnikov S M, Zuev V E, et al. Atmospheric temperature measurements using pure rotational Raman spectrum and Lidar. // Calibration the 9th International Conference on Laser Radar Studies of the Atmosphere Munich. Conference Abstracts, 1979: 21-25. |
| [15] | Hua D X, Masaru U, Kobayashi T. Ultraviolet high-spectral-resolution Rayleigh-Mie lidar with a dual-pass Fabry-Perot etalon for measuring atmospheric temperature profiles of the troposphere. Opt. Lett. , 2004, 29(10): 1063-1065. DOI:10.1364/OL.29.001063 |
| [16] | Souprayen C, Garnier A, Hertzog A, et al. Rayleigh-Mie Doppler wind lidar for atmospheric measurements. Appl. Opt. , 1999, 38(12): 2410-2421. DOI:10.1364/AO.38.002410 |
| [17] | Girolamo P D, Marchese R, Whiteman D N, et al. Rotational Raman Lidar measurements of atmospheric temperature in the UV. Geophys. Res. Lett. , 2004, 31: L01106. DOI:10.1029/2003GL018342 |
| [18] | Sasano Y. Tropospheric aerosol extinction coefficient profiles derived from scanning lidar measurements over Tsukuba, Japan, from 1990 to 1993. Appl. Opt. , 1996, 35(24): 4941-4952. DOI:10.1364/AO.35.004941 |
| [19] | Newsom R K, Turner D D, Mielke B, et al. Simultaneous analog and photon counting detection for Raman Lidar. Appl. Opt. , 2009, 48(20): 3903-3914. DOI:10.1364/AO.48.003903 |
| [20] | Turner D D, Goldsmith J E M. Refurbishment and upgrade of the atmospheric radiation measurement Raman Lidar. // Proceedings of the 15th ARM Science Team Meeting. Daytona Beach, Florida, 2005: 14-18. |
| [21] | BenZvil S Y, Cesterj S, Chiosso M, et al. The Lidar system of the Pierre Auger Observatory. Nuclear Instruments and Methods in Physics Research A: Accelerators, Spectrometers, Detectors and Associated Equipment , 2007, 574(1): 171-184. |
 2012, Vol. 55
2012, Vol. 55


