地球物理学报  2012, Vol. Issue (10): 3420-3426   PDF    
引用本文
李芳, 曹思远, 姚健. 任意各向异性介质相(群)速度的计算. 地球物理学报, 2012, (10): 3420-3426, doi: 10.6038/j.issn.0001-5733.2012.10.025.  
LI F, CAO S Y, YAO J. Calculation of phase and group velocities in an arbitrary anisotropic medium (AAM). Chinese J. Geophys. (in Chinese), 2012, (10): 3420-3426, doi: 10.6038/j.issn.0001-5733.2012.10.025.  
任意各向异性介质相(群)速度的计算
李芳1 , 曹思远1 , 姚健2     
1. 中国石油大学 (北京)油气资源与探测国家重点实验室, 北京 102249;
2. 中海石油(中国)有限公司天津分公司勘探开发研究院, 天津 300452
收稿日期 2011-03-15, 2012-09-15 收修定稿
基金项目: 国家自然科学基金(41140033)资助
作者简介: 李芳,女,1981年生,内蒙古人,博士研究生,主要研究方向是岩石物理基础理论以及裂缝储层岩石物理参数预测.E-mail:lif803@yahoo.com.cn
摘要: 反映弹性波在各向异性介质中传播特性的两个基础的物理量是相速度和群速度.本文在总结前人工作的基础上,提出任意各向异性介质相(群)速度的计算方案:首先推导各自计算公式,其次考虑剪切波奇点的特殊性,再次令其遵循相应约束条件,最后,采用三个计算实例检验该方案的正确性和有效性.通过对计算结果的分析以及各向异性理论预测可以加深对各向异性特有性质(如剪切波奇点、群速度多值性)的理解,有助于增强我们对任意各向异性理论的基本认识.
关键词: 任意各向异性介质      相速度      群速度      极性向量      剪切波分裂     
Calculation of phase and group velocities in an arbitrary anisotropic medium (AAM)
LI Fang1, CAO Si-Yuan1, YAO Jian2     
1. State Key Laboratory of Petroleum Resource and Prospecting (China University of Petroleum, Beijing), Beijing 102249, China;
2. Exploration and Development Research Institute, CNOOC Tianjin Company, Tianjin 300452, China
Abstract: Both phase velocity and group velocity are the essential vectors which could mirror the seismic wave propagation properties of anisotropic media. The shear wave splitting and triplication of group velocity are notable and specific phenomena which often complicate the seismic wave field particularly for anisotropic media with a lower symmetric system. In this paper, we propose an available workflow of calculation on phase (group) velocity in an arbitrary anisotropy medium (AAM). There are two existing obstacles we should focus on, which are shear wave singularity and distinguish of two shear wave. The way to overcome those difficulties is finding more constrain conditions to make the solutions meaningful and continuous. Three examples presented in this paper show that the workflow works well in AAM, however, more attention should be paid to the area around shear wave singularity, particularly for higher-symmetric-system anisotropic media..
Key words: Arbitrary anisotropy medium      Phase velocity      Group velocity      Polarization vector      Shear wave splitting     
1 引 言

早已证实，各向异性在地球介质中普遍存在[1-3]，从地壳一直到地核都存在各向异性.弹性波在各向异性介质中传播特征无论在动力学还是运动学方面均与各向同性存在重大差别.最明显的是各向同性介质中相(群)速度处处相同，而在各向异性波场中包含了相(群)速度大小和方向各不相同的三个体波，即Quasi-P波、Quasi-S1 波和Quasi-S2波.其中，相速度是最基本、最重要的物理量之一，许多物理量都是以它为基础来获得.但实际观测中相速度只有在某些特殊角度或采用特殊手段才能观测到，一般情况下得到的是射线速度和射线方向.在非色散各向异性介质中射线速度等价于群速度.群速度更是实现许多地球物理应用的基础，比如各向异性介质的射线追踪、偏移、层析成像、弹性参数反演、AVO 分析等，因此群速度亦相当重要[1, 3-4].

对于VTI 和HTI 等各向异性对称性弱的介质，目前已经存在该类介质的三种弹性波相(群)速度解析表达式[4-5].但是，任意各向异性的相(群)速度表达式是一个非常复杂的关于弹性模量和传播方向的函数，本文将提出一种适用于任意各向异性介质中三种弹性波的相(群)速度计算方案，有助于更好地理解真实地震波场的传播规律，为实际地震资料处理和解释奠定理论基础.

2 地震各向异性

各向异性定义为物理量沿测量方向变化的属性[6-7]，而地震各向异性特指速度在不同观测方向上各异的性质.诱发各向异性的主要因素[1, 2, 6]有，第一，组成岩石矿物的晶格优势方位排列[1, 3]；第二，裂缝[8]及薄层[2]的作用；第三，地下应力场的变化[2].其中第一个因素能引起很强的各向异性，这是因为组成岩石的各种基本矿物均表现出很强的各向异性.另外，不同裂缝系统(裂缝走向、裂缝密度、裂缝系统间的空间关系等等)也可能产生很强的各向异性[8-9].

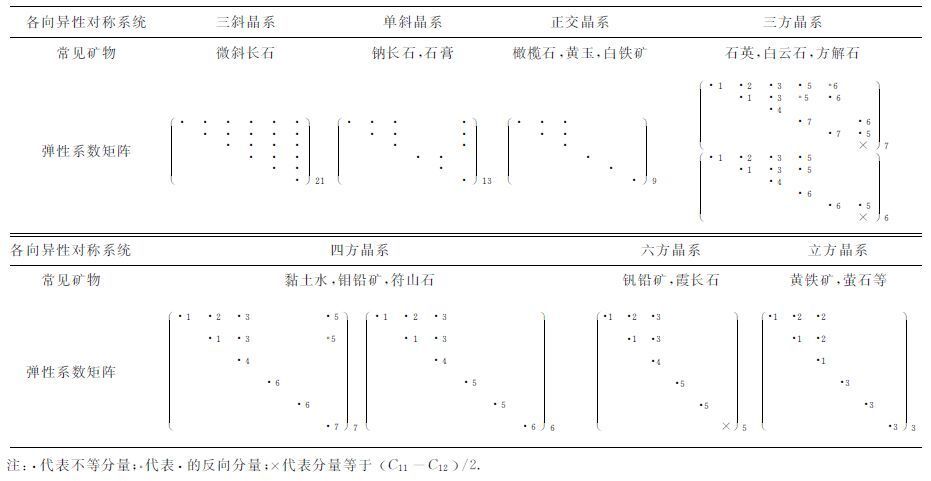
固有各向异性对称系统可分为七类[2, 10]，按照对称程度由低到高依次为三斜晶系、单斜晶系、正交晶系、三方晶系、四方晶系、六方晶系和立方晶系.表 1给出各个对称系统对应的代表矿物和弹性系数矩阵.由于应力张量和应变张量的对称性质，弹性系数矩阵为对称矩阵，表 1只给出其上对角元素.弹性系数矩阵右下角数字代表矩阵中包含不等元素的个数，至多为21个.而且，各向异性对称系统越复杂，不等元素个数越多.

表 1 七类各向异性对称系统及其代表矿物[11-12]和对应的弹性系数矩阵C Table 1 Seven classes of symmetry of anisotropy and corresponding representative minerals[11-12] and elastic tensors
3 相(群)速度的计算

相(群)速度是各向异性介质的两个非常重要的物理量.下面将给出任意各向异性介质相(群)速度的计算方案，包括计算公式的推导，分析可能遇到的问题及对应的解决办法.

3.1 相速度

相速度定义为单一频率平面波等相位面的传播速度，其定义式为:Vp=ω/k，这里，ω 是角频率，k是波数.

首先，从Green-Christoffel方程[6, 13]出发，

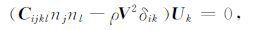
(1)

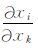
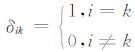
其中Cijkl为弹性系数矩阵，nj为方向余弦，ρ 为密度，V为相速度，δik=为Kronecker-delta函数，有，Uk为单位极性向量(i，j，k，l=1，2，3)，当|Cijklnjnl-ρV2δik|= 0 时，(1)式有唯一解，求解得到三个特征值(三个不同的相速度)和三个特征向量(三个对应的单位极性向量).

对于相速度和极性向量有以下基本性质:

(1) VQP >VQS1 和VQS2，这说明Quasi-P波传播速度最快，其次为两个剪切波(这里不考虑三者相等的特殊情况).同时，各向异性介质的一个显著特征是横波分裂[13-14]的产生，即两个剪切波沿同一方向以不同速度进行传播.

(2) 需要强调的是，只有各向异性对称系统的复杂性低于立方晶系的情况，极性向量的方向才等同于波矢量方向，因此这里P 波改为Quasi-P 波，同理S波改为Quasi-S波.另外，SV 波和SH 波的叫法仅适用于VTI介质，故这里简称为Quasi-S1 波和Quasi-S2波.

(3) 对于任意给定的波矢量，Quasi-P波、Quasi-S1波以及Quasi-S2波的极性向量必定相互垂直.

3.2 群速度

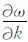
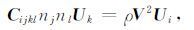
群速度为多个平面波叠加后波群中心的传播速度，其定义式为:Vg =，各个参数含义同上.

首先，改写(1)式[6, 13]，有

(2)

两边同乘Ui，有CijklnjnlUkUi=ρV2Ui2，且Ui2=U12+U22 +U32 =1，则式(2)又写为:

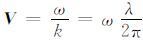
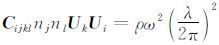
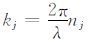
CijklnjnlUkUi=ρV2，由于，则，又因为，(2)式整理后得到[6, 13]

(3)

令(3)式对ω 求导，并依据相(群)速度的定义式，有

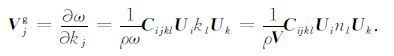
(4)

3.3 剪切波奇点处的极性向量

剪切波奇点是指两个弹性波的慢度面的交点[15-16]，包括三种类型，Kiss 型(如计算实例1)、Wedge型和Conical型(如计算实例2).这些奇点的出现使地震各向异性波场复杂化.因此，需要仔细处理这些奇点.

根据式(4)，可以发现群速度的数值取决于弹性系数矩阵、相速度、方向余弦以及极性向量[17].求解式(1)后，极性向量无法唯一确定，尤其是对于复杂的各向异性介质.BingZhou (2004)提出两种解决办法，第一，特征值方法；第二，特征向量方法.本文采取第一种方法，首先将两个互不相等的特征值(相速度)代入式(1)，得到对应的两个极性向量U1 和U2，然后，利用极性向量性质3，即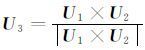，最终获得三个确定的极性向量.

3.4 Quasi-S1波和Quasi-S2波的区分

虽然VQP ≥VQS，但两个剪切波之间不存在与之类似的关系.为了正确分辨Quasi-S1波和Quasi-S2波可以利用以下两个限制条件[13-14]:

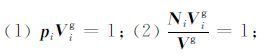
这里，pi为慢度向量，Ni为射线向量，即群速度方向，其它符号同上.另外，根据波前的几何形状，在剪切波奇点附近，两个剪切波的相速度曲线必须连续.根据这三个限制条件，能够达到区分的目的.

4 计算实例

下面给出三个计算实例来测验该方案的应用效果，并全部采用三维曲面图表示三种实例矿物相速度和群速度的三维直观立体图，不同颜色代表随测量方向发生变化的相速度和群速度值，XZ剖面图显示在某一特定剖面内相速度和群速度的变化情况.

4.1 三方晶系:石英

石英的密度ρ=2.65g/cm3，弹性系数矩阵[6, 18]为:

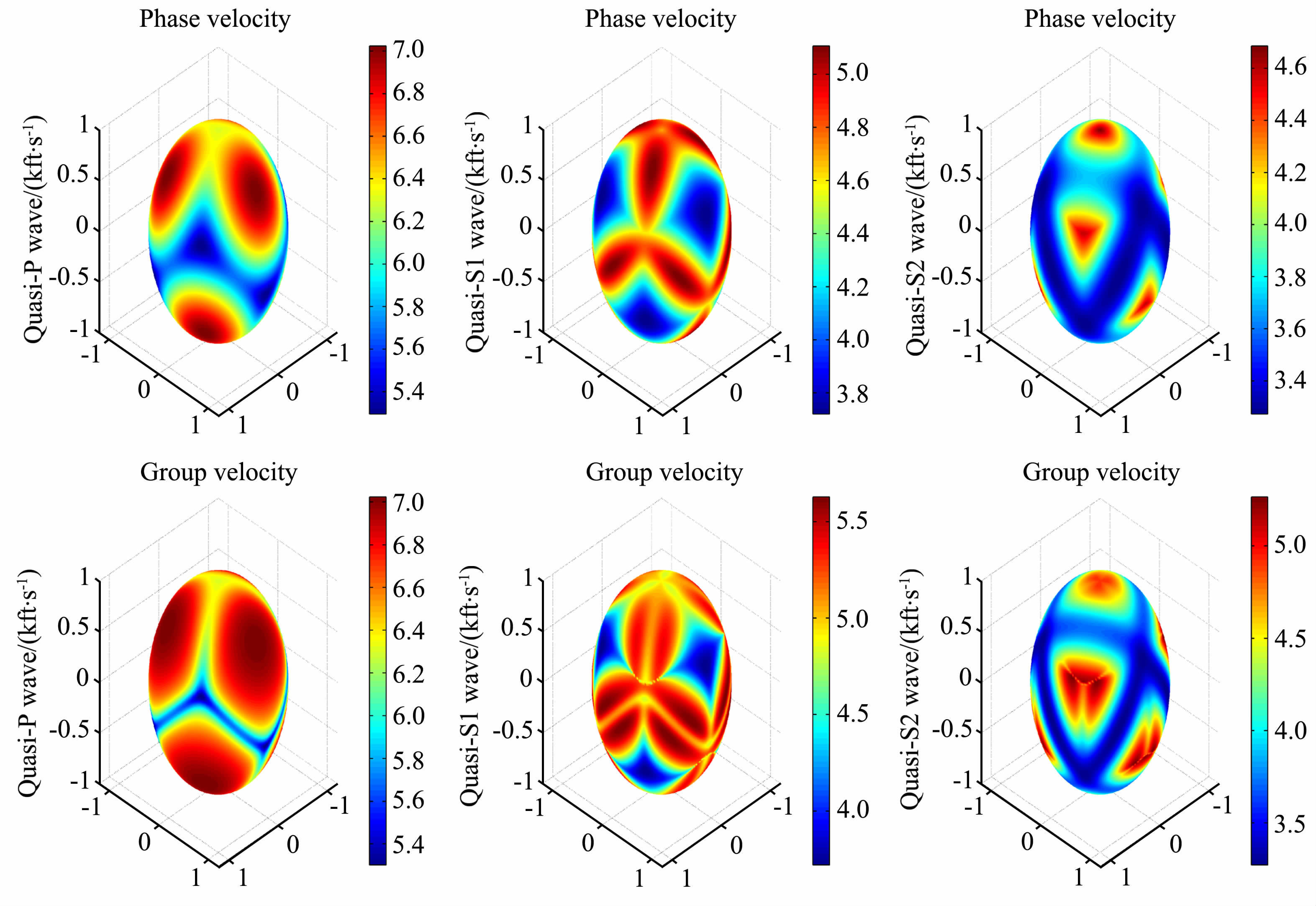
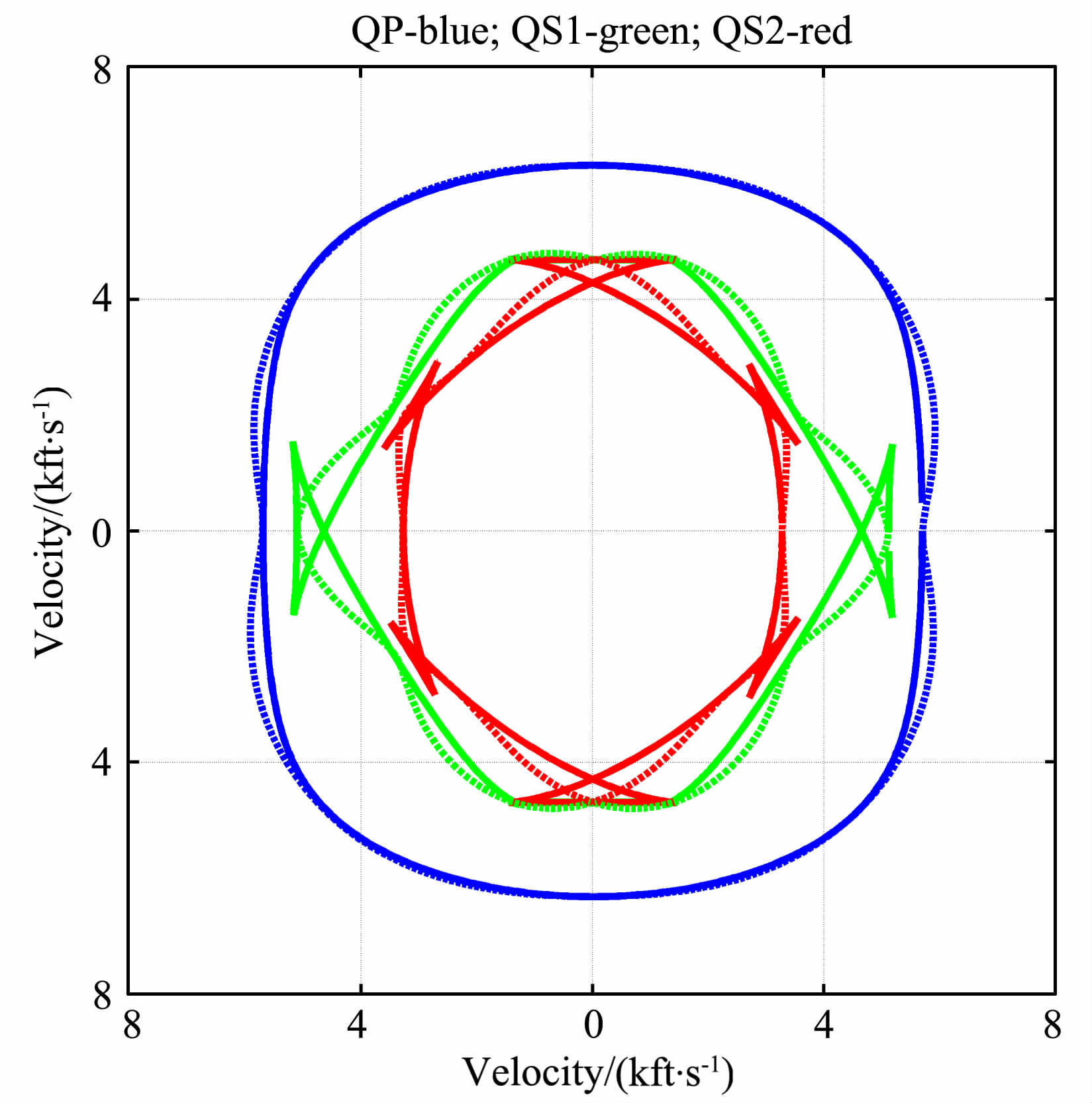
图 1为石英介质的三维相速度面(顶层)和群速度面(底层)，可以看到弹性波沿不同波矢量以不同的速度传播，体现出速度各向异性.图 2为其XZ剖面，图中各个曲线中点线代表相速度而实线代表群速度，蓝色、绿色和红色线分别表示Quasi-P 波、Quasi-S1波和Quasi-S2波.实例2和3的计算结果图中各个曲线的含义与之相同，下面不再赘述.观察图 2发现，群速度剖面比相速度剖面要复杂很多，例如，群速度剖面的多值性[14](又被称作triplication)，即一个射线方向可以同时对应三个互不相同的群速度值.

图 1 石英晶体的3D相速度面和群速度面，不同颜色代表速度，1 kft/s = 0.3048 km/s Fig. 1 3D phase velocity surfaces and group velocity surfaces of quartz，colors denote velocity in kft/s
图 2 石英相速度（点线）和群速度（实线）的XZ剖面 Fig. 2 Phase velocity (dotted line) and group velocity (solid line) of quartz in XZ-plane

CrampinS (1984)从理论上指出三方晶系矿物的剪切波奇点中包含2个Kiss型奇点.在图 2中可以很容易观察到沿垂直轴确实存在两个Kiss型剪切波奇点，验证了计算结果的正确性.另外，已知XZ平面为三方晶系矿物的对称面，因此图中各个曲线均为轴对称.

任意介质的各向异性强度[13] 定义为a=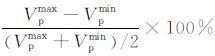，其中Vmaxp 和Vminp 分别代表相速度的最大值和最小值.其实，这里Quasi-P 波对应的a就是Thomsen参数中的ε，而Quasi-S2波对应的a就是γ .经过计算，石英介质的Quasi-P波、Quasi-S1波和Quasi-S2波所对应的各向异性强度分别为15.97%、43.77%和43.77%，其中剪切波表现出很强的各向异性.

4.2 单斜晶系:钠长石

钠长石的密度ρ=2.62g/cm3，弹性系数矩阵[6, 17]为:

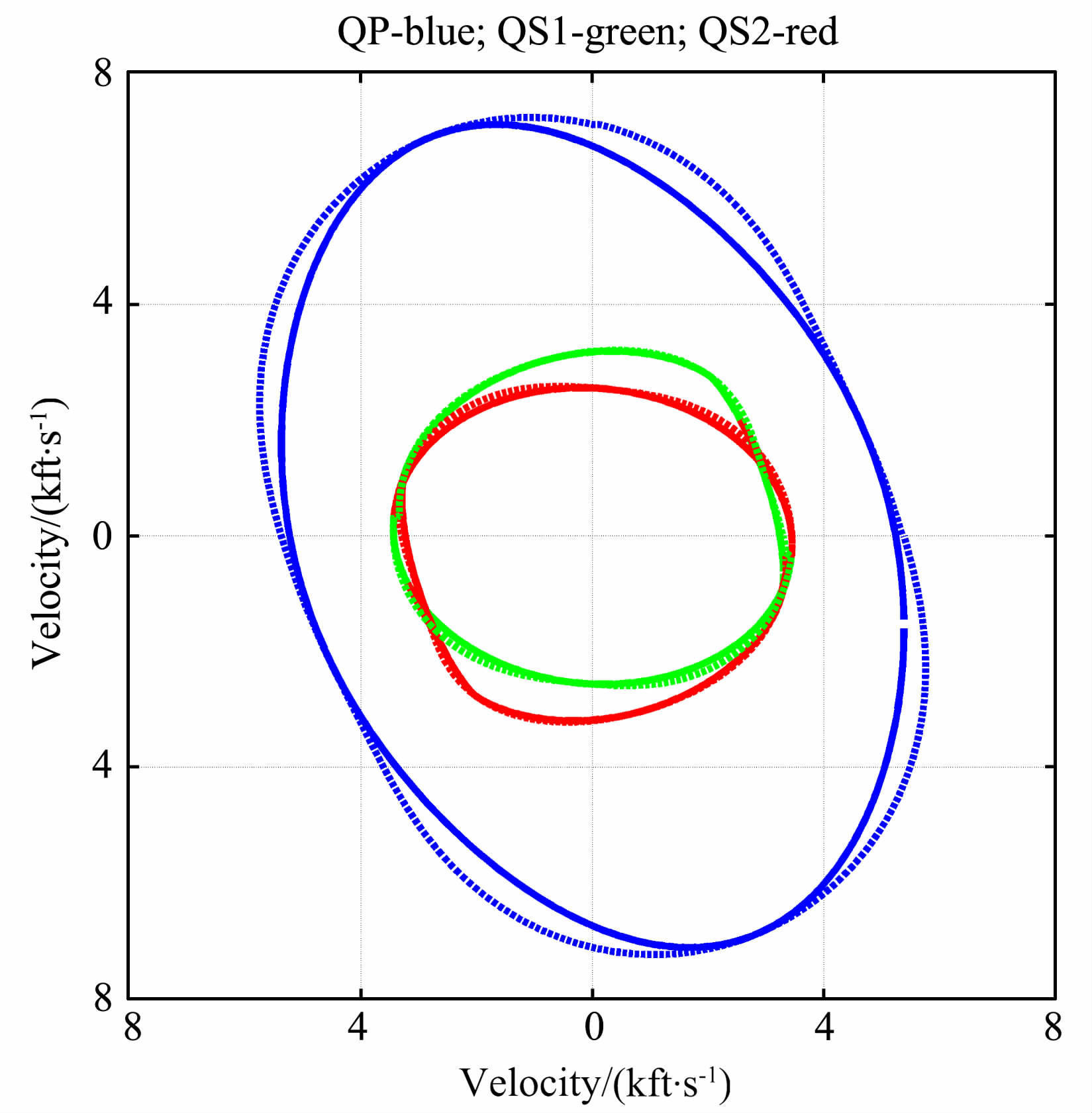
图 3是钠长石相(群)速度XZ剖面.图 4给出其三维相速度面和群速度面.图 3 中所有曲线不存在轴对称性质，这是因为XZ平面并非单斜晶系的对称面.依据理论预测[12]，存在Conical型奇点，图 3也得以证实.另外，钠长石晶体的Quasi-P波、Quasi-S1波以及Quasi-S2波的各向异性强度依次为38.72%、9.25%和29.93%，也表现出较强的各向异性.

图 3 钠长石相速度（点线）和群速度（实线）的XZ剖面 Fig. 3 Phase velocity (dotted line) and group velocity (solid line) of albite in XZ-plane
图 4 钠长石晶体的3D相速度面和群速度面，不同颜色代表速度，1 kft/s = 0. 3048 km/s Fig. 4 3D phase velocity surfaces and 3D group velocity surfaces of albite, colors denote velocity in kft/s
4.3 六方晶系:黏土水

黏土水的密度ρ=2.17g/cm3，弹性系数矩阵[6, 17]为:

从黏土水的弹性系数矩阵看，它属于VTI(transverse isotropy with a vertical symmetry axis)介质.在泥质岩[11]中，该矿物为最基本的组成矿物，表现为黏土和水的混合层状结构.六方晶系的对称轴为Z轴，包含无穷多个通过该对称轴的对称平面(如XZ剖面)，X犢剖面为其各向同性面，如图 5所示.观察图 6，对于Quasi-P 波，当传播方向为0°时，其相速度达到最大值，90°时对应最小值，也就是波动沿着垂直各向同性面传播的速度最小.经过计算发现，该介质表现出非常强的各向异性，Quasi-P波、Quasi-S1波以及Quasi-S2波的各向异性强度依次为53.61%、89.59%和84.38%.

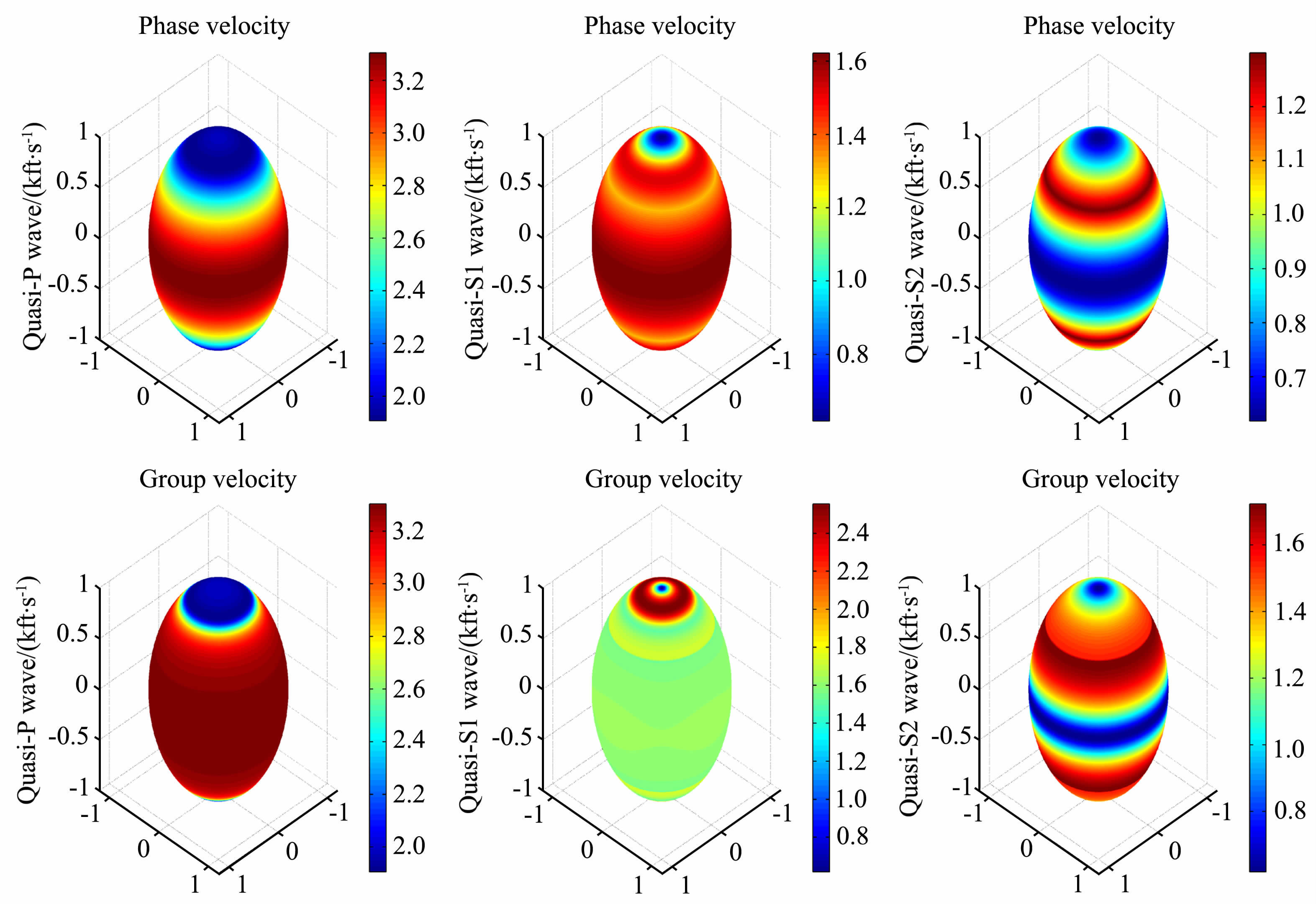
图 5 黏土水晶体的3D相速度面和群速度面，不同颜色代表速度，1kft/s = 0. 3048 km/s Fig. 5 3D phase velocity surfaces and group velocity surfaces of clay-water composite，colors denote velocity in kft/s
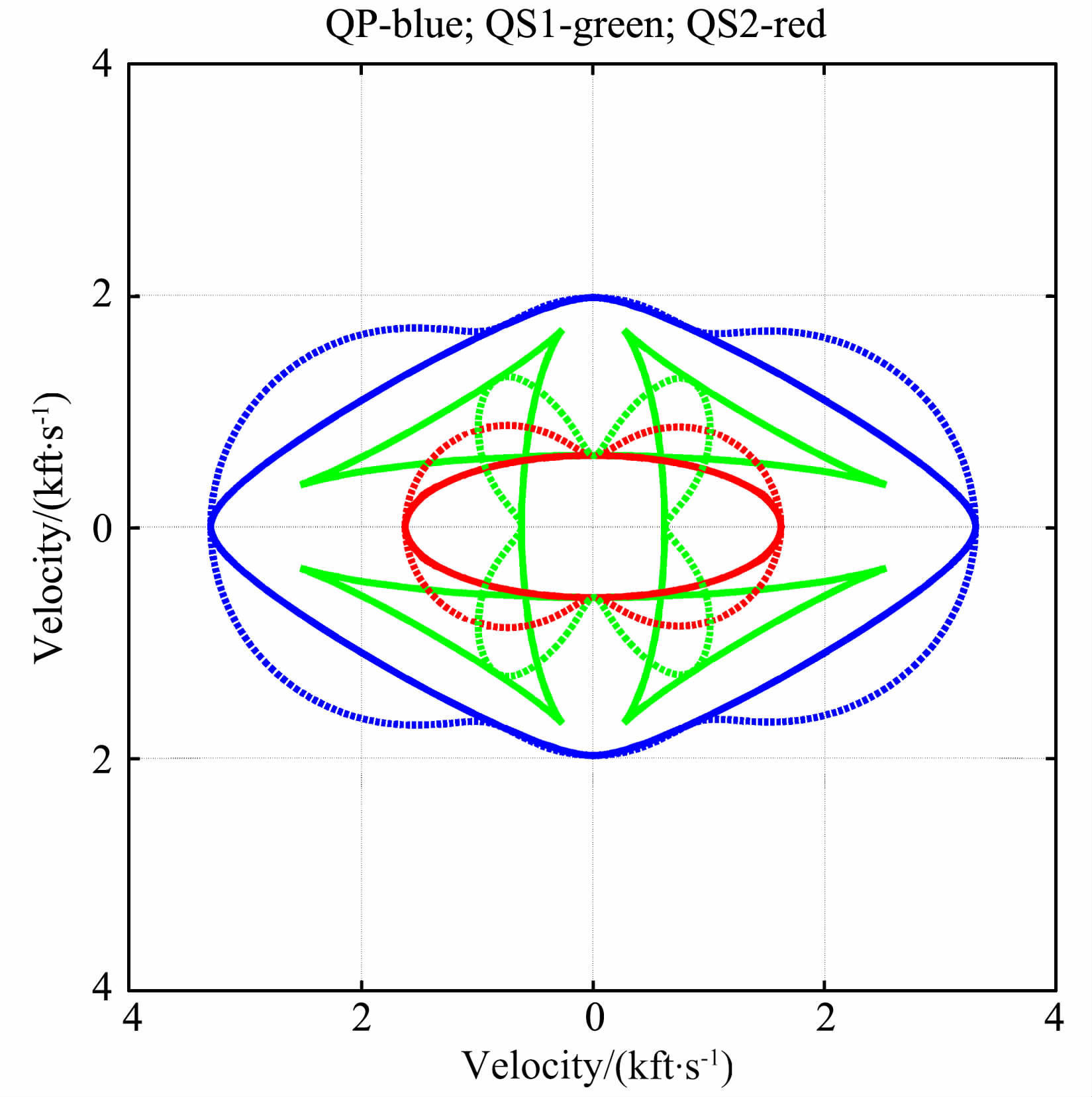
图 6 黏土水相速度（点线）和群速度（实线）的剖面 Fig. 6 Phase velocity (dotted line) and group velocity (solid line) of clay-water composite in XZ-plane
5 结 论

在地震各向异性中，相(群)速度是两个最基本的、非常重要的物理量，这是由于关于各向异性的研究，比如，各向异性波动理论、波场数值模拟、走时正反演、AVO 分析、速度分析、弹性参数反演、裂缝储层的地质评价等等，都离不开相(群)速度的计算.可以说，速度各向异性是各向异性理论的核心，正确理解各向异性介质相(群)速度的基本性质和特点有助于更好地掌握各向异性理论，同时也是对恰当处理实际问题的基本要求.

本文在总结前人工作的基础上，提出计算任意各向异性介质相(群)速度的方案:首先推导各自计算公式，其次考虑剪切波奇点的特殊性，再次须遵循三个约束条件，最后，采用三个实例和各向异性理论预测，检验该方案的正确性和应用效果.这些充分说明:(1)组成岩石的矿物晶体常常表现出较强的各向异性；(2)不同各向异性对称系统相(群)速度的基本性质不同.总体上，群速度场特征明显复杂于相速度，尤其是其多值的特点，突出表现在剪切波奇点附近，而且，三种类型的剪切波奇点表现大不相同；(3)虽然目前人们对实际各向异性地层都简化为VTI或HTI介质，但是必须认识到地下多裂缝系统介质表现出复杂的各向异性，研究其速度场特征和波动传播规律是裂缝性储藏勘探和开发的基础.

致谢

感谢澳大利亚Adelaide University 的BingZhou老师提供了非常好的建议.

参考文献
[1] Helbig K, Thosmen L. 75-plus years of anisotropy in exploration and reservoir seismic: A historical review of concepts and methods. Geophysics , 2005, 70(6): 9ND-23ND. DOI:10.1190/1.2122407
[2] Thomsen L. Understanding Seismic Anisotropy in Exploration and Exploitation. Tulsa: Society of Exploration Geophysics, 2002 .
[3] 李磊. 任意对称系强各向异性介质准纵波相速度和群速度解析表达式. 北京: 中国地震局地质研究所 , 2008: 11–27. Li L. Analytical expressions of phase and group velocities for qP wave propagating in strong anisotropic media of arbitrary symmetry (in Chinese). Beijing: Institute of Geology, China Earthquake Administration (in Chinese) , 2008: 11-27.
[4] 凌云, 郭向宇, 孙祥娥, 等. 地震勘探中的各向异性影响问题研究. 石油地球物理勘探 , 2010, 45(4): 606–623. Ling Y, Guo X Y, Sun X E, et al. Studies on the influence of anisotropy in seismic exploration. Oil Geophysical Prospecting (in Chinese) , 2010, 45(4): 606-623.
[5] Tsvankin I. Seismic Signatures and Analysis of Reflection Data in Anisotropic Media. (Volume 29). New York: Elsevier, 2005 .
[6] Tiwary D K. Mathematical modeling and ultrasonic measurement of shale anisotropy and a comparison of upscaling methods from sonic to seismic. Oklahoma: University of Oklahoma, 2007 .
[7] Sheriff R E. Encyclopedic Dictionary of Applied Geophysics. Houston. 2001.
[8] 裴正林, 董玉珊, 彭苏萍. 裂隙煤层弹性波场方位各向异性特征数值模拟研究. 石油地球物理勘探 , 2007, 42(6): 665–672. Pei Z L, Dong Y S, Peng S P. Numeric simulation of azimuth anisotropic characters of elastic wavefield in fractural coal seams. Oil Geophysical Prospecting (in Chinese) , 2007, 42(6): 665-672.
[9] Gray D. Fracture detection using 3D seismic azimuthal AVO. CSED Recorded , 2008: 41-50.
[10] Hornby B E, Schwartz L M, Hudson J A. Anisotropic effective-medium modeling of the elastic properties of shales. Geophysics , 1994, 59(10): 1570-1583. DOI:10.1190/1.1443546
[11] 路凤香, 桑隆康. 岩石学. 北京: 地质出版社, 2002 . Lu F X, Sang L K. Petrology (in Chinese). Beijing: Geological Publishing House, 2002 .
[12] Crampin S. An introduction to wave propagation in anisotropic media. Geophys. J. R. Astr. Soc. , 1984, 76(1): 17-28.
[13] Vavrycuk V. Calculation of the slowness vector from the ray vector in anisotropic media. Proceedings of the Royal Society , 2006, 462(2067): 883-896. DOI:10.1098/rspa.2005.1605
[14] Vavrycuk V. Behavior of rays near singularities in anisotropic media. Physical Review B , 2003, 67(5): 054105. DOI:10.1103/PhysRevB.67.054105
[15] Vavrycuk V. Parabolic lines and caustics in homogeneous weakly anisotropic solids. Geophys. J. Int. , 2003, 152(2): 318-334.
[16] Zhou B, Greenhalgh S. On the computation of elastic wave group velocities for a general anisotropic medium. Journal of Geophysics and Engineering , 2004, 1(3): 205-215. DOI:10.1088/1742-2132/1/3/005
[17] 郝重涛, 姚陈. 任意空间取向TI介质中体波速度特征. 地球物理学报 , 2007, 50(2): 546–555. Hao Z T, Yao C. Analysis of body-wave velocity characteristic for TI medium with arbitrary spatial orientation. Chinese J. Geophys. (in Chinese) , 2007, 50(2): 546-555.
[18] Bayuk I O, Ammerman M, Chesnokov E M. Elastic moduli of anisotropic clay. Geophysics , 2007, 72(5): D107-D117. DOI:10.1190/1.2757624