2. 中国科学院空间科学与应用研究中心, 北京 100191
2. Center for Space Science and Applied Research, Chinese Academy of Sciences, Beijing 100191, China
关于随机粗糙表面电磁散射建模的研究一直以来都是一个十分重要的研究论题.自20 世纪60 年代以来,人们相继提出了诸如KA 近似(KirchhoffApproximation)、小扰动近似(SPM)、双尺度近似(TSM)[1]、积分方程模型(IEM)[2-4]、小坡度近似(SSA)[5-6]等散射近似模型及其改进的形式.这些模型对于正确理解随机粗糙表面的电磁散射特性、解译归一化雷达截面(NRSC)、反演影响粗糙表面散射的物理参量等方面发挥了重要作用.另一方面,在关于重建雷达后向散射信息方面,Mouche[7]认为以上模型依然不能完全重建雷达后向测量的细节信息,特别是在极化率测量方面,相对于入射角与方位角变化,这些模型的计算结果与实际的测量还存在不一致.例如,在海面后散射系数的计算方面,用基本的SSA 和SPM 模型计算的垂直-垂直极化(V-V)的后向散射系数与实际测量结果的偏差较小,而水平-水平极化(H-H)与实际测量结果的还存在着较大的差异[8-10].当然,新的近似模型还在不断推出中,Elfouhaily及其合作者在SSA 的基础上给出了局地和非局地曲率近似模型(LCA/NLCA)[11-12],而后又推出了权重的曲率近似模型(WCA)[13];在2007 年[14] 又给出了这一模型的改进形式(RLCA3),这是局地曲率近似的三阶表示形式.
在以上这些散射近似模型的研究中,通过Stratton-Chu积分方程[1]和远场的格林(Green)函数[15-16]进行迭代是一个重要的研究思路之一,也是近似模型研究的基础.Elfouhaily[17]采用Holliday[16]的研究思路对模型中的极化核函数进行了分析.与Holliday不同的是Elfouhaily在其分析中试图保留所有的高次项.但是在处理格林函数的展开项时,他简化了斜率线性项在散射积分方程中的表示形式,并给出了称之为补充项的二次迭代结果.为了进一步提高极化核函数的近似程度,在Elfouhaily[11]中他重新恢复了斜率项和高程差项,并在Elfouhaily[17]中进行了分析.
我们通过研究发现Elfouhaily在上述分析中为了将相位项中高度的相关转化为水平分量和高度的梯度项乘积的形式,实际上是假设海面的起伏是小量并且是一阶近似处理.我们知道相位项上的这种转化是一种统计平均,因而可能会引起相位的迁移,并且这种迁移会与极化项产生耦合.因此,基于这种考虑,我们重新推导了二次迭代下的极化核函数(PoKF),得到了PoKF 的相对完整的表示形式,并以后向散射为例计算了归一化雷达散射截面的理论分析结果.PoKF 的完整表示形式能够较为清晰地反映观测配置参数与粗糙面几何特性在散射矩阵中的具体表示形式,更好地揭示粗糙面电磁散射过程与电磁散射特性.
本文第二部分回顾了粗糙面电磁散射的二次迭代形式;第三部分,主要推导了二次迭代形式下PoKF的完整表示形式;第四部分,以后向散射配置为例计算了同极化和交叉极化下的PoKF 的表示,并进行了分析;文章的最后部分进行了简要的分析和总结.
2 粗糙面散射的二次迭代形式应用电磁场理论中的Stratton-Chu 积分方程[1]与格林函数[15]的表示形式,一次与二次迭代的表面电流密度的表示形式可以写为[11, 17]

|
(1) |
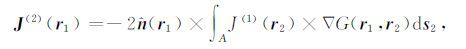
|
(2) |
其中,J(1)(r1)和J(2)(r1)分别表示表面上r1 处的一次与二次迭代的表面电流密度;ξ1 为表面函数,反映了表面的起伏,$\hat{n}$ 表示表面的法向矢量,且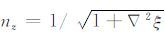
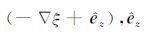

由Stratton-Chu积分方程,在假设表面为理想导体面的情况下,远场区r0 处表面散射场可以表示为
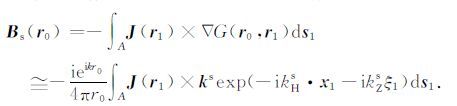
|
(3) |
其中,ks 表示散射方向的传播矢量,可分解为水平分量kHs 和垂直分量kZs,矢量的方向由位置矢量r0确定,即
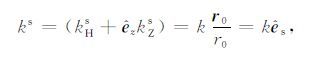
|
(4) |
其中,${{\hat{e}}_{s}}$ 为散射方向的单位传播矢量.
由散射磁场的表示可见,如果将一次与二次迭代得到的表面电流方程代入到式(3)中,通过简化可以得到
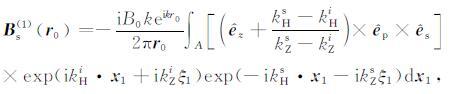
|
(5) |
由式(5)可以定义积分方程经过一次迭代后得到的极化核函数I0(r0,r1),即
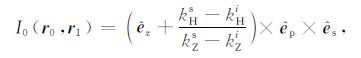
|
(6) |
同样,磁场的二次迭代表示形式Bs(2) 可以表示为
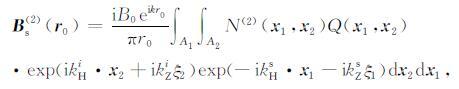
|
(7) |
Elfouhaily称(7)为二次迭代的补充场,实际上是对一次迭代的修正.式中,

|
(8) |
为了便于说明,这里且定义N(2)为二次迭代的极化核函数的“初步"表示式,通过进一步简化可以得到
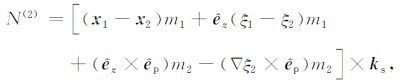
|
(9) |
其中,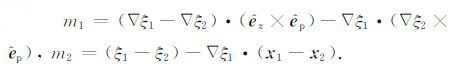
由此看出,在极化核函数这个“初步"的表示式中含有位置矢量差分量,同时也含有表面起伏的梯度分量.同时我们也注意到,在式(9)中,对水平分量的二重积分实际上是一个复杂的四重积分,并且入射-接收的极化配置情况与粗糙面的物理特性耦合在一起,直接分析极为困难.为了能够对散射特性进行分析,就需要对以上积分附加一定的条件并进行解耦处理.
3 二次迭代项的极化分析 3.1 新的二次迭代形式的补充场根据Elfouhaily[11]的考虑,在二次迭代的极化核函数的初步表示式(9)中,-Δξ1·( Δξ2×${{\hat{e}}_{p}}$)为斜率的高阶项,可以在后面的推导过程中忽略.但这里我们保留了两个矢量项${{\hat{e}}_{z}}$(ξ1 -ξ2)项和-Δξ2 ×${{\hat{e}}_{p}}$项,这是与Elfouhaily分析的不同之处.
保留相应的矢量项是进一步分析极化敏感性的一个关键性环节.这是因为散射场的强度在不同的分量(方向)中可能有差异,除了垂直方向以外一般不会为零,因此在极化接收过程中,即便是较弱的方向分量在接收极化方向上的投影也会对接收有贡献.Elfouhaily 在其推导过程中只是保留了含有(x1 -x2)和(${{\hat{e}}_{z}}$×${{\hat{e}}_{p}}$)两个分量项,但是对于后向散射的计算中,(x1-x2)方向项并未对VV 和HH 极化有贡献.
为了进一步说明这一问题,我们先采用小扰动近似的基本假设,即在相关长度范围内高度的变化不大,因而(ξ1-ξ2)可以用斜率项表示,即ξ1-ξ2 ≈(x1 -x2)· Δξ2.
Elfouhaily[17]曾采用了类似的形式对Holliday[16]的形式进行了简化,但是考虑到高程差会与积分变量产生较强的耦合,因而在Elfouhaily[11]中恢复了原有的高程差的表示形式.这样我们可以得到关于磁场的二次迭代新的补充场的表示形式,通过简化可以表示为:
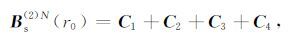
|
(10) |
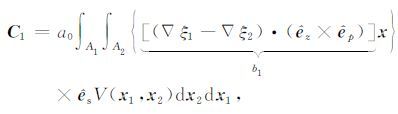
|
(11a) |
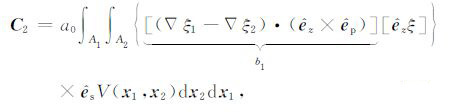
|
(11b) |
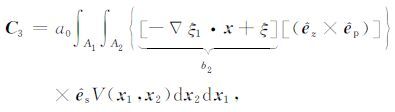
|
(11c) |
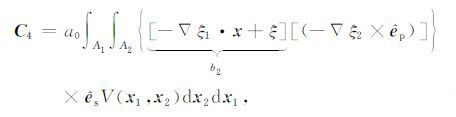
|
(11d) |
其中,
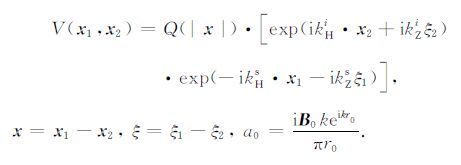
|
为了便于进一步分析,我们希望能够在合理的假设条件下,将上面的表示形式写为单重积分的形式.虽然式(11a-11d)是一组Fourier积分表示式,在形式上可以进行简化[14, 17, 20],但是为了深入分析极化的敏感性这里没有采用类似的形式表示方法,而是根据方程中各项的相互关系进行简化处理.
我们的目的是将二重积分简化为单重积分,为了简化表示,令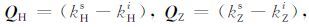
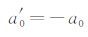
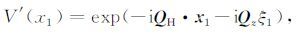
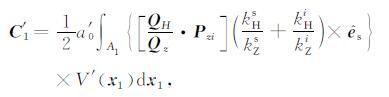
|
(12a) |
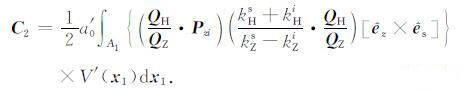
|
(12b) |
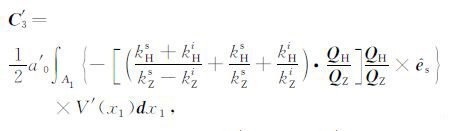
|
(12c) |
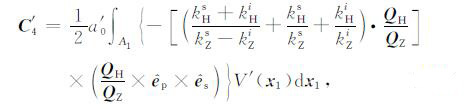
|
(12d) |
由式(12a-12d)并结合上一节中给出的一次迭代极化核函数的表示形式,我们可以定义新的二次迭代极化核函数,该函数的形式区别于一次迭代极化核函数“初步"表示形式,并记为I(N),即
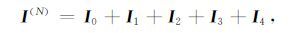
|
(13) |
其中I1-I4,分别表示积分号下花括号中的部分.需要注意的是由式(13)定义的极化核函数,分别是由一次和二次迭代得到,因而符号的选择应协调,即各项中的系数应与I0 所在积分中的系数一致.本例中第二项I1 前有一正号,而I3,I4 项均有一个负号.如果进一步令:
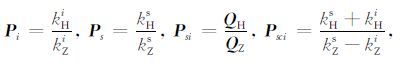
|
(14) |
则(13)式的后四项可以表示为
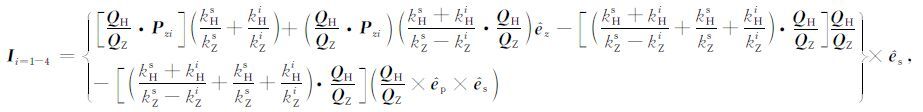
|
(15) |
综合以上各式的表示形式,可以得到
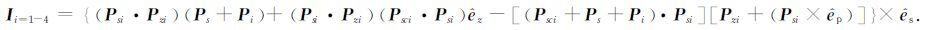
|
(16) |
(16)式就是极化核函数的二次迭代的完整表示形式.该式在简化过程中利用了积分恒等式,同时对相位项也进行了简化处理.另一方面,从极化核函数的表示形式上分析可见,该函数只与入射的相关角度(包括入射角、方位角),散射相关角度(散射射角,散射方位角)以及入射极化等传感器参数相关,而将有关于粗糙面的几何参数解耦到积分号外.
另外,从简式中可以看出,推导过程中我们试图将极化核函数从积分函数中分离出来,然而此过程本身就是一种近似处理.事实上Elfouhaily[12, 18]也曾深刻认识到,试图将极化核函数从积分函数中分离出来的方法由于耦合的原因在高阶近似处理时并不可行,但是如果不进行相应的近似处理无疑会使问题变得更为复杂,并可能使核函数中含有积分项.下面将以后向散射和简化的双站散射为例说明简化后的补充场极化核函数的具体表示形式并与前人的结果进行比较.
4 散射极化敏感性举例根据上一节中给出的极化核函数,下面我们分析在后向散射和散射角变化情况下同极化和(V-V极化,H-H 极化)和交叉极化(V-H 极化)时核函数的分析结果,从而揭示各项对散射极化的贡献.在后向散射的情况下,设入射角为θ,方位角为0°,则入射和散射方向的单位矢量可写为
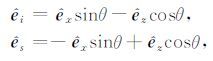
|
(17) |
由此可以得到
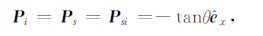
|
(18) |
对于V-V 极化:${{\hat{e}}_{p}}$=${{\hat{e}}_{y}}$,Pzi=-${{\hat{e}}_{x}}$,且接收极化为Pr=${{\hat{e}}_{y}}$,可以进一步得到
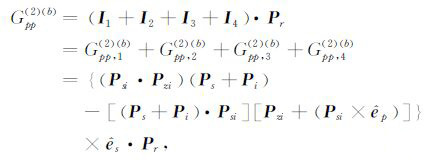
|
(19) |
其中,下标pp可分别取VV、HH、VH 和HV.该式表示了二次迭代极化核函数的极化敏感系数由四项构成,并通过推导可知
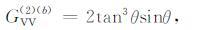
|
(20) |
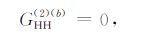
|
(21) |
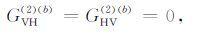
|
(22) |
在上面的推导中,式(21)和式(22)分别表示的是HH 极化和交叉极化的推导结果,该结果与Elfouhaily的结论是一致的.但是式(20)表示VV极化不为零,从推导可知,该结果是由第四项导出,Elfouhaily在分析中忽略了该项的影响.
另外,为了分析极化核函数中的各项在偏离后向散射方向上对散射的影响,我们画出了由式(23)定义的极化敏感性系数(Polarization Coefficient, 无量纲量)与散射角之间的关系.
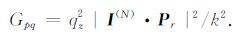
|
(23) |
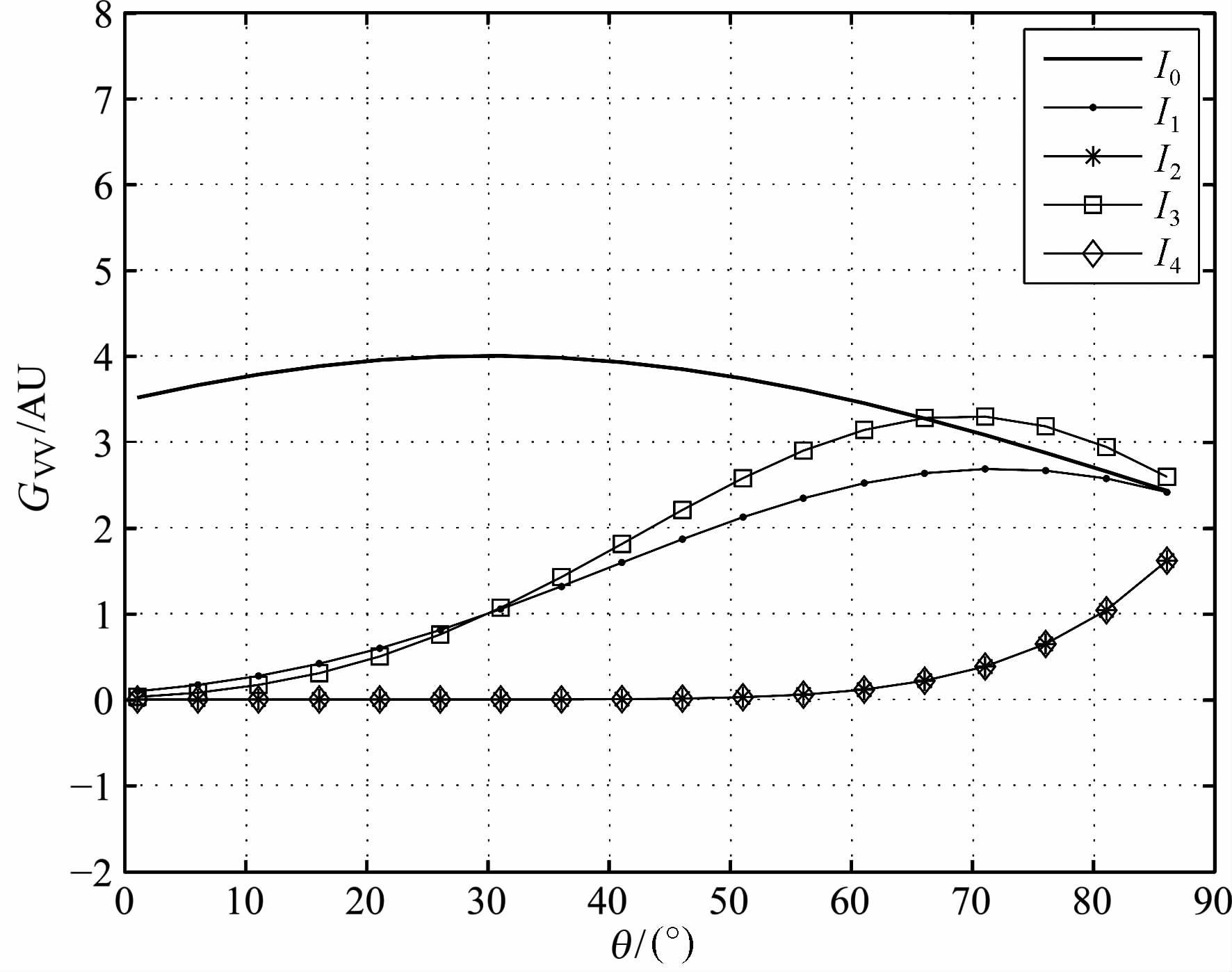
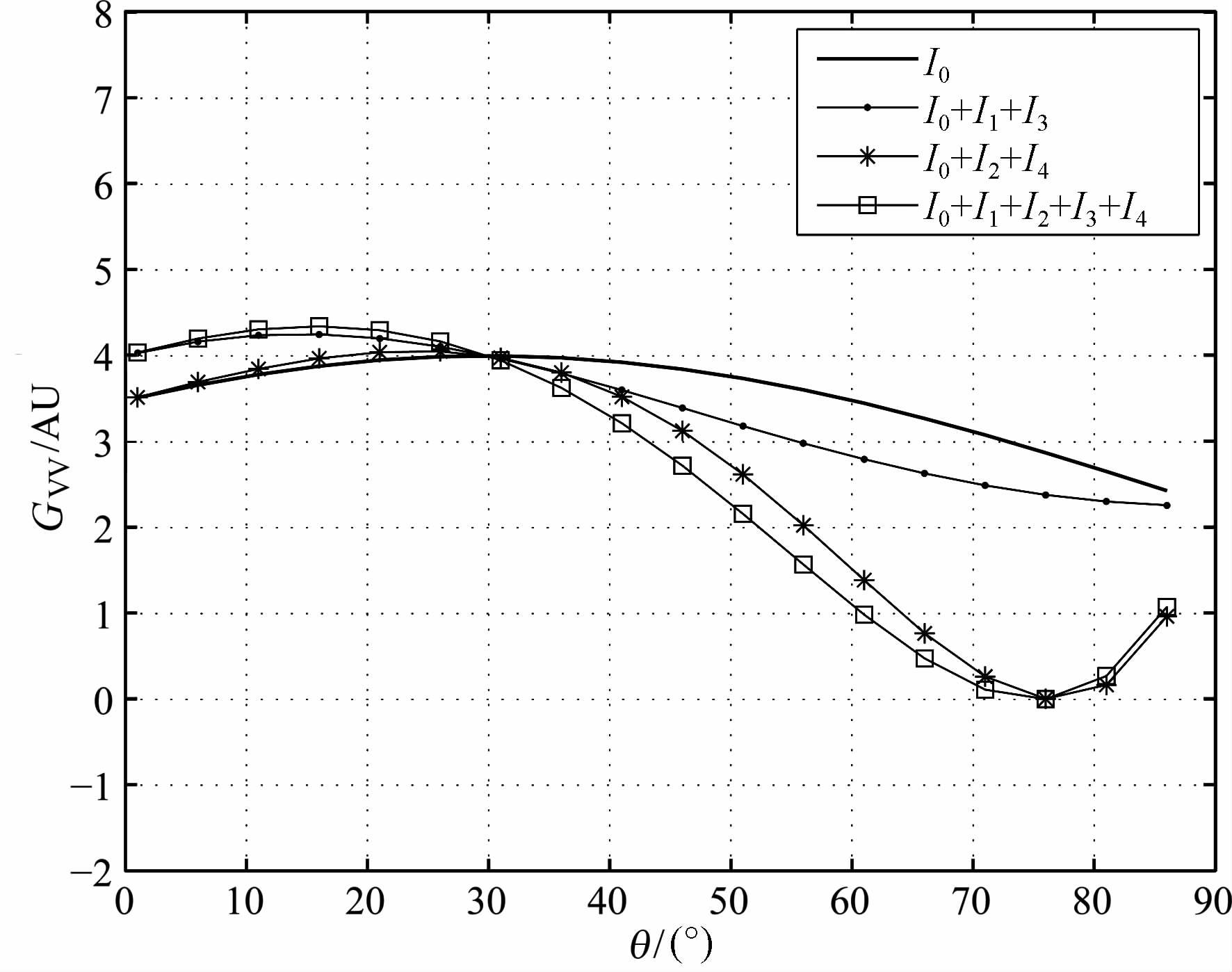
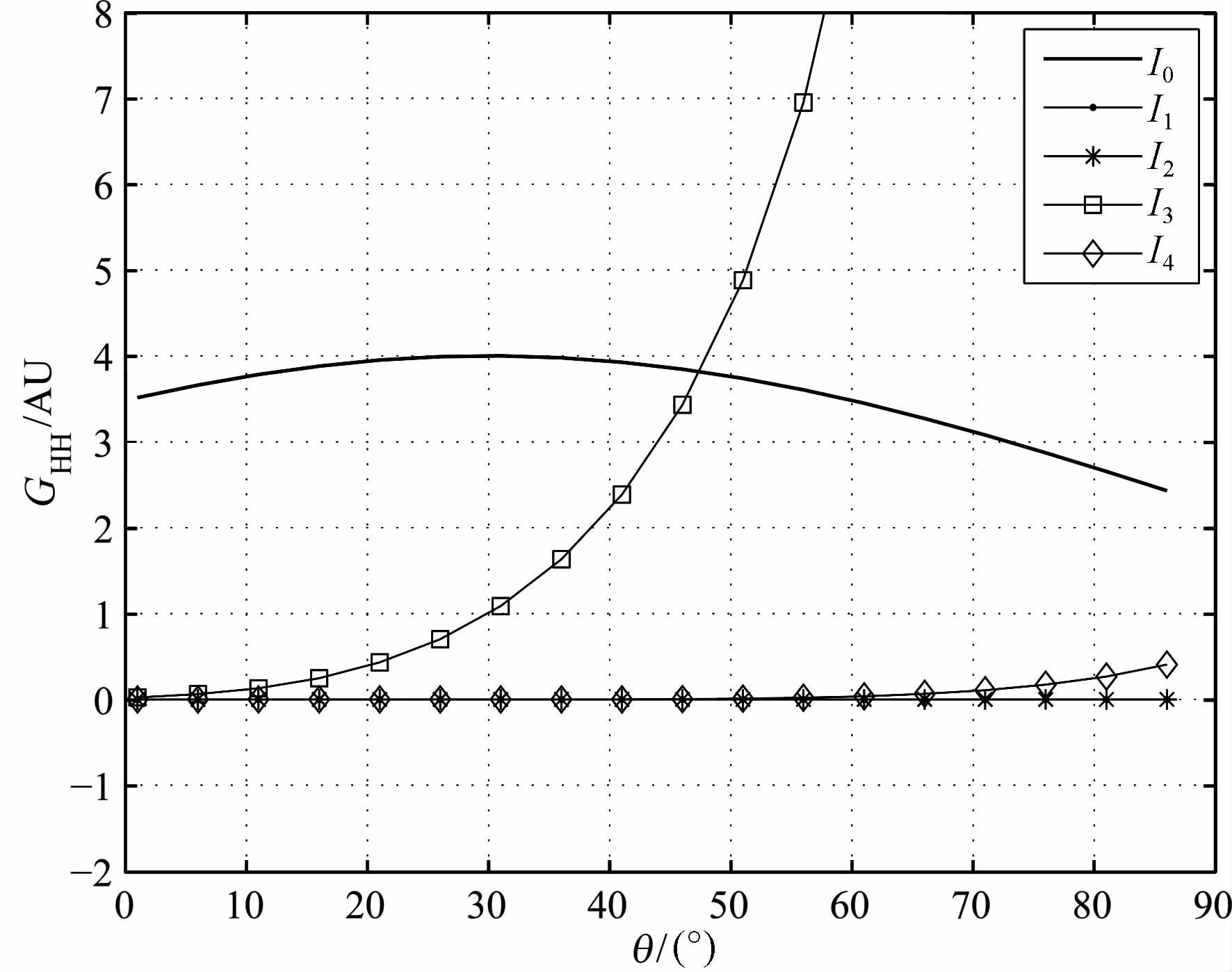
图 1表示的是入射角为30°时核函数中的各项的贡献,可以看出I1和I2的贡献,可能比I3和I4大,但是我们注意到在分析式中I1项与I3项的符号是相反的,因而在量值有相互抵消的作用,这一点也可以从图 2中表现出来,即I0+I1+I3的组合对I0的改变量要小于I0+I2+I4对I0的影响.同样,图 3和图 4 分别表示了H-H 极化时核函数中的各项极化散射的影响.可以看出I1和I2的贡献可以看作是一小量,而I3可能表现出不合理的“发散"特性,这可能是由于在近似表示时引入的.尽管如此,以上结果也表明,在考虑散射的计算问题中,极化核函数中的第I2和I4项是对极化的敏感性是有影响的.
|
图 1 V-V 极化敏感系数各分量与散射角的关系 Fig. 1 Comparison of VV-pol coefficient components as the function of scattering angle |
|
图 2 V-V 极化敏感系数组合分量与散射角的关系 Fig. 2 Comparison of different VV-pol coefficient component combination as the function of scattering angle |
|
图 3 H-H 极化敏感系数各分量与散射角的关系 Fig. 3 Comparison of HH-pol coefficient componentsas the function of scattering angle |
|
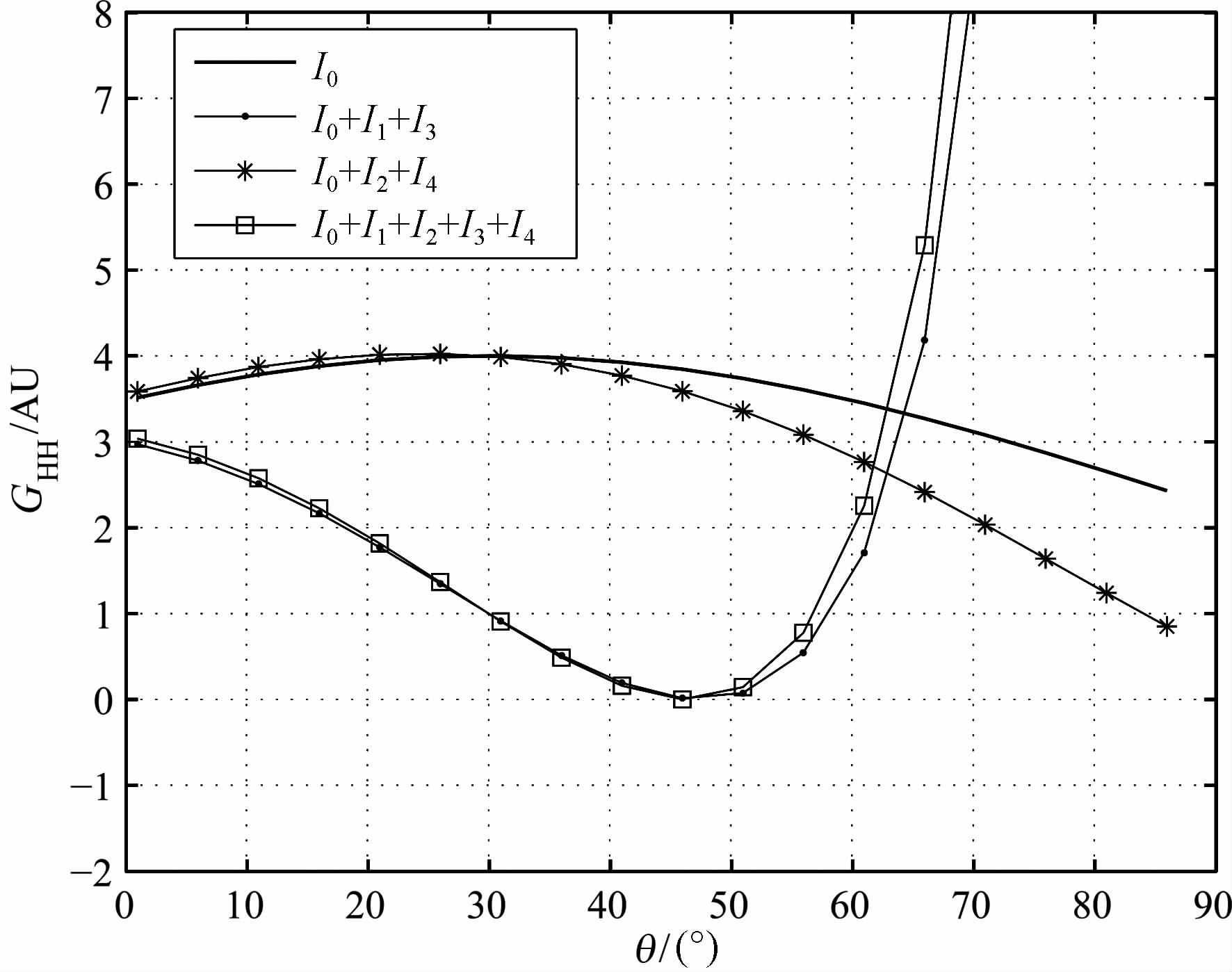
图 4 H-H 极化敏感系数组合分量与散射角的关系 Fig. 4 Comparison of different HH-pol coefficient component combination as the function of scattering angle |
研究随机粗糙表面电磁散射近似模型对于理解与分析粗糙表面(特别是海面)的双站散射特性有重要意义.本文从积分方程出发进一步考虑了Elfouhaily近似的合理性,应用迭代方法推导出了二次迭代条件下粗糙面的电磁散射的极化核函数的完整表示形式,并以后向散射为例计算了后向散射条件下的具体结果.PoKF 的完整表示形式能够较为清晰地反映观测配置参数与粗糙面几何特性在散射矩阵中的具体表示形式,能够更好地揭示粗糙面电磁散射过程与电磁散射特性,对于深入研究粗糙表面特别是海面的双站散射特性,进而应用卫星遥感数据反演影响海面散射特性的海面物理量参数(如海面风场、浪场、流场)等问题的研究具有重要意义.但需要说明的是,由于极化的引入,随机粗糙表面电磁散射不再是标量场而是一种复杂的矢量场,其推导过程极为繁琐,为了简化推导过程,不但需要对研究的随机粗糙表面施以近似假设也需要在推导过程的不同阶段附加合理的近似条件.本文只是从磁场的积分方程的角度出发进行的理论推导,并将在后续的文章中将给出一般的非理想导体随机粗糙表面的相关分析结果.
| [1] | 乌拉比F T, 穆尔R K, 冯健超著. 微波遥感(第二卷)雷达遥感和面目标的散射、辐射理论. 北京: 科学出版社, 1987 : 298 -336. Ulaby F T, Moore R K, Fang A K(Au). Microwave Remote Sensing (Volume II) Radar Remote Sensing and Sruface Scattering and Emission Theory. (in Chinese). Beijing: Science Press, 1987 : 298 -336. |
| [2] | Fung A K, Li Z Q, Chen K S. Backscattering from a Randomly Rough Surface. IEEE Geosci Remore Sensing , 1992, 30(2): 356-369. DOI:10.1109/36.134085 |
| [3] | Fung A K. Microwave Scattering and Emission Models and Their Applications. Boston,MA: Artech House, 1994 . |
| [4] | álvarez-PérezJ L. An extension of the IEM/IEMM surface scattering model. Waves in Random and Complex Media , 2001, 11(3): 307–329. |
| [5] | Voronovich A G. Small-slope approximation for electromagnetic wave scattering at a rough interface of two dielectric half-spaces. Waves in Random and Complex Media , 1994, 4(3): 337-367. DOI:10.1088/0959-7174/4/3/008 |
| [6] | Voronovich A G. Wave Scattering from Rough Surfaces. Berlin: Springer Series on Wave Phenomena, Springer-Verlag, 1999 . |
| [7] | Mouche A A, Reul N, Hauser D,et al. Importance of the sea srface curvature to interpret the normalized radar cross section. J Geophy Res, 2007,112 (C10002): DOI:10.1029/2006JC004010. |
| [8] | Janssen P A E M, Wallbrink H, Calkoen C J, et al. VIERS-1 Scattermeter Model. J Geophy Res , 1998, 103: 7807-7831. DOI:10.1029/97JC02911 |
| [9] | Kudryavtsev V, Hauser D, Caudal G, et al. A semi-empirical model of the normalized radar cross-section of the sea surface:2 radar modulation transfer function. J Geophy Res , 2003, 108(C3): 8055. DOI:10.1029/2001JC001004 |
| [10] | Kudryavtsev V, Akimov D, Johannessen J, et al. On radar imaging of current features:1 model and comparison with observations. J Goephy Research , 2005, 110(C3): C07016. DOI:10.1029/2004JC002505 |
| [11] | Elfouhaily T M, Thompson D R, Freund D E, et al. A new bistatic model for electromagnetic scattering from perfectly conducting random surfaces: numerical evaluation and comparison with SPM. Waves Random Media , 2001, 11: 33-43. DOI:10.1088/0959-7174/11/1/303 |
| [12] | Elfouhaily T, Guignard S, Awadallah R, et al. Local and non-local curvature approximation: a new asymptotic theory for wave scattering. Waves Random Media , 20003, 13(4): 321-337. |
| [13] | Guérin C, Soriano G, Elfouhaily T. Weighted curvature approximation: numerical tests for 2D dielectric surfaces. Waves in Random and Complex Media , 2004, 14(3): 349-363. DOI:10.1088/0959-7174/14/3/009 |
| [14] | Elfouhaily T, Johnson J T. A new model for rough surface scattering. IEEE Geos Remote Sensing , 2007, 45(7): 2300-2308. DOI:10.1109/TGRS.2006.890419 |
| [15] | 宋文淼. 并矢格林函数和电磁场的算子理论. 合肥: 中国科学技术大学出版社, 1991 : 132 -139. Song W M. Dyadic Vector Green Function and Electromagnetic Fields of Operator Theory (in Chinese). Hefei: China University of Science and Technology Press, 1991 : 132 -139. |
| [16] | Holliday D. Resolution of a controversy surrounding the kirchoff approach and the small perturbation method rough surface scattering theory. IEEE antennas and propagation , 1987, 35(1): 120-122. DOI:10.1109/TAP.1987.1143978 |
| [17] | Elfouhaily T M, Thompson D R, Vandemark D, et al. A new bistatic model for electromagnetic scattering from perfectly conducting random surfaces. Waves in Random and Complex Media , 1999, 9(3): 281-294. DOI:10.1088/0959-7174/9/3/301 |
| [18] | Elfouhaily T, Guignard S, Thompson D R. A practical second-order electromagnetic model in the quasi-specular regime based on the curvature of a good-conducting scattering surface. Waves in Random and Complex Media , 2003, 13(3): L1-L6. DOI:10.1088/0959-7174/13/3/101 |
| [19] | Elfouhaily T, Guérin C. A critical survey of approximate scattering wave theories from random rough surfaces. Waves in Random and Complex Media , 2004, 14(4): R1-R40. DOI:10.1088/0959-7174/14/4/R01 |
| [20] | Bourlier C, Déchamps N, Berginc G. Comparison of asymptotic backscattering models (SSA, WCA, and LCA) from one dimensional gaussian ocean-like surfaces. IEEE Antennas and Propagation , 2005, 53(5): 1640-1652. DOI:10.1109/TAP.2005.846800 |
 2012, Vol. 55
2012, Vol. 55

