板块内部弹性部分的厚度可以通过板块的弹性弯曲变形来确定.前人D.W.Forsyth[1],D.P.Mckenzie[2]曾对大陆的岩石圈在负荷的作用下弯曲形变作过深刻的理论和实测数据的研究.A.B.Watts[3]等曾对海山负荷下海洋岩石圈一维的板块弯曲方程进行研究.近十年来随着重力与地形的均衡响应函数的研究的深入,L.M.Kalnins[4]等把均衡响应函数的理论应用到海洋领域探求西太平洋海山区域的岩石圈有效弹性厚度,他应用A..B.Watts[5]板块内覆盖非黏性物质层的均衡响应函数的理论公式到海洋领域,探求了海域的岩石圈有效弹性厚度,并分析了运用该计算时数据取值窗口的技术.我国在研究岩石圈有效弹性厚度方面也取得不少的进展.众多的学者[6-8]从热流变、均衡响应函数等方面对我国的大陆岩石圈有效弹性厚度进行研究.在海洋领域付永涛等[9]研究海洋岩石圈的有效弹性厚度的地质意义.赵俐红等[10]在中西太平洋海山区通过9个剖面的计算,运用弹性板挠曲理论对它们所在处大洋岩石圈的有效弹性厚度进行了理论假设,结合地形数据推求各剖面相应的理论空间重力异常,并与实际测得的空间重力异常进行比较,用最佳拟合方法推求大洋岩石圈的有效弹性厚度.他们深入分析海山区岩石圈有效弹性厚度的地质意义.Lin [11]等运用三个剖面研究了台湾海峡及台湾西部前陆盆地的岩石圈有效弹性厚度约为13km.
在海洋板块上存在的海山、沉积负载、俯冲等都可以使板块弯曲形变,通过对这些区域的研究可探求海洋岩石圈板块的有效弹性厚度.本文在前人研究大陆岩石圈板块有效弹性厚度的基础上,建立研究海洋岩石圈板块有效弹性厚度的理论模型和二维理论计算公式,推导出与大陆岩石圈不同的海洋岩石圈板块响应函数Z(k,Te)理论计算公式.并分析海洋岩石圈板块响应函数Z(k,Te)的特点.
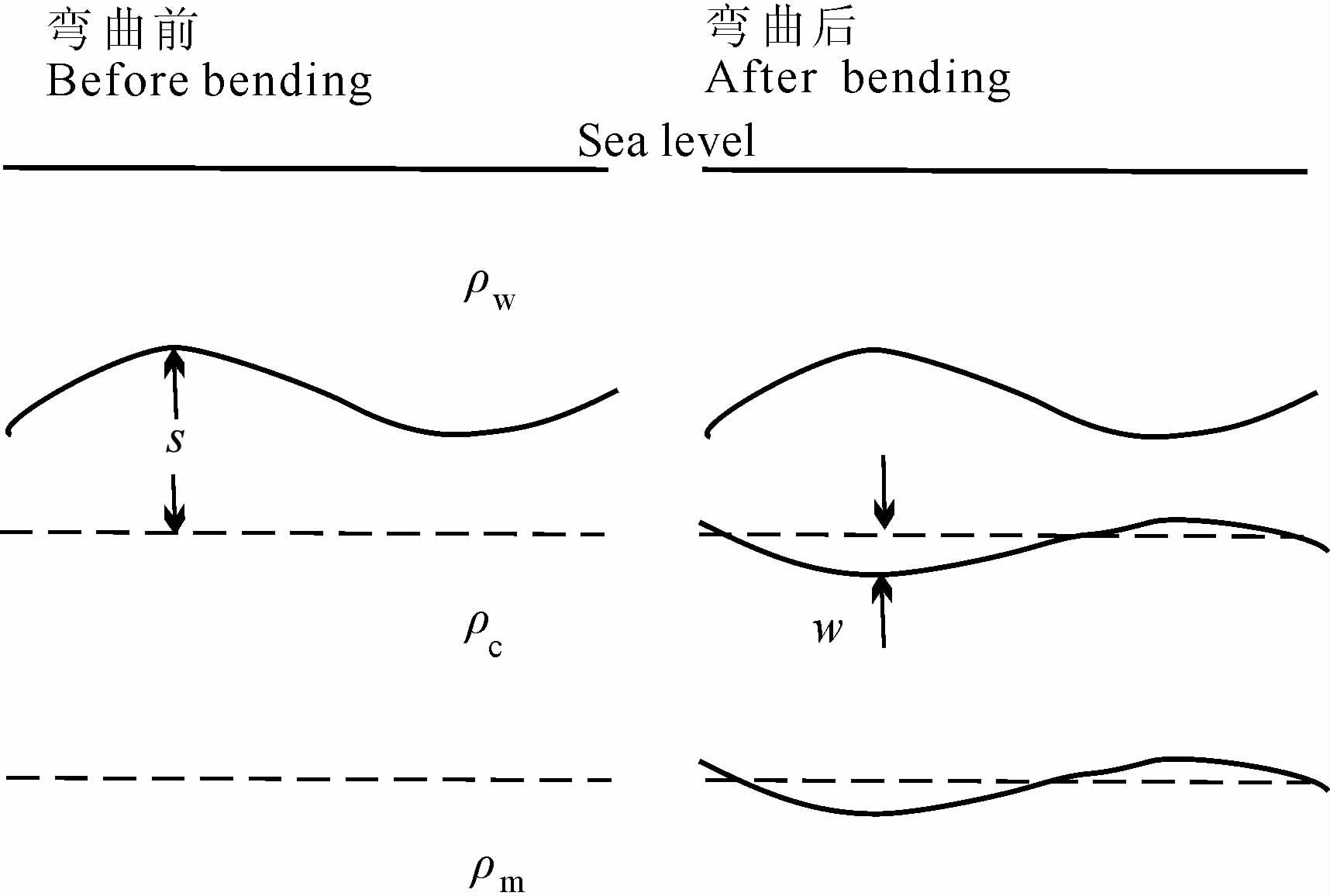
2 基本理论 2.1 曲形变基本方程假设海洋上岩石圈板块弯曲的基本模型如图 1所示.
|
图 1 海洋上岩石圈板块弯曲的基本模型.其中地形负载为s,弯曲形变量w Fig. 1 The model of deformation in the oceanic lithosphere, s is topographic load, w is the deformation of elastic plate |
从一般的弹性力学理论可知,在弹性限度范围内,当板块施加上负载L(x,y)后,会产生形变,其形变量w可由下列方程表示:
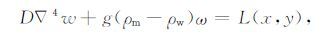
|
(1) |
这里,弯曲刚度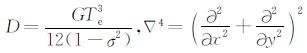
假如海洋上的地形负载为s,则形变方程可改写为:
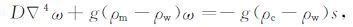
|
(2) |
上述方程(2)在空间域内求解是困难的,应变换到频率域上进行求解.方程(2)进行傅里叶变换得方程(3):
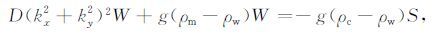
|
(3) |
式中频率域中的变量与空间域的变量一一对应.解(3),可得:

|
(4) |
这里k2 =kx2+ky2.式(4)是频率域内形变量与负荷的关系.
又因为地形E、负荷S和形变量W,存在下列关系:
E=S+W,
因此得:
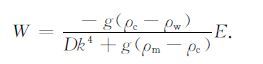
|
(5) |
这是频率域内形变量与地形的关系.
2.2 响应函数Z(k,Te)的计算海洋中地形负载作用下,弯曲板块在海平面上引起的重力异常可由海底地形的起伏界面和板块弯曲形变界面的密度差两部分产生(图 2),即:
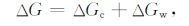
|
(6) |
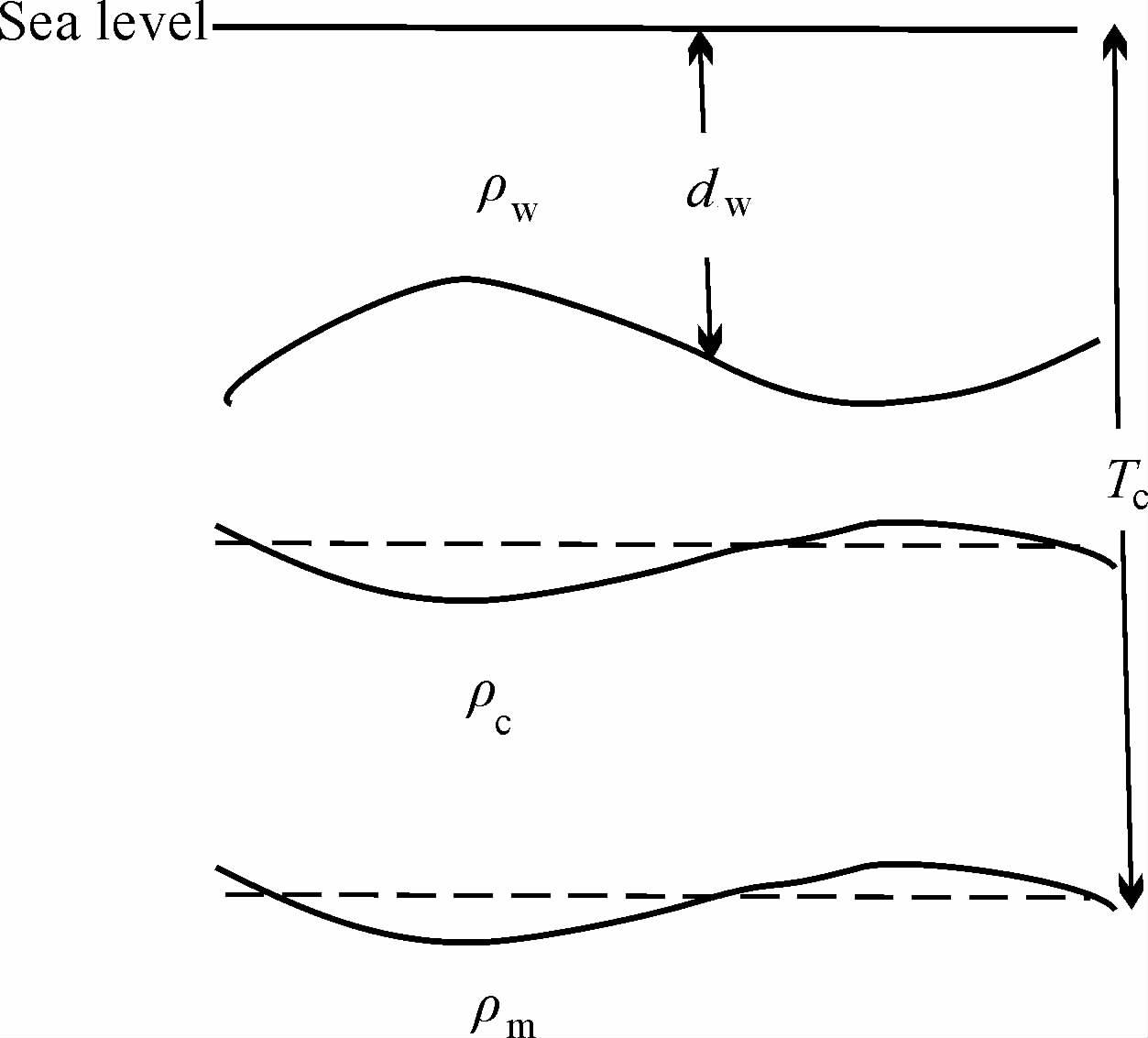
|
图 2 海洋中地形负载作用下,计算弯曲板块引起的重力异常的模型 Fig. 2 The model for calculating gravity anomaly causedby deformation oceanic plate |
而地形的起伏产生的重力异常的傅里叶变换ΔGw可表示为:
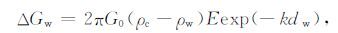
|
(7) |
其中dw 为海底深度,G0 为万有引力常数.E为地形的傅里叶变换.
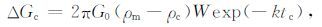
|
(8) |
其中tc 为地壳的厚度.W为板块形变量的傅里叶变换.
综合(6)、(7)、(8)式可得:
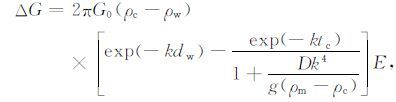
|
(9) |
又因
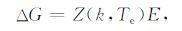
|
(10) |
其中Z(k,Te)为重力与地形变换中的响应函数.对比(9)和(10)可得
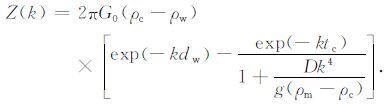
|
(11) |
这就是海洋上重力与地形之间的响应函数Z(k)具体表达式.它是频率k=2π/λ 的函数,也是弯曲刚度D的函数.因为弯曲刚度D是板块厚度Te 的函数,因此响应函数Z(k)也是板块厚度Te 的函数.一般选取一个板块厚度Te 的数值后,就可以作出一条响应函数Z(k)随频率k而变化的曲线.选取多个板块厚度Te 的数值,可作出多条响应函数Z(k)随频率k而变化的曲线,形成理论Z(k,Te)曲线族(图 3).
若(11)式中海底深度dw =0,即转换为陆地情况[2],响应函数Z(k)变为:

|
(12) |
板块厚度Te 的数值确定后,响应函数Z(k)随频率k而变化.这些曲线都有一个极值点.随着频率k=2π/λ的增大,响应函数Z(k)逐步增大达到极值点,通过极值点后,又逐步减少趋向2πG0(ρc -ρ).对于不同的板块厚度Te 值,响应函数Z(k)在极值点前区别较大,通过极值点后,很快趋于一致.在频率k较小区域,也就是重力的长波段,曲线的形态主要决定于板块厚度Te 的数值,也就是深部物质的重力作用;在频率k较大区域,也就是重力的短波段,曲线的形态主要决定于海底深度Wd 的数值,也就是浅部物质的重力作用.为了求取深部岩石圈板块的有效弹性厚度Te, 我们分析极值点前的波段,也就是说频率k较小的重力长波段区域,为了求出极值点,我们令$\frac{dZ}{dk}$=0.
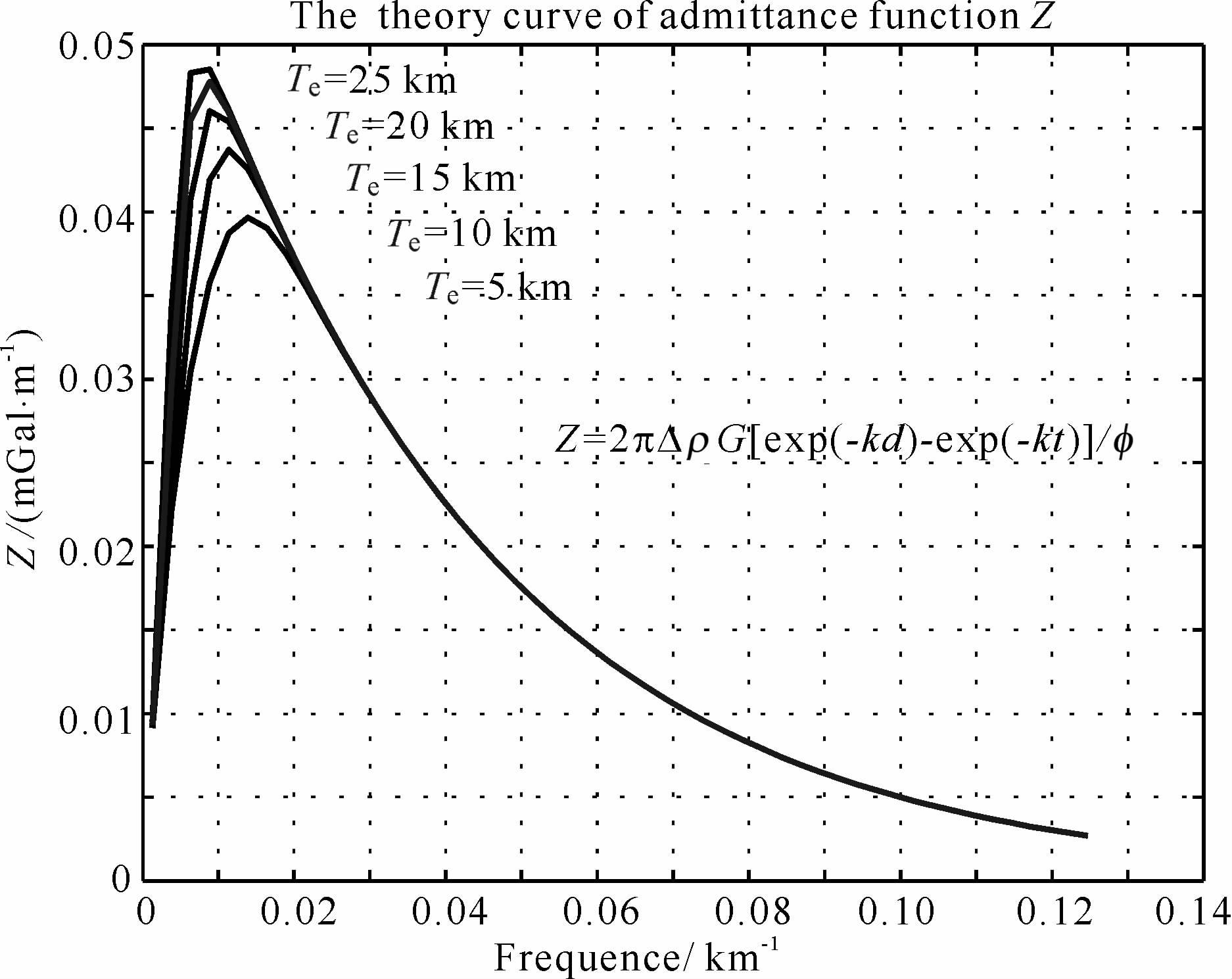
|
图 3 随频率k而变化的不同板块厚度Te 的Z(k,Te)曲线族(从上到下5条曲线分别对应Te的值为25,20,15,10,5km) Fig. 3 The theory curves of isostatic response function Z(k, Te) for different effective elastic thickness of oceanic lithosphere Te |
设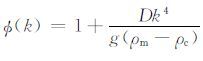
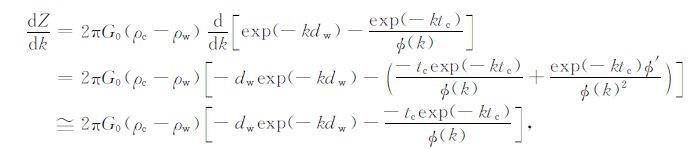
|
令$\frac{dZ}{dk}$=0
得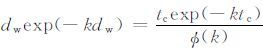
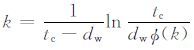
从图 3 来看,在响应函数Z(k,Te)极值点附近,对不同的岩石圈板块有效弹性厚度Te 理论响应函数Z(k,Te)曲线差别较大.在高频部分,对不同的岩石圈板块有效弹性厚度Te 理论响应函数Z(k,Te)曲线差别不大.因此,在分析不同的岩石圈板块有效弹性厚度Te 时,应着重考虑低频部分,特别是在理论曲线的极值点附近.假设海域中tc =20km, dw =5km, 若Φ(k)≈1,即板块的刚度近于零,取极限情况来讨论,则得k≈0.1,即λ≈60km, 曲线取极值.这也就是说,为了求取该海域的岩石圈板块的有效弹性厚度Te, 必须着重考虑波长大于60km的重力异常.
3 实测数据的响应函数Z(k,Te)求取海洋领域中,在海平面上观测的重力异常由自由空间重力异常表示.根据Dorman和Lewis的理论[12],在海洋中海底地形h与自由空间重力异常gf在频率域上的关系为:
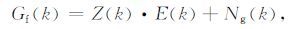
|
(13) |
其中Z(k)为响应函数,它表示单位地形负载和其相关的区域均衡补偿引起的重力脉冲响应,Gf 为自由空间重力异常gf 的傅里叶变换,E为海底地形h的傅里叶变换,Ng 为地球内部各层密度不均匀引起的地质噪音的傅里叶变换.
在实际数据归算中,求取响应函数Z(k)的一般方法是:在频率域内对不同的频率k取δk的圆环,求环内全方位的平均[12],即
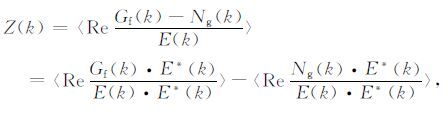
|
式中角括号表示频率域δk的圆环内全方位的平均,Re表示取实数部分,E* 表示E的共轭复数.地质噪音Ng 应与地形E不相关,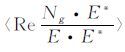
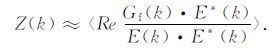
|
(14) |
响应函数Z(k)是单位地形负载和其相关的区域均衡补偿引起的重力z(X)的傅里叶变换,重力z(X)是地心向径X的函数,它的傅里叶变换Z(k)也是实函数[12].
4 南海部分海域岩石圈有效弹性厚度Te 的分析 4.1 南沙海域岩石圈有效弹性厚度Te 的分析我们选取研究范围是109.5°E-118°E,5°N-13.5°N南海的南沙海域.该区域包括整个南海南部海域(图 4,5),纵横跨越约一千公里,与国外学者[2, 5]研究的取值宽度相当.该海域在地质构造上大部分属于南沙地块.该海域有礼乐滩、万安滩等众多的岛礁、广阔的巽它陆架、南沙海槽等复杂的地形地貌.该海域有着复杂的地质构造单元,包括有曾母盆地、万安盆地、南薇盆地、南华盆地、礼乐盆地等众多的盆地、可能是古南海的俯冲带的南沙海槽以及沙巴推复构造带.在该海域研究南海南部岩石圈有效弹性厚度是较合适的,对南海南部的岩石圈及地质构造研究有积极的意义.
|
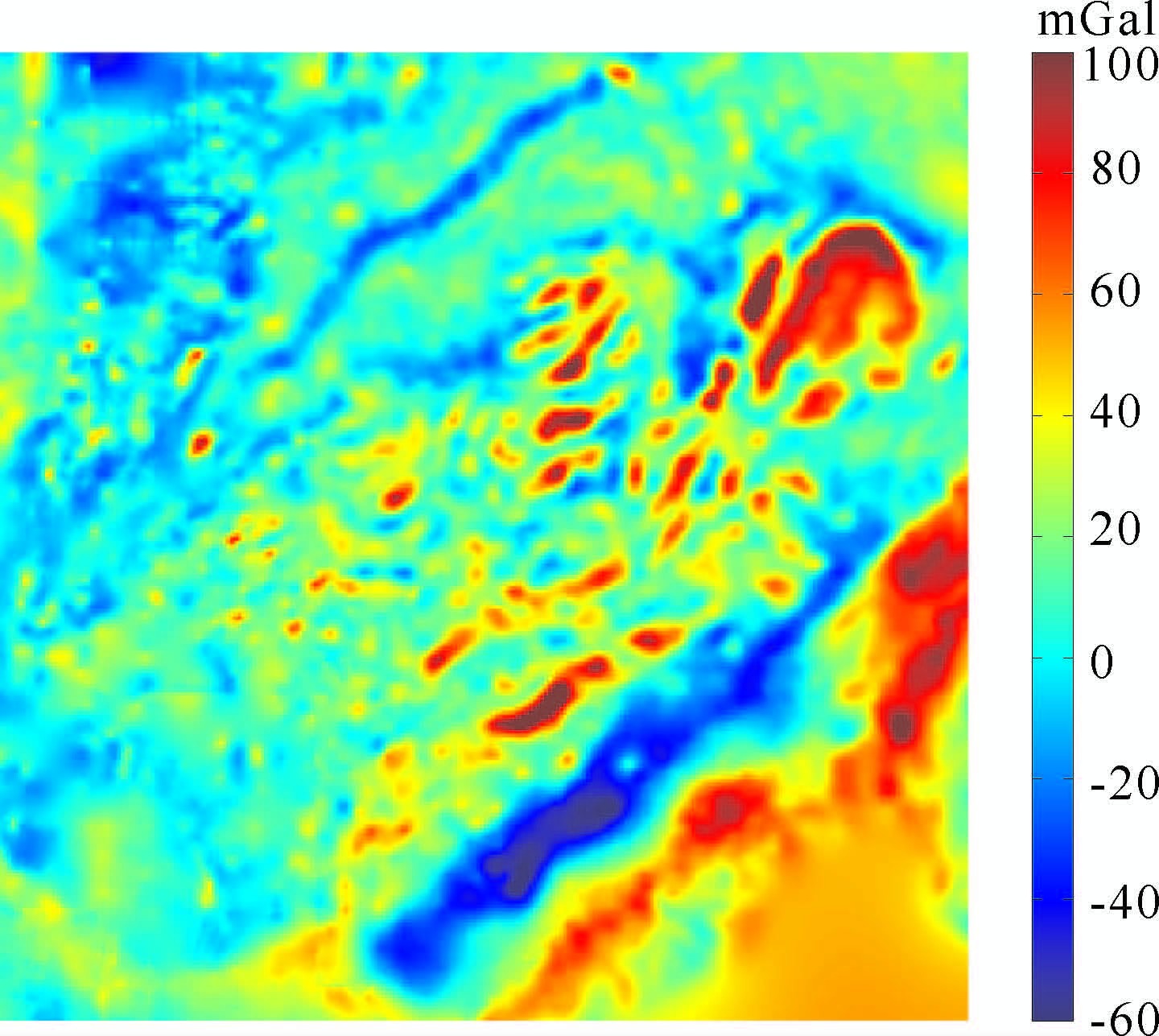
图 4 南沙海域重力影像 Fig. 4 The image of gravity data in Nansha sea area |
|
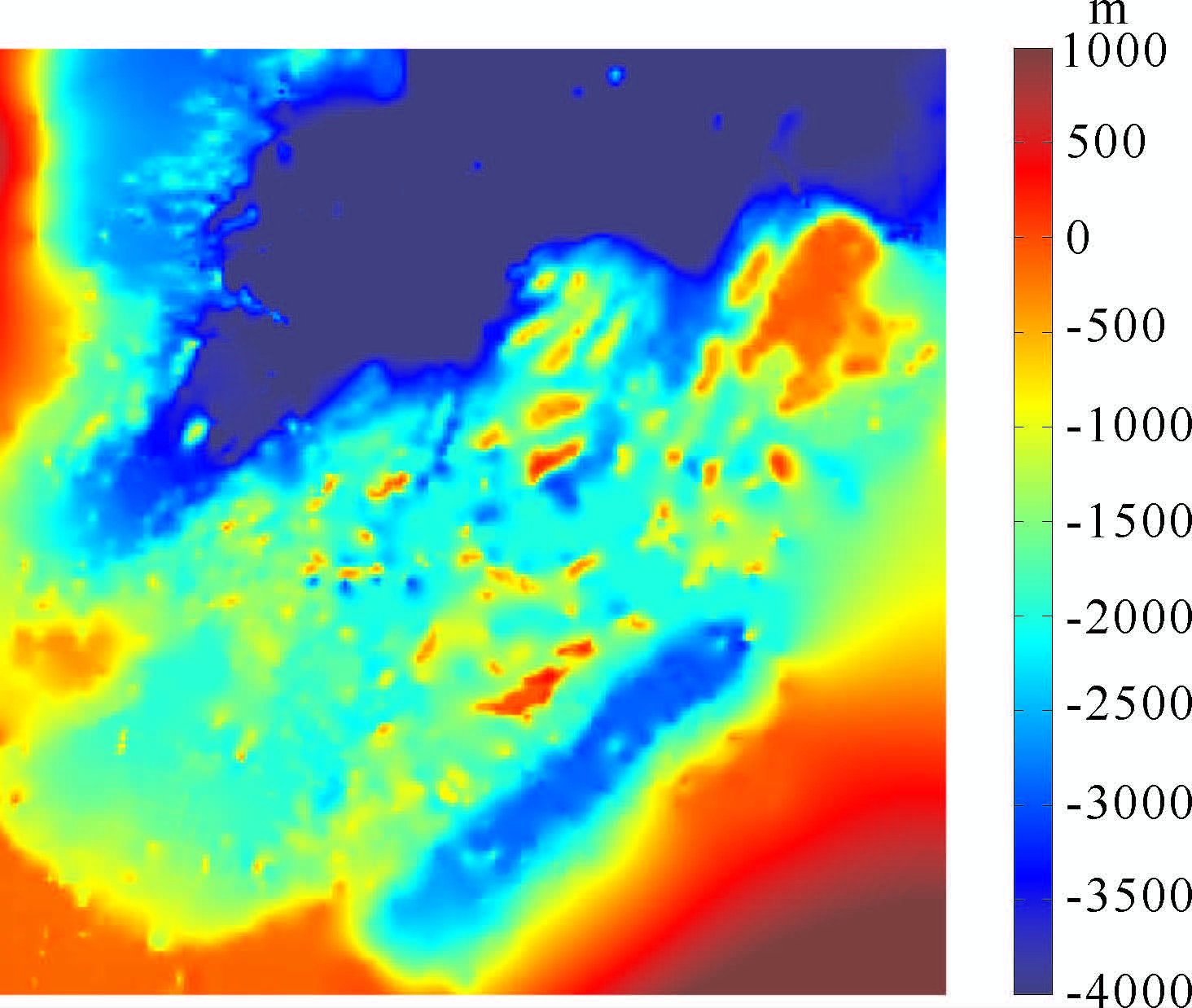
图 5 水深数据的影像 Fig. 5 The image of topographic data in Nansha sea area |
重力数据取自Sandwell的卫星测高重力数据和实测数据,水深数据取自南海多年来测量的实际资料.所有资料经网格化成网格数据,并符合FFT要求,进行FFT 变换.因为重力和水深数据均为实数,重力和水深数据的傅里叶变换对于kx轴和ky轴是对称的,因此仅取频率域的四分之一研究则可(图 6,7).
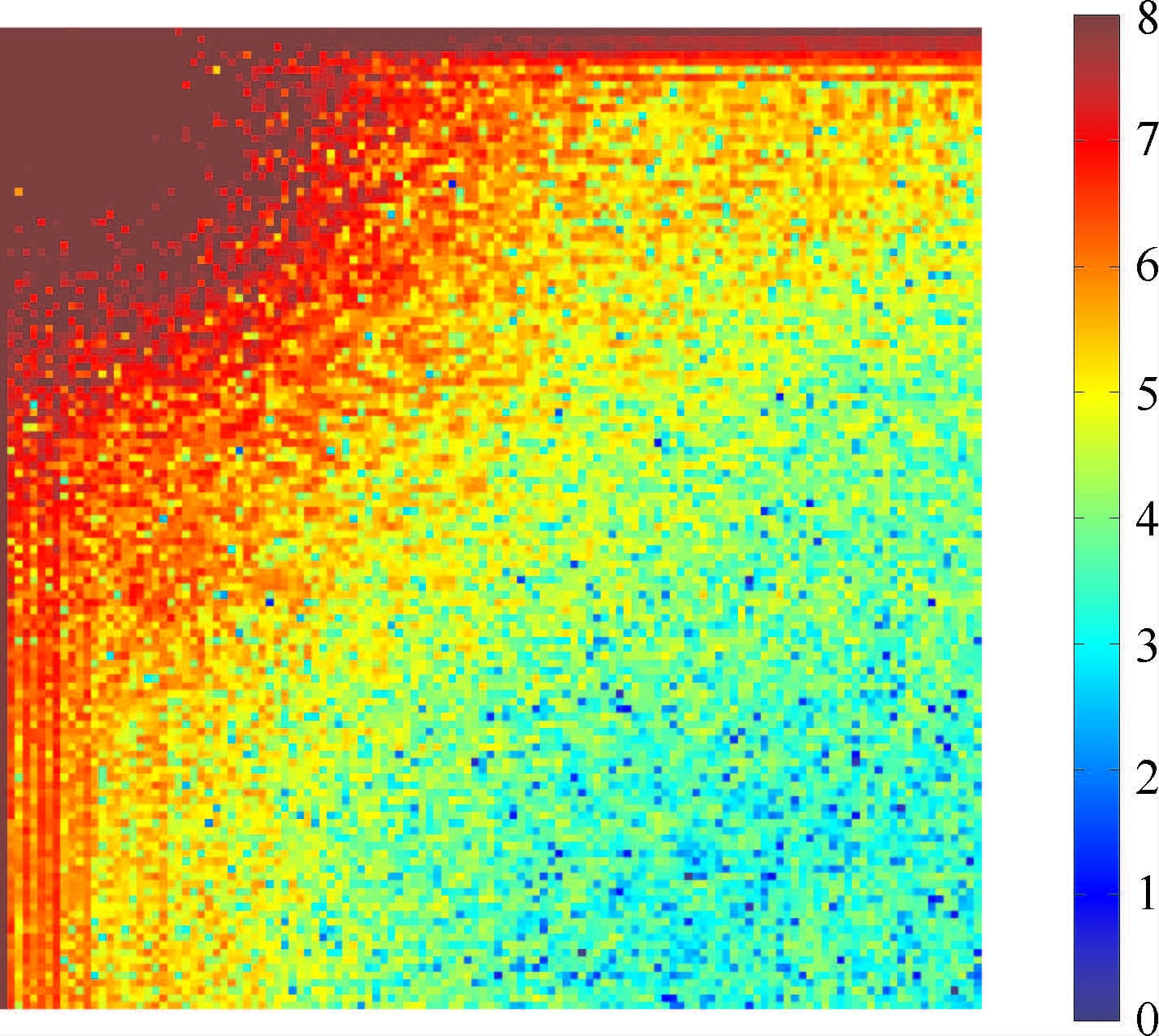
|
图 6 南沙海域重力的二维傅里叶变换后,频率域振幅谱(取自然对数)的四分之一图像 Fig. 6 The quarter image of amplitude spectrum (bylogarithmic conversion) for 2D Fourier transform of gravity in frequency domain in Nasha sea area |
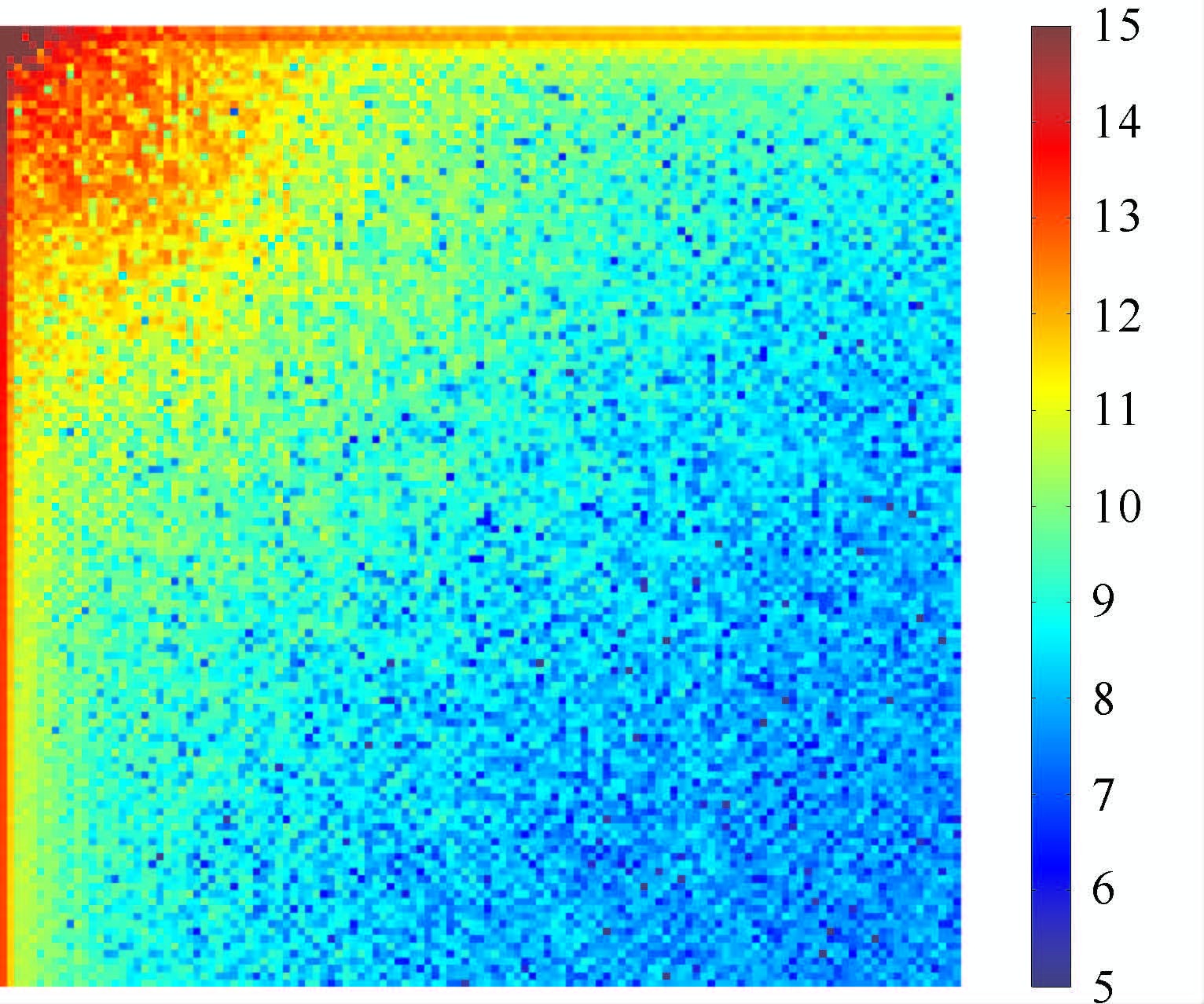
|
图 7 水深数据的二维傅里叶变换后,频率域振幅谱(取自然对数)的四分之一图像 Fig. 7 The quarter image of amplitude spectrum((by logarithmic conversion) for 2D Fourier transform of topography in frequency domain in Nasha sea area |
图 8是根据(14)式计算的实际数据的响应函数Z(k)曲线.实际的响应函数Z(k)与理论公式计算的响应函数曲线族进行比较分析,可得知实际数据的响应函数Z(k)与有效弹性厚度Te=10km 的理论曲线较吻合.因此,得知南沙海域的岩石圈有效弹性厚度Te 为10km.
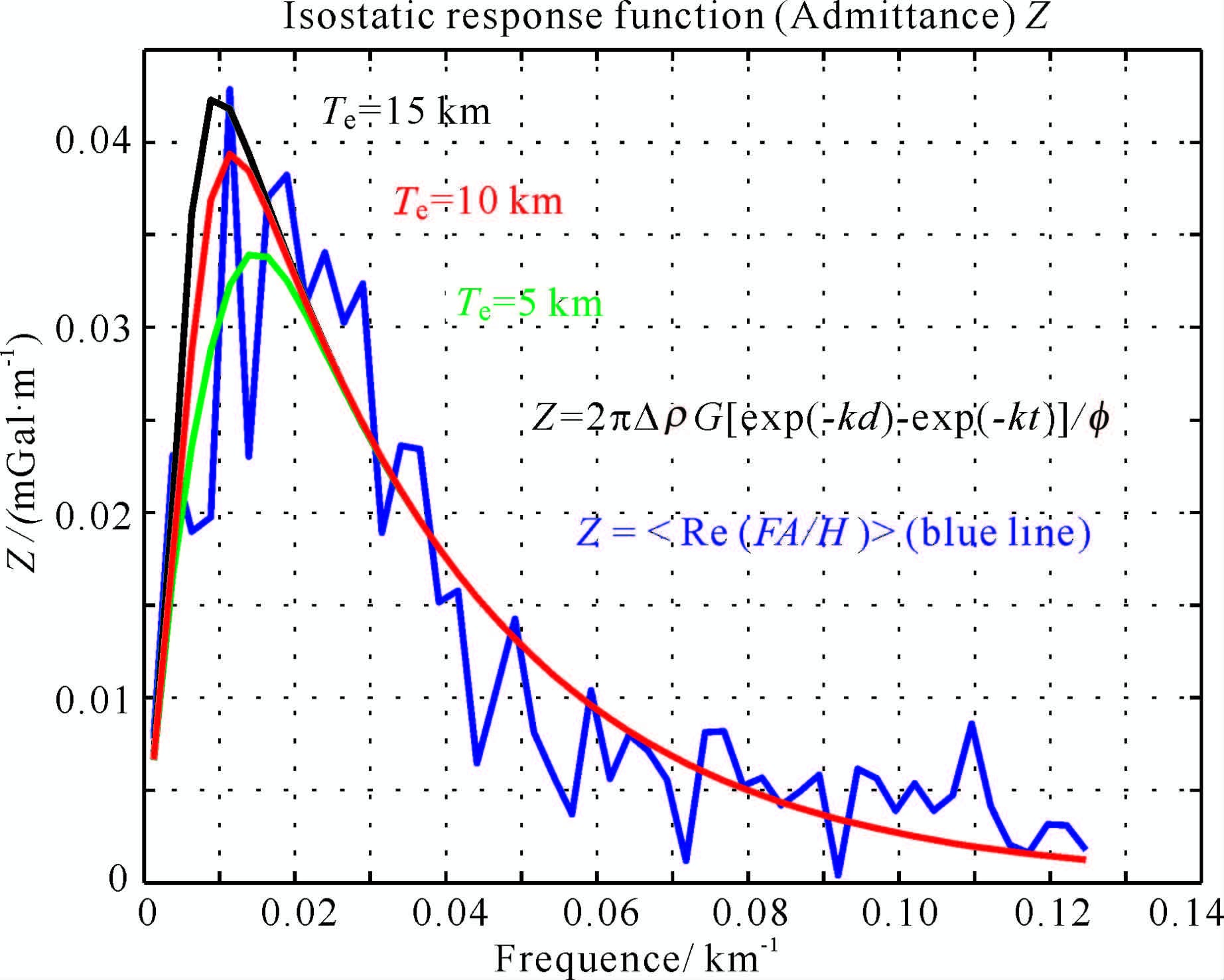
|
图 8 南沙海域实测数据导出的响应函数Z(k)曲线与理论公式计算的响应函数Z(k,Te)曲线族进行对比分析 Fig. 8 The comparison of the isostatic response function Z(k)derived from field data and the curves of theoretical isostatic response function Z(k,Te) in Nasha |
南海中央海盆是张裂的边缘海海盆.我们选取研究范围是115.10°E-119.35°E,13.15°N-17.40°N(图 9、10).该区域纵横跨越约500km.该海域在地壳结构上属于洋壳,地壳厚度为10~12km 左右(包括水深).海盆的深度约4000多米,该海域有黄岩岛等众多的海丘和海山.研究范围的中部15°N 附近东西向展布有黄岩岛等的链状海山,该海山链一般认为是残留的南海扩张中心.研究海域的东缘地质构造上是马尼拉海沟断裂,该断裂以东是北、西吕宋海槽过渡型地壳,断裂以西是南海中央海盆的洋壳.区域的西部边缘是中央海盆西缘断裂.断裂以西是中沙、西沙陆坡区,属过渡地壳.断裂以东为南海中央海盆的洋壳.
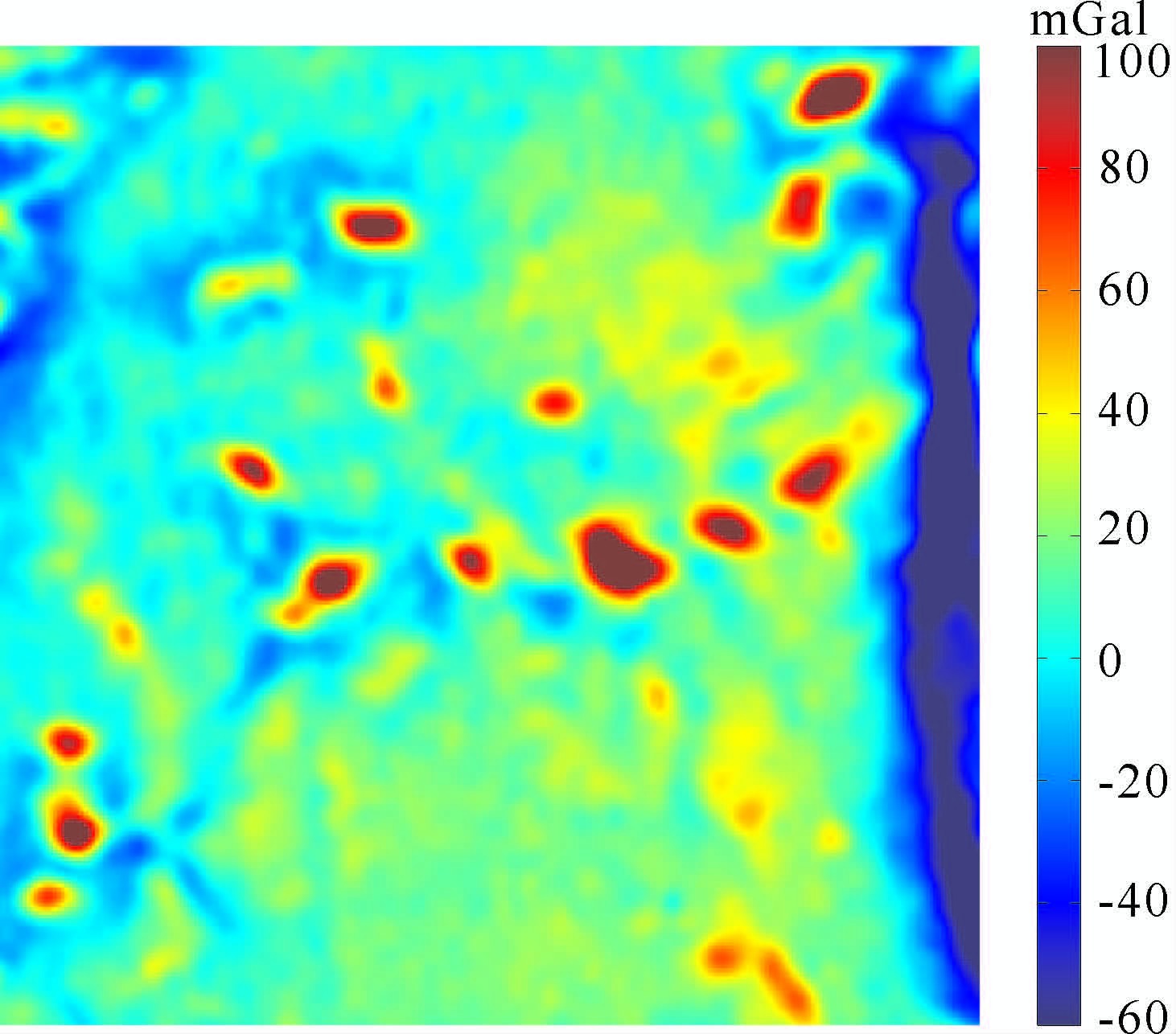
|
图 9 中央海盆重力的影像 Fig. 9 The tmage of gravity data in Centeral Basin of SCS (South China Sea) |
|
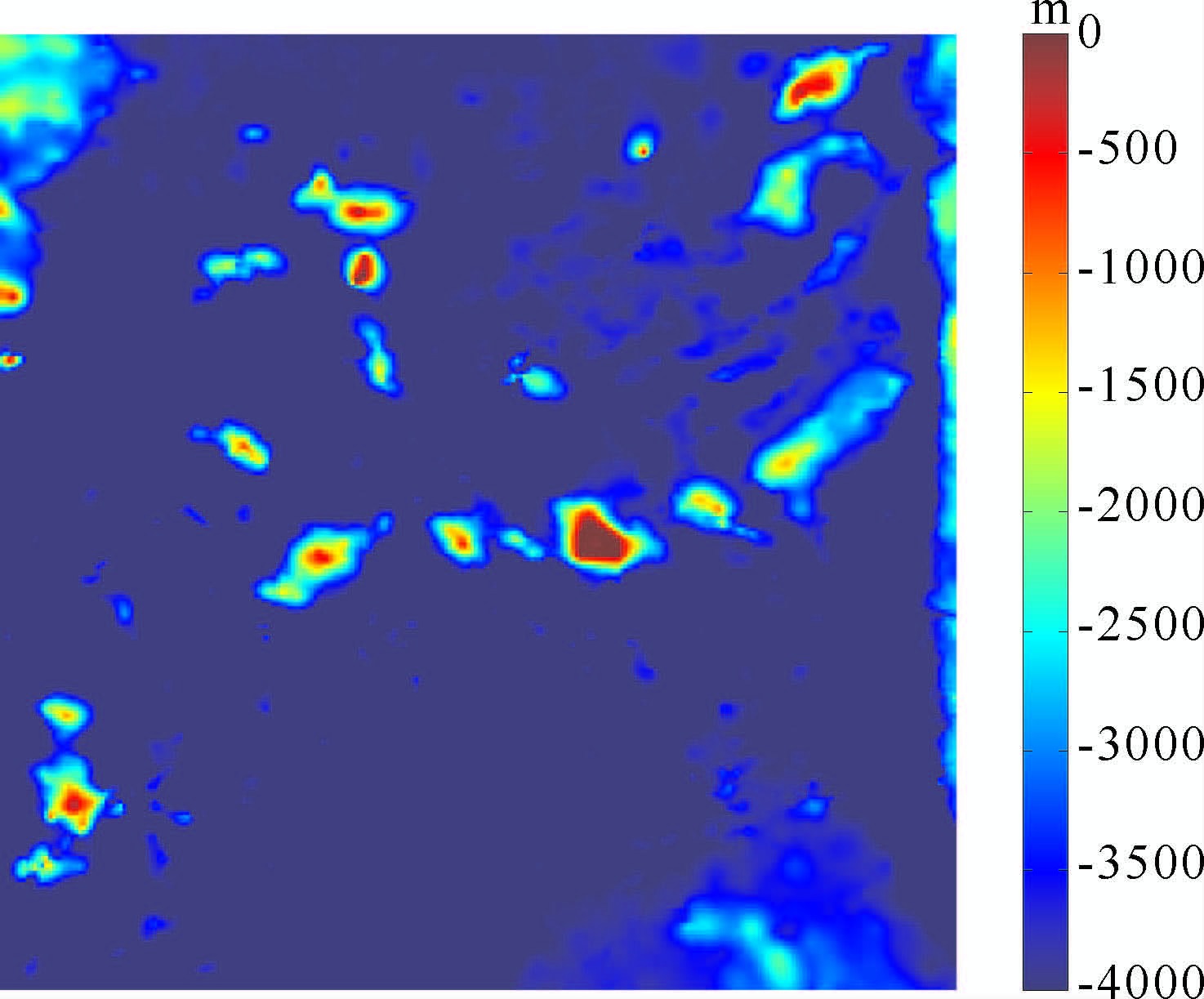
图 10 水深数据的影像 Fig. 10 The tnage of topographic data tn Centeral Basin of SCS |
重力和水深数据来自D.Sandwell的数据和实测数据.同样所有资料经网格化成网格数据,并符合FFT 要求,进行FFT 变换.因为重力和水深数据均为实数,重力和水深数据的傅里叶变换对于kx轴和ky轴是对称的,因此仅取频率域的四分之一研究则可.
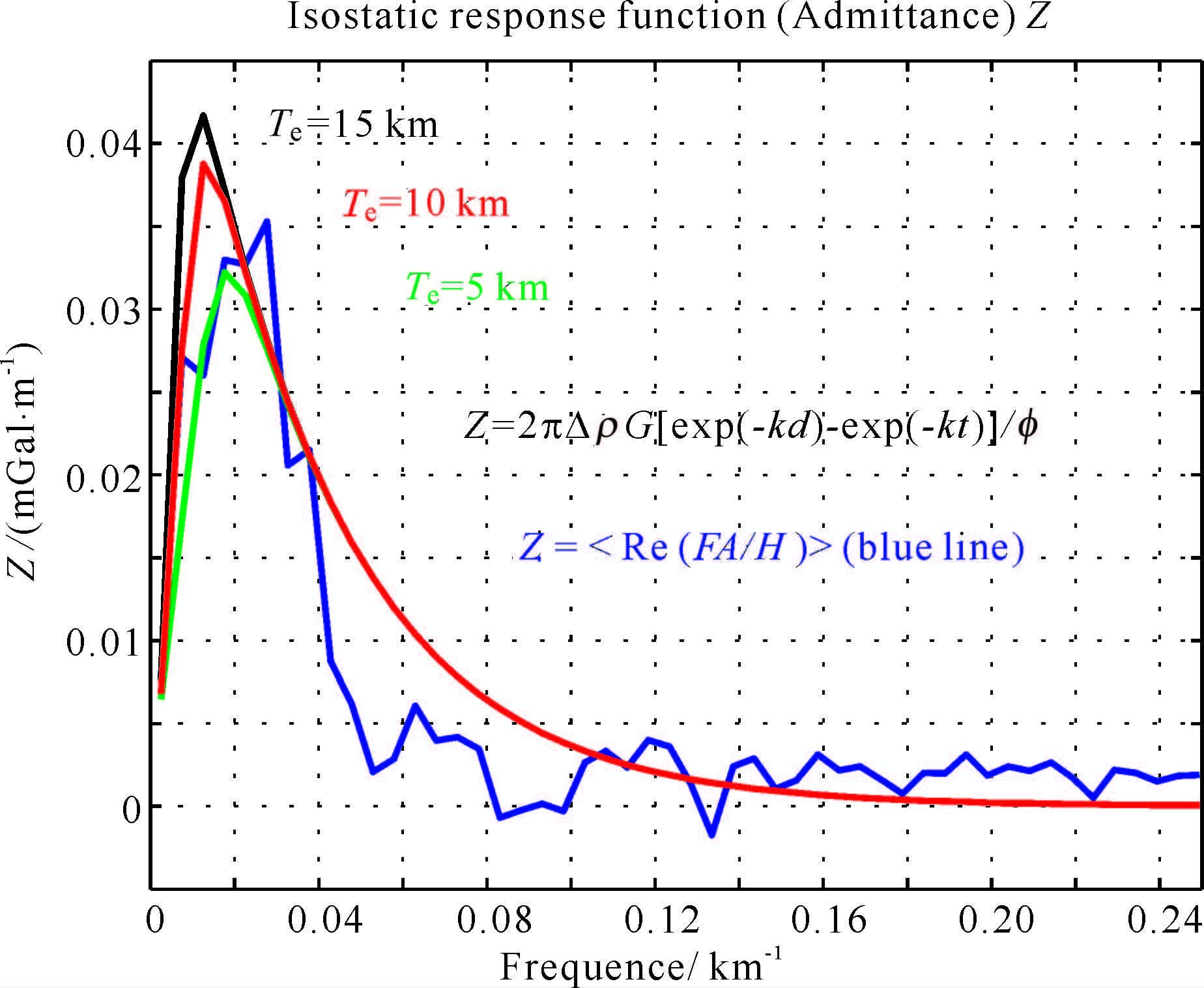
图 11是根据(14)式计算的实际数据的响应函数Z(k)曲线.实际的响应函数Z(k)与理论公式计算的响应函数曲线族进行比较分析,可知实际数据的响应函数Z(k)曲线在理论曲线Te 为10km 和5km 之间.因此,得知中央海盆的岩石圈有效弹性厚度Te 小于10km, 而大于5km, 在6~7km 左右.
|
图 11 南海中央海盆实测数据导出的响应函数Z(k)曲线与理论公式计算的响应函数Z(k,Te)曲线族进行对比分析 Fig. 11 The comparison of the isostatic response function Z(k)derived from field data and the curves of theoretical isostatic response function Z(k, Te) in Centeral Basin of SCS |
本文计算了南海部分海域的岩石圈有效弹性厚度.岩石圈的有效弹性厚度是反映岩石圈一种力学属性,是区域范围内讨论的一种岩石圈属性.本文估算了南海的南沙海域和南海中央海盆两海域的岩石圈有效弹性厚度分别为10km 和6~7km.中央海盆地区是较年轻、洋壳性质的岩石圈,其岩石圈挠曲刚度相对小些,而南沙海域是过渡型地壳,相应地其年龄也古老些,因此其岩石圈挠曲刚度相对强些.但不论是南海中央海盆或南沙海域其岩石圈有效弹性厚度都相对较小,这可能与这些区域的地壳张裂和拉伸有较大的关联,也与台湾西部和台湾海峡的前陆盆地的岩石圈有效厚度情况类似[11].南海是毗邻欧亚大陆的边缘海,它的岩石圈属性应该不同于大陆,也有别于大洋的情况.边缘海岩石圈的有效弹性厚度需要进一步深入研究.
5 结论(1) 基于不同的模型,海域的响应函数Z(k,Te)理论公式(11)与大陆的响应函数Z(k,Te)理论公式(12)是不同的.因此,用响应函数Z(k,Te)估算岩石圈的有效弹性厚度应根据海域与陆地不同情况,采用不同的理论公式.
(2) 对不同的有效弹性厚度Te, 海域的理论响应函数Z(k,Te)曲线在高频处区别不大,在适当的低频处有极值,位于该频域附近对不同的有效弹性厚度Te, 海域的理论响应函数Z(k,Te)曲线差别较大.因此,估算岩石圈的有效厚度应在适当的低频处.
(3) 运用上述的理论,分析实际测量数据的响应函数Z(k,Te),可估算到南沙海域的岩石圈有效弹性厚度约10km.中央海盆的岩石圈有效弹性厚度Te 小于10km, 而大于5km, 在6~7km 左右.
致谢本文的基本理论和分析曾与英国剑桥大学地球科学系的D.P.Mckenzie 教授讨论过,并得到其热情的帮助,在此表深切谢意.
| [1] | Forsyth D W. Subsurface loading and estimates of the flexural rigidity of continental lithosphere. J. Geophys. Res. , 1985, 90(B14): 12623-12632. DOI:10.1029/JB090iB14p12623 |
| [2] | Mckenzie D, Fairhead D. Estimates of the effective elastic thickness of the comtinental lithosphere from Bouguer and free air gravity anomalies. J. Geophys. Res. , 1997, 102(B12): 27523-27552. DOI:10.1029/97JB02481 |
| [3] | Watts A B. The strength of the Earth's crust. Marine Technology Society Journal , 1983, 17(1): 5-17. |
| [4] | Kalnins L M, Watts A B. Spatial variations in effective elastic thickness in the Western Pacific Ocean and their implications for Mesozoic volcanism. Earth Planet. Sci Lett. , 2009, 286(1-2): 89-100. DOI:10.1016/j.epsl.2009.06.018 |
| [5] | Watts A B. Isostasy and Flexure of the Lithosphere. Cambridge: Cambridge University Press, 2001 . |
| [6] | 赵俐红, 姜效典, 金煜, 等. 中国西部大陆岩石圈的有效弹性厚度研究. 地球科学 (中国地质大学学报) , 2004, 29(2): 183–190. Zhao L H, Jiang X D, Jin Y, et al. Effective elastic thickness of continental lithosphere in western China. Earth Science (Journal of China University of Geosciences) (in Chinese) , 2004, 29(2): 183-190. |
| [7] | 付永涛, 李继亮, 周辉, 等. 大陆岩石圈有效弹性厚度研究综述. 地质论评 , 2000, 46(2): 149–159. Fu Y T, Li J L, Zhou H, et al. Comments on the effective elastic thickness of continental lithosphere. Geological Review (in Chinese) , 2000, 46(2): 149-159. |
| [8] | 袁炳强, YvetteH P D, 程顺有, 等. 大陆岩石圈有效弹性厚度的计算及其地质意义. 地球学报 , 2002, 23(3): 269–272. Yuan B Q, Yvette H P Q, Cheng S Y, et al. The estimation of the effective elastic thickness of the continental lithosphere and its geological significance. Acta Geoscientia Sinica (in Chinese) , 2002, 23(3): 269-272. |
| [9] | 付永涛, 李安春, 秦蕴珊. 大洋和大陆边缘岩石圈有效弹性厚度的研究意义. 海洋地质与第四纪地质 , 2002, 22(3): 69–75. Fu Y T, Li A C, Qin Y S. Effective elastic thickness of the oceanic and continental marginal lithospheres. Marine Geology & Quaternary Geology (in Chinese) , 2002, 22(3): 69-75. |
| [10] | 赵俐红, 金翔龙, 高金耀, 等. 中西太平洋海山区的岩石圈有效弹性厚度及其地质意义. 地球科学 (中国地质大学学报) , 2010, 35(4): 637–644. Zhao L H, Jin X L, Gao J Y, et al. The effective elastic thickness of lithosphere in the mid-west Pacific and its geological significance. Earth Science (Journal of China University of Geosciences) (in Chinese) , 2010, 35(4): 637-644. DOI:10.3799/dqkx.2010.078 |
| [11] | Lin A T, Watts A B. Origin of West Taiwan basin by orogenic loading and flexure of a rifted continental margin. J. Geophys. Res. , 2002, 107(B9): 2185. |
| [12] | Lewis B R T, Dorman L M. Experimental Isostasy, 2, An isostatic model for the USA derived from gravity and topography data. J. Geophys. Res. , 1970, 75(17): 3367-3386. DOI:10.1029/JB075i017p03367 |
 2012, Vol. 55
2012, Vol. 55

