2. 北京市地球探测与信息技术重点实验室 中国石油大学, 北京 102249;
3. ERL, Massachusetts Institute of Technology, Cambridge, Massachusetts, US, 02139
2. Key Laboratory of Earth Prospecting and Information Technology, Beijing, China University of Petroleum, Beijing 102249, China;
3. ERL, Massachusetts Institute of Technology, Cambridge, Massachusetts, US, 02139
随钻测井是随着水平井及大斜度井的出现渐渐发展起来的先进测井技术.由于在钻井的同时完成测井作业,节约了完井时间,并能及时测量井下原状地层的参数,进行时间推移测井,因此随钻测井在近年来得到了广泛的应用[1-2].随钻声波测井作为随钻测井的关键技术之一,可以测量地层的纵横波速度信息[3-5],进而可以进行岩性识别、岩石力学分析、超压检测和孔隙度计算等.同时,利用随钻声波测井的反射波信息还可以进行地质导向服务,对钻井进程进行指导.
目前,随钻声波测井仪主要有三种测量方式:单极子、偶极子及四极子测量模式[4-7].通过利用单极子源、偶极子源和四极子源分别激发单极子、偶极子和四极子信号对地层速度信息进行测量.随钻测井环境下,钻杆占据了井孔大部分空间,对井孔波导产生了很大的影响,由于钻杆速度高于地层速度,导致接收到的信号中仪器波占主导地位,无法有效地获得地层纵横波的信号.此外,钻井过程中对钻杆强度的要求使得无法像电缆声波测井那样在仪器上刻槽来消除仪器波的影响.采用非对称偏心的点声源,可以一次激发同时得到单极子、偶极子和四极子信号,不但减少了测井占用时间,获得了更大的数据量,还可以联合利用三种模式波的数据对地层纵横波速度进行反演来消除仪器波的影响.为建立同时利用多极模式波信号测量地层纵横波速度的随钻声波测井实用技术,本文采用1∶12 的缩比模型进行非对称声源多极子随钻声波测井的实验室测量研究,采用6个接收器的接收阵列进行接收,声源和接收器之间用一根中空的钢棒进行连接以模拟实际随钻测井中的钻杆[8].
2 非对称偏心点声源波场的理论分析点声源在充满液体的井中激发得到多极子波直达波的位移势在柱坐标系下的表达式为[9]
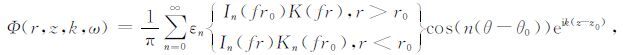
|
(1) |
式中,k为轴向波数;ω 为角频率;r和r0 分别为接收器和声源离井轴的距离,z和z0 分别为接收器和声源在z方向的位置;θ 和θ0 分别为接收器和声源的方位角.其中,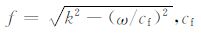
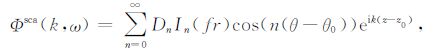
|
(2) |
其中,Dn可以通过对满足边界条件的系数矩阵进行求解得到.井中总的位移势可以表达为Φtot(k,ω)=Φ(k,ω)+Φsca(k,ω).
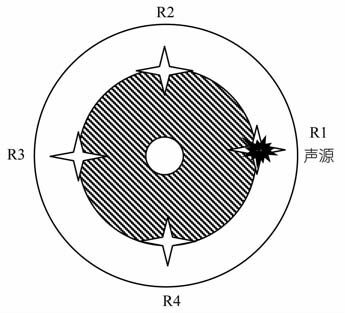
当采用非对称偏心点声源时,可以同时在井中激发各个模式波的信号.由于各模式波对于方位角θ互相正交,我们可以通过在井周方向上按不同的方位角进行接收,分离出各个单独的模式波信号.其中,各接收器到井轴距离是相等的,如图 1 所示,声源放在R1位置,4个接收器R1,R2,R3,R4分别与声源成0°,90°,180°,270°.这4个接收器接收到的总的位移势可表示为
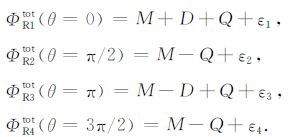
|
(3) |
其中,M、D和Q分别为单极子、偶极子和四极子信号的总的位移势.ε 为所有高阶模式的位移势的总和.通过对各接收器接收到的信号进行加减,就可以分别得到单极子、偶极子和四极子信号.公式如下:
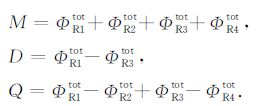
|
(4) |
同时,也可通过增加周向的接收器个数对更高阶模式波的信号进行提取,随钻环境下高阶模式信号能量相对于前三阶模式能量很微弱,此处忽略不记.
|
图 1 声源和接收器的在井周方位的分布位置 Fig. 1 Location of the source and receiver along the circle |
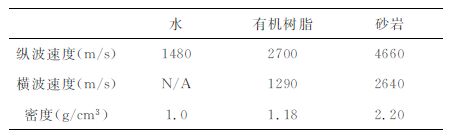
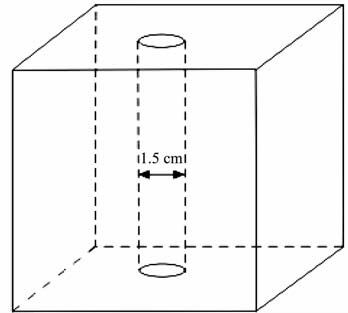
通过在有机树脂和砂岩两种介质中钻孔来模拟井眼,孔的直径为1.5cm(如图 2).有机树脂用来模拟软地层(定义为横波速度小于井眼流体声波速度,通常为泥岩和疏松砂岩类地层),砂岩用来模拟硬地层(定义为横波速度大于井眼流体声波速度,通常为坚实砂岩\碳酸盐岩类地层).在测量时将有机树脂和砂岩放到水槽中,让井眼充满水来模拟随钻声波测井的井眼环境.两种材料的密度和速度参数如表 1所示.
|
图 2 井眼模型示意图 Fig. 2 Schematic of the formation and the scaled borehole in the formation |
|
|
表 1 实验材料的物理参数 Table 1 Parameters of materials used in experiments |
本文中采用缩比的随钻声波测井仪器结构和尺寸如图 3所示.仪器由三部分组成:声源、接收器阵列和连接杆.声源和接收器都由压电陶瓷晶片做成.接收器阵列由6个接收器组成,从声源到第一个接收器的距离为10cm,两个相邻的接收器之间的距离为1.2cm.仪器为中空的结构,内径为0.4cm,外径为1.0cm.声源和接收器之间用中空的刚杆连接,以模拟钻杆.声源中心频率为60kHz,带宽为40kHz,激发波形为正弦波.
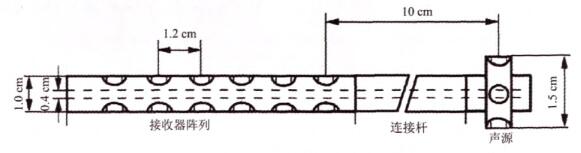
|
图 3 仪器结构示意图 Fig. 3 Schematic of the scaled tool |
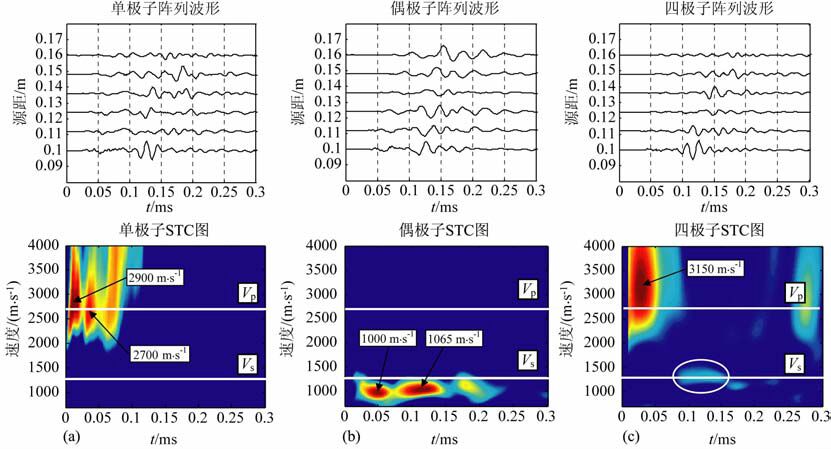
图 4为在有机树脂(软地层)模型中测量的全波列波形及各接受阵列的时间慢度相关图(STC图)[10],图中两条白线分别表示模型的纵波(Vp)和横波(Vs)速度.
|
图 4 软地层(有机树脂)中测量得到的阵列波形及STC相关图 Fig. 4 Acoustic waveforms and their semblance plots in time domain when the tool works in the soft formation (Lucite) |
由单极子的测量结果(图 4a)可以看到,在非对称点声源情况下,仪器的单极子模式波在STC 图上速度显示为2900m/s,可以得到明显的地层纵波速度为2700m/s,与模型纵波速度值吻合.由于本实验采用缩比模型,声源频率较高,换能器尺寸相比井眼尺寸较大,单极子模式时,无法激发有效的斯通利波,故在STC 图上低于地层横波速度的地方并没有出现斯通利波的信号.
由偶极子信号的STC图(图 4b)可以得到,采用非对称点声源在随钻环境下可以得到明显的仪器偶极模式波(1000m/s)和地层的偶极模式波(1065m/s),两种模式波都表现出明显的频散.同时,从图 4 中可知,由于偶极子模式波存在频散,在时间域的时间慢度相关法得到的地层偶极子模式波不能真实地反应地层的横波速度,STC 图上的地层偶极模式波的速度要略低于地层横波速.要确定真实的地层横波速度,需要对偶极模式信号进行频散校正.
由四极子模式波的STC 图(图 4c)分析可以得到,在稍高于地层纵波速度的位置出现了明显的仪器四极子波的信号,STC图上拾取的速度为3150m/s.
实际测量过程中并不能得到纯净的地层四极子信号,仪器波会影响四极子模式时的测量结果.在地层横波速度附近,也得到了明显的地层四极子信号,如椭圆区域所示.通过STC 图的识别,可以得到该信号的速度为1290m/s,为地层的横波速度.同时,由STC 图也可以得到:四极子信号也存在频散,实际处理时需要对四极子信号进行频散校正.
本文通过计算单极子、偶极子、四极子模式波信号的频率-速度相关图[11],对各个信号进行进一步的频域分析,并与理论的频散曲线进行了对比,如图 5所示,其中黑色点线为理论频散曲线.由单极子的频散结果(图 5a)可以得到,本文所采用实验条件无法有效地激发斯通利波信号,在频散图上只有很微弱的反应(椭圆区域).由偶极子和四极子的频散图(图 5(b,c))可以看出,本实验所测得的数据得到的频散曲线和理论曲线有较好的吻合.结合前面STC图的结果可知,由于随钻环境比较复杂,时间域的分析无法确定准确的地层纵横波速度,频散曲线也证实了地层的偶极子和四极子信号的频散曲线的截止值和地层的横波速度并不完全相等,故需要利用频散曲线联合偶极子和四极子信号对地层的横波速度进行反演,提高求取速度的精确性.
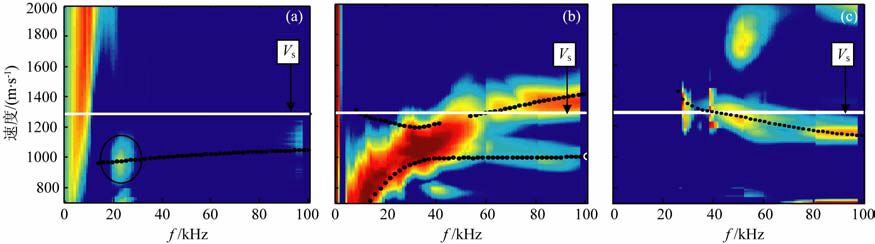
|
图 5 软地层(有机树脂)中各模式波的频散曲线 (a)单极子模式;(b)偶极子模式;(c)四极子模式. Fig. 5 Dispersion curves of the mode waves measured in soft formation (Lucite)(a) Monopole; (b) Dipole; (c) Quadrupole. |
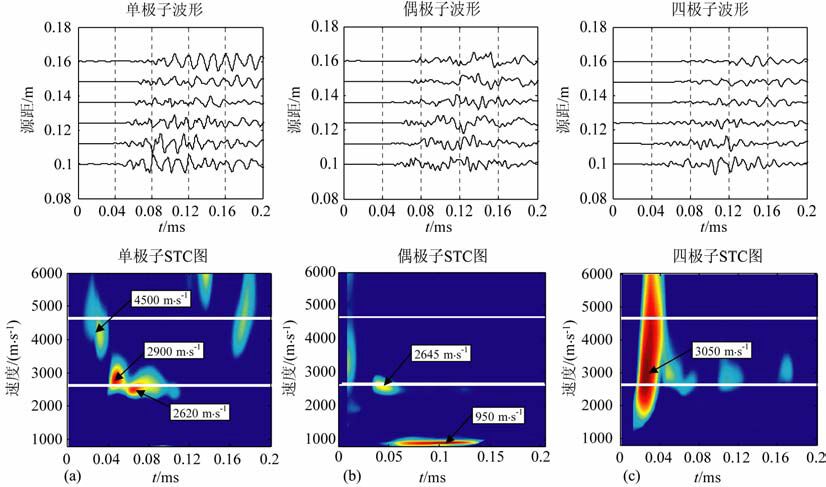
图 6为在砂岩(硬地层)模型中测量的全波列波形及各接受阵列的时间时差相关图(STC 图).图中两条白线分别表示模型的纵波(Vp)和横波(Vs)速度.
|
图 6 硬地层(砂岩)中测量得到的阵列波形及STC相关图 Fig. 6 Acoustic waveforms and their semblance plots in time domainwhen the tool works in the hard formation (Sandstone) |
由硬地层的单极子波形图(图 6a)无法看到明显的斯通利波成分,在STC 图中也说明了这一点现象,原因同软地层,由于缩比模型采用声源频率太高,加之发射探头尺寸相对于井眼尺寸较大,无法有效地激发斯通利波.在STC 图上拾取地层纵波的速度为4500m/s,略低于地层的真实纵波速度.在地层横波速度值上方,有明显的相关值较大的信号响应,拾取其速度为2900 m/s,为仪器波的单极子模式,和软地层情况下得到仪器单极子波速度相同.地层横波信号即为2620m/s的极大值点,比真实的模型横波速度略低.说明由于随钻环境复杂,钻杆的影响,在时间域的处理方法无法得到准确的地层纵横波速度,需要通过其他的处理,尽可能地消除仪器的影响.
硬地层情况下的偶极子STC 图(图 6b)相对于单极子来说,要干净很多.在硬地层情况下,对于偶极子模式,可以得到明显的地层偶极子模式波的信号,即图中2645m/s的信号区域,可以看到偶极子模式波有明显的频散.同时,在偶极子模式下,还可以测得仪器的偶极子模式波,速度为950m/s,此结果也与软地层的偶极子模式一致,只是速度值相比软地层情况下略小.
由四极子模式波STC 图(图 6c)可知,由于仪器的四极子波信号较强,即图中速度值3050m/s的信号部分掩盖了地层的四极子信号,在时域分析的结果无法获得地层四极子波的信息.需要对其进行进一步的频域分析才能获得地层四极子波的信号特征.
图 7 为分别对硬地层中的三种模式波求取频率-速度相关图得到的各模式波的频散图,黑色点线为理论的频散曲线.由单极子的频散图(图 7a)可得,单极子信号相对于偶极子和四极子频率范围稍高.从频散图上可以得到地层的纵横波速度,同时,也验证了单极子模式下本文所采用的模型和声源装置无法得到斯通利波的信号.由偶极子和四极子模式波的频散图和理论频散曲线的对比可以得到,本实验所测得的数据得到的频散曲线和理论曲线有较好的吻合.
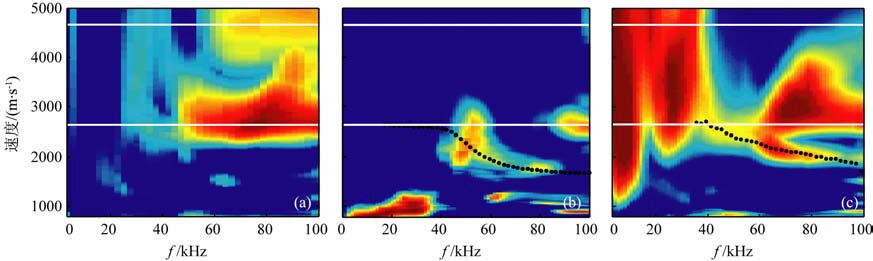
|
图 7 硬地层(砂岩)中各模式波的频散曲线 (a)单极子模式;(b)偶极子模式;(c)四极子模式. Fig. 7 Dispersion curves of the mode waves measured in hard formation (Sandstone) (a) Monopole; (b) Dipole; (c) Quadrupole. |
本文采用缩比模型,用中空的钢杆模拟钻杆,在实验室对随钻声波测井进行了测量研究.采用了非对称点声源作为激发源,采用4 个方位方向分布的6组接收器组成的阵列进行接收.通过对波形的时域及频域的相关分析,可以得出如下结论:
(1) 采用非对称点声源进行随钻声波测量,一次测量,同时得到三种模式波是可行的,能有效地测得地层的单极子、偶极子和四极子信号.
(2) 由于随钻声波测井的环境复杂性,仅仅对随钻声波数据进行时域分析无法得到准确的地层速度信息,需要对测得的各模式波数据进行频率域的分析,结合时间域的分析结果才能更准确地确定地层速度.
(3) 由于采用非对称声源一次测量即可得到三种模式波的信号,故可以联合三种模式波的信息对地层速度进行评价,由此解决随钻声波测井环境下仪器波等造成的干扰问题,获得更准确的地层纵横波速度值.
致谢感谢国家留学基金委资助,可以在美国麻省理工学院进行理论学习及完成文中所述实验.
| [1] | 时鹏程. 随钻测井技术在我国石油勘探开发中的应用. 测井技术 , 2002, 26(6): 441–445. Shi P C. M/LWD technology plays an important role in China oilfield development. Well Logging Technology (in Chinese) , 2002, 26(6): 441-445. |
| [2] | 王华, 陶果, 张绪健. 随钻声波测井研究进展. 测井技术 , 2009, 33(3): 197–203. Wang H, Tao G, Zhang X J. Review on the development of sonic logging while drilling. Well Logging Technology (in Chinese) , 2009, 33(3): 197-203. |
| [3] | Aron J, Chang S K, Dworak R, et al. Sonic compressional measurements while drilling.//SPWLA 35th Annual Logging Symposium.. Tulsa, Oklahoma, United States , 1994: 19-22. |
| [4] | Tang X M, Wang T, Patterson D. Multipole acoustic logging while drilling. //72nd Ann. Internat Mtg. Soc. Expi. Geophys , 2002(364): 368. |
| [5] | Tang X M, Dubinsky V, Wang T, et al. Shear-velocity measurement in the logging-while-drilling environment: modeling and field evaluations. SPWLA 43rd Annual Logging Symposium, Oiso, Japan , 2002: 2-5. |
| [6] | 崔志文. 多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究. 吉林: 吉林大学, 2004 . Cui Z W. Theoretical and numerical study of modified Biot's models, acoustoelectric well logging and acoustic logging while drilling excited by multipole acoustic sources (in Chinese). Jilin: Jilin University, 2004 . |
| [7] | 王华, 陶果, 王兵, 等. 多极子随钻声波测井波场模拟与采集模式分析. 地球物理学报 , 2009, 52(9): 2402–2409. Wang H, Tao G, Wang B, et al. Wave field simulation and data acquisition scheme analysis for LWD acoustic tool. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2402-2409. |
| [8] | Zhu Z Y, Toksoz M N, Rao R M, et al. Experimental studies of monopole, dipole, and quadrupole acoustic logging while drilling (LWD) with scaled borehole models. Geophysics , 2008, 73(4): 133-143. DOI:10.1190/1.2919827 |
| [9] | 唐晓明, 郑传汉. 定量测井声学. 北京: 石油工业出版社, 2004 . Tang X M, Zheng C H. Quantitative Borehole Acoustic Methods (in Chinese). Beijing: Petroleum Industry Press, 2004 . |
| [10] | Kimball C V, Marzetta T L. Semblance processing of borehole acoustic array data. Geophysics , 1986, 49(3): 274-281. |
| [11] | Rao R M, Toks?z M N. Dispersive wave analysis-Method and applications.//Consortium Reports of Earth Resources Laboratory Department in Massachusetts Institute of Technology. Cambridge, MA, USA , 2005. |
 2012, Vol. 55
2012, Vol. 55