2. 电子科技大学宽带光纤传输与通信网技术教育部重点实验室, 成都 611731;
3. 成都理工大学油气藏地质与开发工程国家重点实验室, 成都 610059
2. Key Laboratory of Broadband Optical Fiber Transmission and Communication Networks, University of Electronic Science and Technology of China, Chengdu 611731, China;
3. State Key Laboratory of Oil and Gas Reservoir Geology and Exploration, Chengdu University of Technology, Chengdu 610059, China
地球物理反演起源于20 世纪20 年代,由于观测数据的不完备性和复杂性,在经历了近一个世纪的发展后,反问题求解依然是地球物理研究领域的热点和难点问题.叠后地震数据不能反映反射振幅随偏移距变化等重要信息,无法获得精确的反演结果,难以完全满足岩性油气藏勘探开发的需要.AVO(Amplitude Variation with Offset,地震反射振幅与炮检距的关系)叠前反演利用Zoeppritz方程作为理论基础[1],研究地震道集数据振幅与炮检距的关系,通过利用叠前地震数据同时获得纵波、横波、密度和泊松比等参数,已成为油气储层预测研究的热点技术之一[2-4].
现有地球物理反演方法为了求解方便,大都假设干扰噪声属于高斯白噪声.Arild Buland 在假设噪声服从零均值高斯分布的情况下给出了贝叶斯线性反演流程[5];Ulrich Theune引入数字图像锐化技术,研究了高斯噪声条件下的叠前AVA (Amplitude Variation with Angle,地震反射振幅与入射角的关系)反演方法[6].陈建江等建立了振幅随偏移距变化波阻抗反演公式的一阶差分模型及褶积模型,在噪声为高斯分布的条件下表示了高斯似然函数,推导了基于贝叶斯理论的AVO 波阻抗反演公式[4];杨迪琨等从基于贝叶斯理论的反演观点出发,给出了一种将数据不确定性转移到模型空间概率密度函数的方法,假设噪声服从高斯分布,推导出后验分布概率的计算公式[7].
在噪声为高斯白噪的假设条件下,现有方法对信噪比相对较高的叠后资料反演问题进行了较为成功的反演.对信噪比相对较低的叠前反演问题,尤其是对某些复杂储层(如生物礁储层)的叠前反演问题时,高斯白噪的假设使这些方法在估计系统状态方面可能存在较大的误差,甚至可能发散.我们认为高斯白噪假设可能是阻碍目前地震叠前反演方法技术进步的关键问题之一.基于噪声非高斯的假设已经引起了很多领域学者的关注,而且在盲源分离[8]和脑电图反问题[9]等实际运用中取得了很好的反演效果.OmidKarimi在ArildBuland研究基础上[5],讨论了地震噪声及先验的分布情况,将高斯线性AVO反演进行推广,得到基于偏高斯分布的贝叶斯AVO反演[10].
本文在对A、B 两个地区多口井的噪声进行分布统计后得出结论:在叠前反演中,地震道数据中既包含高斯噪声,同时又包含大量的非高斯噪声,这使得传统的基于噪声高斯分布假设的反演方法性能差强人意.为此,本文提出了基于L1、L2 混合范数的叠前三参数非高斯反演方法,L1范数可以抑制各种非高斯噪声,L2范数可以抑制高斯噪声;鉴于目标函数的不可导性,采用不需要求解目标函数梯度的Powell算法对目标函数进行求解,反演结果验证了算法的有效性.
2 噪声分布的非高斯特征本文采用Gidlow 近似方程表示波阻抗和密度反射系数的近似关系[11]:
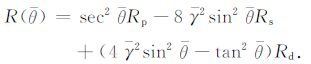
|
(1) |
Daniel P.Hampson等给出了含泥岩线关系的褶积模型[12],地震观测数据d= [d1,d2,…,dN]T可表示为
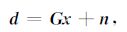
|
(2) |
其中,G为正演模型矩阵,x= [Lp ΔLs ΔLd]T为地层参数,n= [n11,n12,…,nN]T 表示观测噪声.
反演的目标便是利用褶积模型,从收集到的地震数据d中反演出可靠的地层参数x.根据信号处理理论,提取信息的准确程度及精确程度很大程度上取决于所用的概率模型,因此,在实际应用中,必须针对实际情况对噪声的特性进行分析,设计可靠的算法.
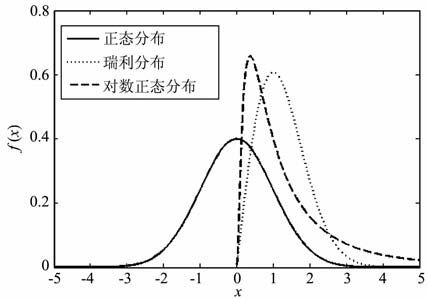
2.1 高斯噪声与非高斯噪声高斯噪声是指概率密度函数服从高斯分布的一类噪声,其概率密度函数呈现对称性;而非高斯噪声是指统计特性偏离高斯分布的噪声,其概率密度函数图像呈现出不对称性和厚尾性(瑞利分布、对数正态分布等),如图 1所示.
|
图 1 常见分布的概率密度函数 Fig. 1 Common probability density functions |
定理1:设随机变量X1,X2,…,Xn相互独立,且任一随机变量Xi的均值、标准差、三阶中心矩和三阶绝对矩分别为:μi,δi,ai,bi,且μi,δi≠0;令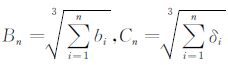
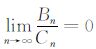
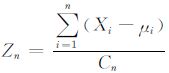
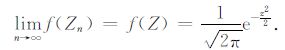
|
根据中心极限定理,足够多独立随机变量之和的分布趋向于高斯分布.因此,在实际应用中大多数情况都假设信号和噪声是满足中心极限定理的,即服从高斯分布.由于基于高斯假设的信号处理算法易于进行理论上的分析,在传统的信号处理中,高斯信号模型占据了主导地位.
尽管高斯噪声模型能很好地描述大多数系统模型,但是在实际应用中,往往存在大量的非高斯噪声.噪声的非高斯特性常常引起基于高斯噪声假设设计的系统性能显著退化,甚至不能正常工作.以雷达系统为例,由于大气和人工产生的各种随机性的脉冲噪声对信道的干扰,总的噪声过程将会偏离高斯分布,而呈现出拖尾分布的特性,使得基于高斯分布假设的经典最优监测器的性能将严重恶化[13],而基于非高斯噪声假设的雷达探测则能在实际处理中取得很好的效果[14].由此可见,尽管基于高斯模型的假设通常可以简化我们算法的设计,但在非高斯噪声干扰的情况下却很难得到可靠的结果.
现有叠前反演为了求解的方便,也大都假设噪声服从高斯模型.针对叠前反演问题,由于地震数据采集时各种杂波和人为噪声的影响,可能会包含各种非高斯噪声,且各地震道采集的数据有限难以满足中心极限定理条件,使得基于高斯噪声假设的叠前反演很难准确地反映出地层异常.所以有必要对实际叠前噪声进行分析,从而设计有效的算法.
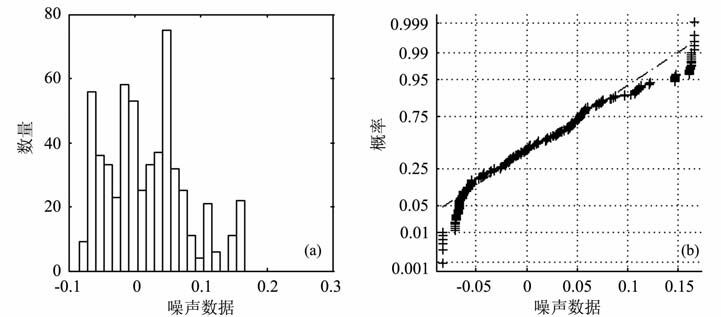
2.2 实际工区叠前噪声数据统计为了探求叠前地震数据的噪声分布情况,对工区A 的A1井、A2 井,工区B 的B1 井储层的叠前噪声数据进行统计,其统计分布图及高斯概率图如图 2~图 4所示.
|
图 2 A 区A1井储层的(a)噪声统计分布图和(b)高斯概率图 Fig. 2 (a) Statistical distribution and (b) Gaussian probabilityplot of then oise of well A1in region A |
|
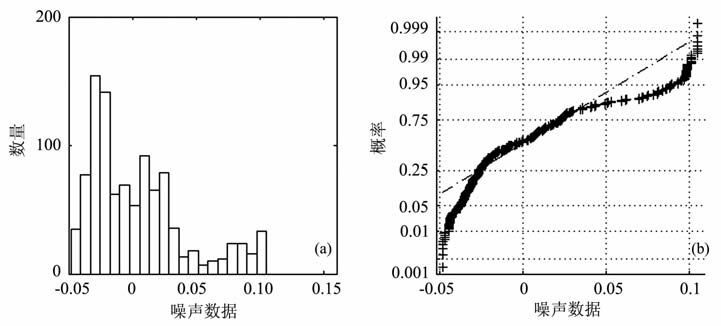
图 3 A 区A2井储层的(a)噪声统计分布图和(b)高斯概率图 Fig. 3 (a) Statistical distribution and (b) Gaussian probability plot of then oise of well A2 in region A |
|
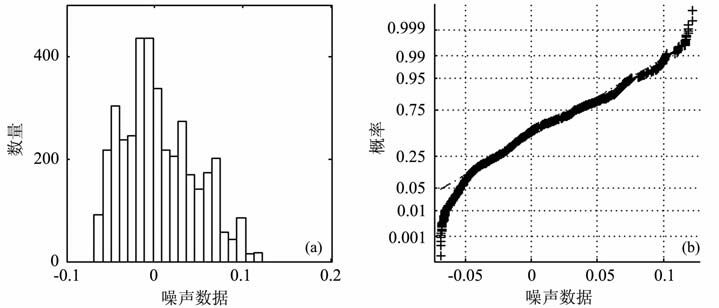
图 4 B区B1井储层的(a)噪声统计分布图和(b)高斯概率图 Fig. 4 (a) Statistical distribution and (b) Gaussian probability plot of the noise of well B1 in region B |
由A、B两个工区三口井的噪声统计分布图可知,叠前储层噪声既有高斯分布的区域集中性,又呈现非高斯分布的偏态性和拖尾性,结合其高斯概率图可知,该地区的地震数据采集噪声的高斯假设是不合理的.基于以上分析,本文将噪声表示为高斯和非高斯两部分:
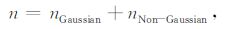
|
(3) |
其中,nGaussian表示噪声的高斯部分,nNon-Gaussian表示噪声的非高斯部分.
3 非高斯噪声模型的反演理论 3.1 混合范数对高斯、非高斯噪声的抑制在求解反演问题时,传统方法常常假设噪声数据是服从高斯分布的,因此采用最小二乘准则构造目标函数,使得观测数据与模型数据达到最优的拟合,即可得到所要反演的地层参数.通常在拟合的时候采用L2范数,误差矢量表示为e=d-Gx,由此可得到基于最小二乘准则的反演目标函数[15]:
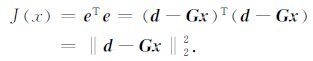
|
(4) |
对目标函数进行求解,便得到传统反问题的最小二乘解.
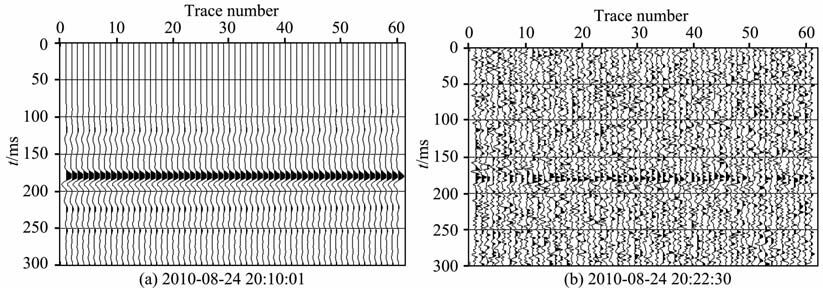
为了研究不同范数准则对各种噪声的抑制作用,构造正演模型如下:采用A 地区A1井实际的测井数据(包括纵波速度、横波速度和密度),通过射线追踪、正演方法构造合成地震记录,正演抽取的角道集如图 5a所示.图 5b为加入信噪比为20的高斯噪声的角道集数据;图 6 为利用L2 范数准则反演的结果,从图中可知,L2范数能很好地抑制高斯噪声.
|
图 5 (a)正演抽取的叠前角道集数据;(b)加入信噪比为20的高斯噪声的角道集数据 Fig. 5 (a) The pre-stack angle gather data from forward calculation; (b) The angle gather data adding Gaussian noise(S/N=20) |
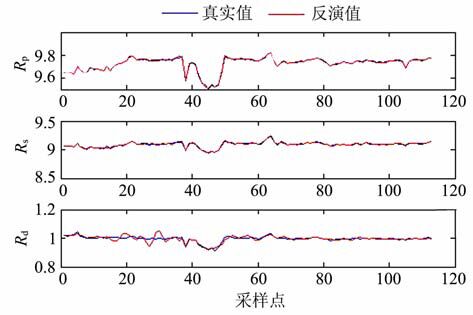
|
图 6 含高斯噪声的L2范数反演结果 Fig. 6 Inversion results with Gaussian noise using L2 norm |
图 7为加入非高斯噪声的角道集数据,圆圈标注部分为加入的非高斯噪声部分;图 8a为L2范数准则下的含非高斯噪声数据的反演结果,可以明显看出,L2范数对非高斯噪声的抑制效果很差.

|
图 7 加入非高斯噪声的角道集数据(圆圈标注为加入非高斯噪声部分) Fig. 7 The angle gather data adding non-Gaussian noise (The circle marke dthepar to fnon-Gaussian noise) |
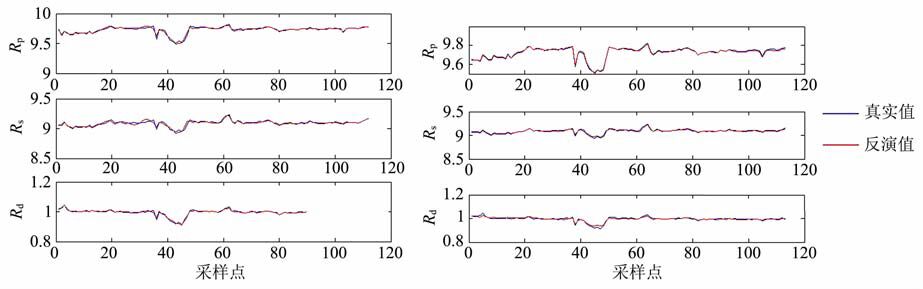
|
图 8 含非高斯噪声的(a)L2范数和(b)L1范数反演结果 Fig. 8 Inversion results with non-Gaussian noise using (a) L2 norm and (b) L1 norm |
利用L1范数准则对含非高斯噪声的数据进行反演,反演结果如图 8b所示.由反演结果可知,由于L1范数相对于L2范数来说,对大的异常有较好的抑制作用,所以在处理非高斯噪声中得到了广泛的运用.
针对海相碳酸盐岩礁滩储层叠前反演问题,由于其数据采集的复杂性和有限性,很难说噪声是高斯白噪的.同时随着前期数据处理手段的进步,叠前数据中的高斯噪声在前期处理中已得到一部分压制,叠前反演所用数据的噪声包括一部分高斯噪声,但还存在大量的非高斯噪声,这点在2.2 节也进行了充分的讨论,由此将式(2)的褶积模型改写为

|
(5) |
其中λ1 +λ2 =1.由上面的仿真分析,传统的基于L2 范数的反演方法只能压制噪声中的高斯部分nGaussian,而基于L1范数的反演方法对噪声中的非高斯部分nNon-Gaussian能起到很好的压制效果.于是,本文利用混合范数对叠前反演中的噪声进行压制,得到基于混合范数的反演目标函数:
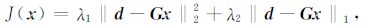
|
(6) |
其中,λ1、λ2 是正则化参数,用来调节两部分的作用大小.当λ1 =0时,式(6)变为犑(x)=λ2‖d-Gx‖1,即为L1范数下的拟合解,用来压制非高斯噪声;当λ2 =0时,式(6)变为犑(x)=λ1‖d-Gx‖22,即为L2范数下的最小二乘解,用来压制高斯噪声.
对式(6)的目标函数进行优化求解,便可以得到混合范数下的反演结果:
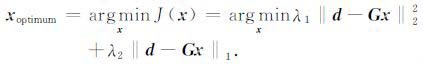
|
(7) |
由于地震记录中的噪声影响、地震数据的带限特性以及正演模型不准确等原因,导致大多数地球物理反演问题都是病态问题.为了克服问题的病态性,往往在模型中加入一些先验信息,对解做必要的约束.
最小长度解是在d-Gx=0的约束下求使L=xTx极小的估计值xoptimum.用拉格朗日乘子法将其化为无条件极值问题:
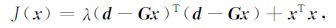
|
(8) |
便可得到最小长度解:
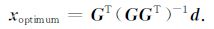
|
(9) |
最小长度解以欧几里德距离作为解的度量,假设所求解距原点的欧式距离最小,当数据噪声比较严重时,最小长度解很难得到理想的反演效果.
本文在最小长度解的基础上,将先验约束信息做一定的改进,利用测井信息$\hat{x}$ 对其进行约束.结合3.1 节提出的压制叠前噪声所用的混合范数,便得到非高斯反演目标函数:
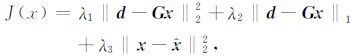
|
(10) |
式(10)的第一部分和第二部分表示数据拟合项;第三部分为约束项.λ1、λ2、λ3 称作正则化参数,用来调节各部分的大小.
3.3 正则化参数λ1、λ2、λ3 取值要求的讨论对式(10)中的λ1、λ2、λ3 取值应根据实际的地震道数据情况遵守以下规则:
(1) 当地震数据信噪比比较高的时候,数据具有较高的可信度,这时候可以由地震数据反演地层参数,可以选用较小的λ3,而选取相对较大的λ1 和λ2;当数据噪声较大的时候,由于数据的失真比较严重,会对反演造成一种假象,使其趋向于非最优解,这时候便可以选择相对较大的λ3,使先验信息能对解起到约束作用.
(2) 由于λ1 是数据拟合的L2 范数部分,即高斯拟合部分,λ2 是数据拟合的非高斯部分,由此可以根据噪声数据的非高斯程度来决定λ1、λ2 的取值大小.当噪声的非高斯性比较强时,可以取较大的λ2;反之亦然.
4 Powell优化算法及其在混合范数反演中的应用由于地球物理反问题是严重病态的,很难通过求逆来求取反问题的解,通常采用迭代法进行求解,传统的迭代法有最速下降法、共轭梯度法[4, 12]等.由于梯度算法的快速性和有效性,通常采用梯度算法对目标函数进行优化.但本文定义的目标函数属于混合范数,很难求得其梯度以及海色矩阵,所以常规的梯度算法并不可行.
Powell方法[16]在求解优化问题时不需要求解一阶导数及海色矩阵,节约了大量的存储空间及时间,对那些不易求导的目标函数最优化问题带来了极大的方便,得到了广泛的运用.由于在搜索过程中,可能搜索方向向量组变得近似线性相关,为了克服这一缺点,朱向阳对共轭方向优化算法中的搜索方向置换策略提出改进,以保证迭代过程中搜索方向组的线性无关性[17].本文便采用朱向阳提出的改进的Powell算法对(10)式的目标函数进行求解.
由此得到叠前三参数非高斯反演的基本流程如下:
Step1:利用测井数据进行射线追踪,将炮检距信息转化为角度信息;
Step2:构建正演模型,产生正演矩阵G′,得到角道集记录;
Step3:通过建立泥岩线约束关系,得到含岩石物理关系的正演矩阵G;
Step4:导入地震道记录,利用产生的AKI角道集对地震道记录进行K值校正,得到K值校正后的地震道记录d;
Step5:利用(10)式建立非高斯反演目标函数;Step6:利用Powell算法对目标函数求解,得到反演所得的地层参数.
5 算法应用 5.1 不同范数准则对噪声的抑制作用为了说明不同范数准则对各种噪声的抑制作用,如3.1节构造正演模型对其进行算法仿真,仿真结果表明了L1范数对非高斯噪声的抑制作用以及L2范数对高斯噪声的抑制作用.
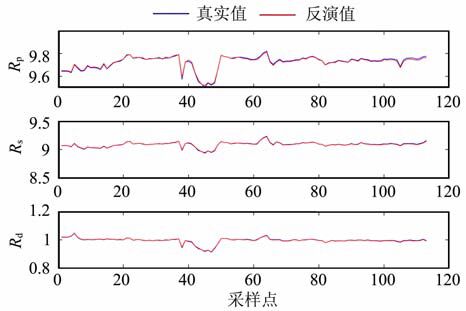
5.2 模型试算采用3.1节构造的正演模型,建立目标函数,对理论数据进行模型试算,其反演结果如图 9所示.从图中可以看出,在没有噪声污染的情况下,反演参数和实际参数能很好地吻合.
|
图 9 反演的波阻抗反射系数与实际波阻抗系数的对比 (Rp 为P波阻抗反射系数,Rs 为S波阻抗反射系数,Rd 为密度反射系数) Fig. 9 The contrast of inversed wave impedance reflection coefficient with the ideal one (Rp is the acoustic impedance reHection coeficient,Rs the shear wave impedance reflection coefficient ,Rd the coefficient for the density) |
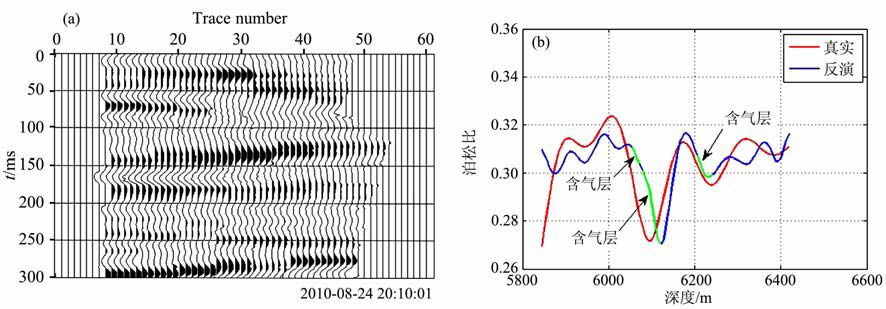
采用A 区A1 井实际地震数据进行反演,图 10a为实际的叠前角道集数据,得到的反演泊松比如图 10b所示,其中绿色线条标注部分为含气层.结果表明,反演结果能准确地反映实际模型,且能准确表示出含气层,证明了本文算法的有效性和鲁棒性.
|
图 10 反演的泊松比与真实泊松比的对比(绿色部分为含气层标注) Fig. 10 The contrast of the Poisson's ratio from mversion with the true value(The green line marks the gas-bearing part) |
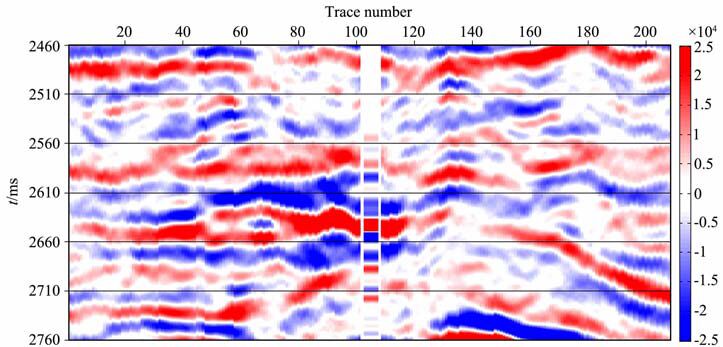
图 11为A1井合成记录的彩色图.井这一道地震数据是利用该工区的测井速度及密度数据,通过射线追踪得到,得到的井的合成记录与邻近的地震记录相比能够较好地吻合.
|
图 11 过A1井合成记录 Fig. 11 Synthetic seismograms passing through Well A1 |
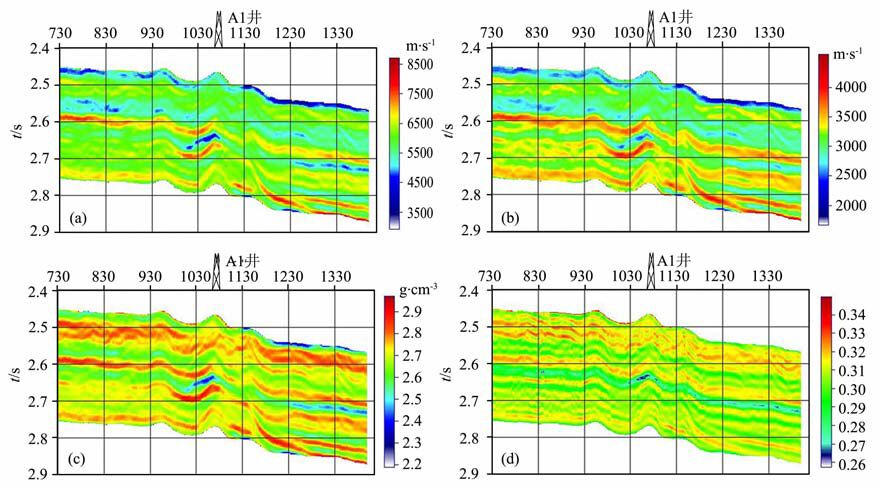
图 12(a,b,c,d)分别为利用本文算法得到的过A1井地区的纵波、横波、密度和泊松比反演剖面图.
|
图 12 过A1井反演剖面 Fig. 12 The inver sionsection through Well A1 |
反演结果与A 区的实际地质构造吻合,反演结果对岩性和含气区域都有很好的分辨率,且通过泊松比剖面能很好地识别A1井的含气性.
6 结 论AVO 反演是提取岩性参数的一种重要途径,随着勘探目标由构造性油气藏转向岩性油气藏,AVO反演得到越来越广泛的运用.传统的反演方法往往采用高斯噪声模型,但对于信噪比相对较低的叠前地震资料来说,噪声往往不完全服从高斯分布,传统反演方法的适定性受到挑战.本文对实际工区的多口井的噪声数据进行统计分析发现:叠前数据噪声中不仅仅含有高斯噪声,还包含了大量的非高斯噪声,由此对基于非高斯噪声模型下的AVO 三参数同步反演进行了研究.基于岩石物理约束的AVO褶积模型,采用L1、L2 混合范数对噪声进行抑制,并利用测井信息对反演进行约束,建立了反演目标函数.鉴于目标函数的复杂性,利用改进的Powell算法对其进行求解.A1井的模型试算和过A1井的剖面反演验证了本文算法的有效性和鲁棒性.
致谢本文得到国家自然科学基金重点项目“海相碳酸盐岩礁滩储层地震预测与识别方法研究"、国家自然科学基金“流水线型自适应多项式滤波理论与方法研究"以及中央高校基本科研业务费专项资金的大力资助,在此向项目组指导老师及参与成员表示感谢.
| [1] | Zoeppritz K. On the Reflection and Penetration of Seismic Waves through Unstable Layers. Goettinger Nachr , 1919: 66-84. |
| [2] | 尚永生, 杨长春, 王真理, 等. 塔里木盆地卡4区块AVO研究. 地球物理学进展 , 2007, 22(5): 1408–1415. Shang Y S, Yang C C, Wang Z L, et al. AVO research in Ka-4 region of Tarim basin. Progress in Geophysics (in Chinese) , 2007, 22(5): 1408-1415. |
| [3] | Smith T M, Sondergeld C H. Examination of AVO responses in the eastern deepwater Gulf of Mexico. Geophysics , 2002, 66(6): 1864-1876. |
| [4] | 陈建江, 印兴耀, 张广智. 基于贝叶斯理论的振幅随偏移距变化三参数同步反演. 中国石油大学学报 (自然科学版) , 2007, 31(3): 33–38. Chen J J, Yin X Y, Zhang G Z. Simultaneous three-term AVO inversion based on Bayesian theorem. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese) , 2007, 31(3): 33-38. |
| [5] | Buland A, Omre H. Bayesian linearized AVO inversion. Geophysics , 2003, 68(1): 185-198. DOI:10.1190/1.1543206 |
| [6] | Theune U, Jensǎs I ?, Eidsvik J. Analysis of prior models for a blocky inversion of seismic AVA data. Geophysics , 2010, 75(3): c25-c35. DOI:10.1190/1.3427538 |
| [7] | 杨迪琨, 胡祥云. 含噪声数据反演的概率描述. 地球物理学报 , 2008, 51(3): 901–907. Yang D K, Hu X Y. Inversion of noisy data by probabilistic methodology. Chinese J. Geophys. (in Chinese) , 2008, 51(3): 901-907. |
| [8] | Alecu T I, Missonnier P, Voloshynovskiy S, et al. Soft/hard focalization in the EEG inverse problem. IEEE Workshop on Statistical Signal Processing , 2005: 978-983. |
| [9] | Tichavsky P, Koldovsky Z, Yeredor A, et al. A hybrid technique for blind separation of non-Gaussian and time-correlated sources using a multicomponent approach. IEEE Transactions on Neural Networks , 2008, 19(3): 421-430. DOI:10.1109/TNN.2007.908648 |
| [10] | Karimi O, Omre H, Mohammadzadeh M. Bayesian closed-skew Gaussian inversion of seismic AVO data for elastic material properties. Geophysics , 2010, 75(1): R1-R11. DOI:10.1190/1.3299291 |
| [11] | Gidlow P M, Smith G C, Vail P J. Hydrocarbon detection using fluid factor traces, a case study: how useful is AVO analysis? Joint SEG/EAEG Summer Research Workshop. Technical Program and Abstracts , 1992: 78-89. |
| [12] | Hampson D P, Russell B H, Bankhead B. Simultaneous inversion of pre-stack seismic data. 75th Annual International Meeting, SEG, Expanded Abstracts , 2005: 1633-1638. |
| [13] | Martin R D, Schiwartz S C. Robust detection of a known signal in nearly Gaussian noise. IEEE Trans. on IT , 1971, JT-17(l): 50-56. |
| [14] | Sangston K J, Gerlach K R. Coherent detection of radar targets in a non-Gaussian background. IEEE Trans. Aerosp. Electron. Syst. , 1994, 30(2): 330-340. |
| [15] | Marquardt D W. An algorithm for least-squares estimation of nonlinear parameters. Journal of the Society for Industrial and Applied Mathematics , 1963, 11(2): 431-441. DOI:10.1137/0111030 |
| [16] | Powell M J D. An efficient method for finding the minimum of a function of several variables without calculating derivatives. The Computer Journal , 1964, 7(2): 155-162. DOI:10.1093/comjnl/7.2.155 |
| [17] | 朱向阳, 熊有伦. 一种改进的Powell共轭方向算法. 控制与决策 , 1996, 11(2): 304–308. Zhu X Y, Xiong Y L. A modification for Powell's method. Control and Decision (in Chinese) , 1996, 11(2): 304-308. |
 2012, Vol. 55
2012, Vol. 55

