2. 中石化石油物探技术研究院, 南京 210014
2. SINOPEC Geophysical Research Institute, Nanjing 210014, China
三维VSP(VerticalSeismicProfile,垂直地震剖面)技术由于结合了VSP 方法和三维地震勘探技术的优点,受到地球物理勘探界的重视.由于VSP数据的主频相对较高,以及其波场路径不像地面反射地震波场那样两次穿越地表低速层,因此三维VSP在井旁构造精细成像、井旁断层识别、井旁地层岩性描述、地震波衰减、速度各向异性、孔隙压力预测和孔隙度估算等方面都取得了许多实际的应用效果[1].
VSP数据经过波场的上下行波分离后,上行(反射)波VSP数据的偏移成像是VSP 数据处理解释中的一个重要环节.VSP 反射波的成像方法主要分两种,一是VSP-CDP变换的成像方法,二是VSP偏移成像方法.VSP-CDP成像是一种基于射线追踪的反射点几何空间归位的方法[2-3].VSP 反射PP 波的偏移成像(PSV 波的偏移成像基本可采用与PP波偏移成像相类似的思路)与常规地面地震反射波数据一样有基于射线的Kirchhoff积分方法和基于波场延拓的单程波波动方程方法和双程波波动方程方法.Kirchhoff方法具有较高的计算效率,并且对各种观测系统和观测方式具有很强的适应性,因此在生产中常用的多为Kirchhoff积分方法[4].但它固有的高频近似假设和射线理论在复杂介质中的缺陷,如焦散和多路径等,使得它在复杂构造区难以取得理想的结果[5].近几年,利用基于波场延拓的波动方程偏移成像方法技术对复杂构造区进行叠前偏移成像,已得到了国内外油气勘探开发业界的普遍认同.VSP数据的波动方程偏移成像主要是在共炮点道集[6-7]和共接收点道集[8-9]上进行.由于在三维VSP地震数据的观测系统中,炮点数目远多于井中检波器数目,因此三维VSP数据的共接收点道集波动方程偏移成像的计算效率也就要远高于共炮点道集波动方程偏移成像的计算效率.两者计算效率上的差异甚至可达到两个数量级.三维VSP 数据的共接收点道集波动方程偏移成像的计算量是与井中检波器数目成正比的,随着三维VSP地震数据采集技术的进展,VSP数据采集中井中检波器的数目越来越多,因此三维VSP共接收点道集波动方程偏移成像的计算量也会随着增大.
为了解决VSP 数据采集中井中检波器数目大时共接收点道集波动方程偏移成像所遇到的大计算量问题,根据波场互易原理可把共接收点道集中的共接收点视为类似于共炮道集中的炮点,把共接收点道集中的炮点视为类似于共炮道集中的接收点,因此用于三维VSP 波动方程偏移成像的共接收点道集可视为在井中检波器位置上激发震源得到的地震记录.本文在陈生昌[10-11]提出的广义地震数据合成及其偏移成像方法理论的基础上,针对VSP 地震数据采集的特殊性,首先通过把广义地震数据合成中的广义合成函数令为井中检波器位置上的δ 函数,对共接收点道集进行广义合成得到一个具有多震源的合成超道集,进而提出一种对超道集进行偏移成像的三维VSP数据高效偏移成像方法.通过对理论和实际三维VSP地震数据试验,并与常规的共接收点道集三维VSP 波动方程偏移成像结果进行比较.
2 方法原理在当前的地震数据叠前深度偏移成像中,最为常用的数据道集有共炮点数据道集、共中心点数据道集、共偏移距数据道集,以及针对VSP 地震数据采集的特殊性而抽取的共检波点数据道集.共炮点数据道集是与野外实际数据采集相一致的,是符合波场传播规律的实际观测道集,而共中心点数据道集、共偏移数据距道集和共检波点数据道集都是人为分选出来的道集.共检波点数据道集也是一种符合波场传播规律的地震数据道集,而共中心点数据道集、共偏移数据距道集在复杂构造区则是不符合波场传播规律的数据排序方式.在地震数据的采集过程中,我们假定地下的地震响应是时不变的(不考虑时延地震数据采集),也就是对于不同时间激发的震源,地下系统有相同的响应函数,因此共炮点道集和共检波点道集的地震波场是满足线性叠加原理的.
2.1 超道集与超震源合成的一般公式对于地面反射地震勘探,令在深度为z的观测面上有频率域共炮点道集波场数据u(sx,sy,gx,gy,z;ω),其中(sx,sy)为炮点坐标,(gx,gy)为检波点坐标,ω 为频率.根据文献[10-11],把下述的线性积分变换称为地震数据的广义地震记录合成:

|
(1) |
式中,k(ξx,ξy,sx,sy;ω)为广义地震数据合成的核函数,也称为广义合成函数;ur(ξx,ξy,gx,gy,z;ω)为由共炮点地震记录波场得到的广义合成地震记录(也称为地震数据的广义合成道集或超道集).
假定与各个共炮点道集波场对应的震源波场具有相同的频谱特性,令为s(ω),则深度z上(sx,sy)处的震源波场u(sx,sy,z;ω)可写为
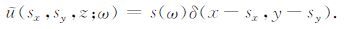
|
同样根据文献[10-11],把下述的线性积分变换称为地震震源的广义震源合成:
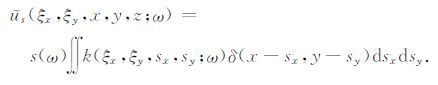
|
(2) |
由于炮点的空间脉冲激发函数为δ(x-sx,y-sy),所以公式(2)也可写为
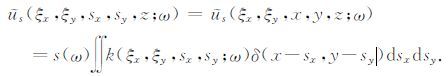
|
(3) |
式(2)、(3)中的k(ξx,ξy,sx,sy;ω)为式(1)中的广义合成函数;us(ξx,ξy,sx,sy,z;ω)称为地震震源波场的广义合成震源(也称为超震源).
公式(1)、(3)称为超道集和超震源合成的一般公式,由这两个公式可知,超道集和超震源分别是多个共炮道集地震记录和多个地震震源的线性组合.Berkhout等[12, 13]在近几年也提出了类似于超道集和超震源的概念,他们称之为Blended Data 和BlendedSource.在公式(1)和(3)中,广义合成函数k(ξx,ξy,sx,sy;ω)可根据偏移成像的需要而由计算得到或人为给定,例如在平面波的偏移成像方法中,k(ξx,ξy,sx,sy;ω)就取为一个平面波函数,在Beam和Beamlet的偏移成像方法[14-15]中,k(ξx,ξy,sx,sy;ω)就取为一个Gauss窗口函数,在BlendedData和BlendedSource中,k(ξx,ξy,sx,sy;ω)就取为一个随机函数.
根据地震的共炮点道集和共检波点道集之间的关系,我们同样可以写出与式(1)、(3)相类似的适用于共检波点道集的超道集与超震源合成公式.
2.2 三维VSP记录的超道集与超震源常规的三维VSP 地震数据采集为地面激发井中接收,由于井中检波器数相对地面激发的炮点数很少,借助波场互换原理,把三维VSP 地震数据的共炮点道集转换为共检波点道集可极大地减少数据的道集数.如果把共检波点道集中的井中检波点假想为炮点,检波点道集中的炮点假想为检波器点,这样就可把三维VSP 地震数据的共检波点道集完全视为井中激发地面接收的共炮点道集(相当于逆VSP共炮点道集).
不同于常规地面观测的共炮点道集地震数据,VSP地震技术中井轨迹一般为垂直、倾斜或不规则,针对井中激发地面z上接收的三维VSP 共炮点道集u(sx,sy,sz,gx,gy,z;ω)的特殊性,令超道集和超震源合成公式(1)、(3)中的广义合成函数k(ξx,ξy,ξz,sx,sy,sz;ω)取为震源点坐标(sx,sy,sz)的δ函数,即
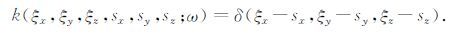
|
(4) |
把式(4)代入式(1)和(3),得到三维VSP 记录的超道集与超震源,即
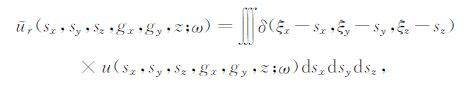
|
(5) |
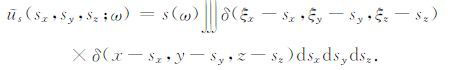
|
(6) |
把公式(5)、(6)写为离散形式,有
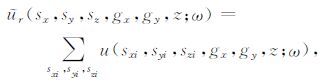
|
(7) |
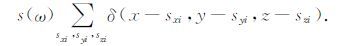
|
(8) |
式中,(sxi,syi,szi)为井中第i个震源点的坐标;ur(sx,sy,sz,gx,gy,z;ω)为经广义合成得到的三维VSP记录的超道集;us(sx,sy,sz;ω)为经广义合成得到的三维VSP 记录的超震源.由公式(7)、(8)可知,三维VSP记录的超道集ur(sx,sy,sz,gx,gy,z;ω)是频率域各个共炮道集数据的直接叠加,三维VSP记录的超震源us(sx,sy,sz;ω)也是井中各个震源点频率域波场的直接叠加.超道集数据ur(sx,sy,sz,gx,gy,z;ω)和超震源波场us(sx,sy,sz;ω)中的震源点坐标变量(sx,sy,sz)只是一种对原所有叠加的共炮点道集中震源点坐标的形式表示,说明超道集数据是由所有震源点(sxi,syi,szi)的共炮点道集组成的多源观测数据,超震源波场是由所有震源点(sxi,syi,szi)的震源波场组成的多源波场.假设VSP中的井轨迹为垂直的,震源点上的震源为炸药震源,则上述合成得到的超震源就相当于由不同深度点上的炸药组成的一个垂直炸药串.
2.3 三维VSP 超道集的偏移成像根据地震波场的线性叠加原理,由式(7)得到的三维VSP超道集记录相当于由式(8)得到的三维VSP超震源波场入射到地下到达反射面产生反射,然后在观测面z上得到的记录波场.对于垂直井中的垂直炸药串超震源,在各个深度上同时激发后,这些不同深度上的具有不同时差的震源波场向下传播到反射面产生反射,在观测面就可得到不同走时的反射波场.因此,超道集地震数据记录的偏移成像可采用与共炮点地震数据偏移成像相同的方式,即在深度方向用上行波方程反向外推广义合成得到的超道集地震数据,同时用下行波方程正向外推广义合成得到的超震源波场(即在深度向下外推过程中,根据超震源中各个震源点的深度由浅到深逐个激发超震源中的震源),并应用超道集波场与超震源波场的时间一致性成像条件[16]提取超道集数据的偏移成像结果.超道集数据的具体偏移成像过程就是在深度外推中逐步使用文献[17]提出的单程波拟线性Born近似波场外推算子,对超道集地震数据和超震源波场进行深度外推和偏移成像.
2.3.1 拟线性Born近似波场外推算子假定深度zi上的频率域波场为u(x,y,zi;ω),深度(zi+Δz)上的频率域波场为u(x,y,zi+Δz;ω);再令(zi,zi+Δz)间的速度场为v(x,y,zi),参考速度场为v0(zi).在由u(x,y,zi;ω)外推u(x,y,zi+Δz;ω)的过程中,可把u(x,y,zi;ω)作为入射波场,而zi+Δz上的波场u(x,y,zi+Δz;ω)是由参考介质中的波场u0(x,y,zi+Δz;ω)和速度扰动产生的散射波场us(x,y,zi+Δz;ω)组成,即

|
(9) |
其中,u0(x,y,zi+Δz;ω)可利用参考速度v0(zi),由下述的相移法得到
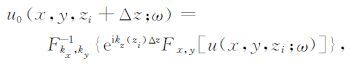
|
(10) |
这里,Fx,y表示x和y方向上的Fourier正变换;Fx,y,ky-1表示x和y方向上的Fourier反变换;kz(zi)为垂向波数,有
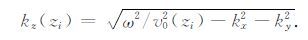
|
对于方程(9)中的散射波场us(x,y,zi+Δz;ω),有

|
(11) |
把上述所介绍的单程波拟线性Born近似波场外推算子应用于超道集地震数据和超震源波场的深度外推,可得到深度zi上的频率域超道集地震波场ur(sx,sy,sz,x,y,zi;ω)和超震源波场us(sx,sy,sz,x,y,zi;ω),略去两波场中的震源点坐标变量,即有ur(x,y,zi;ω)和us(x,y,zi;ω),由波场的时间一致性成像条件提取超道集数据在zi上深度的偏移成像结果I(x,y,zi),即
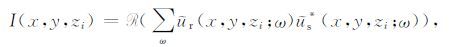
|
式中,R表示复数取实部运算;*代表复数的复共轭运算.
由上述可得到如下的三维VSP 超道集地震数据偏移成像具体计算步骤:
(1) 对分选出的三维VSP共检波点道集应用波场互换原理,把共检波点道集中的检波点视为炮点,共检波点道集中的炮点视为检波点,得到炮点和检波点分别位于井中检波点处和地面炮点处的共炮点道集(也称为逆VSP共炮点道集);
(2) 对经互换原理得到的所有逆VSP 共炮点道集在频率域进行基于相同检波点的直接叠加,得到一个超级炮集,即三维VSP 超道集(它的所有检波点位于地面,所有炮点位于井中);
(3) 在地面对震源波场初始化为零;
(4) 应用单程波拟线性Born近似波场外推算子对三维VSP超道集数据和震源波场进行由浅到深的深度外推;
(5) 当外推深度到达超道集中的第一个炮点深度sz1 时,则在该深度的炮点位置处(sx1,sy1)给震源波场加入第一个震源子波得到新的震源波场;
(6) 在深度循环外推中,应用时间一致性成像条件提取偏移成像结果,并在深度外推中依深度位置激发超道集数据中的各个震源,即在外推深度到达超道集的各个炮点深度szi时,在该深度的炮点位置处(sxi,syi)给震源波场加入一个震源子波得到新的震源波场;
(7) 深度循环结束,完成超道集数据偏移成像.由上述计算步骤可知,超道集数据是各个逆VSP共炮点道集的叠加,而在深度循环外推中又在各个逆VSP共炮点道集的炮点深度上激发了相应的逆VSP共炮点道集的震源波场,因此一次深度循环外推的超道集数据偏移成像就可以完成所有逆VSP共炮点道集数据的偏移成像.
由于震源点激发深度的不同,所以这些逆VSP共炮点道集对应的震源波场间具有相互不同的时差,也意味着这些震源波场间不存在相互干涉.BlendedData和BlendedSource的合成中就是把合成函数取为炮点位置的随机函数减小震源波场间的相互干涉[18],本文的方法通过在井中不同深度激发震源波场使之具有不同的走时来防止震源波场间的相互干涉.
3 数值试验为验证上节提出的超道集高效偏移成像方法的正确性和实用性,分别进行了三维理论模型的三维VSP地震数据和实际三维VSP 地震数据的偏移成像试验.
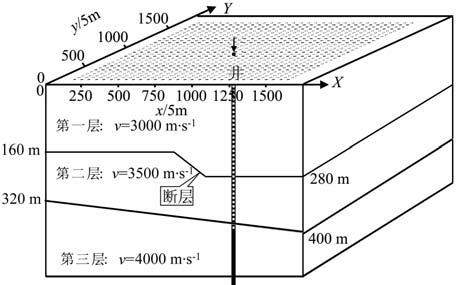
3.1 理论模型数据试验首先验证上节提出的三维VSP 偏移成像方法的正确性,设计了图 1所示的理论模型,并用声波有限差分方程模拟了三维VSP 的共炮点道集地震数据,然后再把共炮点道集数据分选成井中共检波点道集数据.在本次试验中,用井中50、70、90、100m、110m 和120 m 共6 个深度上的共检波点道集数据,应用式(7)和(8)对这6个共检波点道集数据进行广义合成,得到一套三维VSP的超道集记录和超震源.
|
图 1 三维VSP模型图 Fig. 1 3D VSP model |
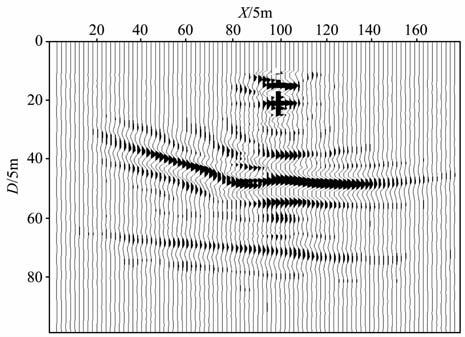
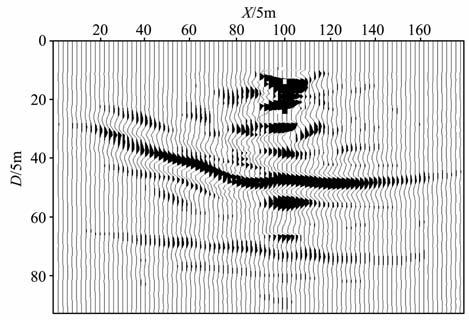
图 2、图 3分别为上述6个共检波点道集常规的共检波点道集波动方程偏移成像结果和本文提出的超道集高效偏移成像方法的结果.比较图 1、2 和3可以看出,成像结果与模型基本一致,说明本文提出的三维VSP高效深度偏移成像的超道集方法的正确性.图 2所示的常规三维VSP共检波点道集波动方程偏移成像结果的计算机耗时是图 3所示的三维VSP超道集波动方程偏移成像结果的6倍,因为通过广义地震数据合成,6 个共检波点道集合成为了一个超道集.用于进行超道集合成的共检波点道集数越多,则超道集偏移成像相对于常规共检波点道集偏移成像的计算效率越高.
|
图 2 三维VSP模型数据的常规偏移成像结果 Fig. 2 Gonvenational migration result of 3D VSP model data |
|
图 3 三维VSP模型数据的超道集偏移成像结果 Fig. 3 Super-gather migration resutt of 3D VSP model data |
为了进一步验证本文方法的实用性,采用我国东部某地采集的三维VSP实际资料进行试验.首先把原始的共炮点道集分选为共检波点道集,然后再对共检波点道集进行广义地震数据合成,得到三维VSP地震数据的超道集.
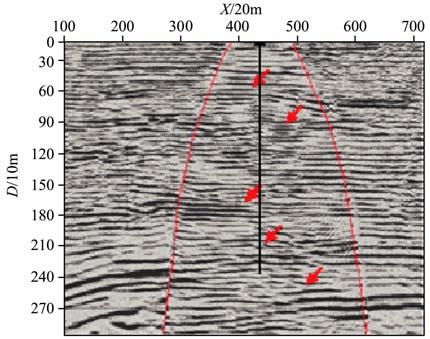
图 4为过井实际三维VSP 数据的超道集波动方程深度成像剖面(中间部分)嵌入到高精度三维地面地震偏移成像剖面的对比图,图中画线的区域就是三维VSP的成像区域.由图 4可看出,三维VSP数据的超道集偏移成像结果相对于高精度三维地面地震偏移成像结果不仅具有很好的可比性与一致性,而且它的分辨率也要明显高于高精度三维地面地震偏移成像结果,说明了本文提出的方法的实用性.
|
图 4 实际三维VSP数据偏移成像(中间部分)与高精度地面地震偏移成像的比较 Fig. 4 Comparison of migration results of real 3D VSP data (middle part) and high precision conventional 3D seismic data |
广义地震数据合成是一种基于波场满足线性叠加原理的地震数据线性变换,其具体的广义合成函数可根据地震数据采集系统和偏移成像目标等因素确定.本文根据VSP 地震数据中炮-检位置的特殊性,把广义合成函数取为δ 函数不仅能保证合成的超道集数据中震源激发具有一定的延迟时间,避免了超道集数据中波场的相干性,还能极大地减少合成的超道集数据的道集数目,有利于提高偏移成像的计算效率,这也正是本文的主要成果.用于进行超道集合成的常规道集(共检波点道集或共炮点道集)数越多,则三维VSP超道集偏移成像相对于常规道集偏移成像的计算效率越高.
| [1] | Boelle J L, Kaiser P, Maocec E. Difficulties and clues in 3-D VSP processing. 72nd Ann. Internat. Mtg. Soc. Expl. Geophys., Expanded abstracts , 1998, 17: 373-376. |
| [2] | Chen G, Peron J F. Mapping of 3-D VSP data using quick ray tracing. 68th Ann. Internat. Mtg. Soc. Expl. Geophys., Expanded abstracts , 1998, 17: 365-368. |
| [3] | Chen G, Peron J, Canales C. Rapid VSP-CDP mapping of 3-D VSP data. Geophysics , 2000, 65(5): 1631-1640. DOI:10.1190/1.1444851 |
| [4] | Bicquart P. Application of Kirchhoff depth migration to 3-D VSP. 68th Ann. Internat. Mtg. Soc. Expl. Geophys., Expanded abstracts , 1998: 389-392. |
| [5] | Yilmaz O. Seismic data analysis. Soc. Expl. Geophys., 2001. |
| [6] | 王华忠, 徐蔚亚, 王建民, 等. VSP数据波动方程叠前深度偏移成像及立体地震成像. 石油地球物理勘探 , 2001, 36(5): 517–525. Wang H Z, Xu W Y, Wang J M, et al. Prestack depth migration of VSP data and stereoscopic seismic imaging. OGP (in Chinese) , 2001, 36(5): 517-525. |
| [7] | 熊高君, 庄志蕾, 张树林, 等. 混合法VSP共炮记录叠前深度偏移. 天然气工业 , 2006, 26(2): 55–56. Xiong G J, Zhang Z L, Zhang S L, et al. VSP common shot pre-stack depth migration with hybrid method. Natural Gas Industry (in Chinese) , 2006, 26(2): 55-56. |
| [8] | Graves J, Checkles S, Leveille J. 3D VSP acquisition and 3C processing on a deep subsalt prospect in the Gulf of Mexico. 82nd Ann. Internat. Mtg. Soc. Expl. Geophys., Expanded abstracts , 2008, 27: 3340-3344. |
| [9] | 陈生昌, 马在田, 陈林. 三维VSP数据的波动方程偏移成像. 天然气工业 , 2008, 28(3): 51–53. Chen S C, Ma Z T, Chen L. Wave equation migration for 3-D VSP data. Natural Gas Industry (in Chinese) , 2008, 28(3): 51-53. |
| [10] | 陈生昌. 波动方程叠前深度偏移成像与速度建模方法研究. 上海: 同济大学, 2002. Chen S C. Research on methods for wave equation pre-stack depth migration and velocity model construction (in Chinese). Shanghai: Tongji University, 2002. http://epub.cnki.net/kns/detail/detail.aspx?QueryID=0&CurRec=1&recid=&FileName=2007224470.nh&DbName=CDFD9908&DbCode=CDFD&pr= |
| [11] | 陈生昌, 马在田. 广义地震数据合成及其偏移成像. 地球物理学报 , 2006, 49(4): 1144–1149. Chen S C, Ma Z T. Generalized synthesis of seismic data and its migration. Chinese J. Geophys. (in Chinese) , 2006, 49(4): 1144-1149. |
| [12] | Berkhout A J. Changing the mindset in seismic data acquisition. The Leading Edge , 2008, 27(7): 924-938. DOI:10.1190/1.2954035 |
| [13] | Berkhout A J, Verschuur D J, Blacquière G. Seismic imaging with incoherent wavefields. 83rd Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded abstracts, 2009: 2894-2898. |
| [14] | Hill N R. Prestack Gaussian-beam depth migration. Geophysics , 2001, 66(4): 1240-1250. DOI:10.1190/1.1487071 |
| [15] | Wu R S, Chen L. Beamlet migration using Gabor-Daubechies frame propagator. 63rd Conference & Technical Exhibition, EAGE, Expanded Abstracts , 2001: 74. |
| [16] | Claerbout J F. Imaging the Earth's Interior. Blackwell Scientific Publication, 1985. |
| [17] | 陈生昌, 曹景忠, 马在田. 基于拟线性Born近似的叠前深度偏移方法. 地球物理学报 , 2001, 44(5): 692–698. Chen S C, Cao J Z, Ma Z T. Prestack depth migration method based on quasi-linear Born approximation. Chinese J. Geophys. (in Chinese) , 2001, 44(5): 692-698. DOI:10.1002/cjg2.v44.5 |
| [18] | Blacquière G, Berkhout A J, Verschuur D J. Survey design for blended acquisition. 83rd Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded abstracts, 2009: 56-60. |
 2012, Vol. 55
2012, Vol. 55

