2. 西安交通大学理学院, 西安 710049;
3. 海洋石油勘探国家工程实验室, 西安 710049
2. School of Science, Xi'an Jiaotong University, Xi'an 710049, China;
3. National Engineering Laboratory for Offshore Oil Exploration, Xi'an 710049, China
Rayleigh面波既是干扰波也可是有效波.在利用Rayleigh面波进行工程勘探中,它被看成有效波[1],在石油地球物理勘探中,面波常常被看成干扰波[2].在这两种情况下,都需要深刻理解Rayleigh面波的传播和频散特性.所谓频散特性,是指Rayleigh面波的相速度随频率变化,面波某一频率分量的传播特征反映了一定深度范围内的地层变化情况.面波的频散特性对于地层的厚度和横波波速十分敏感,利用频散特性可以求得近地表横波速度[3],而横波速度正是许多工程应用的关键参数之一.
目前实际工作中对于面波频散曲线的计算广泛使用基于频散方程的一类方法,如Thomson-Haskell法[4]和Schwab-Knopoff法[5]等.这类方法只能用于一些简单介质(如水平层状介质),不能用于裂隙、空洞等复杂介质中.基于波动方程的数值模拟可以模拟复杂介质中的面波,进而得到其频散曲线.基于弹性波波动方程,采用限差分法对面波进行数值模拟,是一种常用方法.适当的网格对于有限差分法十分重要,交错网格已经被广泛应用于弹性介质、黏弹性介质及各向异性介质中的波场模拟[6-8].但在介质参数剧烈变化的情况下,标准交错网格得到的解可能不稳定.为此,Saenger[9]提出了旋转交错网格,此网格无需对界面处的弹性模量进行平均处理,有效地解决了参数剧变时的稳定性问题.有限差分法模拟面波的关键问题之一是自由表面的处理.Zahradník,Moczo和Hron等人的方法中将自由表面以上的拉梅常数置为0,为避免被零除,令密度大于零且趋近于0[10].Levander和Graves等人的方法则假设应力场关于自由表面两边对称[11-12].近年来还出现了其他一些方法,如:Mittet对自由表面边界条件提出了使用横向各向同性的实现方法[13],徐义贤等对自由表面边界条件提出了一种显式的声学-弹性边界实现方法[14]等.上述方法都假定介质为弹性介质.
然而实际上地球是黏弹性介质,地震波在传播过程中存在衰减,这种衰减现象能够为岩性、物性及岩石饱和度等研究提供信息,Q值通常被用来描述衰减特性.很多学者对黏弹性介质中波场正演的有限差分法进行了研究,例如:Saenger和Bohlen 于2004年将旋转交错网格有限差分法用于模拟黏弹性介质中的波传播[15].Xia在2002 年[16]曾研究了层状介质中纵波和横波的Q值对于面波衰减系数的影响.实际问题中通常需要考虑横向非均匀介质等复杂介质,这对于利用面波进行工程勘探及对浅层地震资料进行补偿有重要意义,本文将对上述复杂介质中面波的特性进行研究.
本文基于由标准线形固体模型得到的二阶位移-应力黏弹性波动方程,采用时域旋转交错网格有限差分法及非分裂卷积形式的完全匹配层[17]边界条件,给出黏弹性介质面波模拟方法.为检验所提出方法的正确性,我们对均匀半空间和2 层介质中的Rayleigh面波进行模拟,将结果与理论值比较.然后分别对弹性及黏弹性横向缓变介质和含有空洞的介质中的面波进行了波场模拟,对比分析了弹性及黏弹性介质中面波的频散特性.最后是结论与讨论.
2 黏弹性介质中波动方程首先给出本文用到的黏弹性介质中有关基本理论.
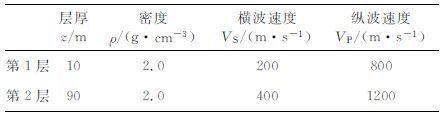
2.1 应力-应变关系在标准线性固体模型中,2 维各向同性黏弹性介质应力-应变关系如下[18-19]:
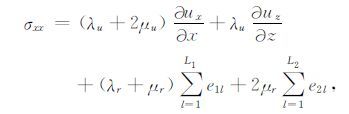
|
(1) |

|
(2) |
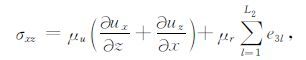
|
(3) |
其中x= (x,z)为直角坐标系坐标,σxx(x,t),σzz(x,t)和σxz(x,t)分别为法向应力和切向应力,ux(x,t)和uz(x,t)分别为质点位移的x和z方向分量,λu= (λr+μr)Mu1-μrMu2 和μu=μrMu2 为非松弛或高频拉梅常数(unrelaxed Lame constants),λr和μr为松弛的或低频的拉梅常数(relaxed Lame constants).Muv,v=1,2为松弛函数在t=0时刻的值,v=1和v=2 依次对应膨胀模式和剪切模式.在广义标准线性固体流变学中,有
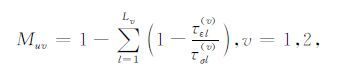
|
(4) |
这里τεl(v)和τσl(v)为材料的松弛时间;e1l(x,t)是与L1个Zener元素相关的记忆变量(memory variables),它描述膨胀波的黏弹性特征;e2l(x,t),e3l(x,t)是与L2 个Zener元素相关的记忆变量(memory variables),它描述拟剪切波的黏弹性特征,其定义如下:

|
(5) |

|
(6) |

|
(7) |
${{\dot{e}}_{1l}}$表示e1l对时间求一次导数.Θ 是膨胀场,Φvl是t=0时刻的松弛响应函数分量,v=1,2依次对应P波和S波.其定义式为
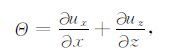
|
(8) |
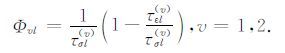
|
(9) |
对于每个l,当τεl(v)→τσl(v)时,Muv→1,Φvl→0,记忆变量为零,黏弹性应力-应变关系蜕化为弹性的情况.
2.2 位移-应力关系质点位移-应力方程时空域形式如下:
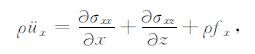
|
(10) |
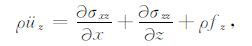
|
(11) |
其中ρ(x)为介质的密度,fx(x,t)和fz(x,t)分别为震源的x分量和z分量,t为时间变量.üz表示uz对时间求两阶导数.
用波动方程对无界区域内地震波场进行波数值模拟时,存在人工边界反射问题,而这种反射在物理上是不存在的.下面针对上述黏弹性波动方程,研究边界的处理.
3 边界的处理使用分裂算法的传统完全匹配层吸收边界条件在弹性介质波场正演模拟中已经得到广泛的应用,但它对于切向入射波仍存在较大的反射.非分裂完全匹配层有效地解决了这一问题[18].本文中采用非分裂完全匹配层作为吸收边界.本节将推导用于二阶位移-应力黏弹性方程的非分裂完全匹配层吸收边界的表达式.
3.1 非分裂完全匹配层吸收边界对于黏弹性二阶位移-应力波动方程,在完全匹配层内其表达式为(详细推导见附录A)
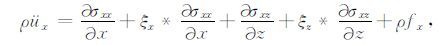
|
(12) |
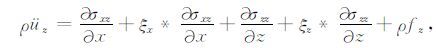
|
(13) |
式中,

|
(14) |
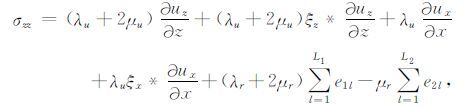
|
(15) |

|
(16) |
在(14),(15)和(16)式中,
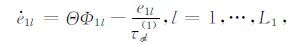
|
(17) |
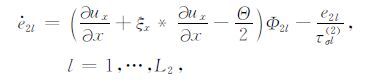
|
(18) |
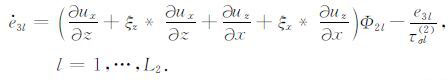
|
(19) |
在(17),(18)和(19)式中,
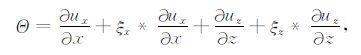
|
(20) |
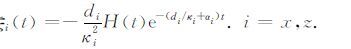
|
(21) |
上面* 代表卷积,H(t)为Heaviside函数.dx、dz、αx、αz、κx和κz为非分裂完全匹配层内的衰减系数,dx衰减x方向传播的波,dz衰减z方向传播的波.在内部区域中dx=0,匹配层内dx>0,dx(x)=d0(x/L)2,L为完全匹配层厚度,d0 =-3Vplog(Rc)/2L,Rc 为数值离散后的目标反射系数,通常取为0.1%,dz的取值与dx类似.αx和αz在完全匹配层内线形变化,在匹配层和内部区域交界处为最大值αmax,在匹配层外边界为0;αmax =πf0 ,f0 为震源主频,κx=κz=1.本文第4节模型计算中可以看到完全匹配层的边界吸收效果.
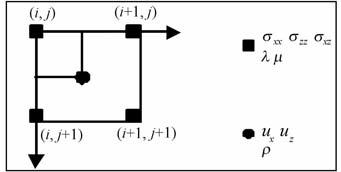
3.2 自由表面的处理为了能适用于强非均匀介质[15],本文使用旋转交错网格有限差分.旋转交错网格中同一物理量在x及z方向上的分量都定义在同一个网格上,如图 2所示.

|
图 1 非分裂完全匹配层吸收边界示意图.匹配层上边 界和下边界衰减z方向传播的波,dx=0,dz> 0;匹配 层左边界和右边界衰减x方向传播的波,dx > 0,dz = 0; 匹配层的四个角则两个方向传播的波都衰减,dx >0,dz> 0. Fig. 1 Structural representation of the unsplitconvolutional perfectly matched layer. The up and bottom boundaries attenuate the wave field propagating in the z direction, dx = 0,dz >0; The left and right boundaries attenuate the wave field propagating in the x direction, dx > 0, dz = 0; The corners attenuate the wave field propagating in both directions. |
|
图 2 物理量在旋转交错网格上分布特点.应力分量定 义在实心方框所在整数网格点,位移分量定义在实心圆 所在非整数网格点上. Fig. 2 The distribution of modeling parameters withinthe Rotated staggered grid (RSG). The stresses are placed at the tilled rectangles, the displacements are placed at the tilled circles. |
我们将自由表面取为z=0处整数网格点所在平面(参见图 4).自由表面的应力分量须满足

|
图 4 模型1示意图 Fig. 4 Structural representation of model 1 |
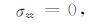
|
(22) |
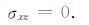
|
(23) |
把式(22)和(23)代入式(2)和(3),注意到式(7)中e3l=0,得到
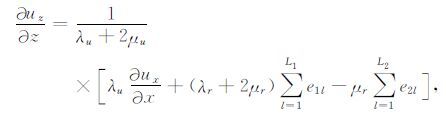
|
(24) |
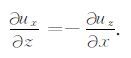
|
(25) |
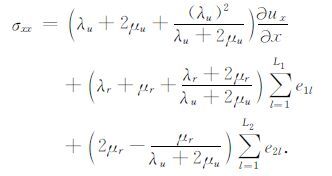
|
(26) |
(26)式即为自由表面处切向应力σxx的计算公式.
4 波场模拟与分析本文有限差分正演过程中计算时间导数使用二阶中心差商,空间导数使用四阶龙格-库塔法.计算的流程图如下:
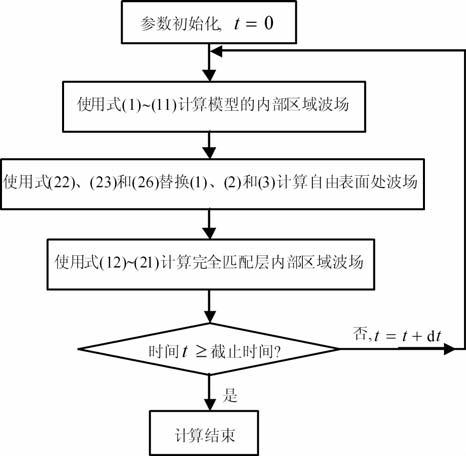
|
图 3 正演模拟流程图 Fig. 3 Forward modeling flowchart |
下面将本文提出的方法用于两个模型的波场模拟,通过与解析解的对比检验其正确性.
4.1 模型1:均匀半空间黏弹性介质模型首先通过模型1中的波场模拟来检验数值解的精度及吸收边界的效果.模型1 尺寸为700 m(宽)×400m(深),匹配层厚度为50m,如图 4所示.介质密度ρ=1g·cm-3,弹性波纵波速度为VP=2000m·s-1,横波速度为VS=1155 m·s-1;震源为垂直方向点力源,埋深为1 m,时间函数为主频f0=20 Hz的Ricker子波,表达式为
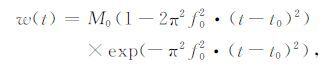
|
(27) |
t0=0.05s,M0 为常数(取为100000);介质的品质因子QP=13,QS=10,表 1 给出了一组数值模拟中使用的松弛时间常数(L1=L2=L=2),可以使品质因子在震源带宽内近似于常值.
|
|
表 1 松弛时间常数(L1=L2=L= 2)QP=13,QS=10 Table 1 Relaxed time constants (L1=L2=L= 2)QX=13,QX=10 |
正演模拟中,垂直和水平方向网格间隔均为2m,时间步长取0.1ms.图 5为面波单炮模拟记录,检波器与震源同深,图中可以看到面波在左、右边界和下边界被很好的吸收,没有反射波进入计算区域.弹性介质中Rayleigh 面波沿自由表面传播,振幅变化缓慢;但黏弹性介质中由于介质的能量吸收特性,Rayleigh面波振幅随着波的传播而逐渐减小.

|
图 5 模型1的模拟单炮记录 (a)弹性介质垂直分量,(b)黏弹性介质垂直分量 Fig. 5 Single-shot seismograms of model 1 (a) Elastic vertical component. (b) Viscoelastic vertical component |
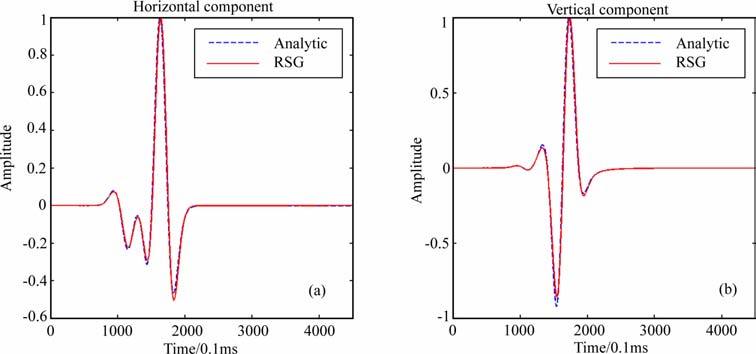
图 6为与震源同深,偏移距为120 m 的检波器接收到的弹性Rayleigh面波波形,将其和解析解[21]进行比较,两者相对误差小于5%.
|
图 6 偏移距为120 m的检波器接收的波形 (a)水平分量,(b)垂直分量.实线为本文所用差分法计算的结果,虚线为解析解. Fig. 6 Seismograms (particle displacement) of analytical and numerical results, the offset is 120 m (a) Horizontal component. (b) Vertical component. |
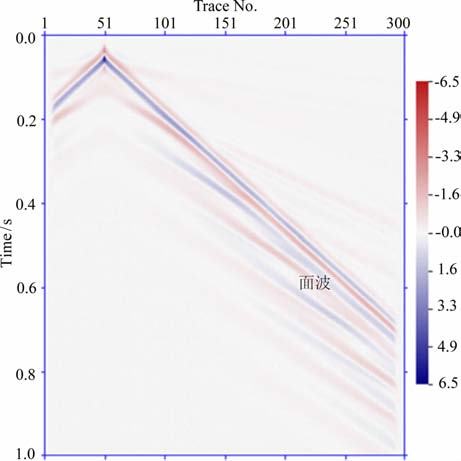
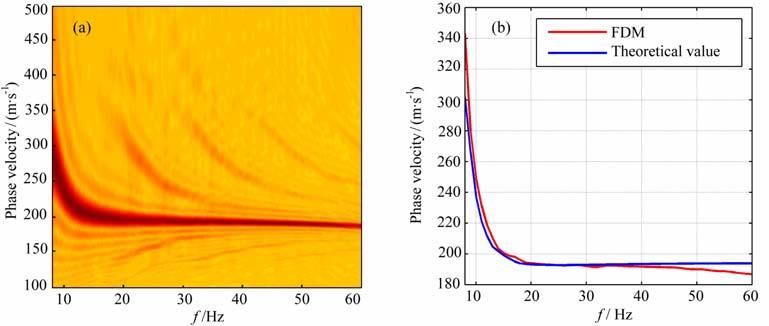
模型尺寸为150m(宽)×100m(深),共2层介质,如图 7 所示,介质参数列于表 2,一垂直方向点力源置于地表,距模型左边界25m,埋深为0.25m,时间函数同式(27),主频f0=20 Hz.水平和垂直网格间距为0.5m,时间步长为0.1ms.图 8为其单炮模拟记录,可以看到层状介质中出现了高阶模式面波以及频散现象.使用MASW 方法[21],我们利用模拟记录在f-k域中的相位信息得到面波的f-c剖面,从中提取出面波的频散曲线(图 9).弹性介质中面波的频散曲线和理论值很好地吻合,表明本文方法有较好的精度,能够正确模拟非均匀介质中的面波传播.
|
|
表 2 层状介质的模型参数 Table 2 Moel parameters of layered media |

|
图 7 模型2示意 Fig. 7 Structural representation of model 2 |
|
图 8 模型2波场垂直分量的模拟单炮记录 Fig. 8 The elastic vertical component of single-shot seismograms of model 2 |
|
图 9 模型2中的面波记录的频散曲线 (a)弹性介质中的f- c剖面,(b)弹性介质中的频散曲线.红线为从f- c剖面提取的结果,蓝线为弹性介质中的理论值. Fig. 9 The dispersion curves of the Rayleigh wave in model 2 (a) f- c profile in elastic medium. (b) Dispersion curves in elasticmedium. The red line is obtained from the f- c profiles, and the blue line s theoretical value rn elastic medium. |
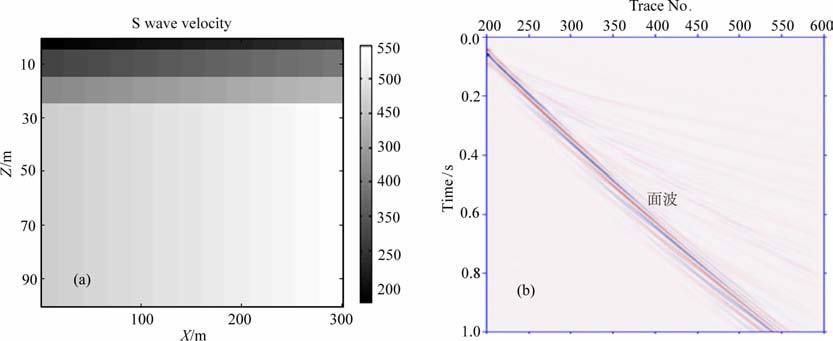
基于频散方程的一类方法只能处理简单情况,无法计算复杂介质中的面波频散曲线;而有限差分法就可以.本模型为横向缓变模型,尺寸为300 m(宽)×100m(深),共4层介质,厚度依次为5m、10m、10m 和75m.四层介质每一层的横波波速自左向右逐渐增加(图 10),左边界处横波波速VS0依次为150m·s-1,250m·s-1,350m·s-1,450m·s-1,横向距离x变化1m,横波波速VS 变化0.5m/s(VS=VS0 +0.5x).此模型将考虑三种不同的泊松比γ(0.2,0.3,0.4),纵波速度可由泊松比计算得出.本文首先计算弹性介质中面波的频散曲线,然后以此为参考值,改变四层介质的Q值(Q1、Q2、Q3和Q4),研究不同参数下的面波频散曲线与参考值的相对变化.一垂直方向点力源置于地表,距模型左边界100m,震源时间函数同式(27),主频为20 Hz.水平和垂直网格间距为0.5m,时间步长为0.1ms.
|
图 10 模型3的横波速度剖面(a)和单炮模拟记录(b) Fig. 10 The profile of the Vsin model 3(a) and the vertical component of single-shot seismograms(b). |
图 10b为泊松比γ=0.2 时弹性介质中的单炮模拟记录,道间距为0.5m.图 11为不同参数下的面波频散曲线.分析图 11中的结果,可以得出如下认识:

|
图 11 不同参数下的频散曲线 (a)Q1 -Q2- Q3-Q4-Q=20, (b)Q1 -Q2-Q3 -Q4 -Q=50 , (c)Q1 -20,Q2 -Q3 -Q4 - ∞, (d) Q1 - 50,Q2 -Q3-Q4-∞ ;(e)Q2 - 20, Q1-Q3-Q4-∞. Fig. 11 The dispersion curves with different parameters (a)Q1 -Q2- Q3-Q4-Q=20,(b)Q1 -Q2-Q3 -Q4 -Q=50 ;(c)Q1 -20,Q2 -Q3 -Q4 - ∞ (d) Q1 - 50,(d) Q1 - 50,Q2 -Q3-Q4-∞ ;(e)Q2 - 20, Q1-Q3-Q4-∞. |
(1) 在横向缓变介质中,Q1=Q2=Q3=Q4=Q=20时,面波的频散特性相比弹性介质出现改变(图 11a),频散曲线的幅值变化明显.
(2) 泊松比越大,频散曲线幅值变化也越大.
(3) Q1=50(图 11d)与Q2=20(图 11e)时频散曲线所产生的变化都比较小,第一层的Q值为影响频散特性的主要因素.
实际介质非常复杂,面波的频散特性的影响因素很多,本文此处只讨论了其中的若干因素,要准确计算面波频散曲线,仍需要对复杂模型的进一步研究.
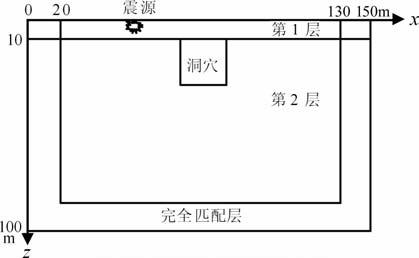
4.4 模型4:含洞穴的两层介质模型在工程勘探中,如溶洞较多的地区,地层中有空洞存在,有必要对其做详细勘察,本模型对此做简单的模拟.模型4参数与模型2相同,第2层介质中有一正方形洞穴(图 12),边长为25m,上表面与两层介质的界面重合,空洞内密度为ρ=0.0001g·cm-3,横波与纵波波速为Vp=Vs=0.1m·s-1.震源距洞穴左边界水平距离为25 m,时间函数同式(27),主频f0=20Hz.水平和垂直网格间距均为0.5 m,时间步长取0.003ms.
|
图 12 模型4示意图 Fig. 12 Structural representation of model 4 |
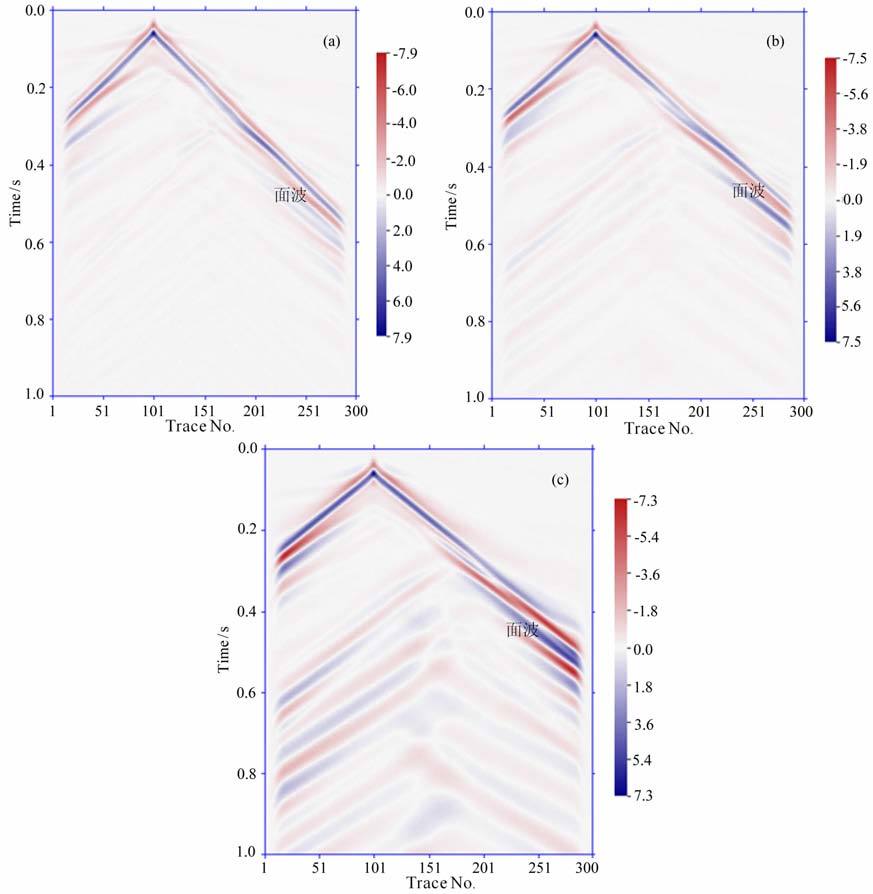
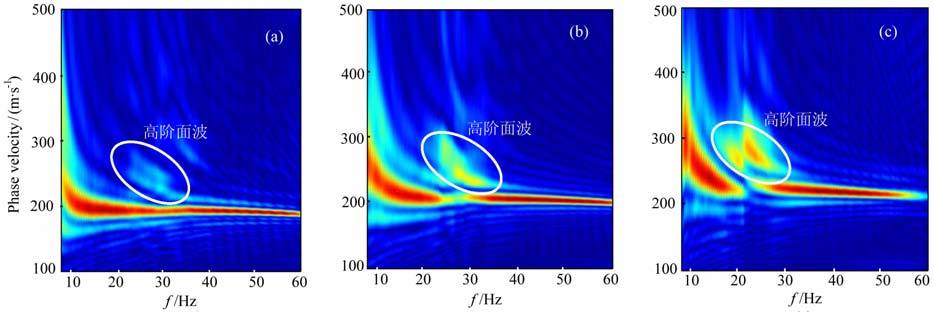
首先我们计算弹性介质中的单炮模拟记录(图 13a),道间距为0.5m,利用单炮纪录得到面波的频率-相速度(f-c)剖面(图 14a),剖面中面波的能量都集中于基阶模式(红色部分).然后我们将第1 层介质的Q值分别设为Q1=30和Q1=20,由单炮记录计算出频率-相速度(f-c)剖面(图 14b和14c),这两个剖面上不单有基阶模式的面波,也可以看到明显的高阶模式面波(图中圆圈所示);并且随着吸收的增强,高阶模式面波能量所占的比重变大.
|
图 13 模型4波场垂直分量单炮模拟记录(a)弹性介质(b) Q1 = 3O; (c) Q1=2O. Fig. 13 The vertical component of single-shot seismograms of model 4 (a) Elasticmedia; (b) Q1 = 3O; (c) Q1=2O. |
|
图 14 模型4中的面波记录的f-c剖面 (a)弹性介质,(b)Q1=30,(c)Q1=20. Fig. 14 The f-c profiles of the Rayleigh wave in model 4 (a) f-c profile in elastic medium; (b) Q1=30; (c) Q1 = 20. |
另一方面,当Q1=20时,我们将震源主频改为15Hz和30 Hz(图 15),面波的频散特性没有出现显著变化,没有受到震源主频变化的影响.
|
图 15 模型4中的面波记录的f-c剖面(a)f0 = 15 Hz, b)f0 = 30 Hz. Fig. 15 The f-c profiles of the Rayleigh wave m model 4(a)f0 = 15 Ⅱz(b)f0 = 30 Hz |
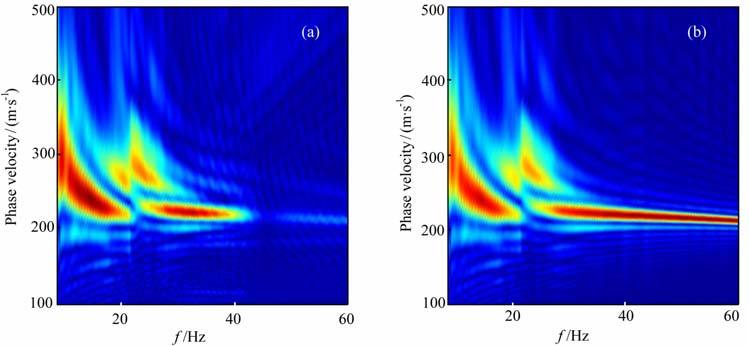
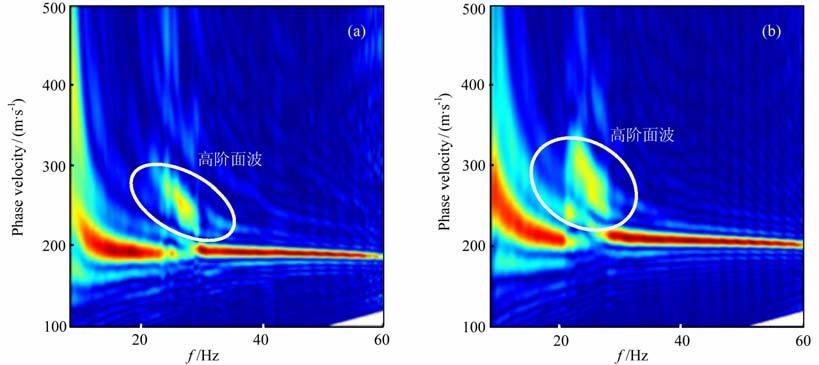
我们也模拟了空洞中充满空气时面波的传播,空洞内纵波波速340 m·s-1.图 16 为从单炮记录得到面波的频率-相速度(f-c)剖面.随着吸收的增强,高阶模式面波能量所占的比重逐渐变大.
|
图 16 洞穴内含空气时面波记录的f-c剖面 (a)弹性介质,(b)Q1=30. Fig. 16 The f-c profiles of the Rayleigh wave with air in the cavity(a) f-c profile in elastic medium; (b) Q1 =30. |
面波的频散特性随着Q值而变化,如果工程勘探中未考虑Q值的影响,结果有可能与实际情况不符,有必要对黏弹性介质中的面波作深入研究.
5 结论与讨论本文提出一种黏弹性介质中的面波模拟方法,该方法模拟的Rayleigh 面波与解析解对比的结果表明:均匀介质中Rayleigh波形的幅值误差小于5%;两层介质中面波的频散曲线与理论值相吻合.此方法能够正确模拟黏弹性介质中的Rayleigh 面波.文中对横向缓变介质及含有空洞的介质中的面波频散特性与Q值的关系进行了对比研究,结果表明:弹性介质与黏弹性介质中面波的频散特性有着显著差异,浅层的Q值对面波的频散特性有着显著影响,强吸收情况下高阶面波能量所占比重变大.此结论可能对利用Rayleigh 面波进行工程勘探有一定的意义.
本文提出的方法为复杂介质中面波的模拟提供了工具.在工程勘探中,可针对实际问题的需要,模拟面波,进行观察系统设计,以便有效的解决实际问题.在油气勘探中,利用该方法可模拟复杂近地表面波,为地震资料噪声衰减研究提供帮助.
附录 A为便于公式推导,将黏弹性二阶位移-应力波动方程(1)~(11)改写为
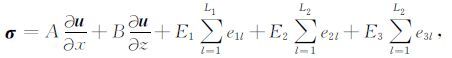
|
(A1) |

|
(A2) |
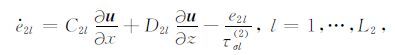
|
(A3) |
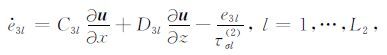
|
(A4) |

|
(A5) |
其中σ = (σxx,σzz,σxz)T,u= (ux,uz)T,f= (fx,fz)T; A、B、C、D、E、O和P皆为与拉梅常数和松弛时间常数有关的系数矩阵.
在弹性波模拟中,完全匹配层的引入可通过引进一个复数扩展坐标系来实现[22].以x轴为例,假设x≥0的区域为完全匹配层,x <0的区域为内部区域.对x轴作如下复数扩展:
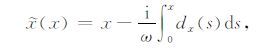
|
(A6) |
其中i= $\sqrt{-1}$,ω为频率,dx 为x方向的衰减系数,在内部区域中dx=0,匹配层内dx>0,dx(x)=d0(x/L)2,L为完全匹配层厚度,d0 =-3cplog(Rc)/2L,Rc 为数值离散后的目标反射系数,通常取为0.1%,dz的取值与dx类似.
对$\tilde{x}$的空间偏导数可写为
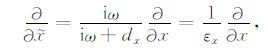
|
(A7) |
其中
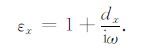
|
(A8) |
对$\tilde{z}$的空间偏导数可写为
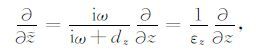
|
(A9) |
其中
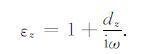
|
(A10) |
非分裂算法完全匹配层引入两个新的变量κ 和α[23],将式(A8)和(A10)推广为
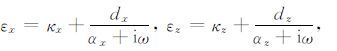
|
(A11) |
αx和αz在完全匹配层内线性变化,在匹配层和内部区域的交界处为最大值αmax,在匹配层外边界为0;αmax=πf0,f0 为震源主频;变量κ 主要用来吸收电磁场模拟中的消逝波,许多数值实验表明它对于吸收地震波没有关键性的影响,因此我们取κx=κz=1[17].
对于黏弹性波动方程,将公式(A1)~(A5)从时间-空间域变换至频率-空间域,其在复数扩展坐标系(${\tilde{x}}$,${\tilde{z}}$)下的表达式为

|
(A12) |
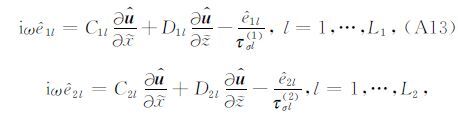
|
(A13) |

|
(A14) |
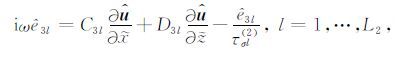
|
(A15) |
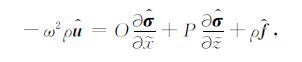
|
(A16) |
其中${\hat{\sigma }}$、${\hat{u}}$、${\hat{e}}$1l、${\hat{e}}$2l、${\hat{e}}$3l和${\hat{f}}$分别为σ、u、e1l、e2l、e3l和f在频域的表达式.
将$\frac{1}{{{\varepsilon }_{x}}}$的逆傅里叶变换记为sx(t),则$\frac{\partial }{\partial \tilde{x}}$可以替换为
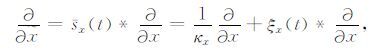
|
(A17) |
其中
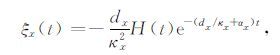
|
(A18) |
式中*代表卷积,H(t)为Heaviside函数.同样z方向有如下关系:
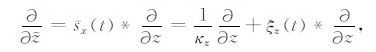
|
(A19) |

|
(A20) |
根据式(A17)和(A20),我们对式(A12)~(A16)做逆傅里叶变换,可得到黏弹性波动方程在完全匹配层内表达式为
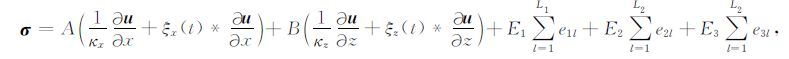
|
(A21) |
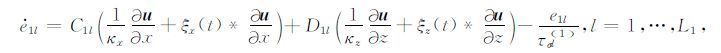
|
(A22) |

|
(A23) |
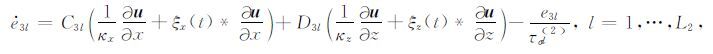
|
(A24) |
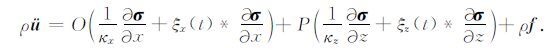
|
(A25) |
整理后即式(12)~(21).式中的卷积项可以使用一种递归卷积方法(recursive-convolution technique)来计算(Roden, Gedney, 2000).对于离散后的第n+1步时间迭代公式为
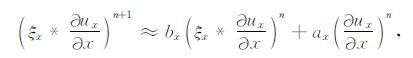
|
(A26) |

|
Δt为离散的时间步长,对于z方向的计算公式与此类似.
| [1] | 张碧星, 肖柏勋. 瑞利波勘探中"之"形频散曲线的形成机理及反演研究. 地球物理学报 , 2000, 43(4): 557–567. Zhang B X, Xiao B X. Mechanism of zigzag dispersion curves in Rayleigh exploration and its inversion study. Chinese J. Geophys. (in Chinese) , 2000, 43(4): 557-567. |
| [2] | 李文杰, 魏修成. 基于频率衰减特性的面波压制方法. 石油物探 , 2008, 47(3): 225–227. Li W J, Wei X C. A method for suppressing surface wave by considering the characteristic of frequency attenuation. GPP (in Chinese) , 2008, 47(3): 225-227. |
| [3] | Haney M M. Imaging lateral heterogeneity at coronation field with surface waves. 80th Annual International Meeting, Expanded Abstracts. SEG. 2010. |
| [4] | Haskell N A. The dispersion of surface waves on multilayered media. Bull. Seism. Soc. Am. , 1953, 43(1): 17-34. |
| [5] | Schwab F. Surface-wave dispersion computations: Knopoff's method. Bull. Seism. Soc. Am. , 1970, 60(5): 1491-1520. |
| [6] | Virieux J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics , 1986, 51(4): 889-901. DOI:10.1190/1.1442147 |
| [7] | Robertsson J O A, Blanch J O, Symes W W. Viscoelastic finite difference modeling. Geophysics , 1994, 59(9): 1444-1456. DOI:10.1190/1.1443701 |
| [8] | Igel H, Mora P, Riollet B. Anisotropic wave propagation through finite-difference grids. Geophysics , 1995, 60(4): 1203-1216. DOI:10.1190/1.1443849 |
| [9] | Saenger E H, Gold N, Shapiro S A. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion , 2000, 31(1): 77-92. DOI:10.1016/S0165-2125(99)00023-2 |
| [10] | Zahradník J, Moczo P, Hron F. Testing four elastic finite difference schemes for behavior at discontinuities. Bulletin of the Seismological Society of America , 1993, 83(1): 107-129. |
| [11] | Levander A R. Fourth-order finite-difference P-SV seismograms. Geophysics , 1988, 53(11): 1425-1436. DOI:10.1190/1.1442422 |
| [12] | Graves R. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences. Bulletin of the Seismological Society of America , 1996, 86(4): 1091-1106. |
| [13] | Mittet R. Free-surface boundary conditions for elastic staggered-grid modeling schemes. Geophysics , 2002, 67(5): 1616-1623. DOI:10.1190/1.1512752 |
| [14] | Xu Y X, Xia J H, Miller R D. Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach. Geophysics , 2007, 72(5). |
| [15] | Saenger E H, Bohen T. Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid. Geophysics , 2004, 69(2): 583-591. DOI:10.1190/1.1707078 |
| [16] | Xia J H, Millera R D, Parka C B, et al. Determining Q of near-surface materials from Rayleigh waves. Journal of Applied Geophysics , 2002, 51(2-4): 121-129. DOI:10.1016/S0926-9851(02)00228-8 |
| [17] | Komatitsch D, Martin R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics , 2007, 72(5): 155-167. DOI:10.1190/1.2757586 |
| [18] | Carcione J M. Seismic modeling in viscoelastic media. Geophysics , 1993, 58(1): 110-120. DOI:10.1190/1.1443340 |
| [19] | Carcione J M. Wave Fields in Real Media: Wave Propagation in Anisotropic, Anelastic, and Porous Media. Amsterdam: Pergamon, An Imprint of Elsevier Science. |
| [20] | Berg P, F If, P Nielsen, & O Skovgaard. Analytical reference solutions: Advanced seismic Modeling // Helbig K, ed. Modeling the Earth for Oil Exploration. Pergamon Press, 1994: 421-427. |
| [21] | Park C B, Miller R D, Xia J. Imaging dispersion curves of surface waves on multi-channel record. 68th Annual International Meeting, Expanded Abstracts. SEG. 1998: 1377-1380. |
| [22] | Chew W C, Liu Q H. Perfectly matched layers for elastodynamics: A new absorbing boundary condition. Journal of Computational Acoustics , 1996, 4(4): 341-359. DOI:10.1142/S0218396X96000118 |
| [23] | Roden J A, Gedney S D. Convolution PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media. Microwave and Optical Technology Letters , 2000, 27(5): 334-339. DOI:10.1002/(ISSN)1098-2760 |
 2012, Vol. 55
2012, Vol. 55