2. 中国科学院地质与地球物理研究所, 北京 100029
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
在天然裂缝性油藏中,通常在同一地层中存在两种不同的孔隙系统,使得整个油藏的孔隙分布不连续而且差异很大,这主要由具有较高储存能力、低流动能力的基质系统和低储存能力、较高流动能力的裂缝系统相互交接而成.由此可见,天然裂缝性油藏是一种双重介质油藏,若研究地震波在其中的传播规律,就要在各向同性孔隙介质模型的基础上,深入研究裂缝对储层的影响,将基质孔隙和裂缝网络两套系统相结合,建立更加符合实际的裂缝性储层双孔隙等效介质模型.
如何建立符合实际的双孔隙介质一直是国际上的一个重要研究方向.1951年,Gassmann[1]提出了关于弹性波在多孔介质中的传播理论,建立了著名的Gassmann 方程.Biot[2-3]在Gassmann 理论的基础上,进一步发展了开放条件下流体饱和多孔隙双相介质理论,发现了第二类纵波,现已成为研究双相介质的理论基础.1960 年,Barrenblatt等[4]提出了均质、各向同性的双孔隙介质模型.1963年,Warren等[5]在此基础上,提出了均质、正交各向异性的双孔隙介质模型.90年代以来,Tuncay等[6]利用体积平均的方法建立了双孔隙介质模型的波动方程.Berryman等[7]把Biot孔隙介质理论推广到了各向同性双孔隙介质模型中,给出了各向同性双孔隙介质的准静态方程,并确定了相关系数.陈勉等[8]通过对双孔隙介质有效应力的研究,建立了多重孔隙介质条件下的有效应力定律.黎水泉等[9]给出了双孔隙介质流- 固耦合方程的数学推导.Berryman等[10]将各向同性双孔隙介质的准静态方程进一步推广到地震波传播过程中,得到了各向同性双孔隙介质的应力应变方程.杜启振等[11]建立了裂缝诱导HTI双孔隙介质等效模型,并研究了地震波在该介质中的传播规律.
有关裂缝岩体渗流模型的理论主要是沿两个方向发展起来的:一是双重介质模型,二是非双重介质模型,它们的主要差别在于是否考虑油藏裂缝系统与孔隙系统之间的流体交换过程[12].双重介质模型根据窜流量和时间的关系又可以分为双重介质拟稳态窜流模型[4-5]和双重介质非稳态窜流模型[13-15],但这些模型要么在时间上作假设,要么在空间上作假设,都偏离了裂缝油藏的实际,计算误差较大[5].非双重介质模型方面,等效连续介质模型是其重要模型.该模型是将裂缝岩体模拟为具有对称渗透张量的各向异性连续体,由于可利用现成的连续介质理论,目前在水体渗流领域应用较广[16].刘建军[16-17]将渗流力学与弹塑性力学相结合,建立裂缝性低渗透油藏的流-固耦合渗流数学模型,并给出了其数值解;建立了油藏渗流和变形的等效连续介质模型.冯金德[18]以平行板理论为基础,将裂缝性低渗透储层模拟为具有对称渗透率张量的各向异性等效连续介质,建立了裂缝性低渗透油藏的等效连续介质模型.
本文针对裂缝诱导HTI双孔隙介质模型,对模型中的三个裂缝参数进行了较为深入的探讨.首先给出了模型的一阶速度-应力方程,并采用交错网格高阶有限差分法对理论模型进行了测试,给出了不同裂缝参数所对应的波场快照;然后分别研究了裂缝弱度与地震波速度、裂缝孔隙度与等效孔隙度、裂缝渗透率与等效渗透率的关系,并给出了相应的数值分析;最后给出了简要的结论.
2 裂缝诱导HTI双孔隙介质模型 2.1 一阶速度-应力波动方程根据双孔隙介质的概念,在实际的裂缝性储层中,孔隙可分为两部分:一部分代表基质孔隙,其孔隙空间大而渗透率低,是流体的主要存储空间;另一部分代表裂缝孔隙,其孔隙空间小而渗透率高,是流体的主要流动通道.基于这一概念,杜启振等[11]将一组垂直定向排列的裂缝嵌入到各向同性孔隙背景岩石中,建立了裂缝诱导HTI双孔隙介质模型(图 1).

|
图 1 裂缝诱导HTI双孔隙介质模型示意图 Fig. 1 Diagram of fracture-induced HTI double porosity medium |
该模型是在开放条件下,基于以下假设建立的[11]:①骨架是统计各向异性的;② 基质孔隙和裂缝相互连通,孔隙内充满各向同性的、具有黏滞性和可压缩性的流体;③骨架和流体之间存在相对位移,流体相对固体的流动属于Poiseuille型流动,流体在模型中的渗流遵守达西定律;④ 在应力作用过程中,模型内部的流体压力处处相等,因而基质孔隙系统和裂缝系统之间不存在流体交换;略去热弹性影响,也不考虑流体与骨架之间的化学作用.
基于以上假设,裂缝诱导HTI双孔隙介质的一阶速度-应力弹性波波动方程可表示为[11]

|
(1) |
其中,T是应力张量,C是刚度系数矩阵,G是微分算子矩阵,V是速度向量,ρ 是密度矩阵,B是流体耗散系数矩阵.
2.2 裂缝参数由文献[11]可知,波动方程(1)中隐含了裂缝参数信息,其中,裂缝的弱度、裂缝系统的孔隙度和渗透率对地震波的传播有很大影响,这里给出其简介.
2.2.1 裂缝弱度据文献[11],裂缝系统的弱度与公式(1)中的刚度矩阵的逆矩阵(柔度系数矩阵)有关,柔度矩阵可具体表示为
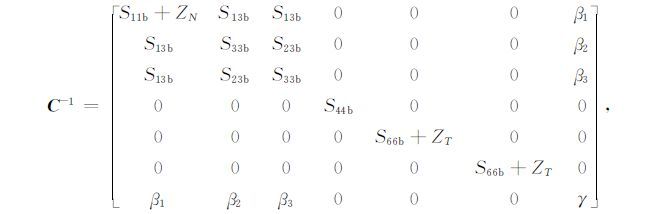
|
(2) |
其中,βi(i=1,2,3)表示固-流耦合柔度系数,且有β2 =β3;γ 是流体的柔度系数;S代表介质的柔度系数分量,下标b表示岩石基质;ZN和ZT分别为裂缝系统的法向弱度和切向弱度.而ZN和ZT又与单个裂缝的弱度参数之间存在如下的关系:
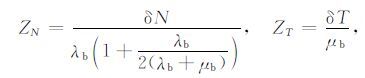
|
(3) |
其中,λb、μb 为各向同性孔隙岩石的弹性常数,δN和δT分别为单个裂缝的法向弱度和切向弱度.
2.2.2 裂缝系统的孔隙度和渗透率由文献[11]可知,裂缝系统的孔隙度和渗透率与方程(1)中的流体耗散系数矩阵B有关,矩阵B可具体表示为
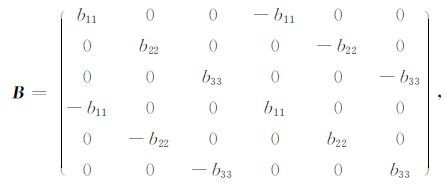
|
(4) |
其中,b11,b22,b33 为介质的耗散系数,其表达式为
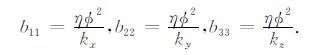
|
(5) |
这里,η 为流体黏滞系数,$\phi $ 和ki(i=x,y,z)分别为模型的等效孔隙度和等效渗透率,其表达式分别为
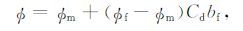
|
(6) |
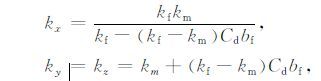
|
(7) |
其中,$\phi $m 和$\phi $f分别为基质系统孔隙度和裂缝系统孔隙度,km 和kf分别为基质系统渗透率和裂缝系统渗透率,Cd 为裂缝线密度,bf 为裂缝宽度.
3 裂缝参数分析 3.1 背景模型为了研究上述参数与地震波在HTI双孔隙介质模型中传播规律的关系,基于文献[11],构造了一个裂缝诱导HTI双孔隙介质模型,其物性参数和裂缝参数如表 1和表 2所示.其中,表 1是各向同性孔隙背景岩石的物性参数,表 2是所引入的裂缝参数.
|
|
表 1 各向同性背景岩石的物性参数 Table 1 Parameters of isotropic matrix system |
|
|
表 2 裂缝参数 Table 2 Parameters of fracture system |
表 1中,Ks、Kw 分别为固体颗粒和流体(水)的体积模量,ρm,ρf,ρa 分别为固体颗粒密度、流体密度以及固-流质量耦合附加密度.
3.2 裂缝弱度参数分析为研究裂缝弱度对地震波传播的影响,在表 1和表 2的基础上,分别将裂缝法向弱度和切向弱度从0.1变化到0.9.采用交错网格高阶有限差分法,对不同弱度情况下的一阶速度-应力方程(式(1))进行了数值试算,这里仅以流相水平分量为例,给出了不同弱度参数所对应的波场快照(如图 2 和图 3 所示).通过波动方程的平面波解析解,分别计算了不同裂缝弱度所对应的快纵波、横波和慢纵波相速度,并给出其关系曲线(如图 4,图 5和图 6所示).

|
图 2 不同裂缝法向弱度所对应的波场快照 (a)δN=0. 3; (b)δN = 0. 6; (c)δN = 0. 9.流相水平分量,t= 500 ms,δT =0. 9. Fig. 2 Snapshots of different fracture normal compliance Horizontal component in fluid phase,t=500 ms,compliance,δT= 0. 9. |
|
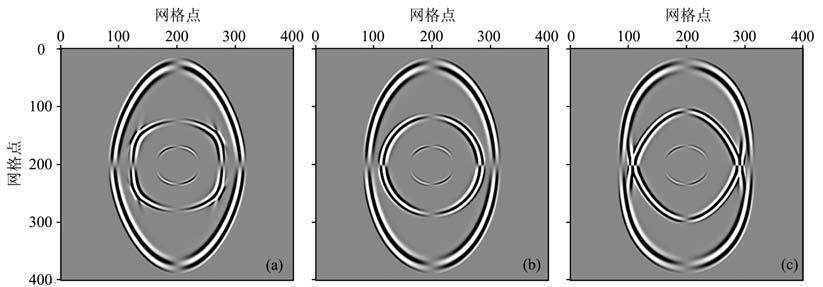
图 3 不同裂缝切向弱度所对应的波场快照 (a)δT=0. 3; (b)δT=0. 6 ; (c)δT=0. 9 ;流相水平分量,t= 500 ms,δN = 0. 3. Fig. 3 Snapshots of different fracture tangential compliance Horizontal component in fluid phase, t= 500 ms, δT = 0. 3. |
|
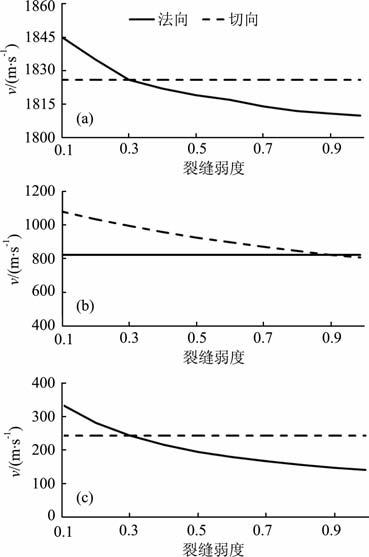
图 4 地震波相速度与裂缝弱度的关系曲线 (a)快纵波;(b)横波;()慢纵波. Fig. 4 Trend curves of seismic wave phase velocities with increasing fracture compliance (a) Fast P-wave; (b) S-wave; (c) Slow P-wave. |
|
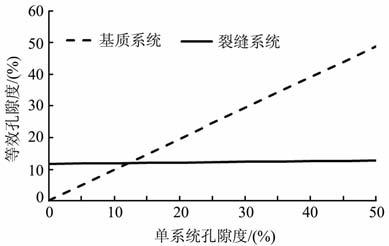
图 5 单系统孔隙度变化与等效孔隙度的对应关系 Fig. 5 Trend curves of equivalent porosity with increasing single system porosity |

|
图 6 裂缝系统的渗透率与等效渗透率的对应关系曲线 Fig. 6 Trend curves of equivalent permeability with increasing fracture permeability |
图 2、图 3所示的波场快照中存在三种波,由内向外分别为快纵波,横波和慢纵波.
从图 2 中可以看出,裂缝法向弱度变化时:①快纵波波前面椭圆的偏心率越来越大,说明介质的各向异性程度越来越强.这是因为,根据表达式(2),裂缝法向弱度δN的增大,会使裂缝系统的法向弱度ZN增大,从而导致介质的柔度系数分量S11由基质孔隙系统的S11b增大到S11b+ZN(式(3)),而其他柔度系数分量保持不变,这就使得介质在裂缝走向即水平方向上的刚度系数分量变小;② 横波波前面在两个正交方向上基本没有变化.因为根据表达式(3),裂缝法向弱度的改变对介质剪切方向的柔度系数分量没有影响,所以介质的刚度系数分量在剪切方向保持不变.
从图 3 中可以看出,裂缝切向弱度变化时:①快纵波的波前面没有变化.据表达式(2),裂缝切向弱度δT的改变不会改变裂缝系统的法向弱度ZN,因而也不会对介质在法向上的刚度系数分量产生影响;②慢纵波波前面椭圆的偏心率逐渐增大,这是因为,根据表达式(2),裂缝切向弱度δT的增大,会使裂缝系统的切向弱度ZT增大,从而导致介质的柔度系数分量S66由基质孔隙系统的S66b增大到S66b+ZT(式(3)),这就使得介质所对应的剪切方向的刚度系数分量减小.
从以上的分析可以看出,法向弱度增大会使快纵波波前面椭圆的偏心率越来越大性,而切向弱度增大则会对横波的波前面产生影响,这表明裂缝弱度是裂缝诱导HTI双孔隙介质中产生各向异性的主要原因,且随着裂缝弱度的增大,介质的各向异性强度逐渐增加.
3.2.2 裂缝弱度对相速度的影响由于裂缝法向弱度δN的增大,会使介质的柔度系数分量S11增大而其他分量保持不变,根据文献[7]可知,介质的体积压缩模量K与柔度系数分量存在如式(8)所示的关系,因此,随着裂缝法向弱度的增大,介质的体积压缩模量减小;而裂缝切向弱度δT的增大,会导致介质的柔度系数分量S66增大,也就导致介质所对应的剪切方向的刚度系数分量减小,即剪切模量减小.所以,裂缝法向弱度δN的增大会减小快纵波和慢纵波的相速度,但不影响横波相速度;而切向弱度δT则正好相反(图 4).
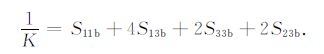
|
(8) |
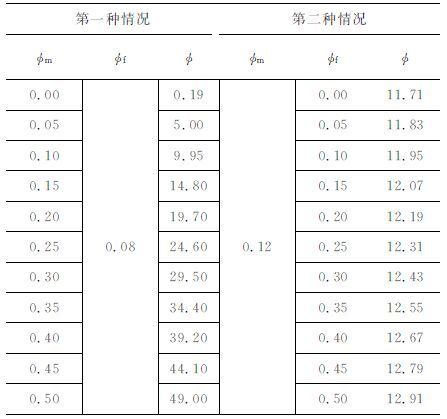
根据等效孔隙度的表达式(公式(6)),分别计算了基质系统孔隙度和裂缝系统孔隙度变化时所对应的等效孔隙度值(表 3),图 5是其关系曲线.
|
|
表 3 基质孔隙度和裂缝孔隙度与总孔隙度的数据对应关系 Table 3 Changes of equivalent permeability corresponding fracture and matrix porosity |
从表 3中可以看出,基质系统孔隙度由0增大到50%时,等效孔隙度由0.1% 增大到49%;而裂缝系统孔隙度按相同数值增大时,总孔隙度仅由原来的11.71%增大到12.91%.从图 5中也可以明显看出,当两套系统的孔隙度都增大相同的数值时,裂缝孔隙度变化对等效孔隙度的影响远远小于基质孔隙度.
以上分析表明,裂缝系统孔隙度的变化对等效孔隙度的变化影响不大,这体现了裂缝系统的“低孔"特性,所以在双孔隙介质中,裂缝所起的储集作用小,而孔隙则是其主要的储集空间.
3.4 裂缝系统的渗透率参数分析根据等效渗透率的表达式(式(7)),在表 1和表 2的基础上,计算了裂缝系统渗透率变化时所对应的介质等效渗透率的数值表(表 4),并绘制了其关系曲线(图 6).采用交错网格高阶有限差分法,分别对不同裂缝渗透率对应的一阶速度-应力方程(式(1))进行了数值计算,图 7 和图 8 分别是其流相水平分量的地震剖面和第190道合成记录.
|
|
表 4 裂缝渗透率与等效渗透率的数据对应关系 Table 4 Data of equivalent permeability corresponding fracture permeability |

|
图 7 不同裂缝系统的渗透率所对应的合成地震记录图(a)kf = 2×l0-9; (b)kf = 2×l0-8; (c)kf = 2×l0-7; (d)kf = 2×l0-6. 流相水平分量,渗透率单位:m2. Fig. 7 Synthetic elastic seismograms of different fracture permeabilities Horizontal component in fluid phase, permeability unit: m2. |
|
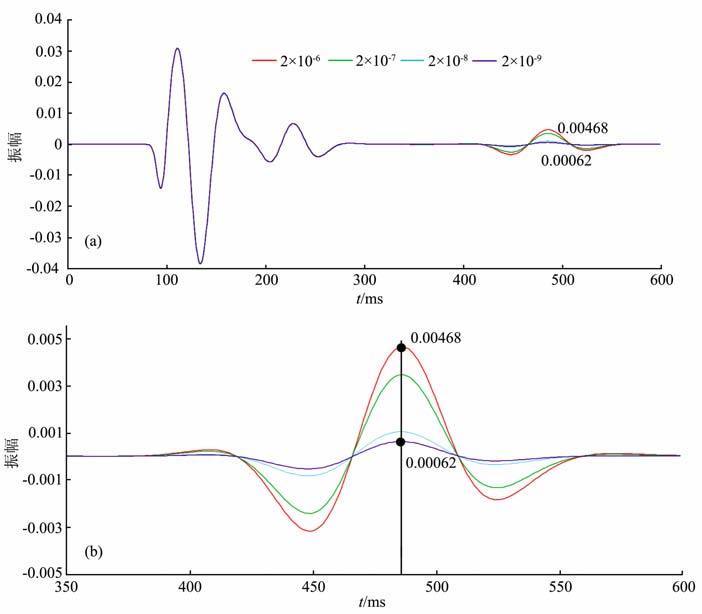
图 8 不同裂缝系统的渗透率所对应的地震波振幅对比图 第190道合成记录,流相水平分量,渗透率单位:m2 (a)快纵波,横波,慢纵波;(b)慢纵波. Fig. 8 Comparison of synthetic seismograms corresponding to different fracture permeabilities The 190th trace, horizontal component in fluid phase,permeability unit: m2 ; (a) fast P-wave,S-wave, slow P-wave; (b) slow P-wave. |
① 从表 4中可以看出,随着裂缝系统渗透率的增大,介质的等效渗透率都有所提高,但是水平方向的渗透率仅提高了0.025,而垂直方向则提高了25倍.② 从图 6中可以看出,裂缝的存在显著提高了双孔隙介质在z方向的渗透率,而对于x方向的渗透率则影响很小.
以上分析表明,裂缝系统渗透率参数的引入会提高HTI双孔隙介质的等效渗透率,尤其在裂缝发育方向,介质的渗透率会得到显著的提高,这体现了裂缝系统的“高渗"特性.所以在双孔隙介质中,裂缝系统是流体的主要流通通道.
3.4.2 裂缝系统的渗透率对慢纵波振幅的影响图 7所示的地震剖面中存在三种波,从上到下分别为快纵波、横波和慢纵波.从图中可以看出,当裂缝渗透率从2×109m2 增大到2×106m2 时,快纵波和横波的振幅没有变化,而慢纵波的振幅则显著增强.这是因为,由关系式(5)可知,裂缝系统的渗透率kf 的增大会使得介质的等效渗透率kx、ky和kz增大,从而导致介质的耗散系数b11、b22 和b33 减小(式(7));而根据文献[2]可知,慢纵波的振幅衰减与介质的耗散系数有关,也就是振幅强度随着介质耗散系数的减小而增大.因此,当裂缝系统的渗透率kf增大时,介质的等效渗透率随之增大,从而使介质的耗散系数减小,慢纵波的振幅逐渐增强.
图 8是不同裂缝渗透率所对应的第190道合成记录.从图中可以看出,裂缝渗透率增大对快纵波和横波振幅没有影响,而对慢纵波影响很大.图 8b明显地显示,当裂缝渗透率为2 ×109m2 时,慢纵波的振幅峰值为0.00062;随着裂缝渗透率的增大,慢纵波的能量显著增强;当裂缝渗透率增大到2 ×106m2 时,慢纵波振幅峰值变为0.00468,增大了6.5倍.
4 结 论本文对裂缝诱导HTI双孔隙介质模型中的裂缝参数进行了深入研究,获得了以下认识:
(1) 裂缝弱度是裂缝诱导HTI双孔隙介质呈现各向异性的主要原因.随着裂缝弱度的不断增大,双孔隙介质的各向异性强度逐渐增强.其中,法向弱度增大会使快纵波波前面的椭圆规律逐渐增强,并不断弱化介质的体积压缩模量,从而使快、慢纵波的相速度减小;切向弱度增大则会使横波的波前面椭圆的离心率逐渐增强,并不断弱化介质的剪切模量,从而使横波的相速度减小.
(2) 裂缝系统的孔隙度对双孔隙介质的等效孔隙度影响不大.根据本文所给的物性参数值,基质系统孔隙度由0增大到50%时,等效孔隙度由0.1%增大到49%;而裂缝系统孔隙度按同样数值增大时,等效孔隙度仅从原来的11.71%增大到12.91%.这是裂缝系统在双孔隙介质中所表现出来的“低孔"特性,由此可见,在双孔隙介质中,基质孔隙系统是流体的主要储集空间.
(3) 裂缝系统渗透率参数的引入会提高HTI双孔隙介质的等效渗透率,尤其在裂缝发育方向,介质的渗透率会得到显著的提高.根据本文所给的物性参数值,随着裂缝渗透率的增大,介质在裂缝发育方向的等效渗透率提高了25倍,这体现了裂缝系统的“高渗"特性,由此可见,在双孔隙介质中,裂缝系统是流体的主要流通通道.另外,当裂缝渗透率从2×109m2 增大到2×106m2 时,快纵波和横波的振幅不发生变化,而慢纵波的振幅则增大了6.5倍,说明裂缝系统渗透率的增大使慢纵波的振幅得到显著增强.
| [1] | Gassmann F. Elastic waves through a packing of spheres. Geophysics , 1951, 16(4): 673-685. DOI:10.1190/1.1437718 |
| [2] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J. Acoust. Soct. Am. , 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [3] | Biot M A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. , 1956, 27: 240-253. DOI:10.1063/1.1722351 |
| [4] | Barenblatt G I, Zheltov Iu P, Kochina I N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. , 1960, 24(5): 1286-1303. DOI:10.1016/0021-8928(60)90107-6 |
| [5] | Warren J E, Root P J. The behavior of naturally fractured reservoirs. Soc. Pet. Engg. J. , 1963, 3(3): 245-255. DOI:10.2118/426-PA |
| [6] | Tuncay K, Corapcioglu M Y. Effective stress principle for saturated fractured porous media. Water Resources Research , 1995, 31(12): 3103-3106. DOI:10.1029/95WR02764 |
| [7] | Berryman J G, Wang H F. The elastic coefficients of double-porosity models for fluid transport in jointed rock. J. Geophys. Res. , 1995, 100(B12): 24611-24627. DOI:10.1029/95JB02161 |
| [8] | 陈勉, 陈至达. 多重孔隙介质的有效应力定律. 应用数学和力学 , 1999, 20(11): 1121–1127. Chen M, Chen Z D. Effective stress laws for multi-porosity media. Applied Mathematics and Mechanics (in Chinese) , 1999, 20(11): 1121-1127. |
| [9] | 黎水泉, 徐秉业. 双重孔隙介质流固耦合理论模型. 水动力学研究与进展 , 2001, 16(4): 460–466. Li S Q, Xu B Y. Theory model of fluid flow through deformable dual porosity media. Journal of Hydrodynamics (in Chinese) , 2001, 16(4): 460-466. |
| [10] | Berryman J G, Wang H F. Elastic wave propagation and attenuation in a double-porosity dual-permeability medium. Int. J. Rock Mech. Min. Sci. , 2000, 37(1-2): 63-78. DOI:10.1016/S1365-1609(99)00092-1 |
| [11] | 杜启振, 孔丽云, 韩世春. 裂缝诱导各向异性双孔隙介质波场传播特征. 地球物理学报 , 2009, 52(4): 1049–1058. Du Q Z, Kong L Y, Han S C. Wavefield propagation characteristics in the fracture-induced anisotropic double-porosity medium. Chinese J. Geophys. (in Chinese) , 2009, 52(4): 1049-1058. |
| [12] | 周德华, 焦方正, 葛家理. 裂缝渗流研究最新进展. 海洋石油 , 2004, 24(2): 34–38. Zhou D H, Jiao F Z, Ge J L. Investigating progress for fluid flowing in fractured media. Offshore Oil (in Chinese) , 2004, 24(2): 34-38. |
| [13] | Streltsova T D. Hydrodynamics of groundwater flow in a fractured formation. Water Resources Research , 1976, 12(3): 405-414. DOI:10.1029/WR012i003p00405 |
| [14] | Bibby R. Mass transport of solutes in dual-porosity media. Water Resources Research , 1981, 17(4): 1075-1081. DOI:10.1029/WR017i004p01075 |
| [15] | Neretinieks I, Rasmuson A. Diffusion in the rock Matrix: an important factor in redounded retardation. Journal of Geophysical Research , 1988, 85(B5): 4379-4397. |
| [16] | 刘建军, 刘先贵, 胡雅礽, 等. 裂缝性砂岩油藏渗流的等效连续介质模型. 重庆大学学报 (自然科学版) , 2000, 23(Suppl): 158–161,180. Liu J J, Liu J G, Hu Y R, et al. The equivalent continuum media model of fracture sand stone reservoir. Journal of Chongqing University (Natural Science Edition) (in Chinese) , 2000, 23(Suppl): 158-161,180. |
| [17] | 刘建军, 杜广林. 裂缝性砂岩油藏流-固耦合数学模型. 新疆石油学院学报 , 2002, 14(3): 36–40. Liu J J, Du G L. Study on mathematic models of fluid-solid coupled flow in fractured oil reservoir of sandy rock. Journal of Xinjiang Petroleum Institute (in Chinese) , 2002, 14(3): 36-40. |
| [18] | 冯金德, 程松林, 李春兰, 等. 裂缝性低渗透油藏等效连续介质模型. 石油钻探技术 , 2007, 35(5): 94–97. Feng J D, Cheng S L, Li C L, et al. Equivalent continuous medium model for fractured low-permeability reservoir. Petroleum Drilling Techniques (in Chinese) , 2007, 35(5): 94-97. |
 2012, Vol. 55
2012, Vol. 55