2. 国家海洋局第二海洋研究所, 杭州 310012
2. Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China
海底表层沉积物介质是一类主要由粘土、粉砂、砂和孔隙流体(含水或含气)组成的孔隙介质,它位于海平面数十米至数千米以下的海底.这类介质颗粒胶结差,平均密度较低(1.2~2g/cm3),具有骨架模量低、孔隙度和渗透率较高的特点[1-2],多种情形下,介质的孔隙被海水充填且介质近似于悬浮液状态[3-5].该类介质具有较强的沉积层序结构,介质速度梯度变化大.声波在该类介质中传播时,由于受到反射、折射和散射的影响,声波耗散很大.通常情况下,海底沉积物介质中的孔隙被液体和一种或者多种气体饱和,气体在孔隙中以小气泡的形式存在,或者大气泡中包含了一定量的介质颗粒而存在,气体的存在改变了孔隙流体性质并与骨架产生耦合作用,对声波速度和衰减影响很大[1, 6].
Biot[7-9]理论是目前研究和应用比较广泛的一种经典的孔隙黏弹性模型,它描述了弹性波在固体和流体应力相互作用下的传播特征.Stoll[1](1998)将Biot理论应用于海底沉积物介质中的声波传播速度和衰减计算,并对该理论进行了扩展,建立了Biot-Stoll模型.该模型考虑了沉积物粒间胶结差、骨架模量低的特点,并指出骨架耗散是导致声波衰减的重要原因,但骨架耗散大小与频率无关.Chotiros[10](2004)考虑了骨架颗粒间的未固结特性,进一步发展了Biot-Stoll模型,提出了基于附加颗粒间喷射流和剪切流的Biot模型.该模型引入了低频极限的剪切模量、体变模量高低频极限差、体积弛豫频率和剪切弛豫频率四个新参数,由于这些参数不能通过实验测量得到,增加了该模型应用的复杂性.Biot-Stoll模型在未固结砂岩的声波速度和衰减计算方面的成果较多,Ohkawa[11](2006)应用Biot-Stoll模型计算了水饱和砂岩的声波衰减,Kimura[12](2007)讨论了Biot-Stoll模型物理参数的简化过程,曹正良[13](2006)应用Biot-Stoll模型研究了海底界面的声波的反射和散射特性.
以往研究海底沉积物这种孔隙介质的声波传播以及孔隙介质模型反演时,均假设孔隙介质是流体饱和的[11-13],而实际上海底沉积物介质的孔隙中可能含有两种或两种以上的流体,例如不但含有海水,而且含有CO2,这种现象在海底沉积物重力取样时已经得到了证实.为了使研究的模型更加符合实际情况,本文对Biot-Stoll模型进行了修正,假设孔隙中含有液体和自由气体,并把孔隙中所含的液体和气体等效为一种孔隙流体.基于此模型,本文详细讨论了海底沉积物中快纵波、慢纵波和横波的传播特性,主要包括流体黏滞系数、骨架耗散系数以及含气饱和度对声波速度和衰减的影响,并把该模型应用于杭州湾海底沉积物样品的声学特性研究中.
2 非饱和Biot-Stoll模型Biot(1962)研究了无边界流体饱和孔隙介质中声波的传播,预测了快纵波、慢纵波和横波的存在,其中,快纵波的衰减受流体黏滞耗散影响很小,而慢纵波的衰减受到的影响很大[9].Stoll考虑到海底沉积物介质的未固结性,对Biot理论进行了修正,以使其适用于海底介质声学特性研究.
2.1 Biot-Stoll 模型早期,海底介质被视为流体介质、弹性或者黏弹性固体介质.实际上,海底介质主要由固体颗粒胶结成孔隙骨架,液体物质填充于固态颗粒的缝隙处.Stoll应用Biot理论研究了声波在海底介质中的声波传播,认为骨架耗散是造成声波衰减的重要原因,因此对Biot理论进行了修正,建立了Biot-Stoll模型.Biot-Stoll纵波波动方程为[14]

|
(1) |

|
(2) |
Biot-Stoll横波波动方程为
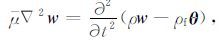
|
(3) |
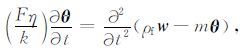
|
(4) |
其中,u和U分别为骨架和孔隙流体位移矢量,e=Δ·u,ζ =$\phi $Δ·(u-U),w=Δ×u,θ =$\phi $Δ× (u-U),$\phi $,η,k分别为孔隙度、黏滞系数和渗透率.Biot弹性模量H、C 和M 用骨架体积模量、孔隙流体体积模量和颗粒体积模量分别表示为

|
其中,Kr,Kf 分别是颗粒体积模量和孔隙流体体积模量,是实数.Kb,μ 是骨架体积模量和剪切模量,是复常数.

|
K0,μ0 是无耗散骨架体积模量和剪切模量,i=$\sqrt{-1}$,δK,δμ 是耗散系数.沉积物密度ρ= (1-$\phi $)ρs+$\phi $ρf,ρs,ρf分别为颗粒密度和流体密度.附加质量m=αρf/$\phi $,α 为孔隙弯曲因子.F是黏滞系数校正因子,与频率有关,以上符号的具体物理意义见文献[1].
2.2 声波频散方程Biot-Stoll模型和Biot理论的声波频散方程具有相似性,主要差别在于Biot-Stoll模型的弹性模量H、C 和M 是复数,本文给出了完整的Biot-Stoll模型声波频散方程的推导过程.考虑一维平面波解,设沿x方向传播的平面波为
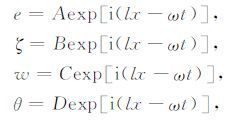
|
式中,l为波数,ω 为角频率.把上述表达式代入方程(1)~(4),可以得到纵波频散方程(5)和横波频散方程(6):

|
(5) |
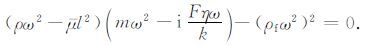
|
(6) |
令Y= (l/ω)2,方程(5)关于Y的两个解分别为Y1,Y2,方程(6)关于Y的解为Y3.则纵波速度Vpi和横波速度Vs 的表达式分别为(i=1,2分别表示快纵波和慢纵波)

|
(7) |
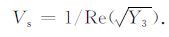
|
(8) |
纵波和横波的衰减系数αpi,αs 以及质量品质因子Qpi,Qs 的表达式分别为
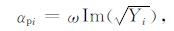
|
(9) |
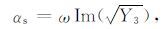
|
(10) |

|
(11) |
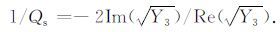
|
(12) |
海底沉积物的孔隙流体中含有气体(如空气、天然气)时,有效孔隙流体更容易被压缩,从而影响了沉积物的声波速度和衰减.基于等效介质理论[15-16],把孔隙中所含的液体和气体等效为一种流体,等效流体的密度一般用线性平均公式计算:
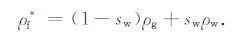
|
(13) |
在计算含有多种矿物颗粒和孔隙的混合物的等效弹性模量时,一般用到两种平均公式,即Voigt和Reuss公式,前者代表坚硬孔隙形状,后者代表柔韧孔隙形状,其表达式如(14)和(15)式所示.

|
(14) |
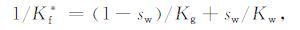
|
(15) |
式中,sw 是液体的饱和度,ρg,ρw 分别是气体和液体的密度,Kg,Kw 分别是气体和液体的体积模量,ρf* ,Kf* 分别是等效流体的密度和体积模量.
上述公式成立的条件是,每个组成成分是各向同性、线性和弹性的.由于液体和气体的体积模量较低,二者的混合物较软,因此采用(15)式求取等效流体的体积模量.用等效流体的密度和体积模量分别替代方程(5)、(6)中流体的密度和体积模量,即可求得孔隙流体含气情况下的声波速度和衰减.
3 声波速度和衰减由式(5)(6)分析可知,对于流体饱和孔隙海底介质,骨架耗散和流体黏滞耗散造成了声波总能量的减小,前者与频率无关,后者随频率的变化而变化.当孔隙流体中同时含气时,孔隙介质的有效流体体积模量和密度会发生变化,这种变化会对声波速度和衰减产生影响.
为了便于对比分析,本文给出了含气非饱和Biot-Stoll模型、Biot-Stoll模型以及Biot模型声波速度和衰减的计算结果,孔隙海底介质参数(来源于Stoll和Kan 数据[17-18])如表 1 所示,根据Biot理论,该介质的Biot特征频率为fc =$\phi $η/(2πρ*fK)=13.3kHz.Biot模型只考虑了流体黏滞耗散对声波能量的影响,Biot-Stoll模型考虑了骨架耗散和流体黏滞耗散对声波能量的影响,非饱和Biot-Stoll模型同时考虑了骨架耗散、流体黏滞耗散和含气饱和度对声波能量的影响.通过对比分析,主要考察了介质在骨架耗散作用下、流体黏滞耗散作用下,以及含气情况下快纵波、慢纵波和横波的传播特性,计算结果见图 1所示.
|
|
表 1 孔隙海底介质参数 Table 1 Marine sediments parameters |
|
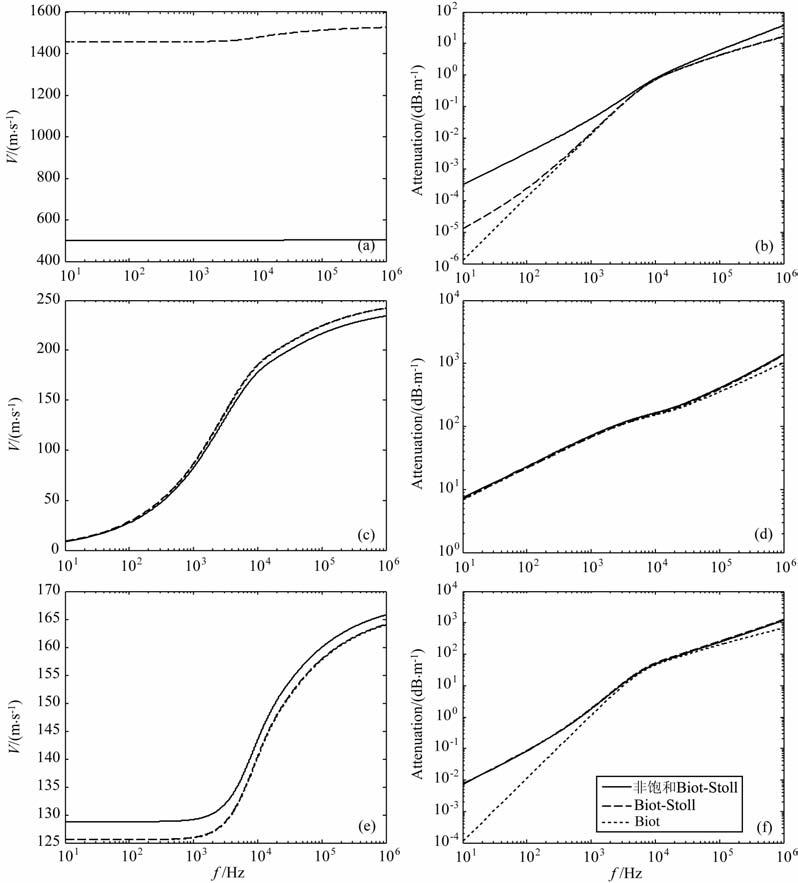
图 1 含气非饱和BOt-Stoll模型声波速度频散(a,c,e)和衰减(b,d,f) (a,b)快纵波;(c,d)慢纵波;(e,_f)横波. Fig. 1 Acoustic wave dispersion of partially gas-saturated Biot-Stoll model (a,b) Fast P-wave; (c,d) Slow P-wave; (e,f) Shear wave. |
从图 1(a,c,e)可知,Biot-Stoll模型和Biot模型预测的三种体波速度的变化趋势是一致的,即骨架耗散对三种体波速度频散影响不大,或者流体黏滞耗散对速度的影响占主要地位.对于非饱和Biot-Stoll模型,在低含气饱和度条件下,快纵波的速度明显低于非含气模型,且速度对频率的依赖性变弱;在低频情况下,气体对慢纵波速度的影响很小,在高频情况下,慢纵波速度略低于非含气的情况,随着频率的变大,这种趋势在增大;横波速度要高于非含气的情况,且对频率的依赖性较强.
图 1b表明,虽然Biot-Stoll模型和Biot模型预测的快纵波速度频散是一致的,但是衰减的变化有较大差别.在低频情况下,Biot-Stoll模型的快纵波衰减要大于Biot模型,且这种趋势随着频率的减小而增大,在高频情况下,两种模型预测的声波衰减较为一致.其物理意义是,低频情况下骨架完全处于松弛状态,骨架耗散造成了较大声波能量的损失,而随着频率的变大,流体和骨架的相对运动增强,流体黏滞耗散导致了较大声波能量的损失.对于非饱和Biot-Stoll模型,在低含气饱和度条件下,快纵波衰减明显要大于非含气的Biot-Stoll模型,这是由于气体的存在导致孔隙流体的可压缩性增大,从而引起更大的声波能量的损失.从图 1d看出,对于非饱和Biot-Stoll模型和其他两种模型,慢纵波衰减都很高,这也是慢纵波在实际中很难被观测到的原因,同时,气体对慢纵波衰减的影响不大.从图 1f看出,对于Biot-Stoll模型和Biot模型,横波衰减性质与快纵波衰减性质类似;对于非饱和Biot-Stoll模型和Biot-Stoll模型,横波衰减基本一致,即气体对横波的影响不大.
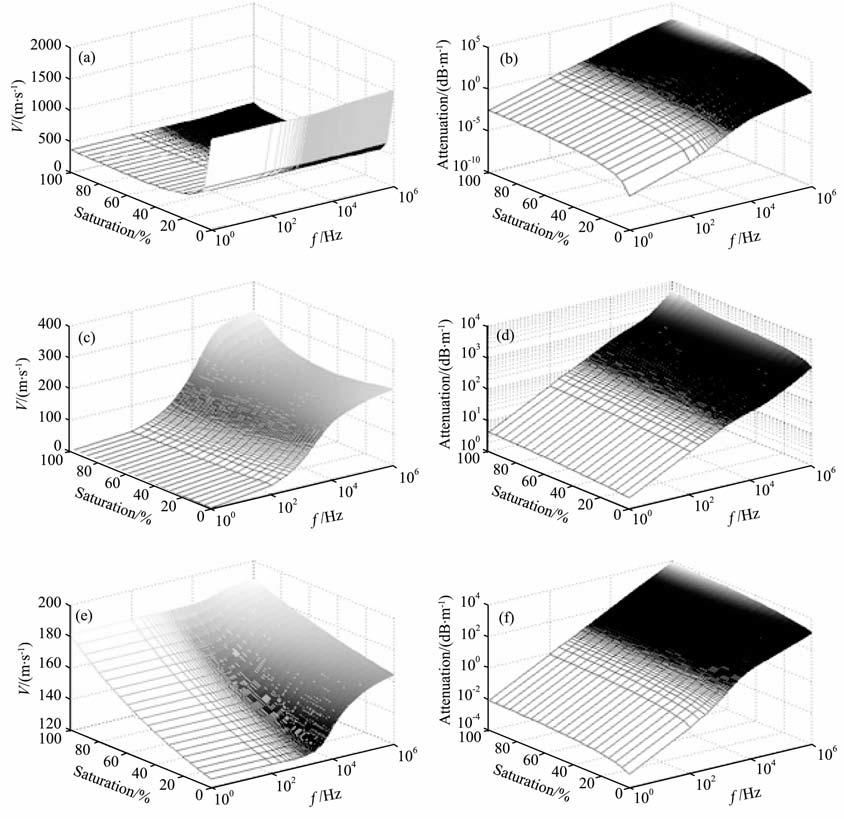
为了进一步说明含气饱和度对声波传播特性的影响,图 2给出了三种体波速度和衰减随频率与含气饱和度的变化关系.从图 2(a,c,e)看出,在低含气饱和度条件下,快纵波速度随含气饱和度的增加而迅速减小,当含气饱和度较大时,快纵波速度基本保持不变,且对频率的依赖性变弱.其物理意义是,气体的存在一方面导致了有效孔隙流体弹性模量的变小,另一方面导致了有效孔隙流体密度的变小,在低含气饱和度条件下,孔隙流体的弹性模量对快纵波速度的影响很大,随着含气饱和度的增加,孔隙流体密度对快纵波速度的影响逐渐增强.含气饱和度对慢纵波速度的影响依赖于频率的变化,在低频情况下,慢纵波速度基本不随含气饱和度的变化而变化,在高频情况下,慢纵波速度随着含气饱和度的增加而增加.同时,随着含气饱和度的增加,慢纵波速度从低频到高频的过渡带逐渐向高频移动.横波速度和慢纵波速度具有类似的特点,但是,在低频情况下,横波速度随着含气饱和度的增加而增加.由图 2(b,d,f)可知,快纵波衰减随着含气饱和度的增加而增加;慢纵波和横波衰减随着含气饱和度的增加而变化不大.同时,三种体波衰减对频率的依赖性很强,频率越高衰减越大.
|
图 2 频率和含气饱和度对声波速度(a,c,e)和衰减(b,d,f)的影响 (a,b)快纵波;(c,d)慢纵波;(e,D横波. Fig. 2 The effects of frequency and gas-saturation on the velocities (a,c,e)and attenuations(b,d,f) (a,b) Fast P-wave; (c,d) Slow P-wave; (e,f) Shear wave. |
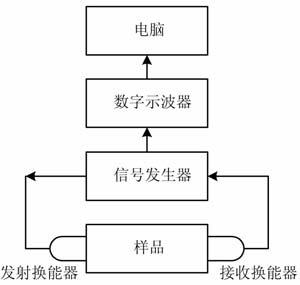
本文采用超声波透射法对海底沉积物样品进行了测量[19],测量系统主要包括
(1) PZT 材料压电换能器,用于发射和接收声波信号;
(2) Model5800信号发器,为发射换能器提供激励信号和预处理接收换能器信号;
(3) TDS3014B数字示波器,用于采集声波数据;
(4) 电脑,用于数据的后处理,如图 3所示.
|
图 3 实验测量系统 Fig. 3 The ultrasonic experiment system |
实验测量时,把待测样品放置在发射换能器和接收换能器之间,保证两个换能器端面平行并且在同一个中轴线上,样品和换能器的耦合用医用耦合剂或者黄油涂抹来实现,实验所使用的纵波换能器频率为50.0、80.0、100.0kHz,频率误差约为10%.
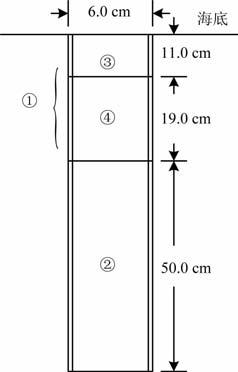
测量样品为杭州湾某海域柱状海底沉积物,其主要成分为粘土、泥和粉砂,颗粒直径为0.1至500μm.样品柱长为80.0cm,柱面直径为6.0cm,长度测量精度为0.02mm,如图 4所示.首先把样品分割成长为30.0cm 和50.0cm 的上下两部分,即图中的①、②两部分;然后把上端部分(即①部分)进行二次分割,切割成实际长为11.0cm 和19.0cm 的上下两部分,即图中的③、④两部分.样品具有方向性,样品的上部靠近海底.图 5(a,b,c,d)为实验接收到的波形,样品长度分别为11.0、19.0、30.0和50.0cm.从接收到的波形可以看出,对于同一长度样品,频率越高纵波传播时间越短,频率高的波形的最大幅度要低于频率低的波形的最大幅度,即声波的传播特性与频率有关.
|
图 4 样品分割示意图 Fig. 4 Schematic diagram of the split sample |

|
图 5 不同长度样品接收到的波形 (a) 11. 0 cm? (b)19. 0 cm? (c)30. 0 cm; (d)50. 0 cm . Fig. 5 The received waveforms in different length sample |
对接收到的波形进行处理后,计算得到频率为50.0、80.0、100.0kHz声波平均速度是1395.5、1471.7、1489.9m/s,即声波速度随频率的增大而增大.声波衰减的测量一般用功率谱和振幅法根据实际测量波形进行衰减计算[20-21],在此,利用功率谱法计算得到声波传播平均衰减分别是28.34、44.22、78.92dB/m.实际测量中发现,样品中夹杂有少量的气体,气体作为孔隙流体的一部分与水共存,致使样品速度低于海水的速度,测量的波形幅度也很小.样品主要为粉砂岩,其参数如表 2 所示(参考文献[22]的数据),所含自由气体一般为CO2.本文采用Biot-Stoll模型考察了孔隙中自由气体对声波传播速度和衰减的影响,其中,骨架耗散系数δμ =0.15和δK=0.1,自由气体含量为0.0025%,用非饱和Biot-Stoll模型计算了样品的纵波速度和衰减,同时和White模型、等效介质理论模型计算结果进行了对比.
|
|
表 2 粉砂沉积物模型参数 Table 2 The parameters of silt sediment |
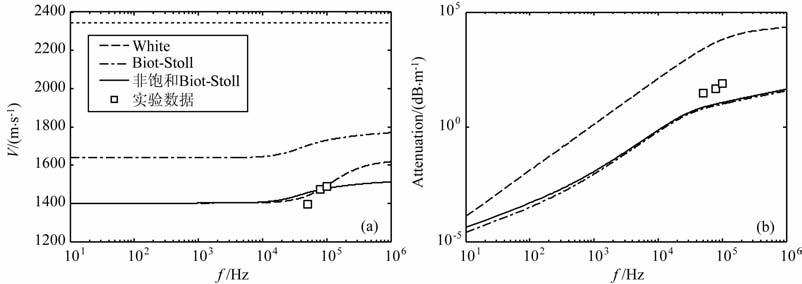
图 6给出了几种理论模型计算的声波速度和衰减与实验数据的比较,由图 6a 可知,非饱和Biot-Stoll模型和White模型在高频下预测的速度与实验测量速度较为一致,不含气的Biot-Stoll模型预测的速度比实验测量速度偏高,等效介质模型预测的速度远远高于实验测量速度.由图 6b看出,所有模型计算的衰减与实验数据差别较大,其中White模型计算的衰减偏高,非饱和Biot-Stoll模型和Biot-Stoll模型在高频下计算的衰减一致,都小于实验数据.上述结果说明,非饱和Biot-Stoll模型含气量接近0%时,高频下预测的速度和实际测量速度较接近,但是不能解释高频下高衰减的原因,虽然Biot-Stoll模型引入了骨架耗散机制,但是只能够解释低频下高衰减现象.实际上,海底沉积物作为一种孔隙介质,其骨架胶结性差,孔隙流体中少量气体或者气泡的存在,一方面使得孔隙流体的可压缩性增大,另一方面孔与孔之间的尺寸不一样导致了气泡可能从较小的孔迁移到较大的孔,从而很大程度上改变了声波在介质中传播的特点.
|
图 6 理论模型与实验数据对比 (a)速度;(b)衰减. Fig. 6 The comparison between theoretical model and experiment data (a) Velocity; (b) Attenuation. |
海底表层沉积介质骨架柔软、颗粒较细,主要表现为高孔隙度和高渗透率,骨架属性和孔隙流体黏滞性质共同影响声波传播特性.为了全面描述海底沉积物介质声学特性,必须考虑孔隙流体中含有气体的情况.利用非饱和Biot-Stoll模型计算了海底沉积物介质中的声波传播速度和衰减,计算结果表明:
(1) 在低频条件下,骨架完全处于松弛状态,由于在外力作用下骨架发生变形且恢复原状需要一段时间,在这一过程中介质内摩擦力做功,从而导致了较大的声波衰减;而在高频条件下,流体相对于固体的运动很强,从而流体黏滞性耗散导致了较大的声波衰减.
(2) 由于气体的存在,一方面导致了有效孔隙流体弹性模量的变小,另一方面导致了有效孔隙流体密度的变小,从而体波速度和衰减表现如下特征:在低含气饱和度条件下( <1%),快纵波速度随着含气饱和度的增加而迅速减小,在高含气饱和度条件下(>1%),快纵波速度变化较小;在低频条件下,慢纵波速度基本不随含气饱和度的变化而变化,在高频条件下,慢纵波速度随着含气饱和度的增加而增加;横波速度在高低频下均随着含气饱和度的增加而增加.快纵波衰减随着含气饱和度的增加而增加,慢纵波和横波衰减随着含气饱和度的增加而变化不大.
(3) 在含气饱和度趋近于0% 时,非饱和Biot-Stoll模型预测的速度与实验测量结果比较一致,但是,非饱和Biot-Stoll模型预测的声波衰减比实验测量结果偏低.上述原因的产生,一方面气体的存在导致了孔隙流体的可压缩性变大,另一方面气体在孔隙中的迁移可能改变了声波在介质中传播的性质.
| [1] | Stoll R D, Bautista E O. Using the Biot theory to establish a baseline geoacoustic model for seafloor sediments. Continental Shelf Research , 1998, 18: 1839-1857. DOI:10.1016/S0278-4343(98)00060-0 |
| [2] | Hamilton E L. Geoacoustic modeling of the sea floor. J. Acoust. Soc. Am. , 1980, 68(5): 1313-1340. DOI:10.1121/1.385100 |
| [3] | Buckingham M J. Theory of compressional and shear waves in fluidlike marine sediments. J. Acoust. Soc. Am. , 1998, 103(1): 288-299. DOI:10.1121/1.421091 |
| [4] | Buckingham M J. Theory of acoustic attenuation, dispersion, and pulse propagation in unconsolidated granular materials including marine sediments. J. Acoust. Soc. Am. , 1997, 102(5): 2579-2596. DOI:10.1121/1.420313 |
| [5] | Buckingham M J. Wave propagation, stress relaxation, and grain-to-grain shearing in saturated, unconsolidated marine sediments. J. Acoust. Soc. Am. , 2000, 108(6): 2796-2815. DOI:10.1121/1.1322018 |
| [6] | Leighton T G. Theory for acoustic propagation in marine sediment containing gas bubbles which may pulsate in a non-stationary nonlinear manner. Geophys. Res. Lett. , 2007, 34: L17607. DOI:10.1029/2007GL030803 |
| [7] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid: I. Low frequency range. J. Acoust. Soc. Am. , 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [8] | Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. , 1956, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [9] | Biot M A. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. , 1962, 33(4): 1482-1498. DOI:10.1063/1.1728759 |
| [10] | Chotiros N P, Isakson M J. A broadband model of sandy ocean sediments: Biot-Stoll with contact squirt flow and shear drag. J. Acoust. Soc. Am. , 2004, 116(4): 2011-2022. DOI:10.1121/1.1791715 |
| [11] | Ohkawa K. Confirmation of the Biot theory for water-saturated sands at high frequencies and effects of scattering on the attenuation of sound waves. J. Acoust. Soc. Am. , 2006, 119(2): 709-711. DOI:10.1121/1.2149770 |
| [12] | Kimura M. Study on the Biot-Stoll model for porous marine sediments. Acoust. Sci. & Tech. , 2007, 28(4): 230-243. |
| [13] | 曹正良, 张叔英, 马在田. BICSQS模型与Biot-Stoll模型海底界面声波反射和散射的比较. 声学学报 , 2006, 31(5): 389–398. Cao Z L, Zhang S Y, Ma Z T. Comparison of reflections and interface scatterings from BICSQS model and Biot-Stoll model seafloors. Acta Acoustica (in Chinese) , 2006, 31(5): 389-398. |
| [14] | Stoll R D. Sediment Acoustics. New York: Lecture Notes in Earth Sciences, 1989. |
| [15] | Mavko G, Mukerji T, Dvorkin J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media. New York: Cambridge University Press, 1998 . |
| [16] | Berryman J G, Thigpen L. Effective constants for wave propagation through partially saturated porous media. Appl. Phys. Lett. , 1985, 46(8): 722-724. DOI:10.1063/1.95487 |
| [17] | Badiey M, Cheng A H D, Mu Y K. From geology to geoacoustics-Evaluation of Biot-Stoll sound speed and attenuation for shallow water acoustics. J. Acoust. Soc. Am. , 1998, 103(1): 309-320. DOI:10.1121/1.421136 |
| [18] | Stoll R D, Kan T K. Reflection of acoustic waves at a water-sediment interface. J. Acoust. Soc. Am. , 1981, 70(1): 149-156. DOI:10.1121/1.386692 |
| [19] | 王东, 李栋梁, 张海澜, 等. 天然气水合物样品声纵波特性和温压影响测量. 中国科学(G辑: 物理学 力学 天文学) , 2008, 38(8): 1038–1045. Wang D, Li D L, Zhang H L, et al. Laboratory measurement of longitudinal wave velocity of artificial gas hydrate under different temperatures and pressures. Science in China (Series G: Physics, Mechanics and Astronomy) (in Chinese) , 2008, 38(8): 1038-1045. |
| [20] | Kibblewhite A C. Attenuation of sound in marine sediments: A review with emphasis on new low-frequency data. J. Acoust. Soc. Am. , 1989, 86(2): 716-738. DOI:10.1121/1.398195 |
| [21] | Tonn R. The determination of the seismic quality factor Q from VSP data: A comparison of different computational methods. Geophysics Prospect , 1991, 39(1): 1-27. DOI:10.1111/gpr.1991.39.issue-1 |
| [22] | 陶春辉, 王东, 金翔龙. 海底沉积物声学特性和原位测试技术. 北京: 海洋出版社, 2006 . Tao C H, Wang D, Jin X L. Marine Sediments Properties and in Situ Acoustic Measurements (in Chinese). Beijing: China Ocean Press, 2006 . |
 2012, Vol. 55
2012, Vol. 55



