2. 中国科学院研究生院, 北京 100049;
3. 澳门科技大学, 澳门
2. Graduated University of Chinese Academy of Sciences, Beijing 100049, China;
3. Macau University of Science and Technology, Macau, China
卫星观测表明磁层空间有大尺度的等离子体对流,这种对流运动过程是磁层最基本的物理过程,和这种大尺度对流运动相对应的是磁层空间存在大尺度的对流电场.该对流电场是在太阳风和磁层相互作用下形成的,对研究磁层物理过程有重要作用[1-2].
目前最简单的磁层电场模式是均匀晨昏电场[1].晨昏电场为假定磁层电场是晨昏方向的均匀电场,带点粒子在磁场和电场作用下做速度为V的漂移运动,由漂移速度可以推导出电场值:E=-V×B,所以磁尾等离子体做日向对流是对流电场作用的结果.均匀对流电场是最简单的电场模式,可以定性讨论磁层对流现象.该电场可用于带电粒子在磁赤道面的运动,考虑到磁尾磁场可近似看成为平行于磁尾方向,它和磁场始终可看成是相互垂直,因此可用于磁尾赤道面以外的整个空间.在近地球区的非磁赤道面和极区,电场方向和磁力线不垂直,粒子沿磁力线方向加速,与磁层磁力线是等势线的基本物理规律不符,均匀晨昏电场在上述区域不可用[2].
在磁层空间中的等离子体为稀薄的等离子体,可不考虑粒子之间的碰撞,沿磁力线的电导率近似无穷大,磁力线为等势线.因此可将观测到的电离层电位沿磁力线推广到整个磁层空间.沿着磁力线将电离层电势投影到磁层空间所得到的电场模式称为投影电场.常用的电离层电场模式为Volland电场,该电场模式简单,其电势仅仅是拉普拉斯方程的零阶近似[3],因此在近地球区简单实用;也可投影到中远磁尾区[4].
目前磁层电场的模式很多[3-5],均匀晨昏电场过于简单,它只适用于磁层和晨昏电场垂直的磁赤道面,因此应用区域有限.Volland电场作为投影电场模式,只对Kp指数作出响应.本文选择Weimer2001电场[5]作为投影电场模式,该电场是根据中高纬度电离层的电势,用拉普拉斯方程的高阶展开,其参数和行星际磁场(IMF)的大小和时钟角(angleclock)、太阳风速度和数密度以及磁轴倾角(tiltangle)有关[6-8].本文选用和Weimer电场变化参数相同的Tsganengko1996(T96)磁层磁场模式[9],将电离层Weimer电场和相同参数的T96磁场,沿其磁力线投影到磁层空间,提出一个新的磁层对流电场模式.该电场能够对太阳风参数、IMF 大小和时钟角、磁轴倾角、亚暴和磁暴作出响应,更加接近实际电场.
2 选取模型与计算方法电离层内的电场模型选取Weimer(2001)电场模式,具体函数表达式可参考文献[6].
磁层磁场选择T96 模式,其源程序从网上下载,内源场选择偶极子磁场.
磁层内的磁力线是等电位线,可以将电离层内的电势值沿磁力线投影到磁层空间,得到磁层内的电势分布.T96 磁场模式是用GSM 坐标系,而Weimer电场模式是用CGM 坐标系,因此在计算空间一点P(Xgsm,Ygsm,Zgsm )的电势时,将P(Xgsm,Ygsm,Zgsm)点沿T96磁力线投影到电离层的P′(X′gsm,Y′gsm,Z′gsm)点,P和P′在同一根磁力线上,利用GSM坐标系与CGM 坐标系的转换关系将P′(X′gsm,Y′gsm,Z′gsm)转换为P′(X′cgm,Y′cgm,Z′cgm),根据Weimer电场模式,计算P′(X′cgm,Y′cgm,Z′cgm)电势值,该电势值即是空间一点P(Xgsm,Ygsm,Zgsm)的电势值.
Weimer电场和T96磁场的输入参数有相同部分,Weimer电场的输入参数:行星际磁场(IMF)的时钟角,对应于T96 的输入参数:IMF 的两个分量By,Bz;T96输入参数:太阳风动压,对应Weimer电场的输入参数:太阳风速度和数密度的函数.因此我们可以用这两种模式的相同输入参数,研究在磁扰期间磁层电场的变化,将电离层观测的电场数据扩展到整个磁层空间.
3 计算结果与分析 3.1 地球磁层的电势根据上面的计算方法,计算2002 年第261 天10时0分0秒,极区电离层的Weimer电场电势分布,并将极区的电势沿T96磁力线投影到磁赤道面上.参数为:太阳风速度V=450km/s,数密度n=8.7cm-3,By=0nT,Bz= -3nT,IMF 时钟角angle=180°,亚暴指数AL= -150nT,磁暴指数Dst=-30nT,磁倾角Tilt=0°.结果如图 1和图 2所示.
|
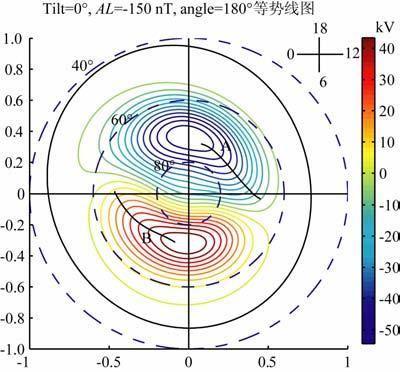
图 1 Weimer电场在极区的电势分布图 Fig. 1 Electric field pattern of Weimer in the polar cap region |
|
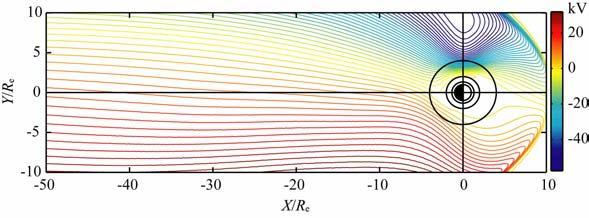
图 2 磁赤道面等势线图,输人参数 Tilt=0°,AL=-150 nT,angle=l80°,Dst=-30 nT Fig. 2 The equipotential lines at magnetic equatorial plane, input conditions are fixed with Tilt=0°,AL=-150 nT,angle=l80°,Dst=-30 nT |
图 3中虚线是磁纬度线,大的椭圆是电势边界线,彩色卵状线是等电位线.从图中可以看出,电位没有晨昏对称性,极盖区等电位线与子午线有顺时针方向10°左右的夹角.极盖区70°以内基本为均匀电场,电场方向不沿晨昏线方向,而与之有一夹角.沿A,B线的电场有明显衰减,晨昏线附近的电场最大.纬度在90°~80°内等势线是相互平行的,且距离基本相同,因此对应的电场基本不变;80°~70°电场逐渐变小;70°~60°电场逐渐变大;60°以外电场变小.
|
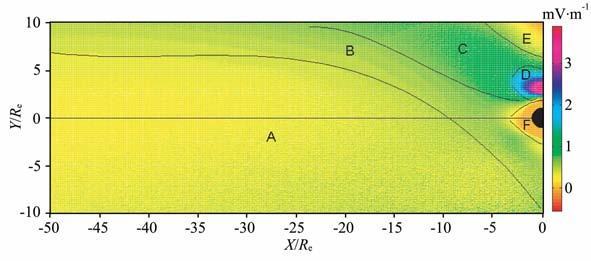
图 3 对应图 2条件下的磁赤道面电场Ey分量分布图 Fig. 3 The pattern of Ey component of electric field corresponding to the conditions of Fig. 2 at magnetic equatorial plane |
在磁层坐标系内,选择-50Re<Xgsm <10Re,-10Re<Ygsm<10Re 作为投影电势区域,Re 代表地球半径.图 2中相邻等势线的电势差为1.8kV,黑色圆圈是纬度线沿磁力线在磁赤道面上的投影位置.其背阳面的等势线形状与文献[4]的结果的等电势线形状大体上相似,但有其特有的特点,如下:
从图 2中可以看出远于-20Re 区域,等势线近似为一组等距离平行于Xgsm的平行线,这说明该区域内电场是沿Y方向即晨昏方向,且各点电场方向和大小基本不变,为均匀晨昏电场.远磁尾区的均匀晨昏电场是极区电离层的均匀晨昏电场的映射,映射场保持了源场的特点,这种特点与磁层的结构有关.
在中远地球区-20Re<Xgsm<-10Re 范围内,晨侧区域的等势线为一组平行Xgsm 的等距离平行线,即各点电场大小相等,方向沿晨昏方向的均匀晨昏电场.昏侧区域等势线不是一组与Xgsm 平行的平行线,而是向昏侧倾斜,这与前面分析的极区等电势线向昏侧倾斜对应,与晨侧区不同,该区域电场不是均匀电场,越靠近磁层边界等势线越密,电场越大,这是由于该区域的投影电场对应的源场是极盖区60°~70°,Weimer电场由外向内变小.
在近地球区-10Re<Xgsm <0Re 范围内,等势线有明显向地球方向弯曲,且越靠近地球区域和晨昏线附近,等势线越密即电场强度越大.随着Y增大,昏侧区的等势线越偏离Xgsm 方向,子午线附近的等势线基本平行于Xgsm方向.该区域电场的非晨昏分量不容忽略.该区域的电势投影与Volland电势的投影结构有高度的相似性,都有U 型弯曲结构,U 型结构是由极区Weimer电场的弧形结构投影得到的.晨侧对应区域没有明显的U 型结构,等势线只是向地球方向弯曲,因为对应的衰减场部分,弧形曲率不大近似平行80°内的等势线.投影场的晨昏不对称性是由于源场的晨昏不对称造成的,负电势区覆盖面积大,电压降比正电势区的电压降大,因此投影电场的昏侧电场比晨侧大.投影电场的非晨昏分量是极区衰减电场投影的结果,衰减电场是指极区的晨昏电场过渡到非晨昏电场,也就是极区等势线的弧形区域.
在向阳面到磁层顶0Re<Xgsm <10Re 区,磁层顶边界区Weimer电场的等势线很密,且等势线与磁层顶边界分布一致.昏侧区的晨昏线附近等势线有U 型结构,但在靠近磁层顶边界附近等势线向内弯曲,这是由于磁层磁力线在该区域被压缩引起的,原因在后面解释.子午线附近非磁层顶边界区的等势线是一组曲线,向晨侧偏转,源场对应的是极区子午线附近的电场,电场的非晨昏分量不可忽略.晨侧区的电势向外弯曲,也是由于衰减场造成的.从上面分析可以看出源场的晨昏不对称且向背阳面偏移对映射场的形态影响很大.其次,磁层顶附近的映射电场形态受磁场形状的影响很大.
子午面附近的磁力线主要沿X轴向磁尾方向延伸,这种延伸对Y轴方向的电场投影影响不大.磁层边界附近的背阳面磁力线除了有沿X轴向背阳面延展,向阳面磁力线向地球方向压缩,还有向子午面的压缩,所以磁层边界的投影电场明显变大.
Weimer电场是中高纬度电场,一般在40°以下区域没有电势值,对应的投影区是磁壳指数L=1.74Re 区域没有电势值.行星际磁场北向时,电势边界向高纬区收缩,最高可到60°区,对应的投影区L=4Re 内没有投影电势值.
3.2 地球磁层的电场特性根据Weimer电场的电势,可计算磁层空间的电场分布.考虑到电场是一个矢量,因此电场可用三个分量的分布来描述.图 2是等电位分布图,其对应的电场分布为图 3、图 4.另外垂直于磁赤道面的电场分量Ez= 0,因此图 3,4 只给出Ex和Ey的分布.在非磁赤道面空间内,该电场模式计算结果有Ez分量.向阳面磁层顶附近的电场值约20mV/m,磁尾电场值较向阳面磁层顶的电场值小两个数量级.为更加直观显示电场分布,图 3、4只画出背阳面电场分布,即X<0,Z=0时的电场强度的分布图.将两图分区讨论,结果如下:
|
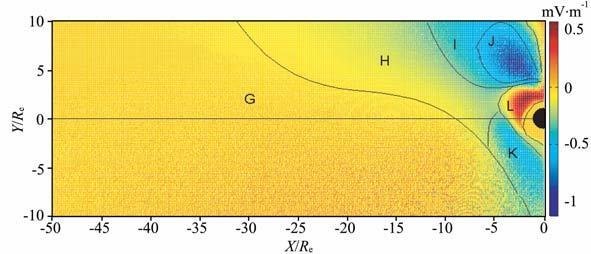
图 4 对应图 2条件下的磁赤道面电场Ex分量分布图 Fig. 4 The pattern of Ex component of electric tield corresponding to the conditions of Fig. 2 at magnetic equatorial plan |
(1) 远磁尾区(X<-15Re)以晨昏电场为主,非晨昏电场很小.由图可以看出,晨昏方向电场(即Ey分量):A 区(X<-15Re)的电场大小约为0.25~0.40mV/m,B区(X<-15Re)的电场大小约为0.40~0.60mV/m,从图中可以看出靠近磁层边界区的电场较子午面附近的电场强.非晨昏方向电场(即Ex分量)在G 区的电场大小约为0,H 区(X<-15Re)电场Ex大于-0.1mV/m,所以远磁尾区的非晨昏电场很小.张天辉等在文献[4]中计算的结果为0.1mV/m,靠近磁层边界的电场较大约为0.3 mV/m,本文与文献[4]的结果相似.Geotail在远磁尾的电场观测值为0.1~1.3 mV/m,同时观测表明电场还有Ez分量[10].该模型的计算电场值在卫星探测的范围之内.
(2) 近地球区(X>-15Re)的晨昏电场值较远磁尾区电场值大,对流电场的非晨昏分量不可忽略.晨昏方向电场Ey值:A 区(X>-15Re)的电场值约为0.5 mV/m,B(X> -15Re)区的电场大小约为0.5~0.7mV/m,C区的电场值为0.7~1.3mV/m,D区电场值为1.3~3.5mV/m,E 区电场值为0.1~0.4mV/m.非晨昏方向电场Ex不可忽略:H(X>-15Re)区非晨昏方向电场约为-0.2~-0.1mV/m;I区非晨昏方向电场约为-0.25~ -0.5 mV/m,J区的非晨昏方向电场约为-0.6~-1.1 mV/m,K区非晨昏方向电场大小为-0.25~-0.5mV/m,L区的非晨昏方向电场约为0.1~0.5 mV/m,G 区(X>-15Re)的非晨昏方向电场为0.通过以上讨论可知昏侧对流电场比晨侧电场大,晨侧的Ex电场较昏侧小.ISEE1卫星探测数据显示,在L=2~6磁赤道平面的电场在0.2~0.8mV/m,发生磁暴时电场可超过2mV/m,在该区域电场有Ex分量,非磁赤道平面有Ez分量[11].GEOS1卫星探测结果显示在中等扰动期间,磁壳数L=5~7 的昏侧区,对流电场值约为2~4 mV/m[12].通过对比,该模型的计算电场值与卫星测量相符.
4 地磁条件及行星际磁场对磁层电场的影响该磁层电场模式是由电离层内的Weimer电场模式和磁层磁场模式T96发展而来,因此磁层电场是上述两个模型的所有参数的函数,参数为:磁倾角、行星际磁场(IMF)的方向和大小、太阳风动压、亚暴AL指数和磁暴Dst指数.下面图 6、8和10是各参数条件下,磁赤道面上沿Y轴(晨昏线)和X轴(日地线)的电场值,该模型在X,Y∈[-2Re,2Re]区间没有投影值,所以图中显示为空.
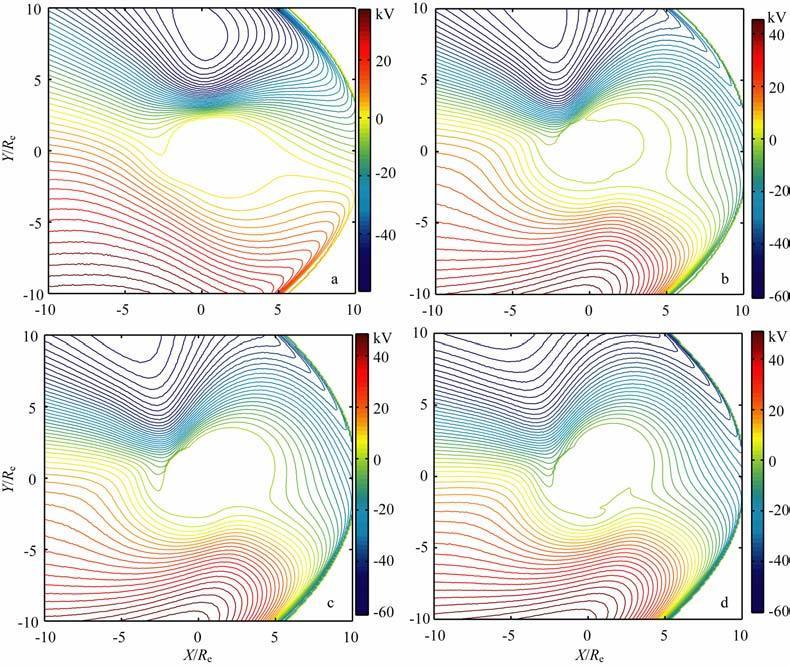
4.1 磁倾角对磁层电场的影响图 5为太阳风速度V=450km/s,数密度n=8.7cm-3,行星际磁场(IMF)By=0 nT,Bz=-4nT,IMF总强度Bt=10nT,IMF时钟角angle=180°,亚暴指数AL= -500nT,磁暴指数Dst=0nT时,不同磁倾角的磁赤道面上的等电位分布图.图 6是沿着图 5 中的晨昏线和日地线的电场值的变化图,an,bn,cn和dn曲线表示沿图 5中的晨昏线和日地线的电场值,n=1和2分别代表沿晨昏线(晨昏电场Ey)与日地线(非晨昏电场Ex)的电场值,其单位为mV/m.
|
图 5 磁赤道面上的等电位分布图,磁倾角分别为0°,10°,20°和30° Fig. 5 The equipotential patterns at magnetic equatorial plane,corresponding tilt angles are 0°,10°,20°and 30° respectively |
图 5中,当磁倾角增大时:
(1) 晨侧区的等电位线向地球方向弯曲,b,c和d图在该区出现U 型结构;等电位线在L=[-9Re,-3Re]区,先变密再变疏,磁倾角越大等电位线越密,反映在图 6中就是电场值Ey在Y<-2Re 区间先变大再变小,磁倾角变大电场值变大.

|
图 6 沿图 5中的晨昏线(晨昏电场Ey;)和日地线(非晨昏电场Ex)的电场值分布 Fig. 6 The plots of fMntensity along the dawn-dusk line (Ey)and the Sun-Earth line (Ex)in Fig. 5 |
(2) 昏侧区U 型等电位线,逆时针转动,等电位线的距离变均匀,所以图 6的电场值Ey在Y>2Re区间,磁倾角越大而电场值变化幅度越小.
(3) 非晨昏电场的值表示的是等电位线与X轴的夹角,Ex为零表示等电位线平行X轴.当磁倾角变大,子夜区(X<-2Re)的等电位线与子午线的夹角变小,而在正午区(X>2Re)的夹角变大,d 图正午区的夹角大于80°.
经分析,当磁倾角增大时,电离层内的Weimer电场分布变化很小,出现上述现象的原因是磁轴向太阳方向倾斜,磁层磁场的位型发生变化,磁力线根部对应的源场位置改变所引起的.
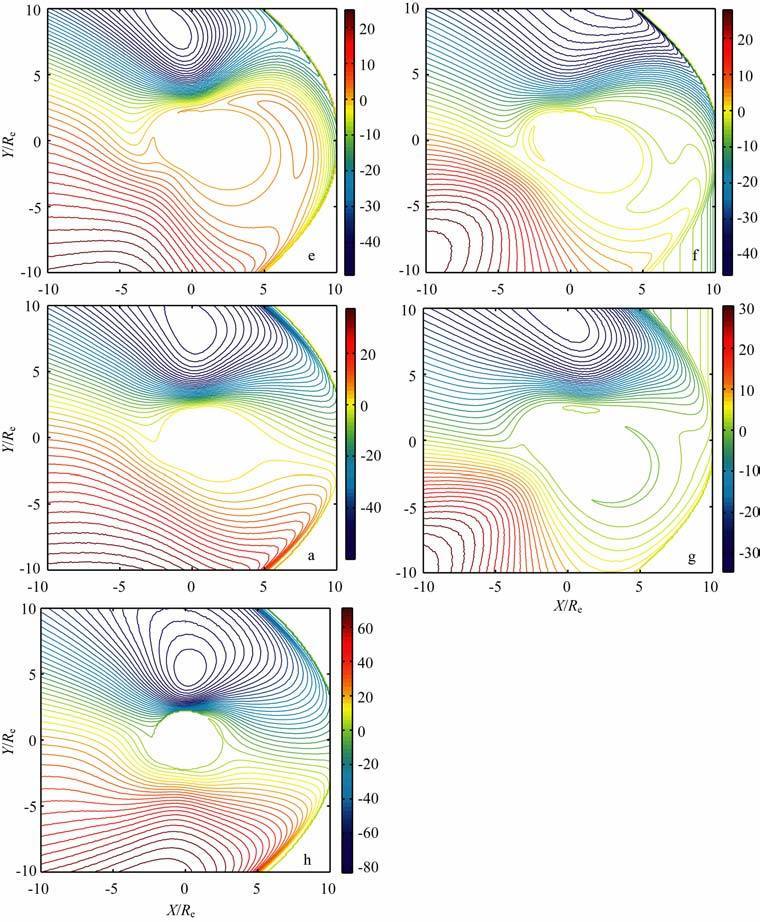
4.2 行星际磁场的方向和大小对磁层电场的影响图 7中的e,f,a和g 图分别是IMF 时钟角为0°,90°,180°和270°时磁赤道面上的等电位分布图,其他参数相同,分别是太阳风速度V=450km/s,数密度n=8.7cm-3,IMF 总强度Bt=10nT,IMF 时钟角angle=180°,亚暴指数AL= -500nT,磁暴指数Dst=0nT.图 7 中的h 图的IMF 总强度为Bt=20nT,其他的输入参数与a图相同,a和h 两图用来说明行星际磁场的大小对磁层电场的影响.
|
图 7 磁赤道面上的等电位分布图.e,f,a和g对应的IMF时钟角分别为0°,90°,180°和270°. a和h的IMF总强度Bt分别为10n丁和20 nT. Fig. 7 The equipotential patterns at magnetic equatorial plane. The panels of e, f,a and g corresponding IMF clock anglesare0°,90°,180°and 270°,respectively. The panels of a and h correspond to IMF magnitude (Bt) 10 nT and 20 nT. |
比较e,f,a和g四个子图:
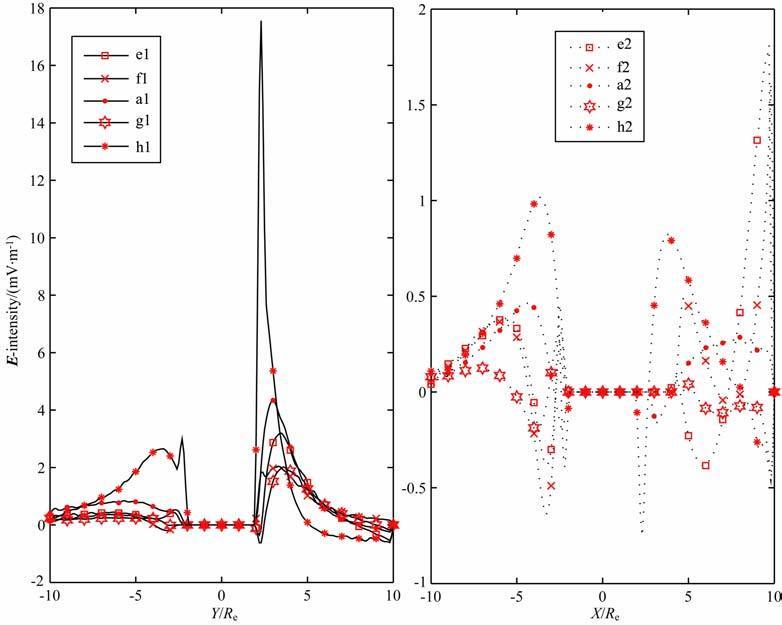
(1)f和g两图后夜区的等电位线向地球方向弯曲,呈现U 型结构,e图也有弯曲但较前两图的弯曲小,在晨侧区的晨昏线附近的等势线与晨昏线(Y轴)的夹角很小,所以图 8中e1,f1和g1的Ey值在Y<-2Re 区间的值很小.
|
图 8 沿图 7中的晨昏线(晨昏电场Ey;)和日地线(非晨昏电场Ex)的电场值分布 Fig. 8 The plots of E-intensity along the dawn-dusk line (Ey) and the Sun-Earth line (Ex)in Fig. 7 |
(2) e和g两图昏侧区的等势线有U 型结构,但较图a的U 型结构向左偏转.图f在该区的等电位线的弯曲较其他三个图(e,a,g)小,等电位线的距离较均匀,所以f1的Ey值在Y>2Re 的近地球区较小,在远地球区较大.
(3) 对子午线附近的等电位线,从图 7中可以看出,子夜区g图的等电位线沿X轴方向分布,其他e,f和a图的等电位线与X轴的夹角较g图的大.图e,f和g在正午区的等电位线分布很复杂,e和g图有闭合新月形等电位线,正午区磁层顶附近的等电位线沿Y轴方向分布.
当行星际磁场南向时,行星际磁场与磁层磁场的作用增强,向阳面的电离层电导率增大,极盖区的总电势降增大,电离层内Weimer电场的正负电势区增大.磁力线根部对应于e,g 两图电离层内Weimer电场相似,f图对应的电离层内Weimer电场,类似图 1中的卵状结构向右偏转达45°,所以出现了图 7中的电势投影图.
行星际磁场大小对磁层磁场的影响,对比图 7中的a和h图,当行星际总磁场Bt 由10nT 增加到20nT 时:
(1) 磁赤道面上投影电场的总电势降增大,a图电势范围-60~40 kV,h 图电势范围-80~70kV.所以图 8 中的h1 与h2 平均电场绝对值比a1与a2平均电场绝对值大.
(2) 与a图相比,h图在晨侧区的等电位线向地球方向弯曲,呈U 型弯曲.昏侧区的等电位线为闭合椭圆形.电势分布区较a图向地球附近扩展.
磁层电场值随IMF大小增大而增大.电离层内的Weimer电势区,随IMF 大小的增大向地球低纬度区扩展,总电势降显著增大,读者可参阅文献[7],如图 1的卵状结构的中心区向低纬度移动,经T96投影后得到的投影场就出现了如上所得的结果.
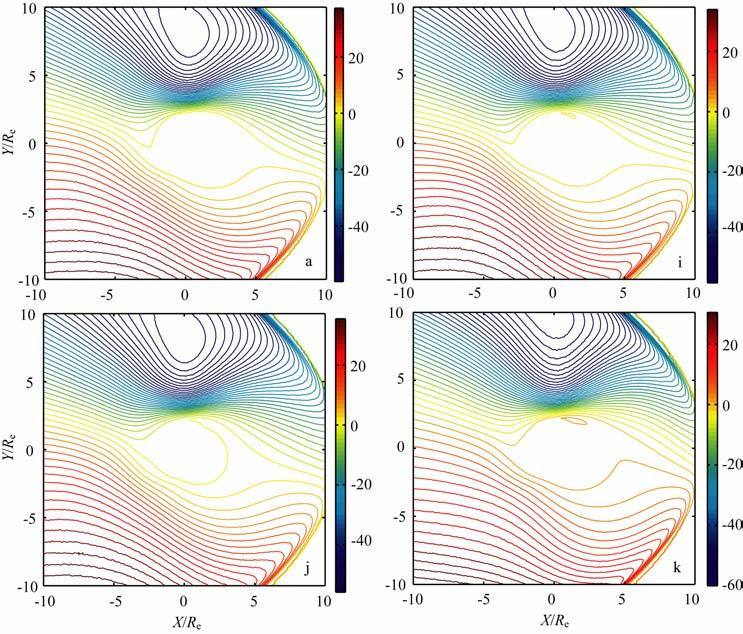
4.3 亚暴指数AL、太阳风参数和磁暴指数Dst对磁层电场的影响图 9中的a图的输入参数是数密度n=8.7cm-3,行星际磁场By=0nT,Bz= -4nT,IMF 总强度Bt=10nT,IMF 时钟角angle=180°,磁倾角为0°,太阳风速度V=450km/s,亚暴指数AL=-500nT,磁暴指数Dst=0nT.图i输入参数为亚暴指数AL=0nT,其他参数与a图相同.图j输入参数为太阳风速度V=400km/s,其他输入参数与a图相同.图k输入参数为磁暴指数Dst=-50nT,其他输入参数与a图相同.
|
图 9 磁赤道面上的等电位分布图.i图AL = 0 nT,j图太阳风速度V=400 km/s,k图Dst= -50nT. Fig. 9 The equipotential patterns at magnetic equatorial plane. In panel i the AL index is 0 nT. In panel j the solar wind velocity is 400 km/s. In panel k the Dst index is -50nT. |
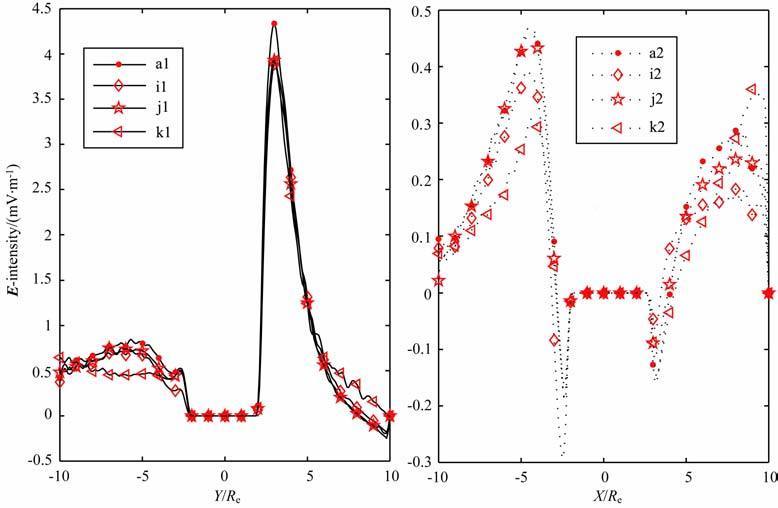
图i与图a用来说明亚暴指数AL对磁层磁场的影响,图i与图a 输入的AL指数分别为0nT、-500nT.AL指数由0nT 减小到-500nT 时,两图的等电位线分布相似,但电场值变大,变化幅度很小,图 10中可以得此结论.
|
图 10 沿图 9中的晨昏线(晨昏电场Ey)和日地线(非晨昏电场Ex)的电场值分布 Fig. 10 The plots of intensity along the dawn-dusk line (Ey) and the Sun-Earth line (Ex)in Fig. 9 |
AL指数只是电离层内Weimer电场的参数,T96磁层磁场模式中没有该参数.当AL指数增大时,Weimer电场的电势边界向低纬度扩展,但是电场分布的整体形状变化很小,因此磁赤道面上的投影场的电势分布基本相同.在实际情况下,亚暴发生伴随着行星际磁场大小和方向的改变,因此单独讨论AL指数的变化与实际情况不符合,这里只是限定条件下的一种讨论方法.
图j与图a用来说明太阳风速度对磁层电场的影响,图j与图a输入的太阳风速度分别为400km/s、450km/s.太阳风速度增大,等电位线分布相似.但电场值变大,变化幅度很小.太阳风速度由400km/s增大到450km/s时,磁赤道面上的电场分布区域只向X负方向移动了0.5Re.
本文没有讨论数密度的影响,因为在Weimer电场模式和T96磁场模式中,太阳风速度和数密度的乘积即太阳风动压作为一个参数影响结果的.
太阳风动压增大时,电离层内的Weimer电场变大,但增加的幅度很小且等电位线的分布相似.太阳风动压增大,磁层被压缩,但磁层的结构和位型没有大的变化,所以磁层内的投影电场出现了上述结果.
图k与图a用来说明磁暴指数Dst对磁层电场的影响,图k与图a输入的Dst指数分别为-50nT、0nT.Dst指数由0nT 减小到-50nT,磁层电场的总电势降没变,等电位线分布的形状大体相同.但晨侧的等电位线变疏,对应图 10 中的情况就是曲线k1的电场值较a1的小.昏侧区,k 图的等电位线分布较a图均匀,所以在Y>2Re 区,曲线k1 的晨昏电场值Ey在Y<5Re 区间比曲线a1的晨昏电场值小,但在Y>5Re 正好相反.Dst指数对磁层电场的影响总体来说是很小的,但是发生磁暴时,同时伴随着行星际磁场和地磁条件的改变,在实际条件下要综合考虑.
Weimer电场模式的输入参数中没有Dst指数,Dst指数只作为T96磁层磁场模式的输入参数,因此是磁层磁场形状的原因引起了上述的电势变化.Dst指数变小时,磁层磁场变小,磁层空间的磁力线变疏,从电离层出发的相邻磁力线投影到磁赤道面的投影点距离变大,出现了上面电场投影结果.
5 讨论与结论本文计算了一个特定的地磁和行星际磁场条件下的电场.计算结果表明,远磁尾区域以晨昏电场为主,但与均匀晨昏电场不同,靠近磁层边界电场越强,昏侧电场比晨侧电场大,该结果与文献[4]的结果一样.该条件下的计算结果也在Geotail和ISEE1卫星探测结果的范围内.
Weimer电场是IMF大小和方向、地磁倾角、太阳风速度和数密度、AL指数的函数,T96磁场模型与太阳风速度和密度、Dst指数、IMF大小和方向有关,所以投影电场也与上述参数有关.本文讨论了各种参数对投影电场的影响,结论如下:
(1) 磁轴倾角的变化对等电位线分布的形状有重大的影响,这在目前其他的磁层电场研究中很少关注,对等离子体层随时间演变的研究将是一个有力的工具.
(2) 行星际磁场的方向和大小对投影电场影响很大,同时还与亚暴和磁暴相关联,所以行星际磁场是影响磁层电场的主要因子.
(3) 亚暴指数AL、太阳风参数和磁暴指数Dst对磁层磁场的影响权重较小,但是上述参数的改变同时伴随着IMF大小和方向的变化,所以在实际情形下对电场有重要影响.
(4) 该方法计算的电场是磁层内的静电场,在磁暴的初相时,δB/δt产生的感应电场不能计算,所以在磁暴初相时计算的电场不准确.
| [1] | 曹晋滨, 李磊, 吴季译. 2001太空物理导论. 北京: 科学出版社, 1995 . Kivelson M G, Russell C T. Introduction to Space Physics. Cambridge University Press (in Chinese). 1995 . |
| [2] | 徐荣栏, 李磊. 磁层粒子动力学. 北京: 科学出版社, 2005 . Xu R L, Li L. The Magnetospheric Particles Dynamics (in Chinese). Beijing: Science Press, 2005 . |
| [3] | Volland H. Models of global electric fields within the magnetosphere. Ann.Geophys. , 1975, 31: 159-174. |
| [4] | 张天辉, 徐荣栏, 李磊. 地球磁尾的电场模式. 空间科学学报 , 2002, 22: 220–225. Zhang T H, Xu R L, Li L. The convection electric field model in the magnetosphere. Chinese J. Space Science (in Chinese) , 2002, 22: 220-225. |
| [5] | McIlwain C E. A Kp dependent equatorial electric field model: The physics of thermal plasma in the magnetosphere. Adv. Space Res. , 1986, 6(3): 187-197. DOI:10.1016/0273-1177(86)90331-5 |
| [6] | Weimer D R. An improved model of ionospheric electric potentials including substorm perturbations and application to the Geospace Environment Modeling November 24,1996,event. J.Geophys.Res. , 2001, 106: 407-416. DOI:10.1029/2000JA000604 |
| [7] | Weimer D R. Models of high-latitude electric potentials derived with a least error fit of spherical harmonic coefficients. J.Geophys.Res. , 1995, 100: 19595-19607. DOI:10.1029/95JA01755 |
| [8] | Weimer D R. Improved ionospheric electrodynamic models and application to calculating Joule heating rates. J. Geophys. Res. , 2005, 110: A05306. |
| [9] | Tsyganenko N A. Modeling of the Earth's magnetospheric magnetic field confined within a realistic magnetopause. J.Geophys. Res. , 1995, 100: 5599. DOI:10.1029/94JA03193 |
| [10] | Tsuruda K, Hayakawa H, Nakamura M, et al. Electric field measurements on the GEOTAIL satellite. J.Geomag.Gedefec. , 1994, 46: 693-711. DOI:10.5636/jgg.46.693 |
| [11] | Maynard N C, Aggson T L, Heppner J P. The plasmaspheric electric field as measured by ISEE1. J.Geophys.Res. , 1983, 88: 3991-4003. DOI:10.1029/JA088iA05p03991 |
| [12] | Pedersen A, Grard R, Knott K, et al. Measurements of quasistatic electric fields between 3 and 7 earth radii on GEOS-1. Space Sci. Rev. , 1978, 22: 333. |
| [13] | 刘卫国. MATLAB 程序设计与应用(第二版). 北京: 高等教育出版社, 2006 . Liu W G. MATLAB Program Design and Application (The Second Edition) (in Chinese). Beijing: Higher Education Press, 2006 . |
| [14] | 王保旗. FORTRAN 95程序设计与数据结构基础教程. 天津: 天津大学出版社, 2007 . Wang B Q. Introduction to FORTRAN 95 Program Design and Data Structure (in Chinese). Tianjin: Tianjin University Press, 2007 . |
 2012, Vol. 55
2012, Vol. 55

