2. 中国气象局国家空间天气监测与预警中心, 北京 100081;
3. NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
2. National Center for Space Weather, China Meteorological Administration, Beijing 100081, China;
3. NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
地球等离子体层主要是由地球磁力线捕获的电子、氢离子(H+ )、氦离子(He+ )和氧离子(O+ )等粒子组成[1-2].等离子体层整体形n受地球磁场位形影响,总体呈现圆环n,其外部边界(等离子体层顶)形n大体与磁力线形n相似,在向阳面受磁层对流影响,还出现等离子体层尾(plume)、等离子体层肩(shoulder)等形n[3].等离子体层中的He+ 会共振散射太阳30.4nm 辐射[4],其强度远大于等离子体层中其他离子的辐射,因而使其成为研究等离子体层整体动力学特征的重要手段.但是,受空间技术和光学技术的限制,直到20世纪末期短波段多层膜技术的发展[5],等离子体层光学探测才逐渐进入应用.
1997年日本火星轨道器Planet-B[6]在飞往火星途中首次进行了等离子体层全局极紫外探测,但由于受视场角和观测周期限制,其并没有得到完整的等离子体层图像[7].2000年美国发射的极轨卫星IMAGE[8]搭载了一台极紫外成像仪[9],首次从极轨对等离子体层30.4nm 辐射进行了全局成像,获得了迄今为止最完善的等离子体层极紫外辐射图像[3].2008年日本月球探测器KAGUYA 在绕月探测过程中用搭载的极紫外望远镜[10]从侧面对地球等离子体层极紫外辐射进行了成像,但由于受视场角和周期限制,以及滤光片故障,并没有得到完整的图像[11].
为解决以前观测中的问题,探月二期嫦娥三号卫星将在着陆器顶部安装一台极紫外相机,对等离子体层30.4nm 辐射进行成像[12-13].该月基极紫外相机将对等离子体层进行全局连续成像观测,并获得投影于子午面上的极紫外光强分布.由于等离子体层30.4nm 辐射强度正比于光线方向的He+ 柱密度,因此从光强分布图可以直接获得He+ 的柱密度分布图.但柱密度分布对研究等离子体层粒子动力学特征并无意义,从柱密度反演得到的三维密度才更有应用意义.反演结果可以用于监测等离子体层顶、等离子体层尾、等离子体层肩以及其他结构的演化,可推导出等离子体层区域内的对流电场分布,而且还可以用于研究等离子体层与电离层、环电流和辐射带之间的耦合动力学.
作为未来月基极紫外图像反演的先导,本文将研究从地球极轨获得的等离子体层极紫外图像的反演方法,因为极轨成像方式较月基成像简单,且美国IMAGE 卫星已经成功实施了极轨成像.本文将引入权矩阵并采用遗传算法反演等离子体层He+ 密度分布,说明反演原理和步骤.最终采用动态全球核心等离子体模式(DGCPM)模拟结果来验证算法的可行性和精度.
2 极紫外成像方法地球等离子体层He+ 共振散射太阳30.4nm辐射,沿某一给定视线方向L的积分光强I由以下积分公式得到:
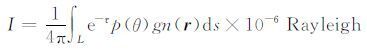
|
(1) |
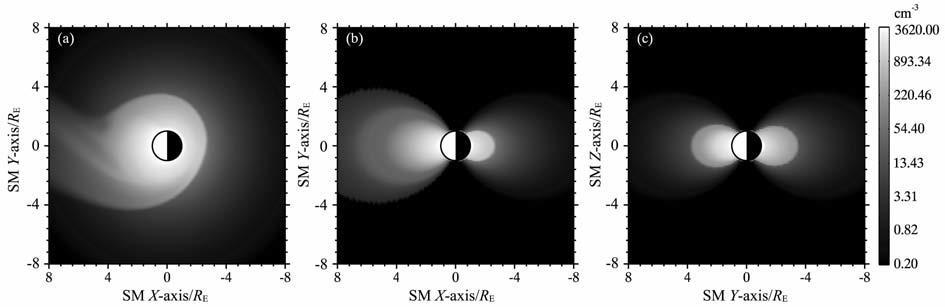
其中,p(θ)=1+1/4(2/3-sin2θ)是共振散射角分布各向异性因子(无量纲)[14],θ是太阳光与散射光之间的夹角,g是He+ 的共振散射因子(与太阳30.4nm辐射通量和He+ 量子力学特性有关,在一个成像周期内可以近似为常数,单位:photons·s-2 ·ion-1),n(r)是空间点r处的He+ 密度(单位:cm-3),τ 是He+ 30.4nm 辐射的光学深度,在高度大于1000km(约1.2RE 处)时τ 可视为0[15-16].当设定坐标系和虚拟成像仪空间坐标后,虚拟像面每一像元对应的各向异性因子都将根据简单的坐标运算得到,剩下的关键部分就是He+ 密度的空间分布.本文采用DGCPM 模式计算He+ 三维密度分布[17-18],图 1 给出了三个不同平面上He+ 密度分布示例.
|
图 1 DGCPM计算的等离子体层密度 (a)磁赤道面;(b)晨-昏子午面;(c)正午子夜子午面 Fig. 1 Plasmaspheric density distribution simulated by DGCPM (a) Magnetic equatorial plane; (b) Dawn-dusk meridian plane; (c) Noon-midnight meridian plane |
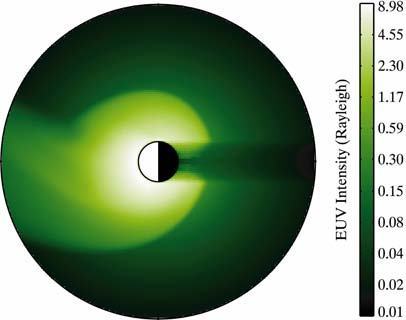
根据以上密度分布,在北极点上空8.0RE 处设置一台虚拟极紫外相机,视场角覆盖范围16.0RE,指向地心,磁赤道面上空间分辨率0.1RE,根据公式(1)模拟得到的投影于磁赤道面的极紫外光强分布如图 2所示.图 2中可以看出从极区成像时,等离子体层辐射光强分布轮廓与磁赤道面等离子体层密度分布轮廓相似(图 1a),只是在光强分布图中,子夜区存在严重的地球遮挡现象.
|
图 2 从北极点上空8.0 RE处模拟得到的等离子体层30.4nm辐射光强分布 Fig. 2 Plasmaspheric 30. 4 nm emission intensity simulated from 8.0 RE above the North Pole |
遗传算法是一种高效的全局优化搜索算法,首先由Holland提出[19].它是进化计算中应用最广泛的算法,并且在人工智能领域得到了极大发展[20-21].遗传算法的原理来源于达尔文进化论中的遗传、变异、杂交、选择和“适者生存”,其理念就是通过模拟自然界进化获取问题的最优解.
遗传算法面对的首先是代表所求解问题的可能解集的一个初始种群,该种群通过将一定量的个体(即所求解问题的可能解)进行编码得到.正如自然界中单个个体一样,遗传算法中的个体包含所求解问题的解的部分特征.根据求解问题的不同,这些个体被编码为二进制串或浮点数组,编码后被称为染色体.本文反演问题的解属于实数集,因此采用实数编码是最方便也是最直接的,即采用实数向量或矩阵表征问题的解[22].所有可能解组成的集合称为遗传算法的搜索空间.对于标量问题,解是实数,则搜索空间就是实数集;对于矢量问题,解是实数向量或平面上的二维曲线,则搜索空间就是二维实数集;而对于矩阵问题,解是实数矩阵或空间的三维平面,则搜索空间就是三维实数集.从地球极轨成像时,公式(1)中的积分可以近似在同一子午面内进行,因此本文反演问题属于上述第二种情况.
搜索最优解等价于在搜索空间中寻找某个函数的最值(最大值或最小值),为此,需要对染色体进行繁殖和选择.正如自然界通过交叉、变异和选择进行进化一样,遗传算法中的个体也通过这些方式进化至最优解.交叉和变异代表了对父代染色体的不同数学操作,前者用于交换父代染色体之间的信息,而后者则在子代染色体中引入新的信息.
在进化过程中,我们面临的一个核心问题就是如何评价个体质量的好坏以及更新种群.办法是计算个体的适应度值并进行选择.当个体的适应度值达到预先设定的阈值时,认为个体接近了问题的最优解,此时的个体可以看作问题解的最佳近似.
遗传算法已经在很多优化问题上,如线路排布、时刻表、自适应控制、认知模拟、输运问题、生产调度、优化控制和数据库优化搜索等问题[20, 22]上得到了很成功的应用.等离子体层密度反演可以转化为对以下目标函数f[n(r)]最小值的最优化搜索:

|
(2) |
其中各个参数定义同式(1).我们的目标是在二维实数空间中寻找一个最优解,使得以下条件成立:f[n(r)]<e(e为预先设定的阈值,e=10-6或更小).遗传算法反演的具体步骤见下节.
4 反演步骤 4.1 权矩阵反演的第1步就是将公式(2)中积分离散化,即将积分转化为求和.由于密度分布是三维的,而从单幅极紫外图像反演三维密度几乎不可能,因此需要先作一些简化.首先是维度简化,将三维转化为二维.根据DGCPM 模式的假设[18],磁赤道面等离子体密度近似等于通量管内平均等离子体密度,也即沿磁通量管密度分布为近似常数,这一假设经常被用于等离子体层研究中[23-24],这也使得构建三维等离子体层和权矩阵更加简便和快捷.因此空间任意一点的密度可以由磁力线追迹到磁赤道面得到,这样只需在磁赤道面设置二维密度网格,根据磁场追迹结果,通过插值方式得到对应空间点密度.第二个简化是在磁场追迹时采用偶极磁场模式,因为在等离子体层所处的空间范围内,实际磁场相对于偶极场的变形较小,可以采用偶极场近似.这样在积分过程中就避免了不同子午面之间的交叉,大大简化了计算过程和计算量,反演过程就在每一子午面中依次进行.
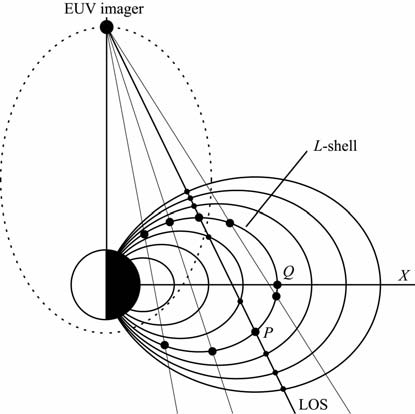
如图 3所示,虚拟相机中任意像元对应的视线方向(LOS)与磁力线交于不同位置,每一条磁力线也与不同的视线方向相交.对于一个确定的视线方向(即光强积分方向),不同L值的磁力线对积分的贡献不同,同一L值磁力线对不同视线方向的贡献也不同.依此,可以建立权矩阵,将积分转化为求和.具体步骤如下:
|
图 3 偶极场中MLT=0子午面上卫星位置和视线方向示意图 Fig. 3 Diagram for satellite position and L0S in meridian of MLT = 0 in dipole field |
(a)在光强分布图中任取一矢径方向,以MLT=0为例(如图 3),得到一列光强值,可以用列向量I=(I1,I2,…,IM)T 表示,其中M表示该矢径方向的光强数据点个数.
(b)在MLT=0的矢径方向设置密度向量D=(D1,D2,…,DN)T,其中N表示密度网格点个数.可知,M个光强数据点中的每一点强度都由这N个网格点密度决定,不同网格点对强度贡献不同.
(c)网格点设置好后,就可以建立权矩阵W,且W满足
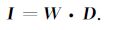
|
(3) |
根据I和D的定义,可知W为N×M维矩阵,即

|
(4) |
(d)求解矩阵元.
在对每一LOS 进行积分的过程中,该LOS 的共振散射角分布各向异性因子p(θ)和共振散射因子g是不变的.积分元ds取值可根据图像分辨率和密度网格分辨率决定,在本文模拟中,图像分辨率和密度网格分辨率均为0.1RE,因此取ds=0.1RE.在每一个积分区域ds内,密度可视为常数,并以积分区域中心的值代替.以该中点(设为P,如图 3)为起点追迹磁力线到磁赤道面,得到的点(设为犙)一般不与密度网格点重合,因此需要进行插值,本文采用拉格朗日插值.则P点的密度为
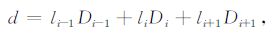
|
(5) |
式中i代表与P点距离最小的密度网格点,li-1,li,li+1为拉格朗日插值系数.积分过程中每一次插值的系数都累加到相应的矩阵元中,积分完成后,相应的矩阵元也确定下来.可以得到
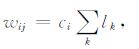
|
(6) |
式中lK为插值系数,ci= p(θ)gds×10-6/4π 为积分公式(1)中的常数项.
(e)最后,积分方程(1)就被转化成了如下线性方程组:

|
(7) |
反演问题被转化为求上述线性方程组的解.式(7)中权矩阵W一般为稀疏矩阵,常规的矩阵求逆解法失效,本文采用实数编码遗传算法[22],通过迭代方式获得物理范围内的最优解.
4.2 实数编码和搜索空间第2步是对密度向量D进行实数编码,产生基因或染色体.染色体是遗传算法中的基本单元,类似于自然界中的单个个体.D中的元素代表了相应网格点的密度值.编码模式、初始值和边界条件决定了遗传算法的搜索空间.原则上,实数编码遗传算法的搜索空间为[- ∞,+ ∞],而根据等离子体层的密度特性,可以大大缩小这一搜索空间,提高算法效率.根据DGCPM 模拟结果[17]和卫星观测结果[3],等离子体层密度峰值低于4000cm-3,而在等离子体层槽内,密度最小值大于0.1cm-3,因此在遗传算法中,搜索空间定义为[0.1,4000].在染色体编码过程中,对于每一个初始染色体,只需要产生一列搜索空间内的随机数,并对其进行降序排列即可(因为等离子体层密度整体上随径向距离递减).
4.3 繁殖规则第3步是定义染色体的繁殖规则.繁殖规则是遗传算法中的核心部分,它决定了下一代染色体如何产生.染色体通过两种方式繁殖,一种是两个染色体之间的交叉或杂交(crossover),另一种是单个染色体的变异(mutation).在实数编码遗传算法中,交叉和变异代表对父代染色体的不同数学运算,交叉用于交换父代两个个体之间的信息,而变异则为子代个体引入新的信息;每一代个体都需要进行交叉,而变异只需隔代进行,本文采用多种交叉方式和变异相结合的繁殖规则[25].在繁殖过程中,父代染色体的一些信息被子代继承,另一些信息被抛弃.子代中的个体根据“适者生存”的法则决定其留存.
4.4 选择规则第4步是定义子代的选择规则.在遗传算法中,如何从子代中选择优秀的个体并抛弃不良个体是至关重要的.本文中子代染色体的适应度定义为
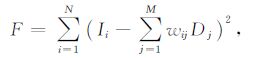
|
(8) |
式中,F为适应度值,它代表了当前染色体对应的积分光强相对于原始光强的差别,差别愈小,即F值愈小,代表该染色体愈接近真实值.根据该判据,适应度值大的染色体将从子代中移除.
4.5 算法步骤描述根据以上描述,本文采用的实数编码遗传算法步骤如下:
第1步:参数定义.
Mp 为每代种群数量,Mp=300;N为单个染色体D长度,本文中反演范围为1.1RE~10.0RE,空间分辨率为0.1RE,因此N=90;M为光强向量I长度,本文中取M=80;PM 为变异概率,本文中取PM=0.05;G为最大繁殖代数,本文中取G=1000;GM 为实施变异的间隔,GM=50;ε为适应度目标值,ε=10-4.
第2步:产生初始种群.
生成Mp 个随机向量,且均为递减向量,每个向量中的数值均在区间[0.1,4000]内;
定义搜索空间,即边界条件为[0.1,4000];
计算每个个体的适应度值,并保存最佳个体及其适应度值.
第3步:产生新种群.
从父代种群中随机选择两个个体进行交叉;
如果迭代次数间隔达到GM ,则对子代中每一个个体进行变异;
根据边界条件对每一个子代个体进行限制.
第4步:选择优秀子代个体.
根据式(8)定义,计算每一个个体的适应度值;
用子代种群中适应度好的个体替代父代种群;
对最佳个体及其适应度值进行替代.
第5步:如果最佳个体的适应度值小于ε,或当前遗传代数已经达到G,则终止遗传算法,输出最佳个体;否则将当前遗传代数加1并返回第3步.
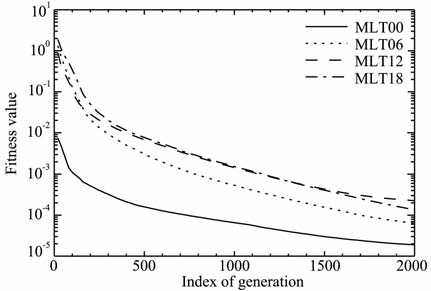
5 反演结果采用图 2中的光强分布,我们分别选取了MLT=0,6,12,18的四条矢径来验证算法的收敛性和精度.图 4给出了四次反演中最佳个体的适应度值随遗传代数的变化曲线.可以看出,在不同的矢径方向,算法的收敛性基本一致,在遗传2000 代时(在PC 上的时间约为1 min)基本达到收敛,收敛速度较快.只是在MLT=0 的矢径方向,由于受地球遮挡,权矩阵W中对应于2.0RE 以内的矩阵元基本为零,因此反演得到的该部分密度不可信.
|
图 4 最佳个体适应度随遗传代数变化曲线 Fig. 4 Variations of fitness values of the best individuals with iteration numbers |
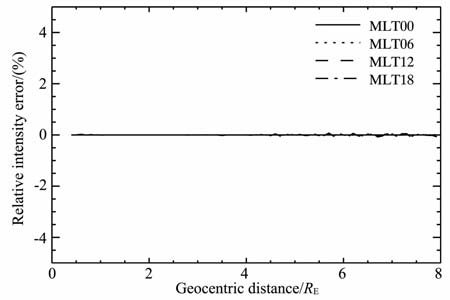
图 5给出了遗传2000代后的密度分布与原始密度分布的对比曲线.图 6给出了光强的相对误差曲线.可知除地球遮挡区域以外(MLT=0),其他矢径方向的反演结果都比较理想,反演得到的光强误差趋于0,而反演得到的密度只在8.0RE 附近出现微小扰动,最大相对误差为8%,在等离子层顶附近和等离子体层内,相对误差趋于0.对于地球遮挡区,由于夜侧等离子体层密度变化较小,因此可以利用插值方法最终得到夜侧等离子体层密度.

|
图 5 反演密度与原始密度对比曲线 (a) MLTOO; (b) MLT06; (c) MLT12; (d) MLT18. Fig. 5 Comparisons between density from inversion and original density at different MLTs |
|
图 6 反演光强与原始光强相对误差曲线 Fig. 6 Relative errors between intensity from inversion and original intensity |
本文介绍了采用一维遗传算法对等离子体层密度进行反演的原理和步骤,通过采用偶极场近似和通量管近似将三维问题转化为一维问题,得到了比较好的反演结果.对不同MLT对应的矢径方向的反演结果显示,密度相对误差<8%,光强相对误差趋于0,证明遗传算法可以有效反演地球等离子体层密度.采用偶极磁场近似和遗传算法的优势在于可以快速精确地反演等离子体层结构和密度.
本文研究结果表明,遗传算法完全可以用于等离子体层极紫外图像反演.但是对于月基极紫外图像,由于每一个LOS的积分都是沿不同的MLT 进行的,因此一维算法需要改进.今后的工作中我们将研究二维遗传算法来反演探月二期工程获得的月基极紫外图像.
| [1] | Farrugia C J, Geiss J, Young D T, et al. Geos-1 observations of low-energy ions in the earth's plasmasphere: a study on composition, and temperature and density structure under quiet geomagnetic conditions. Adv. Space Res. , 1988, 8(8): 25-33. DOI:10.1016/0273-1177(88)90259-1 |
| [2] | Farrugia C J, Young D T, Geiss J, et al. The composition, temperature, and density structure of cold ions in the quiet terrestrial plasmasphere: GEOS-1 results. J. Geophys. Res. , 1989, 94(A9): 11865-11891. DOI:10.1029/JA094iA09p11865 |
| [3] | Sandel B R, Goldstein J, Gallagher D L, et al. Extreme ultraviolet imager observations of the structure and dynamics of the plasmasphere. Space Sci. Rev. , 2003, 109(1): 25-46. |
| [4] | Meier R R. Ultraviolet spectroscopy and remote sensing of the upper atmosphere. Space Sci. Rev. , 1991, 58(1): 1-185. DOI:10.1007/BF01206000 |
| [5] | Yoshikawa I, Nakamura M, Hirahara M, et al. Observation of He II emission from the plasmasphere by a newly developed EUV telescope on board sounding rocket S-520-19. J. Geophys. Res. , 1997, 102(A9): 19897-19902. DOI:10.1029/97JA01530 |
| [6] | Nakamura M, Yamashita K, Yoshikawa I, et al. Helium observation in the Martian ionosphere by an X-ray ultraviolet scanner on Mars orbiter NOZOMI. Earth Planets Space , 1999, 51(1): 61-70. DOI:10.1186/BF03352210 |
| [7] | Nakamura M, Yoshikawa I, Yamazaki A, et al. Terrestrial plasmaspheric imaging by an extreme ultraviolet scanner on Planet-B. Geophys. Res. Lett. , 2000, 27(2): 141-144. DOI:10.1029/1999GL010732 |
| [8] | Burch J L. IMAGE mission overview. Space Sci. Rev. , 2000, 91(1): 1-14. |
| [9] | Sandel B R, Broadfoot A L, Curtis C C, et al. The extreme ultraviolet imager investigation for the image mission. Space Sci. Rev. , 2000, 91(1-2): 197-242. |
| [10] | Yoshikawa I, Yamazaki A, Murakami G, et al. Telescope of extreme ultraviolet (TEX) onboard SELENE: science from the Moon. Earth Planets Space , 2008, 60(4): 407-416. DOI:10.1186/BF03352805 |
| [11] | Yoshikawa I, Murakami G, Ogawa G, et al. Plasmaspheric EUV images seen from lunar orbit: Initial results of the extreme ultraviolet telescope on board the Kaguya spacecraft. J. Geophys. Res. , 2010, 115: A04217. DOI:10.1029/2009JA014978. |
| [12] | 何飞, 张效信, 陈波. 月基观测地球等离子体层极紫外辐射特性. 光学精密工程 , 2010, 18(12): 2564–2573. He F, Zhang X X, Chen B. Moon-based imaging of earth plasmaspheric extreme ultraviolet radiation. Opt. Precision Eng. (in Chinese) , 2010, 18(12): 2564-2573. |
| [13] | 陈波, 何飞. 月基地球等离子体层极紫外成像仪的光学设计. 光学精密工程 , 2011, 19(9): 2057–2062. Chen B, He F. Optical design of moon-based earth's plasmaspheric extreme ultraviolet imager. Opt. Precision Eng. (in Chinese) , 2011, 19(9): 2057-2062. DOI:10.3788/OPE. |
| [14] | Brandt J C, Chamberlain J W. Interplanetary gas, I, Hydrogen radiation in the night sky. Astrophys. J. , 1959, 130: 670-682. DOI:10.1086/146756 |
| [15] | Garrido D E, Smith R W, Swift D W, et al. Imaging the plasmasphere and trough regions in the extreme ultraviolet region. Opt. Eng. , 1994, 33(2): 371-382. DOI:10.1117/12.155909 |
| [16] | Brandt J C. Interplanetary gas, VI, On diffuse extreme ultraviolet helium radiation in the night and day sky. Astrophys. J. , 1961, 134: 975-980. DOI:10.1086/147225 |
| [17] | He F, Zhang X X, Chen B, et al. Calculation of the extreme ultraviolet radiation of the Earth's plasmasphere. Sci. China Tech. Sci. , 2010, 53(1): 200-205. DOI:10.1007/s11431-009-0311-1 |
| [18] | Ober D M, Horwitz J L, Gallagher D L. Formation of density troughs embedded in the outer plasmasphere by subauroral ion drift events. J. Geophys. Res. , 1997, 102(A7): 14595-14602. DOI:10.1029/97JA01046 |
| [19] | Holland J H. Adaptation in Natural and Artificial Systems. Ann Arbor: Univ. of Michigan Press, 1975 . |
| [20] | Sivanandam S N, Deepa S N. Introduction to Genetic Algorithms. New York: Springer-Verlag, 2008 . |
| [21] | Reeves C R, Rowe J E. Genetic Algorithms-Principles and Perspectives: A Guide to GA Theory. Dordrecht: Kluwer Academic Publishers, 2003 . |
| [22] | Michalewicz Z. Genetic Algorithms+Data Structures - Evolution Programs. (3rd Ed). New York: Springer-Verlag, 1996 . |
| [23] | Gurgiolo C, Sandel B R, Perez J D, et al. Overlap of the plasmasphere and ring current: Relation to subauroral ionospheric heating. J. Geophys. Res. , 2005, 110: A12217. DOI:10.1029/2004JA010986. |
| [24] | Larsen B A, Klumpar D M, Gurgiolo C. Correlation between plasmapause position and solar wind parameters. J. Atmos. Sol. Terr. Phys. , 2007, 69(3): 334-340. DOI:10.1016/j.jastp.2006.06.017. |
| [25] | 周永华. 实数编码遗传算法杂交算子组合研究. 广州: 华南理工大学, 2003. Zhou Y H. Research on combination of crossover operators of real coded genetic algorithms (in Chinese). Guangzhou: South China Univ. of Tech., 2003. |
 2012, Vol. 55
2012, Vol. 55


