2. 同济大学海洋与地球科学学院, 上海 200092;
3. 中国科学院地质与地球物理研究所 中国科学院油气资源研究重点实验室, 北京 100029
2. School of Ocean & Earth Science, Tongji University, Shanghai 200092, China;
3. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
VSP和井间地震等井中观测资料由于受表层干扰较小,资料的信噪比和分辨率通常较高,对井旁资料高精度成像具有重要意义.相较地面地震数据,VSP资料中不仅包含上行反射波,还包含丰富的下行反射波信息,并且下行反射波比上行反射波具有更宽的照明范围[1-4].常规VSP 成像方法直接借鉴地面地震成像方法,首先对VSP数据进行上下行波场分离[5],然后只对上行反射波进行成像[6-8],大量的下行波未能得到有效利用.孙文博和孙赞东[9]开展了VSP资料伪谱法逆时偏移研究,对比了全波场偏移和分离后偏移成像效果的对比,指出直达波在炮点和检波点位置成像,并带来较强的成像噪音.近年来,地震干涉[10]成像方法得到地球物理学界的广泛关注,能够较好地对VSP自由表面多次波进行成像,大大扩大了VSP 资料的成像范围,改善了VSP成像效果[1-4].利用地震干涉对高陡倾角构造进行面向目标的成像[11-12],能够对一次下行反射波成像,得到高陡倾角构造的准确成像,在盐丘侧翼的定位方面具有较好的效果.但是,地震干涉仍旧难以处理VSP层间多次波,并且为了得到较好的干涉波场,对VSP波场的分离通常也是必须的[13].另外,吴世萍等[14]通过估计VSP 虚源子波,提高了地震干涉成像对薄层的分辨能力.王臖等[15]利用Kirchhoff偏移算法,实现对P 波和S 波多波资料成像,提高了VSP资料的成像精度.
本文研究的目标是发展VSP 上下行波联合成像方法,首先描述了VSP 资料波场特征,分析了VSP数据中直达波、一次反射波、自由表面多次波、层间多次波等波场的传播路径及照明范围,在此基础上指出了常规成像方法的缺点.根据VSP 资料的特征,给出了新成像算法的处理流程,并结合VSP不同波场的走时特征阐述了本文方法对一次反射波、自由表面多次波、层间多次波的成像原理.本文成像方法具有在不需要进行上下行波场分离的情况下同时对上行反射波和下行反射波成像的优点,可以拓宽VSP资料的成像范围,实现高陡倾角构造成像.理论资料和实际资料测试证明了本文方法的正确性.
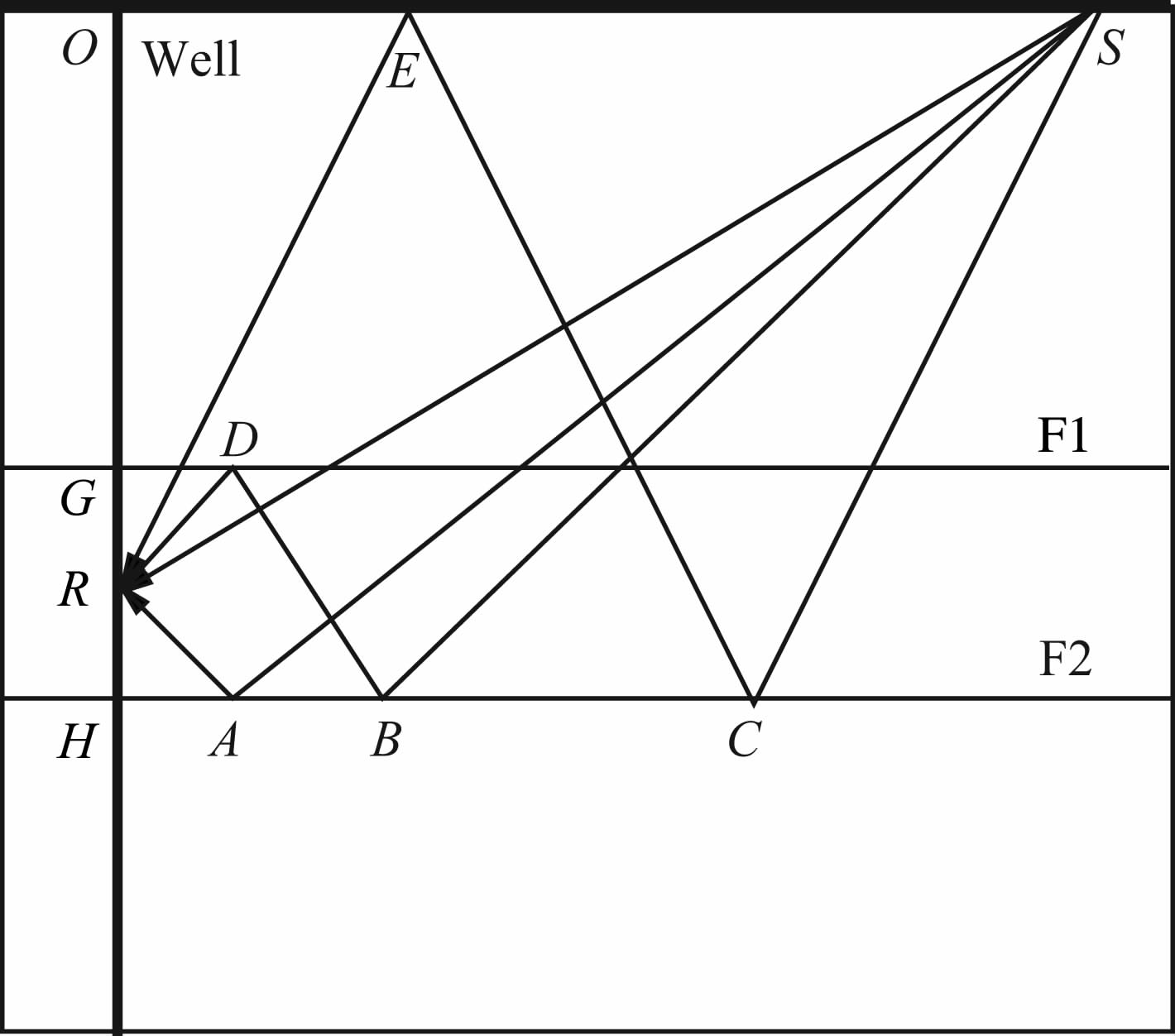
2 VSP波场分析VSP数据地面激发井中接收的观测方式决定了其能够观测到比地面地震更丰富的波场,并且波场受近地表影响较小.在VSP记录中除了常规的上行反射波,还有非常丰富的下行波.通常,下行波包括直达波、自由表面多次波、层间多次波等.如图 1所示,为一简单VSP 观测方式示意图,图中有两个反射界面F1和F2,左侧为一观测井,F1和F2之间有一检波器R,地表S点为一激发震源.我们分析S点激发能量到观测点R的主要传播路径.在R点接收的记录中,首先包含直达波,其传播路径为S→R,一次反射波,路径为S→A→R,层间多次反射波,路径为S→B→D→R,自由表面多次波,路径为S→C→E→R.通常,直达波具有最短走时,然后依次为一次反射波、层间多次波和自由表面多次波.直达波在VSP 记录中为下行波.在地下反射界面水平或者接近水平的情况下,自由表面多次波和层间多次波也为下行波,只有一次反射波为上行波.在高陡倾角构造情况下,一次反射波在记录中也可能为下行波.
|
图 1 VSP观测系统示意图 Fig. 1 VSP geometry sketch map |
如图 1所示的观测系统中,设R点接收的VSP记录为uRA,它满足
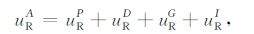
|
(1) |
其中,uRP 表示一次反射波,uRD 表示直达波,uRG 为自由表面多次波,uRI 为层间多次波.在高频近似下,它们分别满足
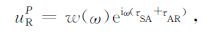
|
(2) |
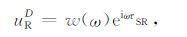
|
(3) |
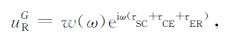
|
(4) |
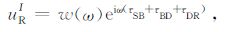
|
(5) |
其中,w(ω)为频率域地震子波,ω 为角频率,i=$\sqrt { - 1} $为虚数单位,τSA 表示波场从S点到A点传播的走时.
不同反射波对于地下构造的照明范围差异较大,图 1中,根据斯奈尔定律,一次反射波、自由表面多次波和层间多次波反射点轨迹分别满足
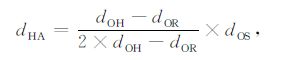
|
(6) |
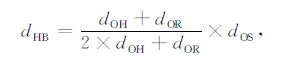
|
(7) |
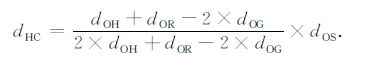
|
(8) |
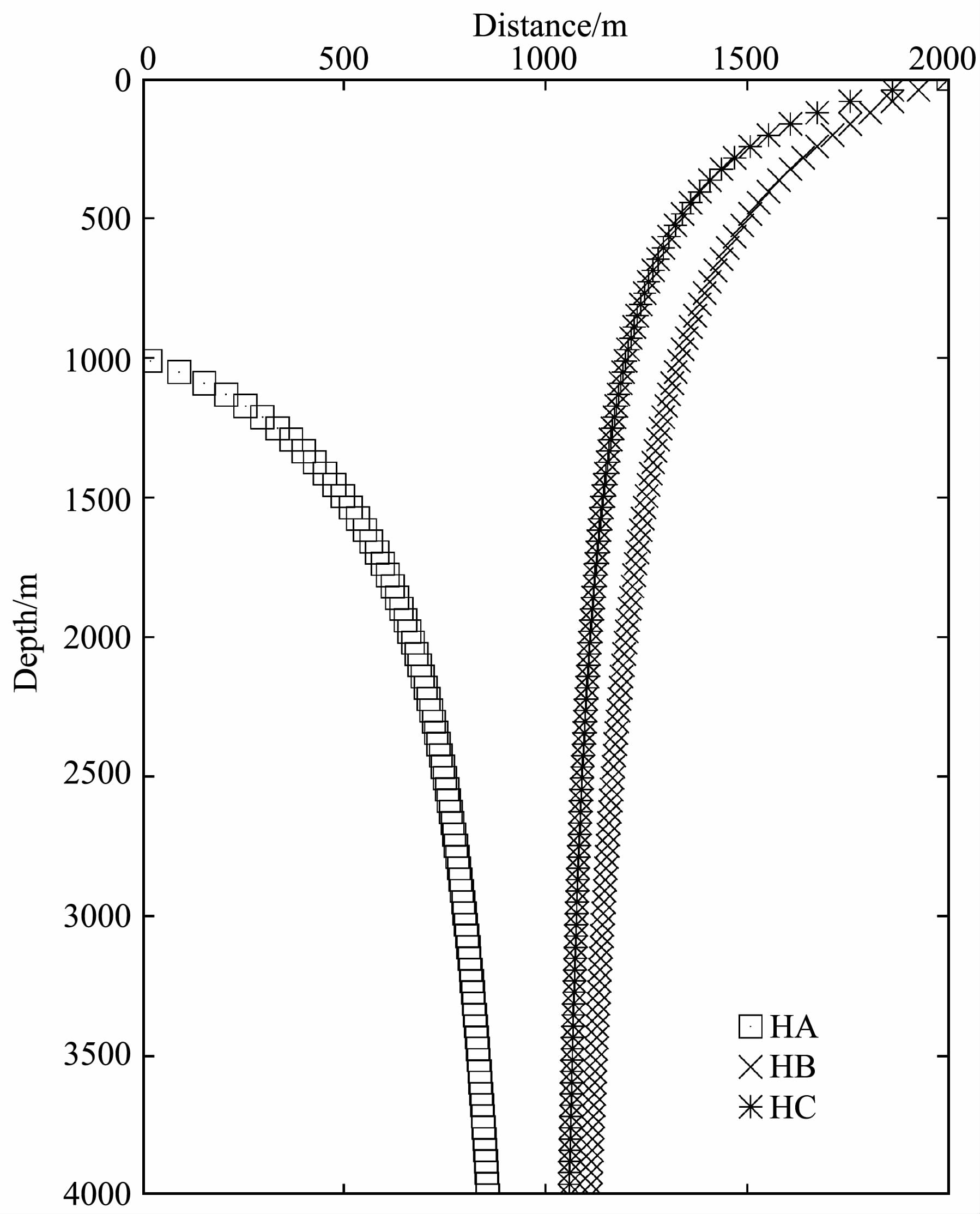
其中,dHA 表示H点到A点横向距离,dOH 表示O点到H点的深度.(6)式需要满足dOH >dOR,即一次反射波只能够照明检波器之下一定区域.(7)、(8)式对反射界面深度没有要求,即多次波能够同时照明检波器上部和下部区域.设检波点深度dOR =1000m,反射界面F1深度dOG=250m,震源S与井O的距离dOS=2000 m,反射界面F2 的深度范围dOH为0到4000m,此时式(6)、(7)和(8)的照明轨迹曲线如图 2 所示,其中□ 表示上行反射波的照明轨迹,×表示自由表面多次波的照明轨迹,*表示层间多次波的照明轨迹.根据式(6)、(7)、(8),随着震源与井的距离dOS逐步减小,波场的照明轨迹也逐步向井的方向靠拢,即当震源从0到2000m分布时,一次反射波、自由表面多次波和层间多次波分别能够照明图 2中对应照明轨迹左侧的区域.容易看出,VSP多次波照明范围比一次波宽得多.
|
图 2 —次波、自由表面多次波和层间多次波照明轨迹图 Fig. 2 Primary, free surface multiple and interbed multiple illumination trajectory |
为了提高VSP成像效率,根据波场的互易性原理,通常将VSP观测系统进行炮检点互换,将VSP数据转化为逆VSP(共检波点道集)数据,然后进行逆VSP数据成像[6-8].即常规VSP 单程波成像算法可以描述为:
第1步:对VSP 资料进行上下行波场分离,并将分离后的上行波场转化为共检波点道集.
第2步:地表共检波点道集波场从地面(z=0)开始逐层向下反向延拓,从深度z到z+Δz的延拓公式为[16]
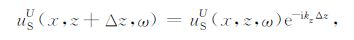
|
(9) |
其中,uSU(x,z,ω)表示坐标(x,z)处的上行共检波点反射波场,kz为z方向波数,这里的波场延拓算法可以根据地下构造的复杂程度选择不同精度的单程波传播算子,如裂步傅里叶算子[17]、傅里叶有限差分算子[18]、广义屏算子[19]等.
第3步:判断当前深度是否小于检波点深度,如果是,返回第2步继续向下反向外推共检波点道集波场.反之,在井中检波点R设置子波(脉冲),并从检波点深度向下正向延拓一个深度Δz:
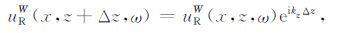
|
(10) |
其中,uRW (x,z,ω)为子波(脉冲)传播到坐标(x,z)处的下行波场.
第4步:正向延拓的下行波场和反向延拓的上行波场在坐标(x,z)处进行互相关,并取零时间成像值[16]
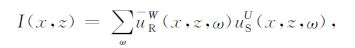
|
(11) |
从而得到空间点(x,z)的像,其中珔uRW (x,z,ω)表示uRW(x,z,ω)的共轭.然后返回第2 步继续进行波场外推,直到执行到最大深度,完成一个共检波点道集数据成像.
常规VSP成像算法需要对VSP 资料进行上下行反射波波场分离,并认为上行反射波主要为一次反射波,在此基础上对上行反射波进行成像.然而,复杂构造区域的波场本身比较复杂,识别和分离不同类型波场也具有较大难度.受VSP观测系统上行反射波照明范围的限制,这种成像算法只能够对井中检波器下方一个很小的钟形区域进行成像,大大限制了VSP资料在成像领域的应用前景.另外,如果地下存在高陡倾角构造,一次反射波在记录中通常表现为下行波,因而针对于上行波的传统VSP 算法很难对高陡倾角构造成像.
4 上下行反射波联合成像方法常规VSP成像方法需要进行上下行反射波场分离,然后利用上行反射波进行成像.近年来发展起来的地震干涉成像法虽然能够利用下行波对高陡倾角构造进行成像,但仅限于自由表面多次波或一次反射下行波,无法利用层间多次波.另外,地震干涉成像需要首先分离出VSP下行反射波和直达波,然后通过互相关或者反褶积等处理将其转化为地面地震资料,操作比较复杂.本文给出上行反射波和下行反射同时成像的方法,这里的下行反射波不仅包括自由表面多次波,而且包含层间多次波.其成像过程可以描述为:
第1步:将VSP数据转化为共检波点道集数据.
第2步:在井中检波点R处设置子波(脉冲),并从该深度开始按照公式
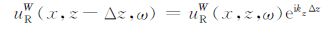
|
(12) |
向上正向延拓一定深度Δz直到地表,在延拓过程中保存每一层的延拓波场.
第3步:从地表开始,读取并累加第2步保存的当前层波场,并按照公式(10)向下正向外推一个深度Δz.同时地表记录波场根据公式(9)向下反向外推一个深度Δz.
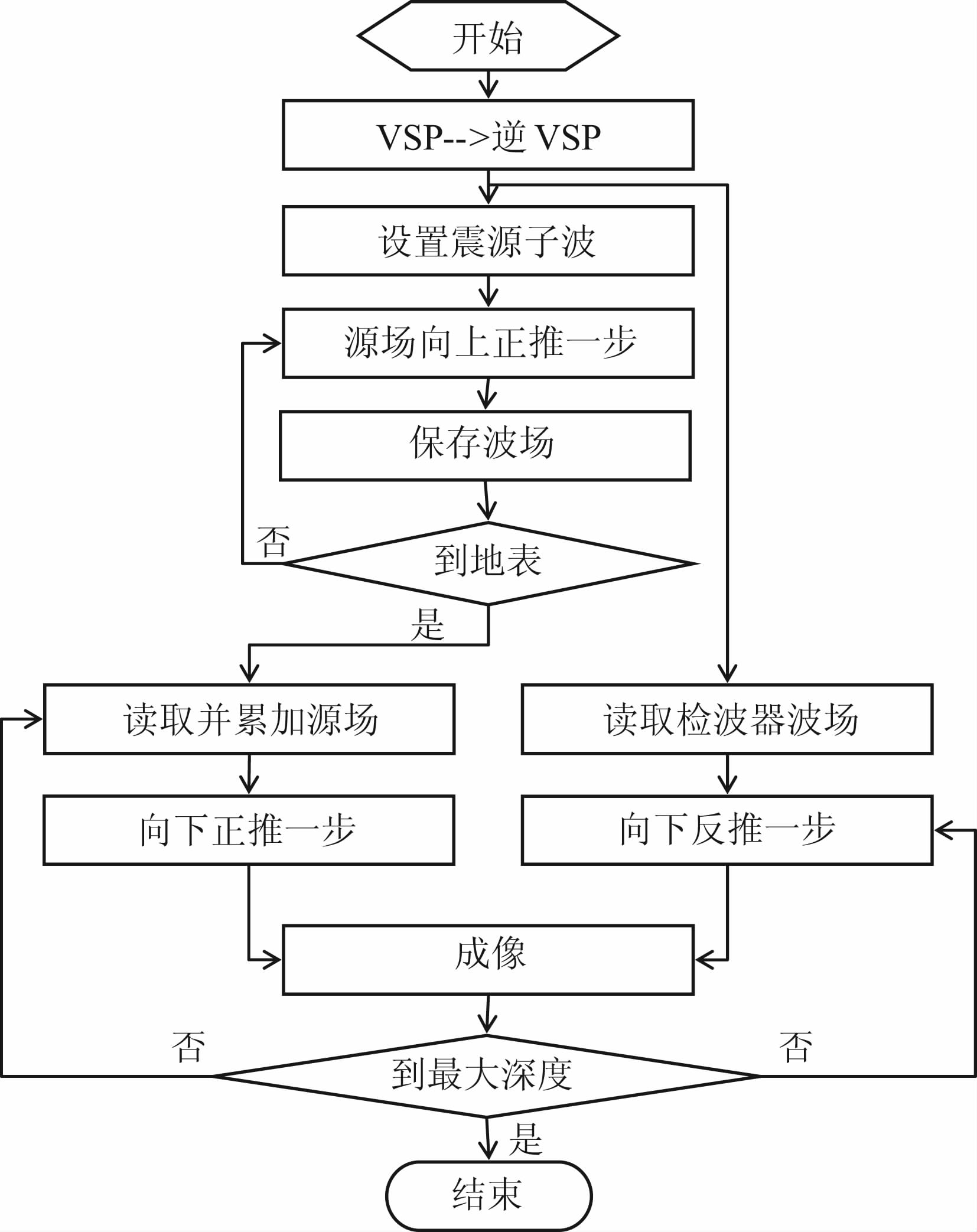
第4步:在每一个外推深度根据公式(11)成像条件提取成像值.整个成像过程如图 3所示.
|
图 3 本文VSP上下行波联合成像方法流程图 Fig. 3 Workflow of VSP upgoing and downgoing joint imaging method |
在高频近似下分析这种成像方法对不同波场的成像能力,将VSP 资料转化为逆VSP 资料,设逆VSP数据震源位于R点,R点上部某个点为X,脉冲震源从R正向延拓到X点的过程可以描述为

|
(13) |
其中,uRX+为从R到X点正向延拓得到的频率域波场,F(δ(t))表示脉冲信号δ(t)的傅里叶变换.当X点位于地面时,则向上延拓到达地表.设空间任意成像点为Y,第3步累加震源波场并将其从X点延拓到Y点的过程可以描述为
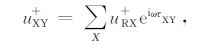
|
(14) |
uXY+为从X点正向延拓到Y点的频率域震源波场.将(13)式代入(14)式,得
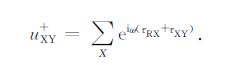
|
(15) |
第3步检波器波场uSA 从地表S点到成像点Y点反向延拓过程可表述为
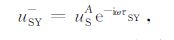
|
(16) |
其中uSY- 为从S点到Y点的频率域波场.
根据(11)式互相关成像条件,成像点Y处的像I(Y)应满足
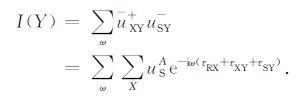
|
(17) |
逆VSP记录uSA 与VSP记录一样由直达波、一次反射波、自由表面多次波和层间多次波等构成,即
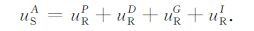
|
(18) |
将(18)式代入(17)式,得
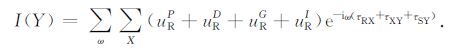
|
(19) |
根据图 1所示的观测系统,结合公式(2—5),有
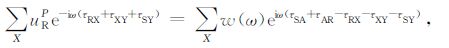
|
(20) |
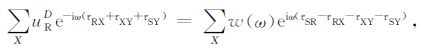
|
(21) |
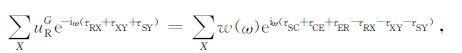
|
(22) |
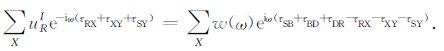
|
(23) |
如果波场在成像点Y成像,(20—23)式必须满足指数项为零.根据这个条件,我们可以分析不同类型波场的成像所对应的X值以及不同类型波场的成像能力.
对于(20)式,当X与R重合时,τRX=0,成像点Y恰好与反射点A重合时,(20)式指数项为零,即在A点能够成像,在其它点其成像值为背景噪音.当X与R不重合时,τRX≠0,成像点Y恰随着X的移动而移动,其叠加效果为背景噪音.这就是VSP 一次波偏移成像的成像值.
对于(22)式,当X与地表E点重合时,成像点Y恰好在反射点C成像,在其它成像点像无法实现同相叠加,其值为背景噪音,这就实现了自由表面多次波成像.对于(23)式的层间多次波,当X点与D点重合时,成像点Y在反射点B成像,当X为其它值时成像值为背景噪音.
对于(21)式,直达波传播路径上每个点都满足指数项为零,即在直达波传播路径上的任意Y都能够成像,其成像值为低频背景噪音.式(20)、(22)和(23)叠加可以得到没有低频噪音干扰的VSP 成像剖面.因此,为了消除低频噪音对成像剖面的干扰,在成像前对VSP 资料进行直达波衰减可以提高偏移剖面的质量.
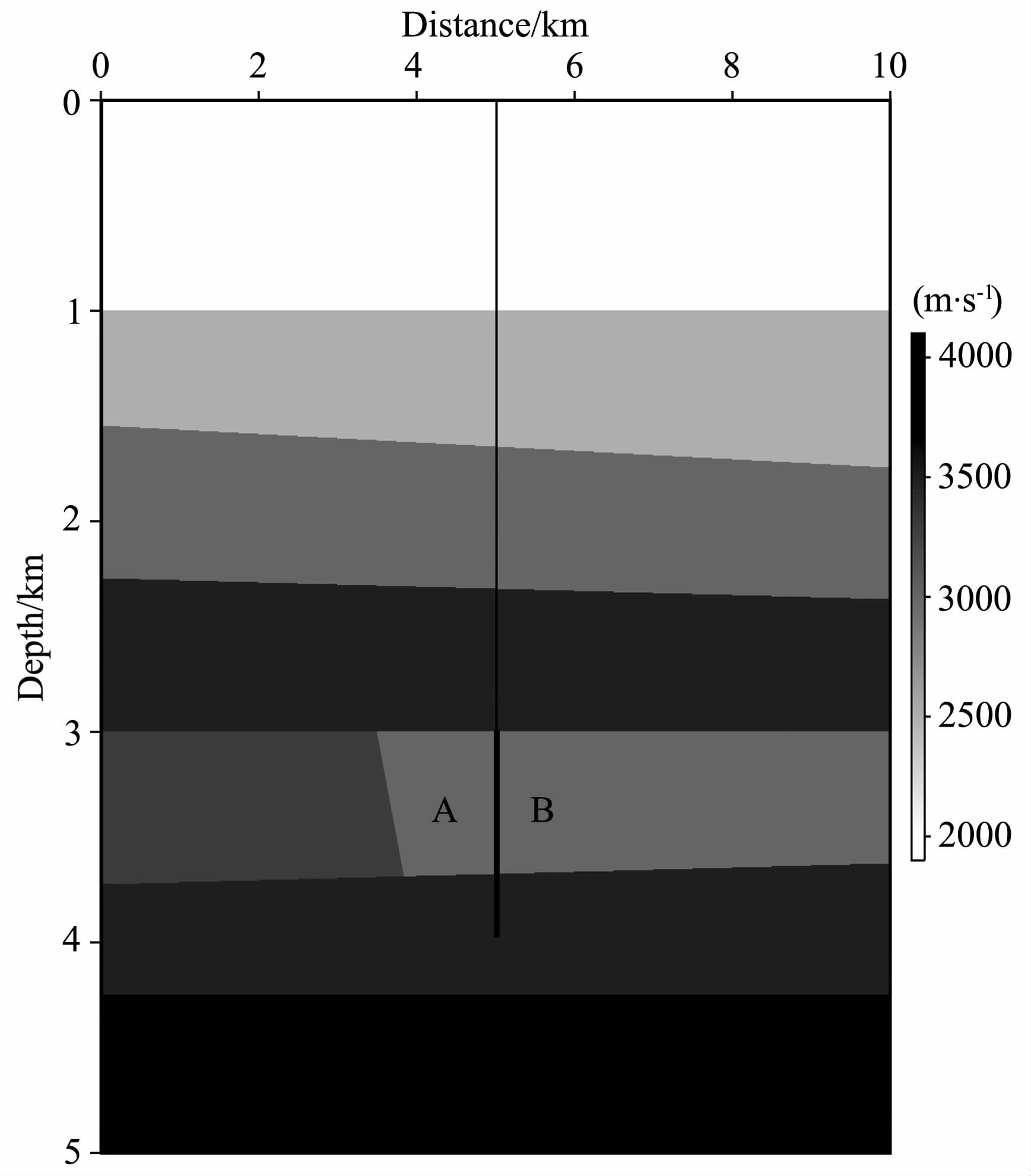
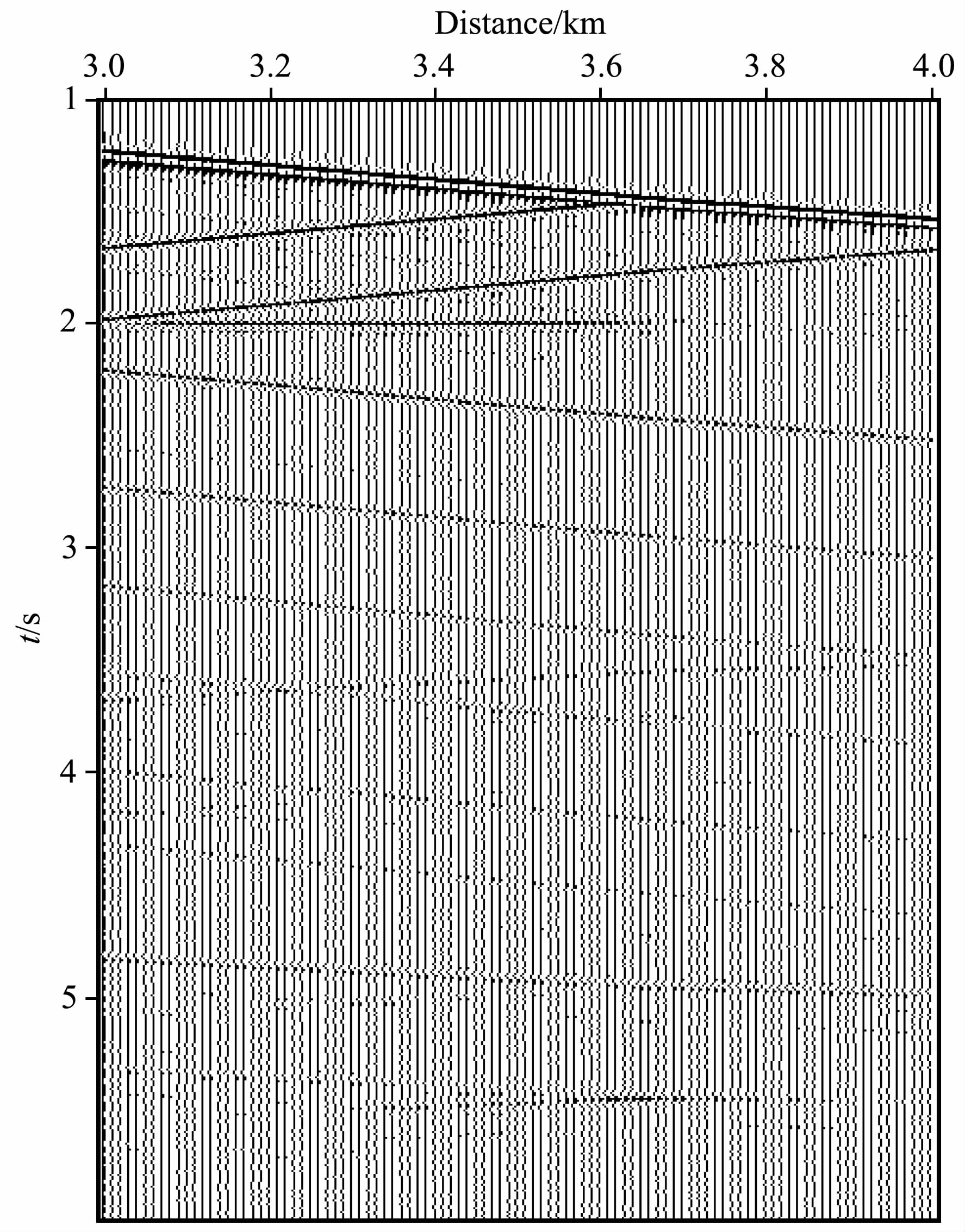
5 模型测试为了验证本文方法的正确性,我们利用如图 4所示的模型进行测试.在模型中部x=5km 处设计一观测井,井中从3km 到4km 每隔10 m 设置一检波器,共101级检波器(图 4中B处所示),地面从0到10km 每隔10m 放一炮,共1001炮.每级检波器记录6s,采样间隔2ms.为了验证本文方法对于高陡倾角构造的成像能力,在VSP 井左侧3km 到3.6km 处设置一65°倾角的反射界面(图 4中A 处所示).图 5 为炮点位于(6km,0)处模拟产生的VSP数据,从图中可以看出,VSP 资料中不仅包含上行反射波信息,同时包含大量下行反射波.如果只用上行反射波进行成像,大量下行波无法参与成像,影响VSP资料成像的范围和效果.
|
图 4 理论速度模型 Fig. 4 Theoretical velocity model |
|
图 5 炮点位于(6000,0)处激发的VSP炮记录 Fig. 5 VSP record of shot location at coordinate (6000,0) |
图 6a为常规VSP成像方法偏移得到的成像剖面,由于VSP上行反射波只能够照明检波器下方较小的一块区域,因此,常规成像算法只能够成像最浅检波器下方较小的一个钟形区域,成像范围较小.由于模型中陡倾角构造A的倾角较大,常规VSP成像方法无法对其成像.作为对比,图 6b为本文成像方法的成像剖面.可以看出,应用本文成像方法能够同时成像VSP资料的上行反射波和下行反射波,有效成像区域大大扩宽,成像效果明显改善.同时,本文方法对模型中陡倾角构造A 能够清晰成像,成像效果较好.

|
图 6 (a)理论资料常规VSP成像剖面;(b)理论资料本文方法成像剖面 Fig. 6 (a)Traditional VSP imaging profile of theoretical data; (b)^Imaging profile of this paper’s imaging method of theoretical data |
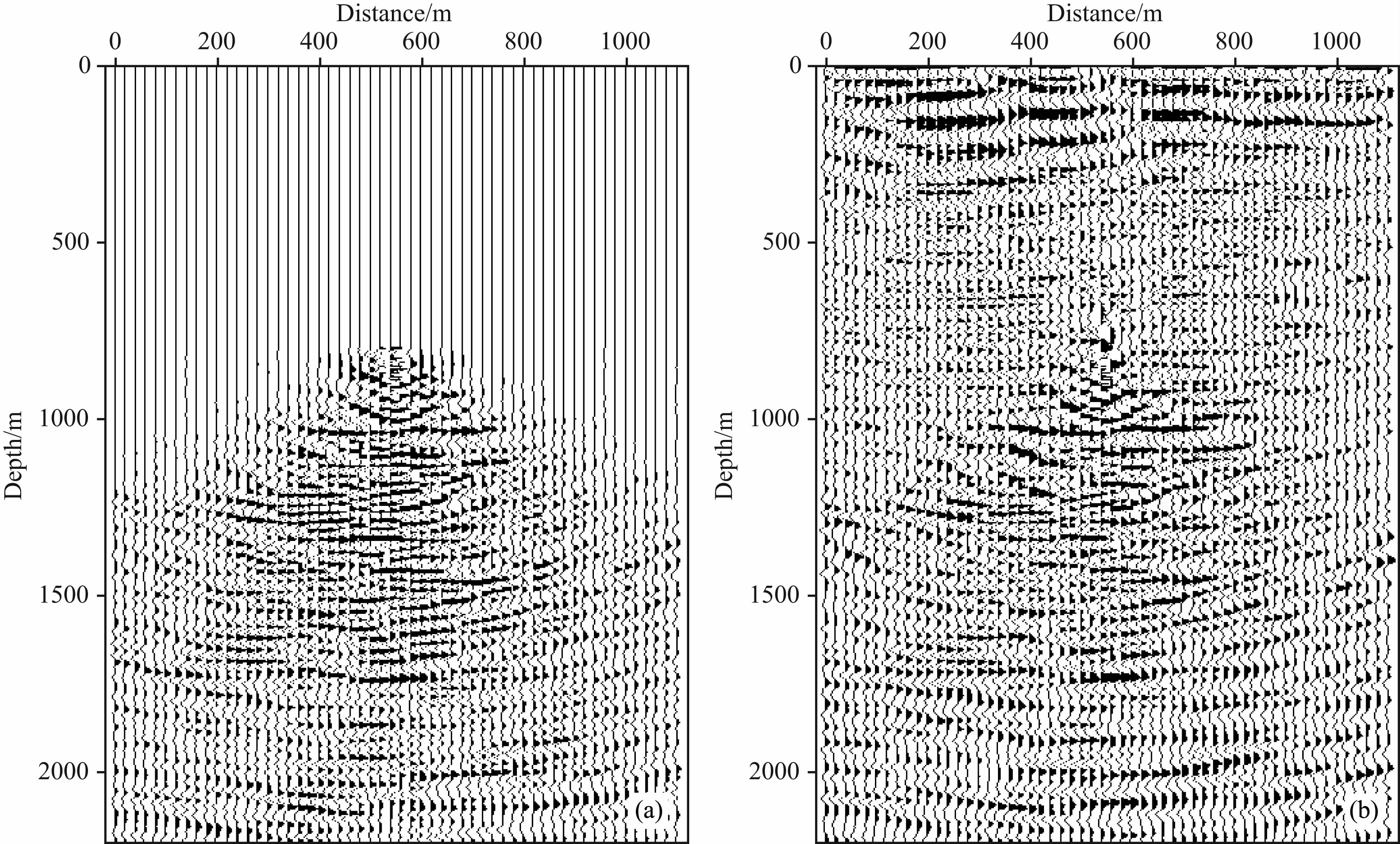
在模型测试的基础上,我们采用中国东部某地VSP资料进行成像试验.该VSP 资料共14级检波器,检波器深度从800~930 m,检波器间距10 m.图 7a为常规成像方法处理得到的成像剖面,可以看出,只有800m 之下的区域能够成像.图 7b为用本文成像方法对该资料处理的成像剖面,对比图 7a,本文成像算法不仅能够对检波器下方一次反射波照明区域进行有效成像,对于检波器之上比较浅的区域,本文方法亦能够取得较好的成像效果,这充分说明了本文方法的正确性.
|
图 7 (a)实际VSP资料常规成像剖面;(b)实际VSP资料本文方法成像剖面 Fig. 7 (a)Traditional imaging profile of real field VSP data; (b)^Imaging profile using this paper’s method of real field VSP data |
本文成像方法不仅能够对反射波进行成像,沿着直达波传播路径,该方法对直达波也能够成像.由于直达波路径上每个点都是成像点,因此直达波在成像剖面中表现为较强的低频噪音.为了消除低频噪音的干扰,我们可以对成像剖面进行适当的高通滤波,消除剖面中低频噪音的干扰.由于高通滤波通常会损伤成像剖面中的高陡倾角构造,因此,首先将VSP资料中的直达波切除,然后对切除直达波的VSP资料进行成像可以得到干净的成像剖面.
地震干涉通过互相关或者反褶积运算消除VSP自由表面多次波中地面反射点到检波器间的走时,将VSP自由表面多次波转化为地面地震一次反射波,然后进行成像.数据域的互相关或者反褶积运算不需要速度模型,能够得到较为精确消除检波器到地面反射点之间(图 1 中ER 段)的走时.本文方法完全利用波场延拓来描述VSP 波场的传播过程,对VSP自由表面多次波成像来说,它对偏移速度模型的依赖性更强.较好的成像效果需要较为准确的偏移速度模型.
多次波比一次波具有更长的传播路径,波场的透射损失、几何扩散以及地下介质的非弹性吸收等因素的作用造成多次波能量通常要比一次波弱得多.为了提高成像剖面的质量,在成像之前建议进行上下行波波场能量的校正,使得VSP记录中下行波场与上行波场能量相当,从而可以提高联合成像的质量.
高陡倾角构造在VSP记录中通常为下行波,常规成像方法无法对其成像.地震干涉成像可以对其进行面向目标的成像,但是该方法需要分离直达波与反射波,处理比较复杂.配合较高精度的波场延拓算子,本文方法对于高陡倾角构造成像也是能够胜任的,式(20)中当X 与Y 重合时,成像点Y恰好能够在高陡倾角构造的反射点成像.
8 结 论针对VSP资料中上下行波均发育丰富的特点,我们提出了新的波动方程上下行反射波联合成像方法.该方法不需要对VSP 资料进行上下行波场分离,能够同时实现上行反射波、下行自由表面多次波和下行层间多次波成像.本文方法大大提高了VSP资料的成像范围,提高了VSP 数据的成像质量.并且,本文方法能够对常规VSP偏移方法无法成像的下行一次反射波进行成像,从而实现高陡倾角构造成像,成像精度较高.理论数据和实际资料试算证明了本文方法的正确性.
| [1] | 常旭, 刘伊克, 王辉, 等. 地震相干偏移与数据自参照偏移的关系. 地球物理学报 , 2009, 52(11): 2840–2845. Chang X, Liu Y K, Wang H, et al. Seismic interferometric migration and data referenced only migration. Chinese J. Geophys. (in Chinese) , 2009, 52(11): 2840-2845. |
| [2] | 吴世萍, 黄录忠, 胡天跃. Walkaway VSP多次波成像技术研究. 石油物探 , 2011, 50(2): 115–123. Wu S P, Huang L Z, Hu T Y. Multiple reflection imaging by using Walkaway VSP data. Geophysical Prospecting for Petroleum (in Chinese) , 2011, 50(2): 115-123. |
| [3] | He R. Wave equation interferometric migration of VSP data. Utah: University of Utah , 2006. |
| [4] | He R Q, Hornby B, Schuster G T. 3D wave-equation interferometric migration of VSP free-surface multiples. Geophysics , 2007, 72(5): S195-S203. DOI:10.1190/1.2743375 |
| [5] | 杜婧, 王尚旭, 刘国昌, 刘洋. 基于局部斜率属性的VSP波场分离研究. 地球物理学报 , 2009, 52(7): 1867–1872. Du J, Wang S X, Liu G C, Liu Y. VSP wavefield separation using local slopes attribute. Chinese J. Geophys. (in Chinese) , 2009, 52(7): 1867-1872. |
| [6] | 王华忠, 徐蔚亚, 王建民, 等. VSP数据波动方程叠前深度偏移成像及立体地震成像. 石油地球物理勘探 , 2011, 36(5): 517–525. Wang H Z, Xu W Y, Wang J M, et al. Prestack depth migration of VSP data and stereoscopic seismic imaging. OGP (in Chinese) , 2011, 36(5): 517-525. |
| [7] | 方伍宝, 陈林. 三维VSP资料波动方程叠前深度偏移研究. 石油物探 , 2006, 45(5): 527–531. Fang W B, Chen L. Wave equation of prestack depth migration of 3-D VSP data. Geophysical Prospecting for Petroleum (in Chinese) , 2006, 45(5): 527-531. |
| [8] | 陈生昌, 马在田, 陈林. 三维VSP数据的波动方程偏移成像. 天然气工业 , 2008, 28(3): 51–53. Chen S C, Ma Z T, Chen L. Wave equation migration for 3-D VSP data. Natural Gas Industry (in Chinese) , 2008, 28(3): 51-53. |
| [9] | 孙文博, 孙赞东. 基于伪谱法的VSP逆时偏移及其应用研究. 地球物理学报 , 2010, 53(9): 2196–2203. Sun W B, Sun Z D. VSP reverse time migration based on the pseudo-spectral method and its applications. Chinese J. Geophys. (in Chinese) , 2010, 53(9): 2196-2203. |
| [10] | Claerbout J F. Synthesis of layered medium from its acoustic transmission response. Geophysics , 1968, 33(2): 294-269. |
| [11] | Brandsberg-Dahl S, Van Gestel J P, Etgen J T, et al. VSP salt flank imaging through wavefield continuation: 65th annual EAGE conference, Extended Abstracts, B14, 2003. |
| [12] | Hornby B, Yu J H. Interferometric imaging of a salt flank using walkaway VSP data. The Leading Edge , 2007, 26(6): 760-763. DOI:10.1190/1.2748493 |
| [13] | Mehta K, Bakulin A, Sheiman J, et al. Improving the virtual source method by wavefield separation. Geophysics , 2007, 72(4): V79-V86. DOI:10.1190/1.2733020 |
| [14] | 吴世萍, 彭更新, 黄录忠, 等. 基于虚源估计的复杂上覆地层 下地震相干成像. 地球物理学报 , 2011, 54(7): 1874–1882. Wu S P, Peng G X, Huang L Z, et al. Seismic interferometry imaging based on virtual source estimation with complex overburden. Chinese J. Geophys. (in Chinese) , 2011, 54(7): 1874-1882. |
| [15] | 王珺, 杨长春, 刘海河, 等. 克希霍夫法VSP多波联合成像. 地球物理学进展 , 2006, 21(3): 845–855. Wang J, Yang C C, Liu H H, et al. VSP multiwave image with Kirchhoff Method. Progress in Geophysics (in Chinese) , 2006, 21(3): 845-855. |
| [16] | Claerbout J F. Imaging the Earth's Interior. Cambridge, MA: Black-Well Scientific Publications, Inc. 1985. |
| [17] | Stoffa P L, Fokkema J T, de Luna Freire R M, et al. Split-step Fourier migration. Geophysics , 1990, 55(4): 410-421. DOI:10.1190/1.1442850 |
| [18] | Ristow D, Ruhl T. Fourier finite-difference migration. Geophysics , 1994, 59(12): 1882-1893. DOI:10.1190/1.1443575 |
| [19] | 金胜汶, 许士勇, 吴如山. 基于波动方程的广义屏叠前深度偏移. 地球物理学报 , 2002, 45(5): 684–690. Jin S W, Xu S Y, Wu R S. Wave equation based prestack depth migration using generalized screen propagator. Chinese J. Geophys. (in Chinese) , 2002, 45(5): 684-690. |
 2012, Vol. 55
2012, Vol. 55

