2. 大庆油田有限责任公司勘探开发研究院, 大庆 163712
2. Exploration and Development Research Institute of Daqing Oil field Company Ltd., Daqing 163712, China
多次波在地震勘探资料,尤其是海洋地震勘探资料中普遍存在,通常作为噪声予以压制.压制多次波的主要方法可分为两类:滤波法和基于波动理论预测的方法.在滤波法中,广义Radon 变换法可在叠前高效地衰减多次波,该方法对地震资料沿给定的路径进行积分,将地震数据变换到新域后,再设计滤波器滤波得到衰减多次波后的成果剖面.由求和路径不同,Radon 变换可分为线性Radon 变换,抛物Radon变换以及双曲Radon变换.
Radon变换压制多次波方法来源于Ryu[1]提出的速度滤波的概念,当多次波和一次波存在速度差时,多次波能量与一次波能量成像至不同的速度空间,在该速度空间,应用滤波方法可将一次波与多次波分离.随着模型空间域分辨率的日益提高,基于Radon变换的多次波压制方法获得了快速发展.Hampson[2]提出在部分动校正(NMO)的地震数据中快速应用抛物Radon变换压制多次波的实用方法,随后诸多学者对该方法进行了完善[3-5].Yilmaz[6]引入t平方算子,以代替对数据进行NMO 校正.地震勘探资料的共中心点(CMP)道集或共炮点(CSP)道集上的同相轴大多近似为双曲线形状,因此,应用双曲Radon变换进行滤波,可以有效模拟波场的性质,时空域的双曲同相轴经双曲Radon 变换后可成像为点.Foster等[7]提出双曲Radon变换压制多次反射的方法,首先需要估计变换域中多次波的能量,然后将估计出的多次波能量做双曲Radon逆变换,再将其从原始数据中减去.当地震数据的一次波和多次波有足够的时差差别时,其正变换后在模型空间可获得较高的分辨率,Radon多次波压制方法效果较好.尽管如此,抛物和双曲Radon 变换实质上仍是利用了一次波比多次波动校时差小这一特性,因此在地下介质速度逆转或存在较小的速度梯度时,多次波衰减效果并不好.
基于波动方程预测的方法可以压制来自复杂地下介质地震资料的表面多次波,通常包括波场延拓法[8]、反馈迭代法[9]和逆散射级数法[10],其中反馈迭代法常用于表面多次波压制,逆散射级数法常用于层间多次波压制.基于波动方程预测的方法计算成本较高,除多次波预测算法外,自适应相减算法对多次波压制效果也有重要的影响.
近三十年来,尽管多次波压制技术获得了空前的发展,但是目前还没有任何一种多次波压制技术能在实际处理中完美应用.然而,联合应用不同的方法技术却可以取长补短,发挥优势.曾有学者考虑结合基于波动方程预测的方法和滤波法压制表面多次波,Zhou 等[11]提出采用波场延拓法产生多次波模型道,再联合滤波法压制多次波,波场延拓方法虽然可处理复杂地下介质数据,但是该方法不但计算成本高,而且属模型驱动的方法,实际应用中受到较大的限制.Zhang等[12]提出结合波动方程预测的反馈迭代法(SRME 方法)和抛物Radon 变换方法压制表面多次波.反馈迭代法虽为数据驱动的方法,但实际对多次波的粗略预测时,计算成本较高,也需要考虑计算效率问题.
随着GPU(图形处理器)硬件技术的发展、可编程性的不断提高,其在处理能力和存储器的带宽上相对CPU 有明显优势,GPU 的通用计算优势在地震勘探领域日益凸显,也获得了较为成功的应用[13-17].为此笔者利用GPU 和CPU 协同并行加速文中表面多次波预测的密集型运算.
本文利用反馈迭代法和双曲Radon 变换方法联合压制表面多次波,并引入GPU 加速计算,该方法一方面节约了Zhang等[12]采用基于波动方程的反馈迭代法预测和Zhou等[11]采用基于波动方程的波场外推法预测多次波的计算成本,另一方面避免了常规反馈迭代方法级数展开或迭代[18-19]压制多次波的自适应相减计算,文中算法依据原始数据完成空间褶积运算,可精确预测多次波在输入数据中的位置(走时),而对多次波振幅和相位仅粗略预测,无需严格匹配原始数据中多次波的振幅和相位.文中也在双曲Radon 变换域比较预测的多次波和原始数据所包含的多次波能量,并设计有效的自适应滤波器完成对多次波能量的滤波,所采用的时不变双曲Radon变换滤波方法符合地震同相轴的双曲特性,在双曲Radon 域,多次波和一次波可较好地分离,获得理想的多次波压制效果.另外,该方法在频率域解耦计算,计算效率较高.
2 基于波动方程多次波预测和双曲Radon变换基本理论 2.1 基于波动方程的反馈迭代法预测表面多次波基于波动方程的反馈迭代表面多次波预测方法为叠前的完全数据驱动的方法,在预测过程中,无需震源特性、表面反射的信息,也无需地下介质的任何信息,只需要含多次波的总波场就可以实现多次波的预测,并且该方法能有效地处理非均质地层以及速度逆转等复杂的地下介质.
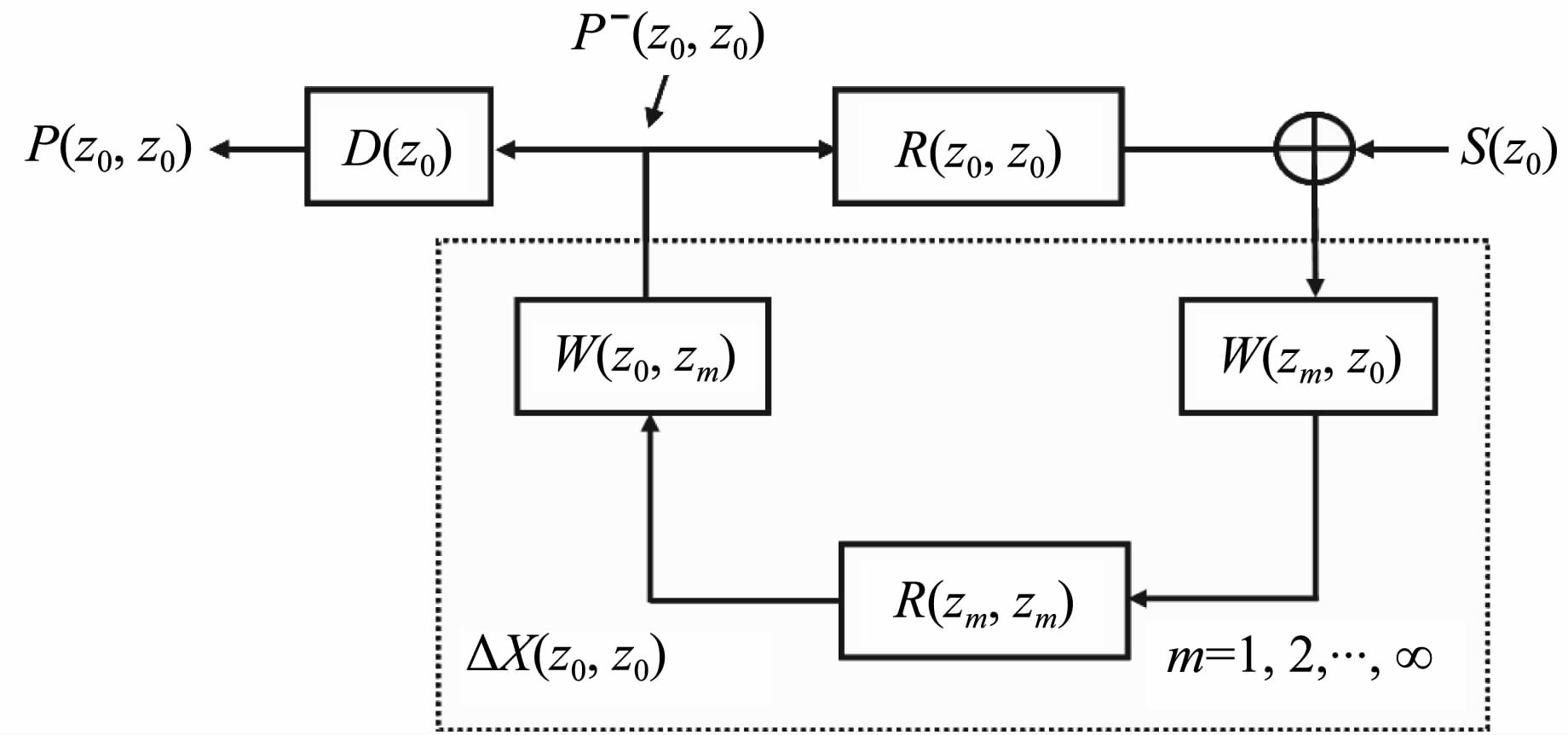
Berkhout[20]最初引入数据矩阵的概念,用以表示叠前地震数据,并用其构建表示地震波传播和反射的WRW 模型.将波场延拓表示成空间褶积过程是WRW 模型[20-21]的基础,WRW 反馈模型如图 1所示.
|
图 1 含有一次波和多次波的正演WRW 反馈模型 Fig. 1 WRW feedback model with primary and multiples |
含有一次波和多次波的波场传播可由WRW反馈模型表示为
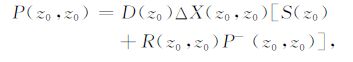
|
(1) |

|
(2) |
式中,P(z0,z0)表示自由界面z0 处包含表面多次波的总波场;D(z0)表示检波器特性矩阵;ΔX(z0,z0)表示自由界面不发生反射时的地下介质的脉冲响应;S(z0)表示震源特性矩阵;R(z0,z0)表示自由界面处对上行波场的反射矩阵;P- (z0,z0)表示自由界面处的上行波场.$\sum\limits_{m = 1}^\infty {} $表示所有层的传播效应的叠加;m表示自由界面以下的反射层序号;W(z0,zm)表示从zm到z0 的上行传播矩阵;W(zm,z0)表示从z0 到zm的下行传播矩阵;R(zm,zm)表示第zm层的反射系数矩阵.
实际上,没有多次波的脉冲响应ΔX是无法应用的,因此,对2D 地震数据,预测的多次波M0 可由总波场P(有效波和多次波的和)和一次波的估计数据${{\hat p}_0}$褶积得到,即
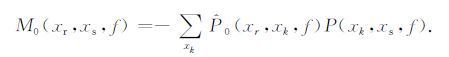
|
(3) |
基于波动方程的反馈迭代表面多次波压制方法可由级数展开法或迭代法实现.应用级数展开法时,用地震数据本身(总波场)代替一次波估计,即:
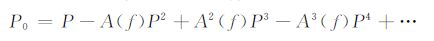
|
(4) |
式中,多次波预测由矩阵相乘来实现,具体实现时,在每个频率分量上计算一组矩阵乘法,应用加权因子-A(f),A2(f),-A3(f),…,后再求和,使得预测的多次波在振幅和相位上匹配地震数据中待压制的多次波.
利用迭代法压制表面多次波的基本迭代方程为
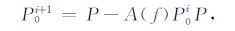
|
(5) |
式中,i为迭代次数,P0i 为前次多次波压制结果.应用迭代法时,可以利用迭代过程更新有效波的估计.
由(4)式可知,若选择利用级数展开法压制表面多次波,则需尽可能地预测到高阶项,再进行自适应相减,若选择利用迭代法计算,通常也需要三次迭代能获得满意的结果.文中算法对表面多次波粗略预测,只需要一次空间褶积运算,即计算P2 项,大大节约了计算成本.
2.2 时不变双曲Radon变换广义Radon 变换是沿给定的路径进行积分计算的,积分路径越接近地震同相轴的时差曲线,得到的正变换效果就越好,模型空间域的分辨率就越高.在对地震数据做部分NMO 的CMP道集上,多次波的剩余时差更加接近于双曲线,当有效波和多次波存在足够的时差差别时,应用双曲Radon变换进行多次波的衰减,能得到较理想的多次波衰减效果.
由于双曲Radon变换是时变的,无法在频域完成,因此,直接进行双曲Radon变换成本非常高,以致较难实现.因此本文采用时不变双曲Radon 变换,其优点是能在频率空间域进行计算,即求解方程对频率是解耦的,因此,提高了双曲Radon 正变换的计算效率.另外,对于均匀采样的地震数据,时不变双曲Radon变换法所形成的频率空间域矩阵具有Toeplitz结构,应用Levinson递推算法可大大提高矩阵求解计算的效率.
双曲Radon变换压制多次波的基本思想是利用了在变换域中一次波和多次波同相轴的可分离性质.将变换域中的多次波能量做反变换,再在原始的CMP道集中将其减去,就获得了只有一次波的道集.
时不变双曲Radon变换的定义如下[7]:
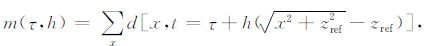
|
(6) |
式中,m(τ,h)为沿路径$t = \tau + h\left( {\sqrt {{x^2} + z_{{\text{ref}}}^2} - {z_{{\text{ref}}}}} \right)$积分得到的双曲Radon 正变换剖面,d(x,t)为时空域地震数据,τ为截距时间,h为射线参数,zref 为参考深度.只有在参考深度处所定义的积分路径才是Dix所定义的双曲线.
因为时间参量t和τ 有着线性关系,同抛物Radon变换一样,可应用Fourier变换在频率域进行时不变双曲Radon变换的计算.所以文中方法和传统时变双曲Radon变换法相比,其计算效率有数量级的提高.
对式(6)两端进行Fourier变换,可得
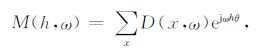
|
(7) |
其中,

|
(8) |
结合方程(7),对于单频分量,双曲Radon正反变换可用矩阵形式表示为
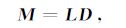
|
(9) |
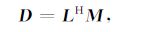
|
(10) |
式中:LH 是矩阵L的共轭转置,矩阵L的元素可表示为:
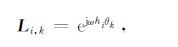
|
(11) |
同抛物Radon变换[22]一样,对于超定系统方程,式(9)可写为如下的最小平方形式:
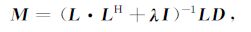
|
(12) |
若射线参数等间隔采样,则L·LH为主对角线元素相等Toeplitz 矩阵,可用Levinson 递推法进行求解,计算效率很高.
对于双曲Radon变换,射线参数h的采样间隔为
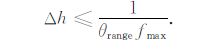
|
(13) |
一般情况下,参考深度zref 选为最大偏移距xmax,在这种假设下,θrange =0.4xmax.
如果zref =xmax,双曲Radon变换中射线参数的取值范围为
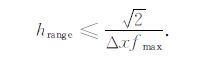
|
(14) |
如前所述,时不变双曲Radon变换可在频率域解耦计算,因此计算效率较高,但该方法难以处理复杂介质地震资料,诸如速度逆转介质,而且,通常需要假定一次波和多次波有足够大的时差差别,在许多情况下,假设不成立,多次波衰减的有效性和一次波信号的保护被降低.基于波动方程预测的反馈迭代方法可应对复杂的地下介质,但在利用级数展开或迭代形式压制多次波时需要较高的计算成本.文中将基于波动方程预测和双曲Radon 变换滤波的方法相结合,可有效地降低多次波残余和近偏移距处一次波振幅的损伤,该方法在Radon域引入一个自适应滤波器,通过比较所记录数据和粗略预测多次波的Radon 成像结果,构建自适应滤波器.多次波的粗略预测只包含所记录数据的空间褶积,无需复杂的迭代过程.基于Radon变换的多次波衰减通常需对所记录数据的CMP 道集执行Radon 变换,再进行滤波衰减.实际上,传统滤波切除函数是在稀疏的CMP道集上进行的,而其他CMP 道集的滤波切除曲线可通过插值获得.文中采用自适应滤波器在每个CMP道集上自动完成切除,无需人工干预.通过在双曲Radon 域比较多次波模型道的能量以及含多次波和有效波的原始数据的能量可自动确定含多次波区域,多次波模型道的能量由原始数据通过基于波动方程预测的反馈迭代方法产生,由产生的多次波模型道,可预测输入数据中多次波的位置.因此,在双曲Radon 域,可选择合理有效的滤波器进行滤波,从而提高了计算精度.
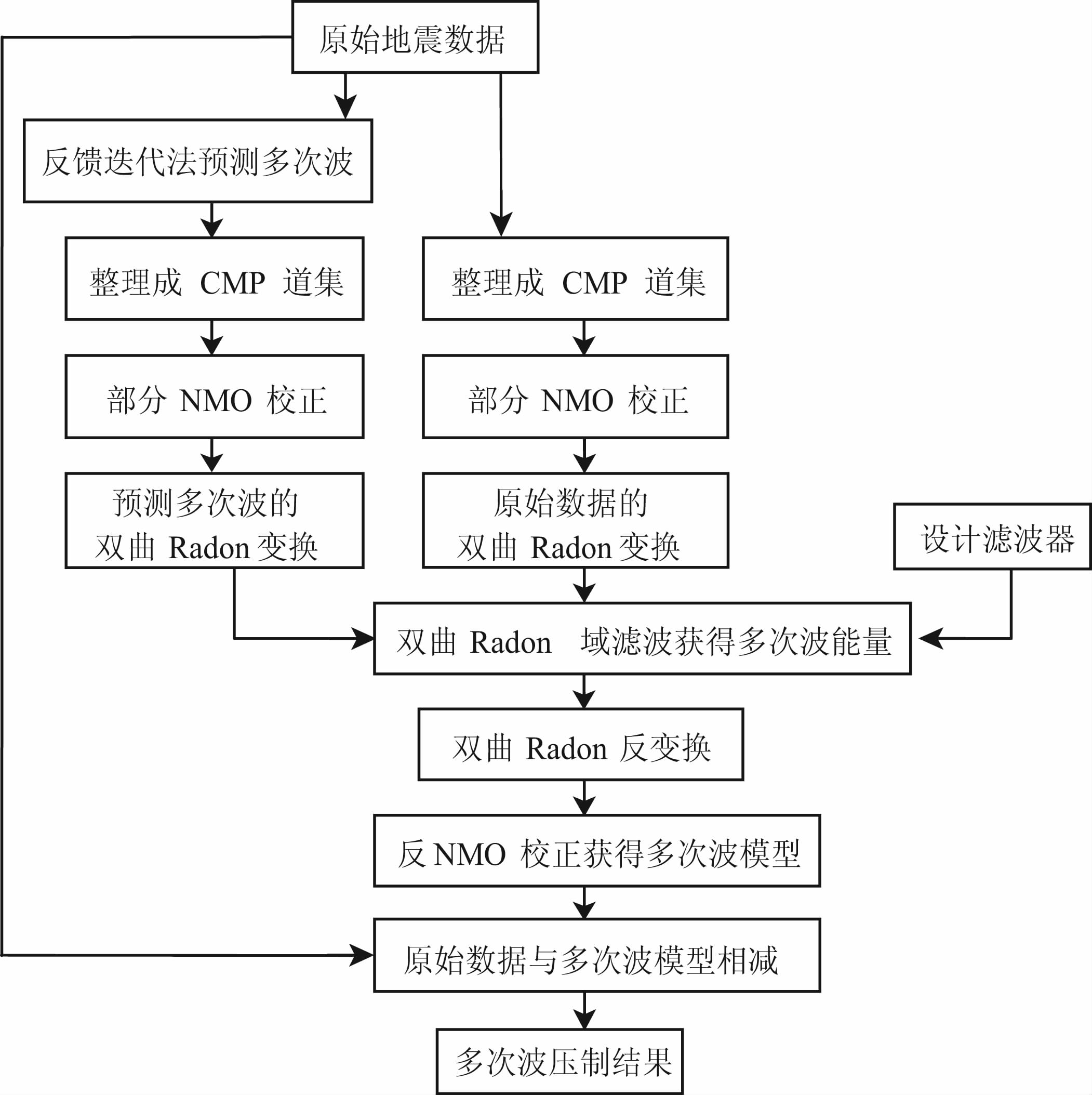
文中首先对含多次波的原始数据应用反馈迭代方法粗略预测表面多次波,所谓粗略,就是预测的多次波模型道不需与输入数据中的多次波严格匹配.在对含多次波的原始数据和预测的多次波数据分别应用NMO 校正后,分别对其执行双曲Radon 变换,在Radon 变换域,多次波能量通常集中在具有较大曲率参数的道上,参照预测多次波的Radon域的能量,设计最优的滤波器,对原始数据的Radon域能量利用自适应切除滤波器滤除一次波存在的区域,获得多次波能量,随后对其执行双曲Radon 反变换,再进行反NMO 校正,获得滤波后的多次波模型,即仅有多次波同相轴存在的道集数据,从原始数据中减去多次波数据,得到多次波压制结果.多次波反射被有效地去除,一次波反射能量更好地得到保护.图 2所示为结合反馈迭代和双曲Radon变换压制表面多次波的方法流程图.
|
图 2 结合波动方程预测和双曲Radon变换压制表面多次波的方法流程图 Fig. 2 Flow chart for suppressing surface-related multiples by combining wave equation prediction and hyperbolic Radon transform |
在双曲Radon 域应用自适应滤波器滤除有效波能量,保留多次波能量,所以定义正确的有效波去除区域是决定多次波压制效果优劣的关键环节,良好的自适应滤波器将有效地区分有效波和多次波,获取理想的滤波效果.Zhou等[23-25]将Butterworth型非线性滤波器应用于t-x域、τ-p域和f-k域的多次波压制中,通过研究成像域局部2D 窗内的振幅谱之和,确定自适应滤波器.文中将Butterworth型滤波器引入到双曲Radon域滤波中,通过比较所记录数据和预测多次波的Radon 域成像自动确定如下的自适应滤波器:
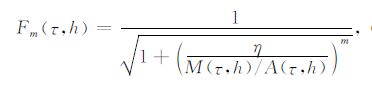
|
(15) |
式中,M(τ,h)为多次波模型数据的双曲Radon变换;A(τ,h)为含多次波原始地震数据的双曲Radon变换;m为控制滤波的平滑参数,通常可在小于10的偶数中取值;η 为滤波器的剔除参数,与海底反射系数有关,通常可取为海底反射系数的绝对值.当M(τ,h)/A(τ,h)远小于η 时,认为无多次波存在,滤波器Fm(τ,h)近似为0,当M(τ,h)/A(τ,h)大于η 时,多次波存在,滤波器Fm(τ,h)近似为1.实际应用中,需根据有效波保护和多次波衰减的平衡关系适当选择η 和m的值.
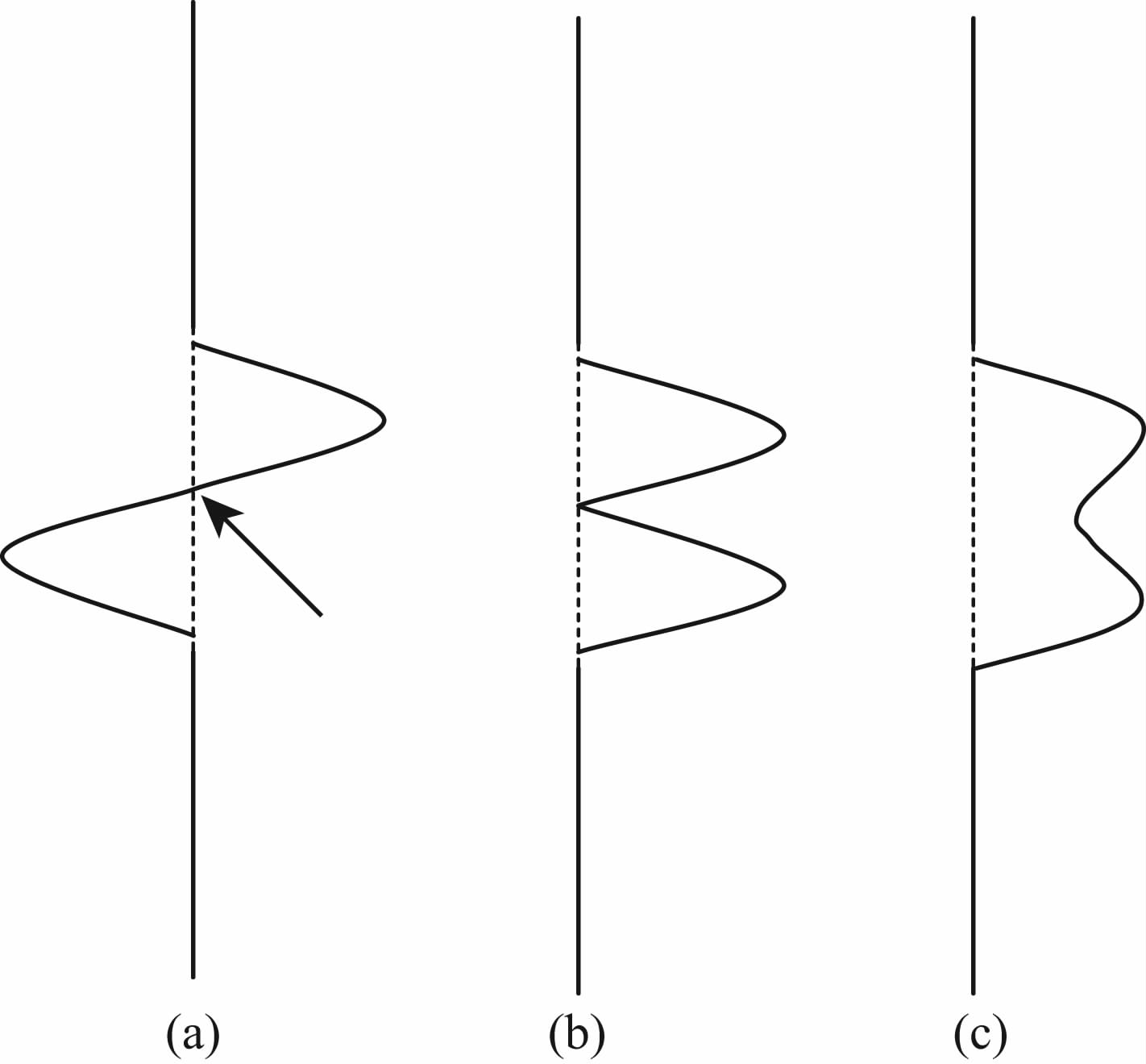
值得提出的是,Zhou等[23-25]对成像域2D 窗内的能量进行研究,而本文对每个成像点分别进行研究,以确定精度更高的自适应滤波器.自适应滤波器对预测的多次波和原始数据的波形变化较为敏感,即波形变化对自适应滤波器的设计有较大影响.假定M(τ,h)如图 3a所示,则图中箭头及其附近位置能量较弱,因此这些区域的M(τ,h)/A(τ,h)小于η,由其所确定的自适应滤波器Fm(τ,h)=0,但实际上该区域附近的多次波能量要完整保留.同理,假定图 3a所示为A(τ,h)为有效波,在箭头所示及其附近能量较弱位置,M(τ,h)/A(τ,h)的值较大,由此确定的Fm(τ,h)=1,会将此处的有效波信号误判断为多次波.为此,有必要对预测的多次波和原始数据进行平滑滤波处理,文中对预测的多次波和原始数据逐道采用7点平滑,并迭代三次,以削弱其高频成分,平滑滤波过程如图 3b和3c所示.从图 3c易知,文中确定比值M(τ,h)/A(τ,h)时,实际利用了Radon域成像的包络,而并非真实的Radon域成像能量,因此利用平滑后的有效波和多次波能量合理确定自适应滤波器,完全消除了由波形变化对自适应滤波器带来的影响.
|
图 3 有效波和多次波能量的平滑滤波示意图 Fig. 3 Smoothing filter for primary and multiple energy |
基于波动方程的反馈迭代法预测表面多次波需要在每个频率分量上进行空间褶积运算,具体表现为每个单频分量上的大尺度的矩阵乘法运算,以常用的测试多次波压制算法优劣的SMAART 模型为例,通常要对1387×1387的方阵做自乘运算,常规的CPU 串行计算成本较高,导致表面多次波预测算法的计算效率低.本文利用GPU 与CPU 联合运算加速多次波预测算法,即利用GPU 执行表面多次波预测中计算密集度高的矩阵乘法运算,预测中其他串行计算由CPU 执行.
本文采用的计算平台为GPU NVIDIA Quadro4000,计算能力为2.0,GPU 主频为0.95 GHz,而另一计算环境为主频2.8 GHz的六核CPU,计算SMAART 模型,CPU 计算矩阵乘法耗时14838s,GPU 运算矩阵乘法耗时199s,计算效率提高约75倍,如图 4所示.

|
图 4 GPU与CPU预测表面多次波计算时间对比 Fig. 4 Calculation time comparison for predicting surface-related multiple between GPU and CPU |
为了验证文中所述联合多次波压制方法的有效性,对单炮数据、SMAART 模型数据以及实际地震数据分别进行了计算.
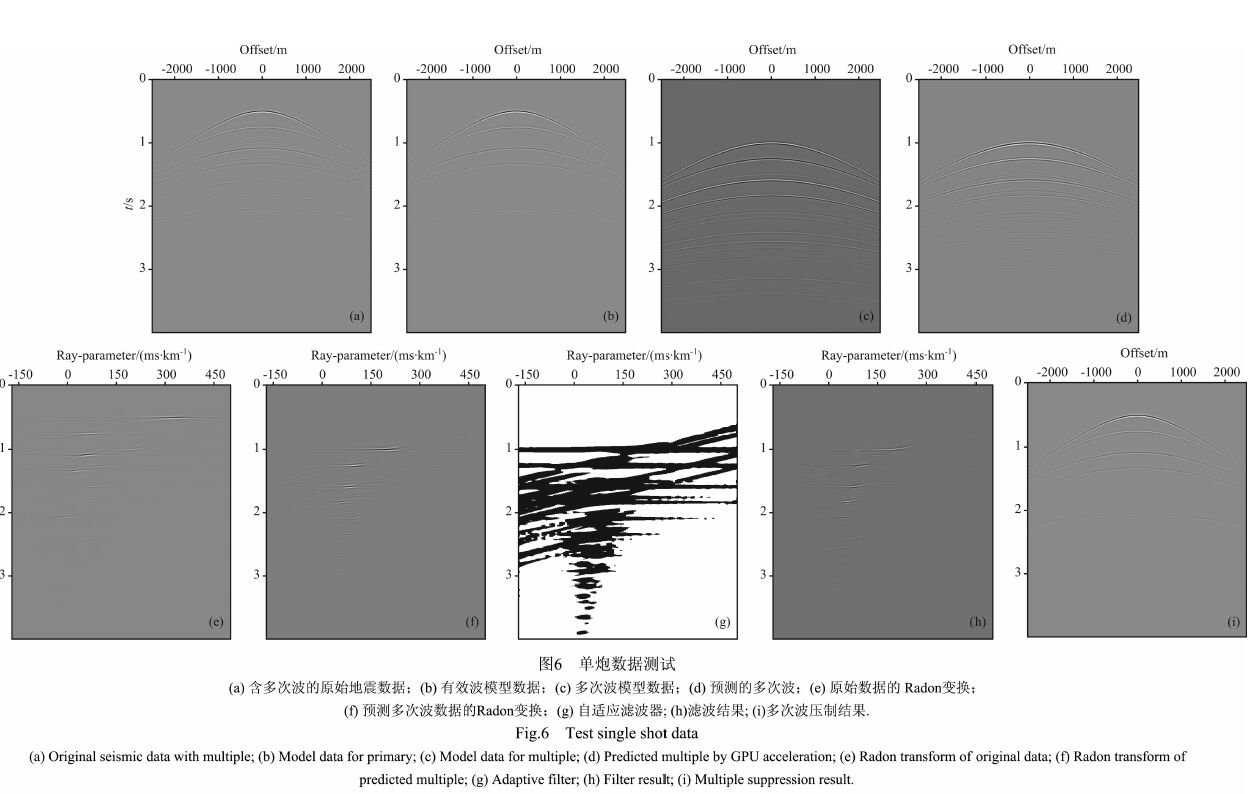
4.1 单炮数据一般而言,双曲Radon 变换是在CMP 道集上计算的,对水平层状介质来说,在CMP 道集和炮集计算可得到同样的多次波压制效果,此处对模拟的单炮记录进行计算.已知水平层状各向同性的一维介质,速度模型如图 5 所示,模型介质最大埋深为3000m,速度变化范围为2000~3600m/s.图 6a为模拟的含表面多次波的炮记录,共200道数据,道间距为25 m,每道的采样点为1000,采样间隔为4ms,采取中间放炮形式,模拟用子波为主频25 Hz的零相位Ricker子波.图 6b 为模拟的只含有效波地震记录,6c为理论的多次波地震记录,基于图 6a含多次波的地震数据,利用反馈迭代法预测的多次波数据,如图 6d所示.将原始地震数据和预测得到的多次波数据用同样校正速度进行部分NMO 后得到的双曲Radon域剖面分别为图 6e和6f所示.分析可知,x-t域相交干扰的同相轴,在双曲Radon域得到很好地分离,参照基于波动方程方法预测的多次波,合理有效地设计自适应滤波器如图 6g 所示,将该滤波器作用于图 6e所示Radon 域含多次波的原始数据,结果如图 6h 所示,将图 6h 进行反Radon变换后,再将其从原始数据中减去,即得到多次波压制结果,如图 6i所示.理论合成的炮记录证明,应用波动方程预测的多次波设计滤波函数,在双曲Radon域可有效实现多次波压制.

|
图 5 速度模型 Fig. 5 Velocity model |
|
图 6 单炮数据测试 (a)含多次波的原始地震数据;(b)有效波模型数据;(c)多次波模型数据;(d)预测的多次波;(e)原始数据的Radon变换;⑴预测多次波数据的Radon变换;(g)自适应滤波器;(h)滤波结果;①多次波压制结果. Fig. 6 Test single shot data (a) Original seismic data with multiple; (b) Model data for primary; (c) Model data for multiple; (d) Predicted multiple by GPU acceleration; (e) Radon transform of original data; (f) Radon transform of predicted multiple; (g) Adaptive filter; (h) Filter result; (i) Multiple suppression result. |
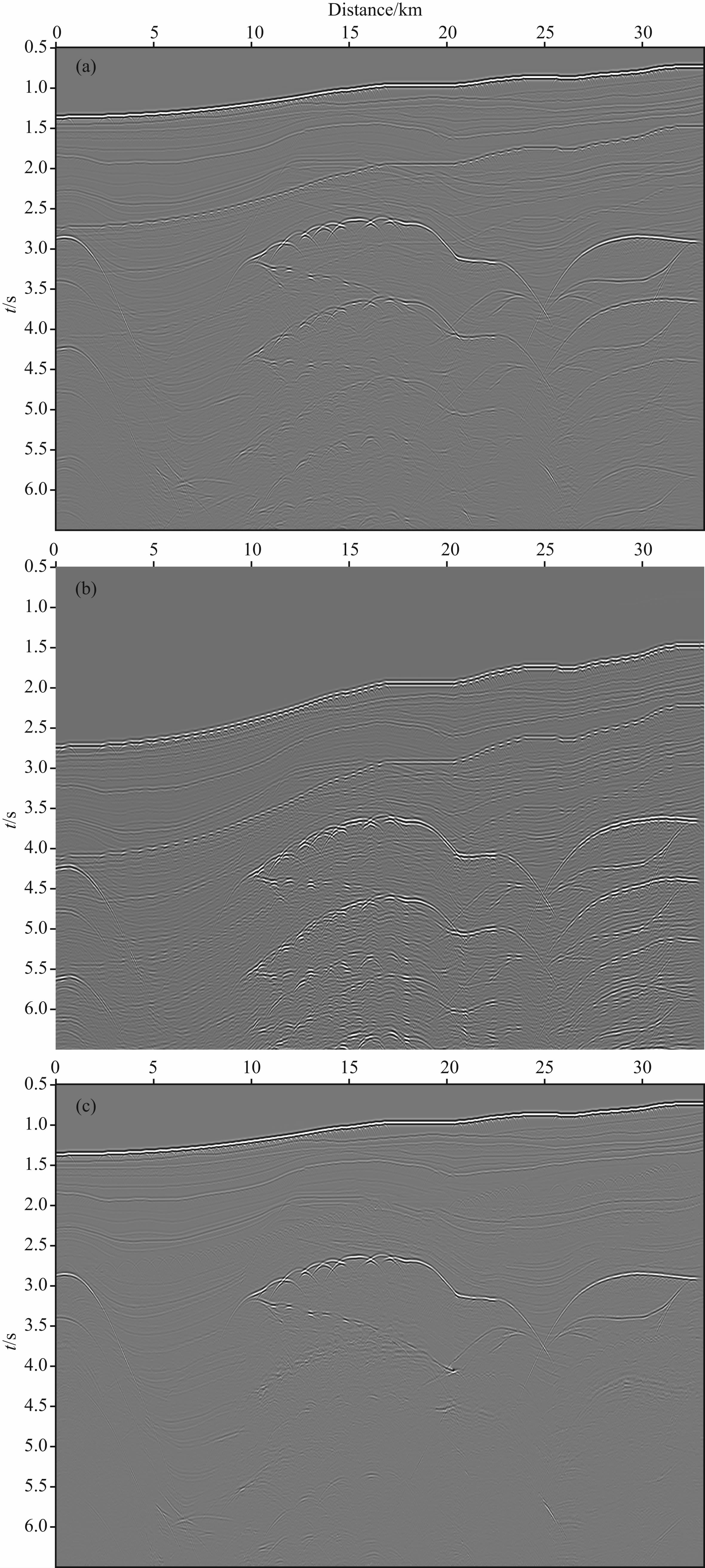
上面对水平层状介质模型进行了算法测试,为进一步验证文中所提出的结合波动方程预测和双曲Radon滤波的多次波压制方法,对复杂的2DSMAART模型合成数据体进行计算.SMAART 模型含有很强的水底表面多次波和三个盐丘顶底界面的表面多次波,是测试多次波压制算法的常用模型[26],其共零偏移距剖面如图 7a所示,利用反馈迭代法粗略预测的表面多次波的共零偏移距剖面如图 7b所示,图 7c为文中所述的结合波动方程预测和双曲Radon滤波方法的多次波压制结果,表明多次波被有效地压制,有效波振幅得到较好保持,复杂SMAART 模型算例表明结合多次波预测和双曲Radon 变换的方法,可有效压制复杂介质的表面多次波.
|
图 7 SMAART模型表面多次波压制效果 (a)原始数据共零偏移距剖面;(b)粗略预测多次波的共零偏移距剖面;(c)多次波压制结果的共零偏移距剖面. Fig. 7 urface-related multiple suppression on theoretical SMAART model (a) Common zero-offset section for raw data; (b)Common zero-offset section for sketchy multiple predication result; (c) Common zero-offset section for multiple suppression result. |
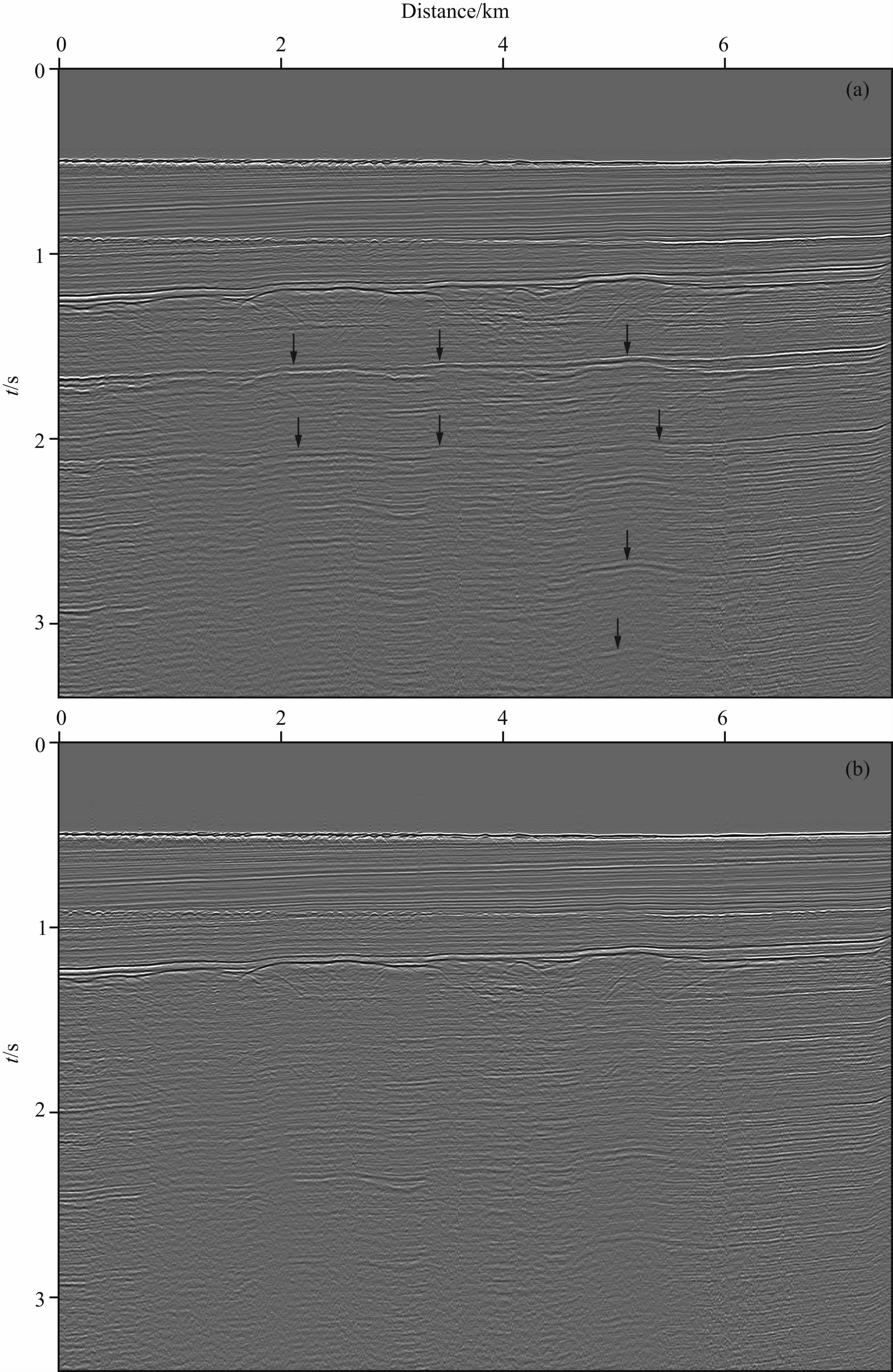
利用文中所提出的多次波压制方法,对中国某探区海洋地震数据进行多次波压制试算,该区水深为300~450 m 左右,浅水勘探导致地震资料中表面多次波较为发育,可见到较为明显的一阶和二阶表面多次波,如图 8a所示,基于波动方程方法对表面多次波粗略预测后,再在双曲Radon域进行滤波压制,图 8a中箭头所示的强能量多次波,尤其是双程走时为1.7s附近的强能量一阶表面多次波,均得到了较好的压制,如图 8b所示.同时对比分析多次波压制前后数据发现,海洋地震数据的有效波信号在地震资料多次波压制预处理中得到了较好的保护,这进一步表明了本文多次波联合压制方法的有效性和实用性.
|
图 8 实际地震数据多次波压制 (a)含多次波数据的共偏移距剖面;(b)压制多次波后的共偏移距剖面. Fig. 8 ultiple suppression on the field data (a) Common offset section with multiple data; (b) Common offset section after suppressing multiple. |
基于波动方程预测和基于滤波的多次波压制方法在地震资料多次波压制领域均发挥着重要的作用,但是两种方法都有瓶颈制约,前者计算成本高,且对数据观测有严格要求,后者则无法处理复杂介质的地震资料,本文将基于波动方程的多次波预测方法和双曲Radon变换滤波方法有效地结合,充分利用两种方法各自的优势,依照基于波动方程方法对多次波的粗略预测结果,对含多次波的地震数据进行双曲Radon变换滤波,避免了常规的基于波动方程方法的自适应匹配相减工作带来的计算压力,同时也改善了常规双曲Radon 变换法无法适应速度逆转等复杂介质的状况.水平层状介质模型、复杂SMAART 模型和实际地震资料的多次波压制试算表明本文算法的有效性和实用性,在计算精度和计算效率上都有一定程度改善.同时,本文也发展了GPU 和CPU 协同并行计算加速地震数据多次波压制算法,从硬件层面上进一步提高了计算效率
| [1] | Ryu J V. Decomposition (DECOM) approach applied to wave field analysis with seismic reflection records. Geophysics , 1982, 47(6): 869-883. DOI:10.1190/1.1441354 |
| [2] | Hampson D. Inverse velocity stacking and multiple elimination. Journal of the Canadian Society of Exploration Geophysicists , 1986, 22(1): 44-55. |
| [3] | Zhou B Z, Greenhalgh S. Linear and parabolic τ-p transform revisited. Geophysics , 1994, 59(7): 1133-1149. DOI:10.1190/1.1443669 |
| [4] | Landa E, Belfer I, Keydar S. Multiple attenuation in the parabolic τ-p domain using wavefront characters of multiple generating primaries. Geophysics , 1999, 64(7): 1806-1815. |
| [5] | Wang Y H. Multiple attenuation: coping with the spatial truncation effect in the Radon transform domain. Geophysical Prospecting , 2003, 51(1): 75-87. DOI:10.1046/j.1365-2478.2003.00355.x |
| [6] | Yilmaz O. Velocity-stack processing. Geophysical Prospecting , 1989, 37(4): 357-382. DOI:10.1111/gpr.1989.37.issue-4 |
| [7] | Foster D J, Mosher C C. Suppression of multiple reflections using the Radon transform. Geophysics , 1992, 57(3): 386-395. DOI:10.1190/1.1443253 |
| [8] | Wiggins J W. Attenuation of complex water-bottom multiples by wave-equation-based prediction and subtraction. Geophysics , 1988, 53(12): 1527-1539. DOI:10.1190/1.1442434 |
| [9] | Verschuur D J, Berkhout A J, Wapenarr P A. Adaptive surface-related multiple elimination. Geophysics , 1992, 57(9): 1166-1177. DOI:10.1190/1.1443330 |
| [10] | Weglein A B, Gasparotto F A, Carvalho P M, et al. An inverse-scattering series method for attenuating multiples in seismic reflection data. Geophysics , 1997, 62(6): 1975-1989. DOI:10.1190/1.1444298 |
| [11] | Zhou B Z, Greenhalgh S. Multiple suppression by 2D filtering in the parabolic τ-p domain: a wave-equation-based method. Geophysical Prospecting , 1996, 44(3): 375-401. DOI:10.1111/gpr.1996.44.issue-3 |
| [12] | Zhang J F, Wang W H. Multiple attenuation: an approach by incorporating multiple prediction with Radon transform. Journal of Seismic Exploration , 2006, 15: 81-99. |
| [13] | Zhang J H, Wang S Q, Yao Z X. Accelerating 3D Fourier migration with graphics processing units. Geophysics , 2009, 74(6): WCA129-WCA139. DOI:10.1190/1.3223186 |
| [14] | Clapp R G, Fu H H, Lindtjorn O. Selecting the right hardware for reverse time migration. The Leading Edge , 2010, 29(1): 48-58. |
| [15] | 李博, 刘国峰, 刘洪. 地震叠前时间偏移的一种图形处理器提速实现方法. 地球物理学报 , 2009, 52(1): 245–252. Li B, Liu G F, Liu H. A method of using GPU to accelerate seismic pre-stack time migration. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 245-252. |
| [16] | 刘国峰, 刘洪, 李博, 等. 山地地震资料叠前时间偏移方法及其GPU实现. 地球物理学报 , 2009, 52(12): 3101–3108. Liu G F, Liu H, Li B, et al. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation. Chinese J. Geophys. (in Chinese) , 2009, 52(12): 3101-3108. |
| [17] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implemenation. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1725-1733. |
| [18] | Berkhout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion, partⅠ: Theoretical considerations. Geophysics , 1997, 62(5): 1586-1595. DOI:10.1190/1.1444261 |
| [19] | Verschuur D J, Berkhout A J. Estimation of multiple scattering by iterative inversion, partⅡ: Practical aspects and examples. Geophysics , 1997, 62(5): 1596-1611. DOI:10.1190/1.1444262 |
| [20] | Berkhout A J. Seismic Migration: Imaging of Acoustic Energy by Wave Field Extrapolation. New York: Elsevier Science Publishing Company, Inc, 1982 . |
| [21] | Berkhout A J, Verschuur D J. Removal of internal multiples with the common-focus-point (CFP) approach: Part 1-Explanation of the theory. Geophysics , 2005, 70(3): V45-V60. DOI:10.1190/1.1925753 |
| [22] | Schonewille M A, Duijndam, A J W. Parabolic Radon transform, sampling and efficiency. Geophysics , 2001, 66(2): 667-678. DOI:10.1190/1.1444957 |
| [23] | Zhou B, Greenhalgh S A. Multiple suppression by a wave-equation extrapolation method. Exploration Geophysics , 1991, 22(2): 481-484. DOI:10.1071/EG991481 |
| [24] | Zhou B, Greenhalgh S A. Dereverberation of seismic data by 2-D non-linear filter: A wave-equation-based approach. 61th Ann. Internat. Mtg., Soc. of Expl. Geophys., Expanded Abstracts , 1991: 1315-1318. |
| [25] | Zhou B, Greenhalgh S A. Wave-equation extrapolation-based multiple attenuation: 2D filter in the f-k domain. Geophysics , 1994, 59(9): 1377-1391. DOI:10.1190/1.1443696 |
| [26] | Huo S D, Wang Y H. Improving adaptive subtraction in seismic multiple attenuation. Geophysics , 2009, 74(4): V59-V67. DOI:10.1190/1.3122408 |
 2012, Vol. 55
2012, Vol. 55

