2. 国家海洋环境预报中心海洋灾害预报技术研究国家海洋局重点实验室, 北京 100081
2. Key Laboratory of Research on Marine Hazards Forecasting, National Marine Environmental Forecasting Center, State Oceanic Administration, Beijing 100081, China
海底地震是诱发海啸的主要原因,所以海啸通常也被称为“地震海啸",据不完全统计全球90%左右的海啸事件是由海底地震引发[1],海啸的能量大约为1014 ~1017J,一般为引发海啸的地震能量的0.005%~10%[2].海底地震引发地壳大规模的垂向错动(“倾滑型")会使变形区上覆盖的水体以波动形式向外传播,形成海啸.地震海啸在深水洋区传播时波长与震源的长轴相当,可达数百海里,周期10~120min,波速高达700~900km/h;海啸进入浅水区,水深沿着波向线逐渐变浅、波能传播速度减慢,巨大水体的动能在垂直和水平方向上都将变得聚集,表现为波高陡增,流速变急,会对沿岸海湾、河口地区人民的生命、财产带来巨大灾害.
自2004年印度洋大海啸后,全世界对海啸灾害的关注度达到前所未有的高度;同时这次巨灾也促使世界很多滨海国家开始加大对海啸物理机制研究和海啸预警系统建设的投入,也进一步推动了各国在应对海啸灾害方面的交流与合作.虽然海啸事件特别是大海啸事件属于低频灾害,但它给人类带来的损失和伤痛时刻提醒人类:应对海啸潜在的威胁必须保持清醒认识,加强相关研究.近年来,各国也相继建立了各自的海啸预警系统,初步具备了应对越洋海啸和区域海啸[3]的能力,但对局地海啸[3]的应对能力仍存在较大不足.研究表明:我国沿海地区特别是东海、南海以及台湾地区主要面临琉球海沟和马尼拉海沟潜在的地震海啸的威胁[4-7],也会受到越洋海啸的威胁[8-9].
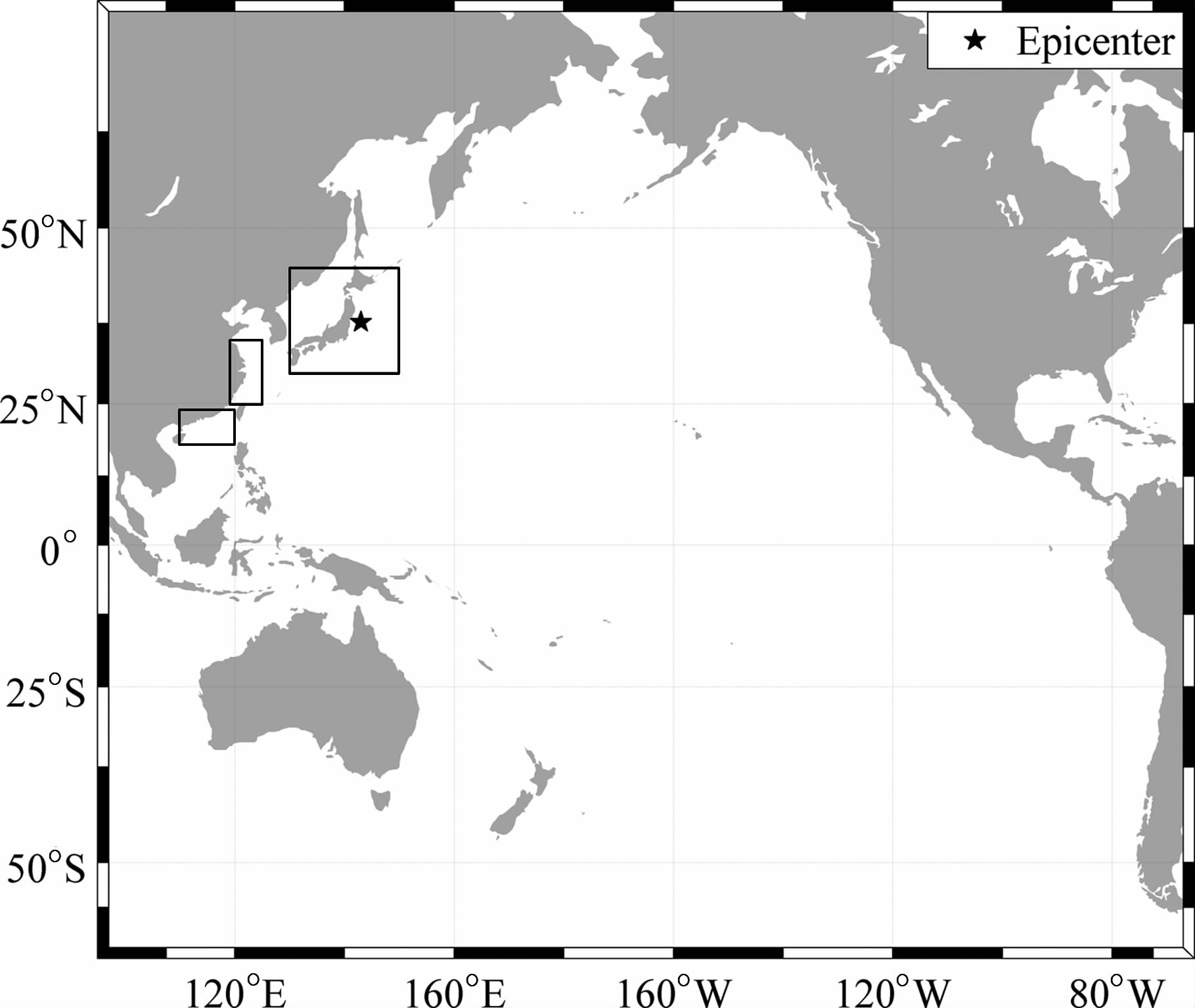
2011年3月11日13时46分(北京时间),在日本本州东北部海域(38.3°N,142.4°E)发生Mw9.0级特大地震,震源深度20km(图 1).这是日本近海发生最强列的一次大地震,并引发了太平洋范围的海啸.地震和海啸造成的福岛第一核电站核泄漏事故等级达到最高7级;截止2011年4月30日,地震和海啸共造成14704人死亡,10969人失踪,直接经济损失3100多亿美元,造成日本战后60年来最为“严重"的伤亡.虽然日本在防震技术、海啸研究及海啸预警技术等方面一直处于世界领先水平,但海啸仍然对该国造成了巨大灾害;其中最主要的一个原因:沿海经济规划与重大工程海啸评估工作中低估了潜在的地震海啸源和最大海啸波.此次海啸除了对近场的日本东北部沿岸地区造成了巨大灾难,太平洋东岸的部分国家和地区也监测到1.5~2.0m 的海啸波,并对这一区域造成了一定程度的影响.中日两国隔海相邻,此次事件虽未对我国造成灾害性影响,但日本东北近岸潜在的地震海啸威胁却不能忽视;本文通过数值模拟的方法再现了此次地震海啸越洋传播情景,海啸主轴能量的空间分布特征;重点模拟分析了海啸波在日本近岸及中国东南沿海的传播特性,定量阐述了日本东北部近海潜在地震海啸对中国的风险估计.
|
图 1 模拟区域及网格设置 (★为震中位置,矩形框为近岸加密区域分辨率1) Fig. 1 Nested grid setup of the simulation domain, with the star and rectangle indicating the epicenter and refined regions for 1 resolution |
地震海啸模型是探索海啸生成机制、评估海啸灾害和建立实时海啸预警系统的重要工具和技术手段.根据海啸波的物理特性,海啸数值模型通常由:计算海啸初始位移场的断层模型(Generation);基于非线性浅水方程或类Boussinesq方程,计算海啸波传播的传播模型(Propagation);考虑沿岸地形、地物、采用动态移动边界技术来实现海啸爬高及与海岸相互作用的淹没模型(Inundation)[8, 10-12].
1) 如无特殊说明,本文后续篇幅中所提及的海啸均为地震海啸.
2.1 海啸源模型(断层模型)海啸源模型是海啸数值模型研究的基础,它的适用性直接关系到海啸波的传播及海啸与海岸的相互作用.断层模型通过利用海床位移量来估算地震引起的初始水面高度,为海啸数值模型计算提供初始条件.目前,Mansinha & Smylie[13]以及Okada[14]基于弹性错移理论发展的两套断层模型被广泛应用,大量的研究和应用实例表明此类模型对大部分海啸源计算具有较好的适用性[8, 15-16].
2.2 海啸传播数值模型2)海啸在大洋和大陆架传播时,水质点的垂直加速度与重力加速度相比可看做一小量,这时水质点的垂直运动对压力分布的影响可以忽略,所以不考虑频散项的非线性浅水方程通常被用来作为海啸的传播模型.在近岸此类模型对海啸波到达时间和海啸波首波波高均能给出较精确的模拟结果,但对首波后的系列波形的预报却有较大的偏差.Imamura F和Liu P.L 认同频散作用的重要性,认为模型物理频散效应可以通过选择适当的时间和空间步长,用差分方程的数值频散代替微分方程的物理频散(physicaldispersion)[17, 18]既保持了海啸传播过程的物理本质,又降低了求解物理频散项的机时代价.
2) 由于基础地理信息数据所限,本文研究不涉及海啸上岸部分.
本文选用美国Cornell 大学开发COMCOT(Cornell Multi-grid Coupled Tsunami Model)海啸模型作为本文的研究模型.该模型采用基于多层网格嵌套的有限差分法.针对海啸波不同物理特性,模式可以灵活配置所需坐标系(直角/球面)和控制方程类型(线性/非线性)[19-21].本次模拟采用两层嵌套网格(图 1).
本文中深水模块采用球坐标系下线性方程:
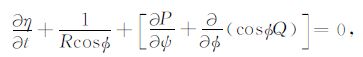
|
(1) |
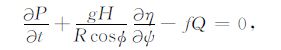
|
(2) |

|
(3) |
浅水模块采用球坐标系下非线性方程:

|
(4) |
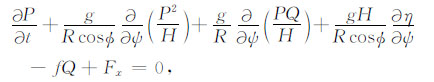
|
(5) |
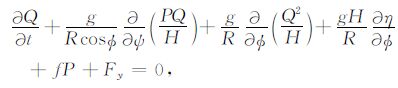
|
(6) |
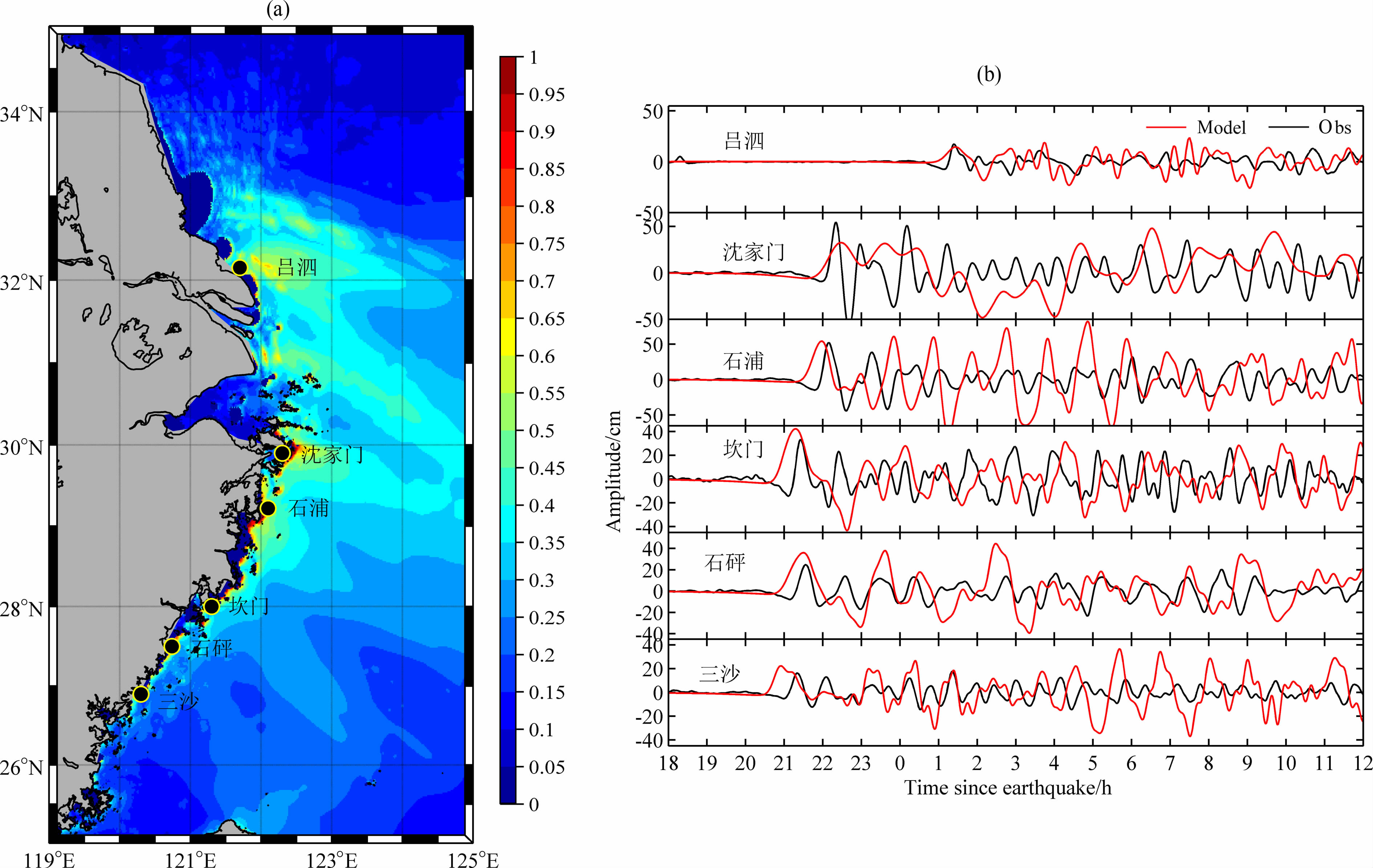
式中η 为相对于平均海平面的自由表面位移;$\phi $ 为纬度;ψ 为经度;R为地球半径;h为净水深,H=h+η为总水深;P为沿经度单位宽度的通量;Q为沿纬度单位宽度的通量;f为科氏力系数;g为重力加速度.Fx,Fy分别为经度和纬度方向的底摩擦力.
模式采用交错显示蛙跳格式求解长波方程.波高η 及流通量P,Q在时间和空间上都是交错进行,波高及水深定义在网格中心,体积通量定义在网格边的中点,因此波高及体积通量的计算是在不同的时间步长上,利用物理量在空间上的交错方式来计算,可以增加数值稳定性.采用蛙跳格式可以利用差分方程的数值频散近似代替波在浅水中传播所带来的物理频散.
3 日本海啸越洋传播的数值分析 3.1 震源参数的选取及海啸初始场计算地震海啸的波长、波高以及能量大小不仅与震级有关,与地震断层的几何特性、震源深度也有很大关系,对于近场海啸影响更为显著;因此,海啸源模型的精度很大程度上决定了海啸波模拟的精度.目前地震海啸初始场的确定均是基于1969年Aida的假设[22]:“由于地震地壳破裂时间远小于海啸波的周期,所以主震发生时刻即为海啸发生的初始时刻;地壳破裂后的形状为海面的初始位移."本文引用GCMT 的震源机制解作为震源参数,断层长度(L),宽度(W)根据相关经验公式计算[8].本文采用Okada的理论模型进行海啸初始场的计算.计算结果见图 2.从断层模型计算的结果可知,最大海面抬升为+8.86m,最大下沉位移量为-4.99m.

|
图 2 海啸初始位移场和沿图中直线方向的剖面曲线 Fig. 2 Tsunami initial conditions and profile of seafloor displacement along arrow line |
本文的模拟采用两层嵌套网格(图 1),基础地理信息数据为NGDC 的ETOPO5 和ETOPO1 海底地形资料(http://www.ngdc.noaa.gov/mgg/gdas/gd_designagrid.html),海底变形采用前节中的计算结果,模拟时间为发震后24h.采用的模拟方案见表 2.
|
|
表 2 模拟方案 Table 2 Modelling scheme |
震后约30min,位于日本近岸的验潮站监测表明强震引发的第一波海啸已经袭击了震中附近的Ofunato、Miyako港,记录到的海啸波幅分别为8.0m、8.5m[23](见图 3a、图 3b);随后海啸袭击了仙台机场和福岛第一核电站.大海啸肆虐日本沿岸后,迅速抵达太平洋中部岛国及沿岸国家.巴布亚新几内亚北部岛屿监测到1.04 m 的海啸波,波浪衰减因子为0.1224,海啸到达夏威夷群岛时的最大海啸波为1.27m,美国Crescentcity验潮站监测到最大1.88m海啸波,波浪衰减因子为0.2212;在南美洲智利沿岸测得最大1.5m 海啸波,波浪衰减因子为0.1765.此次海啸波穿越整个太平洋所需时间23个小时(见图 3a、图 3b),平均传播速度达到700km/h.
|
图 3 (a)日本地震海啸能量越洋传播及海啸先导波到达时间(★为震中位置)(b)太平洋区域海啸高度观测及传播时间(据文献 [24]) Fig. 3 (a) Energy propagation of the 2011 Japan tsunami calculated from COMCOT and arrival time contours of the leading wave (2-hours contour interval & epicenter location marked by black star) ; (b) Observed water heights and computed tsunami travel times (after ref. [24]) |
从数值模拟结果(图 3a)来看此次海啸波能主传播方向为东南方向,另外北东北及南东南两个方向为海啸波能的次传播方向.这与太平洋区域实测海啸高度(图 3b)的分布特征相吻合.从图 3a分析知:当海岭的走向不偏离海啸传播的方向时,洋中脊和环绕大陆的陆架区是海啸波传播的天然波导管和海洋地震波能量聚集器,远离海啸源决定波能量流方向的唯一因素就是海底地形.大洋中脊对引导波能分布(主传播方向、次传播方向)起着重要的作用,而主要的能量流也都在主要的海岭处聚集,并呈现带状分布.
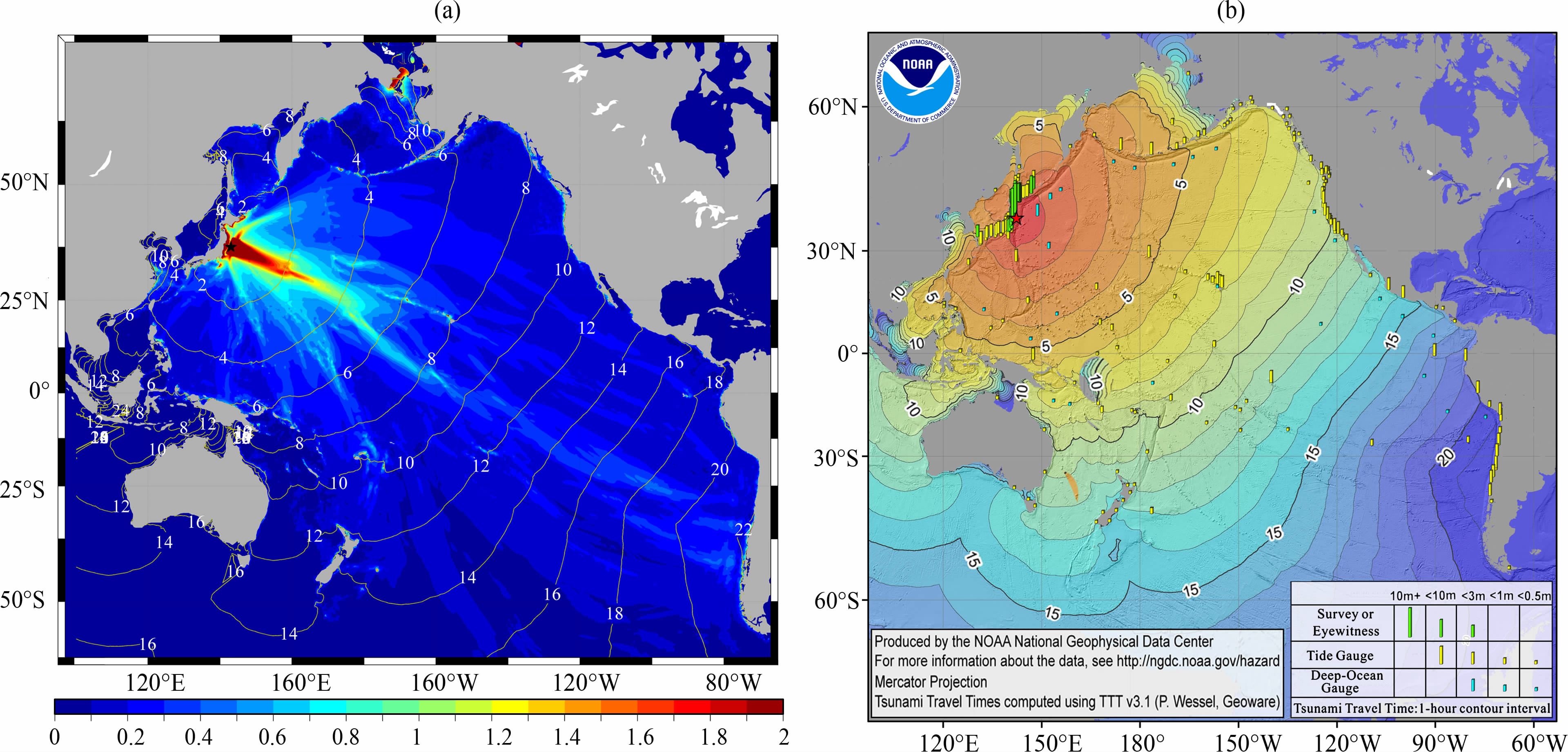
3.3 海啸近场传播特征数值模拟地震发生1小时后,观测资料表明地震产生的海啸已经袭击了日本本州东北大部分沿海城市.日本沿岸Miyako、Ofunato 两个验潮站分别监测到8.0m+的海啸波,随后两个站位的验潮仪被海啸摧毁,据图 3b 中的数据显示以及本文的模拟结果(图 4)来看,上述两处的海啸波应该在9~10 m.图 4中可以清楚的看出:无论是深海浮标站、还是近岸的验潮站,本文的模拟结果无论是振幅还是海啸波位相均与实测数据吻合良好,说明所用模型对近场海啸的模拟精度是非常可信的;通过波谱分析可知海啸波主周期为30~50 min,根据当地的水深可以推算海啸波到达近岸时波长可以达到20km+.从模拟的结果来看,仙台机场和福岛第一核电站处的海啸波达到10m+,最大平均流速超过9m/s.在这样的“巨浪"面前世界第一防波堤瞬间被摧毁.由此我们不难想象位于海啸能量传播主轴方向上的仙台机场和福岛第一核电站两地为何受到如此重创.
|
图 4 海啸能量近场传播特征(a)及典型站点海啸时间序列数值模拟分析(b) Fig. 4 Characteristic of tsunami energy propagating in near field (a) and comparison of numerical simulation result (b) with tidal gages measurements at typical sites |
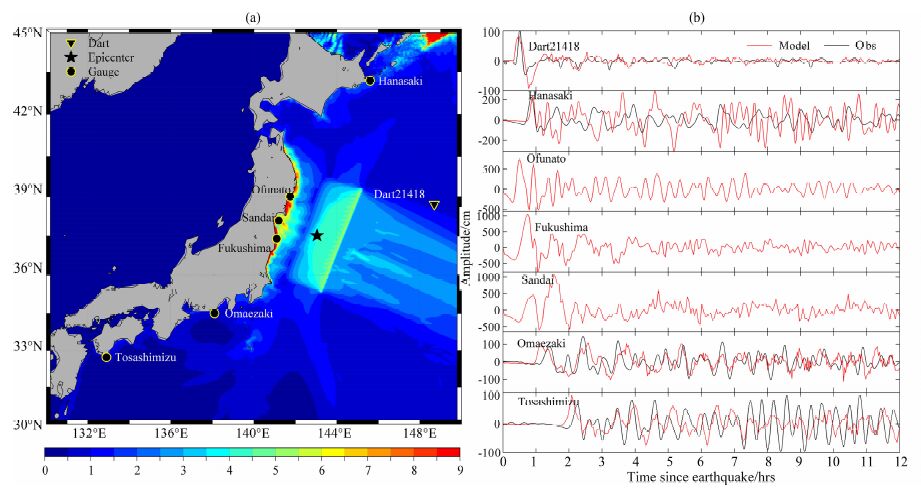
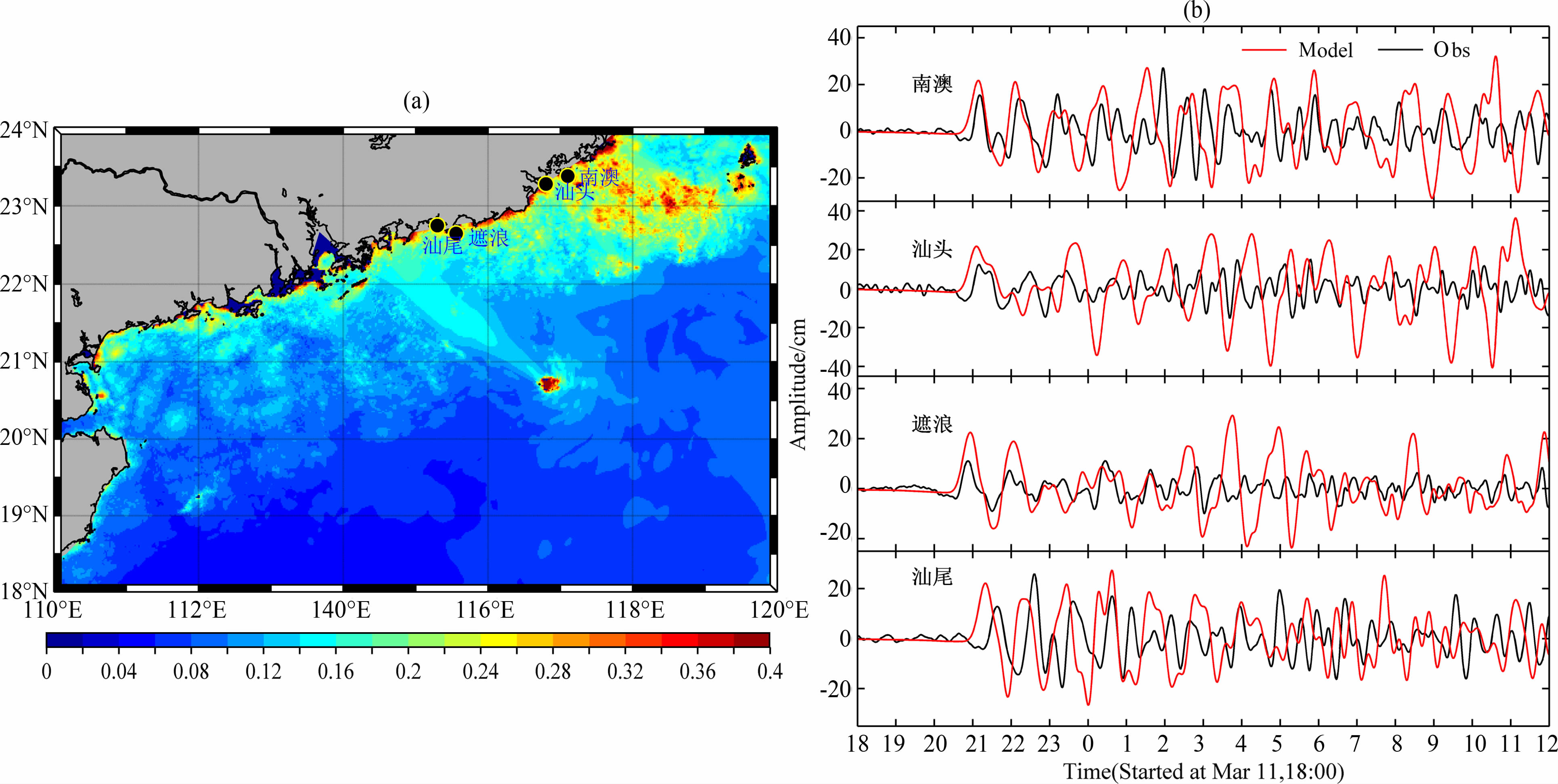
海啸波于11日17时40分开始影响我国台湾东部沿海,台湾花莲、成功、苏澳、基隆、龙洞等地监测到5~20cm 的海啸波振幅.11 日晚间20 时20分起,我国浙江、福建及广东沿岸陆续受到海啸波影响(图 5、图 6),浙江沈家门、大陈、坎门、石坪、石浦、健跳、福建东山及广东汕头、汕尾等潮位站先后监测到振幅为10~55cm 的海啸波,其中浙江石浦和沈家门潮位站监测到的海啸波最大,分别为55cm 和52cm,波高衰减因子为0.0647.也是建国以来我国仪测最大海啸波记录.震后20 min,国家海洋预报台综合地震信息和海啸数值预报结果对预计受影响沿海地区发布了我国首个海啸“蓝色"警报,监测数据证明此次海啸预警是非常成功的.从模拟结果来看,我国的江苏南部至福建北部(图 5)、闽南至珠江口沿岸(图 6)为主要受影响区域,其中,浙江中部至长江口一带沿海为严重影响区域,近岸海啸达到1m+,根据工程推算,1 m 以上的海啸波足以对海上和岸边的固定建筑物构成危害.图 5中我们还可以发现,苏北辐射沙洲群对海啸波的传播起到了非常好的抑制作用,扮演了一个天然消波器的角色.
|
图 5 福建北部至江苏南部一带沿海海啸能量分布(a)及典型站点海啸时间序列数值模拟分析(b) Fig. 5 Tsunami energy distribution around coastal region from northern Fujian to southern Jiangsu (a) and comparison of numerical simulation result (b) with tidal gages measurements at typical sites |
|
图 6 闽南至粵东沿海海啸能量分布(a)及典型站点海啸时间序列数值模拟分析(b) Fig. 6 Tsunami energy distribution around coastal region from eastern Guangdong to southern Fujian (a) and comparison of numerical simulation result (b) with tidal gages measurements at typical sites |
模型计算的海啸先导波波幅和到达时间均与观测数据吻合良好,但对各验潮站海啸波的初始扰动以及后续波动的模拟相对近场传播结果(图 4)仍存在一些差距.可能原因如3.1节所述,远离海啸源决定波能量的唯一因素就是海底地形,受海底地形精度所限,加之微地形变化对海啸波的影响显著[25];海啸源模型的精度对模拟的结果也有一定的影响.
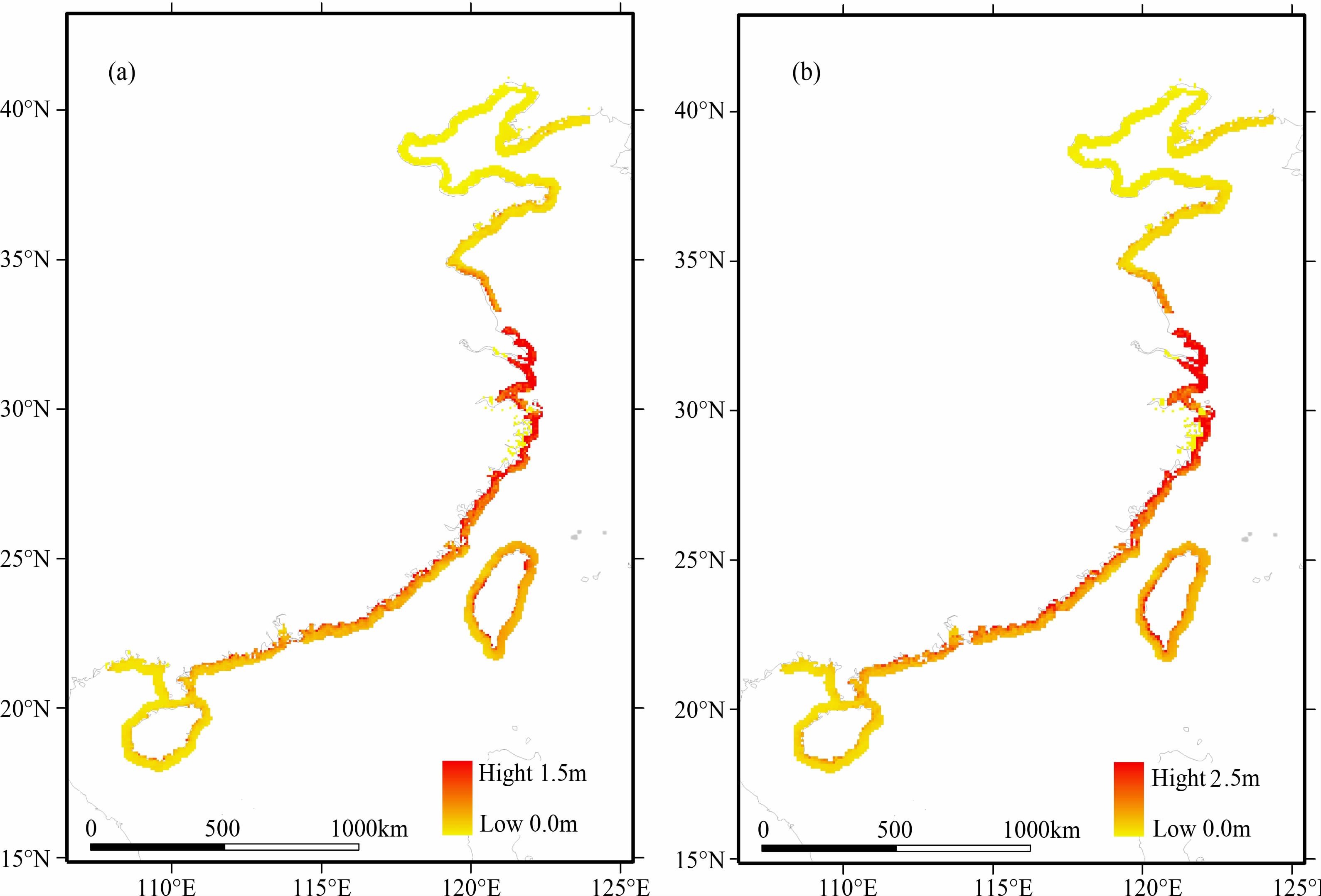
4.2 海啸对中国沿海的影响分析中日两国隔海相邻,仪测最大海啸波幅却仅50多厘米.主要原因:本次引发海啸的海底断层呈东北偏北走向,海底断层断裂造成的海啸的能量分布与断层走向垂直,呈西北—东南方向分布.我国沿海不处在海啸能量传播的主要分布方向上,加之琉球岛链的阻挡和大陆架的能量衰减作用故未对我国造成灾害性影响.尽管如此,我国面临的日本东北近岸潜在的地震海啸威胁却不能忽视(图 7),左图为此次海啸对中国沿岸的影响分布,采用格林函数订正数值模拟结果[8],杭州湾至长江口一带沿海的海啸波达到1.5 m.假定在相同位置处Mw =9.3 级地震(走向角、倾角、滑动角取自表 1)引发海啸,到达中国沿海后最大波高可达2.5m(图 7b).
|
|
表 1 2011年3月11日本海啸震源参数 Table 1 Fault parameters of Japan tsunami (11/3/2011) |
|
图 7 日本东北海啸对中国危险性分布((a) Mw = 9.0,(b) Mw = 9.3) Fig. 7 Risk distribution on China coasts due to Tohoku Tsunami ((a) Mw = 9. 0,b) Mw = 9. 3) |
日本东北特大地震海啸除给近场的日本造成了严重灾难外,在海啸波越洋传播过程中,也给其他沿岸国家造成了一定的影响,但未形成明显的破坏和灾难.这主要归功于太平洋沿岸国家初步具备了应对远源海啸的能力及各国海啸预警系统的成功预警;但也清醒的认识到:面对近场海啸,具有全球领先水平的日本海啸预警和防范体系仍存在诸多不足;完善海啸监测及预警系统,开展海啸灾害风险评估及区划工作,势在必行.
利用海啸数值模型模拟分析了海啸波的越洋传播及在日本近海和我国东南沿海的传播特征;模拟结果与观测数据拟合良好.通过对数值模拟结果的分析获得了日本海啸能量分布特征、得出仙台机场及福岛第一核电站处海啸波剖面,分析了近场海啸传播特征及致灾原因;海啸波传播到中国沿海,波浪衰减因子为0.0647.我国的江苏南部至福建北部、闽南至珠江口沿岸为主要受影响区域,其中,浙江中部至长江口一带沿海为严重影响区域,近岸海啸达到1m+.研究发现:苏北辐射沙洲群对海啸波的传播起到了非常好的抑制作用.通过数值模拟定量分析了日本东北海啸(Mw=9.0,9.3)对中国沿海的危险性分布,得出日本东北海啸对中国沿海具有造成灾害的风险,应给予高度重视.
致谢感谢两位评审专家对本文提出的宝贵意见.
| [1] | 王培涛, 于福江, 赵联大, 等. 越洋海啸的数值模拟及其对我国的影响分析. 海洋学报 , 2012, 34(2): 39–47. Wang P T, Yu F J, Zhao L D, et al. Numerical simulation of trans-oceanics tsunami and its impact analysis on Chinese coasts. Acta Oceanologica Sinica (in Chinese) , 2012, 34(2): 39-47. |
| [2] | Alexander B. R, Rogerio N. C. Richard E.T. Energy decay of the 2004 Sumatra Tsunami in the World ocean.. Pure and Applied Geophysic , 2011, 168: 1919-1950. DOI:10.1007/s00024-011-0279-1 |
| [3] | UNESCO-IOC. Tsunami Glossary.IOC information document O.1221.Paris,UNESCO,2006. |
| [4] | 温燕玲, 朱元清, 宋治平, 等. 冲绳海槽地震海啸的数值试验研究. 地球物理学进展 , 2008, 23(2): 326–332. Wen Y L, Zhu Y Q, Song Z P, et al. Numerical experiment of earthquake tsunami in Okinawa Trough. Progress In Geophysics (in Chinese) , 2008, 23(2): 326-332. |
| [5] | 温燕林, 朱元清, 宋治平, 等. 东海海域潜在地震海啸的数值模拟研究. 地震学报 , 2008, 30(5): 456–463. Wen Y L, Zhu Y Q, Song Z P, et al. Preliminary numerical simulation of potential earthquake-induced tsunami in East China Sea. Acta Seismologica Sinica (in Chinese) , 2008, 30(5): 456-463. |
| [6] | 潘文亮, 王盛安, 蔡树群. 南海潜在海啸灾害的数值模拟. 热带海洋学报 , 2009, 28(6): 7–14. Pan W L, Wang S A, Cai S Q. Simulation of potential tsunami hazards in the South China Sea. Journal of Tropical Oceanography (in Chinese) , 2009, 28(6): 7-14. |
| [7] | Liu Y C, SantoS Angela, Wang S M, et al. Tsunami hazards along Chinese coast from potential earthquakes in South China Sea. Physics of the earth and planetary interiors , 2007, 163: 233-244. DOI:10.1016/j.pepi.2007.02.012 |
| [8] | 于福江, 王培涛, 赵联大, 等. 2010年智利地震海啸数值模拟及其对我国沿海的影响分析. 地球物理学报 , 2011, 54(4): 918–925. Yu F J, Wang P T, Zhao L D, et al. Numerical simulation of 2010 Chile tsunami and its impact on.Chinese coasts. Chinese J. Geophys. (in Chinese) , 2011, 54(4): 918-925. |
| [9] | 于福江, 原野, 赵联大, 等. 010年 2 月 27日智利 8.8 级地震海啸对我国影响分析. 科学通报 , 2011, 56(1): 1–8. Yu F J, Yuan Y, Zhao L D, et al. Evaluation of potential hazards from teletsunami in China: Tidal observations of a teletsunami generated by the Chile 8.8 Mw earthquake. Chinese Science Bulletin. (in Chinese) , 2011, 56(1): 1-8. |
| [10] | 姚远, 蔡树群, 王盛安. 海啸波数值模拟的研究现状. 海洋科学进展 , 2007, 25(4): 487–494. Yao Y, Cai S Q, Wang S A. Present Status of Study on Numerical Simulation of Tsunami Wave. Advances in Marine Science(in Chinese (in Chinese) , 2007, 25(4): 487-494. |
| [11] | 李燕林, 毛献忠. 深圳海域潮汐海啸波耦合数值研究. 海洋学报 , 2012, 34(3): 11–18. Li Y L, Mao X Z. Numerical study for tide-tsunami coupling model in Shenzhen Waters. Acta Oceanologica Sinica (in Chinese) , 2012, 34(3): 11-18. |
| [12] | 张超凡, 石耀霖. 海啸灾害的数值模拟研究. 中国科学院研究生院学报 , 2008, 25(3): 289–296. Zhang C F, Shi Y L. Numerical simulation research on tsunami hazards. Journal of the Graduate School of the Chinese Academy of Sciences (in Chinese) , 2008, 25(3): 289-296. |
| [13] | Mansinha L, Smylie D E. The displacement fields of inclined faults. Bulletin of the Seismological Society of America , 1971, 61(5): 1433-1440. |
| [14] | OkadaY. Surface deformation due to shear and tensile faults in a half-space. Bulletin of the Seismological Society of America , 1985, 75(4). |
| [15] | Wu T R, Chen P F, Wu T T, et al. Numerical study on Tsunamis excited by 2006 Pingtung earthquake doublet. Terr. Atmos.Ocean.Sci. , 2008, 19(6): 705-715. |
| [16] | Dao M H, Pavel T, Chan E S, et al. Tsunami propagation scenarios in the South China Sea. Journal of Asian Earth Sciences , 2009, 36: 67-73. DOI:10.1016/j.jseaes.2008.09.009 |
| [17] | Imamura F, Goto C. Truncation error in numerical tsunami simulation by the finite difference method. Coastal Engineering (in Japanese) , 1988, JSCE31: 245-263. |
| [18] | Liu P L, Cho Y S, Yoon S B, et al. Numerical simulations of the 1960 Chilean tsunami propagation and inundation at Hilo, Hawaii//In Tsunami Progress in Prediction, Disaster Prevention and Warning, edited by Y. Tsuchiya and N. Shut o, Kluwer Academic Publishers, Netherlands, 1995: 99-115. |
| [19] | Liu P L-F, Wang X M, Andrew J S. Tsunami hazard and early warning system in South China Sea. Journal of Asian Earth Sciences , 2009, 36: 2-12. DOI:10.1016/j.jseaes.2008.12.010 |
| [20] | Wang X M, Liu P L-F. An analysis of 2004 sumatra earthquake fault plane mechanisms and indian ocean tsunami. J. Hydraulic Res. , 2006, 44(2): 147-154. |
| [21] | Wang X M and Liu P L-F. Numerical simulations of the 2004 Indian Ocean tsunamis coastal effects. Journal of Earthquake and Tsunami , 2007, 1(3): 273-297. DOI:10.1142/S179343110700016X |
| [22] | Aida I. Numerical experiments for the tsunami propagation—the 1954 Niigata tsunami and 1968 Tokachi-oki tsunami. Bulletin of the Earthquake Research Institute , 1969, 47: 498-512. |
| [23] | Nobuhito Mori, Tomoyuki Takahashi, Tomohiro Yasuda, et al. Survey of 2011 Tohoku earthquake tsunami inundation and run-up. Geophysical Research Letters , 2011, 38: L00G141-6)... |
| [24] | Charles S. McCreery. Pacific Tsunami Warning Center Intersessional Activities for the PTWS. The 24th conference of ICG/PTWS. Beijing, China. in 2011. |
| [25] | Harold O M, Frank I G, Titov V V. Tsunami Scattering and Earthquake Faults in the Deep Pacific Ocean. Oceanography , 2004, 17(1): 38-46. DOI:10.5670/oceanog |
 2012, Vol. 55
2012, Vol. 55



