2. 江苏省地质勘查技术院, 南京 210008
2. Geological Exploration Technology Institute of Jiangsu Province, Nanjing 210008, China
地壳应力状态是地壳最重要的性质之一,地壳表面和内部发生的各种地质构造现象(包活浅源地震的发生)及其伴生的各种物理现象与化学现象都与地壳应力的作用密切相关.了解认识地壳应力分布状态,特别是地壳深部应力状态,是解决地球动力学有关科学问题的基础,如板块驱动机制、地球能量平衡、地震发生机制、区域地壳稳定性等,地壳应力状态及其分布特征成为地学界和工程学界所关注的主要问题之一.
原地应力测量是获取浅层地壳应力状态最直接的途径,国内外许多学者利用原地应力测量数据对浅层地壳应力状态进行了研究.1958 年Hast[1]率先利用地应力实测资料研究了芬兰Scandinavia地区的应力场,表明地壳浅部的水平应力为垂直应力的几倍,并通过回归分析发现,水平应力的大小随深度呈线性增加.在之后的几十年中,水平应力随深度呈线性增加的特征在不同地区的应力测量和研究结果中得到了印证[2-5],并且发现,在全球的许多地区,地壳浅部水平应力大于垂直应力,并且可为垂直应力的数倍乃至更高[5-8].E.T.Brown等[7]归纳了世界范围内地应力测量结果,发现平均水平应力与垂直应力之比随深度的变化在两个双曲线之间分布.此后,包括我国在内的许多学者对全球多个地区的原地应力测量数据进行了研究,发现不仅平均水平应力与垂直应力之比随深度的变化呈双曲线形式,水平最大主应力与垂直应力之比(σH/σv)、水平最小主应力与垂直应力之比(σh/σv)、水平最大主应力与水平最小主应力之比(σH/σh)等多个应力比值随深度的变化也呈双曲线形式[9-11].P.R.Sheorey[8]通过构建理论应力模型,对地壳浅部水平应力及其影响因素进行了分析,尝试性地对水平应力与垂直应力之比随深度的双曲线变化形式给予解释.
在利用原地应力测量数据研究浅层地壳应力方面,以往的研究工作大多是通过回归分析等方法,侧重展现某一地区地壳应力随深度的变化规律[6, 9, 12],或是讨论不同地区地壳应力分布特征的差异[13-14],或是研究岩性、地形地貌、地质构造对地壳应力及其分布特征的影响[15-17].对回归分析结果的深入研究,包括对回归分析结果的可靠性进行检验等,则相对较少.直接探测地壳深部(地下数千米)应力状态,技术难度大,费用昂贵,只有个别科学深钻获取了少量5000m 以下应力观测资料[18].从力学的角度阐明不同应力参数随深度的变化特征,不仅有助于更加全面认识浅层地壳应力状态分布规律,并且对推断地壳深部(地下数千米)应力状态具有重要的意义.
本文从建立应力参数随深度变化的回归关系式入手,利用中国大陆1780条水压致裂和应力解除二维原地应力实测数据,深入分析了中国大陆地壳应力状态随深度的分布特征,并就不同应力参数的回归分析结果带给我们的启示进行了讨论.
本文统一用以下符号表示相关的物理量和参数:σH 为水平最大主应力,σh 为水平最小主应力,σh,ave为平均水平应力,σv 为垂直应力,单位为MPa;z表示深度,单位为km;ρ 为地壳上部物质密度,取值2.65×103kg/m3;g为重力常数,取值9.8m/s2;KH、Ka、Kh表示侧压系数,无量纲; μm 为剪应力相对大小,无量纲;a、b、c为相应回归关系式中的参数,无量纲.
2 应力参数随深度变化的回归关系式影响地壳应力状态的因素有很多,使得地壳应力呈现非均匀分布[19-21],因此,利用不同地区原地应力实测数据得到的应力随深度变化的回归分析结果不尽相同.但前人大量的研究成果有一点是相同的,即:在地壳浅部,水平最大和水平最小主应力随深度呈线性增加[2-5],而水平主应力与垂直主应力之比等多个应力参数随深度的变化则呈现双曲线形式[9-11].这一点已得到地学界和工程学界的广泛认同.
实际上,根据水平最大和水平最小主应力随深度呈线性增加这一得到广泛认可的结果,可以从数学上建立其他应力参数随深度变化的关系式,包括平均水平应力与垂直应力之比(σh,ave/σv)、水平最大主应力与垂直应力之比(σH/σv)、水平最小主应力与垂直应力之比(σh/σv)、水平最大主应力与水平最小主应力之比(σH/σh)等.
2.1 双曲线回归关系式的建立水平最大和水平最小主应力随深度变化的回归关系式一般可描述为
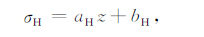
|
(1) |

|
(2) |
垂直应力用上覆岩层的重力来估算:
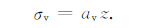
|
(3) |
用两个水平应力与垂直应力(岩体自重)之比来描述地下某点的应力状态具有一定的合理性,不仅是工程设计和建设中常用的方法,国内外许多学者也利用它们来展现地壳浅部应力状态随深度的变化特征.为叙述方便,本文将水平最大主应力与垂直应力之比、平均水平应力与垂直应力之比、水平最小主应力与垂直应力之比统称为侧压系数,分别用字母KH、Ka、Kh 表示:
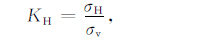
|
(4) |
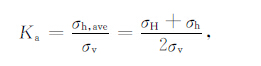
|
(5) |
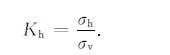
|
(6) |
将(1)-(3)式分别代入(4)-(6)式可得:
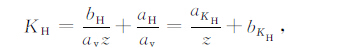
|
(7) |

|
(8) |
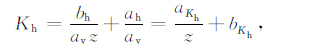
|
(9) |
其中,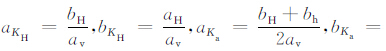
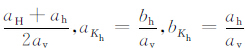
水平最大与最小主应力之比表征了两个水平应力的关系,同样是地壳应力的一个重要参数,由式(1)和式(2)可得:
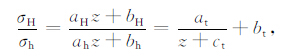
|
(10) |
其中,
由于二维原地应力测量数据只给出了水平面内的最大和最小主应力,如果将水平最大和最小主应力近似看作二维坐标系下的2 个应力主轴,根据岩石力学中的定义[22],水平面内最大剪应力τm 为

|
(11) |
μm 则可以用来表示根据二维原地应力测量数据给出水平面内最大剪应力的相对大小[22]:
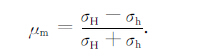
|
(12) |
为叙述方便,本文称 μm 为剪应力相对大小,在第4节中,我们将结合具体回归分析结果对其物理意义作进一步讨论.根据式(1)和式(2),式(12)可写为

|
(13) |
其中,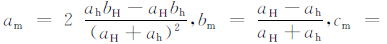

可以看出,式(7)、(8)、(9)、(10)和(13)可统一表示为
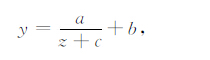
|
(14) |
式(14)是离心率为$\sqrt 2 $ 的双曲线.对于式(7)、(8)、(9),式(14)中的c等于0,正好是前人在对侧压系数进行回归分析时所采用的关系式.
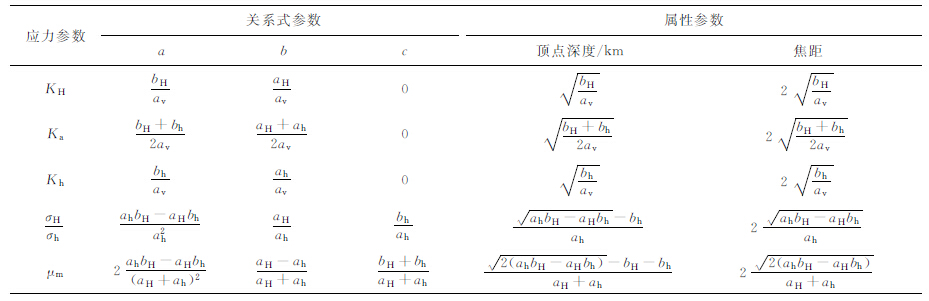
2.2 双曲线的几何性质根据双曲线的几何性质,可以用顶点、焦距和渐近线来描述双曲线的形状.对于式(14)的双曲线,其顶点为($\sqrt a $+b,$\sqrt a $-c),焦距为2$\sqrt a $,其中一条渐近线为y=b.那么对于实际回归拟合结果来说,顶点的纵坐标($\sqrt a $-c)表示顶点距离地表的深度,本文称其为顶点深度.顶点的位置越接近地表,焦距越小,双曲线在顶点附近的曲率就越大,其形状就越接近于以顶点为对称点的折线.随着深度的增加,双曲线逐渐趋向渐近线,回归拟合结果y的值逐渐趋向b,本文称b为双曲线的趋向值.
对于式(7)、(8)、(9)、(10)和(13),可以直接写出它们的顶点深度、焦距等属性.具体结果列于表 1.
|
|
表 1 双曲线的几何参数 Table 1 Geometric parameters of hyperbolic curves |
上述分析表明,在两个水平主应力随深度呈线性增加的前提下,通过简单的数学推导,可以建立3个侧压系数、水平最大与水平最小主应力之比(σH/σh)以及剪应力相对大小 μm 随深度变化的关系式.这些关系式在理论上呈现双曲线形式,并且,双曲线的几何参数均可以通过水平最大与最小主应力的线性回归拟合参数确定.
3 中国大陆实测地应力数据回归分析为了深入分析中国大陆地壳应力状态,我们依据原地应力实测数据,对侧压系数、水平最大与水平最小主应力之比(σH/σh)以及剪应力相对大小 μm 进行了回归分析.
3.1 数据资料“中国大陆地壳应力环境基础数据库"集成了遍布中国大陆范围内的6类地应力观测数据资料[23],并且处于不断更新之中,相对来说,该数据库是我国目前收录数据种类最全、数据量最为丰富的地应力数据库.其中,该数据库给出的原地应力实测量值中包含二维应力数据的有2 类,即水压致裂和应力解除原地应力测量数据.为了使所分析的数据具有一致性,本文只选取了数据库中测试深度大于25 m的二维水压致裂和应力解除的数据,共403个钻孔,包括了1780个测试段的数据.数据测试地点几乎涵盖了整个中国大陆,既有大型工程建设中获取的原地应力实测数据,也有油田地区的实测数据,这些数据具有广泛的代表性.其中二维水压致裂数据有360个钻孔,1737 组(测试段),最大的测试深度为3712m;二维应力解除有43个钻孔,最大的测试深度为498m.
3.2 利用实测数据的回归分析 3.2.1 水平最大和水平最小主应力随深度变化的回归分析我们首先采用式(1)和式(2)的线性回归关系式,对中国大陆1780组原地应力实测数据的水平最大主应力σH 和水平最小主应力σh 进行了回归拟合,结果为(图 1)
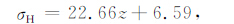
|
(15) |

|
(16) |

|
图 1 中国大陆水平最大与水平最小主应力随深度分布的散点图及拟合结果 (左下角小图为拟合结果的离差分布) Fig. 1 Scatter plot and fitting results of maximum and minimal horizontal principals tresses in China main land Lower-left corner is the deviation distribution of fitting results. |
回归结果的相关系数均大于0.83,表明σH 和σh 随深度都具有较好的线性关系.而aH、ah、bH、bh 在置信度为95%时置信区间较窄(见下节表 2)则反映出该拟合结果的可信度较高.另外,从图 1 中可以看出,在1km 以下,σH 和σh(尤其是σh)的离散性逐渐变小.浅部数据的离散性可能与地壳浅部的岩性、地表覆盖层、地形地貌等因素有关[15-17],另外,关于不同地区原地应力测量数据的差异,已有许多文献作了分析[13-14, 17],本文主要是从力学的角度探讨整个中国大陆地壳应力状态随深度的分布特征,故没有对浅部数据的离散性进行详细分析,只是简单给出了拟合结果的离差分布(见图 1左下角).
3.2.2 侧压系数随深度变化的双曲线拟合垂直应力用上覆岩层的静岩压力来估算,通过式(7)-(8),即可根据原地应力实测数据给出的σH和σh 计算出相应的侧压系数.然后采用式(14)的双曲线形式(此时取c=0),对3个侧压系数随深度的变化进行回归分析,拟合结果为
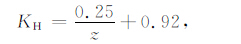
|
(17) |
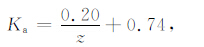
|
(18) |

|
(19) |
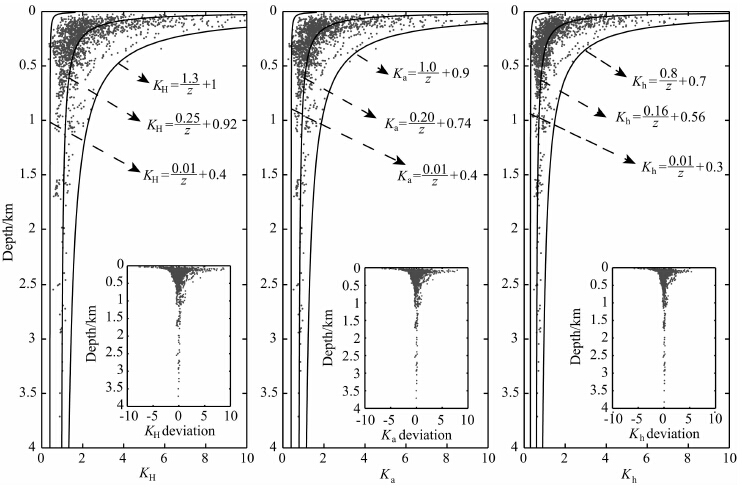
同样,我们也对三个侧压系数的外包络线进行了双曲线拟合,拟合结果如下:
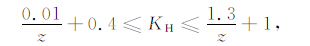
|
(20) |
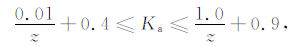
|
(21) |
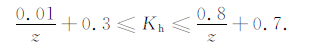
|
(22) |
图 2为侧压系数随深度变化的散点图及拟合结果(各拟合参数的置信区间见3.2.3 节表 2),右下角小图为拟合结果的离差分布,从中可以看出,在深度小于200 m 的浅地表,三个侧压系数均十分离散,在200~800m 之间侧压系数变化较大,而深度到了800 m 以下,三个侧压系数开始趋于稳定.本文给出的中国大陆侧压系数随深度变化的总体特征与前人的分析结果相一致.
|
图 2 中国大陆侧压系数随深度分布的散点图及拟合结果 (右下角小图为拟合结果的离差分布) Fig. 2 Scatter plot and fitting results of the lateral pressure coefficients with depth in China continent Lower-right corner is the deviation distribution of fitting results. |
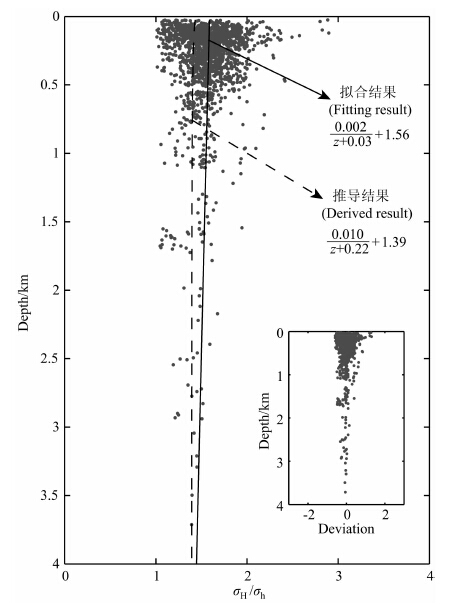
大量的研究结果表明,水平构造应力在我国现今地应力场中起着重要的作用[17, 19, 24-25].对原地应力测量获取的水平最大主应力和水平最小主应力进行分析,能够进一步展现我国水平构造应力场的特征.水平最大与最小主应力之比表征了两个水平应力的关系,因此,本文对水平最大与最小主应力之比(σH/σh)进行了回归分析,拟合关系式采用式(10),回归拟合结果为(图 3)
|
图 3 中国大陆水平最大与水平最小主应力之比随深度分布的散点图及拟合曲线 (右下角小图为拟合结果的离差分布,图中的推导结果见3.3节) Fig. 3 Scatter plot and fitting results of the ratio of maximum to minimal horizontal principal stress with depth in China main land Lower-right corner is the deviation distribution of fitting results.Derived result is in the Section3.3. |

|
(23) |
虽然在拟合分析时采用的是双曲线形式,图 3显示(左下角小图为拟合结果的离差分布),原地应力测量数据给出的σH/σh 以及拟合结果总体上更接近线性分布,随深度并无明显变化.σH/σh 在浅部较为离散,深部比较集中.在500 m 以上,σH/σh 取值范围大部分在1.0至3.0之间,在500~2000 m 深度段,σH/σh 取值范围基本上在1.0至2.5之间,开始趋向集中,在2000~4000m的深度段,σH/σh基本上位于1.0至1.8之间.式(23)表明,回归拟合结果的第一项远小于第二项(拟合参数b),随着深度的增加,σH/σh 逐渐趋向于1.5 左右.各拟合参数的置信区间见表 2.
|
|
表 2 拟合结果中关系式参数的置信区间 Table 2 Confidence intervals of relation coefficients in fitting results |
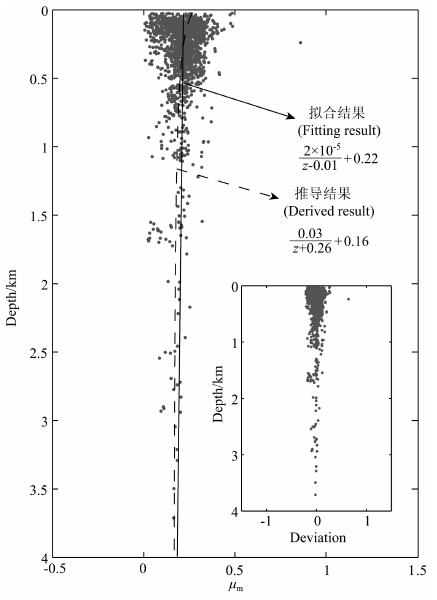
剪应力相对大小 μm 是反映地壳水平最大剪应力状态的一个重要特征参数[26-27].通过式(12),即可根据原地应力实测数据给出的σH 和σh 计算出相应的 μm .本文采用式(14)的双曲线形式,对 μm 随深度的变化进行了回归分析,回归拟合结果为(图 4,右下角小图为拟合结果的离差分布)
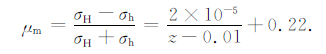
|
(24) |
|
图 4 中国大陆剪应力相对大小 μm 随深度分布的散点图及拟合曲线 (右下角小图为拟合结果的离差分布,图中的推导结果见3.3节) Fig. 4 Scatter plot and fitting results of μm with depth in China main land Lower-right corner is the deviation distribution of fitting results.Derived result is in the Section3.3. |
由图 4 中的黑色实线可以看出,与σH/σh 随深度变化的散点图一样,原地应力实测试数据给出的 μm ,总体上呈线性条带分布,随深度没有明显变化,并且分布的线性条带较σH/σh 更为集中.在深度小于500m时, μm 的取值范围在0至0.5之间;在深度为500~2000m 深度段, μm 的取值范围为0.1 至0.4;在深度大于2000 m 时, μm 的线性集中度更好,取值在0.2左右.回归拟合结果第一项的值几乎为零,式(24)可以等效为横截距为0.22的垂直线.各拟合参数的置信区间见表 2.
3.3 关于回归参数的分析对回归拟合的公式相对于数据样本的代表程度,常采用显著性检验,当回归效果显著时,常需要对拟合参数(a,b,c)作区间估计[28].对于3.2 节的回归拟合结果(式(15)-(19)、式(23)、式(24)),在置信度取95%时,各关系式参数的拟合值及其置信区间列于表 2.总体来看,各关系式拟合参数的置信区间都较窄,而本文所取的数据量较大(接近两千条),表明参数真值的可信程度较高.
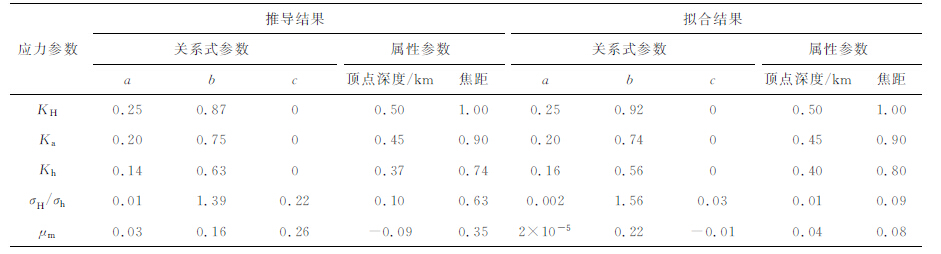
本文第2节阐述了可以根据水平最大和水平最小主应力随深度线性增加的关系式,从数学上建立其他应力参数随深度变化的关系式.也就是说,可以依据式(15)和式(16)的水平最大和水平最小主应力随深度变化的线性拟合结果,直接写出KH、Ka、Kh、σH/σh 和 μm 随深度变化的双曲线关系式,以及相应的顶点和焦距等双曲线属性参数,为叙述方便,本文将据此得到的KH、Ka、Kh、σH/σh 和 μm 随深度变化的关系式称为推导结果,具体相关参数列于表 3.
|
|
表 3 推导结果与直接拟合结果的对比 Table 3 Comparison of derived results and direct fitting results |
根据式(17)-(19),以及式(23)和式(24)的回归拟合双曲线表达式,也可以计算出它们的顶点和焦距,本文称其为拟合结果.为了对比,将直接拟合结果相应参数同时列于表 3.
由表 3可以看出,侧压系数KH、Ka、Kh 的推导结果与拟合结果,包括关系式参数和属性参数,均十分接近.从关系式参数上看,σH/σh 和 μm 的推导结果与其拟合结果有一定的差异,实际上,它们的焦距都很小,也就是说,σH/σh 和 μm 的推导结果与拟合结果在地表以下都接近垂直线.由图 3 可以看出,σH/σh 的推导结果与拟合结果可以看成是近乎平行的2条垂直线,它们的偏差在合理范围内.据此我们认为,在中国大陆地壳浅部,σH/σh 随深度没有明显变化,拟合值可能在1.3至1.6之间.同理, μm 的推导结果与拟合结果的间距可以看成 μm 的拟合偏差(图 4), μm 随深度没有明显变化,拟合值在0.1 至0.3之间.
朱焕春等[15]给出了全球范围内σH 和σh 随深度变化的拟合结果:
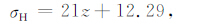
|
(25) |
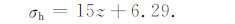
|
(26) |
据此可以推导出KH、Ka、Kh、σH/σh 和 μm 随深度变化的关系式,其相应参数列于表 4.从中可以看出,在地表以下侧压系数KH、Ka 和Kh 随深度的变化是完整的双曲线形态,相应的关系式参数和属性参数与本文的结果比较接近.而σH/σh 的顶点深度很小, μm 的顶点深度为负,即在地表以下,σH/σh 和 μm 随深度的变化不大,整体上呈现线性,并且 μm 的线性性质最好,与本文的结果相一致.
|
|
表 4 全球范围内KH 、Ka、Kh、σH/σh 和 μm 的关系式参数(根据朱焕春结果[15]推导) Table 4 Relation parameters of KH 、Ka、Kh、σH/σh and μm around the world (after Zhu [15]) |
另外,我们还利用其他学者[9-11]给出的σH 和σh随深度变化的线性拟合结果,对KH、Ka、Kh、σH/σh和 μm 随深度变化的关系式进行了计算,得出了同样结论,即在地表以下,侧压系数KH、Ka 和Kh 随深度的变化是完整的双曲线形态,而σH/σh 和 μm 随深度的变化不大,整体上呈现线性.
4 稳定性检验由于受技术条件和资金的制约,利用原地应力测量技术直接获取的地下数千米的地应力实测数据还很少,本文所使用的数据中,2000 m 以下的地应力实测数据也只占了很少一部分.那么,缺少较深的地应力实测数据对KH、Ka、Kh、σH/σh 和 μm 等应力参数的回归拟合结果有何影响,就成为人们关心的一个问题.在此,本文仅以侧压系数的回归分析为例,从拟合参数误差分析的角度,对回归分析结果的稳定性进行了研究.
具体思路是,分别选取不同深度段的侧压系数KH、Ka 和Kh 进行回归拟合,起始深度固定为25m,逐渐增加下部截止深度.也就是说,分别选择25~100m,25~200 m,25~300 m,…,25~3800 m内的数据进行分段回归拟合,下部截止深度增加表示逐渐加入了深部数据,数据总量在增多,最后一组25~3800m 即为全部数据.每个深度分段都可得到一组侧压系数的回归关系式参数ai和bi.然后以全部数据拟合结果给出的关系式参数为参照值(具体结果见式(17)-(19)或表 3),计算各分段关系式参数与参照值的相对偏差:
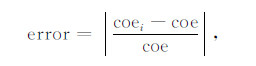
|
(27) |
其中,coe为参照值的关系式参数a和b,coei代表分段关系式参数ai和bi,error即为各分段内拟合参数的相对偏差.通过参数拟合相对偏差的分布状况来检验拟合结果的稳定性.图 5 给出了稳定性检验的结果.其中,图 5a为侧压系数KH 的拟合参数相对偏差分布图,aKH-err、bKH-err分别为KH 的回归关系式参数aKH、bKH的相对偏差;图 5b 为侧压系数Ka 的拟合参数相对偏差分布图;图 5c为侧压系数Kh 的拟合参数相对偏差分布图,aKa-err、bKa-err、aKh-err、bKh-err的含义同上;图中的纵坐标均为下部截止深度.
通过稳定性检验发现,在数据段的下部截止深度达到1500m 左右时,侧压系数KH、Ka 和Kh 的回归关系式参数a、b的相对偏差开始小于10-2,即当参与回归拟合的数据的深度大于1500 m 时,拟合结果开始趋于稳定.也可以这样来理解稳定性检验的结果,当利用1500 m 以上的浅部数据给出回归拟合曲线后,为数不多的深部数据恰好也落在这些曲线附近,表明了回归拟合结果的稳定性和可延伸性.
另外,我们根据各深度段的回归拟合结果,推算了4000m 深处的三个侧压系数KH、Ka、Kh,推算结果显示在图 5d中,图中纵坐标同样为不同数据段的下部截止深度,横坐标为4000 m 处侧压系数的推算值.从中可以看出推算的4000 m 处侧压系数KH、Ka、Kh 随下部截止深度的变化情况,当下部截止深度大约超过1500 m 后,4000 m 深处的侧压系数的推测值开始趋向稳定,直至趋于定值.

|
图 5 侧压系数稳定性检验结果 (a)KH 的拟合参数相对偏差分布;(b)Ka 的拟合参数相对偏差分布;(c)Kh 的拟合参数相对偏差分布;(d)不同数据段推算的4km 处侧压系数. Fig. 5 Stability test results of lateral pressure coefficients |
上述稳定性检验初步表明,即使缺少较深(地下数千米)的地应力实测数据,只要有一定数量的测试深度超过1500 m 的原地应力测量数据,仍然有可能得到比较可信的侧压系数回归分析结果.当然,深部原地应力测量数据量越多,数据的测试深度越深,侧压系数回归分析结果的可靠性也就越高.
5 讨论 5.1 关于侧压系数本文从理论关系式的建立和实测地应力数据的回归分析2个方面,进一步验证了中国大陆地壳浅部的侧压系数KH、Ka 和Kh 随深度的变化呈完整的双曲线形态.由于地壳物性和应力的非均匀分布,不同地区的侧压系数不尽一致,使得中国大陆地壳浅部侧压系数的分布具有一定的离散性,但总体上,3个侧压系数随深度的变化均在2 条双曲线(图 2中的外包络线)之间分布,2条双曲线可以认为是相应侧压系数的上下限.
4 节的稳定性检验结果表明,即使缺少较深的地应力实测数据,只要有一定数量的测试深度超过1500m 的原地应力测量数据,仍然有可能得到比较可信的侧压系数回归分析结果.侧压系数的回归分析结果是稳定的,这就给我们带来一个启示,能否根据侧压系数随深度的变化规律对整个地壳上部的地应力状态进行推断?一般认为在脆性的上地壳(10km左右),其应力状态与地壳物性参数等因素有关,并且受地壳内部已有断层的摩擦强度控制[17].据此是否可以这样认为,在地壳物性参数没有本质改变的整个脆性上地壳,地壳应力随深度的变化特征也没有本质的变化.如果这个假设成立,则可以利用一个地区(如中国大陆或华北地区)地壳浅部原地应力测量数据给出的侧压系数回归分析结果,推测地壳数千米深处的侧压系数,进而借助地壳岩石自重,对数千米深处2个水平主应力的取值范围给出较为可靠的推断.
例如,根据本文的回归分析结果,在中国大陆地表以下平均7km 深处,侧压系数KH 的推测值为0.96,其下限与上限(左右两侧外包络线的值)分别为0.40和1.19.依据岩石自重,7km 深处的水平最大主应力的推测值为170 MPa左右,并且水平最大主应力的推测值在70MPa至220MPa之间都是可能的.同理,7km 深处的水平最小主应力的推测值为100MPa左右,其取值范围在50 MPa至130 MPa.
侧压系数反映的是水平应力相对于垂直应力的强弱,在浅部侧压系数较大,随深度增加侧压系数逐渐变小,大约在地下1km 左右侧压系数KH 开始趋于1,表明在1km 以下岩石的自重作用凸显出来.
5.2 关于σH/σh 和 μm依据现有的认识,中国大陆构造应力的作用可能更多地体现在水平向[17, 19, 24-25],侧压系数随着深度的加深,先减小后稳定,单纯用侧压系数来反映构造应力作用的强弱是不全面的.而σH/σh 和 μm 则反映了2个水平主应力的关系,能够从一个侧面反映构造应力作用的特征.从本文的回归拟合结果来看,相对于侧压系数,σH/σh 和 μm 的顶点深度较低,甚至是负值,即在中国大陆地表以下到几千米深度,σH/σh 和 μm 的变化不大,更接近线性分布,在地表1000m 以下更加集中,σH/σh 的拟合值在1.5左右, μm 的拟合值在0.2左右.
地壳内的破裂现象极其复杂,但从本质上来看,是剪应力增大而产生滑动破坏,控制这种破坏的力学因素是断层面上的剪应力和正应力[26]. μm 虽然反映的是水平面上剪应力的相对大小,由于我国大部分地区最大主应力位于水平方向上,因此, μm 可以在一定程度上反映中国大陆地壳剪应力状态.有学者通过研究表明,地壳内的 μm 值一般不应超过0.5~0.7[26-27],否则,则可能产生剪切滑动破坏.从本文的研究结果来看,虽然原地应力测量数据给出的σH 和σh 比较离散,但根据这些数据求出的 μm 却比较集中,并且随深度没有明显变化,除个别数据点外, μm 值很少有超过0.5的,大部分处于0.1~0.4之间.从力学的角度可以这样来理解:地壳应力本身与地壳的力学环境(如构造应力的作用)、构造环境以及岩石的物理性质等多种因素有关,中国大陆地壳应力呈现非均匀分布,并存在着应力集中和释放的情况,地下岩体的剪切破坏(如地震)与剪应力相对大小相关.在正常情况下,地壳内的 μm 与深度无关,与应力量值本身的相关程度可能也不大(高应力并不一定意味着高剪应力),从而使地壳在绝大部分时间里处于一种相对稳定的力学状态.
由于深部岩体材料的内聚力、内摩擦以及结构面的摩擦和粘结,在地质构造运动和自重应力作用下,地下岩体积累了弹性应变能.此时岩体宏观能量平衡是在一定的约束条件下维持的,表现出 μm 处于一个相对稳定的范围.当岩体附近出现扰动,约束条件被破坏时, μm 开始发生偏离,当达到岩体的承受极限时,应变能转化为动能,发生相应的地震.田中丰等[26]研究发现,1995年日本兵库县7.2级地震前十多年的时间里,该地区2 个钻孔的原地应力重复测量数据给出的 μm 出现了明显变化,从1978 年的0.2左右逐渐增加到震前的0.6左右,震后 μm 恢复到0.2.并提出可以通过用原地应力重复测量,观测 μm 的变化,来分析地壳应力的改变,进而为判断地震危险性提供依据.这一观点也得到国内一些学者的认同,并开始尝试用 μm 的大小来判断活动断裂的地震危险性[27].然而,类似日本兵库县地震的观测实例还太少,需要在这一方面作进一步的研究.
根据本文的研究结果,用 μm 作为判断活动断裂地震危险性的力学依据具有一定的合理性.由于在地表1km 以下 μm 的线性集中程度更好,其随时间的变化应更具代表性,因此,利用1km 以下 μm 的变化来分析活动断裂的地震危险性可能更好些.
6 结论(1) 在两个水平主应力随深度呈线性增加的前提下,通过简单的数学推导,可以建立侧压系数(KH、Ka、Kh)、水平最大与水平最小主应力之比(σH/σh)以及剪应力相对大小 μm 随深度变化的关系式.这些关系式在理论上呈现双曲线形式,并且,双曲线的几何参数均可以通过水平最大与最小主应力的线性回归拟合参数确定.
(2)从数学回归关系式的建立和实测地应力数据的回归分析两个方面,进一步验证了中国大陆地壳浅部的侧压系数KH、Ka 和Kh 随深度的变化呈完整的双曲线形态.通过稳定性检验说明,即使缺少较深(地下数千米)的原地应力实测数据,只要有一定数量的测试深度超过1500m 的原地应力测量数据,仍然可以得到比较可信的侧压系数回归分析结果.并据此提出,在整个脆性上地壳的物性参数没有本质变化的前提下,可以利用地壳浅部的侧压系数回归分析结果,以及地壳岩石自重,对整个脆性上地壳的2个水平主应力的取值范围进行推断.例如,根据本文的回归分析结果,在中国大陆地下7km 深处,水平最大主应力推测为170 MPa,其上、下限分别为220 MPa和70 MPa,水平最小主应力的推测为100 MPa 左右,其上、下限分别为130 MPa 和50 MPa.
(3) 相对于侧压系数(KH、Ka、Kh),水平最大与水平最小主应力之比(σH/σh)以及剪应力相对大小 μm 的顶点深度较低,甚至是负值,即在中国大陆地表以下几千米深度范围,σH/σh 和 μm 的变化不大,更接近线性分布,在地表1000 m 以下更加集中.σH/σh 的拟合值在1.5 左右, μm 的拟合值在0.2 左右.并且 μm 的线性集中程度更好,利用 μm 的大小来判断活动断裂的地震危险性具有一定的合理性.
本文通过对一千多条的原地应力测量数据的回归分析,展现了多个应力参数随深度的变化特征.应力大小是了解应力状态最直接的参数,但差应力和剪应力与地壳形变更加相关,基于中国大陆构造应力的作用可能更多地体现在水平向上这一认识,本文尝试通过侧压系数、σH/σh 和 μm ,来分析2个水平应力之间,以及它们与垂直应力之间的关系,研究结果从一个侧面反映了构造应力作用的特征,对更加全面地认识中国大陆地壳上部应力状态将起到积极作用.
| [1] | Hast N. The Measurement of Rock Pressure in Mines. Stockholm: Norstedt, 1958. |
| [2] | Hast N. The state of stress in the upper part of the Earth's crust. Tectonophysics , 1969, 8(3): 169-211. DOI:10.1016/0040-1951(69)90097-3 |
| [3] | Wyss M. Stress estimates for south America shallow and deep earthquakes. J. Geophys. Res. , 1970, 75(8): 1529-1544. DOI:10.1029/JB075i008p01529 |
| [4] | Hast N, Kropotkin P N. The state of stress in the Earth's crust as based on measurements in mines and on geophysical data. Phys. Earth Planet. Inter. , 1972, 6(4): 214-218. DOI:10.1016/0031-9201(72)90002-7 |
| [5] | Haimson B C. The hydrofracturing stress measuring method and recent field results. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. , 1978, 15(4): 167-178. DOI:10.1016/0148-9062(78)91223-8 |
| [6] | Gay N C. In-situ stress measurements in Southern Africa. Tectonophysics , 1975, 29(1-4): 447-459. DOI:10.1016/0040-1951(75)90173-0 |
| [7] | Browm E T, Hoek E. Technical note trends in relationships between measured in-situ stresses and depth. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. , 1978, 15(4): 211-215. DOI:10.1016/0148-9062(78)91227-5 |
| [8] | Sheorey P R. A theory for in-situ stresses in isotropic and transversely isotropic rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. , 1994, 31(1): 23-24. DOI:10.1016/0148-9062(94)92312-4 |
| [9] | 高建理, 丁建民, 梁国平, 等. 华北地区盆地内地壳应力随深度的变化. 中国地震 , 1987, 3(4): 82–89. Gao J L, Ding J M, Liang G P, et al. Variation of crustal stress with depth in the basin of north China. Earthquake Research in China (in Chinese) , 1987, 3(4): 82-89. |
| [10] | 赵德安, 陈志敏, 蔡小林, 等. 中国地应力场分布规律统计分析. 岩石力学与工程学报 , 2007, 26(6): 1265–1271. Zhao D A, Chen Z M, Cai X L, et al. Analysis of distribution rule of geostress in China. Chinese Journal of Rock Mechanics and Engineering (in Chinese) , 2007, 26(6): 1265-1271. |
| [11] | 景锋, 盛谦, 张勇慧, 等. 中国大陆浅层地壳实测地应力分布规律研究. 岩石力学与工程学报 , 2007, 26(10): 2056–2062. Jing F, Sheng Q, Zhang Y H, et al. Research on distribution rule of shallow crustal geostress in China mainland. Chinese Journal of Rock Mechanics and Engineering (in Chinese) , 2007, 26(10): 2056-2062. |
| [12] | 李方全, 王连捷. 华北地区地应力测量. 地球物理学报 , 1979, 22(1): 1–8. Li F Q, Wang L J. Stress measurements in north China. Chinese J. Geophys. (in Chinese) , 1979, 22(1): 1-8. |
| [13] | Ogasawara H. Flexure of the crust estimated from in-situ stress measurements and its relation to tectonics. Tectonophysics , 1992, 201(3-4): 303-315. DOI:10.1016/0040-1951(92)90238-2 |
| [14] | 康红普, 林健, 颜立新, 等. 山西煤矿矿区井下地应力场分布特征研究. 地球物理学报 , 2009, 52(7): 1782–1792. Kang H P, Lin J, Yan L X, et al. Study on characteristics of underground in-situ stress distribution in Shanxi coal mining fields. Chinese J. Geophys. (in Chinese) , 2009, 52(7): 1782-1792. |
| [15] | 朱焕春, 陶振宇. 不同岩石中地应力分布. 地震学报 , 1994, 16(1): 49–63. Zhu H C, Tao Z Y. State of in-situ stress in different rocks. Acta Seismologica Sinica (in Chinese) , 1994, 16(1): 49-63. |
| [16] | 薛玺成, 郭怀志, 马启超. 岩体高地应力及其分析. 水利学报 , 1987(3): 52–58. Xue X C, Guo H Z, Ma Q C. High ground stresses in the rock masses and their analysis. Journal of Hydraulic Engineering (in Chinese) , 1987(3): 52-58. |
| [17] | 谢富仁, 崔效锋, 赵建涛, 等. 中国大陆及邻区现代构造应力场分区. 地球物理学报 , 2004, 47(4): 654–662. Xie F R, Cui X F, Zhao J T, et al. Regional division of the recent tectonic stress field in China and adjacent areas. Chinese J. Geophys. (in Chinese) , 2004, 47(4): 654-662. |
| [18] | Brudy M, Zoback M D, Fuchs K, et al. Estimation of the complete stress tensor to 8 km depth in the KTB scientific drill holes: Implications for crustal strength. J. Geophys. Res. , 1997, 18(B8): 18453-18475. |
| [19] | 李方全, 刘光勋. 我国现今地应力状态及有关问题. 地震学报 , 1986(8): 156–171. Li F Q, Liu G X. The present state of stress in China and related problems. Acta Seismologica Sinica (in Chinese) , 1986(8): 156-171. |
| [20] | Seagar J S. Pre-mining lateral pressures. Int. J. Rock Mech. Min. Sci. , 1964, 1(3): 413-419. DOI:10.1016/0148-9062(64)90007-5 |
| [21] | Zoback M L. First and second order patterns of stress in the lithosphere: the world stress map project. J. Geophys. Res. , 1992, 97(B8): 11703-11728. DOI:10.1029/92JB00132 |
| [22] | Jaeger J C, Cook N G W, Zimmerman R W. Fundamentals of Rock Mechanics. London: Chapman and Hall Press, 1979 : 97 . |
| [23] | 谢富仁, 陈群策, 崔效锋, 等. 中国大陆地壳应力环境基础数据库. 地球物理学进展 , 2007, 22(1): 131–136. Xie F R, Chen Q C, Cui X F, et al. Fundamental database of crustal stress environment in continental China. Progress in Geophysics (in Chinese) , 2007, 22(1): 131-136. |
| [24] | 徐纪人, 赵志新, 石川有三. 中国大陆地壳应力场与构造运动区域特征研究. 地球物理学报 , 2008, 51(3): 770–781. Xu J R, Zhao Z X, Yuzo I. Regional characteristics of crustal stress field and tectonic motions in and around Chinese mainland. Chinese J. Geophys. (in Chinese) , 2008, 51(3): 770-781. |
| [25] | 李瑞莎, 崔效锋, 刁桂苓, 等. 华北北部地区现今应力场时空变化特征研究. 地震学报 , 2008, 30(6): 570–580. |
| [26] | 田中丰, 藤森帮扶, 大塚成昭. 地壳应力·歪の测定·观测による大地震发生の预测. 地震 , 1998, 50(2): 201–208. |
| [27] | 李宏, 谢富仁, 刘凤秋, 等. 乌鲁木齐市区断层附近原地应力测量研究. 地震地质 , 2007, 29(4): 805–812. Li H, Xie F R, Liu F Q, et al. Studies on in-situ stress measurement near fault in Urumqi city. Seismology and Geology (in Chinese) , 2007, 29(4): 805-812. |
| [28] | 盛骤, 谢式千, 潘承毅. 概率论与数理统计. 北京: 高等教育出版社, 2001 : 303 -305. |
 2012, Vol. 55
2012, Vol. 55