2. 海岛(礁)测绘技术国家测绘局重点实验室, 青岛 266510;
3. 中国科学院测量与地球物理研究所, 武汉 430077
2. Key Laboratory of Surveying and Mapping Technology on Island and Reef, State Bureau of Surveying and Mapping, Qingdao 266510, China;
3. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China
目前,潜艇水下导航定位主要采用惯性导航方式,但惯性导航系统(InertialNavigationSystem)的定位误差随时间积累发散,无法满足潜艇长期潜航及隐蔽性要求,因此有必要借助其它辅助导航手段实时或定期校正INS.重力匹配辅助导航系统能在保障高隐蔽性的前提下有效地对惯性导航系统误差进行水下重调校正,极具军事价值,该技术已引起各国极大的关注,美国于1983年成功地在海上进行了水下载体重力匹配导航系统实验测试,后来该系统部署在美国海军三叉戟潜艇上,大大改善了该型潜艇惯性导航系统性能.20世纪80年代,美国贝尔实验室、Lockheed Martin 公司开展重力匹配导航技术研究,并取得了一系列的成果[1-4].贝尔实验室研制出了重力梯度仪导航系统[1](Gravity Gradiometer Navigation System,GGNS)和重力辅助惯性导航系统[2](Gravity Aided Inertial Navigation System,GAINS),Lockheed Martin公司研制出了通用重力模块[3-4](UniversalGravity Model,UGM).
重力辅助惯性导航系统中的核心部分是匹配算法,它包括基于卡尔曼滤波的匹配算法和相关序列匹配算法两类.基于卡尔曼滤波的匹配算法主要有SITAN(Sandia Inertial Terrain-Aided Navigation)算法[5-10],序列相关匹配算法主要有ICCP(Iterative Closest Contour Point)算法[11-15]、TERCOM(Terrain Contour Matching)算法[16-19] 及相关极值匹配算法[20-22].许多学者对这些算法进行了研究并取得了大量有价值的成果,其中苏联学者克拉索夫斯基等在文献[22]中对相关极值导航理论做了详细的论述.考虑到重力异常基准图具有连续分布特性,本文对2′×2′卫星测高反演重力异常格网数据进行二维高斯基函数逼近以获取局部重力异常基准图解析表达式,在该解析式的基础上对相关极值匹配算法进行重新设计,并针对算法在实际应用中的一些问题做出了改进.
2 重力相关极值匹配算法基本原理设INS 指示航迹点序列为(P1,P2,…,Pn),INS指示航迹序列点上的重力量测值序列为(g1,g2,…,gn).根据(P1,P2,…,Pn)及一定的置信区域在重力异常基准图中搜索若干与(g1,g2,…,gn)等序列长度的参考重力序列(g′1,g′2,…,g′n),最后通过重力量测值序列与参考重力值序列之间某种相关分析算法获取位置最优估计.常用的相关分析算法分三种,它们分别是互相关(COR,Cross Correlation)算法、平均绝对差(MAD,Mean Absolution Difference)算法以及均方差(MSD,Mean Square Difference)算法,其定义如下式:
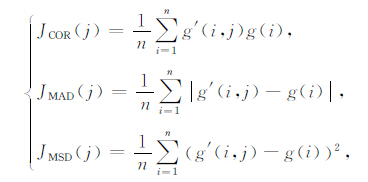
|
(1) |
当JCOR(j)达到最大或JMAD(j)和JMSD(j)达到最小时,位置估计达到最优.一般来说,MSD 算法性能最优,MAD 算法次之,而COR 算法由于相关处理的数据长度有限,通常互相关算法得不到真正的最大值,因而精度不高.
3 重力异常离散基准图的二维高斯基函数解析逼近设高斯基函数表达式为G(x)=e-x2/a2,设局部重力异常基准图等分格网点集合为{(xi,yj,zij)|i=1,2,…,m;j=1,2,…,n},则其x方向一维高斯基函数解析式为Lx= Span{Gx((x-xi)/δx)},y方向一维高斯基函数解析式为Ly= Span{Gy((y-yj)/δy)},其中δx、δy为格网点分辨率,则XY平面的二维高斯基函数可以写成Lx与Ly的张量积形式:
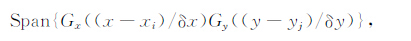
|
(2) |
即得
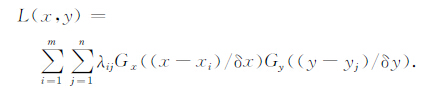
|
(3) |
设
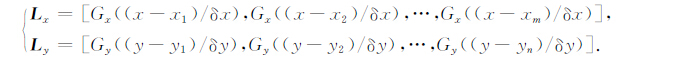
|
(4) |
则(4)式可以简化为矩阵形式:
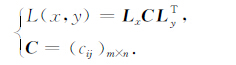
|
(5) |
根据插值条件{L(xi,yj)=f(xi,yj)i=1,2,…,m;j=1,2,…,n},有如下线性方程:
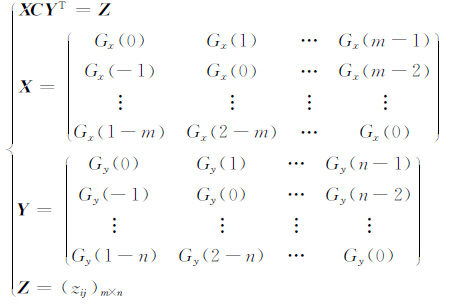
|
(6) |
已知X,Y均为非奇异矩阵,即上式有唯一解,解方程即得到系数矩阵C,将系数矩阵代入式(5)便得到该局部重力异常基准图二维高斯基函数逼近解析式.需要注意的是,参数a的取值对高斯基函数逼近效果影响很大,a过大或过小都将导致很大的逼近误差,因此需要通过建立调优模型并进行解算获取参数a的最优值.限于篇幅,本文对参数a调优过程不作介绍,最后仿真试算取a为2 即可获得较高的逼近精度.
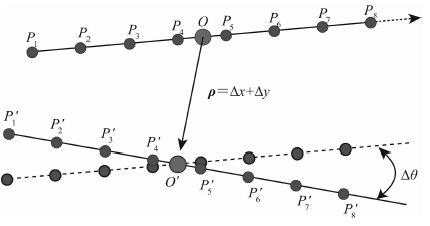
4 基于连续解析重力场的相关极值匹配算法设计如图 1所示,设INS指示航迹序列为Pi(i=1,2,…,n),该序列几何中心为o,对应序列点上的重力量测值为gi(i=1,2,…,n).假定INS 在采样序列短时间内无相对漂移误差,即将匹配过程视为旋转平移变换过程T(Δx,Δy,Δθ)(其中,Δx,Δy为序列几何中心平移变换量,Δθ为绕序列几何中心旋转变换量),设参考航迹序列为P′i(i= 1,2,…,n).这里采用MSD 性能指标展开基于连续解析重力场的相关极值匹配算法设计,如式(7)当目标函数I(Δx,Δy,Δθ)最小时(其中G(x,y)为二维高斯基函数逼近局部重力异常基准图解析式),估计航迹达到最优.
|
图 1 相关极值匹配算法模型 Fig. 1 Model of maximum correlation algorithm for matching |
依据INS 指示航迹将置信区间设定为Δx∈[-a,a];Δy∈ [-b,b];Δθ∈ [-c,c],则基于局部连续解析重力异常基准图的相关极值匹配过程转化为(7)式在该三维置信区间非线性寻优过程.采用BFGS拟牛顿方法对该非线性寻优数学模型进行解算,其尺度矩阵迭代公式如公式(8),其中X(k)为第k次迭代点旋转平移变换三维坐标值,g(k)为X(k)处对应梯度,H(k)为X(k)处尺度矩阵.
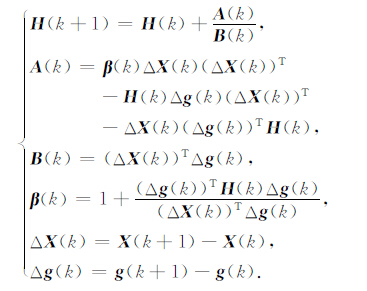
|
(8) |
考虑到BFGS拟牛顿法最优解容易收敛于初值附近,而当置信区间较大时有可能存在多局部最优解情况,为了获取在置信区间内全局最优解,可以引入平均分布随机数以产生随机初值进行多次迭代计算寻优实现全局寻优.
5 新算法的两点改进 5.1 采用TERCOM算法进行粗匹配TERCOM 算法基本原理是在预先存储在匹配导航计算机内的重力异常基准图中找出一系列平行于INS指示航迹序列的参考航迹序列,然后采用相关分析算法分别计算各参考航迹序列重力异常剖面与实测重力异常剖面的相关程度,从中选出相关程度最高的一条作为最佳匹配剖面.从TERCOM 基本原理可以看出,传统的TERCOM 最大的缺点是无法对航向误差进行修正,且只能匹配到格网点,匹配精度受限于基准图分辨率,该算法优点是算法简单、计算量小.而新设计的相关极值匹配算法优点是能同时对位置漂移误差及航向误差进行精确修正,但考虑到当定位漂移误差较大时搜索区间较大,非线性寻优过程存在多局部最优解情况,由此增加了迭代次数,从而影响算法速度.综上所述,上述两种匹配算法优缺互补,我们采用TERCOM 算法进行粗匹配获取一条离实际航迹较为接近的估计航迹作为迭代初值,然后在该迭代初值基础上用新设计的相关极值算法进行精匹配,此时置信区间已经大大减小,搜索范围及迭代次数也得到有效地减小,匹配算法效率将得到大幅提高.
5.2 采用差分法对实测序列数据进行预处理海洋重力仪的测量精度受水平加速度、垂直加速度、交叉耦合效应以及厄特弗斯效应等因素影响,其中前三项改正由重力仪系统内部自行进行改正,而厄特弗斯效应则需要通过外部提供的速度、位置、姿态信息进行改正.假定载体的航向角为A,载体运动速度为V,地球平均半径R,载体所在处纬度φ,则厄特弗斯效应的改正量如下式所示:
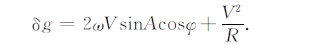
|
(9) |
厄特弗斯改正对潜艇速度测量精度要求较高,且正常重力计算也要求精确的纬度信息,而INS定位误差随时间积累无法满足这两项要求,两者对重力异常观测量所产生的误差不可忽视.为此,采用相邻重力异常测量值差分形成一个新的观测序列,采用新的观测序列以减小上述两项误差及其它系统误差,在此基础上对相关极值目标函数重新设计如式(10).
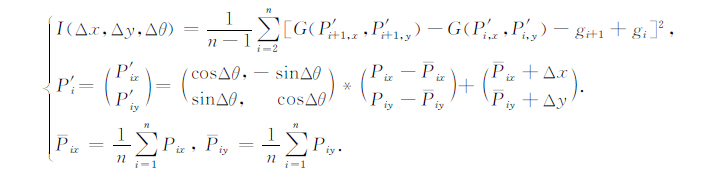
|
(10) |
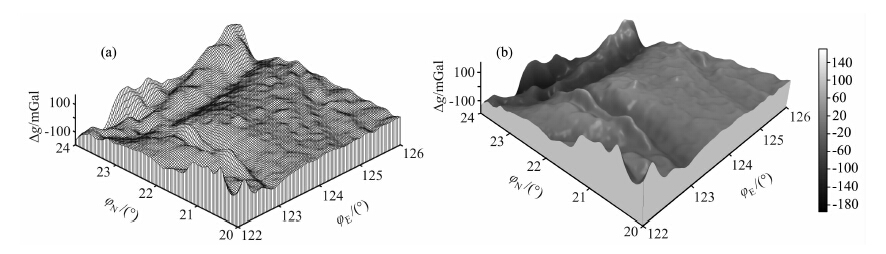
取范围为122°E-126°E,20°N-24°N,分辨率为2′×2′卫星测高反演重力异常数据作为仿真用重力异常基准图.首先对该范围局部重力异常基准图进行二维高斯基函数逼近,获得该范围局部重力异常基准图解析表达式.如图 2所示,由二维高斯基函数逼近获取的基准图解析式能较好的描述这一范围的重力异常变化.
|
图 2 2′×2′局部重力异常基准图三维图 (a)标准格网重力异常基准图;(b)二维高斯基函数逼近重力异常基准图. Fig. 2 The 3D map of2′×2′local gravity anomaly field |
下面对该方域二维高斯基函数逼近精度进行分析.采用该方域4′×4′格网处重力异常数据作为已知数据点,以此为基础通过逼近获得该局部基准图解析表达式.然后在解析式基础上计算该区域其余4′×4′格网点处重力异常逼近值并与对应的已知重力异常值进行比对分析(如图 3).从图 3可以看出,该次逼近试算边缘效应得到有效抑制且逼近误差呈明显的高斯分布.误差分析表明,试算区域4′×4′格网点处逼近绝对误差均值为0.3155mGal、误差均值为-0.000417 mGal且95.56% 计算点绝对误差小于1 mGal,逼近精度可满足匹配导航要求(本次试算若直接采用2′×2′数据进行逼近,其精度将得到较大提高,但无法进行误差分析).

|
图 3 4′×4′局部重力异常基准图二维高斯逼近试算 (a)4′×4′格网点处逼近误差图;(b)4′×4′格网点处逼近误差统计直方图. Fig. 3 The simulation of 4′×4′local gravity anomaly map′s approximation with 2-D Gausssp line |
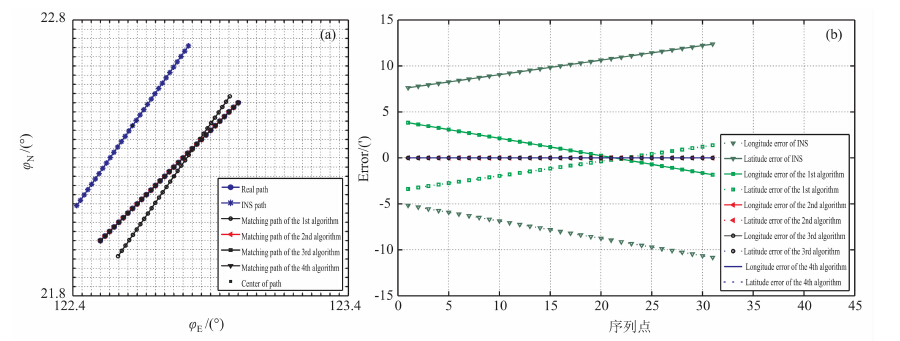
采用直线段航迹进行仿真,设定航迹序列点数为31,采样点距为1.414′,迭代最大次数为20.为验证算法最佳精度,首先设计在理想条件下的仿真实验一(设重力观测噪声及重力仪系统误差均为零).设定INS 指示航迹误差分别为(-8′,10′,pi/18)(括号内第一个值为INS航迹序列几何中心点经度方向误差,第二个值为INS航迹序列几何中心点纬度方向误差,第三个值为INS航迹航向误差).仿真实验一结果如图 4所示(匹配结果图经局部放大处理.图中算法1 表示TERCOM 算法,算法2 表示TERCOM 算法粗匹配+差分相关极值匹配算法精匹配组合算法,算法3表示TERCOM 算法粗匹配+ 相关极值匹配算法精匹配组合算法,算法4 表示相关极值匹配算法).
|
图 4 仿真实验一 (a)仿真结果图;(b)误差分析图. Fig. 4 The first matching simulation experiment |
从匹配结果图中可以清楚地看出传统的TERCOM 算法无法对航向误差进行修正,从图中序列几何中心点的位置可以看出传统的TERCOM 算法只能匹配到格网点上,这两方面对TERCOM 算法匹配精度影响很大.后面三种算法匹配精度都达到了10-6分量级的精度,由于算法2与算法3采用TERCOM 算法作为粗匹配,使得相关极值匹配过程寻优区间大大减小,迭代2次就收敛于最优解,而算法4由于寻优范围大,迭代次数为9次.由理想条件下仿真实验可以看出,改进的相关极值匹配算法可以克服TERCOM 算法和单纯相关极值算法的缺点,在保障快速性的同时提高匹配精度.
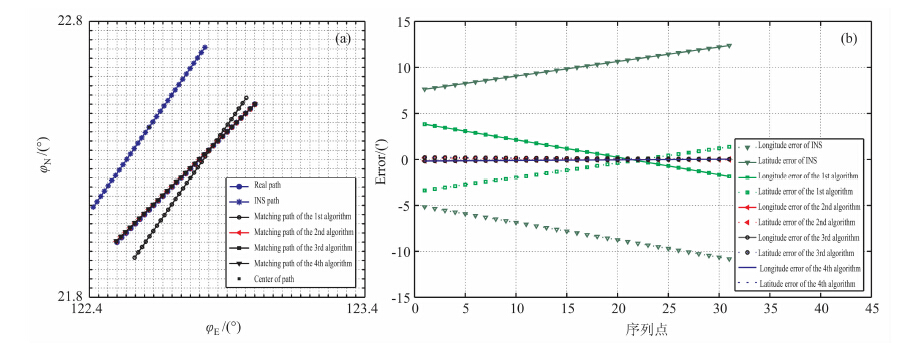
考虑到卫星测高数据反演重力场与真实重力场之间的误差及重力仪观测误差,下面设计两组带重力仪观测误差及系统误差的仿真实验对上述四种算法进行对比仿真.将重力量测噪声取均方差为10mGal2的高斯白噪声,系统误差设为零,INS指示航迹误差保持不变进行仿真实验二,仿真结果如图 5所示.与实验一相比,TERCOM 算法的匹配误差没有变化,而其它三种匹配算法由于观测误差较大,匹配误差明显增大.在仿真实验二中,后三种算法匹配精度没有实质差别.算法2 匹配由于采用观测数据差分预处理使得数据信噪比降低,算法匹配略受影响,又由于在仿真实验二中未加入系统误差,算法2与算法3 匹配精度相差不大.算法4 由于未经过粗匹配导致寻优范围变大,迭代9 次才收敛到最优解,而算法2与算法3仅迭代了4次.
|
图 5 仿真实验二 (a)仿真结果图;(b)误差分析图. Fig. 5 The second matching simulation experiment |
|
|
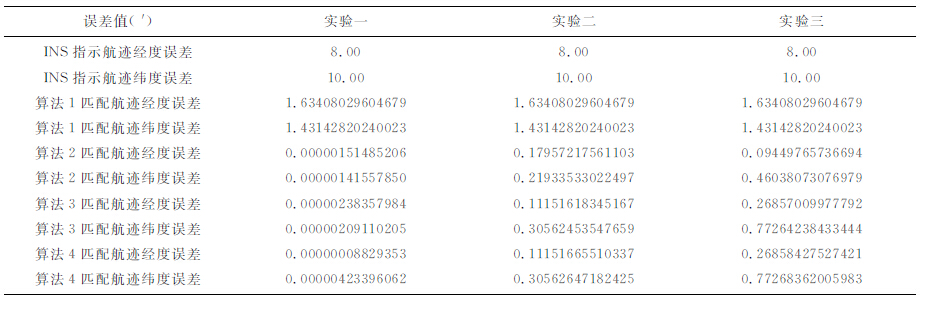
表 1 仿真实验各匹配算法误差统计表 Table 1 Statistics of simulation errors between gravity matching algorithms |
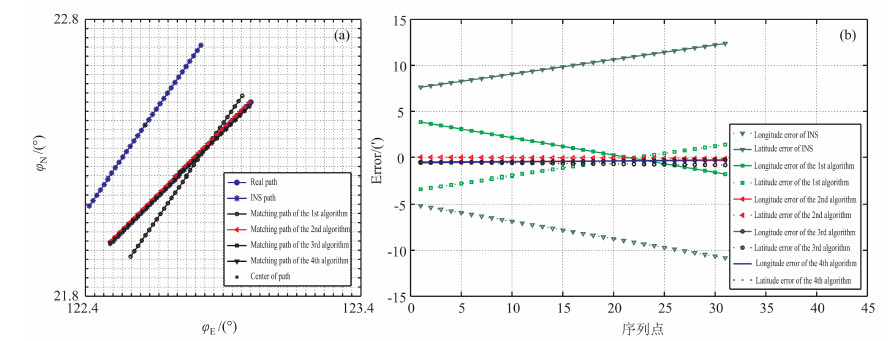
将重力量测噪声取均方差为10 mGal2 的高斯白噪声,系统误差设为2 mGal,INS 指示航迹误差不变,对四种匹配算法进行对比仿真实验三,仿真结果如图 6所示.在仿真实验三中,TERCOM 算法的匹配误差相比实验二没有变化,算法2 匹配误差较实验二没有实质差别,表现出较好的抗系统误差性,而后面两种匹配算法由于加入了系统误差,匹配误差较实验二中对应算法匹配误差有明显增大.在此次仿真实验中,算法4迭代9次才收敛到最优解,而算法2与算法3仅迭代了3次.
|
图 6 仿真实验三 (a)仿真结果图;(b)误差分析图. Fig. 6 The third matching simulation experiment |
匹配算法作为重力辅助惯性导航系统中核心技术之一,其优劣与否决定了重力辅助惯性导航系统定位精度.传统的匹配算法大多建立在离散基准图基础上,匹配精度很大程度上受限于基准图分辨率,基于这方面考虑,本文首先对局部重力异常基准图逼近进行研究,通过高斯基函数逼近获取局部重力异常基准图逼近解析式,然后在连续形式的局部重力异常基准图上进行基于非线性寻优方法的相关匹配算法建模与解算研究,最后采用数据预处理及粗、精两级组合匹配对算法进行改善,最后的仿真实验结果表明了该组合算法能在较大量测误差及系统误差条件下实现高精度匹配定位.本文为匹配算法设计研究提供了一种新的思路,具有一定现实意义.
| [1] | Clive A A, Albert J. Passive Gravity Gradiometer Navigation System. // IEEE PLANS'90: Position, Location and Navigation Symposium, 1990: 60-66. |
| [2] | Jircitano A, Dosch D. Gravity Aided Inertial Navigation System (GAINS). ION 47th Annual Meeting Proceedings , 1991: 21-229. |
| [3] | Moryl J. Advanced submarine navigation systems. Sea Technology , 1996, 37(11): 33-39. |
| [4] | 蔡体菁, 周百令. 重力梯度仪的现状和前景. 中国惯性技术学报 , 1999, 7(1): 39–42. Cai T J, Zhou B L. Status and prospects of gravity gradiometers. Journal of Chinese Inertial Technology (in Chinese) , 1999, 7(1): 39-42. |
| [5] | Hollowell J. HELI/SITAN: A terrain referenced navigation algorithm for helicopters. IEEE Position, Location and Navigation Symposium 1990 (PLANS'90), Las Vegas, NV, USA , 1990: 616-625. |
| [6] | 许大欣. 利用重力异常匹配技术实现潜艇导航. 地球物理学报 , 2005, 48(4): 812–816. Xu D X. Using gravity anomaly matching techniques to implement submarine navigation. Chinese J. Geophys. (in Chinese) , 2005, 48(4): 812-816. |
| [7] | Wang Z G, Bian S F. A local geopotential model for implementation of underwater passive navigation. Progress in Natural Science , 2008, 18(9): 1139-1145. DOI:10.1016/j.pnsc.2008.02.011 |
| [8] | Wu L, Gong J Q, Cheng H, et al. New method of underwater passive navigation based on gravity gradient. Proc. of SPIE , 2007, 6790: 67901V. |
| [9] | Jamshaid A, Fang J C. SINS/ANS Integration for augmented performance navigation solution using unscented Kalman Filtering. Aerospace Science and Technology , 2006, 10(3): 233-238. DOI:10.1016/j.ast.2005.11.009 |
| [10] | Xiao S H, Bian S F. Research on regional model of continuous fourier series of marine magnetic anomaly field using for the geomagnetic navigation. // International Conference on Industrial and Information System , 2010: 437-440. |
| [11] | Kamgar-Parsi B. Matching Sets of 3D line segments with application to polygonal arc matching. IEEE Trans on Pattern Analysis and Machine Intelligence , 1997, 19(10): 1090-1099. DOI:10.1109/34.625109 |
| [12] | Bishop G C. Gravitational field maps and navigational errors. IEEE Journal of Oceanic Engineering , 2002, 27(3): 726-737. DOI:10.1109/JOE.2002.1040954 |
| [13] | 王志刚, 边少锋. 基于ICCP算法的重力辅助惯性导航. 测绘学报 , 2008, 37(2): 147–157. Wang Z G, Bian S F. ICCP algorithm for gravity aided inertial navigation. Acta Geodaetica et Cartographica Sinica (in Chinese) , 2008, 37(2): 147-157. |
| [14] | 朱海, 王顺杰, 蔡鹏. 基于ICCP的水下直线段地磁匹配. 中国惯性技术学报 , 2009, 17(2): 153–155. Zhu H, Wang S J, Cai P. Straight-line geomagnetic matching for underwater base on ICCP. Journal of Chinese Inertial Technology (in Chinese) , 2009, 17(2): 153-155. |
| [15] | 童余德, 边少锋, 蒋东方, 等. 实时ICCP算法重力匹配仿真. 中国惯性技术学报 , 2011, 19(3): 340–343. Tong Y D, Bian S F, Jiang D F, et al. Gravity matching simulation of real-time ICCP algorithm. Journal of Chinese Inertial Technology (in Chinese) , 2011, 19(3): 340-343. |
| [16] | Priestley N. Terrain Referenced Navigation. PLANS'90 , 1990: 482-489. |
| [17] | Cowie M, Wilkinson N, Powlesland R. Latest development of the TERPROM digital terrain. // Position, Location and Navigation Symposium , 2008: 1219-1229. |
| [18] | 闫利, 崔晨风, 吴华玲. 基于TERCOM算法的重力匹配. 武汉大学学报(信息科学版) , 2009, 34(3): 261–264. Yan L, Cui C F, Wu H L. A gravity matching algorithm based on TERCOM. Geomatics and Information Science of Wuhan University (in Chinese) , 2009, 34(3): 261-264. |
| [19] | 赵建虎, 王胜平, 王爱学. 一种改进型TERCOM水下地磁匹配导航算法. 武汉大学学报·信息科学版 , 2009, 34(11): 1320–1323. Zhao J H, Wang S P, Wang A X. An improved TERCOM algorithm for underwater geomagnetic matching navigation. Geomatics and Information Science of Wuhan University (in Chinese) , 2009, 34(11): 1320-1323. |
| [20] | 夏冰, 王浩. 相关极值的重力匹配辅助导航. 光学精密工程 , 2009, 17(4): 832–837. Xia B, Wang H. Gravity matching aided navigation of maximum correlation. Optics and Precision Engineering (in Chinese) , 2009, 17(4): 832-837. |
| [21] | 刘飞, 周贤高, 杨晔, 等. 相关地磁匹配定位技术. 中国惯性技术学报 , 2007, 15(1): 59–62. Liu F, Zhou X G, Yang Y, et al. Geomagnetic matching location using correlative method. Journal of Chinese Inertial Technology (in Chinese) , 2007, 15(1): 59-62. |
| [22] | 克拉索夫斯基 A A. 相关极值导航系统理论, 任思聪译. 北京: 航空工业出版社, 1986. Krasovski A A. Theory of Maximum Correlation Navigation System (in Chinese). Translated by Ren S C. Beijing: Aviation Industry Press, 1986. |
 2012, Vol. 55
2012, Vol. 55