2. 中国科学院大学, 北京 100049;
3. 同济大学测绘与地理信息学院, 上海 200092;
4. 同济大学空间信息科学及可持续发展应用中心, 上海 200092;
5. 广东工业大学土木与交通工程学院, 广州 510006
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. College of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China;
4. Center for Spatial Information Science and Sustainable Development, Tongji University, Shanghai 200092, China;
5. Faculty of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou 510006, China
自从1960年Baker提出应用卫星观测数据反演地球重力场的理论[1],国外很多专家已进行了大量论证和数值模拟工作,如Kaula、Colombo等人做了大量研究[2-3].在经过国际同行30多年的努力后,CHAMP (Challenging Minisatellite Payload),GRACE (GravityRecoveryandClimateExperiment)和GOCE (Gravityfield and steady-state OceanCirculationExplorer)卫星相继成功发射,并计划再发射GRACE Follow-On 和GRAIL (GravityRecoveryandInteriorLaboratory).从20 世纪90年代开始,国内许多学者也开展了相关的研究工作,对发展我国重力卫星起到了很大的推动作用,如陈俊勇、宁津生、许厚泽、孙文科和罗志才等对卫星重力技术提出讨论[4-8],姜卫平等对卫星载荷做出了定性分析[9],章传银等导出了以距离的二次变率为观测值的反演方法[10],罗佳、郑伟和王正涛等用能量法进行了相关的研究[11-15],徐天河、沈云中、肖云、周旭华和邹贤才等用动力学法或基线法进行了重力场的反演工作[16-22].虽然国外的重力卫星项目已经取得长足进步,但很多关键技术对我国保密.近年来,我国正努力推进自主知识产权的重力卫星项目.重力卫星的发射可以获取全球的卫星重力观测数据,促进我国在地球科学领域的发展,提高我国在该领域的国际地位.基于我国重力卫星计划的需求,针对符合国情的重力卫星的指标论证方面的研究国内正逐步展开,比如郑伟在多篇文章里进行了论证,说明了能量法对GRACE 卫星部分指标的敏感度;然而直到目前为止,利用动力学法在重力卫星指标论证方面的国内相关研究大多都是针对低阶重力场位系数的讨论,如40 阶,60 阶等,取得了很多有意义的成果.但是重力卫星的很多指标特性在低阶位系数上得不到完整的体现,所以仍需要对高阶位系数继续展开讨论.鉴于此,本文利用动力学法反演较高阶次(130阶)来对我国未来重力卫星的各项指标进行系统的完善的论证研究,以期为我国重力卫星计划提供参考.
此外,卫星重力反演地球重力场的算法分为时域法和空域法.时域法主要包含Kaula线性摄动法、动力学法、基线法、能量法、加速度法和短弧边值法等,适合于GRACE 卫星的解算;空域法主要适合于利用GOCE 卫星数据解算地球重力场.时域法中,大部分方法需要顾及较多的局部参数(如两颗卫星的初始位置向量和加速度计的尺度偏差等参数).这些局部参数处理的好坏,对最后重力场解算的精度存在较大影响.其原因如下,首先,在单独利用星间距离或者星间距离变率来求解地球重力场模型时,无法对存在着误差的初始位置参数进行有效校正.因为星间距离和星间距离变率都是相对量,而初始位置参数是绝对量,无法仅用相对量来校正绝对量.其次,这些局部参数之间还存在着相关性,从而导致解算地球重力场时局部参数矩阵病态,而难以得到满意的解.针对这两类问题,国外学者进行了很多的研究,如Mayer等利用QR 分解法可以降低局部矩阵的病态性[23-24].在国内,也有一些学者进行了相关的研究,如张兴福通过只估计两颗卫星之间的相对速度误差的方法对卫星初始状态误差进行校正[25],肖云通过转换为基线参数的基线法来解决该问题[20].在本文里,笔者采用通过融合卫星精密轨道数据和星间距离或星间距离变率数据来求解地球重力场模型.这方法存在着如下优点:第一,以精密的双星轨道数据(绝对量)作为观测值,再融合星间距2899地球物理学报(ChineseJ.Geophys.) 55卷 离或星间距离变率数据(相对量)来校正初始位置误差,解决了上述仅由相对量无法校正绝对量的问题;第二,通过把双星轨道数据和星间距离或者星间距离变率数据结合起来,可以有效地降低局部参数矩阵的病态性;第三,重力卫星的轨道数据里包含了大量的地球重力场的低频信息,如果仅仅利用星间距离或者星间距离变率数据则没有充分挖掘GRACE卫星提供的数据信息.本方法融合了轨道数据和星间距离或者星间距离变率数据,从而充分利用了GRACE 卫星任务提供的数据.
2 理论与方法 2.1 基于轨道和星间距离以及距离变率反演重力场的基本观测模型根据牛顿运动定律,
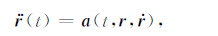
|
(1) |
式中,r,$\dot r$ ,$\ddot r$(t)分别为卫星在t时刻的位置、速度与加速度向量,a(t,r,$\dot r$)为卫星运行时所受到的加速度.通过积分可得卫星位置r与初始状态向量r(t0)、$\dot r$ (t0)、重力场位系数u、卫星所受加速度a(t),以及时间t的函数关系如下:
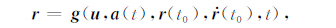
|
(2) |
式中,加速度a(t)包含中心引力、非球形引力、日月引力和各种潮汐以及太阳光压、大气阻力等各种非保守力.对于双星编队飞行的GRACE,利用公式(2)可得到基于轨道扰动Δr(t)的观测模型,
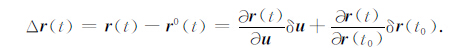
|
(3) |
若令y(t)= [r(t),$\dot r$ (t)],则可得到星间距离Δρ(t)和距离变率Δρ · (t)的观测模型,
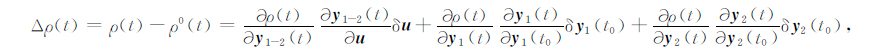
|
(4) |
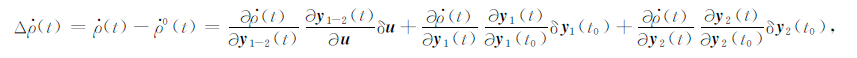
|
(5) |
式中,δy1 和δy2 分别为两颗GRACE 卫星的初始位置参数改正数(因为每个弧段都有不同的初始位置改正数,因此δy1 和δy2 也称为局部参数),δu为位系数改正数(因为每个弧段都有相同的位系数改正数δu,因此δu也称为全局参数).t0 表示初始时刻,t表示任意时刻.r0(t)、ρ0(t)与$\dot \rho $0(t)为用初始重力场模型计算的值.式中的下标1,2分别表示两颗GRACE 卫星.
2.2 联合轨道数据和星间测距数据反演地球重力场的理论两颗GRACE 卫星一直在同一轨道上相距约220km 的位置编队飞行,若单独使用星间距离或者距离变率数据,在消去局部参数的时候,必然会引起局部矩阵严重病态,从而无法求得精确解.所以,本文采用融合GRACE 轨道数据和K 波段数据来解算地球重力场模型,这不仅充分利用GRACE 卫星提供的轨道数据和K 波段数据,而且还有效地降低局部矩阵病态的问题,此外还可以在相对量(星间距离或者星间距离变率)的基础上,结合绝对量(精密轨道)来校正轨道初始位置(局部参数)误差.其观测模型如下:
融合轨道数据和K 波段星间距离数据的观测模型:

|
(6) |
合轨道数据和K 波段星间距离变率数据的观测模型:
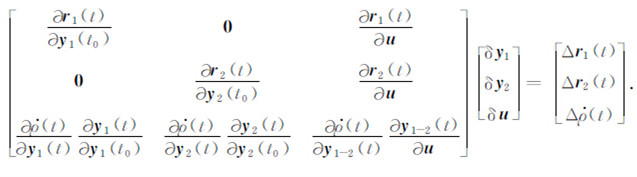
|
(7) |
对式(6)和式(7),其误差方程为
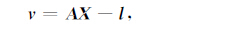
|
(8) |
式中,v为改正数,A为设计矩阵,l为常数项,X为未知数,包括局部参数δy1 与δy2 和全局参数δu,
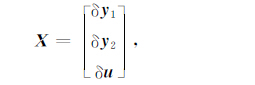
|
(9) |
法方程形式可统一表示为

|
(10) |
式中,
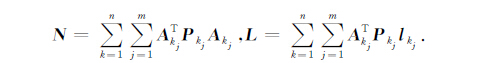
|
(11) |
设共n个弧段,每个弧段有m个历元,Akj和lkj分别为第k弧段里第j历元形成的设计矩阵和常数项,N和L分别为叠加后的法方程和常数项.在融合星间距离或者星间距离变率时,Akj和lkj的表达式不尽相同,其详细表达式为:
(1) 当轨道和星间距离数据融合时,
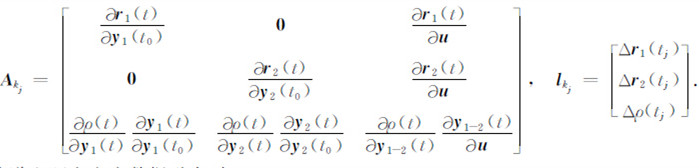
|
(12) |
(2) 当轨道和距离变率数据融合时,
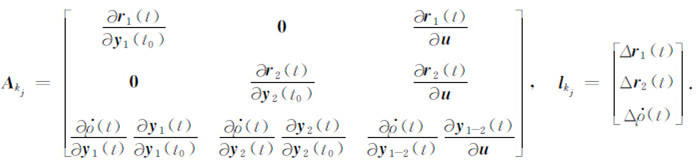
|
(13) |
式(11)中,
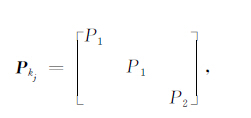
|
(14) |
P1 为GRACE 卫星精密轨道数据对应的权,P2 为GRACE 卫星K波段数据对应的权.由定权原理,设轨道对应的权P1 为1,星间距离变率或星间距离的权P2由轨道精度和距离变率或星间距离精度确定.
每个弧段的未知数包含局部参数改正数δr(表示δr1 和δr2)和位系数改正数δu,而作为全局变量的δu才是需要求解的量.因此需要消去这些局部参数得到仅含有全局变量的表达式,消去方式如下:
对式(10)可以细化为N
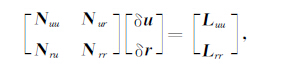
|
(15) |
式中,Nuu、Nur、Nru、Nrr分别为对应的子块,
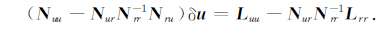
|
(16) |
式(16)为消去局部参数后的法方程,通过直接矩阵求逆或者PCCG(预条件共轭梯度法)或者其他方法,即可求解出位系数改正数.但是如果仅由星间距离或者星间距离变率数据(即式(12)或者式(13)中Akj矩阵的第三行)作为观测值,再根据与式(15)相同的方法消去局部参数后得到的局部参数矩阵Nrr呈严重的病态性,其条件数cond (Nrr)≈1020,但在融合轨道数据和星间距离或者星间距离变率数据后,cond (Nrr)≈107,条件数降低了13 个量级,再利用QR分解,可把cond(Nrr)降到103 左右,法方程矩阵已经较为稳定,可以得到很好的地球重力场反演结果.
3 指标论证与分析利用上述的融合卫星轨道数据和星间距离或距离变率数据的函数模型进行模拟计算分析,模拟计算以EIGEN-5C 作为“真实"模型,结合各种星载设备载荷的精度指标,模拟出30 天10 秒采样间隔的观测数据;以EGM96 作为初始模型,解算出130阶的地球重力场模型系数,其理论值应该等于EIGEN-5C 与EGM96 的模型系数之差.根据反演的系数与其理论值之差,探索与我国重力卫星计划的各种星载设备载荷相匹配的精度指标.
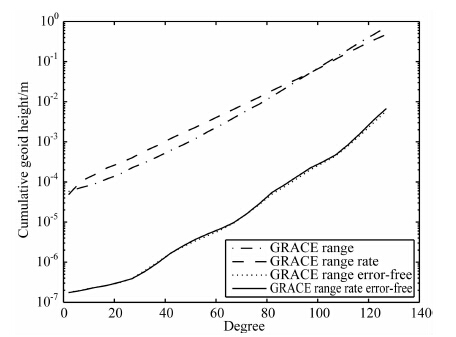
表 1 为目前运行的GRACE 卫星的设计指标.在不引入误差的情况下,分别用轨道与星间距离数据为观测值,和轨道与星间距离变率数据为观测值,反演了两组120阶重力场模型,在图 1中分别用GRACE range error-free和GRACE range rate error-free表示.从图可知,截断到120 阶的累积大地水准面差距分别为0.0023m 和0.0026m,该误差主要是计算机的舍入误差和模型线性化误差导致,可忽略不计.从而验证了本算法的正确性.
|
|
表 1 GRACE卫星计划各项设计指标 Table 1 The error configuration of GRACE |
高精度的星间测距系统数据是低低卫-卫跟踪技术反演高精度地球重力场模型的重要保证.在GRACE 的设计指标下,通过使用一个月数据的模拟验算得知,如图 1所示,在约前90阶时,用融合轨道和星间距离反演出的重力场模型(GRACE range)精度相对于融合轨道和星间距离变率数据(GRACE range rate)反演的结果体现出较大的优势,90 阶之后,前者反演出的重力场模型的精度低于后者反演出的精度,截断到130 阶时两者的累积大地水准面差距达到0.41m.
|
图 1 轨道数据和星间距离或星间距离变率数据融合解算的重力场模型的累积大地水准面差距 Fig. 1 The cumulative geoid errors of the gravitational potential model recovered from combined measurements of orbit and range or range rate data |
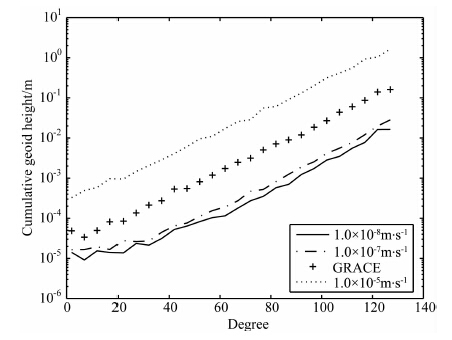
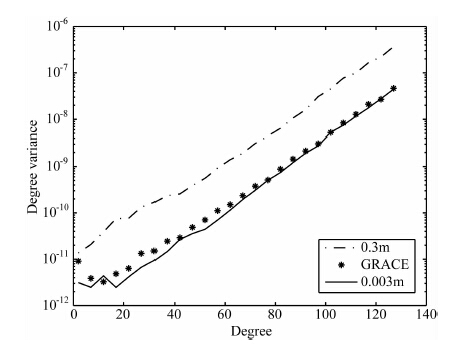
目前国际上各大机构在用GRACE 卫星实测数据反演地球重力场时通常使用星间距离变率数据,而较少使用星间距离数据.图 2表示利用不同精度的星间距离变率数据融合轨道反演的地球重力场的每阶大地水准面差距.从图 2可知,当把星间距离变率精度从1.0×10-6m·s-1降低到1.0×10-5m·s-1,其余载荷的指标与现行GRACE 保持一致时,所反演的地球重力场精度也随之降低,截断到130 阶的累积大地水准面差距增大了4.9倍.把星间距离变率分别提高到1.0×10-7m·s-1和1.0×10-8m·s-1,其余载荷的指标与现行GRACE 保持一致时反演的重力场模型,与目前运行的GRACE 卫星反演的重力场模型相比,精度大幅度提高.对于星间距离变率精度为1.0×10-6m·s-1(现行GRACE)时截断到130阶时的累积大地水准面差距为99.2cm.对于星间距离变率为1.0×10-7m·s-1时,截断到130 阶时的累积大地水准面差距为8.6cm ,较现行GRACE 任务提高10.6倍.当星间距离变率精度为1.0×10-8m·s-1时,截断到130 阶时的累积大地水准面差距为6.2cm,较GRACE 任务提高约15.2倍.即当从1.0×10-6 m·s-1提高到1.0×10-7m·s-1时,反演的重力场精度可以得到大幅度提高,大约提高一量级,与文献[28]所得结论一致,但是当从1.0×107m·s-1提高到1.0×10-8m·s-1时,反演的重力场的精度提高的幅度小于从1.0×10-6 m·s-1提高到1.0×10-7m·s-1时的幅度.
|
图 2 不同精度的星间距离变率反演的地球重力场模型的每阶大地水准面差距 Fig. 2 The geoid errors for every degree of the gravitational potential model recovered from different accuracies of range rate measurements |
从上述分析可知,随着星间距离变率精度的提高,所反演重力场精度有显著提高.结合上述分析,建议我国未来重力卫星计划采用激光干涉系统,其可把星间距离变率测量提高至1.0×10-8m·s-1.此外,从图 2可知,单独提高星间距离变率精度可以等量级地提高反演地球重力场的精度.
3.1.2 星间距离精度对反演地球重力场的影响利用精度分别为1.0×10-8m、1.0×10-7m、1.0×10-6m、1.0×10-5m 和1.0×10-4m 的星间距离观测值,其余载荷的指标与现行GRACE 卫星一致,融合轨道数据反演了130阶的重力场模型,其累积大地水准面差距的精度列于表 2.由表 2可知,星间距离精度从目前GRACE 卫星的1.0×10-5m 降低到1.0×10-4 m 时,截断到130 阶的累积大地水准面差距的精度相应降低了344.12%.当星间距离精度分别提高到1.0×10-8 m、1.0×10-7 m 和1.0×10-6m,其余载荷指标不变时所反演重力场的累积大地水准面差距与GRACE 卫星相比,精度分别只提高了3.02%、3.01%和2.85%.由此可见,在其余载荷与目前GRACE 卫星相同的情况下,单独提高星间距离精度,难以像距离变率那样大幅度提高所反演出的重力场模型精度.
|
|
表 2 不同精度的星间距离反演的地球重力场的累积大地水准面差距(m) Table 2 The cumulative geoid height of the global gravity field recovered by different accuracies of range data(m) |
在上述分析里可以发现,单独提高星间距离精度并不会大幅度地提高反演重力场的精度.但3.1.1节建议采用激光干涉系统,可使星间距离变率精度达到1.0×10-8m·s-1,相应的星间测距精度也可提高到1.0×10-7m 量级.因此,建议我国未来重力卫星的星间距离精度为1.0×10-7m.
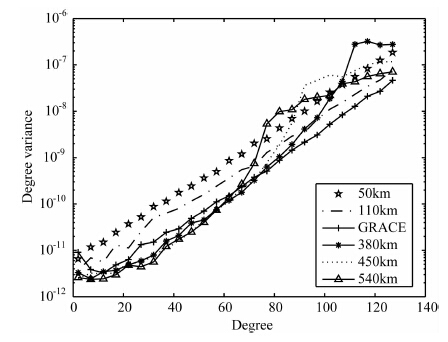
3.1.3 星间间隔对反演地球重力场的影响目前运行的GRACE 双星之间距离保持220km左右.图 3 为利用轨道和星间距离为观测值,在500km 轨道高度上,基于50km、110km、220km(现行GRACE)、380km、450km 和540km的星间间隔,其余载荷指标与现行GRACE 相同时,反演的地球重力场模型的精度分布图.由图可知,220km 的星间间隔为精度的分界线.当星间间隔从50km 变化到110km 和220km 的时候,无论是高阶还是低阶,阶方差都整体大幅降低,截断到130阶时的阶方差分别为1.13×10-7、2.93×10-7和6.56×108.当星间间隔从380km 增加到450km 以及540km 的时候,与220km 相比,其阶方差距分别约在105阶、89阶和74阶附近存在波峰,并且随着星间间隔的增加,出现阶方差波峰的阶次依次降低,从约105阶降低到74阶左右.此外,在出现波峰之前的低阶位系数阶方差里,GRACE 卫星相距越远,精度越高.由此可知,较长的星间间隔利于地球重力场长波的恢复,而较短的星间间隔利于重力场中长波的恢复.
|
图 3 不同的星间间隔反演的地球重力场模型的每阶大地水准面差距 Fig. 3 The geoid errors of the gravitational potential model recovered from different inter-satellite distances |
在卫星跟踪卫星(SST)观测方程里包含sin(ηβ),η表示用角度表示的星间间隔的一半,β为正则化的SST 观测频率[26].由于该观测方程特性,将使反演出的地球重力场位系数产生如图 3 所示的波峰现象.出现波峰现象的阶次计算公式如下:
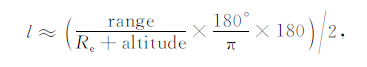
|
(17) |
式中,l表示阶数,range表示星间间隔,Re 表示地球平均半径,altitude表示卫星轨道高度.对于这种波峰现象,在设计重力卫星的时候应尽量避免其出现在重力卫星所能反演的有效阶次内.220km 的星间间隔虽然在反演重力场的低阶位系数的精度上,比50km 以及110km 高,但其会在180 阶的时候出现波峰现象,这将因为星间距离问题影响该阶次的重力场信号的提取.表 3 为不同的星间间隔出现波峰现象的阶次.
|
|
表 3 不同星间间隔所对应的首次波峰出现阶次 Table 3 The degree of the first peak for different ranges |
在对星间距离变率指标的论证时,已建议下一代重力卫星选择基于激光干涉的测量系统.综合避免波峰现象,激光干涉系统的最佳有效测量距离,以及确定重力场长波分量(较短星间间隔)与短波分量(较长星间间隔)的平衡等三方面的影响,建议我国未来重力卫星星间间隔定为100km 左右[27].
3.2 星载加速度计精度对反演地球重力场的影响由于难以用精确的模型对大气阻力、太阳光压和地球反照辐射压等非保守力进行建模,所以通常使用加速度计来测量非保守力.非保守力测量精度的高低直接关系到卫星定轨和重力场反演的精度.表 4所示为利用轨道和星间距离为观测值,在不同精度的星载加速度计指标,其余载荷保持和现行GRACE相同时,反演出的地球重力场模型的累积大地水准面差距.在加速度计精度为3.0×10-10m·s-2,3.0×10-11 m·s-2和3.0×10-12 m·s-2,其余指标与GRACE 卫星相同的情况下,反演出的重力场模型的精度依次提高,但是相差很小,如表 4 所示.当星载加速度计精度降为3.0×10-9m·s-2时,反演出的重力场模型精度降低,截断到130阶,比现行GRACE 卫星任务降低4.16倍.
|
|
表 4 不同精度加速度计指标反演的地球重力场的累积大地水准面差距精度(m) Table 4 The cumulative geoid height of the global gravity field recovered by different accuracies of acceleration data(m) |
在星载加速度的测量方面,目前国际上比较流行采用drag-free控制系统,该方法可以把非保守力测量精度在目前GRACE 的测量基础上,提高两量级左右.但表 4数据显示,星载加速度计精度提高两量级对反演地球重力场的精度提高并不明显.因此,如果从反演地球重力场精度的角度考虑,目前GRACE 卫星所搭载的加速度计精度已经满足要求,建议我国未来重力卫星的星载加速度计指标定为3.0×10-10m·s-2.
3.3 低轨卫星定轨精度对反演地球重力场的影响利用卫星轨道和星间距离为观测值,在定轨精度分别为3mm、3cm 和3dm,其余载荷指标与现行GRACE 相同时,反演出一组重力场模型,其阶方差如图 4所示.图 4表明,定轨精度为3dm 的阶方差比3cm(现行GRACE)大,其累积大地水准面差距截断到130 阶时,增大了692.48%.对于定轨精度为3mm 与3cm 反演出的重力场模型,约在前80阶时,3mm 的轨道比3cm 的轨道反演的重力场模型的精度高.在80阶到130阶时虽有所提高,但相差的幅度较前80阶小很多.其原因在于卫星轨道摄动受重力场模型的长波部分影响较大,但受短波部分影响较小,因此在反演地球重力场时,轨道对短波部分的贡献也相对较小,所以在提高轨道精度后反演出的地球重力场模型在长波部分精度提高幅度较大,在短波部分提高幅度不明显.
|
图 4 不同精度的轨道反演的地球重力场模型的阶方差 Fig. 4 The cumulative geoid height of the global gravity field recovered by different accuracies of orbit data |
通过利用融合轨道和星间距离数据的模拟可知,分米级(3dm)轨道所反演的重力场模型精度明显低于厘米级(3cm)轨道反演的重力场模型精度,与厘米级轨道相比截断到130阶时的累积大地水准面差距增大了6.92倍.毫米级(3 mm)轨道反演的重力场模型与厘米级轨道相比虽然在低阶位系数上有所提高,但是在高阶位系数上的提高幅度不大.考虑到目前的定轨技术,建议中国的重力卫星的轨道精度定为厘米级(3cm 左右).
3.4 低轨卫星速度精度对反演地球重力场的影响GRACE 卫星的速度对反演重力场存在着重要的影响.如果利用经典动力学法反演地球重力场,则容易发现速度误差对状态转移矩阵和参数敏感矩阵影响较大.表 5表示利用轨道和星间距离为观测值,在速度误差分别为3.0×10-4m·s-1,3.0×10-5 m·s-1和3.0×10-6 m·s-1,其余载荷与现行GRACE 保持相同时,反演出的重力场模型精度信息.如表 5 所示,速度误差精度为3.0×10-4 m·s-1 和3.0×105 m·s-1时,反演的重力场模型精度相差不大.当速度误差为3.0×10-6 m·s-1时反演出的重力场精度比误差为3.0×10-5 m·s-1时提高约1.48倍.因此,建议我国重力卫星的速度精度定为3.0×106m·s-1.
|
|
表 5 不同精度的星间速度反演的地球重力场的累积大地水准面差距(m) Table 5 The cumulative geoid height of the global gravity field recovered by different accuracies of velocity data(m) |
轨道倾角越接近90°卫星所覆盖的地面范围越大.现行的GRACE 卫星轨道倾角为89°,分别在南北极存在着1°的空白区域.表 6表示利用轨道和星间距离为观测值,在轨道倾角为88.5°,89°和89.5°,其余指标和现行GRACE 相同时,反演出的重力场模型的精度信息,截断到130 阶时的累积大地水准面差距分别为1.19×10+0m,9.91×10-1 m 和1.04×10+0m,相差幅度很小,说明在该幅度变化的轨道倾角对反演地球重力场的影响不明显.因此建议中国重力卫星的轨道倾角定为89°左右,与现行GRACE 保持一致.
|
|
表 6 不同轨道倾角反演的地球重力场的累积大地水准面差距(m) Table 6 The cumulative geoid height of the global gravity field recovered by different inclination of orbit (m) |
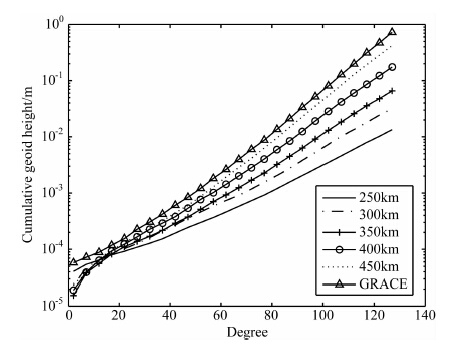
现行GRACE 任务的初始轨道高度为500km,在所有的载荷中,影响重力场最大的就是轨道的高低.卫星轨道越低所探测到的重力场信息越多,反演出的重力场精度越高.也正因此,GOCE 卫星的轨道降为250km,但轨道越低,卫星受到的中心引力和大气阻力等越大,卫星的运行时间也越短.因此需在轨道高度和运行时间之间做出折中选择.图 5 表示在利用轨道和星间距离为观测值,轨道高度分别为250,300,350,400,450km 和500km,其余载荷指标和现行GRACE 相同时,反演出的重力场模型的精度信息,截断到130 阶的累积大地水准面差距分别为1.63×10-2,3.79×10-2,8.09×10-2,2.14×10-1,5.23×10-1 m和9.91×10-1 m.对卫星轨道高度从250km增加到450km时与现行的GRACE(500km)相比,精度提高约5985.98%,2512.43%,1125.12%,363.33%和89.37%.虽然轨道越低越利于提高重力场模型的精度,但是卫星的在轨运行时间也会相应降低很多;高轨卫星虽然寿命较长,但是反演的重力场模型的精度较低,因此必须采取折中选择,轨道不宜过高,也不宜过低.目前GRACE 卫星的运行时间即将到第十年,为长期监测地球重力场的质量分布等信息提供了宝贵的数据.因此建议下一代重力卫星的在轨运行时间也可考虑维持在10 年左右[28].从轨道高度和运行时间的关系[28],建议我国未来重力卫星轨道高度定为300km 左右.
|
图 5 不同轨道高度反演的地球重力场模型的累积大地水准面差距 Fig. 5 The cumulative geoid height of the global gravity field recovered by different altitudes |
度的预期估计通过综合上述对重力卫星各项关键载荷精度指标的系统分析和建议,并且结合我国目前仪器研制的情况,笔者分别采用两组指标对我国的重力卫星任务进行讨论.
第一,若保守估计各项主要指标分别比现行GRACE 精度指标降低一个数量级时,如表 7所示,即星间距离精度为1.0×10-4m,星间距离变率精度为1.0×10-5 m ·s-1,星载加速度计精度为3.0×10-9m·s-2,其余指标和现行GRACE 保持一致,分别用精密轨道融合星间距离数据和星间距离变率数据反演了两个地球重力场模型(本文称之为LOW-GRACE range 和LOW-GRACE range rate),如图 6a所示.从图 6a可知,与现行GRACE相比,用轨道融合星间距离数据和星间距离变率数据所反演的地球重力场截断到130阶累积大地水准面差距分别增大5.27和5.10倍.
|
|
表 7 LOW-GRACE和Advanced GRACE Ⅱ的各项载荷的精度指标 Table 7 Error configuration for LOW-GRACE and Advanced GRACE |
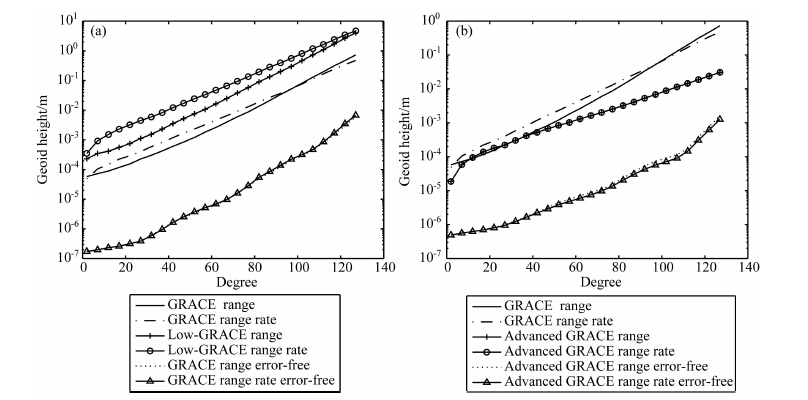
|
图 6 下一代重力卫星的预期精度图 Fig. 6 The expected accuracy of global gravity field of future satellite gravity mission |
第二,如果我国重力卫星采用先进的激光干涉测量系统,并适当地降低卫星轨道,即采用表 7中的相应指标.分别用精密轨道数据融合星间距离和星间距离变率数据可反演出两个地球重力场模型(本文称之为Advanced GRACE range 和AdvancedGRACE range rate),如图 6b 所示.在图 6b,Advanced GRACE range error-free 和Advanced GRACE range rate error-free这两个模型表示在观100测值不加误差的情况下反演出的120阶的重力场模型.从图可知,Advanced GRACE 的精度比GRACE和Low-GRACE 大幅度提高,与GRACE 相比,由轨道分别融合星间距离数据与星间距离变率数据所反演的地球重力场,截断到130 阶时累积大地水准面差距的精度分别提高24.38和121.37倍.
5 结论与建议本文研究了融合轨道数据和星间距离或星间距离变率数据反演高阶地球重力场的方法,并对算法的正确性进行了验证.在此基础上,对我国自主的重力卫星的指标进行论证,得到了如下结论和建议.
(1) 在算法上,本文的融合方法避免仅用星间距离或星间距离变率无法对卫星初始状态向量进行校正的弊端;此外,通过融合双星精密轨道数据,充分挖掘了精密轨道数据中含有的地球重力场的低频段信息;通过融合轨道数据和星间距离或者星间距离变率数据作为观测值,可以使局部参数矩阵的条件数降低13 个量级,从而有效地降低了矩阵病态性.
(2) 鉴于我国目前仪器研制水平和卫星方面的实力,如果达不到现行GRACE 指标,则发射的重力卫星反演的重力场精度会在一定程度上降低.如,各项载荷指标取为Low GRACE 时,分别用精密轨道融合星间距离数据或星间距离变率数据反演了两个地球重力场模型,与现行GRACE 相比,截断到130阶地球重力场精度最少降低5.10倍.
(3) 用本文推荐的Advanced GRACE 指标,分别用精密轨道融合星间距离数据或星间距离变率数据反演了两个地球重力场模型,较目前的GRACE卫星反演的重力场模型的精度提高幅度明显.与现行GRACE 卫星相比,截断到130阶时,融合轨道和星间距离数据所解算的模型的累积大地水准面差距为0.10m;融合轨道和星间距离变率数据所解算的模型的累积大地水准面为0.0027 m,分别提高约24.38和121.37倍.
(4) 在把星间距离变率精度从1.0×10-6m·s-1提高到1.0×10-7m·s-1,其余指标保持与现行GRACE 卫星一致时,截断到130 阶时的累积大地水准面差距为8.6cm,较现行GRACE 任务提高10.6倍.即把现行GRACE 卫星的星间距离变率指标提高一个量级,可以使地球重力场的精度等量级提高.
致谢感谢中国科学院测量与地球物理研究所郑伟副研究员和慕尼黑工业大学(TUM)易维勇博士给予的帮助.
| [1] | Baker R M L. Orbit determination from range and range-rate data // Semi-Annual Meeting of the American Rocket Society. Los Angeles: ARS Preprint, 1960: 1220-1260. |
| [2] | Kaula W M. Inference of variations in gravity field from satellite to satellite range rate. J. Geophys. Res. , 1983, 88(B10): 8345-8349. DOI:10.1029/JB088iB10p08345 |
| [3] | Colombo O L. The global mapping of gravity with two satellites. Netherlands Geodetic Commission, New Series , 1984, 7(3): 1-253. |
| [4] | 陈俊勇. 现代低轨卫星对地球重力场探测的实践和进展. 测绘科学 , 2002, 27(1): 8–10. Chen J Y. Recent development in the earth gravity field determination by modern LEO satellite. Science of Surveying and Mapping (in Chinese) , 2002, 27(1): 8-10. |
| [5] | 宁津生, 罗志才. 卫星跟踪卫星技术的进展及应用前景. 地球科学进展 , 2000, 25(4): 1–4. Ning J S, Luo Z C. The progress and application prospects of Satellite-to-Satellite Tracking technology. Advances in Earth Science (in Chinese) , 2000, 25(4): 1-4. |
| [6] | 许厚泽. 卫星重力研究: 21世纪大地测量研究的新热点. 测绘科学 , 2001, 26(3): 1–3. Xu H Z. Satellite gravity missions-new hotpoint in geodesy. Science of Surveying and Mapping (in Chinese) , 2001, 26(3): 1-3. |
| [7] | 孙文科. 低轨道人造卫星(CHAMP、GRACE、GOCE)与高精度地球重力场——卫星重力大地测量的最新发展及其对地球科学的重大影响. 大地测量与地球动力学 , 2002, 22(1): 92–100. Sun W K. Satellite in low orbit (CHAMP, GRACE, GOCE) and high precision earth gravity field: the latest progress of satellite gravity geodesy and its great influence on geoscience. Journal of Geodesy and Geodynamics (in Chinese) , 2002, 22(1): 92-100. |
| [8] | 罗志才. 利用卫星重力梯度数据确定地球重力场的理论和方法. 武汉: 武汉大学, 1996. Luo Z C. The theory and methodology for determining the Earth's gravity field using satellite gravity gradiometry data (in Chinese). Wuhan: Wuhan University, 1996. http://www.oalib.com/references/18987363 |
| [9] | 姜卫平, 章传银, 李建成. 重力卫星主要有效载荷指标分析与确定. 武汉大学学报(信息科学版) , 2003, 28(S1): 104–109. Jiang W P, Zhang C Y, Li J C. Analysis and determination of the major payload indexes for gravity exploring satellite. Geomatics and Information Science of Wuhan University (in Chinese) , 2003, 28(S1): 104-109. |
| [10] | 章传银, 胡建国, 党亚民, 等. 多种跟踪组合卫星重力场恢复方法初探. 武汉大学学报(信息科学版) , 2003, 28(S1): 137–141. Zhang C Y, Hu J G, Dang Y M, et al. Gravity field recovery method with several kinds of satellite tracking data. Geomatics and Information Science of Wuhan University (in Chinese) , 2003, 28(S1): 137-141. |
| [11] | 罗佳. 利用卫星跟踪卫星确定地球重力场的理论和方法. 武汉: 武汉大学, 2003. Luo J. Theory and methodology of Earth gravity field determination using satellite-to-satellite tracking (in Chinese). Wuhan: Wuhan University, 2003. http://cdmd.cnki.com.cn/Article/CDMD-10486-2006031869.htm |
| [12] | 郑伟. 基于卫星重力测量恢复地球重力场的理论和方法. 武汉: 华中科技大学, 2007. Zheng W. Theory and methodology of Earth's gravitational field recovery based on satellite gravity measurement (in Chinese). Wuhan: Huazhong University of Science and Technology, 2007. |
| [13] | 郑伟, 许厚泽, 钟敏, 等. 卫-卫跟踪测量模式中轨道高度的优化选取. 大地测量与地球动力学 , 2009, 29(2): 100–105. Zheng W, Xu H Z, Zhong M, et al. Optimal design of orbital altitude in satellite-to-satellite tracking model. Journal of Geodesy and Geodynamics (in Chinese) , 2009, 29(2): 100-105. |
| [14] | 郑伟, 许厚泽, 钟敏, 等. 卫星跟踪卫星模式中轨道参数需求分析. 天文学报 , 2010, 51(1): 65–74. Zheng W, Xu H Z, Zhong M, et al. Requirement analysis of orbit parameters in the satellite-to-satellite tracking model. Chinese Astronomy and Astrophysics (in Chinese) , 2010, 51(1): 65-74. |
| [15] | 王正涛. 卫星跟踪卫星测量确定地球重力场的理论与方法. 武汉: 武汉大学, 2005. Wang Z T. Theory and methodology of Earth gravity field recovery by satellite-to-satellite tracking data (in Chinese). Wuhan: Wuhan University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10486-2006031327.htm |
| [16] | 徐天河, 杨元喜. 利用CHAMP卫星几何法轨道恢复地球重力场模型. 地球物理学报 , 2005, 48(2): 288–293. Xu T H, Yang Y X. CHAMP gravity field recovery using kinematic orbits. Chinese J. Geophys. (in Chinese) , 2005, 48(2): 288-293. |
| [17] | 沈云中, 许厚泽. 应用CHAMP星历精化地球重力场的正则化算法与模拟结果. 测绘学报 , 2003, 32(1): 11–14. Shen Y Z, Xu H Z. The regularization solution model and simulating results of modifying the geopotential model with the ephemerides of CHAMP. Acta Geodaetica Et Cartographica Sinica (in Chinese) , 2003, 32(1): 11-14. |
| [18] | 沈云中, 许厚泽. 卫-卫跟踪重力卫星测量模式的模拟与精度分析 // 大地测量与地球动力学进展. 武汉: 湖北科学技术出版社, 2004. Shen Y Z, Xu H Z. Simulation of recovering the geopotential model based on the Satellite to Satellite Tracking gravity mission // Progress in Geodesy and Geodynamics (in Chinese). Wuhan: Hubei Science and Technology Press, 2004. |
| [19] | 肖云, 夏哲仁, 王兴涛. 高低卫卫跟踪模式恢复地球重力场的误差分析. 测绘学报 , 2006, 35(2): 106–111. Xiao Y, Xia Z R, Wang X T. Error analyses for recovery of the earth's gravity field by HL-SST technique. Acta Geodaeticaet Cartographica Sinica (in Chinese) , 2006, 35(2): 106-111. |
| [20] | 肖云. 基于卫星跟踪卫星数据恢复地球重力场的研究.郑州:信息工程大学测绘学院,2006. Xiao Y. Analysis of earth gravity field recovery by satellite-to-satellite tracking data (in Chinese). Zhengzhou: School of Geodesy and Geomatics, Information Engineering University, 2006. |
| [21] | 周旭华. 卫星重力及其应用研究. 武汉: 中国科学院测量与地球物理研究所, 2005. Zhou X H. Study on satellite gravity and its application (in Chinese). Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2005. |
| [22] | 邹贤才. 卫星轨道理论与地球重力场模型的确定. 武汉: 武汉大学, 2007. Zou X C. Theory of satellite orbit and earth gravity field determination (in Chinese). Wuhan: Wuhan University, 2007. |
| [23] | Mayer-Gürr T, Ilk K H, Eicher A, et al. ITG-CHAMP01: a CHAMP gravity field model from short kinematic arcs over a one-year observation period. J. Geodesy , 2005, 78(7-8): 462-480. DOI:10.1007/s00190-004-0413-2 |
| [24] | Mayer-Gürr T. Gravitationsfeldbestimmung aus der analyse kurzer Bahnboegen am Beispiel der Satellitenmissionen CHAMP und GRACE. Bonn: Institute Fuer Theoretische Geodaesi der Universitaet Bonn, 2006. |
| [25] | 张兴福. 应用低轨卫星跟踪数据反演地球重力场模型. 上海: 同济大学, 2007. Zhang X F. The earth's field model recovery on the basis of satellite-to-satellite tracking missions (in Chinese). Shanghai: Tongji University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10247-2007222863.htm |
| [26] | Nico S, Jakob F, Reiner R. Science requirements on future missions and simulated mission scenarios. Earth, Moon, and Planets , 2005, 94(1-2): 113-142. |
| [27] | Wiese D N, Nerem R S, Lemoine F G. Design considerations for a dedicated gravity recovery satellite mission consisting of two pairs of satellites. J. Geodesy , 2011, 86(2): 81-98. |
| [28] | 张兴福, 沈云中. 联合GRACE卫星轨道及距离变率数据反演地球重力场方法研究. 大地测量与地球动力学 , 2011, 31(2): 66–70. Zhang X F, Shen Y Z. Method of gravity field inversion with combining GRACE orbits and range-rate observations. Journal of Geodesy and Geodynamics (in Chinese) , 2011, 31(2): 66-70. |
 2012, Vol. 55
2012, Vol. 55









