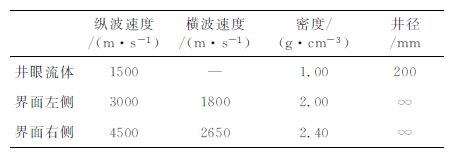
随着石油、天然气及矿藏勘探和开发需求的增长及测井技术的发展,需要对井周围数米到数十米范围内的地层构造及地质体进行探测.这些构造或地质体的具体例子如,地层界面、裂缝、断层、溶洞和矿体等等.在井中对这些构造地质体的测量技术称为远探测技术.它把常规测井技术的测量范围从井周一米左右提高到几十米.该技术应用前景十分巨大,可以用来显示与井相交的地质界面;可以用来探测井旁的倾斜地层界面、裂缝、断层、尖灭及盐丘内部构造等[1-7];在水平井中用来追踪油储边界[8];这项技术还有可能用来在钻井过程中探测钻头前面地层的信息,以决定钻井的下一步走向和位置,进行地质导向.
目前的远探测技术有声和电两种,电法远探测由井中的仪器向地层深部发射低频电磁波,用以探测井周围地质异常体与背景地质电阻率的差异造成的电阻率异常.然而,低频电磁波的分辨率很低,所以电法远探测往往只能感知异常体的存在而难以确定其具体位置,而用于地质导向的方位电磁波的频率较高,只能探测数米范围内的地质体[9].
声波的远探测技术分单极纵波法和偶极横波法两种.前者利用井中单极子声源向井外辐射的纵波,并接收从井外地质体反射回来的波来确定地质体的位置.1998 年,Schlumberger公司推出了利用单极纵波法进行单井反射波成像的测井仪BARS(Borehole Acoustic Reflection Survey)[10];国内,在薛梅、楚泽涵(2002)[11]、车小花、乔文孝(2003)[12-14]、CNPC 大港测井公司(2001)以及何峰江、陶果(2005)[15]等的研究基础之上,针对单极声源条件下的反射声波,于2005年研制了新型远探测声波反射波测井仪器,取得了一定的应用效果.但是,由于采用无方向性的单极声源激发,因而该方法不能确定反射体的方位,只给出地层三维空间中界面的二维图像;另外,单极纵波的频率一般在10kHz左右,较高频率的波衰减造成其探测范围有限,约为数米到十数米的范围.
基于以上单极纵波法的不足和存在的问题,TangX.M.于2004年首次把偶极子用于单井反射声波测井中[16],并提出了偶极横波的远探测声波成像方法,该方法采用偶极子声源在井中向井外发射横波,并在井中接收由井外地质体反射回来的横波.TangX.M.和PattersonD.J.(2009)利用四分量偶极数据对井旁裂缝和盐丘内部的精细构造进行了成像[17].与单极纵波法相比,偶极声源使用的频率约为2~5kHz.由于频率较低,该方法有较深的横向探测距离,可达二、三十米的范围.此外,由于偶极子声源的指向性具有方向性,采用多分量(实际中为四分量)的偶极发射和接收,可以确定反射体界面的方位.结合数值模拟计算结果,本文进一步指出,在慢速地层中使用偶极声源辐射的纵波进行远探测测井具有较高的探测灵敏度,并可同时确定反射体的位置和方位.偶极声源的方位灵敏度使得偶极声波法不但能确定发射体的位置,还能确定其方位,因而较单极声波法有相当的优越性.
虽然偶极声波测井技术已经问世了三十多年[18],但用井中的偶极声源来做远探测测井,只是最近才发展起来的,也存在一个发现和认识的过程.一种观点认为偶极声源的用途是在井中产生弯曲波来进行横波和横波各向异性测井,在物理直观上难以把井的弯曲振动与井外的辐射声场联系起来,因而不能用于远探测测井;另一种观点则认为用偶极这种指向声源发射信号,当源指向发射体时可以得到反射信号,而当源指向偏离反射体时,反射便消失,不利于进行远探测测井.针对以上偶极远探测的种种不完整的认识,并加深对偶极远探测技术的理解,有必要对其基本原理和方法做一系统的论述.
下文中,我们从井中偶极声场的基本理论出发,详尽地推导了其远场辐射的渐进表达式,从中可以明确理解其远场辐射特征;首次全面系统地结合对偶极辐射声场的数值模拟,加深了远场辐射特征及反射声场的理解.更为重要的是,通过对偶极远探测测井数据成像处理结果,我们可以从实际数据中看到这些特征的具体体现及其远探测成像的效果.
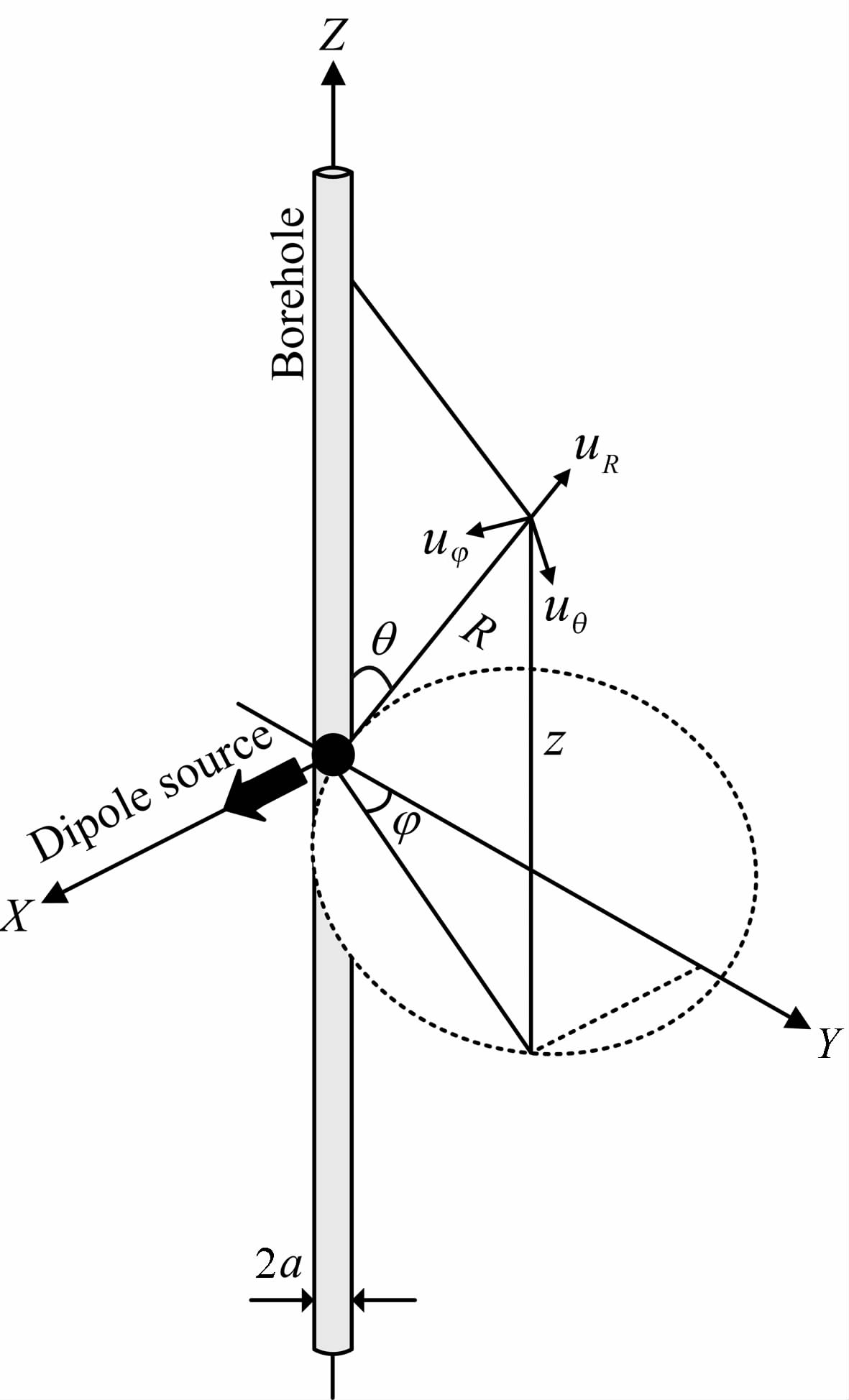
2 基本理论/方法 2.1 井中偶极声源的远场辐射特征我们首先对位于井中的偶极声源在井中和井外产生的声场进行理论分析.如图 1所示,将一偶极声源置于充液井孔中,该声源在井中产生沿井轴传播的波.在数千赫兹频率范围内,这种波一般是以弯曲波的形式传播.井中流体波动的位移可用势函数Φf表示为:
|
图 1 充液井孔中的偶极声源在激发沿井传播的波动 的同时也向井外地层辐射声波.辐射声场采用图示的柱 坐标系描述 Fig. 1 A dipole source in a fluid-filled borehole generates wave propagation along borehole and radiates elastic waves into formation. A cylindrical coordinate system is used to analyze the far-field radiation of a dipole source in a fluid-filled borehole of radius a |
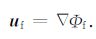
|
(1) |
在偶极声源工作的同时,它还向井外地层辐射出弹性波.井外辐射的弹性波包括纵(P)波,及在竖直(SV)和水平面(SH)内偏振的两种横波.井外弹性波的位移场为:
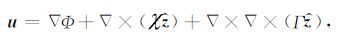
|
(2) |
其中,${\hat z}$竖直向的单位向量;井外P 波、SV 波和SH波,及其井中流体声波的位移势函数Φ、χ、Γ 和Φf分别为:
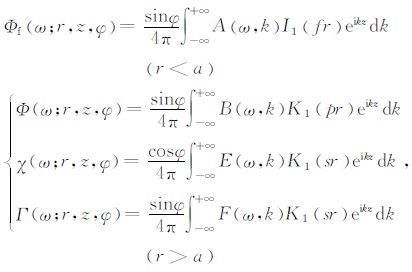
|
(3) |
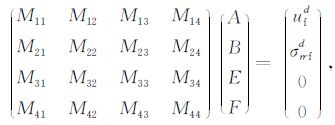
其中,r和z为径向和轴向距离,a为井的半径,φ 为波场产生的质点振动所在竖直平面的方位与偶极指向的夹角的余角(见图 1:这样选择方位角是为了方便以下波场反射和接收的讨论),ω 为圆频率;A、B、E和F分别为井中声波、井外P 波、SV 波和SH 波的振幅系数,由下面的矩阵方程确定[19]:
|
(4) |
设声源随频率变化的谱函数为S(ω),则上式中偶极源辐射到井壁的径向位移和应力分别由下式表示:
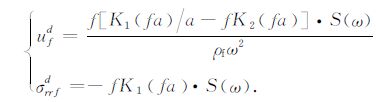
|
(5) |
(4)式中的矩阵各个元素的数学表达式如下:
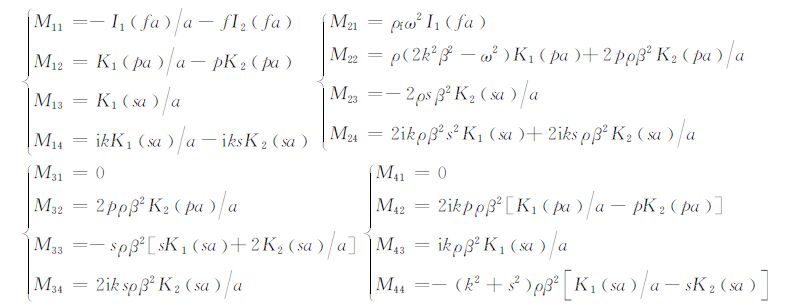
|
(6) |
其中,In和Kn(n=0,1,2…)分别为第一类、第二类n阶变型贝塞尔函数;$p = \sqrt {{k^2} - {\omega ^2}/{\alpha ^2}} $,$s = \sqrt {{k^2} - {\omega ^2}/{\beta ^2}} $和$f = \sqrt {{k^2} - {\omega ^2}/\alpha _{\rm{f}}^2} $分别为纵波、横波和井中流体声波的径向波数;α、β 和αf 分别为纵波速度、横波速度和井孔流体速度;k为轴向波数.
偶极声场的远场辐射表达式可以将最速下降法[20]用于(3)式中的井外声场(r>a)的积分表达式,由此有
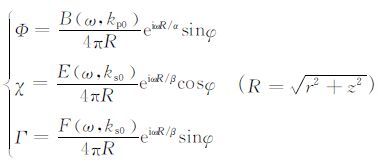
|
(7) |
其中,Kp0 =cosθ·ω/α、ks0 =cosθ·ω/β分别为纵波和横波轴向波数的最速下降解,再在低频(波长远大于井径)的条件下求出(4)式中的振幅系数:
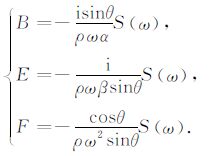
|
(8) |
最后,代入(2)式得到P波、SV 波和SH 波位移的远场渐近表达式:
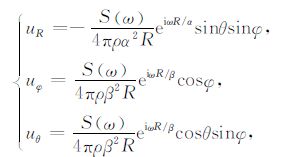
|
(9) |
式中,R为源到接收点的距离;uR为R向质点位移,即为纵波的位移;uφ 为平行于水平面的质点位移,即SH 型横波,而uθ 为与垂直向夹角为θ 的方向上的SV 型横波.(9)式的数学表达式与无穷大弹性介质中一集中力源(力的方向和偶极指向相同)的远场辐射表达式完全一致[21].由此可见,位于充液井中低频偶极声源的远场辐射与无限介质中的单力源的辐射是完全等同的[22].辐射场中不但有纵波,而且还有SH 和SV 型横波.
根据(9)式我们可以比较偶极辐射与单极辐射的异同.井中单极辐射的远场位移场[22]为
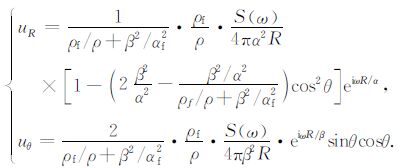
|
(10) |
两种辐射场随距离的几何扩散因子均为1/R,说明两辐射场均以球面波形式向外传播.与单极场最大不同之处是偶极辐射中含有SH 横波((9)式中uφ项),它不随垂直向角度θ 变化,具有良好的辐射覆盖特征.偶极辐射的远场与井中流体性质无关,而单极辐射则相关,这是因为单极在井中产生的声压靠流体的体积变化传递,而偶极在井中产生的流体体积的总体变化为零,故其声场对流体的依赖性较低,低频时更是如此.与单极辐射场的另一主要区别是偶极辐射场随方位变化.将(9)式中的方位角φ 取为偶极指向与反射体(视为平面)走向的夹角.当偶极指向反射体平面时,即φ=90°,可以向其辐射纵波和SV 波;当偶极指向与反射体平面平行时,即φ=0°时,显然这时辐射的纵波和SV 波消失,但这时却能获得SH 辐射的最大振幅.利用SH 波辐射的反射成像---是偶极横波远探测的一个重要依据.
2.2 偶极辐射声场的反射和接收我们来讨论一下井外反射体对偶极辐射声场的反射以及井中的接收换能器对经反射回到井中的反射波的接收.为了更方便地讨论反射体对辐射声场的反射,我们选垂直于反射体平面的波入射面作为参考面.当偶极指向位于入射面时,将在入射面内振动的纵波和横波定义为P 和SV 波;当偶极指向平行于反射体走向时,将沿此方向偏振的横波定义为SH 波.这样定义的好处是可以直接引用以入射面为参考的P 波,SV 波及SH 波的反射理论和结果(如反射系数等).我们从(9)式已经知道偶极辐射声场是具有方向(θ,φ)调制的球面波,这从声场的球面波几何扩散因子1/R可以看出.在波长小于反射体尺度的条件下,将反射体近似为一无穷大平面,对于以$\frac{1}{R}{{\rm{e}}^{{\rm{i}}\omega R/v}}$(v为波速)形式入射到平面上的球面波,其反射波的形式为[3]
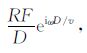
|
(11) |
其中,RF为(入射波为平面波时的)反射系数;D为从源到反射点,再从反射点到接收点波的传播总距离.考虑到波在传播过程中的非弹性吸收(用品质因子Q表示),上式可进一步写为
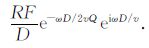
|
(12) |
当反射波从地层向井中入射时,随相对于井轴的入射角度的不同,充液井孔对波的振幅也有调制作用,叫做井的接收角度调制[24].调制后的声场从(12)式变为
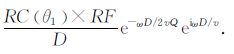
|
(13) |
其中,RC(θ1) 为接收角度调制因子,θ1 为入射角.事实上,接收因子与辐射因子有相同的函数关系.根据弹性波的互易原理,井中声源远场的辐射指向与其远处声场向井入射的接收方向因子是相等的[25].
综上所述,我们把通过低频声源远场辐射((9)式)、反射和非弹性传播衰减,以及受到井的接收调制后的P波,SV 波及SH 波的位移写为
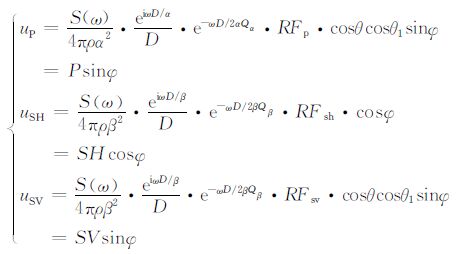
|
(14) |
其中,RFp、RFsh、RFsv分别为P 波、SV 波和SH 波的反射系数;θ 和θ1 分别为波从井中的出射角及反射回来后相对于井轴的入射角;Qα和Qβ分别为地层纵、横波的品质因子;SH、P和SV分别表示偶极声源指向与反射体入射面垂直、共面时在井中得到的SH、P和SV 波.
现在考虑在井中用两组正交的偶极发射和接收系统来接收这些入射波.一组系统的指向为x向,另一组系统的指向为y向.接收到的信号实际上就是把入射的位移矢量投影到x和y方向,得到两个分量:
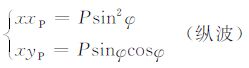
|
(15) |
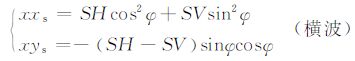
|
(16) |
类似地,我们把x向声源换到y方向,由此得到y和x方向的两个接收分量:
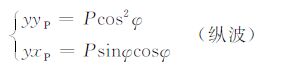
|
(17) |
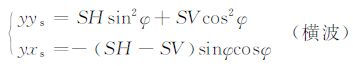
|
(18) |
对于P波,只需两个分量便可确定最大反射波(即声源正对反射体的情况)
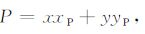
|
(19) |
而比较xxP 和yyP 两分量的相对大小,便可确定反射体的方位角φ.
对于横波,需要把四个接收分量组合起来才能得到SH 和SV 波.

|
(20) |
在SV 波很小或忽略不计的条件下(这种情况在反射体与井大致平行或者夹角较小时发生,见(9)式或(14)式),横波的情况可以简化到与纵波相似的情况,即仅利用SH 横波便可以确定反射体的大小和方位.
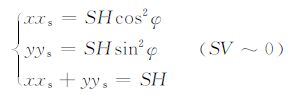
|
(21) |
以上的分析结果也指出了偶极声波存在的180°不确定性.在(15)到(21)式中,将φ 置换为φ+180°将得到同样的结果,对于一反射体来说,这意味着该方法不能确定该反射体是在井的右侧(φ=0°),还是在井的左侧(φ=180°).换言之,偶极方法只能确定反射体的走向,而不能确定其倾向.但是,在很多地质问题中(如裂缝探测)得到地质体的走向也是非常重要的.
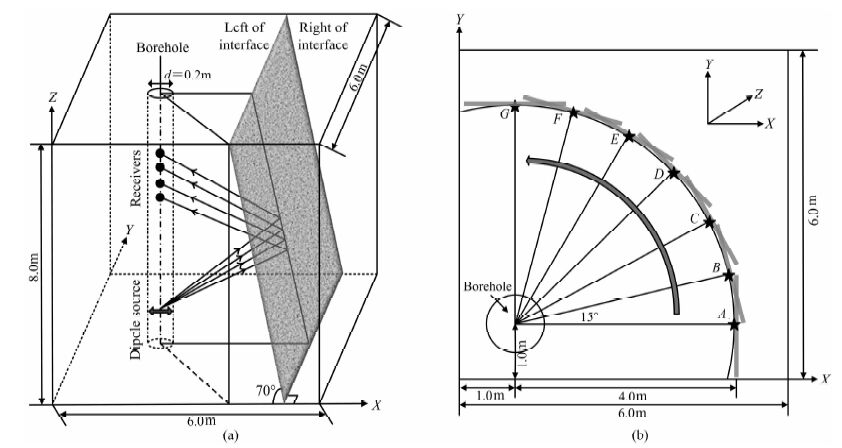
3 模拟结果及分析 3.1 快速地层下的反射声场我们采用三维时域有限差分的数值模拟方法对偶极辐射声场的上述特征进行阐述.模拟过程中所用模型如图 2所示:模型大小为x=6m、y=6m 和z=8 m,充液井孔半径为0.1 m,井眼中心在x=1m、y=1 m 处,偶极声源位于z=0.3 m 处,采用了非均匀的网格,井孔附近网格为1cm,井外较远处网格为1.5cm,时间步长为1.65μs.图 2a表示了偶极声源激励下的三维井旁地层界面计算模型,图 2b表示了2a的xoy横切面示意图.为了考察偶极声源的偏振方向对于反射声场的影响,模拟中以井轴在xoy面投影为圆心,设置一个半径为4m 的1/4圆周(图中A→G),将固定倾角为70°的井旁地层界面从A点以15°等间距间隔依次旋转至G点位置,移动方向如图中箭头所示.为了方便计算,偶极声源指向始终为x轴,中心频率为3kHz,考察偶极声源指向与井旁反射体相对关系对于反射横波的振幅的影响.计算模型中采用相关参数见表 1.
|
图 2 3D井旁地质界面计算模型 (a) 偶极声源和单个反射面;(b) 偶极声源与不同交角的反射面组成的xoy横切面. Fig. 2 The 3D calculation model with a near-borehole geological interface (a) Dipole source with an reflector; (b) The cross-section xoy with various reflector of different angles. |
|
|
表 1 理论模拟参数设置 Table 1 Model parameters of wire logging |
本文规定地层界面最大倾斜线下倾方向与它在水平面上(xoy平面)的投影所夹的角度为井旁地层界面的倾角,为了方便表示,地层界面位置用相应的空间方位角表示,如地层界面位于A点表示为A(0°,70°),位于G点表示为G(90°,70°),其它7个位置表示方法类似,以下模拟结果均按此方式进行说明.
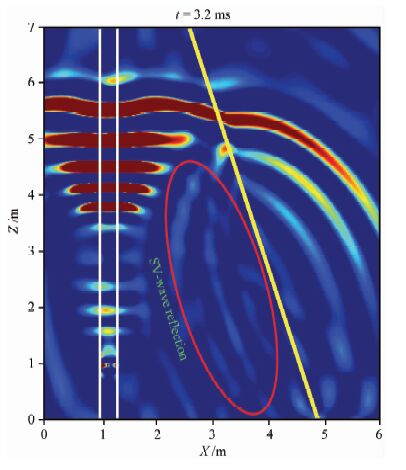
图 3和图 4 分别显示了过井轴的xoz截面和yoz截面上t=3.2 ms时刻x分量声场快照,图 3为地层界面位于A点时的快照,图 4为地层界面位于G点时的快照.根据前述基本理论和方法分析可知,当偶极指向与反射体走向垂直,即φ=90°时,可得到反射纵波和反射SV 波.因此,图 3声场快照中红线所标椭圆区域出的是SV 反射波;而图 4 偶极指向与反射体走向平行,即φ=0°,红线所标椭圆区域出现了明显的SH 反射波,而且图示的声场中没有其它波,如反射纵波、SV 波及转换波的干扰(这也是SH 波反射成像的一大优点).从两种情况的反射横波幅度来看,SV 反射波的幅度较小,而SH 反射波大约是SV 反射横波幅度的3~4倍.这也再次验证了上述的理论分析(见(14)式).
|
图 3 界面位于A点时,在t= 3.2 ms偶极 声源在xoy截面内的SV波场快照 Fig. 3 Dipole wave snapshot at t=3.2 ms,reflector is at point A in the xoz section |

|
图 4 界面位于G点时,在t=3.2 ms偶极 声源在xoy截面内的SH波场快照 Fig. 4 Dipole wave snapshot at t=3. 2 ms, reflector is at point G in the xoz section |
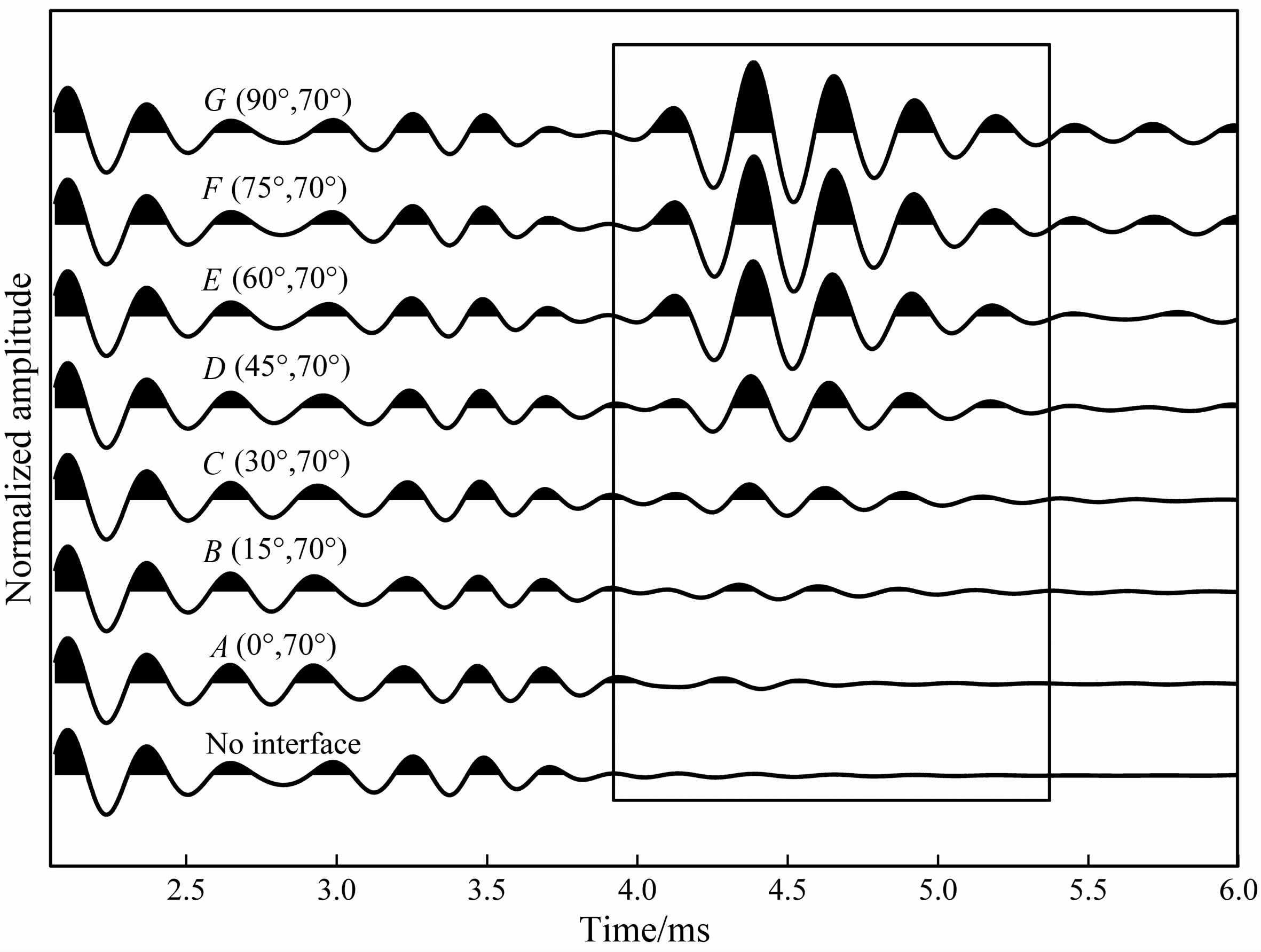
我们现在来分析同一源距,不同界面位置处所对应的井孔全波波形情况.图 5 显示了源距为1 m时反射界面位于A、B、C、D、E、F、G7 个位置时均匀地层下充液井孔接收到的全波波形对比图.为了方便分析,图中仅显示了反射横波部分(图中实线方框区域).可以看出,随着偶极声源指向与反射界面垂直到平行时,即井旁反射界面从A点移动至G点,反射横波幅度单调递增(均匀地层作为参考).由于偶极声源可以等价于无穷大弹性介质中的集中力源,当偶极声源偏振方向和井旁地层界面夹角在0°<θ<90°范围时,可将偶极声源以反射界面为参考,分解为垂直于反射界面和平行于反射界面的两个偏振方向.由于接收到的反射横波就是SV 反射波和SH 反射波的线性组合(见(16)式),在SV 波较小的条件下(见图 3,这是反射体倾角较大所致),接收到的横波基本上是SH 波的贡献,其随方位的变化如(21)式所示,呈cos2φ 的变化规律.
|
图 5 xoz横切面中从不同方位的地层界面接收到的反射波全波波形 Fig. 5 The received reflection waveform for all reflectors of different angles in cross-section xoz |
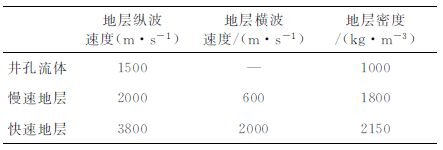
我们对慢速地层进行数值模拟,并对比慢速地层和快速地层的计算结果.和图 2a的计算模型类似,井旁反射界面倾角设置为80°,模型大小增至x=8m,y=8m,z=10m,声源中心频率为3kHz,位于空间(1,1,0.3)处,网格划分和时间步长同上,计算中设置了偶极声源指向垂直于和平行于反射体走向两种情况,模拟中采用的相关参数见表 2所示.
|
|
表 2 慢速地层和井孔流体弹性参数 Table 2 Soft formation and borehole fluid elastics parameters |
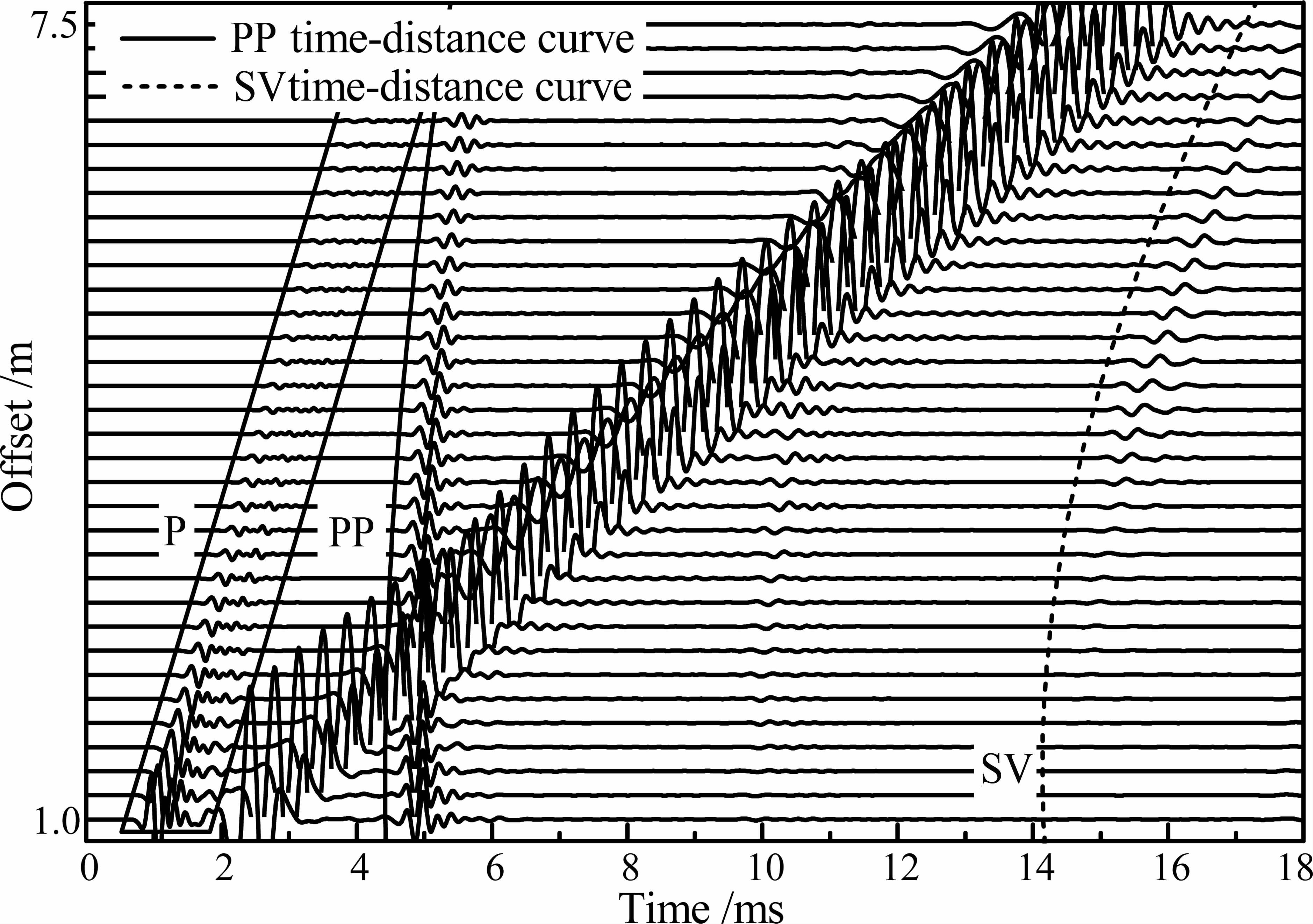
图 6给出了在慢速地层中,偶极声源指向垂直于反射体走向时井孔共源阵列,图中同时还显示了理论计算得到不同类型反射波的到时曲线,与模拟结果对应较好.从图中可以看到,振幅较强的偶极辐射的反射纵波(波至为实线轨迹),相对于SV 反射横波(波至为虚线轨迹),其灵敏度更高.
|
图 6 慢速地层条件下,偏振方向垂直于反射界面时的全波波形及对应的时距曲线 Fig. 6 Full waveforms and corresponding travel times in the fluid-filled boreholeCdipole polarization is normal to the reflector plane) |
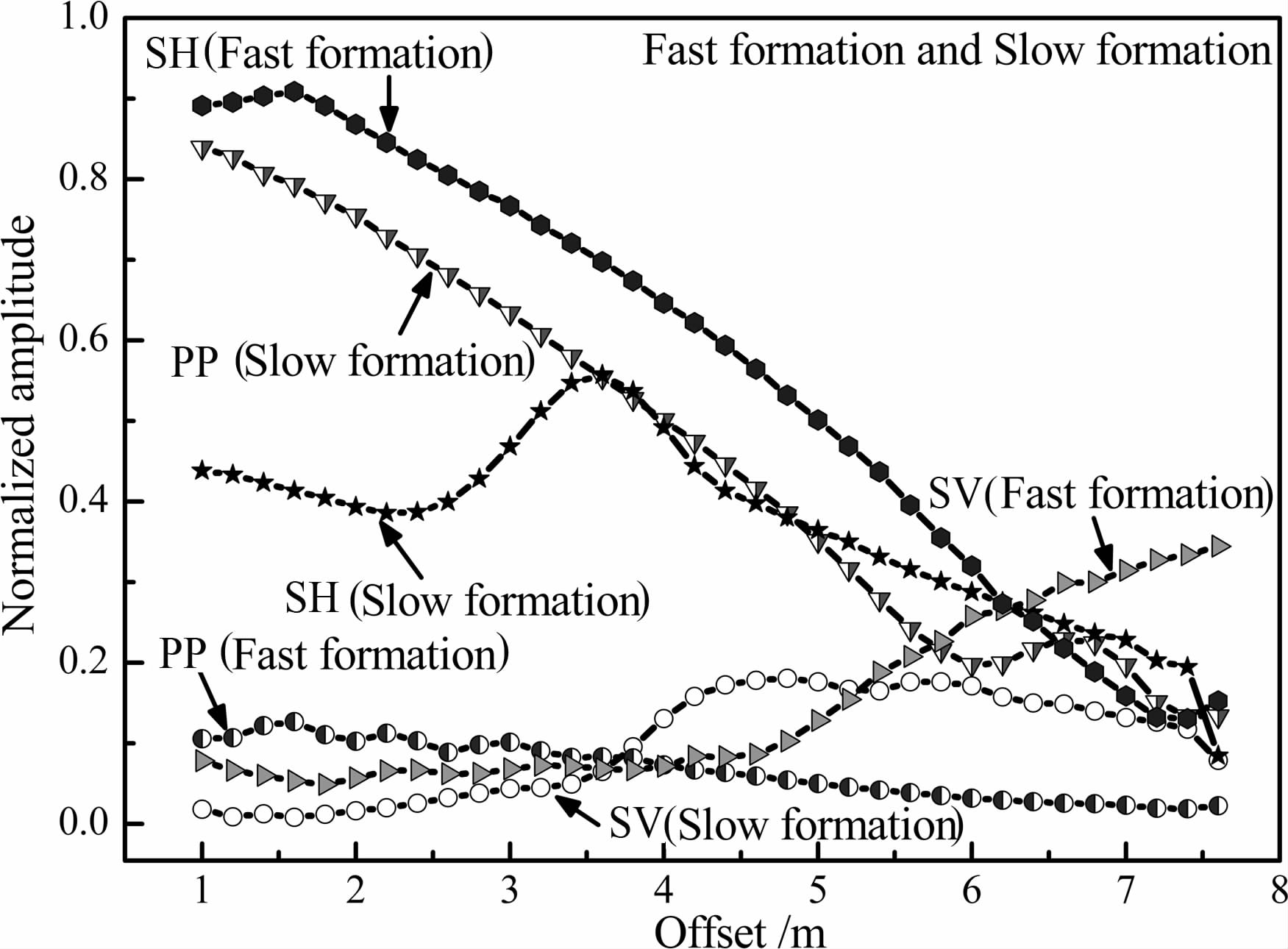
最后,我们将快速地层(表 1)和慢速地层(表 2)不同偶极声源指向,井孔中得到三种反射波的模拟结果绘制在源距和幅度的坐标系中,如图 7所示.根据(14)式,反射波随源距的变化实际上是波随出射角、入射角、反射系数及传播距离的变化.以接收到的反射波振幅或强度为前提,可以看出,在慢速地层中,可以通过PP 反射波和SH 反射波进行井旁反射体追踪和成像;快地层中则可以利用SH 反射波.对比结果显示,慢速地层中偶极辐射的纵波具有振幅强、灵敏度高,源距覆盖范围大的特征,也可以用于远探测测井[23].而且,与单极反射纵波相比,偶极声源激发的反射纵波振幅具有随反射体方位变化的特征,即具有方位灵敏度.
|
图 7 两种地层特性下,偶极产生的反射SH、PP和 SV反射波幅度随源距的变化曲线图 Fig. 7 Dipole-generated SH、PP and SV wave reflection amplitude versus receiver offset for the fast and slow formations |
我们用两个偶极声波远探测成像处理的实际例子来说明偶极辐射和反射的重要特征;第一个例子是慢速地层中纵波远探测成像的例子,第二个是快速地层中SH 横波成像的例子.
图 8是慢速地层的例子.钻井以45°的倾角穿过水平状的慢速地层.采用正交偶极仪测井,测井时,x向偶极置于水平方向;y向偶极置于垂直平面内.该慢速地层的纵横波速度约为2200m/s和800m/s.在这样的低速地层采用横波进行远探测成像需要在声波测井时采用超长的记录长度,而使用纵波进行远探测,则常规测井记录长度便能满足要求.根据图7的计算结果,慢地层中偶极反射纵波具有较高的灵敏度,可以用作远探测.
|
图 8 慢速地层偶极纵波反射成像的例子 Fig. 8 Example of dipole PP reflection wave imaging in a slow formation |
采用yy分量进行远探测反射波偏移成像,使用频率的范围为2~6kHz,成像结果见图 8.图中标出了井的位置,由图可见一系列与井交角约为45°的地层,以变密度图的形式给出.在离井约20m的距离上这些地层的轨迹清晰可辨,这是由于使用频率较低,偶极声波测井记录长度较长的缘故.值得指出的是,利用xx进行的成像却看不到这些地层(为节省篇幅起见,xx分量进行的成像图未给出).正如(15)式所示,当偶极指向(x向)与水平向的反射体平行时,没有反射纵波产生,而当偶极指向反射体时(y向),将产生反射纵波.综上所述,图 8 所示的偶极纵波反射成像例子很好地证明了慢速地层中偶极纵波具有较强的反射振幅和方位灵敏度.
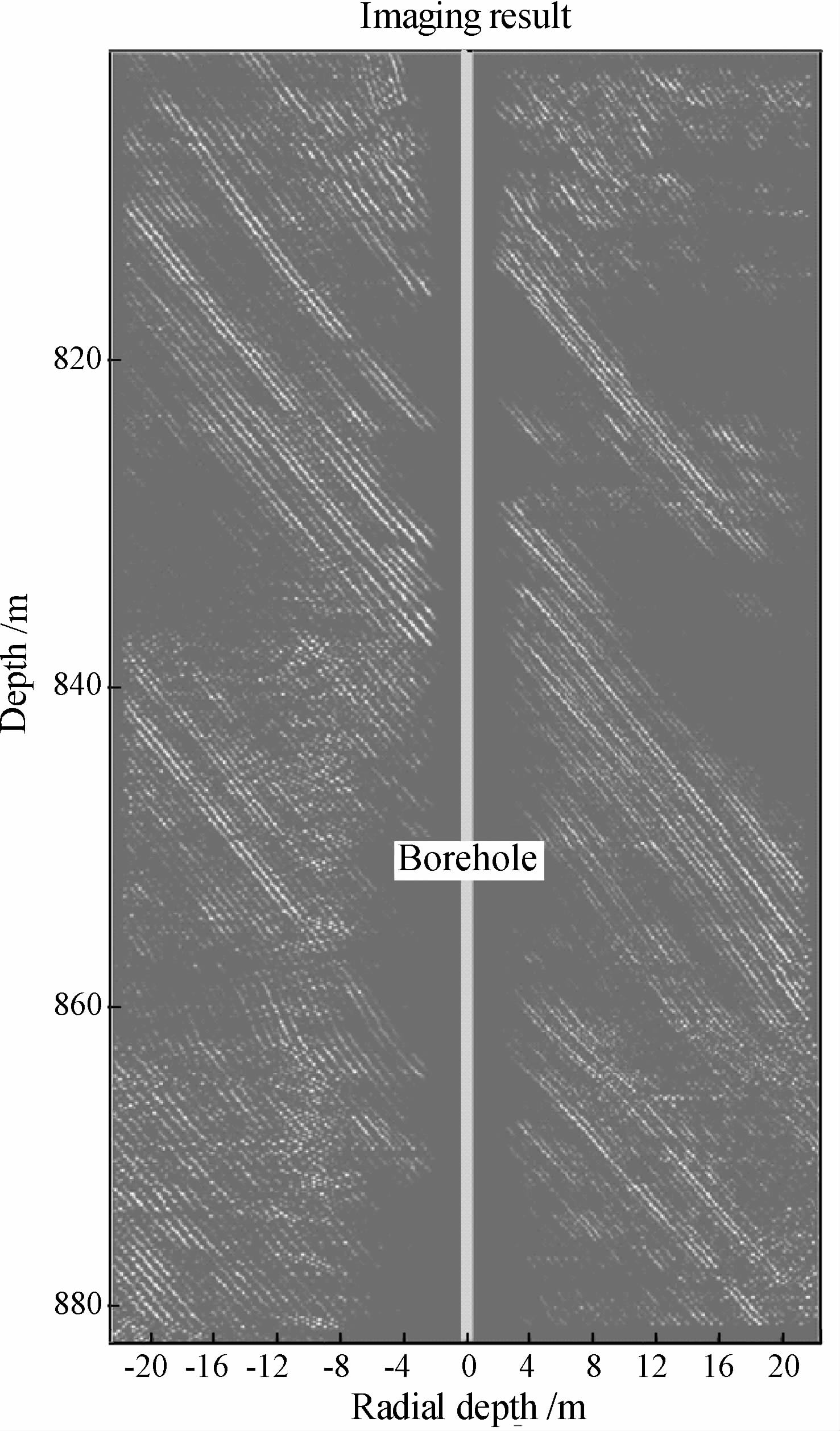
在图 9的例子中,采用了SH 横波来探测井周围的地质体,地层的横波速度约为2100 m/s,为快速地层.图示成像为井深400 m 左右,径向深度为20m 的范围,在径向距离5 m 以外,图中的成像显示了一些高倾角的地质体,而5m 之内的直条则是井中直达波的残差所致(应忽略).在径向与井轴向1∶1的尺度下,这些地质体与井基本上与井平行.在这种情况下,偶极声波从井中的出射和反射后的入射都几乎与井轴垂直.根据(14)式这时的SV 波几乎为零,接收到的横波基本上为SH 波.图 9就是利用(21)式求出方位后,再由(20)式求出SH 成像得到的,而由(20)式求出的SV 波成像却得不到这些地质体(为节省篇幅起见,成像图未给出).横波成像时采用的频率范围为1~4kHz.

|
图 9 快速地层偶极SH 横波反射成像的例子 Fig. 9 Example of dipole SH reflection wave imaging in a fast formation |
除了证明SH 横波成像的有效性外,图 9 还指出了偶极横波成像中存在的180°方位不确定性.图9钻井左边和右边的图像存在着相当的对称性.若根据地质体在钻井两边弯曲的形态(如图中箭头所指界面),可以将其解释为褶皱构造,但褶皱弯曲的方向是向右(细箭头所指界面),还是向左(粗箭头所指界面)需要用其它信息来确定.尽管存在这种180°的不确定性,图 9 中显示的偶极横波远探测的成像结果,证明了这种方法的有效性和方位灵敏度,同时还说明了该方法中SH 型横波所占的重要地位.
5 结 论充流体的井孔中偶极声源可向井周围地层辐射出纵波、SV 波和SH 型横波.在低频远场条件下,该声源的辐射特性与无限大介质中的集中力源的辐射特征相同,其中SH 型横波具有良好的辐射覆盖特性,是偶极横波远探测的重要依据.慢速地层中的纵波具有较高的灵敏度,也可以用于远探测测井.采用四分量的发射和接收可以从偶极辐射的纵波或横波中获得地质反射体的位置及其走向的方位,但不能确定其倾向.数值模拟计算和实际测井数据的成像处理进一步证明了偶极声源的辐射、反射特征以及偶极声源反射成像的可行性和有效性.
| [1] | Hornby B E. Imaging of near-borehole structure using full- waveform soncc data. Geophysics , 1989, 54(6): 747-757. DOI:10.1190/1.1442702 |
| [2] | Chabot L, Henley D C, Brown R J, et al. Single-well imaging using the full waveform of an acoustic sonic. 71st Ann. Internal. Mtg. Soc. Expl. Geophys , 2001: 420-423. |
| [3] | Yamamoto H, Watanabe S, Mikada H, et al. Fracture imaging using borehole acoustic reflection survey. //Proceedings of the 4th SEGJ International Symposium. Tokyo, 1998: 375-382. |
| [4] | Yamamoto H, Watanabe S, Mikada H, et al. Borehole acoustic reflection survey experiments in horizontal wells for accurate well positioning. SPE/PS-CIM International Conference on Horizontal Well Technology. Calgary, Alberta, Canada , 2000: 1-7. |
| [5] | Yamamoto H, Haldorsen J, Mikada H, et al. Fracture imaging from sonic reflections and mode conversion. SEG International Exposition and the 69th Annual Meeting , 1999: 148-152. |
| [6] | Tang X M, Glassman H, Patterson D, et al. Single-well acoustic imaging in anisotropic formations. SEG/San Antonio Annual Meeting , 2007: 109-113. |
| [7] | PattersonD, TangX M, RatiganJ. Iligh-resolution borehole acoustic imaging through a salt dome. SEG, Annual Meeting , 2008: 319–323. |
| [8] | Esmersoy C, Chang C, Kane M R, et al. Sonic imaging: A tool for high resolution reservoir description. SEG 67th Annual Meeting, Extended Abstracts , 1997: 250. |
| [9] | TangX M, WangT. Method and apparatus for imaging bed boundaries using azimuthal propagation resistivity measurements. US: 7912648 , 2011: 3–22. |
| [10] | Schlumberger Geoquest. Geoframe BARS user'Guide. Version 1. 0. Kanagawa: Schlumberger K K, 1998 : 1-6. |
| [11] | 薛梅.远探测声波反射波测井方法研究和声系设计[博士论文].北京:石油大学(北京),2002. XueM. Study on remote exploration acoustic reflection well logging & it;s acoustic sonde design [Ph. D. dissertation] (in Chinese). Beijing: University of Petroleum (Beijing) , 2002. |
| [12] | 车小花, 乔文孝, 阎相祯. 相控线阵声波辐射技术在反射声 波测井中的应用探讨. 测井技术 , 2004, 28(2): 108–111. Che X I, Qiao W X, Yan X Z. The effectivity of applying linear phased array transmitter in borehole acoustic reflection logging. Well Logging Technology (in Chinese) , 2004, 28(2): 108-111. |
| [13] | 乔文孝, 车小花, 李刚, 等. 反射声波成像测井的物理模拟. 石油物探 , 2004, 43(3): 294–297. Qiao W X, Che XI, L iG. The physical modeling of acoustic reflection image logging. Geophysical Prospering forPeirole (in Chinese) , 2004, 43(3): 294-297. |
| [14] | 车小花, 乔文孝. 充液井孔中的相控线阵声波辐射器在地层 中产生的声场. 地球物理学报 , 2004, 47(4): 731–736. Che XI, Qiao W X. Acoustic field in formation generated by linear phased array transmitters in fluid-filled boreholes. Chinese J. Geophys (in Chinese) , 2004, 47(4): 731-736. |
| [15] | 何峰江.声反射成像测井仪器仿真及波形处理技术研究[博 士论文].北京:石油大学(北京),2005. IIe F J. The study on the simulation of the borehole processing method [ Ph. D. dissertation ] (in Chinese). Beijing: University of Petroleum (Beijing),2005. |
| [16] | Tang X M. Imaging near borehole structure using directional acoustic wave measurement. Geophysics , 2004, 69(6): 1378-1386. DOI:10.1190/1.1836812 |
| [17] | Tang X M, Patterson D. Single-well S-wave imaging using multi-component dipole acoustic log data. Geophysics , 2009, 74(6): 211-223. DOI:10.1190/1.3227150 |
| [18] | Zemanek J,Williams F,Caldwell R. Continuous shear-wave logging. // 25th Annual Logging Symposium Transactions. Society of Professional Well Log Analysts,1984 : 1-11. |
| [19] | 唐晓明, 郑传汉. 定量测井声学. 北京: 石油工业出版社, 2004 . Tang X M, Zheng C II. Quantitative Borehole Acoustic Methods (in Chinese). Beijing: Petroleum Industry Press, 2004 . |
| [20] | 郭敦仁. 数学物理方法. 北京: 人民教育出版社, 1978 . Guo D R. 数学物理方法 (in Chinese). 北京: 人民教育出版社, 1978 . |
| [21] | Aki K,Richards P. Quantitative Seismology Theory and Methods. San Francisco: W. II. Freeman & Co, 1980. |
| [22] | Ben-Menahem A? Kostek S. The equivalent force system of a monopole source in a fluid-filled open borehole. Geophysics , 1991, 56: 1477-1481. DOI:10.1190/1.1443168 |
| [23] | 魏周拓.反射声波测井数值与物理模拟研究[博士论文].青 岛:中国石油大学(华东),2011. WeiZT. Research on single-well acoustic imaging logging by using numerical modeling and experimental measurement [Ph. D. dissertation] (in Chinese). Qingdao: China University of Petroleum (East China),2011. |
| [24] | Peng C B. Borehole effects on downhole seismic measurements [Ph. D. dissertation]. Cambridge, MA: Massachusetts Institute of Technology,1994. |
| [25] | White J E. Use of reciprocity theorem for computation of low-frequency radiation patterns. Geophysics , 1960, 25(3): 613-624. DOI:10.1190/1.1438742 |
 2012, Vol. 55
2012, Vol. 55