2. 吉林大学仪器科学与电气工程学院, 长春 130026
2. College of Instrumentation and Electrical Engineering, Jilin University, Changchun 130026, China
对航空TEM 的响应数据进行预处理与定量解释时需要各种系统参数,如飞行参数(吊舱的姿态、位置),等效面积,发射波形等等,而实测参数由于受到各种因素的影响,不可避免地含有系统误差,所以需要对系统进行标定,获得系统的有效参数[1-12].通常的做法是在已知地质条件的区域飞行进行标定,但是这种方法比较耗时也比较昂贵,同时受到地质条件的影响,很难获得精确的标定结果[2].近年来随着商业系统的不断完善,利用地回路对航空系统进行精确标定的方法受到越来越广泛的关注[1-12].
地回路是指精心铺设在地面的多匝闭合回线(导线),以回线作为目标体具有模型简单、响应规律易于计算等优点,从而可以实现对航空系统各项参数的精确标定[1-12].大地对系统响应的影响是制约标定精度的主要原因,如何消除这些影响是目前研究的热点[1-7].有文献表明,只有当大地电阻率大于1000Ωm 时,才可以忽略大地响应对标定结果的影响[1, 3],但这样的地质条件实际中很难满足,因此有研究者利用已知大地电阻率,通过正演计算的方法扣除大地响应对标定的影响[4].目前关于航空电磁法的正、反演计算[13-14],其所用系统参数均未经标定.对航空TEM 系统开展全面、准确的标定工作是十分必要的.
本文在文献[3]的基础上发现,无论均匀大地,还是层n大地,只要大地响应沿测线不变,则完全可以通过增加恒定参量的拟合参数获得系统参数,该方法在获得大地响应的同时也获得了系统的有效参数,避免了大地响应计算和扣除等繁琐过程,简单明了且易于实现.文献[3]未考虑低阻大地与地回路之间由于二次感应形成的响应,经研究发现,该响应在剖面曲线上与地回路响应相似,早期时域信号具有过零特点,通过选取零点附近的抽道进行参数拟合,可以有效抑制二次感应信号对标定结果的影响.本文通过建立更完善的大地响应模型,并结合多参数最小二乘拟合,消除和显着降低了低阻大地对标定结果产生的影响,使标定结果能够准确反映系统自身性质,从理论上证实了在低阻地区利用地回路标定航空TEM 系统的可行性与准确性.
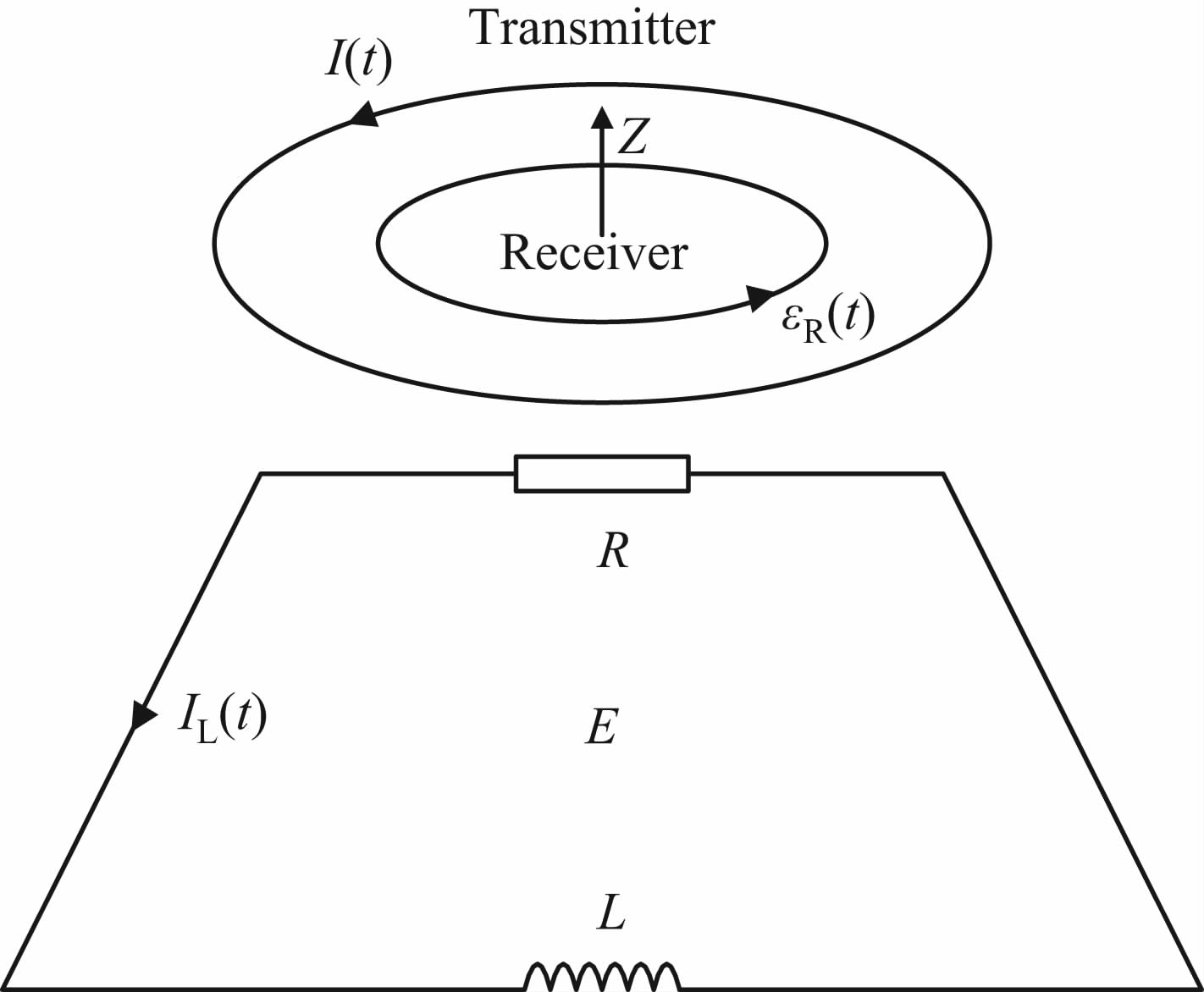
2 系统响应模型和基本参数 2.1 响应模型和类型图 1 为基于地回路的航空TEM 系统响应模型,其中I(t)为发射电流,IL(t)为地回路感应电流,εR(t)为接收线圈感应电动势,R和L分别为回线的电阻和电感,E表示均匀大地.
|
图 1 地回路系统响应模型 Fig. 1 Response model of ground loop system |
由发射线圈激发的能量经五种不同耦合路径最终到达接收线圈:由发射线圈直接耦合到接收线圈(TR,transmitter-receiver);由发射线圈经过地回路再耦合到接收线圈(TLR,transmitter-loop-receiver);由发射线圈经均匀大地再耦合到接收线圈(TER,transmitter-earth-receiver);由发射线圈首先激励地回路,再由地回路中感应电流激励均匀大地,最后达到接收线圈(TLER,transmitter-loop-earth-receiver);由发射线圈首先激励均匀大地,再由均匀大地中感应电流激励地回路,再耦合到接收线圈(TELR,transmitter-earth-loop-receiver).
2.2 系统的基本参数对航空TEM 数据进行解释时需要吊舱的位置、姿态、接收线圈的等效面积、发射电流等基本参数,由于系统误差的存在,实际测量的基本参数往往与数据解释模型下的等效值不符,获得该等效值则需要对系统进行标定.
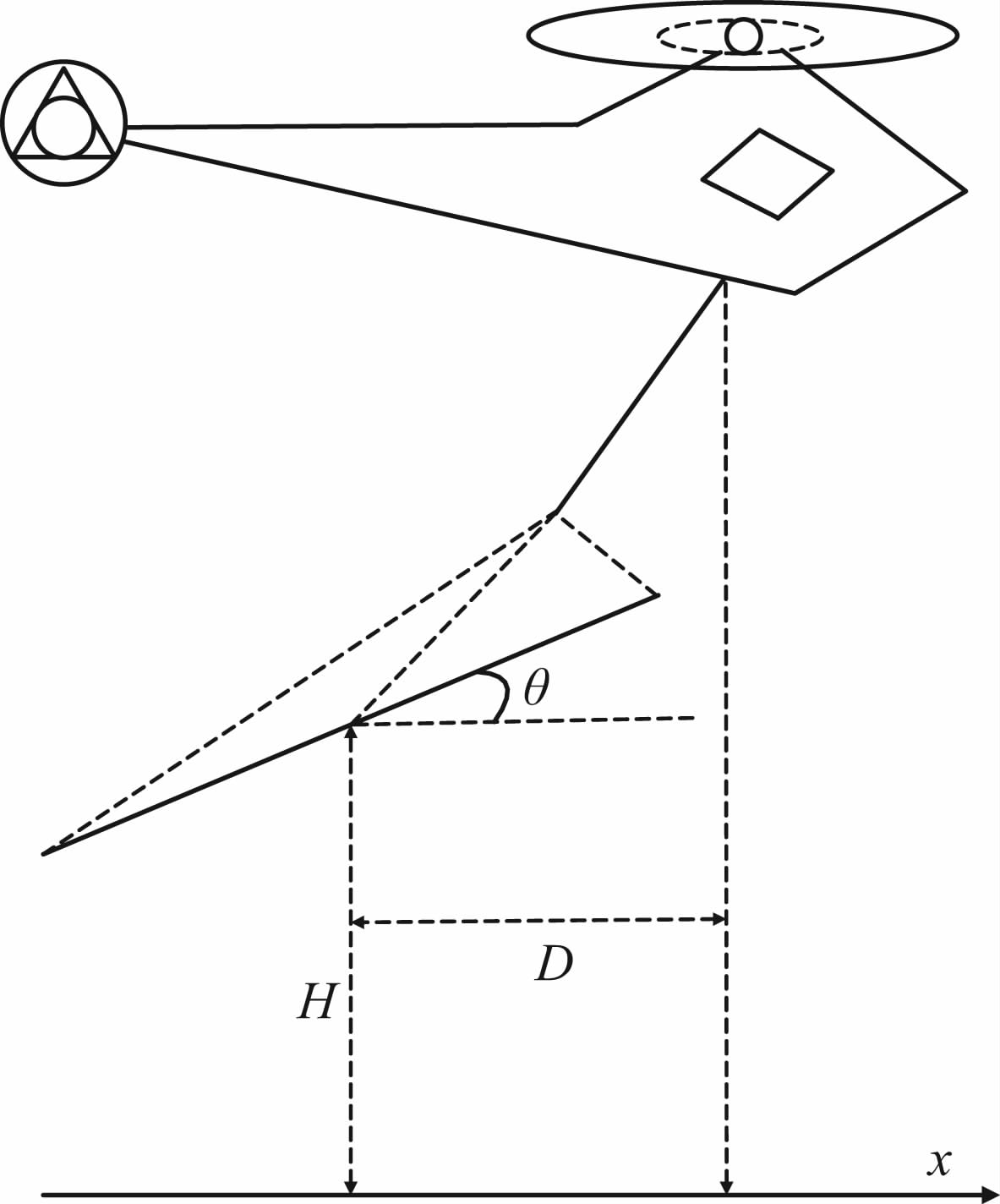
图 2中H表示吊舱中心高度,D表示吊舱中心与GPS定位仪的水平距离,θ 表示吊舱倾角,设接收系统的等效面积为S,则系统的基本参数可以表示为(S,D,H,θ).本文将通过对地回路响应进行多参数最小二乘拟合,以获得系统参数的标定值,即等效值(S,D,H,θ).
|
图 2 系统参数 Fig. 2 System parameters |
TLR 模型是只包含发射线圈、接收线圈和地回路的理想系统,本文将从这种简单模型出发,逐渐构建出更接近实际的标定模型,最终得到优化的拟合算法,以消除大地响应对标定结果的影响,准确获得系统等效参数.
3.1 TLR模型响应关系推导假定发射电流为I(t),发射线圈与地回路间的互感为MTL,得到地回路中的感应电动势εL(t)为

|
(1) |
设地回路电感为L,电阻为R,电流为IL(t),可以得到:
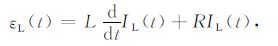
|
(2) |
假设接收线圈与地回路的互感为MLR,接收线圈的感应电动势为
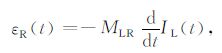
|
(3) |
利用拉氏变换,根据发射电流计算地回路中的电流以及接收线圈的感应电动势为
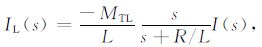
|
(4) |
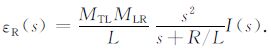
|
(5) |
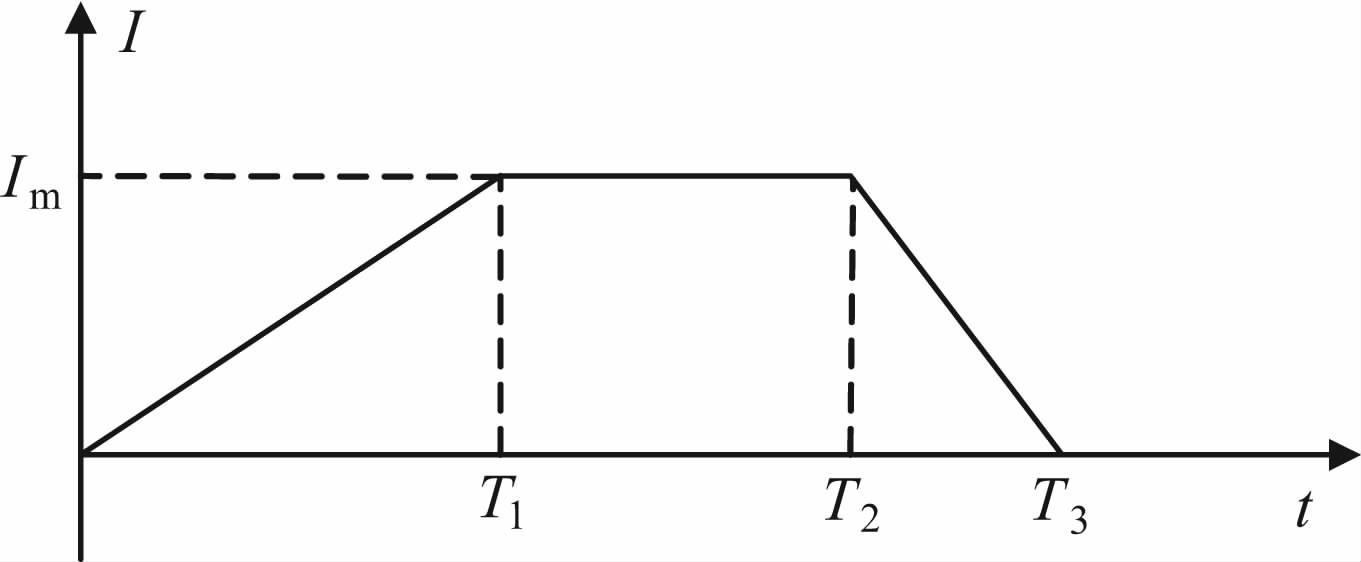
图 3为本文讨论的航空TEM 系统的发射电流波形,其中Im 为发射电流峰值,T1、T2、T3 为电流变化的拐点.首先将上面的发射电流分解为四个不同起始点的斜阶跃波:
|
图 3 系统发射电流波形 Fig. 3 Waveform of transmitter current |
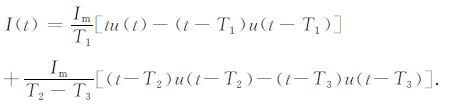
|
(6) |
将发射电流进行拉氏变换并且代入到(4),(5)式,得到地回路中电流与接收线圈的感应信号分别为
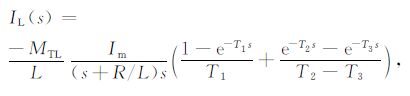
|
(7) |
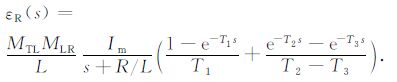
|
(8) |
经过反拉氏变换得到地回路中的电流与接收线圈中的感应电动势分别为
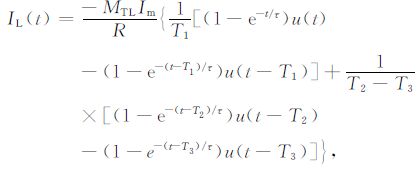
|
(9) |
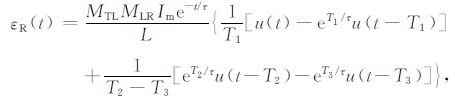
|
(10) |
其中$\tau = \frac{L}{R}$为地回路的时间常数.当发射电流关断后,一次场信号消失,线圈中的电压只有二次场与线圈本身过渡过程,如果只考虑线圈感应电压,忽略线圈过渡过程,认为线圈中只有按照指数衰减的二次场信号,则系统响应为
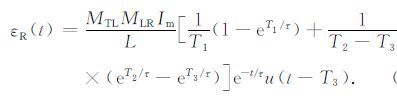
|
(11) |
实际系统发射的是双极性周期脉冲,周期为T,设接收系统的增益为A,计算得到在双极性周期脉冲激励下系统的响应为
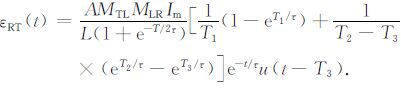
|
(12) |
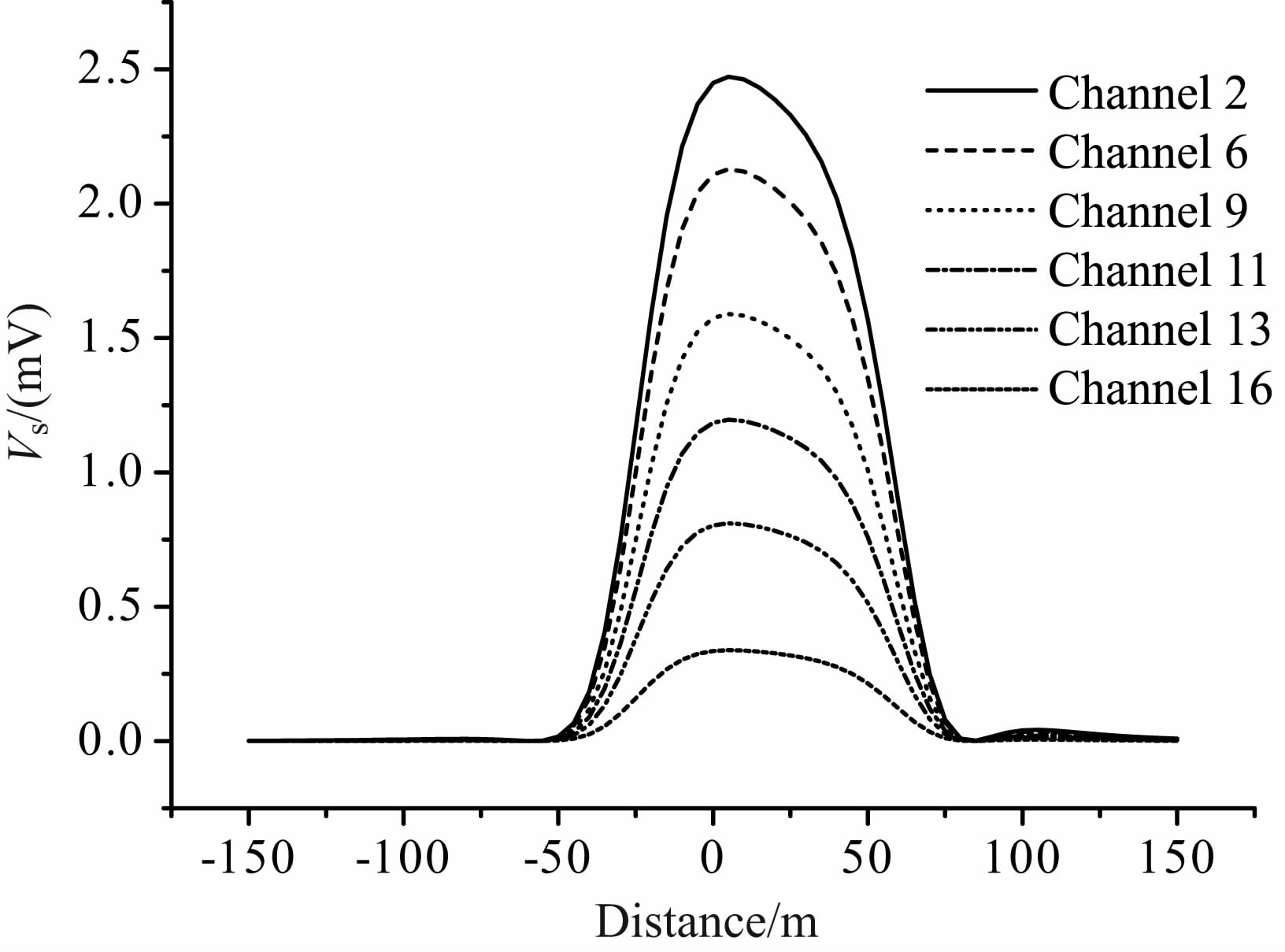
航空TEM 系统的参数如下:发射线圈直径15m,5匝,发射电流峰值300A,发射基频为25Hz,图 3中T1、T2、T3 分别为4.2ms,5.93ms,7.38ms.接收系统的等效面积为440 m2.地回路边长100 m,1匝,电感830μH,电阻0.83Ω,整个剖面曲线长为300m,飞机航速为90km/h,吊舱高度为32 m,吊舱中心与GPS 的水平距离为20 m,吊舱倾角为10°,空间分辨率为5m.系统基本参数(S,D,H,θ)真值为(440,20,32,10),根据(12)式,计算得到自由空间中地回路响应如图 4.
|
图 4 TLR 响应剖面曲线 Fig. 4 Profile curves with TLR |
假设系统剖面曲线为f(S,H,D,θ),拟合得到剖面曲线为f(S,H,D,θ),二者差值定义为ε,则拟合关系可表示如下:
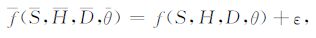
|
(13) |
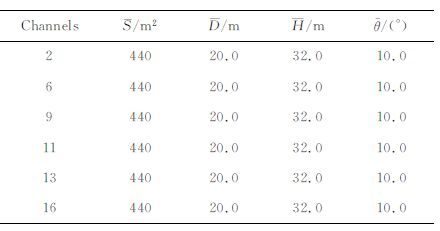
利用最小二乘的方法对误差进行限制,得到各个道等效的系统参数见表 1.
|
|
表 1 TLR响应的拟合结果 Table 1 Fitting results of TLR response |
表 1结果表明,TLR 模型下利用最小二乘拟合算法能够精确拟合出系统等效参数,在高阻地质条件下,可以作为航空TEM 标定的有效方法,为航空数据解释与正反演提供准确的系统参数.上述讨论忽略了大地响应的影响,下面将讨论存在大地响应的情况下,通过改进模型和算法,从而消除大地响应对标定结果的影响.
4 TER 模型下系统参数的标定 4.1 TER响应的计算有文献表明,大地电阻率大于1000Ωm 时,才可以忽略大地对系统响应的影响[3],这种地质条件并不容易找到,所以必须考虑到大地电阻率对系统响应的影响.
下面首先计算均匀半空间条件下航空TEM 系统的TER 响应,吊舱式航空TEM 系统采用中心回线装置,发射线圈半径为a,高度为h,得到均匀大地的响应[15-18]:
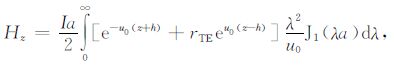
|
(14) |
考虑准静态条件与中心装置,(14)式可以化简为
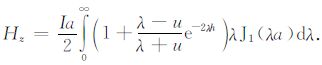
|
(15) |
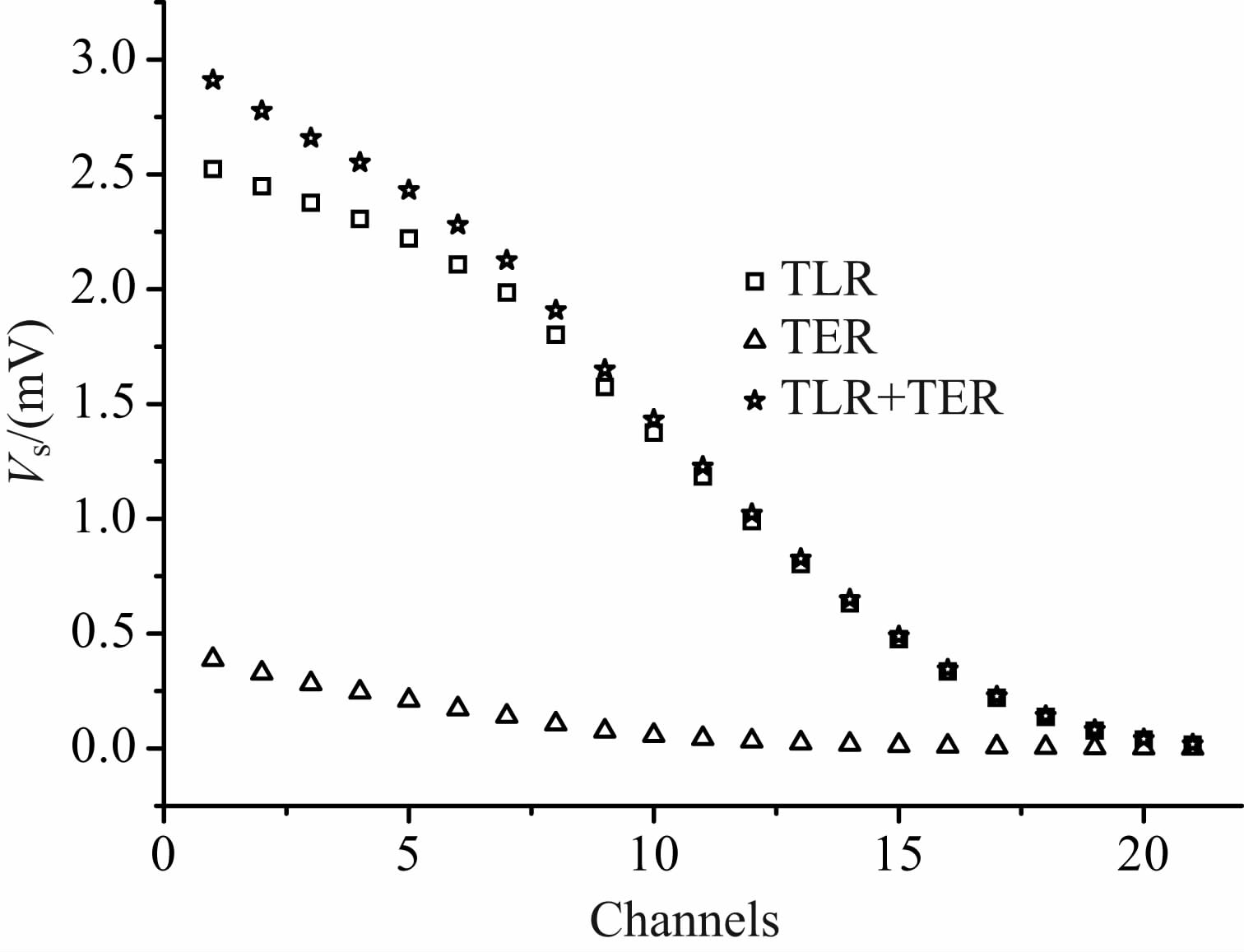
根据(15)式,并利用汉克尔变换[19-21]和G-S变换[22]可以计算出不同电阻率TER 响应,设置大地电阻率为50Ωm,对响应结果进行抽道,结果见图 5.
|
图 5 TLR和TER响应 Fig. 5 Responses of TLR and TER |
由图 5 可知,早期TER 的响应幅度达到TLR的15%,直接利用(13)式进行参数拟合,会使参数估计出现较大的误差.下面将给出改进的拟合方法,以消除TER 对系统响应的影响,准确地获得系统参数.
4.2 改进的系统参数提取算法设置系统的参数为:(440,20,32,10),在50Ωm时,根据(12)式和(15)式,计算得到下面的剖面曲线:
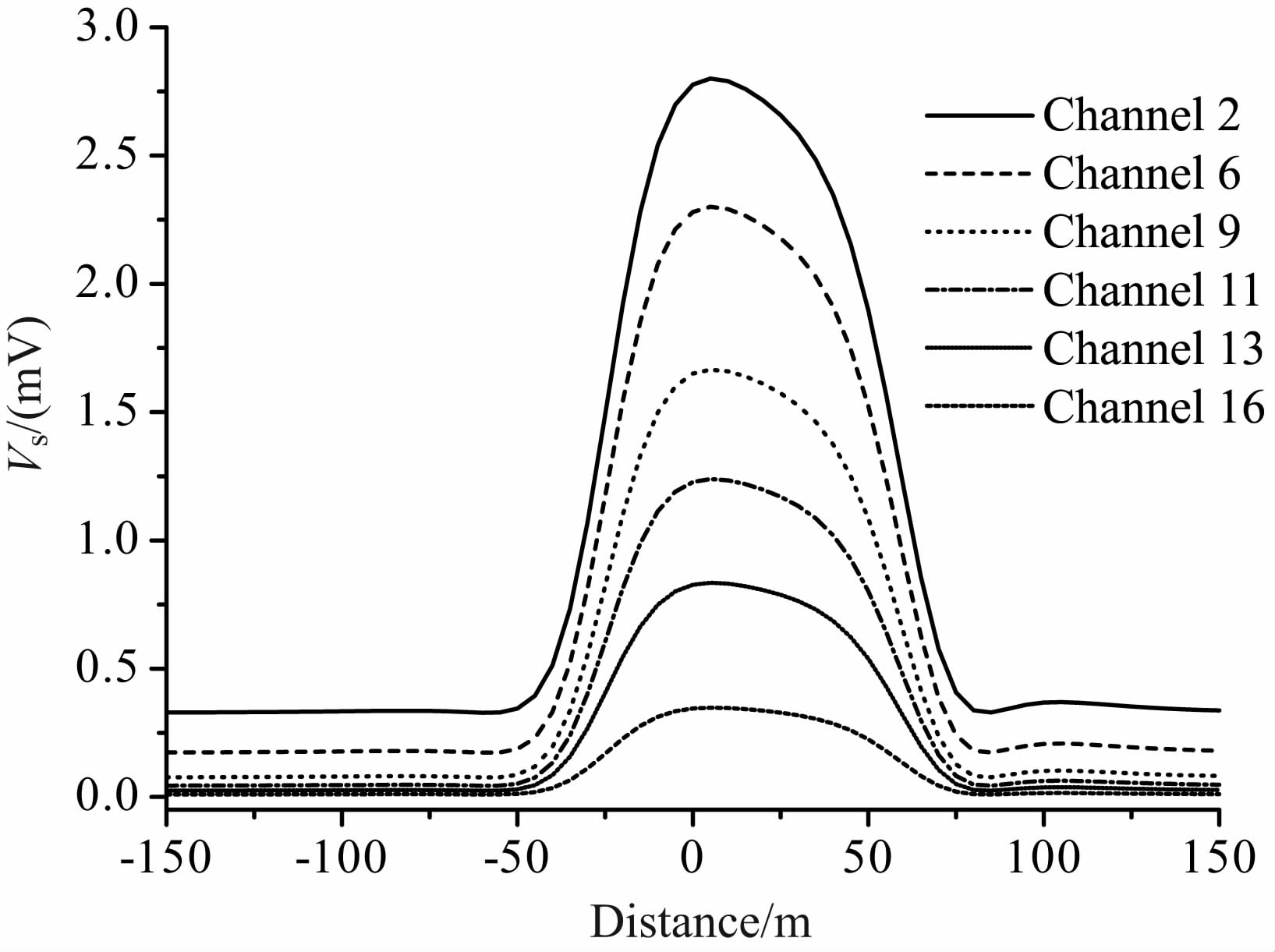
对比图 4和图 6可见,TER 响应使整个系统的响应幅度提升,对于某一道而言,TER 响应相当于加上一个常数,根据TER 响应的这种特点,将拟合关系(13)式改进如下:
|
图 6 含有TLR 和TER 的剖面曲线 Fig. 6 Profile curves with TLR and TER |
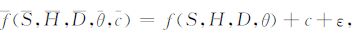
|
(16) |
|
|
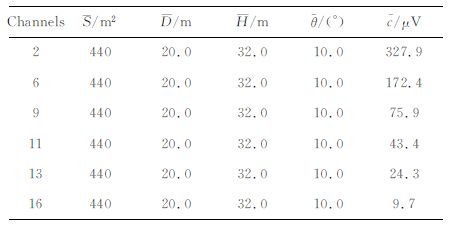
表 2 TLR+TER响应的拟合结果 Table 2 Fitting results of TLR+TER response |
表 2结果表明,无论是早、中、晚期,拟合得到的等效参数与所设置的真值完全吻合,即大地电阻率对拟合结果的影响可以被忽略.(16)式具有普适性,不论是均匀大地、层状大地响应,还是直升机对系统的响应影响,只要响应在整个飞行区间上固定,都可以通过本文的拟合方法将其消除.
5 TELR 与TLER 模型下系统参数的标定上面仅讨论了TLR 和TER 响应,忽略了地回路与大地之间的二次感应响应,下面将详细讨论二次感应的特点及其对系统参数估计的影响及消除.
5.1 TELR与TLER响应的计算首先讨论均匀半空间条件下系统的响应,圆形回线激励均匀大地的响应可以按照文献[17]进行计算,式中h,z分别表示发射线圈高度和接收线圈位置,a表示发射线圈半径,ρ 表示接收线圈与发射线圈在水平方向的距离:
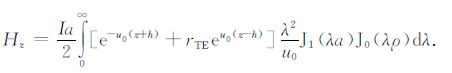
|
(17) |
TELR 响应分两步计算,第一步是计算TEL 响应,第二步是计算地回路与接收线圈之间的响应.TEL 响应条件为:发射线圈离地面32m,地回路铺设在地面,准静态条件下,不考虑一次场e-u0(z+h)项,将(17)式化简为
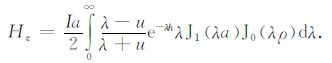
|
(18) |
利用(18)式可以计算得到地回路的感应电压,根据(2),(3)式可以计算得到接收线圈的感应电压,从而获得TELR 响应.
TLER 响应计算分为两步,第一步根据(1),(2)式计算得到发射线圈在航线上任意一点地回路中电流;第二步以地回路中电流激励均匀大地,计算接收线圈中的感应电压,将地回路分割为若干正方形,利用与这些正方形等面积的圆进行计算,这些圆均铺设在地面,接收线圈位置为z,可以得到
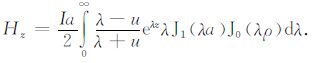
|
(19) |
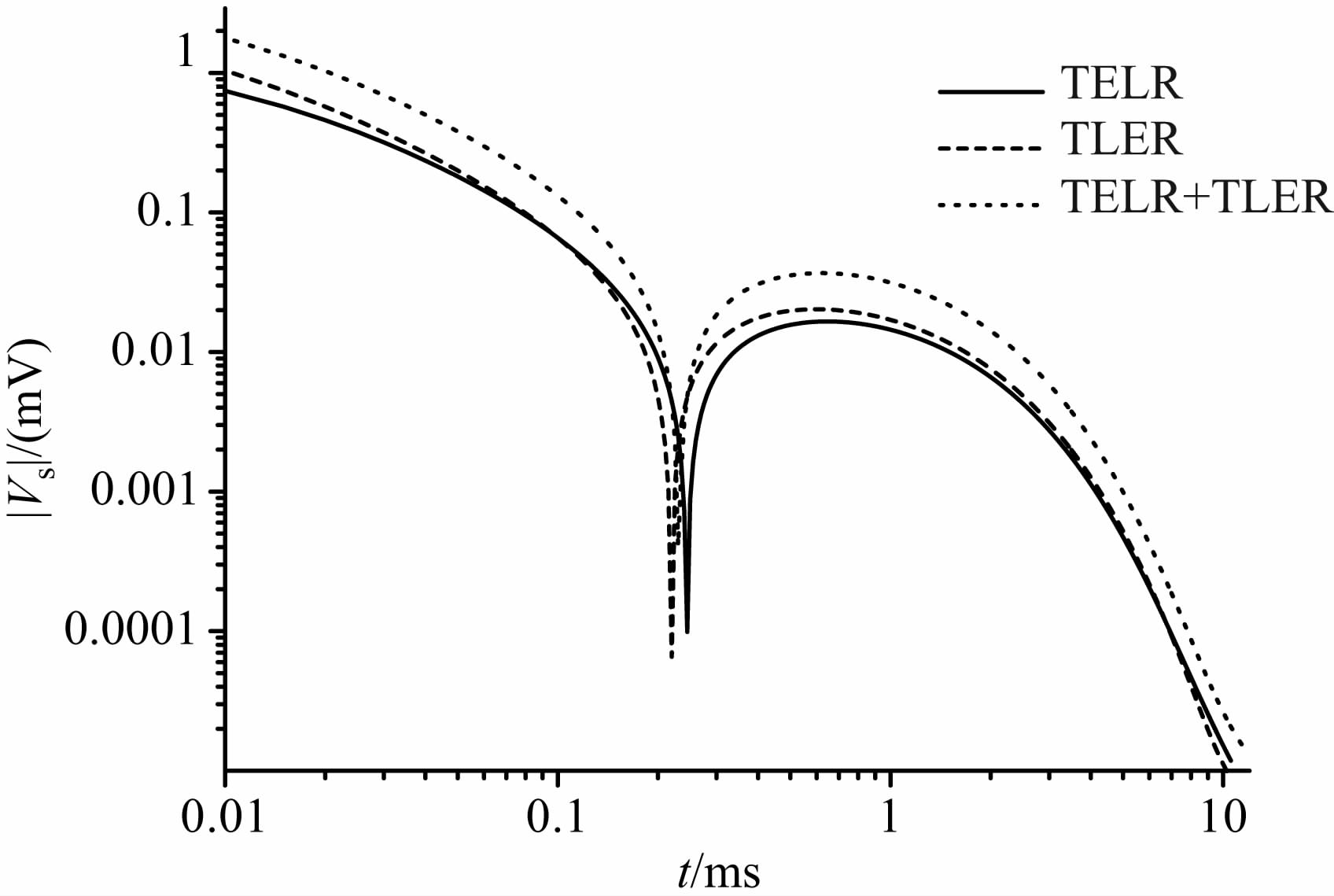
为了研究这两种响应的特征,本文选取了当线圈系统处于地回路正上方时系统的时域响应,取大地电阻率为50Ωm,计算得到如图 7的结果.
|
图 7 中心点处的TELR 和TLER 响应 Fig. 7 TELR and TLER responses at central poin |
如图 7 所示,TELR 与TLER 响应规律相似,前半部分都小于零,为了能够在对数坐标下观察,取信号绝对值进行对比,在双对数坐标下可以看到,在0.2~0.3ms内,两种信号都过零点,此时对整个系统响应的影响最小.
本文采用21道的抽道方法,在关断后延时0.2ms开始抽道,将TELR 与TLER 抽道结果与TLR、TER以及全部响应的抽道结果进行比较,结果见图 8.
|
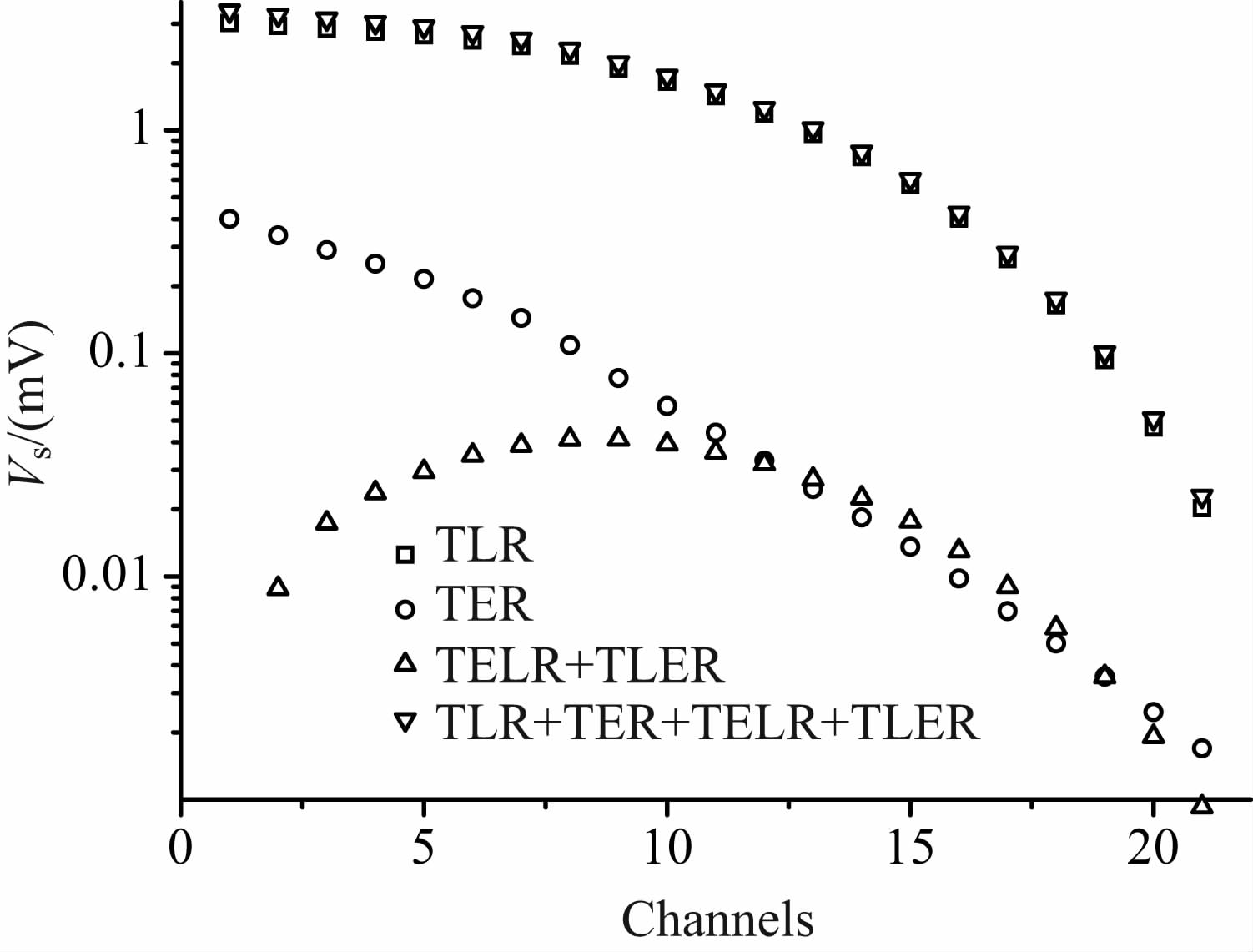
图 8 系统各部分响应的抽道结果 Fig. 8 Different responses of the system in channels |
图 8为线圈系统在地回路正上方时的响应结果,分析这些响应可以看到:(1)在早期道中,TLER+TELR 响应幅度最低,对TLR 响应影响最小,早期道中TER 对TLR 响应的影响最大.(2)在中期道中,TER 响应迅速降低,在13~19 道之间,TER响应小于TELR+TLER 响应,TELR+TLER 响应在中期道时影响最大.(3)晚期道中,TLR 幅度迅速降低,TER 和TELR+TLER 信号对系统总响应的影响增加.图 9为TELR+TLER 的剖面曲线.
|
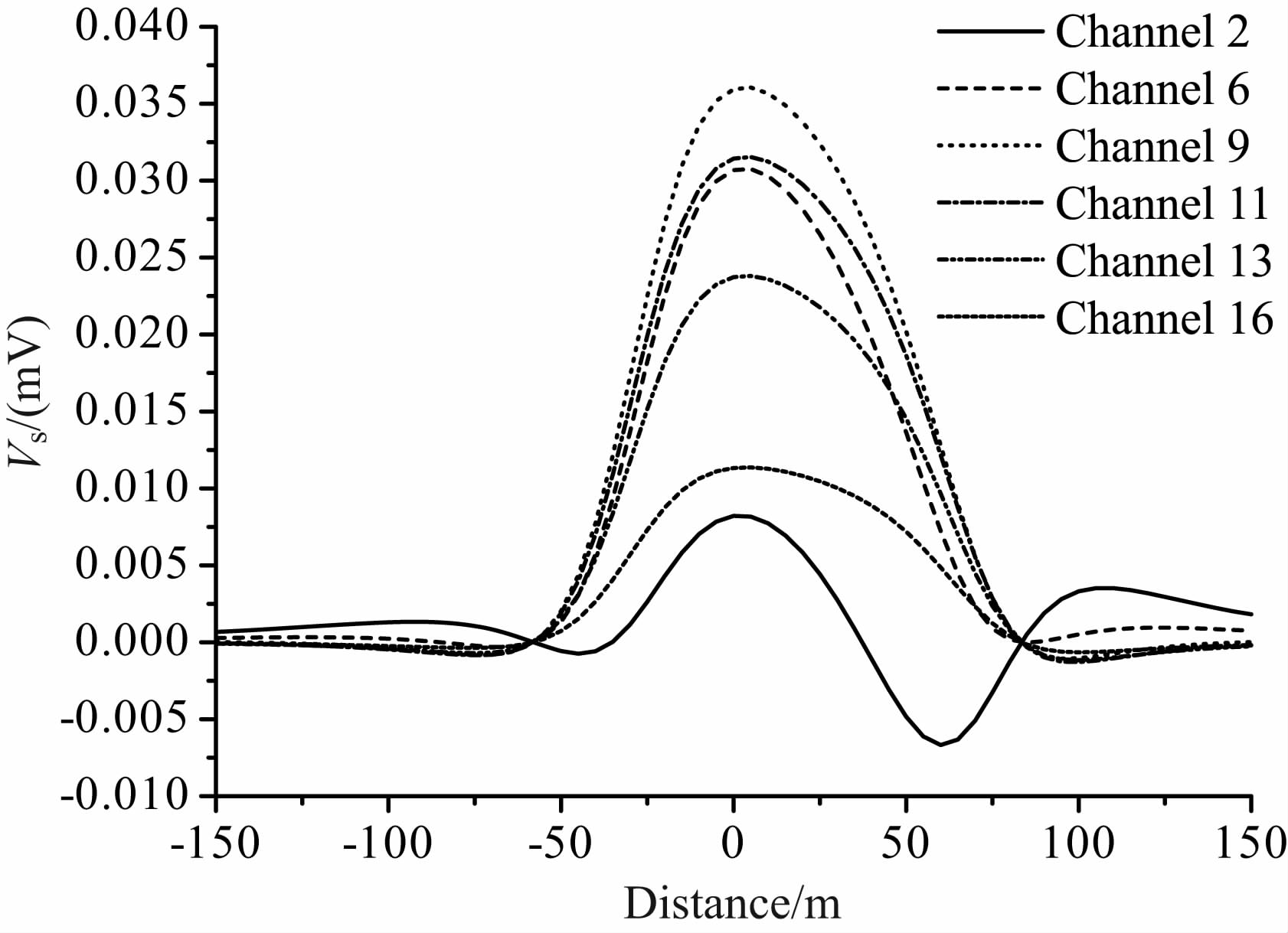
图 9 TELR+TLER 响应剖面曲线 Fig. 9 Profile curves of TELR+TLER response |
由图 9 可见,TELR+TLER 响应的剖面曲线与TLR 响应的剖面曲线形态相似,但是各个道的剖面曲线形态又有所不同:(1)早期道响应沿航线变化极为剧烈,第二道剖面曲线在回路上方发生变号,与线圈系统存在大倾角的情况相似,所以这种响应在拟合时会使线圈倾角的拟合结果偏大,但是整个响应幅度最低,所以对有效面积的拟合结果影响最小.(2)中期道的剖面曲线形态与TLR 剖面曲线形态最为相似,所以对倾角的拟合结果不会产生影响,但是中期道信号幅度大,会使有效面积拟合结果偏大.(3)晚期道信号幅度有所降低,同时变得较为平坦,但是由于TLR 信号幅度也迅速降低,所以还是会对有效面积产生较大的影响,同时由于平坦的剖面曲线与小角度TLR 响应相似,倾角的拟合结果相对偏小.
5.2 低阻区提取系统参数的方法设置系统的参数真值为:(440,20,32,10),在50Ωm 时,将图 6 的系统响应中加入TLER+TELR 响应,同时为了模拟野外实测的条件,还在数据中加入试验场地的实测噪声,在进行十次叠加后,系统噪声等效为高斯白噪声,均方根为13.56μV,最终得到模拟状态下系统的总响应剖面曲线,如图 10所示.
|
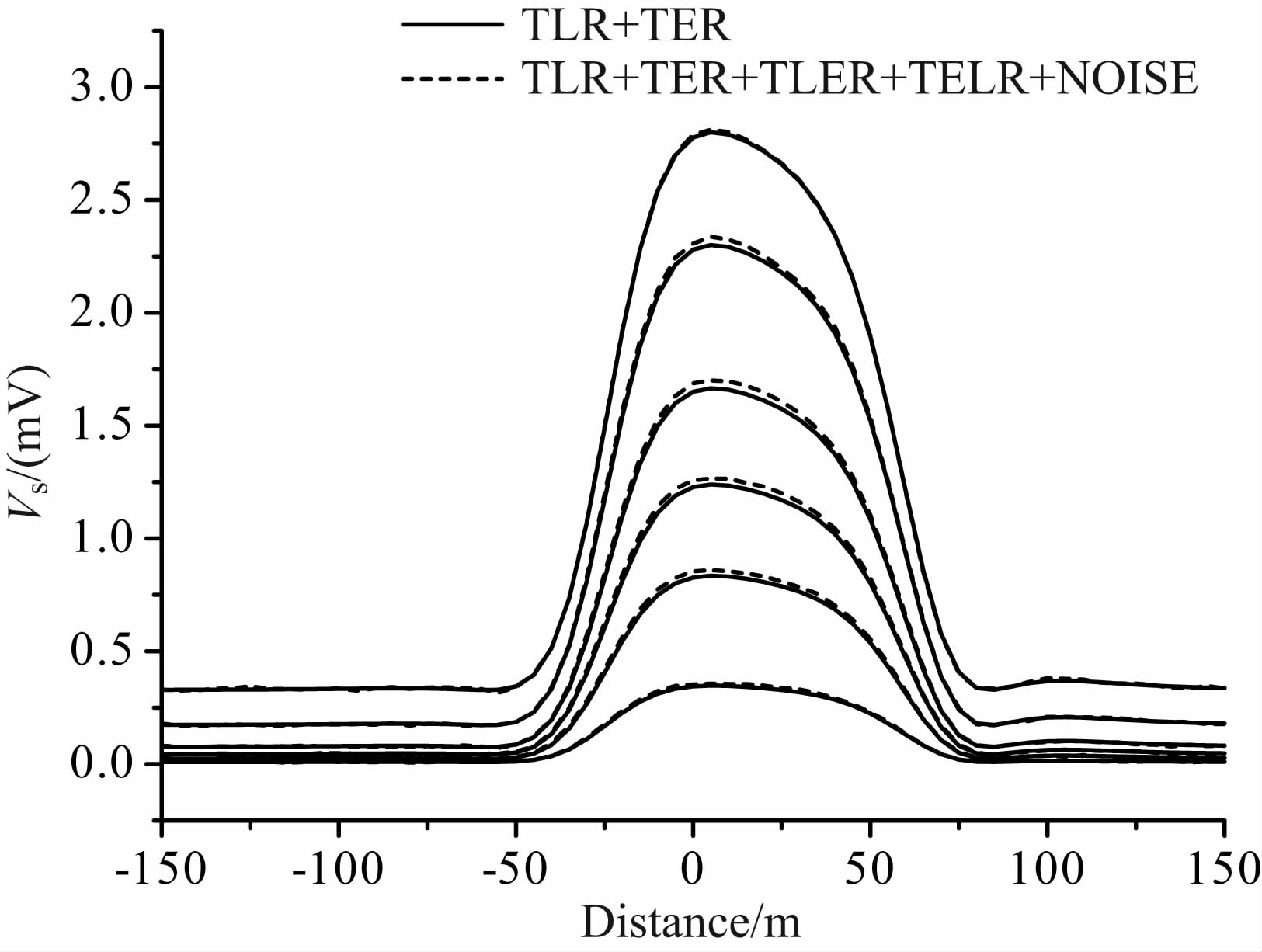
图 10 含有TLR、TER、TLER、TELR 与噪声的剖面曲线 Fig. 10 Profile curves with TLR,TER,TLER, TELR and nois |
对比图 10和图 4可见,TLER+TELR 响应在剖面曲线上与TLR 响应比较类似,不能够直接消除,因此需要引入新的拟合函数,图 10 的剖面曲线反映了TLER+TELR 响应对总响应的贡献.根据以上分析,拟合关系在(16)式的基础上可改写为
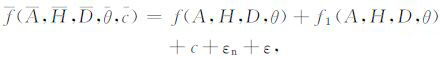
|
(20) |
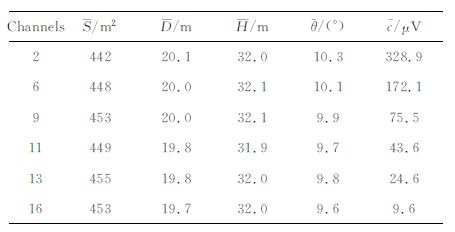
其中f(A,H,D,θ)表示TLR的响应;f1(A,H,D,θ)则表示TLER+TELR 响应;常数c表示TER 响应;εn 表示系统实测的噪声.将图 10的数据按(20)式拟合,结果见表 3.
|
|
表 3 TLR+TER+TLER+TELR+NOHSE响应的拟合结果 Table 3 Fitting results of TLR+TER+TLER+TELR+NOISE response |
表 3结果显示,由于TLER+TELR响应在这一段时间中均为正,整个系统的响应大于真实值,所有道等效面积的拟合值均大于真值,其中早期道拟合得到的有效面积与真值最接近,其他道差异较大,这是由于早期道互感信号幅度小,TLR 响应幅度大.但是早期道倾角的拟合值与真值差异较大,这是由于二者的形态差异较大.从表 3可以看出,中期道拟合值中,等效面积比真值高3%,但是倾角拟合差异较小;晚期道由于信号幅度的降低,噪声对系统影响增大,拟合结果不确定性增加.
在整个拟合结果中,早期道的拟合结果综合效果最佳.这一方面因为均匀大地响应为常量,通过改变拟合公式的方法消除了TER 响应,另一方面因为TLER 与TELR 响应幅度较小,对整个系统的结果影响有限.即在大地电阻率均匀的情况下,即使在低阻区也可以使用地回路对航空TEM 系统进行标定.
6 结 论对自由空间中地回路的响应研究表明,当大地响应可以忽略时,基于TLR 模型的多参数最小二乘拟合方法可以准确获得系统的等效参数.当大地呈现低阻性质时,大地响应会以不同的方式影响系统标定结果,使所获得的有效参数无法反映系统本身特性,从而丧失标定的意义.本文将大地响应的影响分为两类,一类为TER 响应,另一类为TELR 与TLER 响应.理论上只要大地在测线方向上各向同性,则TER 响应沿测线不变,根据这一特点可以通过增加拟合参数的方法,直接拟合得到各测道的大地响应,同时也得到系统的等效参数从而完成对系统的标定.TELR 与TLER 响应在时域中具有过零特点,利用这一特点,可以选取近零点的测道以消除其影响.拟合结果表明,在误差不超过3% 的情况下,该方法能准确获得系统参数,从而实现低阻区航空TEM 标定.
| [1] | Davis A C. Quantitative characterization of airborne electromagnetic systems . Melbourne: RMIT University, 2007. |
| [2] | Yin C C, Hodges G. Wire-loop surface conductor for airborne EM system testing. Geophysics , 2009, 74(1): F1-F8. DOI:10.1190/1.3008055 |
| [3] | Davis A C, Macnae J. Quantifying AEM system characteristics using a ground loop. Geophysics , 2008, 73(4): 179-188. DOI:10.1190/1.2943189 |
| [4] | Yin C C, Douglas C F. Attitude corrections of helicopter EM data using a superposed dipole model. Geophysics , 2004, 69(2): 431-439. DOI:10.1190/1.1707063 |
| [5] | Davis A C, Macnae J. Measuring AEM waveforms with a ground loop. Geophysics , 2008, 73(6): F213-F222. DOI:10.1190/1.2976791 |
| [6] | Fitterman D V. Sources of calibration errors in helicopter EM data. Exploration Geophysics , 1998, 29(2): 65-70. DOI:10.1071/EG998065 |
| [7] | Davis A C, Macnae J. Calibration of Time Domain AEM Systems Using a Ground Loop. Canning Bridge, West. Aust.: Promaco Conventions, 2007. |
| [8] | Davis A, Macnae J, Hodges G. Predictions of bird swing from GPS coordinates. Geophysics , 2009, 74(6): F119-F126. DOI:10.1190/1.3237143 |
| [9] | Ley-Cooper Y, Macnae J. Amplitude and phase correction of helicopter EM data. Geophysics , 2007, 72(3): F119-F126. DOI:10.1190/1.2717498 |
| [10] | Macnae J, Aaron Davis A. An AEM system calibration. ASEG Extended Abstracts , 2010(1): 1-4. DOI:10.1071/ASEG2010ab230 |
| [11] | Ley-Cooper Y, Macnae J, Robb T. Identification of calibration errors in helicopter electromagnetic (HEM) data through transform to the altitude-corrected phase-amplitude domain. Geophysics , 2006, 71(2): G27-G34. DOI:10.1190/1.2187741 |
| [12] | Davis A C, Macnae J, Robb T. Pendulum motion in airborne HEM systems. Exploration Geophysics , 2006, 37(4): 355-362. DOI:10.1071/EG06355 |
| [13] | 嵇艳鞠, 林君, 关珊珊, 等. 直升机航空TEM中心回线线圈姿态校正的理论研究. 地球物理学报 , 2010, 53(1): 171–176. Ji Y J, Lin J, Guan S S, et al. Theoretical study of concentric loop coils attitude correction in helicopter-borne TEM. Chinese J. Geophys (in Chinese) , 2010, 53(1): 171-176. |
| [14] | 朱凯光, 林君, 韩悦慧, 等. 基于神经网络的时间域直升机电磁数据电导率深度成像. 地球物理学报 , 2010, 53(3): 743–750. Zhu K G, Lin J, Han Y H, et al. Research on conductivity depth imaging of time domain helicopter-borne electromagnetic data based on neural network. Chinese J. Geophys (in Chinese) , 2010, 53(3): 743-750. |
| [15] | 蒋邦远. 实用近区磁源瞬变电磁法勘探. 北京: 地质出版社, 1998 . Jiang B Y. Applied near Zone Magnetic Source Exploration of Transient Electromagnetic Method (in Chinese). Beijing: Geological Publishing House, 1998 . |
| [16] | 罗延钟, 张胜业, 王卫平. 时间域航空电磁法一维正演研究. 地球物理学报 , 2003, 46(5): 719–724. Luo Y Z, Zhang S Y, Wang W P. A research on one-dimension forward for aerial electromagnetic method in time domain. Chinese J. Geophys (in Chinese) , 2003, 46(5): 719-724. |
| [17] | 米萨克N纳比吉安. 勘查地球物理电磁法. 北京: 地质出版社, 1992 . Nabighian M N. Electromagnetic Methods in Applied Geophysics (in Chinese). Beijing: Geological Publishing House, 1992 . |
| [18] | 李貅. 瞬变电磁测深的理论与应用. 西安: 陕西科学技术出版社, 2002 . Li X. The Theory and Application of Transient Electromagnetic (in Chinese). Xi'an: Science and Technology Press of Shaanxi, 2002 . |
| [19] | Kong F N. Hankel transform filters for dipole antenna radiation in a conductive medium. Geophysical Prospecting , 2007, 55(1): 83-89. DOI:10.1111/gpr.2007.55.issue-1 |
| [20] | Guptasarma D, Singh B. New digital linear filters for Hankel J0 and J1 transforms. Geophysical Prospecting , 1997, 45(5): 745-762. DOI:10.1046/j.1365-2478.1997.500292.x |
| [21] | 张伟, 王绪本, 覃庆炎. 汉克尔变换的数值计算与精度的对比. 物探与化探 , 2010, 34(6): 753–755. Zhang W, Wang X B, Tan Q Y. Research and application on numerical integration of Hankel transforms by digital filtering. Geophysical & Geochemical Exploration (in Chinese) (in Chinese) , 2010, 34(6): 753-755. |
| [22] | 罗延钟, 昌彦君. G-S变换的快速算法. 地球物理学报 , 2000, 43(5): 684–690. Luo Y Z, Chang Y J. A rapid algorithm for G-S transform. Chinese J. Geophys (in Chinese) , 2000, 43(5): 684-690. |
 2012, Vol. 55
2012, Vol. 55