2. 中南大学数学与统计学院, 长沙 410075;
3. 湖南师范大学数学与计算机科学学院, 长沙 410081;
4. 高性能计算与随机信息处理教育部重点实验室, 长沙 410081
2. School of Mathematics and Statistics, Central South University, Changsha 410075, China;
3. College of Mathematics and Computer Science, Hunan Normal University, Changsha 410081, China;
4. HPCSIP Key Laboratory, Ministry of Education, Changsha 410081, China
直流电阻率法是寻找金属、非金属矿床、勘查地下水资源和能源以及研究地质构造的常用方法[1].1971 年,Coggon[2] 首次将有限单元法(FiniteElementMethod,FEM)应用到直流电阻率数值模拟.此后,地球物理学家徐世浙、周熙襄和罗延钟等,发表了一系列FEM 在电阻率法中应用的论文[3-9].现在,FEM 以其理论完备、不用考虑内部界面条件、且能模拟复杂边界、程序通用性强等优点得到了广泛的研究和应用,已成为直流电阻率法数值模拟最主要的方法[10-14].
尽管FEM 在直流电法数值模拟中取得了长足的发展,但问题依然存在.由于地球物理勘探所涉及的研究区域具有无界性,因此实际模拟计算中必须把无界区域截断为有界区域.为了减小计算误差,必须要求截断区域足够大;另一方面,点电源附近FEM 网格必须足够密;均匀剖分势必会大大增加FEM 的计算工作量与存贮量.吴小平[15-18]等1998年引进不完全Cholesky共轭梯度(ICCG)法求解Possion 方程边值问题,明显提高了计算速度,应用于三维直流电法正、反演也取得了很好的效果.陈小斌与胡文宝[19]1999 年基于源点附近局部加密网格,利用有限元直接迭代算法求解线源频率域大地电磁正演问题,揭示了自适应有限元中单元大小及密度不均匀分布的优点.2009 年以来,汤井田[20-25]等采用非结构化网格的自适应有限元,通过加密奇异点(点电源)处网格密度以减小有限元的计算误差,提高了有限元的正演速度.尽管目前比较热门的自适应有限元,在提高点电源或异常地质体等附近的精度、减小计算量方面取得了较大的成果,但由于其网格结构的任意性破坏了FEM 固有的超收敛结构,提高了局部精度的同时却降低FEM 整体的收敛速度.
多重网格法(MG)是20世纪60年代由苏联计算数学家Fedorenko[26]提出最初思想,现已成为快速求解大规模科学工程计算问题最有效的方法之一,在计算地球物理领域亦渐渐得到关注[27-31].数学上已严格证明:至少对线性椭圆型偏微分方程,多重网格方法是最优的,其计算量仅与节点数的一次方成正比.然而,经典的多网格法采用三种基本算子:插值、限制和迭代,在粗细网格之间需要反复迭代求解,程序比较麻烦.1996年,德国Bornemann[32]等提出了瀑布式多网格法(CMG),是一种从粗网到细网的单向计算,只采用了插值和迭代两种运算,没有粗网格上的修正,程序实现更简单.1999年,我国学者陈小斌[33]提出用自动网格剖分法求解二阶椭圆型偏微分方程,加快了收敛速度,其思想与CMG 法完全一致.2008年,陈传淼[34-37]等基于有限元误差展开式提出外推瀑布型多网格法(EXCMG).该方法沿用CMG 的思想,但将粗网上的线性插值改为“外推+二次插值”,为密网提供更好的初值,对提高精度和加速收敛起着关键作用.
本文利用EXCMG 方法求解点源2.5 维电阻率法正演问题,详细比较了不同网格尺寸下EXCMG 方法和ICCG 方法的计算速度和精度,并通过典型地电模型模拟验证了方法的正确性和有效性.
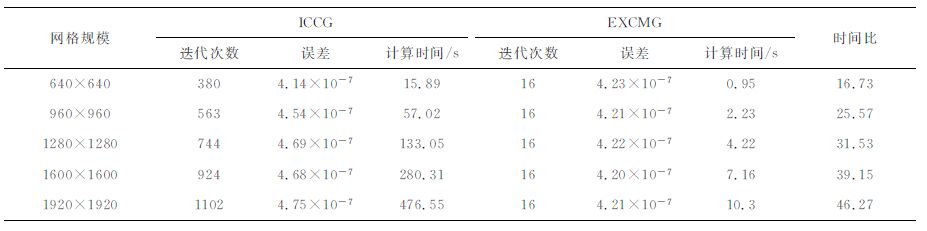
2 点源稳定电场边值问题及其有限元逼近 2.1 点源稳定电场边值问题电阻率法常用点电源供电,点电源产生的电场为三维的,满足如下变系数Possion方程边值问题:
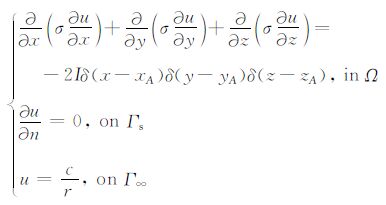
|
(1) |
其中,Ω 为地表以下求解区域,Γs 为地表-空气界面,Γ∞ 为截断边界,r为点电源A 到无穷远边界的距离.σ 为电导率,u为电位,I为电流强度,c是常数,均匀场时c=I/(2πσ),n为边界∂Ω 的外法向,δ(x)为狄垃克函数.
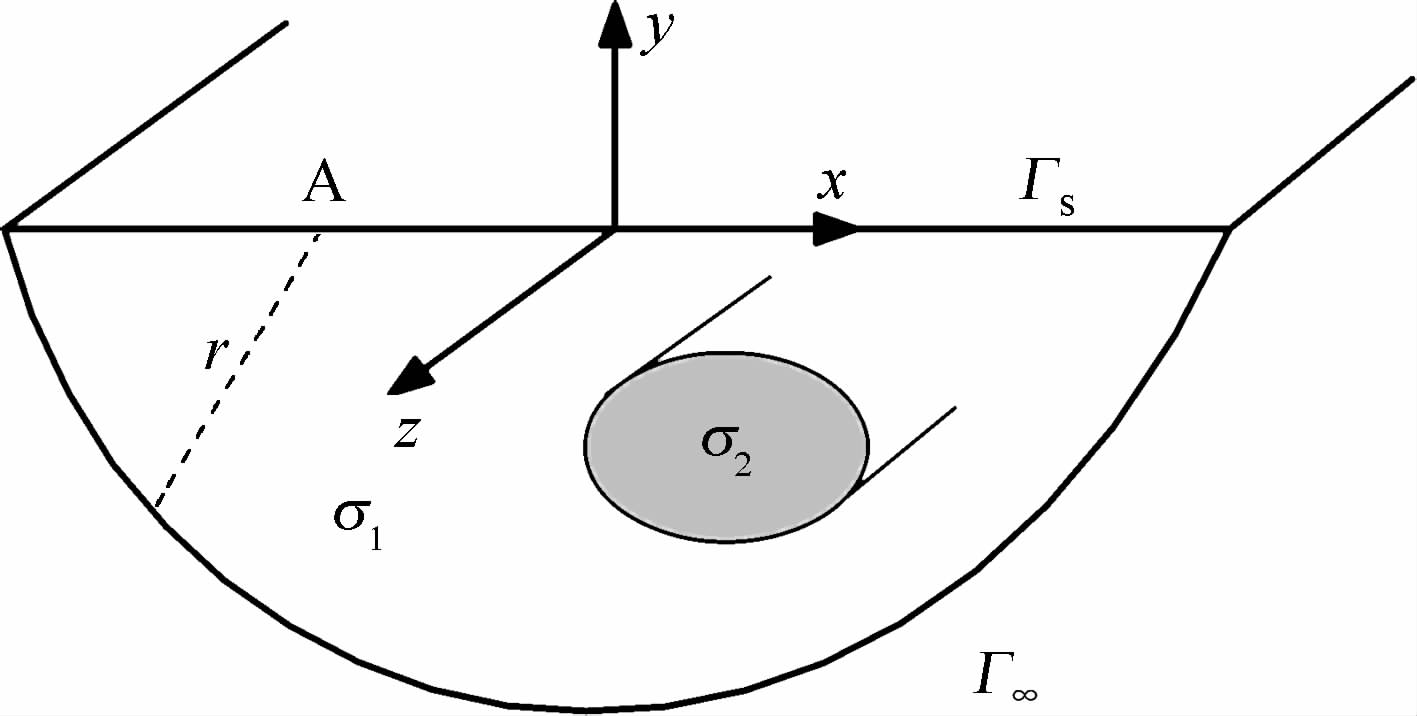
实际中,大多地质具有一定的走向,建立如图1所示坐标系,使得z轴平行于构造走向.图 1 中σ1 为地下半空间电导率,σ2 为地下异常体的电导率.对于此类三维问题,可利用Fourier变换将其变成二维问题简化计算.由于地质构造关于xoy平面对称,故电位u(x,y,z)关于z为偶函数,其Fourier变换即为余弦变换
|
(2) |
|
图 1 二维结构模型 Fig. 1 Model of 2D structure |
对微分方程和边界条件同时进行Fourier变换,可得如下带参数(波数k)的二维变系数非齐次亥姆霍茨(Helmholtz)方程边值问题:
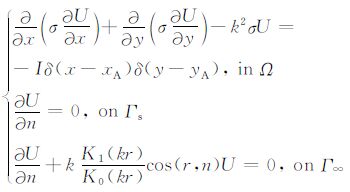
|
(3) |
此处,Ω 为二维区域,Γs,Γ∞ 为区域边界.K0,K1 分别为第二类零阶、一阶修正贝塞尔函数.
2.2 电阻率法有限元公式对微分方程边值问题,采用Galerkin加权余值法,可导出其相应的有限元方程:
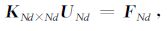
|
(4) |
其中:
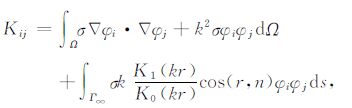
|
(5) |
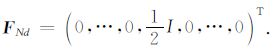
|
(6) |
式中,Nd为总的节点数,UNd为未知的电位向量,荷载向量FNd仅点电源所在的节点处分量为I/2,其余节点处为0,φi为第i个节点处的基函数.在有限单元法实际计算过程中,通常先利用形函数计算单元刚度矩阵,再组装成总体刚度矩阵.由式(5)易知总体刚度矩阵K为对称正定矩阵,故可用共轭梯度法(CG)求解有限元方程得到各个位置的电位.
2.3 最优化离散波数的计算通常,我们只对通过点电源剖面上的电位感兴趣.此时z=0,由Fourier逆变换式知
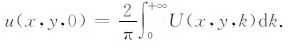
|
(7) |
可利用数值积分将上式写成
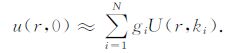
|
(8) |
其中N为离散波数的个数,本文实际计算中取为5,ki为根据文献[38]中计算最优化波数的基本原理得到的离散波数,gi为相应的权系数,详见表 1.
|
|
表 1 波数ki及相应的gi Table 1 Wavenumber ki and corresponding gi |
利用离散Fourier逆变换求得各个位置的电位U之后,便可采用如下公式计算各个位置的视电阻率:
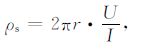
|
(9) |
其中,r为极距,I为微分方程中所设定电流强度.
3 外推瀑布式多网格法 3.1 外推和二次插值以一维为例,考虑三层嵌套网格Zi和步长hi=h0/2i,相应的线性有限元解为Ui.Z0 的粗单元Ij= (xj,xj+1),被加密为Z1,Z2 的单元,增加了一个中点和两个四分点,组成5点集合:
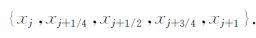
|
设已知相应的两组有限元节点值为
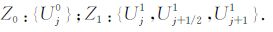
|
利用这5个节点值可提供密网Z2 上有限元解U2 的好初值${\tilde U^2}$[36]:
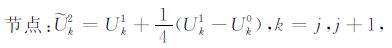
|
(10) |
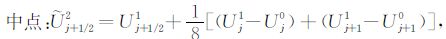
|
(11) |
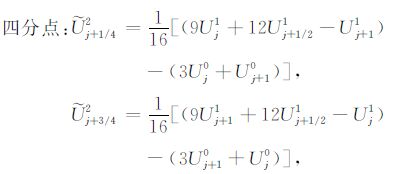
|
(12) |
其中,Z2 网格节点和中点初值由Z0,Z1 网格上的五个初值外推得到,而Z2 网格两个四分点初值利用外推得到的3 个(2 节点和1 中点)初值二次插值得到.
对如图 2所示二维三层矩形嵌套网格,和一维情形类似,4个节点‘·’可利用前两层网格节点值由公式(10)外推得到、4 个边中点‘▲’初值可利用x,y方向中点外推公式(11)得到,中心点‘*’看成对角线的中点,同样由中点外推公式(11)得到.而其余未知的16 个四分点‘■’初值可由已得到的9个节点(4节点、4 边中点、1 中心点)初值作双二次完全多项式插值得到.
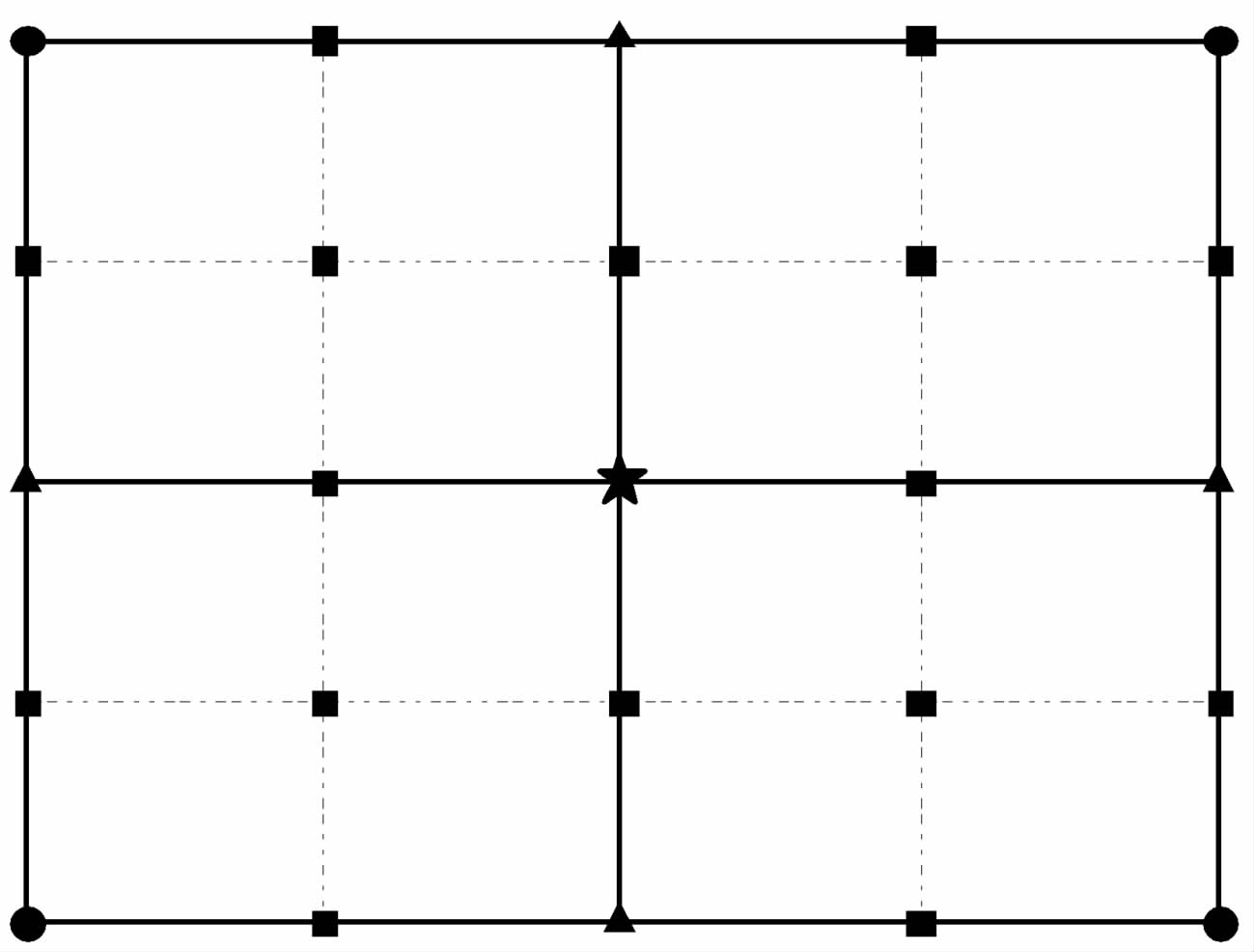
|
图 2 三层矩形嵌套网格 Fig. 2 Three nested rectangular grids |
外推瀑布型多网格法,利用外推及二次插值公式构造密网上的初值,逼近有限元解U,而不是微分方程真解u.典型三重外推瀑布式多网格算法具体步骤如下[34-37]:
步骤1:先求解最粗两层网格Z0,Z1 上的准确有限元解U0,U1;
步骤2:对i=1,2,…,L执行
(a)利用外推公式(10)-(12),构造密网Zi上初值珟${\tilde U^i}$],
(b)对密网Zi上有限元方程(4),由初值珟${\tilde U^i}$利用CG 迭代mi次求得近似解Ui;
步骤3:输出近似解UL,退出程序.
网格Zi上的CG 迭代次数mi通常取为

|
(13) |
m* 为最密网格ZL上的迭代次数,一般取为4-20,|_·_|表示取下整;而1<β≤2d,d为求解区域的维数.本文第四节所有算例中均取m* =16,β =4.
值得指出的是,一旦得到最密几层网格上很精确的有限元解,可利用经典Richardson外推进一步提高精度,或作后验误差估计,这种高精度后处理也是本算法最大优点之一.
3.3 刚度阵压缩存贮总体刚度矩阵K是具有高度稀疏性的对称正定矩阵.为了采用共轭梯度法求解有限元方程,对刚度矩阵必须采取压缩存储,即只记录和存贮矩阵非零元素.等带宽存储和变带宽存储为两种最常用的存储方式,它们都适用于线性方程组的直接解法,也适用于迭代解法.不过这两种存储方式没有充分利用网格的均匀性(EXCMG 算法采用的是均匀的嵌套网格),节省内存效率并不是特别高.
本文提出基于地址矩阵的压缩存贮方式:采用两个矩阵,一个整型矩阵G记录非零元素的地址,另一个实型矩阵M记录相应非零元素的数值.例如,n阶方阵A,若它每行最多有m个非零元素,则采用n×m阶矩阵G记非零元素的地址,用n×m阶矩阵M记非零元素的数值.CG 迭代中需要计算矩阵向量乘法,计算Ax的第i个分量简化为计算m个乘法
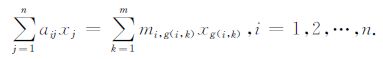
|
(14) |
作一次迭代Ax的计算工作量为mn=O(n).
考虑二维1600×1600 矩形剖分,节点总数为1601×1601=2563201,采用矩形双线性元,每个节点只与周围相邻的9 个节点有关系(包含该点本身),即总体刚度矩阵每行最多9个非零元.若总体节点编号规则为自下而上,自左至右,则第3行第4个节点的总体编号为(3-1)×1601+4=3206,故2563201×9阶整型地址矩阵G的3206行为
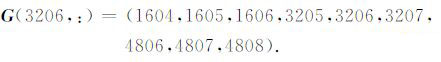
|
(15) |
若采用8字节双精度存贮刚度阵,其压缩率达到
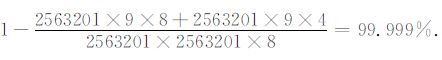
|
(16) |
因此,以上压缩存储方式是非常有效,并且矩阵规模越大,压缩比例越大.
4 数值计算结果与分析采用擅长数值计算的Fortran90语言,编写了2.5维直流电阻率法模拟的外推瀑布式多网格法程序.采用均匀矩形剖分,单元为矩形双线性元.本文的数值测试平台为CPUi57602.8G,RAM2G;测试系统为Compaq VisualFortran ProfessionalEdition6.6,自带IMSL 国际数学和统计链接库,调用贝塞尔函数比较方便.
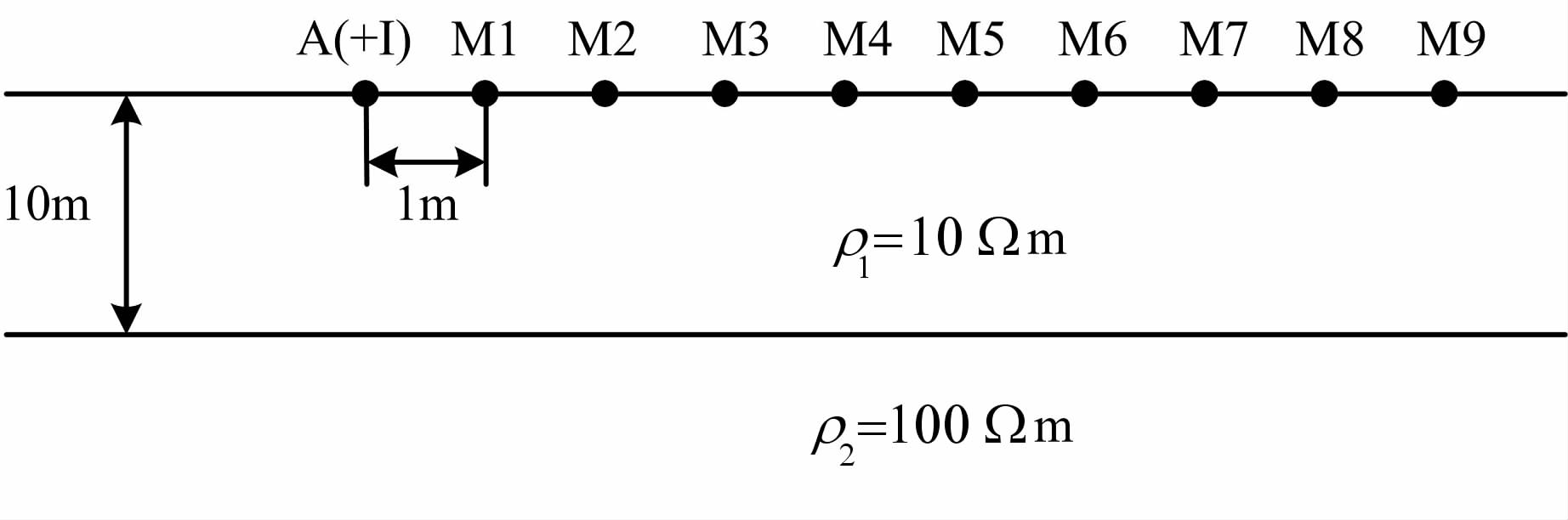
4.1 EXCMG算法效率分析考虑如图 3所示两层地电模型,第一层电阻率为ρ1=10Ωm,厚度h=10m;第二层电阻率为ρ2=100Ωm.采用单极供电(电流强度为I=1A),供电电极A 位于坐标原点.
|
图 3 两层地电断面示意图 Fig. 3 Schematic diagram of two-layer geoelectric section |
有界化计算区域取为400 m×400 m,采用均匀矩形剖分,取表 1 中最小的离散波数k=0.0031677(波数越大,有限元离散后得到的刚度阵对角优势越明显,条件数越小,求解更容易)将问题有限元离散后,分别用ICCG 及EXCMG 算法求解离散后得到的大型线性方程组.
EXCMG 算法采取6层均匀矩形嵌套网格,建立5个有限元模型,最粗网格分别取为20×20、30×30、40×40、50×50、60×60,最密网格为640×640、960×960、1280×1280、1600×1600、1920×1920,每层网格上CG 迭代次数mi=16×46-i.为了便于比较,ICCG 法的停机标准取为残差达到与EXCMG 算法相同的精度要求.
表 2是不同网格尺寸下ICCG 和EXCMG 的迭代次数和运行时间.从表 2中可看出,从640×640到1920×1920 的不同网格尺度,EXCMG 最密网格均为16 次迭代,且残差能达到相同的精度,约4.2×107,这证明了EXCMG 算法的收敛速度与网格尺寸无关.而ICCG 方法随着网格逐次加密,迭代次数明显增多.表 2最后一列给出了两种方法的计算时间比,可以看出,EXCMG 比ICCG 方法快几十倍,并且随着计算规模的增大,优势更加明显,1920×1920 网格下ICCG 方法的计算时间为EXCMG 算法的46.27倍.
|
|
表 2 不同网格尺寸下ICCG与EXCMG程序运行时间及迭代次数 Table 2 Running time and iteration number of ICCG and EXCMG method for various grid sizes |
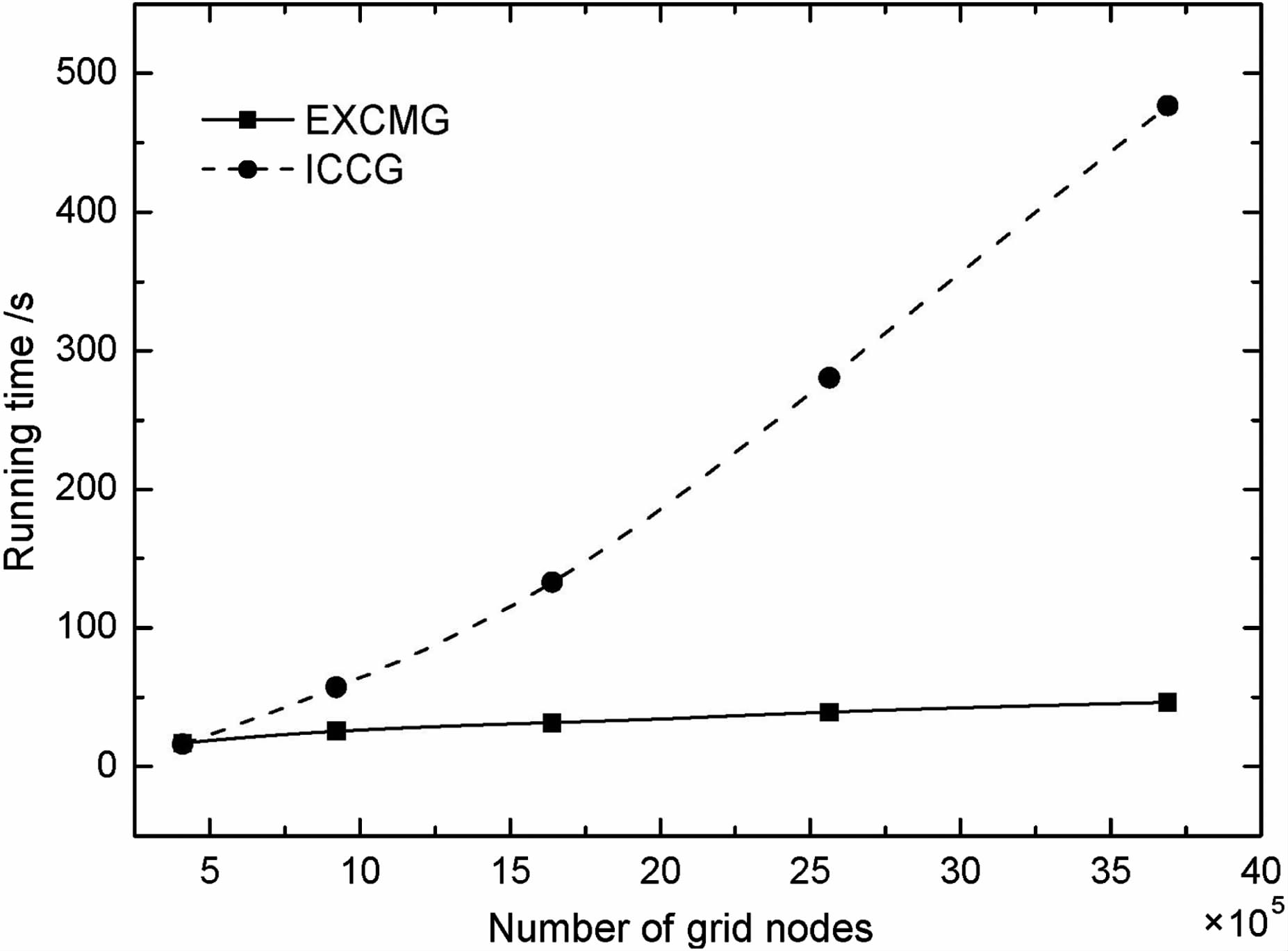
图 4为ICCG 和EXCMG 法的不同网格节点数下的计算时间.对比两种方法的时间曲线可以看出,ICCG 法所需计算时间随网格节点数增长明显比EXCMG 法要快,且时间曲线有明显的向上弯的趋势,而EXCMG 法的时间曲线基本为直线且微微向下弯曲,这意味着随着网格节点的增加EXCMG法在计算速度上的优势更加明显,也进一步验证了EXCMG算法的计算量仅与节点数的一次方成正比.
|
图 4 不同网格尺寸下ICCG与EXCMG的计算时间 Fig. 4 Running time of ICCG and EXCMG method for various grid sizes |
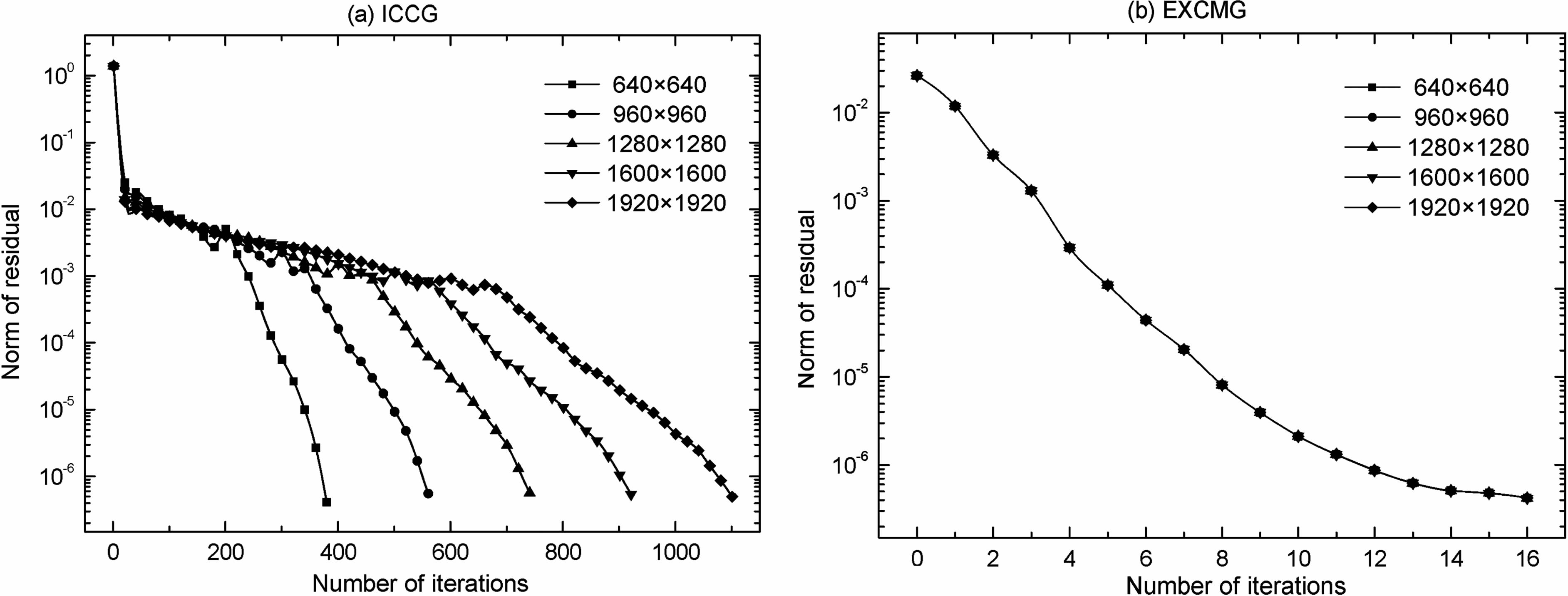
图 5为ICCG 法和EXCMG 法在不同网格尺寸下的收敛曲线.在不同网格尺寸下,EXCMG法迭代次数保持不变且残差范数几乎完全重合.而ICCG 算法随着网格节点数的增加收敛明显减慢,迭代次数由380 次(网格640×640)增至1120 次(网格1920×1920).实际上,ICCG 算法能保证收敛到问题的精确解,但迭代过程中误差出现震荡;而EXCMG 算法单调、迅速收敛到问题的精确解.
|
图 5 不同网格尺寸下ICCG 与EXCMG 的收敛曲线 Fig. 5 Convergence curves of ICCG and EXCMG methods for various grid sizes |
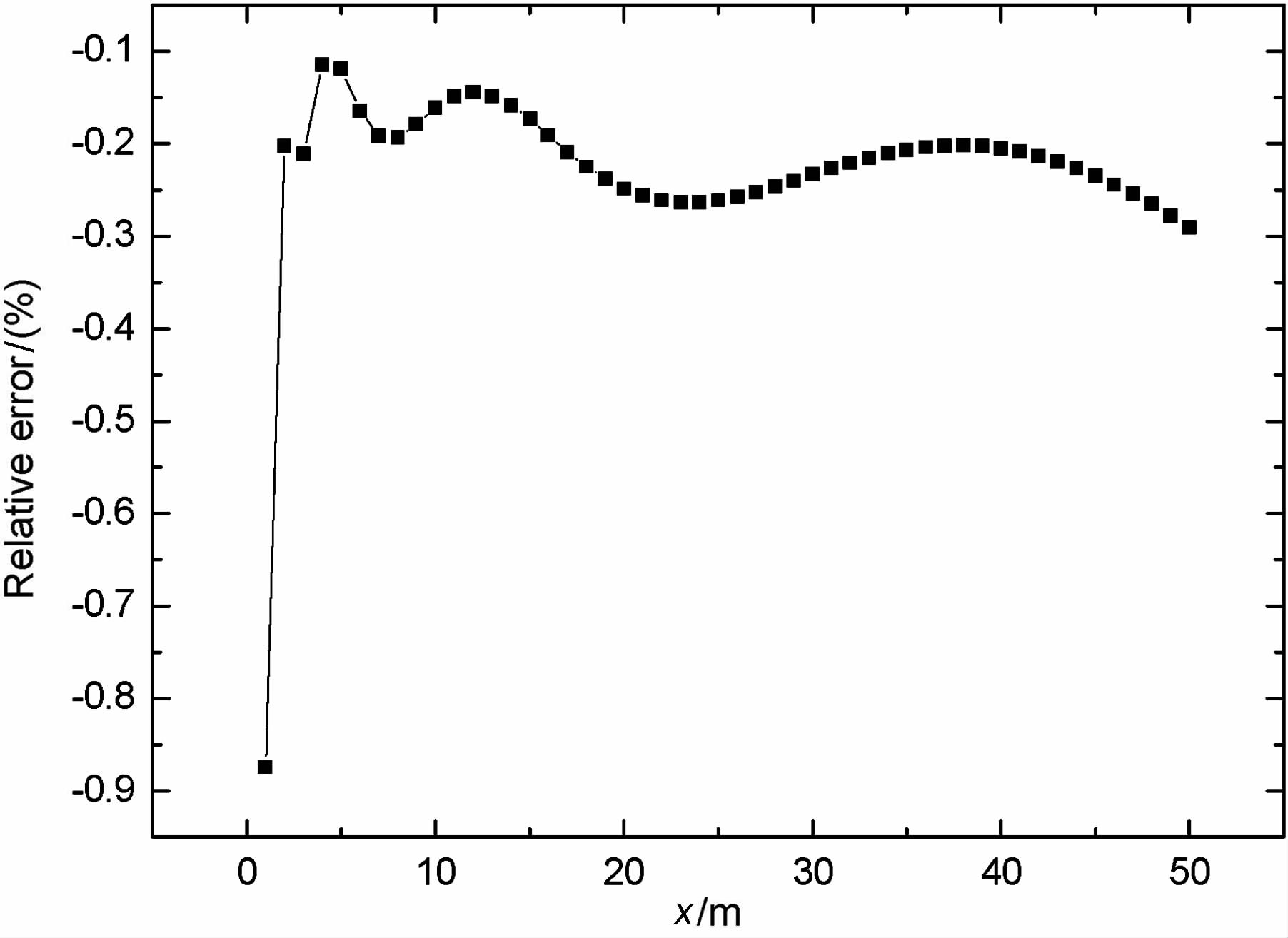
对如图 3所示具有解析公式的二层地电模型,有界化计算区域为400 m×400 m,初始网格规模为50×50,采用6层嵌套矩形均匀网格,最密网格为1600×1600(2563201个节点,2560000个单元),2.5维电阻率法模拟的EXCMG 程序在PC 机上仅耗时28s.视电阻率ρs 的平均相对误差为0.22%,均方误差为0.09Ωm.最大相对误差出现在离电源最近的M1点,为-0.87%,除M1 点相对误差均在-0.3%之内,详见图 6.
|
图 6 视电阻率相对误差曲线 Fig. 6 Relative errors of apparent resistivity |
均方误差MSE 按下式定义:
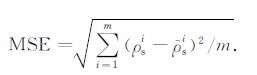
|
式中,m为电极距个数,ρsi,$\tilde \rho _{\rm{s}}^i$分别为第i个位置的视电阻率理论值和计算值.
4.3 DiKe模型Dike模型是垂直的三层介质,中间层厚度很薄,如图 7 所示.计算中取中间层电阻率为ρ2 =10Ωm,厚度为5 m,左右两边的电阻率ρ1 =100Ωm.单点电源A 位于坐标原点,采用二极AM 测深装置,侧线从10~35m,点距为0.5m.
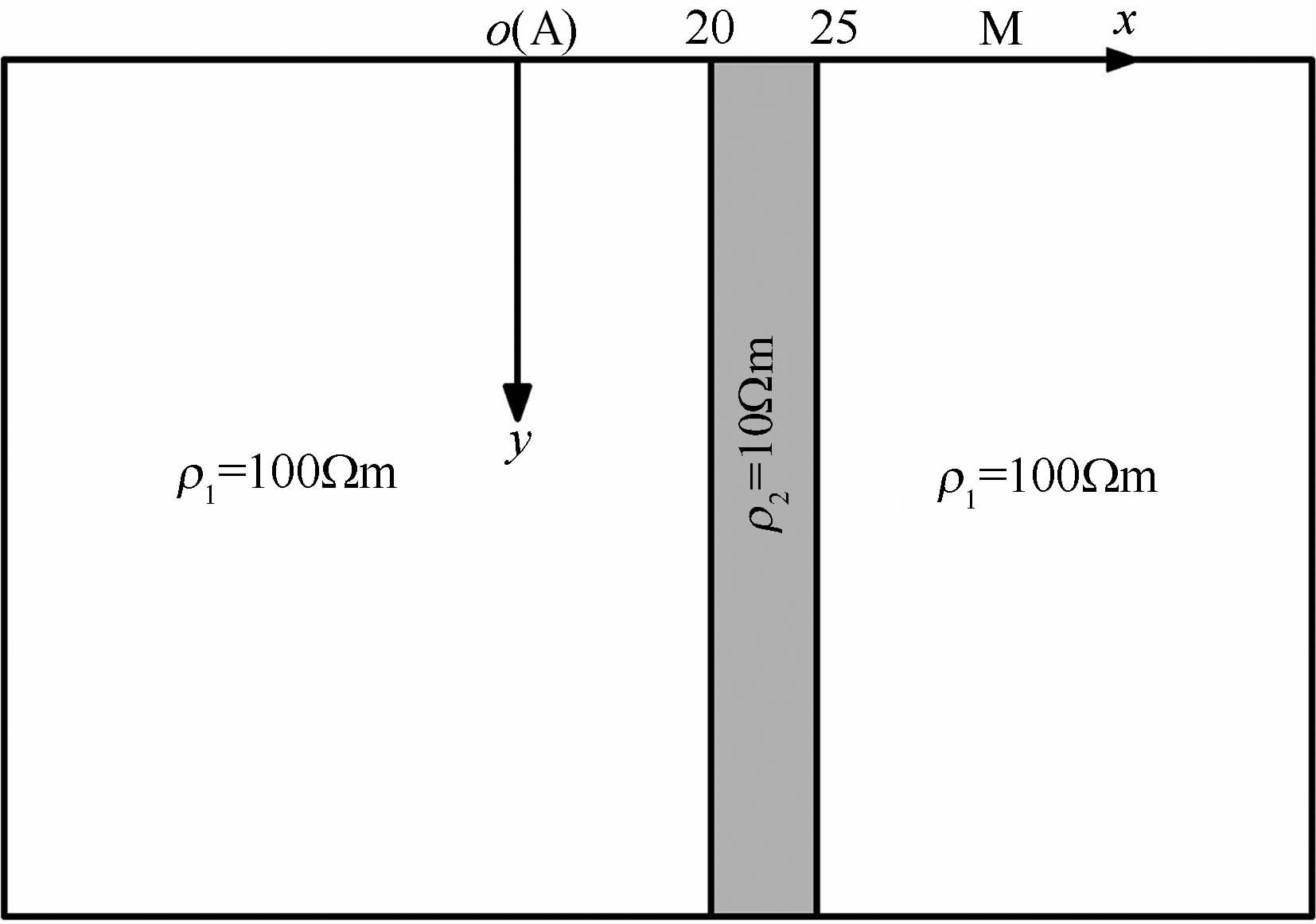
|
图 7 Dike模型示意图 Fig. 7 Schematic diagram of the Dike model |
有界化计算区域为800 m×400 m,初始网格规模取为50×25,采用6层嵌套矩形均匀网格,最密网格分别为1600×800(1282401 个节点),正演程序耗时12s,数值模拟结果如图 8所示.
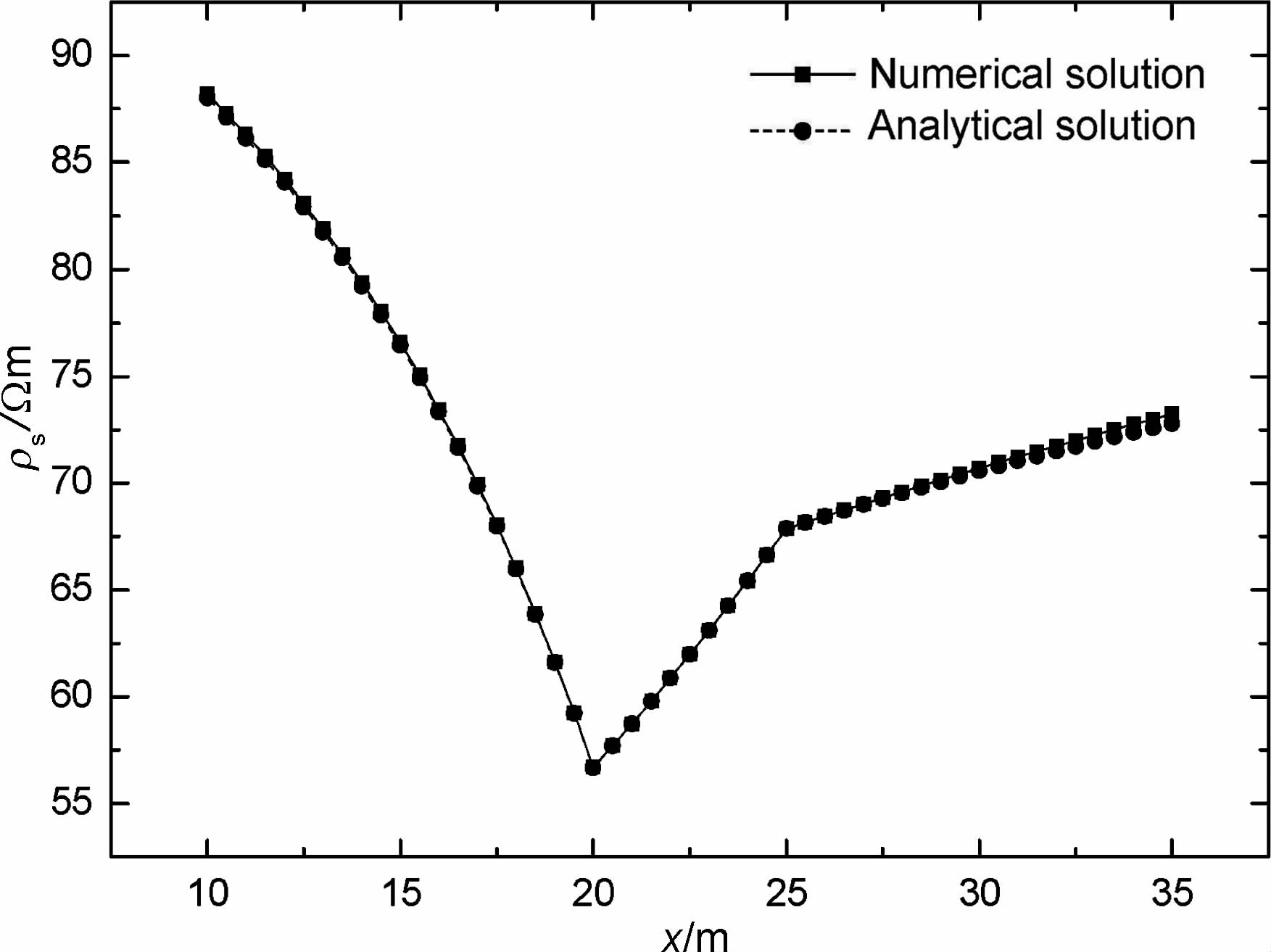
|
图 8 Dike模型视电阻率曲线 Fig. 8 Apparent resistivity curve for Dike model |
从图 8可以看出,数值解与精确解的视电阻率曲线几乎完全吻合.实际上,视电阻率最大相对误差为0.62%,平均相对误差为0.16%,均方误差为0.17Ωm.
为了研究电性差异对EXCMG 算法精度的影响,将如图 7 所示Dike 模型中电阻率改为ρ1 =1000Ωm,ρ2=1Ωm,在同样的网格剖分和CG 迭代次数下重新进行计算,计算结果如图 9所示.从图 9可以看出,较大电性差异下EXCMG 法得到的视电阻率和精确解亦几乎完全重合.最大相对误差正好出现在低阻薄层20~25 m 之间,且远离薄层相对误差迅速趋于零,平均相对误差为2.74%,均方误差为2.66Ωm.
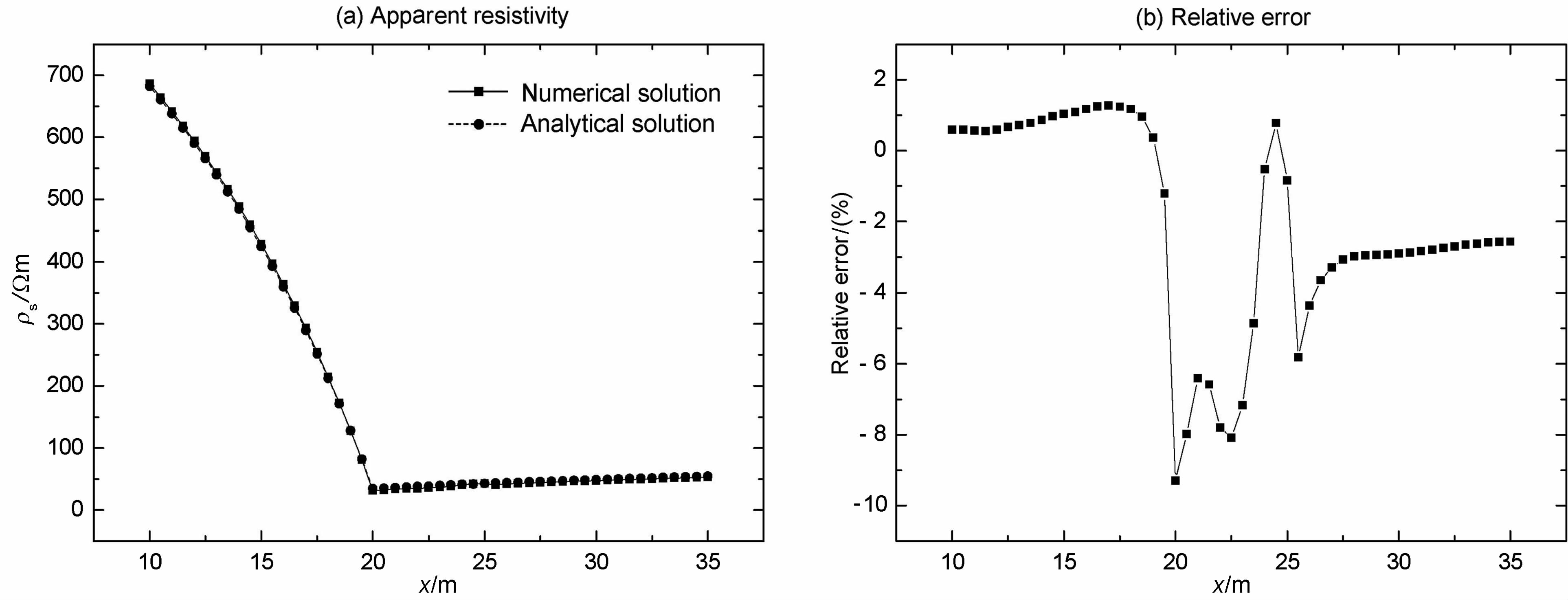
|
图 9 大电性差异Dike模型计算结果 Fig. 9 Numerical results for Dike model with high contrast conductivity |
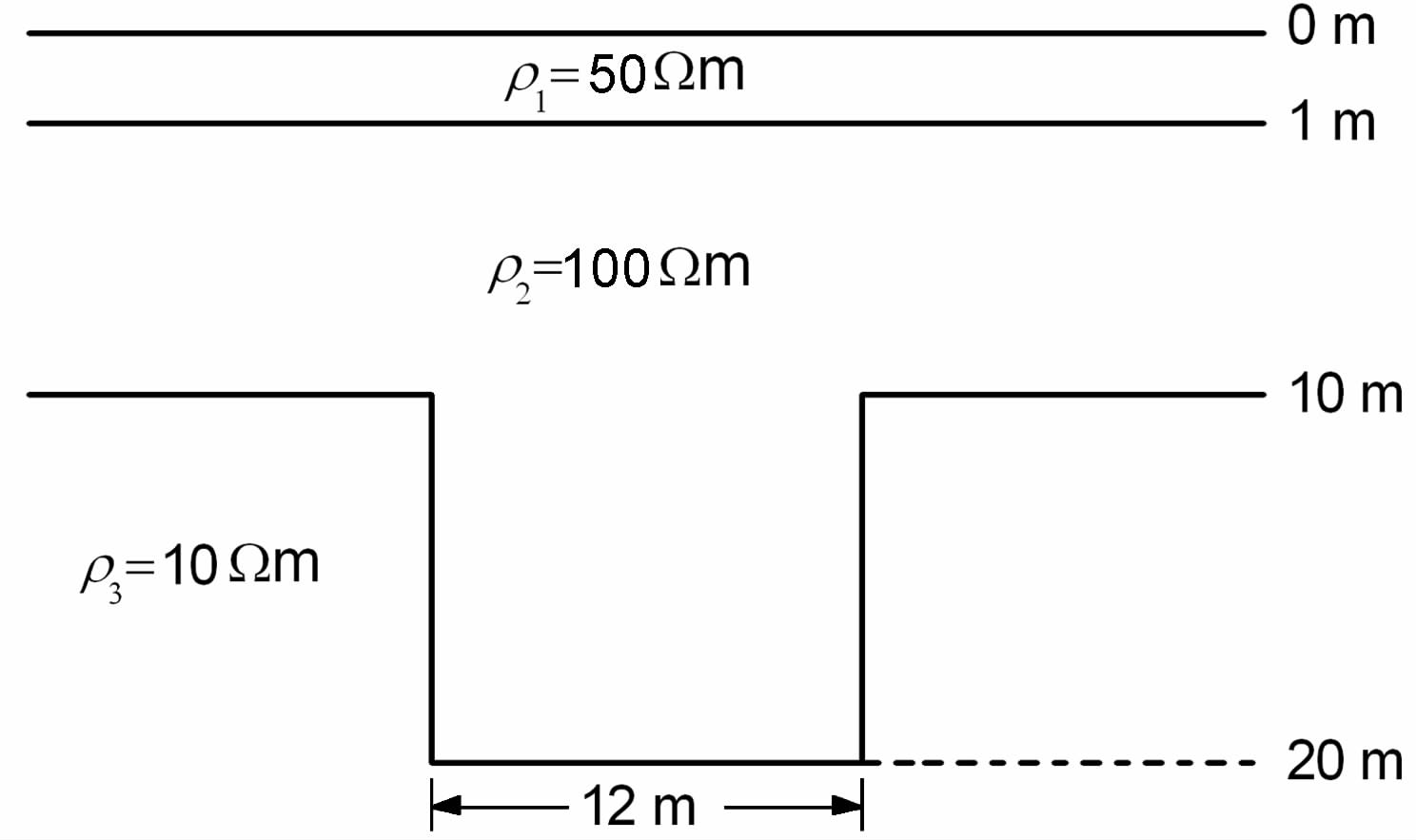
考虑如图 10 所示的三层地堑模型,第一层地表层电阻率ρ1=50Ωm,厚度为1m;第二层地堑层电阻率ρ2 =100 Ωm,厚度为9 m,地堑宽度为12m;第三层背景层电阻率ρ3=10Ωm.
|
图 10 地堑模型示意图 Fig. 10 Schematic diagram of the graben model |
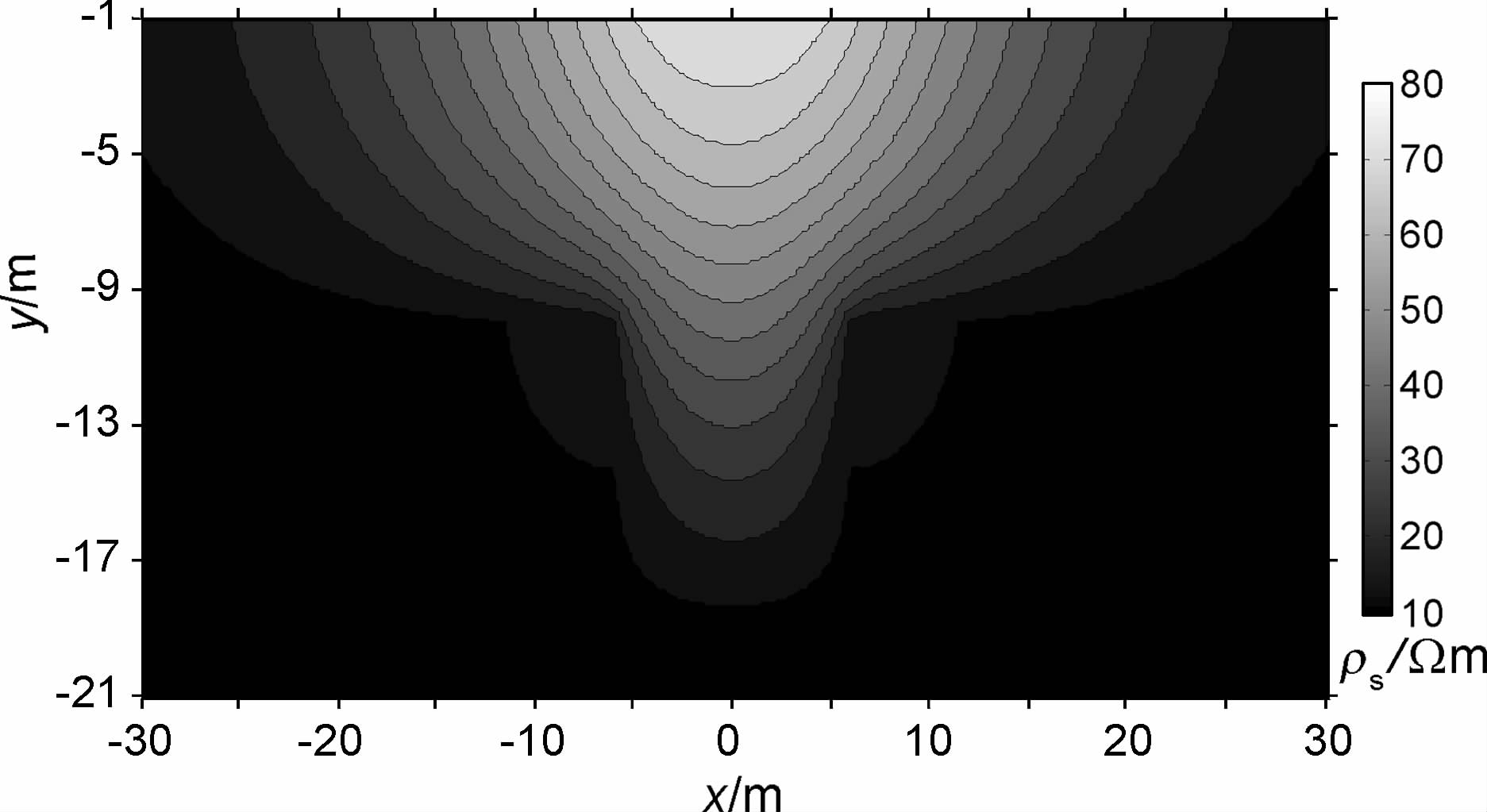
计算区域取为400 m×200 m,初始网格规模为100×100,采用5层嵌套矩形均匀网格,最密网格为1600×1600(2563201个节点).电阻率法正演的EXCMG 程序在PC 机上耗时29s,主剖面视电阻率断面图见图 11.
|
图 11 视电阻率断面图 Fig. 11 Cross-section of apparent resistivity |
从图 11可以看出,地堑轮廓非常明显:地堑宽度约为12m,亦在深度为10~20 m 范围,这与正演所设定地电模型完全吻合,进一步验证了正演程序的正确性.
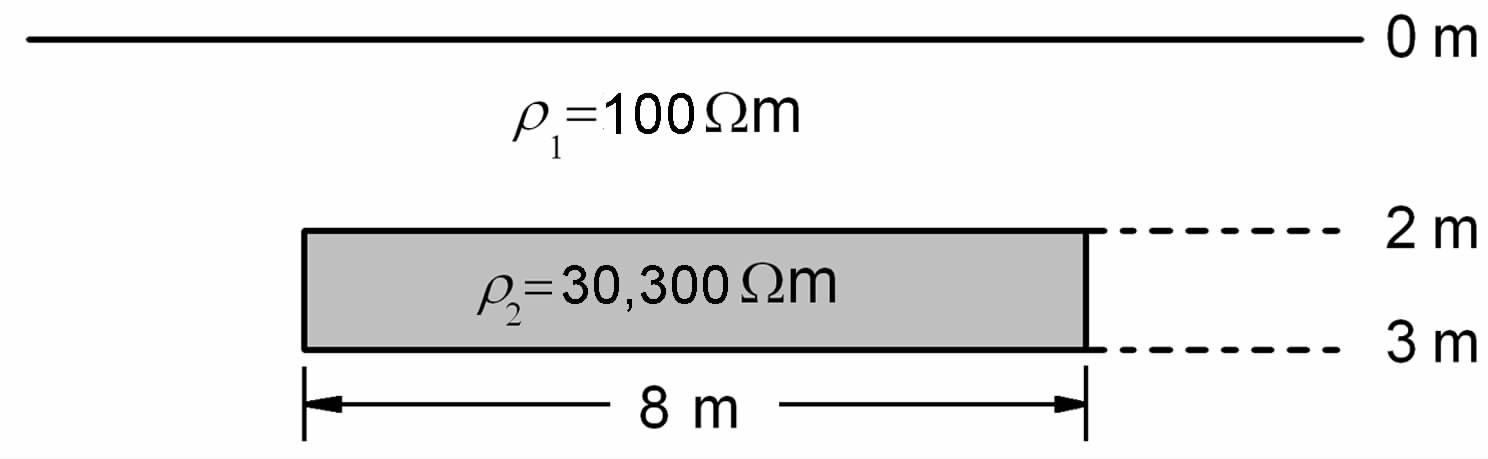
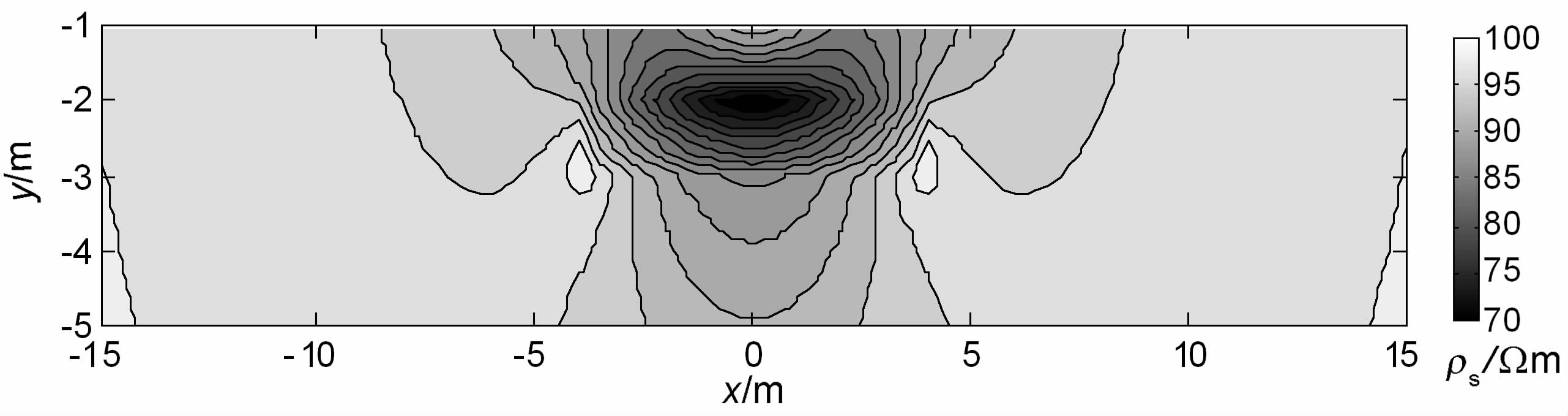
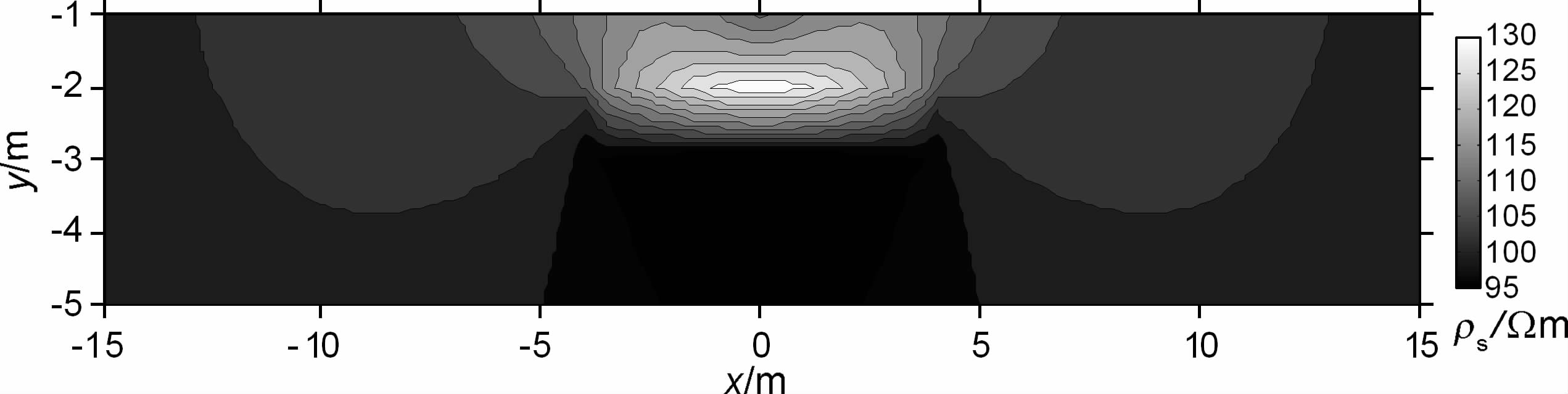
4.5 异常板状体模型考虑图 12所示的低阻和高阻水平板状体模型,板状体宽8m,厚1m,埋深2m,围岩电阻率ρ1=100Ωm,低阻体电阻率为30Ωm,高阻体电阻率为300Ωm.采用与地堑模型相同的计算规模和程序参数设置,电阻率法正演的EXCMG 程序在PC 机上耗时27s,低阻和高阻情形主剖面视电阻率断面图分别见图 13和图 14.
|
图 12 水平板状异常体示意图 Fig. 12 Schematic diagram of plate-like body in the horizontal direction |
|
图 13 低阻板状体正演模拟结 Fig. 13 Forward modeling results of low-resistivity plate-like body |
|
图 14 高阻板状体正演模拟结果 Fig. 14 Forward modeling results of high-resistivity plate-like body |
从图 13和图 14可以看出,低(高)阻板和异常形态为一封闭的低(高)阻圈,其宽度与低(高)阻板的宽度大致相同,厚度与低(高)阻板的厚度大致相同,且其位置亦与正演模型完全吻合.
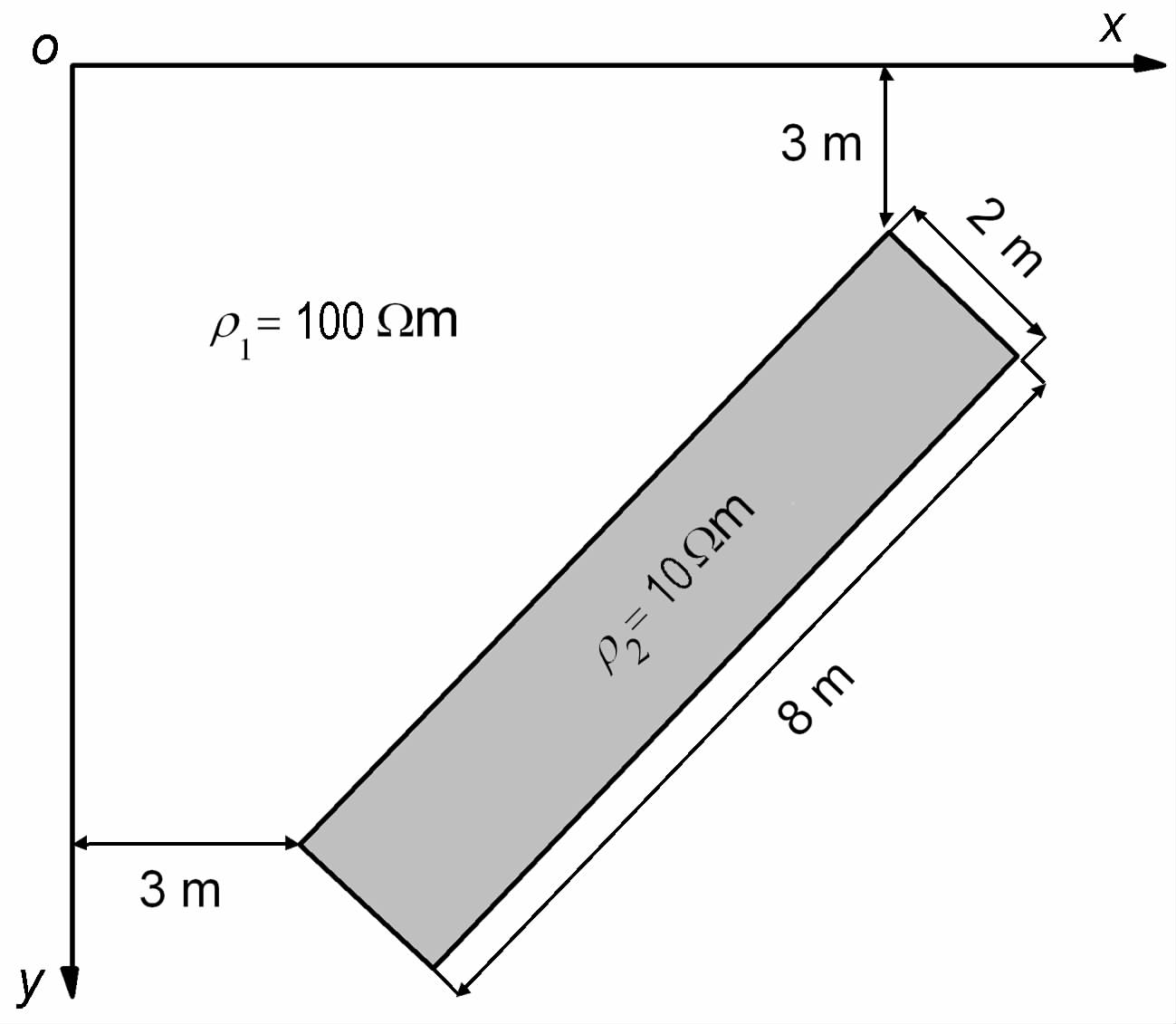
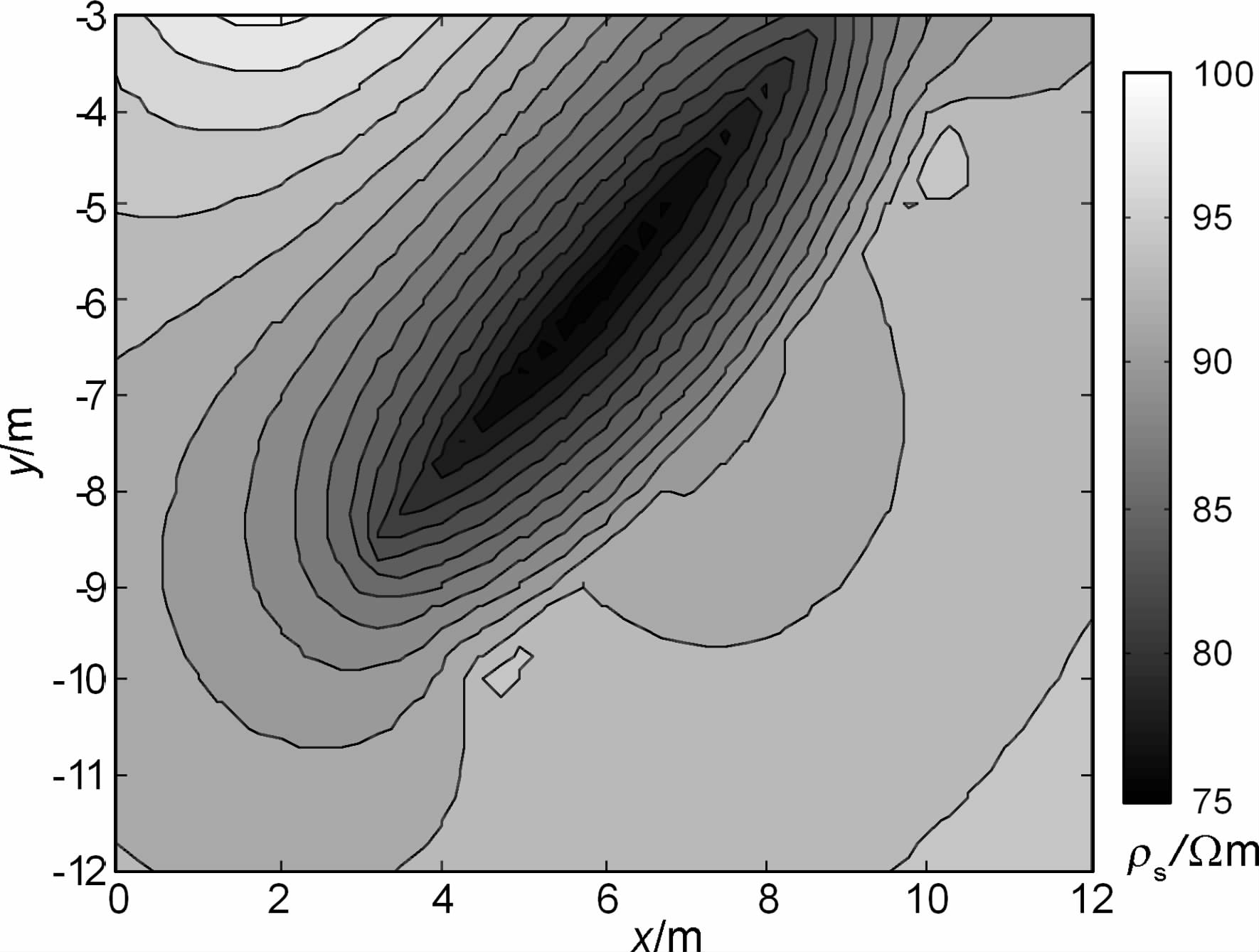
考虑图 15所示的倾斜板状体模型,板状体宽2m,长8 m,向右倾斜,倾角为45°.顶部埋深3m,围岩电阻率ρ1=100Ωm,低阻异常体电阻率为ρ2=10Ωm.取计算区域为600m×300m,初始网格规模为150×75,采用5层嵌套矩形均匀网格,最密网格为2400×1200(2883601 个节点).正演EXCMG 程序PC 机上耗时38s,主剖面视电阻率断面图见图 16.
|
图 15 倾斜板状体空间位置图 Fig. 15 Locations of plate-like body titled in the subsurface |
|
图 16 倾斜板状体正演模拟结果 Fig. 16 Forward modeling results of plate-like body titled |
从图 16可明显地看出在-10 m~ -3 m 之间有一明显的低阻异常体,其形n为一右倾45°的矩形,这与正演模型完全吻合.并且,将最密层网格迭代次数m* 从16改为128(保证最密网格层上的求解精度),得到几乎完全相同的模拟结果,这表明了外推瀑布式多重网格法对较复杂的地电模型同样适用,且其收敛速度与模型的复杂性及其未知数的个数基本无关.
5 结 论本文将求解大规模椭圆边值问题的外推瀑布式多网格法应用到2.5 维直流电阻率法正演计算中,实现了快速、精确的直流电阻率法有限元正演,为进一步研究反演奠定了基础.
(1)基于地址矩阵的压缩存贮模式,非常适合EXCMG 算法的规则网格剖分,且压缩效率极高,如采用矩形双线性元,1600×1600 网格剖分压缩率可达99.999%.
(2)EXCMG 算法计算速度比基于单重网格的ICCG 算法快几十倍,且随着网格加密优势更加明显.
(3)EXCMG 算法收敛速度与网格节点数无关,在保持同等精度的前提下计算时间随节点数线性增加.
(4)EXCMG 算法对大电性差异和较复杂的地电模型(如斜向界面模型)同样适用.
(5)几何多网格法的局限:求解区域不宜太复杂(如起伏地表),否则无法进行多网格剖分.
致谢特别感谢任政勇博士(ETH Zurich,Switzerland)提供的Dike模型及理论计算程序以及两位审稿专家的宝贵修改意见.
| [1] | 徐世浙. 地球物理中的有限单元法. 北京: 科学出版社, 1994 : 178 -188. Xu S Z. The Finite Element Method in Geophysics (in Chinese). Beijing: Science Press, 1994 : 178 -188. |
| [2] | Coggon J H. Electromagnetic and electrical modeling by the finite element method. Geophysics , 1971, 36(1): 132-145. DOI:10.1190/1.1440151 |
| [3] | 徐世浙. 电导率分段线性变化的水平层的点电源电场的数值解. 地球物理学报 , 1986, 29(1): 84–90. Xu S Z. A numerical method for solving electric field of point source on a layered model with linear change of conductivity in each layer. Chinese J. Geophys (in Chinese) , 1986, 29(1): 84-90. |
| [4] | 徐世浙, 刘斌, 阮百尧. 电阻率法中求解异常电位的有限单元法. 地球物理学报 , 1994, 37(S2): 511–515. Xu S Z, Liu B, Ruan B Y. The finite element method for solving anomalous potential for resistivity surveys. Chinese J. Geophys (in Chinese) , 1994, 37(S2): 511-515. |
| [5] | 徐世浙, 刘斌. 电导率分层连续变化的水平层的大地电磁正演. 地球物理学报 , 1995, 38(2): 262–268. Xu S Z, Liu B. A numerical method for calculating MT field on a layered model with continuous change of conductivity in each layer. Chinese J. Geophys (in Chinese) , 1995, 38(2): 262-268. |
| [6] | 阮百尧, 徐世浙. 电导率分块线性变化二维地电断面电阻率测深有限元数值模拟. 地球科学——中国地质大学学报 , 1998, 23(3): 303–307. Ruan B Y, Xu S Z. FEM for modeling resistivity sounding on 2D geoelectric model with line variation of conductivity within each block. Earth Science——Journal of China University of Geosciences (in Chinese) , 1998, 23(3): 303-307. |
| [7] | 周熙襄, 钟本善, 严忠琼, 等. 电法勘探正演数值模拟的若干结果. 地球物理学报 , 1983, 26(5): 479–491. Zhou X X, Zhong B S, Yan Z Q, et al. Some results of resistivity modelling. Chinese J. Geophy (in Chinese) , 1983, 26(5): 479-491. |
| [8] | 罗延钟, 孟永良. 关于用有限单元法对二维构造作电阻率法模拟的几个问题. 地球物理学报 , 1986, 29(6): 613–621. Luo Y Z, Meng Y L. Some problems on resistivity modeling for two-dimensional structures by the finite element method. Chinese J. Geophys (in Chinese) , 1986, 29(6): 613-621. |
| [9] | 强建科, 罗延钟. 三维地形直流电阻率有限元法模拟. 地球物理学报 , 2007, 50(5): 1606–1613. Qiang J K, Luo Y Z. The resistivity FEM numerical modeling on 3-D undulating topography. Chinese J. Geophys (in Chinese) , 2007, 50(5): 1606-1613. |
| [10] | Zhou B, Greenhalgh S A. Finite-element 3D direct current resistivity modelling: accuracy and efficiency considerations. Geophysical Journal International , 2001, 145(3): 679-688. DOI:10.1046/j.0956-540x.2001.01412.x |
| [11] | 熊彬, 阮百尧. 电位双二次变化二维地电断面电阻率测深有限元数值模拟. 地球物理学报 , 2002, 45(2): 285–295. Xiong B, Ruan B Y. A numerical simulation of 2-D geoelectric section with biquadratic change of potential for resistivity sounding by the finite element method. Chinese J. Geophys (in Chinese) , 2002, 45(2): 285-295. |
| [12] | 阮百尧, 熊彬. 电导率连续变化的三维电阻率测深有限元模拟. 地球物理学报 , 2002, 45(1): 131–138. Ruan B Y, Xiong B. A finite element modeling of three-dimensional resistivity sounding with continuous conductivity. Chinese J. Geophys (in Chinese) , 2002, 45(1): 131-138. |
| [13] | 李长伟, 阮百尧, 吕玉增. 点源场井-地电位测量三维有限元模拟. 地球物理学报 , 2010, 53(3): 729–736. Li C W, Ruan B Y, Lü Y Z, et al. Three-dimensional FEM modeling of point source borehole-ground electrical potential measurements. Chinese J. Geophys (in Chinese) , 2010, 53(3): 729-736. |
| [14] | 底青云, 王妙月. 稳定电流场有限元法模拟研究. 地球物理学报 , 1998, 41(2): 252–260. Di Q Y, Wang M Y. The real-like 2D FEM modeling research on the field characteristics of direct electric current field. Chinese J. Geophys (in Chinese) , 1998, 41(2): 252-260. |
| [15] | 吴小平, 徐果明, 李时灿. 利用不完全Cholesky共轭梯度法求解点源三维地电场. 地球物理学报 , 1998, 41(6): 848–855. Wu X P, Xu G M, Li S C. The calculation of 3-D geoelectric field yielded by point source using incomplete cholesky conjugate gradient method. Chinese J. Geophys (in Chinese) , 1998, 41(6): 848-855. |
| [16] | Wu X P, Xiao Y, Qi C, Wang T. Computations of secondary potential for 3-D DC resistivity modelling using an incomplete Choleski conjugate gradient method. Geophys Prospect , 2003, 51(6): 567-577. DOI:10.1046/j.1365-2478.2003.00392.x |
| [17] | Wu X P. A 3D finite-element algorithm for DC resistivity modelling using the shifted incomplete cholesky conjugate gradient method. Geophys. J. Int , 2003, 154(3): 947-956. DOI:10.1046/j.1365-246X.2003.02018.x |
| [18] | 吴小平, 汪彤彤. 利用共轭梯度算法的电阻率三维有限元正演. 地球物理学报 , 2003, 46(3): 428–432. Wu X P, Wang T T. A 3-D finite-element resistivity forward modeling using conjugate gradient algorithm. Chinese J. Geophys (in Chinese) , 2003, 46(3): 428-432. |
| [19] | 陈小斌, 胡文宝. 有限元直接迭代算法及其在线源频率域电磁响应计算中的应用. 地球物理学报 , 2002, 45(1): 119–130. Chen X B, Hu W B. Direct iterative finite element (DIFE) algorithm and its application to electromagnetic response modeling of line current source. Chinese J. Geophys (in Chinese) , 2002, 45(1): 119-130. |
| [20] | 任政勇, 汤井田. 基于局部加密非结构化网格的三维电阻率法有限元数值模拟. 地球物理学报 , 2009, 52(10): 2627–2634. Ren Z Y, Tang J T. Finite element modeling of 3-D DC resistivity using locally refined unstructured meshes. Chinese J. Geophy (in Chinese) , 2009, 52(10): 2627-2634. |
| [21] | 汤井田, 王飞燕, 任政勇. 基于非结构化网格的2.5-D直流电阻率自适应有限元数值模拟. 地球物理学报 , 2010, 53(3): 708–716. Tang J T, Wang F Y, Ren Z Y. 2.5-D DC resistivity modeling by adaptive finite-element method with unstructured triangulation. Chinese J. Geophys (in Chinese) , 2010, 53(3): 708-716. |
| [22] | 汤井田, 公劲喆. 三维直流电阻率有限元—无限元耦合数值模拟. 地球物理学报 , 2010, 53(3): 717–728. Tang J T, Gong J Z. 3D DC resistivity forward modeling by finite-infinite element coupling method. Chinese J. Geophys (in Chinese) , 2010, 53(3): 717-728. |
| [23] | Ren Z Y, Tang J T. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method. Geophysics , 2010, 75(1): 7-17. DOI:10.1190/1.3298690 |
| [24] | Ren Z Y, Tang J T, Wang F Y, et al. Object-oriented implementation of 3D DC adaptive finite element method. Front. Earth Sci , 2010, 4(2): 229-236. DOI:10.1007/s11707-009-0065-x |
| [25] | Tang J T, Ren Z Y, Wang F Y, et al. 3-D direct current resistivity forward modeling by adaptive multigrid finite element method. J. Cent. South Univ. Technol , 2010, 17(3): 587-592. DOI:10.1007/s11771-010-0527-z |
| [26] | Fedorenko P R. The speed of convergence of one iterative process, USSR Comp. Math. Math. Phys , 1964, 4(3): 227-235. DOI:10.1016/0041-5553(64)90253-8 |
| [27] | Moucha R, Bailey R C. An accurate and robust multigrid algorithm for 2D forward resistivity modelling. Geophys| Prospect , 2004, 52(3): 197-212. |
| [28] | Mulder W A. A multigrid solver for 3D electromagnetic diffusion. Geophys| Prospect , 2006, 54(5): 633-649. |
| [29] | 鲁晶津, 吴小平, SpitzerK. 直流电阻率三维正演的代数多重网格方法. 地球物理学报 , 2010, 53(3): 700–707. Lu J J, Wu X P, Spitzer K. Algebraic multigrid method for 3D DC resistivity modelling. Chinese J. Geophys (in Chinese) , 2010, 53(3): 700-707. |
| [30] | 柳建新, 郭荣文, 童孝忠, 等. 基于多重网格法的MT正演模型边界截取. 中南大学学报 (自然科学版) , 2011, 42(11): 3429–3437. Liu J X, Guo R W, Tong X Z, et al. Boundary truncation of magnetotelluric modeling based on multigrid method. Journal of Central South University: Science and Technology (in Chinese) , 2011, 42(11): 3429-3437. |
| [31] | 柳建新, 郭荣文, 童孝忠, 等. 大地电磁法正演中多重网格法求解的广义傅里叶谱分析. 吉林大学学报(地球科学版) , 2011, 41(5): 1587–1595. Liu J X, Guo R W, Tong X Z, et al. General Fourier analysis of multi-grid in magnetotelluric modeling. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2011, 41(5): 1587-1595. |
| [32] | Bornemann F, Deuflhard P. The cascadic multigrid method for elliptic problems. Numer. Math , 1996, 75(2): 135-152. DOI:10.1007/s002110050234 |
| [33] | 陈小斌, 张翔. 用自动网格剖分法求解二阶椭圆型偏微分方程. 江汉石油学院学报 , 1999, 21(3): 93–95. Chen X B, Zhang X. On the computational aspects of auto grid splitting for solving second order elliptic equations. Journal of Jianghan Petroleum Institute (in Chinese) , 1999, 21(3): 93-95. |
| [34] | Chen C M, Hu H L, Xie Z Q, et al. Analysis of extrapolation cascadic multigrid method. Science China, Series A , 2008, 51(8): 1349-1360. DOI:10.1007/s11425-008-0119-7 |
| [35] | Chen C M, Hu H L, Xie Z Q, et al. L2-error of extrapolation cascadic multigrid. Acta Mathematica Scientia, Series B , 2009, 29(3): 539-551. DOI:10.1016/S0252-9602(09)60052-7 |
| [36] | 胡宏伶, 陈传淼, 谢资清. 外推瀑布多网格法(EXCMG)—求解大规模椭圆问题的新算法. 计算数学 , 2009, 31(3): 275–288. Hu H L, Chen C M, Xie Z Q. Extrapolation cascadic multigrid method (EXCMG)—A new algorithm for solving large scale elliptic problems. Mathematica Numerica Sinica (in Chinese) , 2009, 31(3): 275-288. |
| [37] | Chen C M, Shi Z C, Hu H L. On extrapolation cascadic multigrid method. J. Comp| Math , 2011, 29(6): 684-697. |
| [38] | Xu S Z, Duan B C, Zhang D H. Selection of the wavenumbers k using an optimization method for the inverse Fourier transform in 2. Geophysical Prospecting , 2000, 48(5): 789-796. DOI:10.1046/j.1365-2478.2000.00210.x |
 2012, Vol. 55
2012, Vol. 55