2. 成都理工大学地球物理学院地球物理与勘察技术系, 成都 610059;
3. 中国石油大学CNPC物探重点实验室, 北京 102249
2. Department of Geophysics and Exploration, College of Geophysics, Chengdu University of Technology, Chengdu 610059, China;
3. CNPC Key Laboratory of Geophysical Prospecting, China University of Petroleum, Beijing 102249, China
弹性波在流体饱和孔隙介质传播过程中会诱发孔隙压力的变化而形成孔压梯度,孔压梯度引起黏性孔隙流体与固体岩石骨架间的相对运动从而使介质在宏观性质上表现出衰减、速度频散等非弹性行为.孔隙介质内的孔压梯度可形成于三种情况下:其一,弹性波在均匀孔隙介质传播过程中由波峰与波谷之间振幅变化所形成的孔隙压力梯度,这种孔压梯度形成波长尺度上的流体流动即Biot流或宏观流动作用[1-3];其二,均匀孔隙介质中所含孔隙的不同部分存在刚性差异,在弹性波的作用下孔隙不同部分所诱发的孔隙压力存在差异而造成的流体流动,即喷射流作用,通常这种作用所产生的速度频散和衰减作用主要发生在超声频段(如岩石样品对超声波的衰减作用)[4-7];其三,孔隙介质内部在介观尺度上存在不均匀,在弹性或者物性特征上存在差异(如弹性性质不均匀、饱和度分布不均匀、渗透率不均匀等),在弹性波作用下不均匀体间的孔隙压力存在差异而形成的孔隙介质中不同部分间的流体流动,这种流体流动在尺度上远大于介质组成孔隙的尺度同时小于弹性波传播的波长是介观尺度上(厘米或分米级)的流体流动作用,可使岩石介质在地震频段也表现出较为明显的速度频散和衰减特征[8-13].
White首先利用“球状气包”模型讨论了介观尺度孔隙流体流动作用对介质宏观性质的影响,随后用相同的方法研究了含气、含水层交错排列的周期层状孔隙介质中纵波衰减与频散特征,但在White模型中并不要求含气层与饱水层之间孔隙压力连续,因此其求解过程在物理意义上并不严格[14].随后Dutta等基于Biot理论用更严格的方法对“球状气包”模型进行了研究,并修正了White 计算公式[15-16].之后层状孔隙介质一直是研究介观尺度下流体流动耗散机制的重要模型,Norris利用该模型通过均匀化方法研究了介观尺度流体流动作用对纵波衰减和频散特征的影响[17];Vogelaar等基于Biot理论将White周期性层状孔隙介质模型扩展到全频段,并利用数值解研究了介质的纵波频散特征与衰减特[18-19];Gurevich等对随机排列的层状孔隙介质中的纵波传播特征进行了研究[20-21];Brajanovski与Gurevich 等将周期性层状孔隙介质中厚度较薄的一层替换为具有高孔隙度的柔性层,藉此研究纵波在含裂隙孔隙介质中的传播特征[22-23].上述研究结果均表明介观尺度上的流体流动作用会在地震频段形成较强的纵波速度频散与衰减作用,可以定性解释地震频段下纵波衰减的现象.但现有相关研究结果中尚未对弹性波作用下White模型中孔隙压力、孔隙流体相对运动速度以及固体骨架位移等物理量的变化规律给出相关的理论计算公式及理论分析,因此无法对建立它们与介质的频散与耗散特征之间的直接联系.本文利用White周期性层状孔隙介质模型,基于准静态孔弹性理论给出了模型介质中孔隙压力、孔隙流体相对运动速度以及固体骨架位移等物理量的数学解析表达式,克服了White模型中介质分界面处流体压力不连续的假设,并以此为基础系统讨论了波在模型中的传播特征.同时在准静态与全频段下对介质中孔隙压力、孔隙流体相对运动速度变化形式进行了研究,讨论了快、慢纵波在介质中所诱发的孔隙压力及孔隙流体相对流动速度的形式,为更有效地理解介观尺度上流体流动耗散机制提供依据.
2 Biot方程与孔弹性关系弹性波在孔隙介质中的传播特征不但受孔隙介质自身性质的影响,同时还与弹性波的频率特征有明显关系.弹性波在均匀各向同性流体饱和孔隙介质中的传播规律可由Biot理论描述,其时间域弹性动力学方程组可以表示为[1-3]:
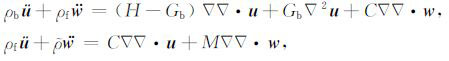
|
(1) |
式中u为孔隙介质固体骨架位移向量,如定义U为平均流体位移向量,则孔隙流体相对位移向量w=$\phi $(U-u),$\phi $ 为介质孔隙度;用ρs、ρf 分别代表固体骨架组成物质密度与孔隙流体密度,则孔隙介质总密度ρb为
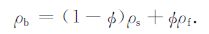
|
(2) |
公式(1)中ρ 为表征孔隙流体与固体骨架间惯性耦合作用与黏滞力作用的总有效密度:
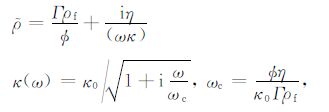
|
(3) |
式中Γ 为孔隙介质曲折度,κ0、κ 分别为孔隙介质的绝对渗透率和动态渗透率[24],μ 为孔隙饱和流体黏度,ω 为平面波角频率,ωc 为Biot临界频率.Gb、H、C、M是孔隙介质的四个独立弹性常数,在以知孔隙介质固体骨架体积模量kb、固体骨架剪切模量Gb、饱和流体体积模量kf 与固体骨架组成颗粒体积模量ks 的情况下,弹性参数H、C、M可分别表示为
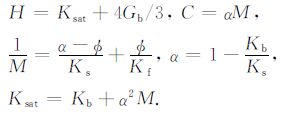
|
(4) |
式中ksat为不排水条件流体饱和孔隙介质的体积模量,α 为孔隙介质的Biot系数.在Biot方程中包括两种流体与固体骨架的相互作用,即黏性拖曳与惯性耦合作用,以Biot临界频率ωc 作为区分两种作用机制的频率界限,当传播弹性波的频率小于该临界频率时流体固体骨架相互作用以黏性拖曳为主,而大于该临界频率时则以惯性耦合作用为主.
作用于孔隙介质上的总应力张量τij与平均孔隙压力p可分别表示为:
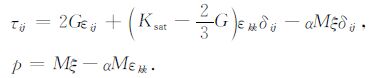
|
(5) |
式中εij为孔隙介质骨架应变张量,εkk=Δ·u为孔隙介质固体骨架的体应变,孔隙流体增量ξ=Δ(u-U).
如定义孔隙流体与固体骨架相对运动速度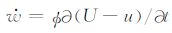
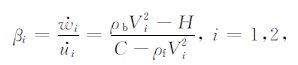
|
(6) |
式中Vi为孔隙介质中纵波速度,下标i=1,2 分别代表快纵波与慢纵波速度.在零频率下快纵波速度V1 与弹性参数H满足关系:H=ρbV12,同时对于通常储层岩石弹性参数H远大于参数C,因而公式(6)中的分母C-ρfV12与弹性参数H在量级上一致;由于快纵波速度频散很小,即在不同频率条件下公式(6)中的分子H-ρbV12仍会远小于模量H,造成β1 近于零值,即快纵波形成的流体相对运动速度很小并趋近于零.在零频率下慢纵波速度V2=0,则β2=-H/C,同样当传播弹性波的频率小于Biot临界频率时慢纵波的速度频散很小,β2≈-H/C仍近似成立,而模量H通常又远大于模量C,因此在低频下慢纵波形成的流体相对运动速度可表现为较高的值.
对于均匀孔隙介质可存在四种不同的临界频率,分别代表不同的衰减/频散作用机制.其一为Biot临界频率ωc,此时黏性趋附深度与组成孔隙具有相同尺度;其二为喷射流作用频率;其三为组成孔隙介质颗粒发生瑞利散射或米氏散射所对应的频率,此时弹性波传播波长λ 与颗粒平均粒径d具有相同尺度,这种情况下波长与颗粒粒径比应小于10;其四为黏弹性频率,在此频率下孔隙流体复剪切模量与其体积模量具有可比性而不能忽略.Biot方程虽然适用于全频段,但由于不同频率下流体饱和孔隙介质中起主导作用的衰减/频散作用机制存在明显差异,如仅考虑弹性波诱发流体流动作用对介质宏观衰减/频散特征的影响,则需要对Biot方程的设定高频截止频率.对于以储层砂岩为代表的流体饱和孔隙介质,组成颗粒发生瑞利散射或米氏散射所对应的频率通常低于其黏弹性频率,可将孔隙介质发生瑞利散射的频率作为Biot方程的高频截止频率,即满足关系λ≥10d,那么文中全频段其最高频率也应小于该截止频率.当传播弹性波的频率远小于Biot临界频率时(ω<0.15ωc)孔隙介质与饱和流体的应力、应变耦合作用可用固结理论表述(准静态作用域),介质中的快纵波与横波具有非频散特征,而慢纵波传播表现为扩散特征,孔隙介质位移与应力场的变化仅与骨架与孔隙流体间的摩擦机制有关,同时黏性动力学算符退化为摩擦系数,该条件下Biot方程可忽略惯性项而简化为:
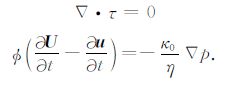
|
(7) |
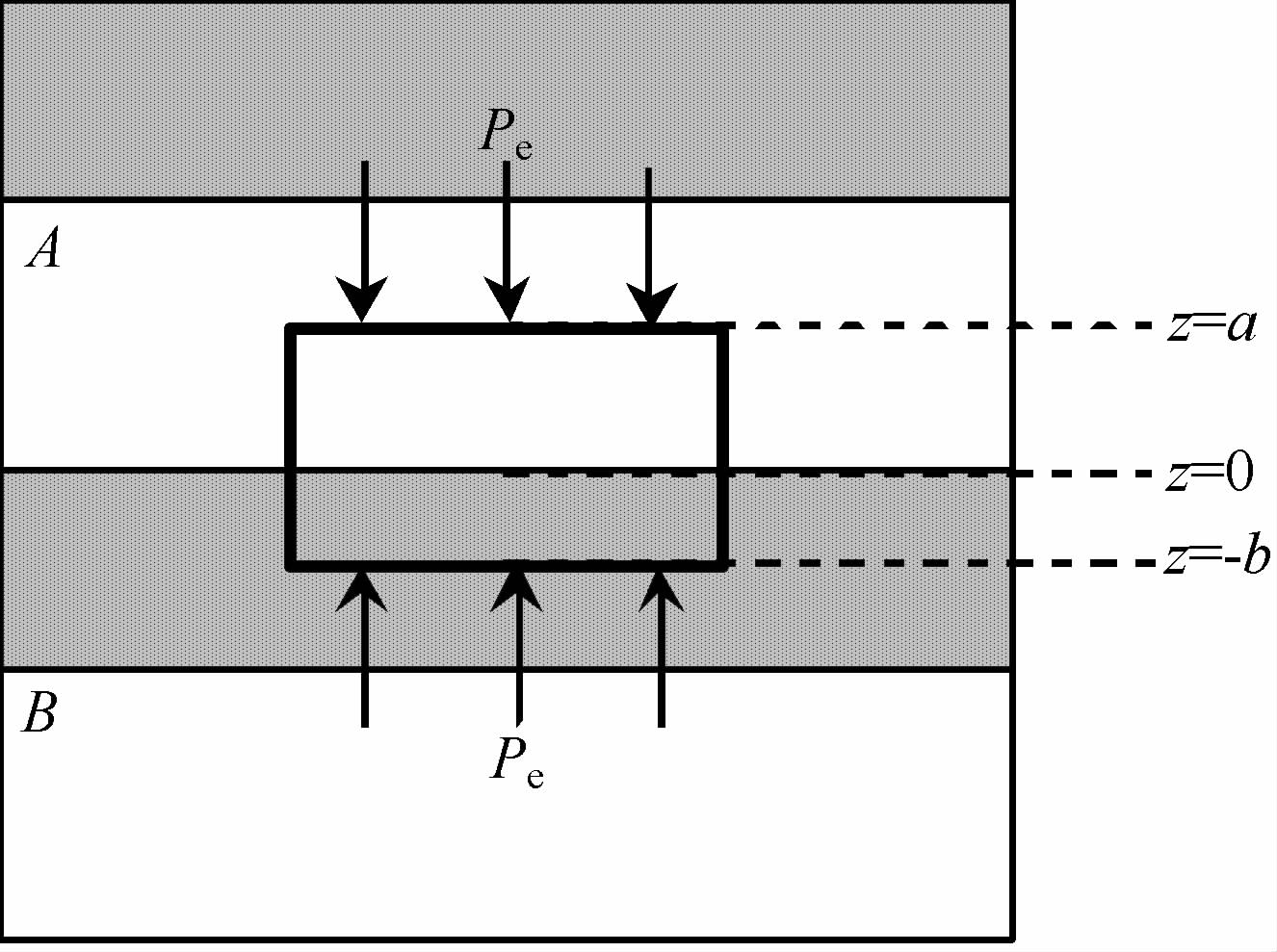
周期性层状孔隙介质模型又可称为White模型,是表征及研究不均匀孔隙介质在介观尺度上流体流动耗散机制的重要物理模型,如由含液孔隙层与含气孔隙层交错排列所构成的斑块饱和模型、由背景孔隙介质层与高孔隙度软薄层交错排列所构成的裂隙孔隙介质[18-19, 22].图 1为由A、B孔隙介质层交错排列所构成的周期性层状介质,每层在横向上均假设为无限延伸.取由A层与B层所构成的等效体元进行分析,在垂直层面的稳态纵波作用下,外加应力亦与层面垂直使孔隙介质整体表现为单轴应变状态,同时等效体元中的每一层均满足Biot方程.对于由A、B层所构成的等效体元建立如图 1所示的坐标系统,并取层界面为坐标原点,A、B层的半厚度分别为a与b.可对所建立的等效体元建立孔隙压力平衡条件,则有A、B层分界面处存在孔隙压力相等及孔隙流体流动连续:
|
图 1 周期性层状孔隙介质模型 Fig. 1 Schematic of periodic layered model composed of two fluid-saturated porous medi |
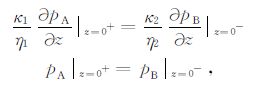
|
(8) |
式中pA 、pB 分别为A、B层中的孔隙压力,κ1、κ2 分别为A层与B层孔隙介质的绝对渗透率,η1、η2 分别为A、B层孔隙介质中饱和流体的黏度.考虑到模型结构的对称性,每层孔隙介质的中间面不存在流体流动,即在等效体元的边界上孔压梯度为零:
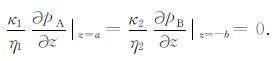
|
(9) |
构成图 1 中等效体元中的每一层介质均满足Biot方程,同时在低频准静态条件下Biot方程可简化为总应力场平衡方程及达西流方程的形式(公式(7)).将达西方程代入本构方程中可得到准静态条件下孔隙压力p与轴向应力τzz的耦合关系,即A、B层中孔隙压力满足如下渗流关系:
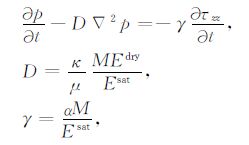
|
(10) |
式中D为扩散系数,γ 为单轴应变条件下的Skempton系数[25],弹性参数Edry = kb +4Gb/3、Esat = ksat+4Gb/3分别为排水与非排水条件下的单轴应变模量,其它弹性参数的物理意义以及计算过程与公式(4)中相同(胡恒山教授交流).
分别在等效体元的顶、底面沿垂直层面的z轴方向作用简谐正应力Pe =-τ0exp(iωt),其中τ0 为弹性波振幅.在该外加应力作用下的孔隙压力p可表示为
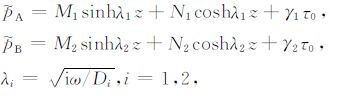
|
(11) |
式中M1、N1 为A层中孔压振幅待定系数,M2、N2为B层中孔压振幅待定系数,D1、D2 分别为A层与B层的扩散系数,γ1、γ2 分别为单轴应变条件下A层与B层的Skempton系数.将(11)式式带入边界条件(8)、(9)式中可解出上述4个待定系数.此时A、B层中的诱发孔隙压力${{\tilde p}_{\rm{A}}}$与${{\tilde p}_{\rm{B}}}$分别表示为
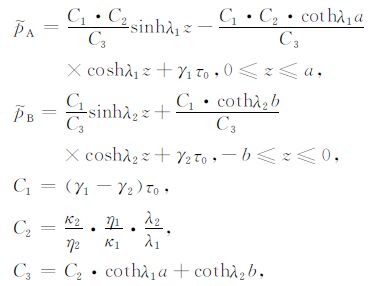
|
(12) |
式中参数的意义与前面公式中相同,coth为双曲余切函数.在上述孔隙压力计算公式中的第三项γ1τ0与γ2τ0 分别为谐波作用下A、B层中快纵波所诱发孔隙压力,也为高频极限下A、B层中的孔隙压力;式中的前两项则为A、B层间孔隙压力梯度作用下的孔隙流体相对流动所引起的孔压变化,表现为孔隙流体扩散作用下的慢纵波诱发孔隙压力.将孔隙压力的计算结果代入公式(7)的达西方程中可分别得到A、B层中孔隙流体与固体骨架相对运动速度${\dot w}$的计算公式.
3.3 孔隙介质固体骨架位移表示孔隙介质的控制方程可表示为
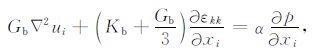
|
(13) |
对(13)式沿xi方向求偏导可得到
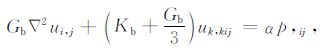
|
(14) |
i与j缩并,得标量方程
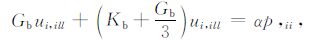
|
(15) |
即
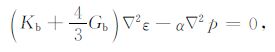
|
(16) |
式中ε=ui,i为孔隙介质固体骨架的体应变.在轴向应变条件系kb +4Gb/3 即为排水条件下的一维应变模量,记为Edry,则(16)式可表示为
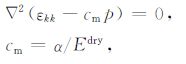
|
(17) |
式中cm 为均匀孔隙介质Geertsma单轴孔弹性膨胀系数[25].同时体应变εkk与固体骨架法向位移u存在关系${\varepsilon _{ii}} = \partial u/\partial z$(其它轴向应变为0),则(17)式又可以可表示为
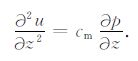
|
(18) |
对(18)式积分可得到法向位移u的计算方程:
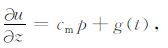
|
(19) |
式中g(t)是一个只与时间有关的函数,可通过相应边界条件求取.在边界z=a处,孔隙压力p(a,t)=γ1τ0exp(iωt),同时位移u满足如下关系:
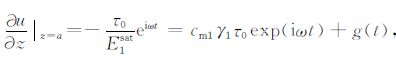
|
(20) |
式中E1sat、cm1分别代表A层流体饱和孔隙介质在单轴应变条件下的非排水应变模量与Geertsma系数.利用(20)式函数g(t)可表示为
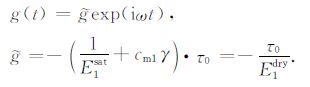
|
(21) |
在确定了函数g(t)后,可通过(18)式分别求A、B层中不同位置的固体骨架位移u(z).可将A、B层的固体骨架位移u(z)表示为
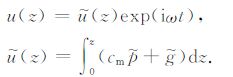
|
(22) |
综合方程(12)、(21)、(22)层可计算出A、B层的固体骨架位移振幅$\tilde u\left( z \right)$,在模型单元边界z=a处位移振幅$\tilde u\left( a \right)$为
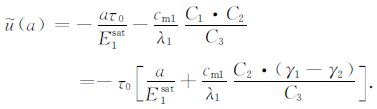
|
(23) |
模型单元边界z=-b处位移振幅$\tilde u\left( { - b} \right)$为
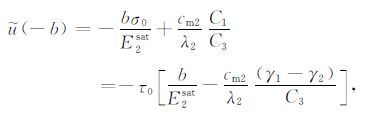
|
(24) |
式中E2sat、cm2分别代表B层流体饱和孔隙介质在单轴应变条件下的非排水应变模量与Geertsma系数.A、B层位移表达式中的第一项为非排水条件下各层孔隙介质在外加正应力作用下的位移,第二项则为层间流体流动作用所引起的介质固体骨架位移.
3.4 等效模量表示定义复纵波模量H(ω)=-Pe/ε,其中作用于等效体元上的外加应力Pe =-τ0exp(iωt),可令等效体元的总长度为L,则复纵波模量可表示为
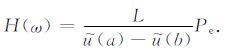
|
(25) |
利用方程(23)、(24)、(25)等效体积模量H(ω)可表示为
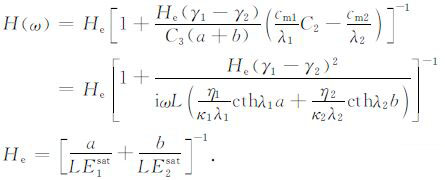
|
(26) |
在高频条件下复纵波模量为
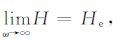
|
(27) |
上式与孔隙流体具有斑块分布形式时的介质等效体积模量计算公式一致[26].在低频极限下有
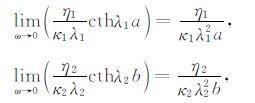
|
(28) |
则在低频极限下等效体积模量可表示为
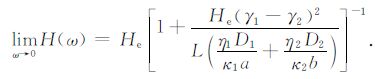
|
(29) |
利用复体积模量可计算出纵波相速度Vp与纵波衰减的逆品质因子Q-1:
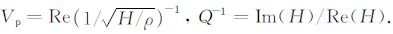
|
(30) |
式中ρ 为等效体元的密度.如分别用lm、ρsm、ρfm、$\phi $m分别代表孔隙介质层的厚度、构成骨架颗粒、饱和流体密度与孔隙度,下标m=1,2分别代表A、B两层孔隙介质,则密度ρ 可表示为
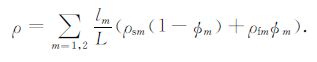
|
(31) |
与频散特征在周期性层状孔隙介质外力已知的情况下,对介质复纵波模量的计算问题转化为对等效体元应变的求取,进而利用公式(30)研究纵波在介质中传播时的衰减和速度频散特征,在等效体元上、下界面同时施加沿z轴方向的简谐外力时,体元中A、B层孔隙介质的孔隙压力pA 与${{\tilde p}_{\rm{B}}}$可以写成如下调谐形式:
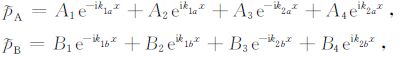
|
(32) |
式中k1a、k2a分别为外力作用下A层孔隙介质中快、慢纵波的波数,k1b、k2b分别为B层孔隙介质中快、慢纵波的波数,它们可以通过求解频率域Biot方程获得[26];A1、A2、B1、B2 为快纵波诱发孔压待定系数,A3、A4、B3、B4 为慢纵波诱发孔压待定系数.利用Biot方程也可以分别得到A、B层中用孔隙压力所表示的总应力、固体骨架位移以及孔隙流体位移等物理量[3, 18].
同样对于所构建的等效体元可通过边界条件建立方程组来确定方程(32)中的孔压待定系数.在单轴应力条件下,相接触的A、B层孔隙介质在分界面(z=0)处的总法向应力τ、孔隙压力p、固体骨架在法向上的位移u、法向孔隙流体位移U或渗流速度连续有如下四个边界方程:
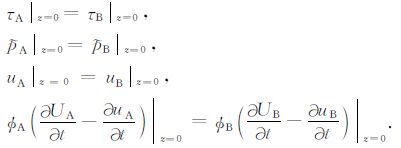
|
(33) |
在等效体元的顶、底界面有孔隙介质的总法向应力τ 与外加应力Pe 相等,同时在等效体元为不排水状态其边界上孔压梯度为零,这样在模型介质等效体元顶、底界面的四个边界条件为:
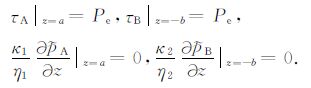
|
(34) |
上述边界方程中的下标A、B分别代表层A、B层孔隙介质中的相应物理量.
将用孔隙压力所表示的A、B层的总法向应力τ、孔隙压力p、固体骨架在法向上位移u、法向孔隙流体位移U带入上述八个边界方程中构成以A1、A2、A3、A4、B1、B2、B3、B4 为未知量的线性方程组.该方程成组的系数矩阵为8×8的方阵,对于通常砂岩类孔隙介质的弹性参数与物性参数的取值范围该系数矩阵表现出明显病态矩阵的特征,因此采用奇异值分解法对该方程组求解以确定方程(30)中A、B层孔隙压力的四个待定系数.在此基础上可利用固体骨架位移与孔隙压力关系计算A、B层的固体骨架位移uA、uB 的值,从而得到体元在顶、底界面的骨架位移uA|z=a与uB|z=-b,并通过公式(25)计算复纵波模量H(ω).在得到复纵波模量后可利用公式(30)计算出全频段下的纵波速度频散特征与纵波衰减的逆品质因子变化特征.
5 数值计算结果及分析可用周期性层状孔隙介质构成介观尺度上弹性性质、孔隙流体分布存在差异的简单不均匀孔隙介质模型,从而研究介观尺度上的流体流动对传播弹性波的衰减与频散作用机理.
5.1 饱和流体差异的斑块饱和模型对于图 1中所构建的周期性层状孔隙介质,当A、B孔隙介质层仅表现为饱和流体差异时,孔隙介质层整体上可等效为典型的斑块饱和介质,弹性波传播时会形成层间的流体流动以使孔隙压力在界面上达到平衡状态.对文献[4]中的周期性层状孔隙介质模型进行计算,其中A层为饱水层,B层为饱和气层,介质模型等效体元的总长度取定值L=0.2m.通过改变A、B的相对厚度达到不同含水饱和度的情况,如含水饱和Sw=0.9时,A层厚a=0.18m,B层厚b=0.18 m.孔隙介质层的骨架参数与饱和流体参数见表 1.
|
|
表 1 孔隙介质骨架与饱和流体参数(引自文献[18]) Table 1 Poroelastic properties of skeleton and saturated fluid (from Ref.[18]) |
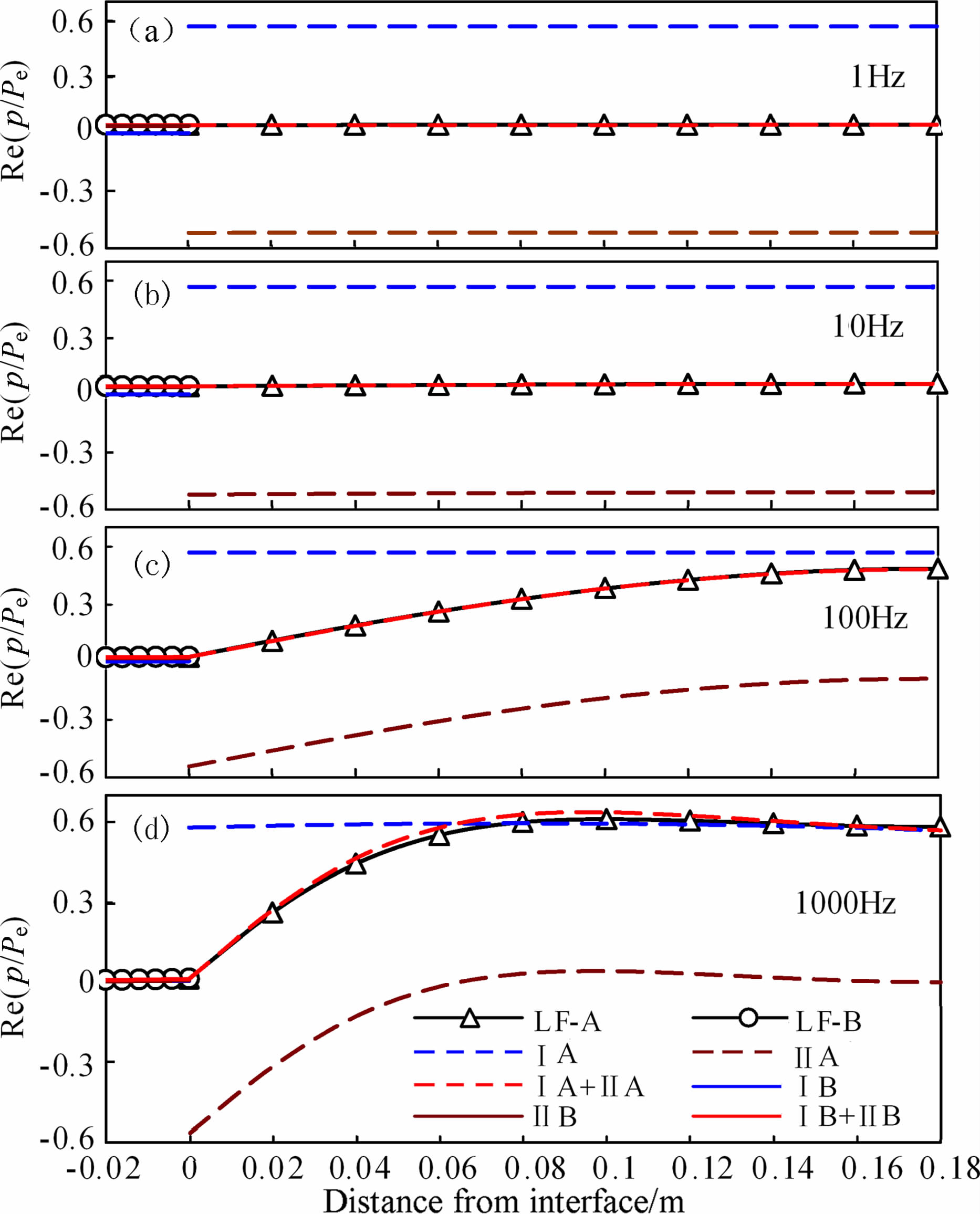
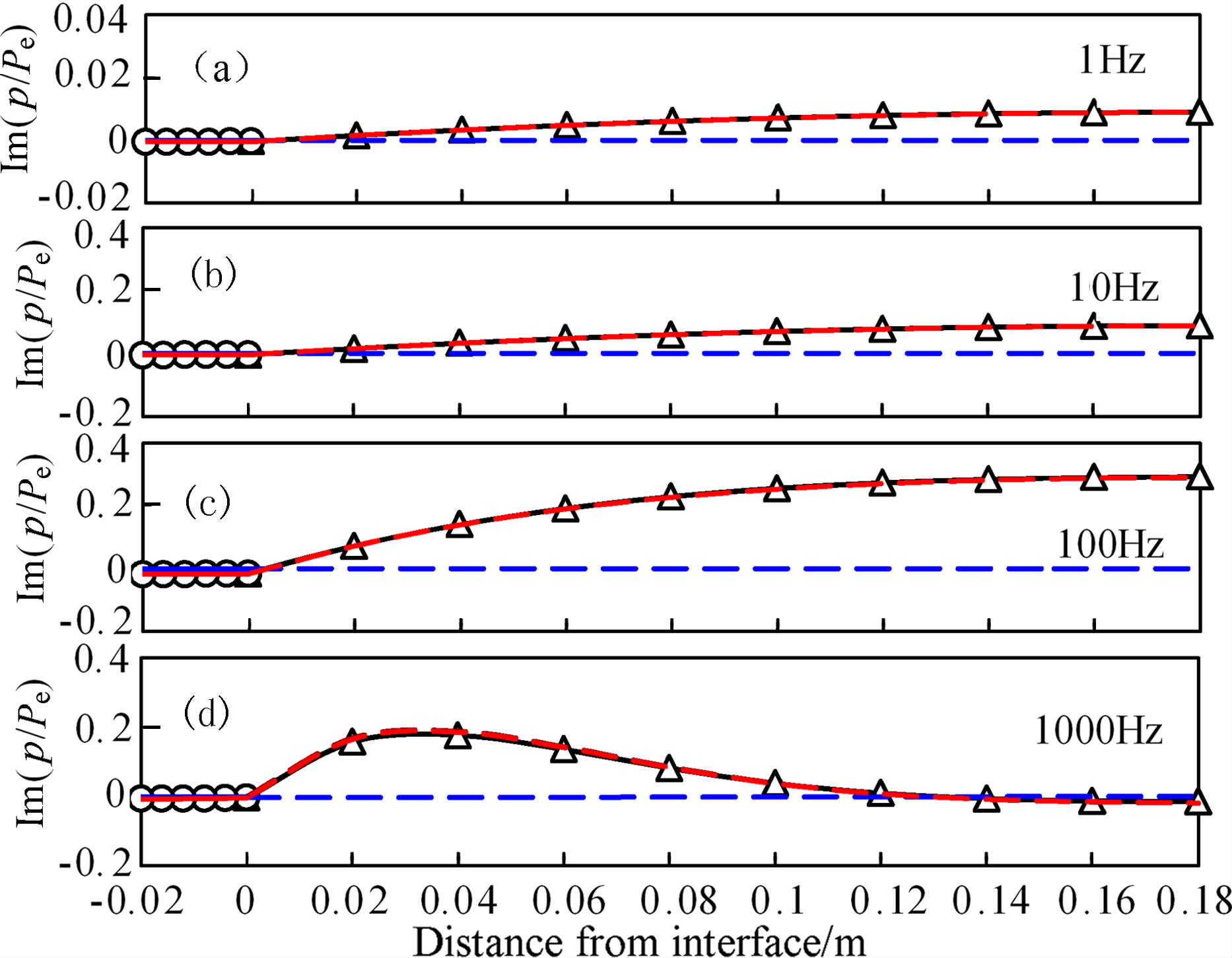
图 2与图 3中别给出Sw=0.9时孔隙介质模型中归一化孔隙压力(p/Pe)实部、虚部变化特征.利用公式(12)所计算的准静态条件下的孔隙压力(LF-A、LF-B)与全频条件下所计算的孔隙压力(ⅠA+ⅡA、ⅠB+ ⅡB)仅在较高的频率下表现出微小差异.在图中所给出的频率范围内,快纵波所诱发孔隙压力的实部与虚部在A、B层内均表现为定值,该定值在A、B层内分别约为γ1 与γ2;A、B层分界面处快纵波所诱发孔隙压力存在明显的压力梯度,由于该分界面处快、慢纵波所诱发的孔隙压力符号相反,因此总孔隙压力连续.A、B层中慢波诱发孔隙压力的实部与虚部在相对低频下随距离界面的距离变化很小,但随频率增加慢波诱发孔隙压力在两层内均出现明显变化(图 2、3),反映出随频率的增加流体扩散长度的减少(见公式(11)),即慢纵波通过流体扩散作用对孔隙压力的影响范围减小.在频率为1000Hz时由于孔隙压力与外加应力的二次耦合作用慢波孔压的实部出现正值特征,此时慢波孔压与快纵波孔压在符号上不再相反,致使总孔隙压力大于快纵波孔隙压力(图 2d);慢波孔压的虚部控制总孔隙压力虚部的变化(图 3).在相对低频条件下,由A、B层中快纵波所形成的压力梯度可通过慢波扩散作用平衡,因此在A、B层内总孔隙压力的实部近于零(图 2(a、b)),即介质体系的边界条件为不排水条件,但体系内孔隙压力却为近于零孔压的排水条件,此时虽然对介质整体而言孔隙流体是不均匀分布的,但其对介质等效弹性性质的影响与孔隙流体均匀分布的情况并无明显差异;随频率的增加扩散长度逐渐减小,慢纵波所引起的孔隙压力变化仅局限在距离界面较近的范围内(图 2(c、d)),在该范围内总孔隙压力迅速降低,而该范围之外孔隙压力又与快纵波诱发孔隙压力一致,孔隙流体逐渐接近非弛豫状态,造成等效体积模量增加.
|
图 2 孔隙介质层归一化孔隙压力(p/Pe)实部分布特征(图中Ⅰ和Ⅱ分别代表快、慢纵波) Fig. 2 Real part of the pore pressure relative to the effective pressure throughout the unit cell for four frequency values |
|
图 3 孔隙介质层归一化孔隙压力(p/Pe)虚部分布特征(图例与图 2相同) Fig. 3 Imaginary part of the pore pressure relative to the effective pressure throughout the unit cell for four frequency values |
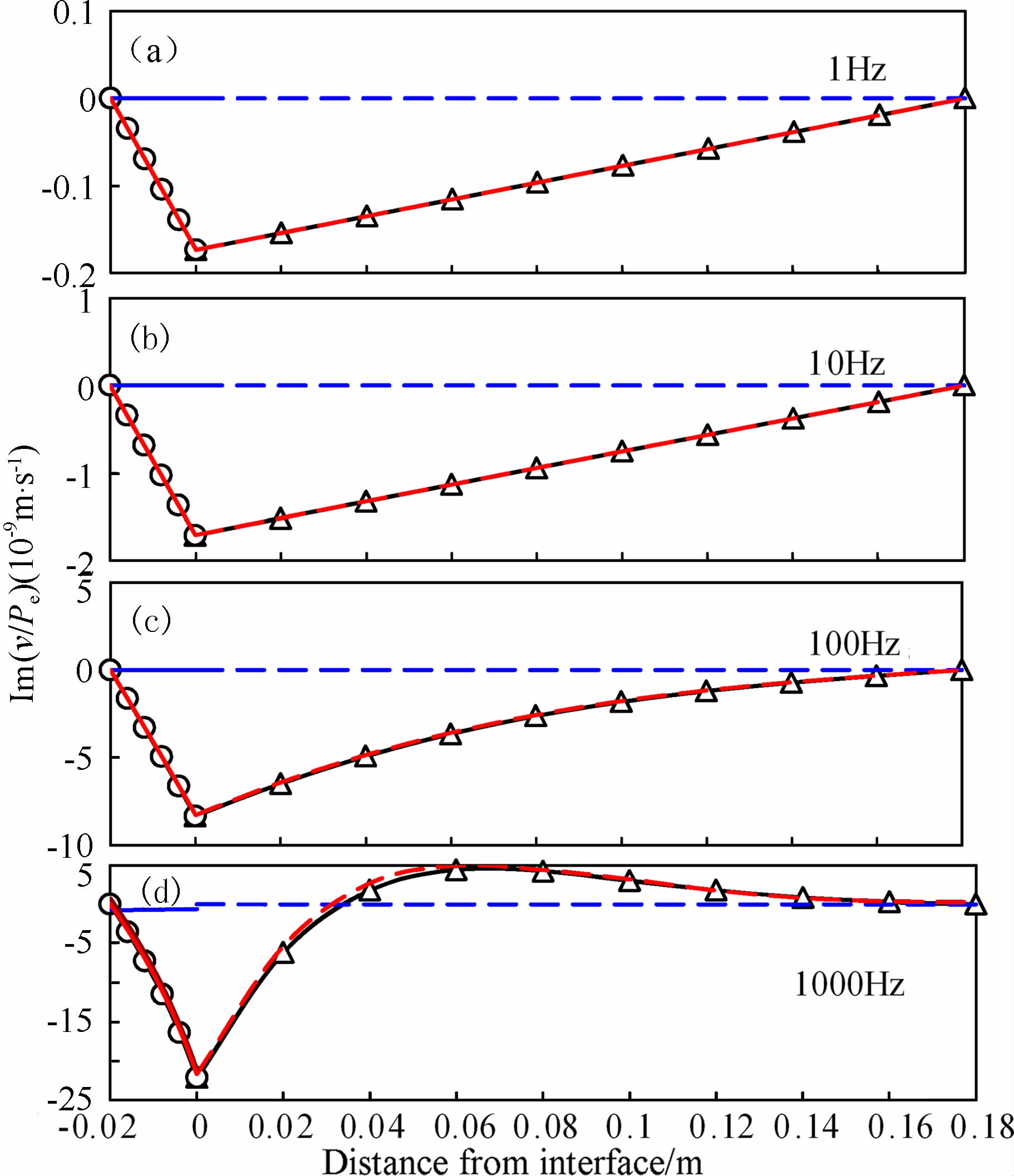
图 4与图 5分别给出Sw=0.9时介质模型中孔隙流体相对运动速度的实部、虚部变化特征(图中用字母v代表相对运动速度${\dot w}$).利用公式(12)与公式(7)所计算的准静态条件下孔隙流体相对运动速度(图中LF-A、LF-B)及全频条件下所计算的孔隙流体相对运动速度(图中ⅠA+ ⅡA、ⅠB+ ⅡB)也仅在较高的频率下表现出微小差异.快纵波(ⅠA、ⅠB)与慢纵波(ⅡA、ⅡB)传播所形成的孔隙流体相对运动速度的实部及虚部在界面处均不连续,但总速度和连续.根据公式(7),孔隙流体相对运动速度应与孔隙压力的变化率一致.图 2 中已知快纵波诱发孔隙压力在介质层内近于定值,其变化率也近于零,因此快纵波传播所形成的孔隙流体相对运动速度在A、B层内均表现出近于零值的特征且随距离的变化也较为平缓(尤其低频条件下),同时层内不同位置的速度绝对值会随频率的增加而略有增加,这些特征均也与公式(7)所反映的特征一致.慢纵波传播所形成的相对运动速度在A、B层内表现出明显变化,在界面处具有最大的视速度,向层中心位置逐渐减小直至在A、B层的中间位置相对速度为零;慢纵波通过流体扩散作用以降低快纵波所诱发孔压,随频率的增加流体扩散距离减小,慢纵波孔压作用范围减小,此时孔隙压力变化仅局限在距离界面较近的范围内,在该范围内慢波孔压迅速变化,因此A、B层分界面处的流体相对运动速度在量值上会随频率的增加而增加,但在层内可发生相对流动的孔隙流体范围则随频率的增加而减少(对比图 4c与4d);在频率为1000Hz时同样由于二次耦合作用致使孔隙流体相对运动速度出现正值特征(图 4d、5d).由于慢纵波所形成的孔隙流体相对运动速度在量值上远大于快纵波的流体相对运动速度,因此总的流体相对运动速度与慢纵波的流体相对运动速度变化形式一致,即低频下慢波所形成的流体相对流动起主导作用.在低频下慢纵波所形成的流体相对运动速度较低,同时虚部在量级上远大于其实部值;随频率的增加,相对速度的实部与虚部在量级上逐渐趋于一致.

|
图 4 模型介质孔隙流体相对运动速度实部变化特征(图中Ⅰ和Ⅱ分别代表快、慢纵波) Fig. 4 Real part of the relative flow velocity relative to the effective pressure throughout the unit cell for four frequency values |
|
图 5 模型介质孔隙流体相对运动速度虚部变化特征(图例与图 4相同) Fig. 5 Imaginary part of the relative flow velocity relative to the effective pressure throughout the unit cell for four frequency values |
孔隙流体的相对流动是造成孔隙介质中传播弹性波发生衰减的主要原因,从前面的分析可知快纵波所形成的孔隙流体相对运动速度近于零,因此快纵波所引起的流体流动对传播弹性波的衰减是可忽略的;快纵波在层分界面处形成的压力梯度通过慢纵波所表现出的流体扩散作用得以平衡,慢波所形成的流体相对流动起主导作用,因此模型介质中传播弹性波的衰减主要表现为慢纵波的耗散作用,即低频下慢纵波所形成的流体扩散作用是介观尺度主导的流体流动耗散机制.在入射波传播的半时间周期内,如果当慢纵波所表现的扩散孔压扰动距离达到最大,即该距离等于模型介质组成层的半厚度时慢纵波的耗散作用最强,此时介质对传播弹性波的衰减应达到最大值.
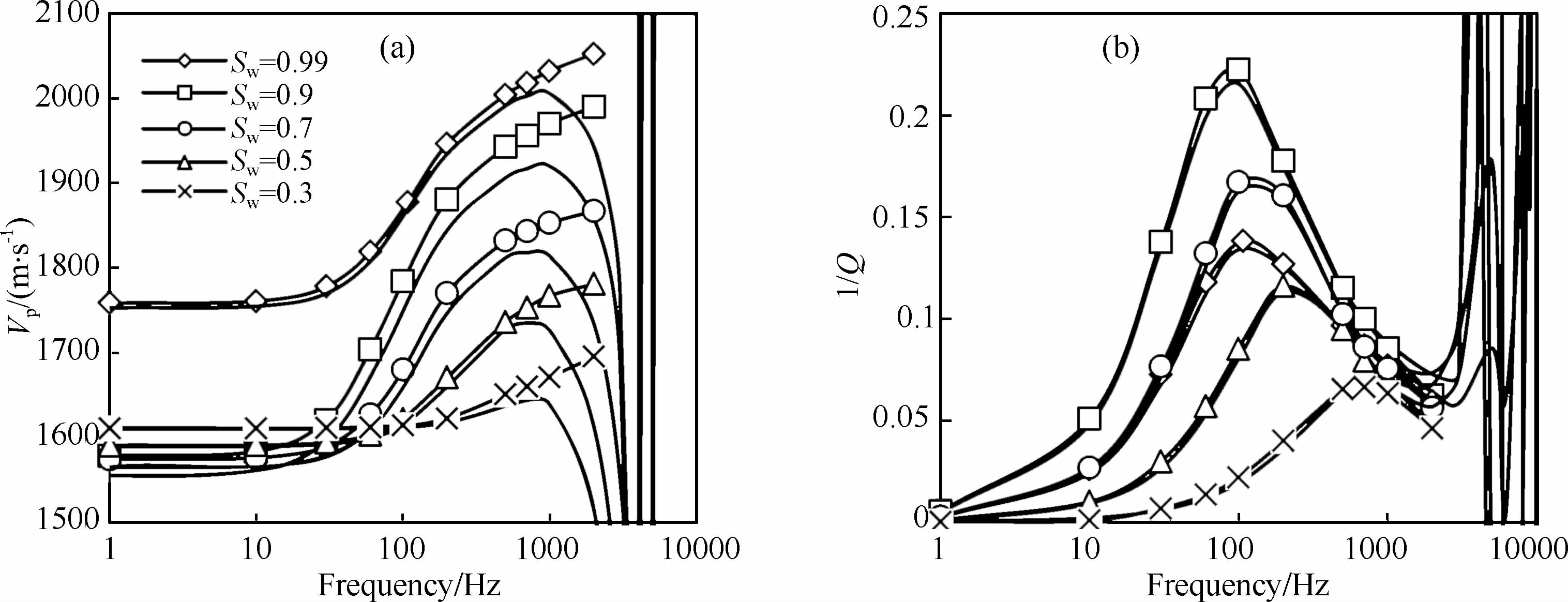
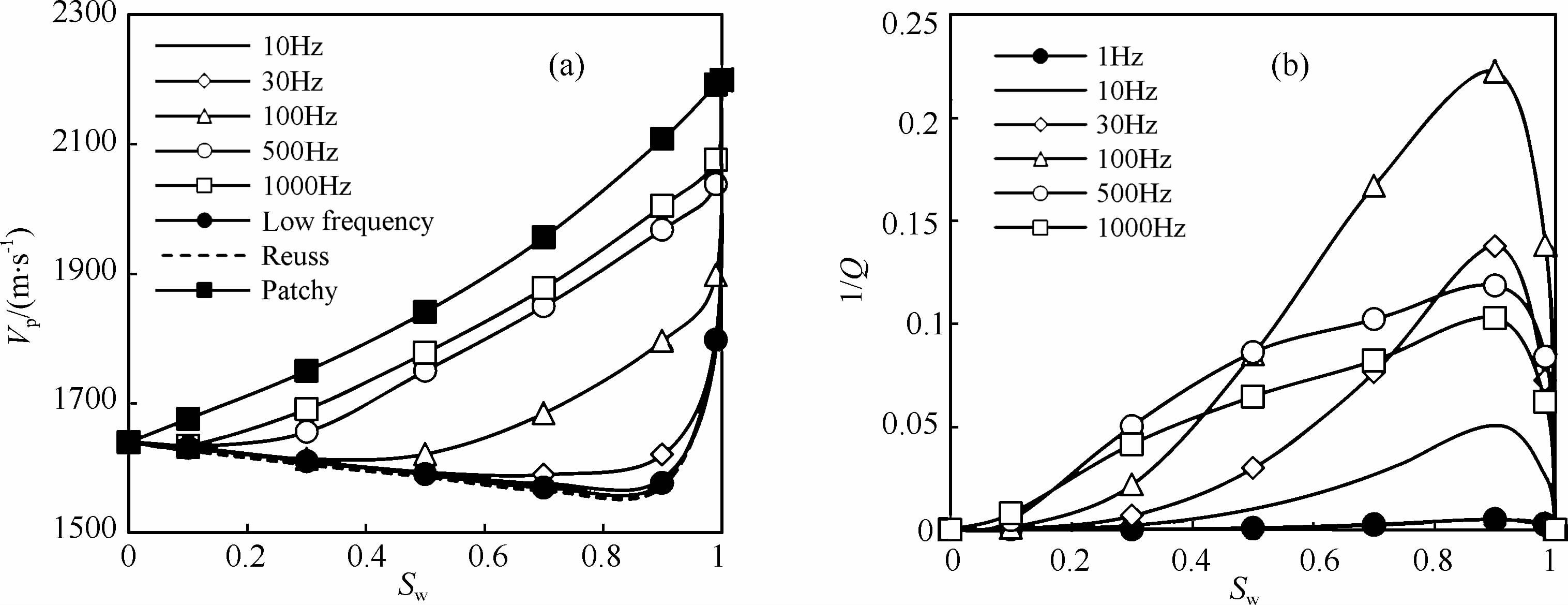
5.4 衰减与速度频散特征改变周期性层状孔隙介质中A、B层的相对厚度可形成具有不同含水饱和度值的等效孔隙介质.利用公式(30)可分别计算出准静态与全频段下部分饱和孔隙介质的速度频散与衰减变化特征(图 6).在传播弹性波频率近似小于1000 Hz时,两种方法的计算结果差异很小,准静态低频近似表达所计算的纵波速度仅略大于全频段White模型扩展结果,其原因为准静态结果给出更高的总孔隙压力(图 2),模型介质具有负频散特征,即纵波速度随频率的增加而增大.在频率高于1000 Hz时两种方法结果表现出明显的差异,此时传播弹性波波长等于或小于等效孔隙介质的厚度而出现共振现象,在模型中传播的纵波进入了声子晶体的能量禁带[18-19],此时全频段方法所计算出的纵波速度与逆品质因子具有明显的高、低值振荡跳跃变化特征.模型介质的衰减主要通过慢纵波所形成的孔隙流体相对流动或流体扩散产生,当流体扩散长度等于模型介质中不均匀体(水层)厚度时衰减具有最大值,对应最高衰减的临界频率可表示为
|
图 6 部分饱和孔隙介质在低频近似及全频段下(实线)的速度频散(a)与衰减特征(b) Fig. 6 Phase velocity and attenuation as a function of frequency for low frequency approximation model and full frequency model(solid curves)of partially saturated porous media(a)Phase velocity as a function of frequency;(b)Attenuation1/Q as a function of frequency |
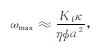
|
(35) |
从上式可以看出临界频率会随含水饱和度的增加而降低,与图 6b结果一致.含水饱和度Sw=0.9时模型介质在相同频率下具有最大衰减值.
图 7中给出了利用准静态方法所计算的不同频率下纵波速度与逆品质因子随含水饱和度的变化特征.利用公式(29)计算的低频极限条件下的Vp-Sw变化关系与孔隙流体均匀分布的Reuss公式计算结果差异很小,均表现为纵波速度先随含水饱和度的增加而减小,当饱和度大于0.9 时纵波速度又随饱和度的增加而迅速增大;同时介质中传播弹性波频率小于10Hz时,所得到的Vp-Sw 变化形式也仅与低频极限结果在Sw 为0.7~0.9 的范围时出现较小差异.随频率的增加,Vp-Sw 变化形式出现明显变化,纵波速度随含水饱和度的变化逐渐呈单调增加的形式,并接近于公式(27)所计算的高频极限(斑块饱和)结果.在低频条件下(本例中小于20 Hz),由快纵波所形成的孔隙压力可通过慢纵波的流体扩散作用而迅速降低而接近零孔压的弛豫状态(图 3a、b),虽然介质中总孔隙压力会随含水饱和度的增加而增大,致使介质的等效体积模量增大,但在含水饱和度较低时该增量相对于介质密度的增加(密度随含水饱和度的增加而增加)仍较小,因此模型介质速度特征表现为速度首先随含水饱和度的增大而减少,而在含水饱和度较高时纵波速度又会随其增加而增大.在高频条件下(本例中大于500Hz),A、B层中诱发孔隙压力差异所造成的流体流动仅局限在距离分界面较近的范围内(图 4d),即慢纵波通过流体流动来减少A层中快纵波诱发孔隙压力的作用较弱,A、B层中总孔隙压力近似等于快纵波诱发孔压,孔隙流体为非弛豫状态,此时模型介质的等效体积模量可通过公式(27)计算,纵波速度随含水饱和度的增加而增大.
|
图 7 不同频率下孔隙介质速度(a)与衰减特征(b)随含水饱和度变化关系 Fig. 7 Phase velocity and attenuation as a function of water saturation (Sw)at different frequency (a)Phase velocity as a function of water saturation;(b)Attenuation1/Q as a function of water saturation. |
逆品质因子在含水饱和度为0.9 时出现最大值,同时在勘探地震频段(30~100 Hz)该值大于0.15,最高可达0.23,远高于Biot流在地震频段下的衰减值,表明介观尺度的流体流动作用所造成的衰减可能是地震频段下储层岩石中主导的衰减机制.同时也能看出在地震频段下,对于一定的储层岩石在完全饱水及高含气(Sw <40%)的情况下在衰减上并无明显差异.如前所述,慢纵波所表现的孔隙流体相对运动是形成介质衰减的主要原因,其耗散势正比于孔隙流体相对流动速度的平方[1];图 8中可以看出在频率为100Hz时(该频率下不同含水饱和度介质具有最大衰减值)介质在不同含水饱和度下的衰减值与慢纵波所形成的孔隙流体相对流动速度具有明显的相关性,所能形成的相对流动速度越大,其衰减越大,如Sw =0.9 时衰减与相对运动速度具有最大值,而Sw=0.3时衰减与相对运动速度具有最小值.如果将图 8 中孔隙流体相对流动速度与x轴所围成的图形近似看做三角形,对于所研究模型该三角形底面长度为定值0.2,则所围成三角形具有最大面积时也一定对应最大孔隙流体相对流动速度.
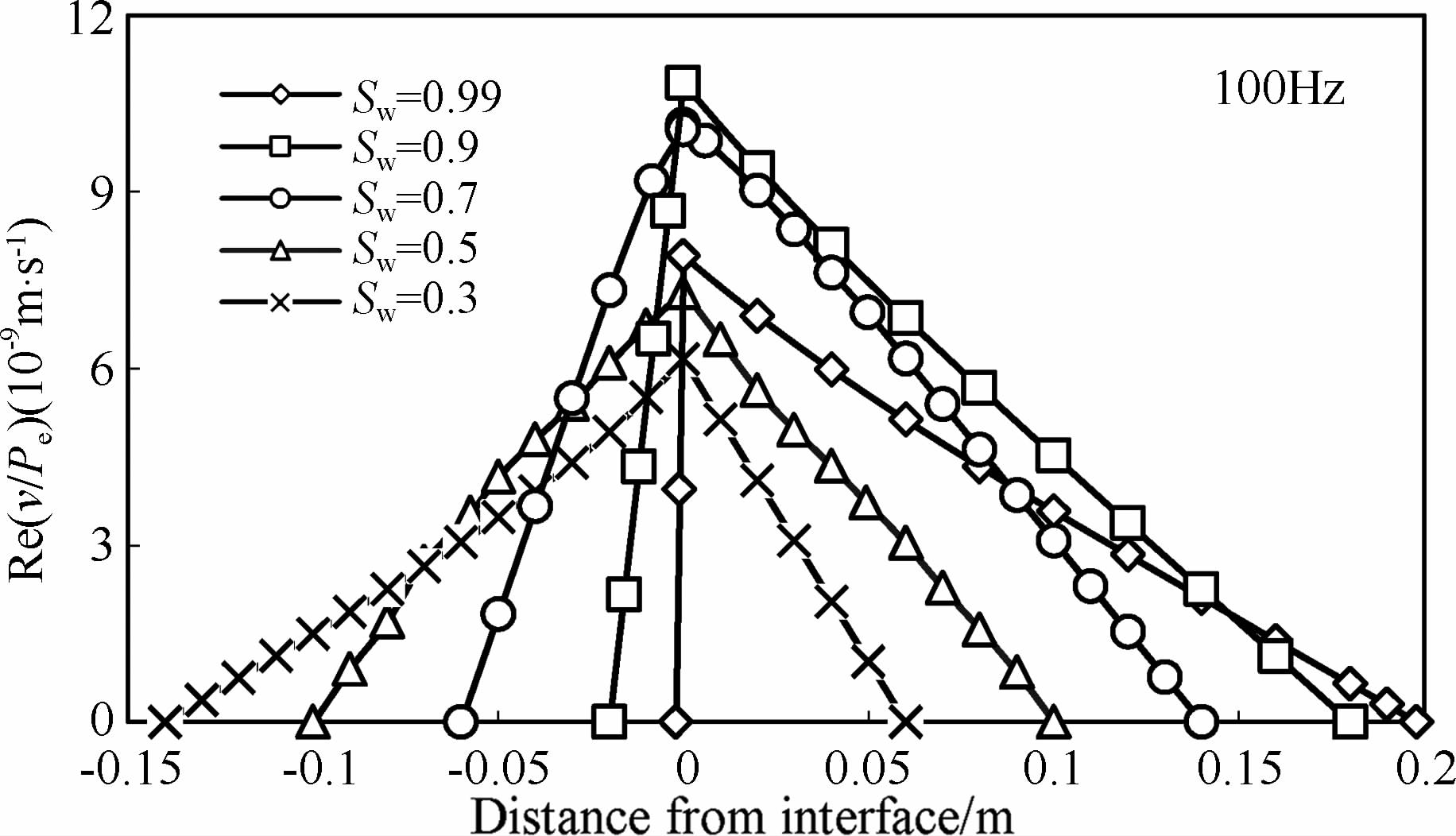
|
图 8 不同含水饱和度下模型介质慢纵波孔隙流体相对运动速度实部变化特征 Fig. 8 Real part of the relative flow velocity relative due to slow wave throughout the unit cell for different water saturations |
基于准静态孔弹性理论和严格边界条件给出了White周期性层状孔隙介质模型在低频下的孔隙压力、相对流体流动速度、固体骨架位移等物理量的解析表达,并以此为基础讨论了介质中纵波传播特征,同时利用Biot理论将White模型推广到全频条件下,对比两种方法得到如下结论:
(1)在传播纵波频率满足等效介质假设条件下,快纵波诱发孔隙压力的实部与虚部在模型介质的组成层内表现为不随距离变化的定值,并在分界面处表现明显的孔压力不连续;当传播纵波频率较低时,慢纵波形成的孔隙压力与快纵波孔压符号相反、大小相等,致使介质中总孔压较低;随频率的增加慢纵波孔压在层内表现出明显变化,慢纵波通过流体扩散作用对孔隙压力的影响范围减小,总孔隙压力逐渐与快纵波孔压一致;在较高频率下可能出现二次耦合作用使得慢波孔压的实部与快纵波孔隙压力符号相同,造成总孔隙压力超过快纵波孔压.
(2)在传播纵波频率满足等效介质假设条件下,慢纵波所形成的孔隙流体相对运动速度在量值上远大于快纵波所形成的孔隙流体相对运动速度,总的流体相对运动速度与慢纵波形成的流体相对运动速度变化形式一致,即低频下慢波所形成的流体相对流动起主导作用;孔隙流体的相对流动是造成传播弹性波衰减的主要原因,因此低频下慢纵波所形成的流体扩散作用是介观尺度主导的流体流动耗散机制.
(3)在低频时两种方法的计算结果差异很小,准静态低频近似模型计算的纵波速度仅略大于全频段White模型扩展结果,其原因为低频近似结果给出更高的总孔隙压力;随着频率的增加,传播地震波波长等于或小于等效孔隙介质的厚度而出现共振现象,两种方法结果表现明显的差异,此时全频段White模型扩展方法所计算出的纵波速度与逆品质因子具有明显的高、低值振荡跳跃变化特征.
(4)对于文中所采用的模型参数,介观尺度流体流动作用在勘探地震频段(30~100 Hz)所引起的速度频散与衰减作用远强于Biot流作用;随频率的增加,孔隙流体逐渐从排水的弛豫状态过渡到非弛豫状态,介质的纵波速度-含水饱和度变化形式也从符合孔隙流体均匀分布模式过渡到完全斑块分布模式;不同频率下介质均在含水饱和度为90%时出现最强衰减作用,介质在不同含水饱和度下的衰减峰值与慢纵波所形成的孔隙流体相对流动速度之间具有明显的相关性.
致谢感谢两位匿名评阅人对本文所提出的宝贵意见,文中公式(17)的推导过程根据胡恒山教授的建议进行了修改,在此表示感谢.
| [1] | Biot M A. Theory of propagation of elastic waves in a fluid saturated-porous solid I. low frequency range. J. Acoust. Soc. Am , 1956, 28(2): 168-178. |
| [2] | Biot M A. Mechanics of deformation and acoustic propagation in porous media. J. Appl.Phys , 1962, 33(4): 1482-1498. DOI:10.1063/1.1728759 |
| [3] | 胡恒山, 王克协. 孔隙介质声学理论中的动态渗透率. 地球物理学报 , 2001, 44(1): 135–141. Hu H S, Wang K X. Dynamic permeability in poroelastic medium acoustics. Chinese J. Goephys (in Chinese) , 2001, 44(1): 135-141. DOI:10.1002/cjg2.v44.1 |
| [4] | Dvorkin J, Nur A. Dynamic poroelasticity: a unified model with the squirt and the Biot mechanisms. Geophysics , 1993, 58(4): 524-533. DOI:10.1190/1.1443435 |
| [5] | Dvorkin J, Nolen-Hoeksema R, Nur A. The squirt-flow mechanism: macroscopic description. Geophysics , 1994, 59(3): 428-438. DOI:10.1190/1.1443605 |
| [6] | Yang D H, Zhang Z J. Poroelastic wave equation including the Biot/squirt mechanism and the solid/fluid coupling anisotropy. Wave Motion , 2002, 35(3): 223-245. DOI:10.1016/S0165-2125(01)00106-8 |
| [7] | Deng J X, Wang S X, de Han H. The velocity and attenuation anisotropy of shale at ultrasonic frequency. J. Geophys. Eng , 2009, 6(3): 269-278. DOI:10.1088/1742-2132/6/3/006 |
| [8] | Berryman J G, Wang H F. Elastic wave propagation and attenuation in a double-porosity dual-permeability medium. International Journal of Rock Mechanics and Mining Sciences , 2000, 37(1-2): 63-78. DOI:10.1016/S1365-1609(99)00092-1 |
| [9] | Pride S R, Berryman J G. Linear dynamics of double-porosity dual-permeability materials. I. Governing equations and acoustic attenuation. and II. Fluid transport equations. Physical Review E , 2003, 68(3): 036603-036604. DOI:10.1103/PhysRevE.68.036603 |
| [10] | Pride S R, Berryman J G, Harris J M. Seismic attenuation due to wave-induced flow. J. Geophys. Res , 2004, 109: B01201. DOI:10.1029/2003JB002639 |
| [11] | Carcione J M, Picotti S. P-wave seismic attenuation by slow-wave diffusion: Effects of inhomogeneous rock properties. Geophysics , 2006, 71(3): O1-O8. DOI:10.1190/1.2194512 |
| [12] | Müller T M, Gurevich B. Wave-induced fluid flow in random porous media: Attenuation and dispersion of elastic waves. J. Acoust. Soc. Am , 2005, 117(5): 2732-2741. DOI:10.1121/1.1894792 |
| [13] | Müller T M, Gurevich B, Lebedev M. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks-A review. Geophysics , 2010, 75(5): 75A147-75A164. DOI:10.1190/1.3463417 |
| [14] | White J E. Computed seismic speeds and attenuation in rocks with partial gas saturation. Geophysics , 1975, 40(2): 224-232. DOI:10.1190/1.1440520 |
| [15] | Dutta N C, Odé H. Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation(White model)-Part 1: Biot theory. Part II: Results. Geophysics , 1979, 44(11): 1777-1805. |
| [16] | Dutta N C, Seriff A J. On White’s model of attenuation in rocks with partial gas saturation. Geophysics , 1979, 44(11): 1806-1812. DOI:10.1190/1.1440940 |
| [17] | Norris A N. Low-frequency dispersion and attenuation in partially saturated rocks. J. Acoust. Soc Am , 1993, 94(1): 359-370. DOI:10.1121/1.407101 |
| [18] | Vogelaar B, Smeulders D. Extension of White’s layered model to the full frequency range. Geophysical Prospecting , 2007, 55(5): 685-695. DOI:10.1111/gpr.2007.55.issue-5 |
| [19] | 刘炯, 马坚伟, 杨惠珠. 周期性成层Patchy模型中纵波的频散和衰减研究. 地球物理学报 , 2009, 52(11): 2879–2885. Liu J, Ma J W, Yang H Z. Research on dispersion and attenuation of P wave in periodic layered-model with patchy saturation. Chinese J. Goephys (in Chinese) , 2009, 52(11): 2879-2885. |
| [20] | Gurevich B, Lopatnikov S L. Velocity and attenuation of elastic waves in finely layered porous rocks. Geophys. J. In , 1995, 121(3): 933-947. DOI:10.1111/gji.1995.121.issue-3 |
| [21] | Gurevich B, Zyrianov V B, Lopatnikov S L. Seismic attenuation in finely-layered porous rocks: Effects of fluid flow and scattering. Geophysics , 1997, 62(1): 319-324. DOI:10.1190/1.1444133 |
| [22] | Brajanovski M, Gurevich B, Schoenberg M. A model for P-wave attenuation and dispersion in a porous medium permeated by aligned fractures. Geophys. J. Int , 2005, 163(1): 372-384. DOI:10.1111/gji.2005.163.issue-1 |
| [23] | Gurevich B, Brajanovski M, Galvin R J. P-wave dispersion and attenuation in fractured and porous reservoirs-poroelaticity approach. Geophysical Prospecting , 2009, 57(2): 225-237. DOI:10.1111/gpr.2008.57.issue-2 |
| [24] | Johnson D L, Koplik J, Dashen R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. Journal of Fluid Mechanics , 1987, 176(1): 379-402. |
| [25] | Wang H F. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology. Princeton and Oxford: Princeton University Press , 2000: 27-149. |
| [26] | Mavko G, Mukerji T, Dvorkin J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media. New York: Cambridge University Press , 2009: 266-281. |
 2012, Vol. 55
2012, Vol. 55


