储层随机反演与建模方法一直是工业界与学术界关注的热点问题.随着地质统计学建模与反演方法的日益成熟,该方法已经进入商业软件并在波阻抗反演与储层建模应用中得到了广泛使用[1-6].随机反演方法中最经典的当属Monte Carlo 方法,MonteCarlo方法随机地遍历(或采样)模型空间,寻找与观测数据及先验信息具有最佳匹配的采样模型.由于尝试性模型的选取与参数修改具有很强的随机性,使得该方法在搜索过程中可以避免陷入局部极值,实现对模型空间的全局寻优.为了能够提高采样效率,MonteCarlo方法出现了很多变种,其中最具代表性的当属模拟退火算法与遗传算法,但是由于模型空间往往很大,再高效的采样方法在遍历模型空间时都需要高额的计算成本,因此两者的计算效率都不甚理想[7].
当介质参数可以用统计学语言(如均值、方差、变差函数、直方图)进行描述时,就提供了高效率的、基于地质统计学随机模拟对模型空间进行采样的可能性.与传统的克里金插值得到一个过于光滑的拟合结果不同,在地质统计学随机模拟中,先验信息可以以协方差函数的形式或者是训练图像的方式给出,然后结合先验观测信息以序贯拟合的方式得到多个等概率的实现,相比MonteCarlo方法,基于序贯拟合的地质统计学模拟在计算效率方面的优势十分明显[8].
利用地质统计学模拟在计算效率方面的优势并结合传统的反演思想,Haas和Dubrule[9]提出了地质统计学反演方法.该方法基于已知的测井信息实施序贯模拟并在地面地震数据的约束下判断拟合结果的合理性.通过不同的随机路径得到不同的全局实现,然后基于多个全局实现(也就是多个采样结果)来评估反问题的解[10-11].由于地质统计学反演的实现过程可以认为是一个基于测井资料并在地震数据约束下的随机建模过程,因此这种建模(反演)方法天然具有整合不同尺度数据的能力.目前,如何在序贯拟合的框架下融合更多的先验信息以进一步降低建模的不确定性并提高地质统计学反演的精度已经成为下一步需要深入研究的课题.
Hansen等[12]深入讨论了将地质统计学随机模拟用于求解线性高斯反问题的可能性,并提出可以将测井数据与井间地震数据这两种先验信息统一考虑作为条件数据实施序贯模拟,这样得到的模拟结果自然同时忠实于先验的测井数据与井间地震数据.由于综合了更多的先验信息,随机模拟的不确定性自然会降低.显然这是一种更优秀的地质统计学随机模拟方法.如果能够在方法基础上进一步将地面地震数据加入约束实施地质统计学建模(反演),应该会得到优于以往的反演结果.
基于上述考虑,本文首先实现了文献[12]提出的基于测井信息与井间地震信息的地质统计学模拟方法,然后将这种方法纳入到传统地质统计学反演的框架中,提出一种能够融合测井、井间地震信息与地面地震信息、具有更高精度的地质统计学反演方法.基于二维理论数据的测试表明,该方法可以明显降低地质统计学建模的多解性,有效提高反演精度,是一种具有应用潜力的地质统计学反演方法.
2 测井与地面地震信息联合约束下的传统地质统计学反演思路传统的地质统计学反演实质是一个在序贯拟合思想指导下,在测井信息与地面地震信息共同约束下的地质统计学随机建模过程(Haas andDubrule[9]).其中每一个需要反演的波阻抗道都是基于序贯拟合的思想生成的,具体的拟合地震道的顺序则完全按照随机路径来决定.
传统地质统计学反演实现思路如下:在拟合一个新位置处的波阻抗道之前,需要将已有的工区内测井信息与已经反演得到的波阻抗道作为先验信息;然后通过克里金插值拟合得到一个新的波阻抗道,随即实施褶积正演,并将正演结果与当前位置已有的叠后偏移数据体中的地震道相比求取残差.将多次拟合结果中残差符合给定的精度要求或者残差最小的加以保留,保留之后该道随即被认为是已知的先验测井信息,被用于拟合下一个位置的波阻抗道.将上述过程重复应用于工区中所有需要拟合的位置,当工区内所有位置的波阻抗道都拟合得到之后,就得到了一个全局实现结果.
显然,仅得到一个全局实现是不够的,我们需要得到多个全局实现---即对模型空间进行多次采样才有可能对模型空间有比较充分的了解.因此需要生成多个随机路径,重复上述过程,得到多个新的全局实现;当得到了足够多的全局实现之后,这时可以认为对模型空间的采样已经比较充分,整个地质统计学反演过程结束.
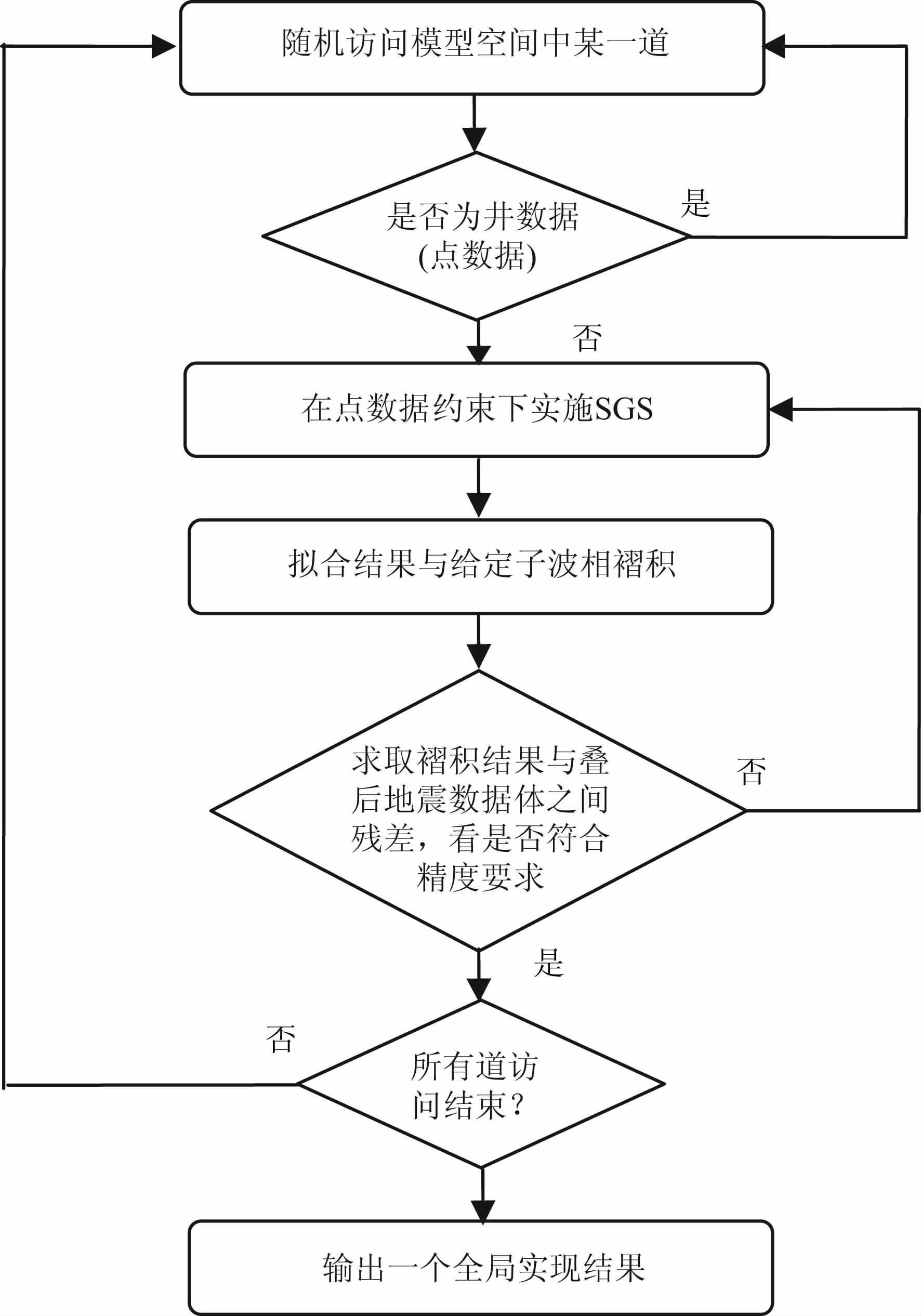
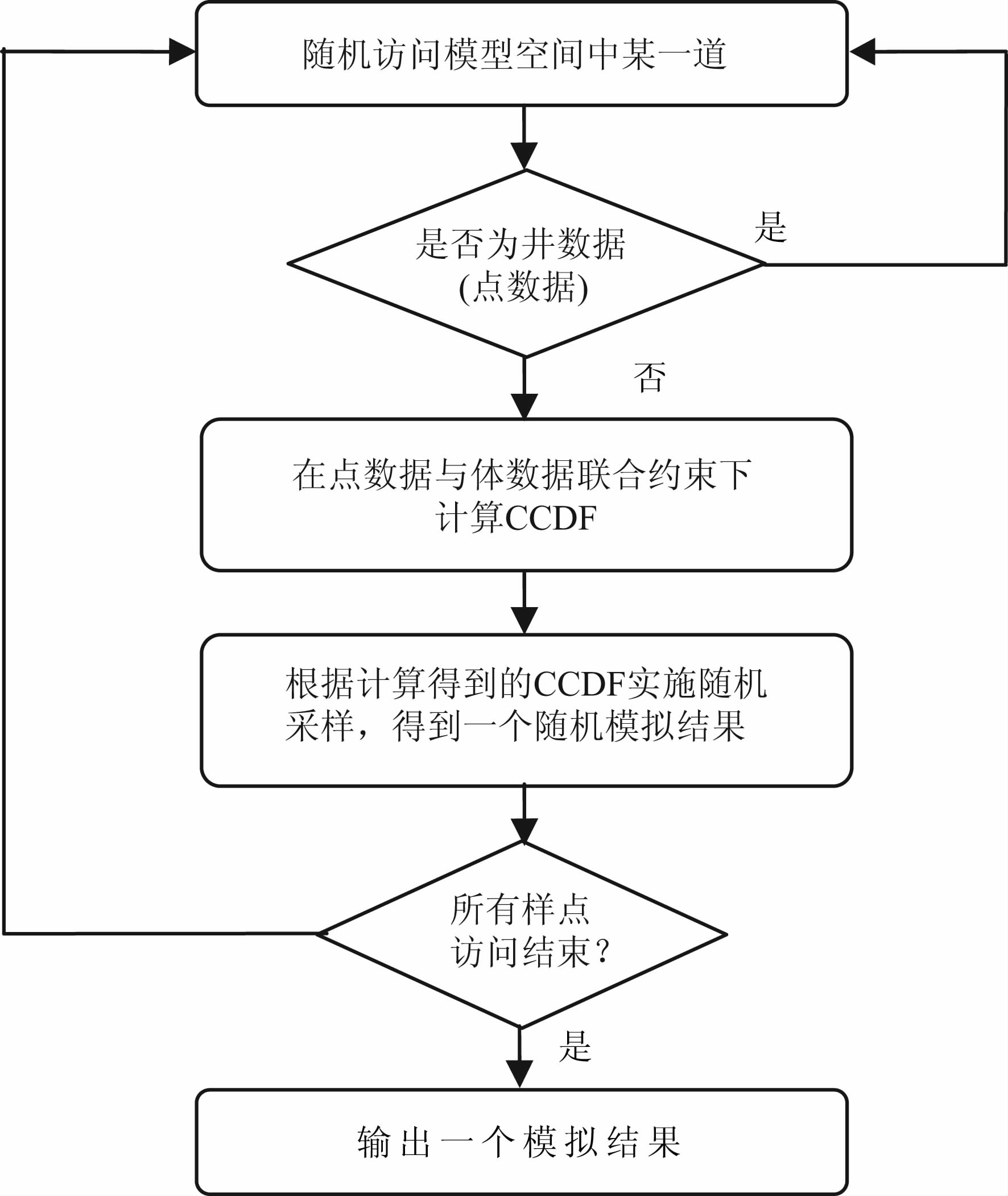
本文中沿用Hansen等[12]的表达方式,用A 类数据(或点数据)代表测井信息;用B 类数据(或体数据)代表井间地震数据或者地面地震数据,建立基于测井与地面地震信息的传统地质统计学建模(反演)的工作流程(图 1).图中的点数据即表示测井信息,SGS 代表序贯高斯序贯模拟(Sequential Gaussian Simulation).注意图 1仅仅表达了如何得到一个全局实现的工作流程,实际应用时还需要将图 1所示流程重复多次得到多个全局实现才可以算是一个完整的地质统计学反演/建模过程.
|
图 1 测井与地面地震信息联合约束下的 地质统计学反演工作流程图 Fig. 1 A work-flow for geostatistical inverseon constrained by logging and surface seismic data |
Hansen等[12]提出可以利用地质统计学模拟的等概率采样方式求解线性高斯反问题,这个思路无论对于线性反问题的求解还是地质统计学模拟来说都是一个重要的贡献.更值得注意的是,他们在实施序贯模拟的过程中成功地将测井信息与井间地震信息同时当作条件数据来构造条件累积分布函数(Conditional Cumulative Distribution Function,以下简称CCDF),因此对构造出的CCDF 进行采样时,就实现了同时忠实于测井信息与井间地震信息的序贯模拟.根据文献[12],假设A 类数据对应于模型参数的直接测量值a0,B 类数据对应于模型参数的线性平均值b0,可以有如下表达:
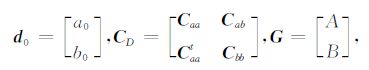
|
(1) |
这里Caa和Cbb是观测数据a和b的数据协方差,Cab是两类数据间的协方差.观测值d通过线性算子G与模型m相联系:
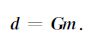
|
(2) |
根据Tarantola[13]对高斯概率密度方程求取最小二乘解的思路,可导出任意位置x的后验平均值和协方差在最小二乘意义下的解为
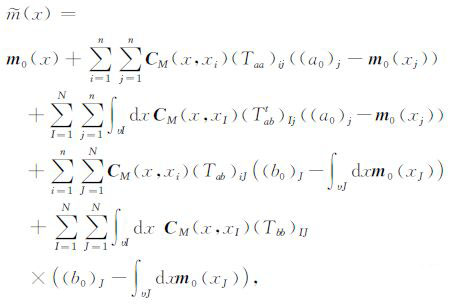
|
(3) |
后验协方差表示为
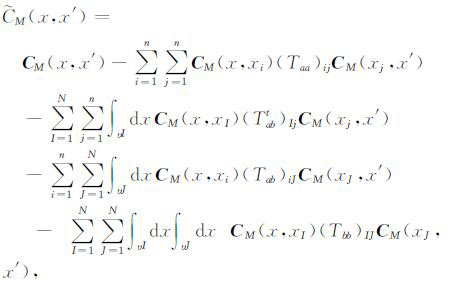
|
(4) |
其中m0 为模型的均值;CM为先验协方差模型;矩阵T为一个4×4矩阵,是模型协方差矩阵CM与数据协方差矩阵CD的一个线性组合.n为A 类数据的可用数量;N为线性平均数据(B类数据)的数量.图 2显示了在这两类数据条件约束下的序贯模拟流程图.注意模拟方式可以根据介质分布规律不同有所区别:当模拟的介质参数符合高斯分布规律时,可以使用序贯高斯模拟;当模拟的介质参数不符合高斯分布规律时,可以使用直接序贯模拟.以下以序贯高斯模拟为例,说明在点数据(测井信息)与体数据(井间射线信息)联合约束下该方法的有效性.
|
图 2 基于测井与井间地震信息的序贯模拟流程图 Fig. 2 A work-flow for sequential simulation constrained by logging and cross-hole seismic data |
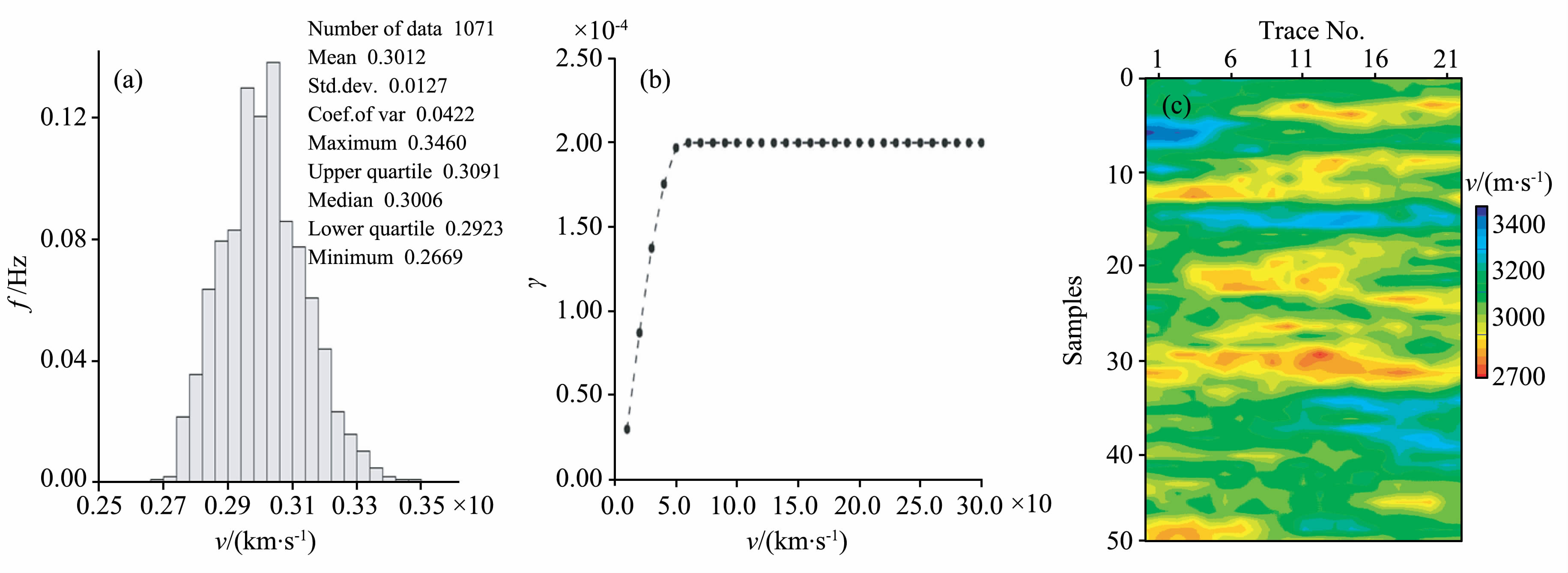
首先设计一个服从高斯分布的速度模型.作为先验信息的速度分布直方图与变差函数模型如图 3a与图 3b所示,这里使用了球型变差函数模型,其一般公式为
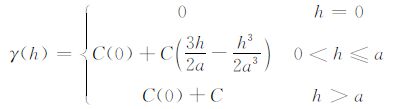
|
(5) |
式中,C(0)为块金常数;C为拱高;C(0)+C为基台值;a为变程.本文使用的参数为变程a= 5,C(0)=0,C=0.0002;利用高斯序贯拟合(SGS)方法对模型进行模拟.随机生成高斯分布的速度场如图 3c所示,该模型将作为后续模拟的标准答案使用.为了对比的方便,在垂向不赋予该模型一个明确的物理量纲,就以样点数为单位;稍后提供的雷克子波在垂向的量纲也是样点数,读者可以将其理解为深度域子波即可.这样处理可以省略时深转换操作,同时不影响对问题的理解.
|
图 3 速度分布直方图(a);球型变差函数模型(b);高斯速度模型(c). Fig. 3 (a) The histogram of velocity distribution; (b) Spherical Variogram model; (c) Velocity modfl in Gaussian distribution. |
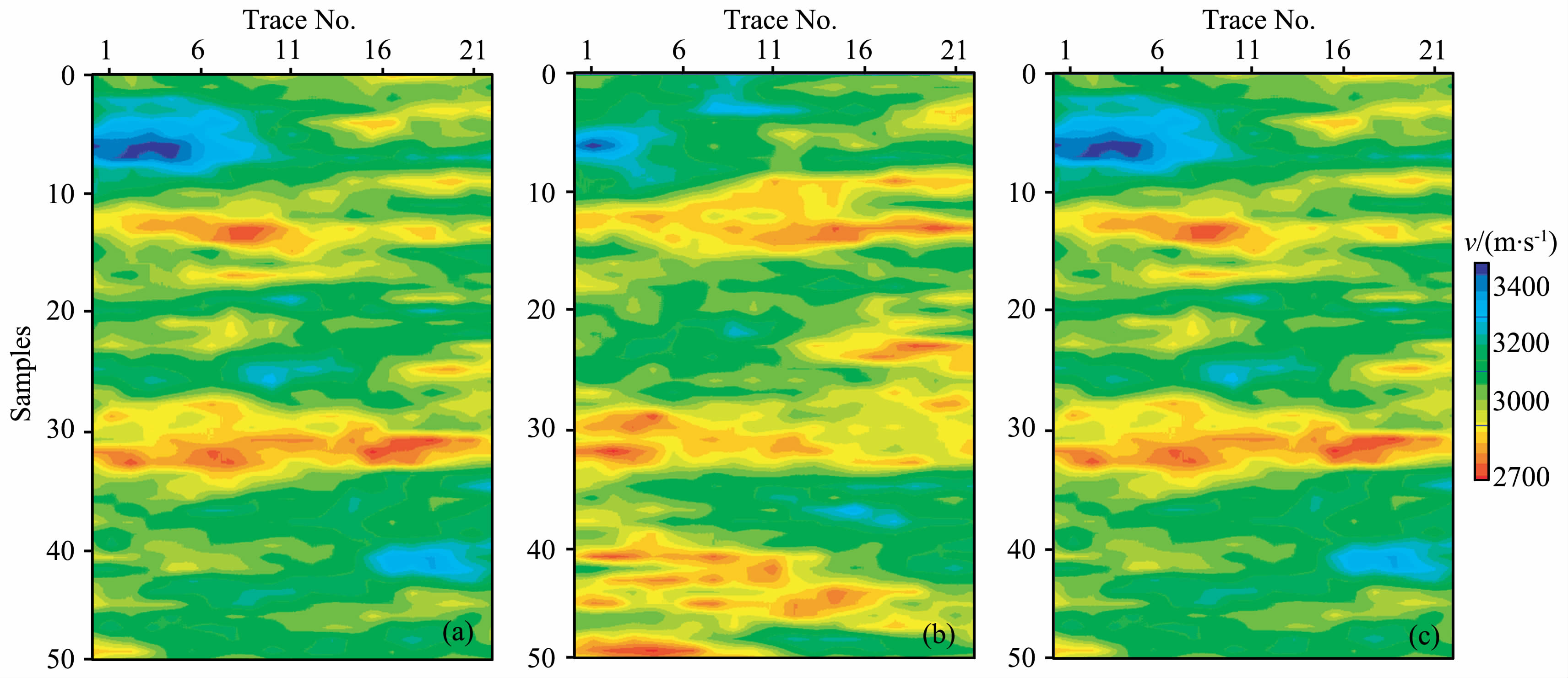
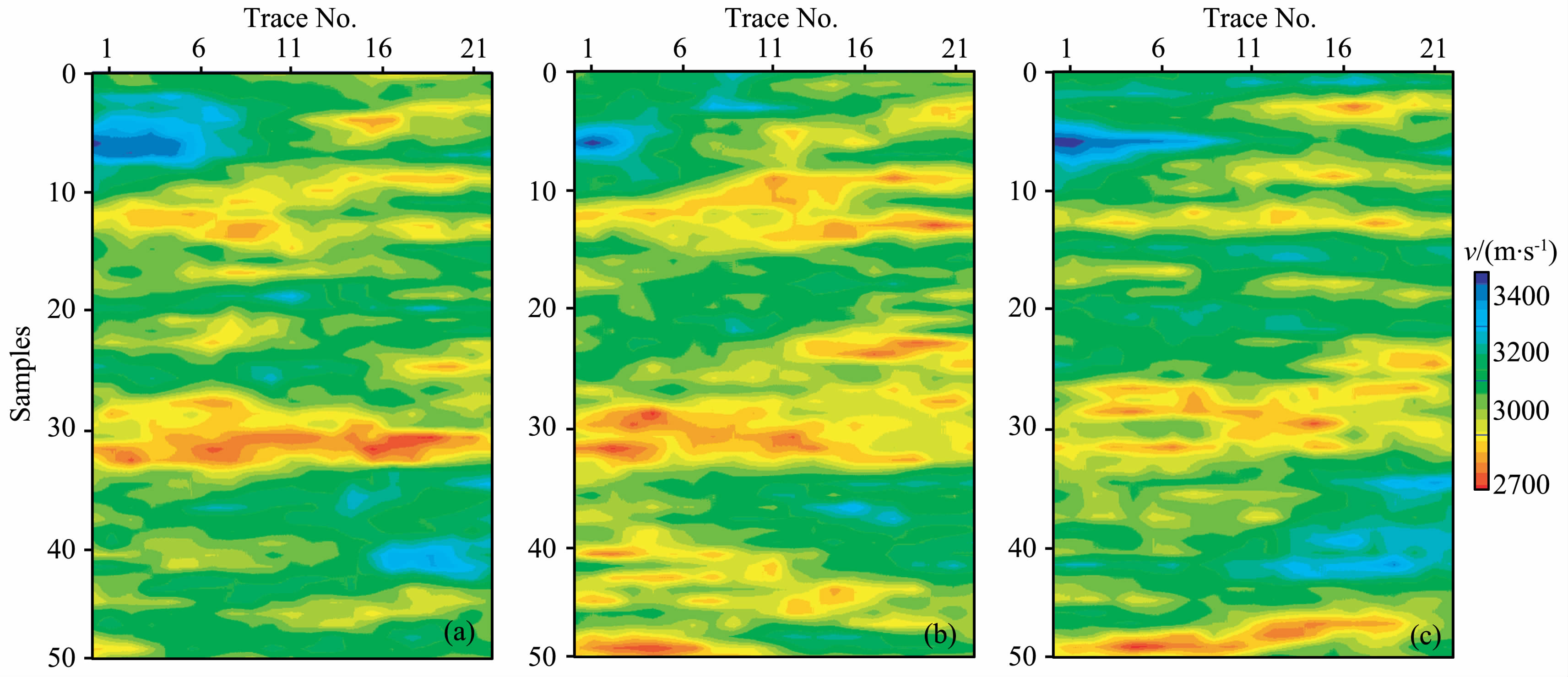
图 4a为使用的点数据示意图,测井信息被安置在模型的两侧.图 4(b,c)分别对应于25 根射线和100根射线时的体数据示意图.图 5(a-c)显示了仅在点数据约束(射线根数=0)下的三个模拟结果;图 6(a-c)显示了在点数据和体数据联合约束(射线根数=25)下的三个模拟结果;图 7(a-c)显示了在点数据和体数据联合约束(射线根数=100)下的三个模拟结果.

|
图 4 使用的点数据(0射线)(a);体数据射线路径示意图(25射线)(b);体数据射线路径示意图(100射线)(c) Fig. 4 A geostatistical simulation constrained by logging and different borehole seismic rays |
|
图 5 0根射线模拟的结果1(a)、模拟结果2(b)、模拟结果3(c) Fig. 5 Three geostatistical simulations constrained by logging and zero borehole seismic rays |
|
图 6 25根射线的模拟结果1(a)、模拟结果2(b)、模拟结果3(c) Fig. 6 Three geostatistical simulations constrained by logging and 25 borehole seismic rays |

|
图 7 100根射线的模拟结果1(a)、模拟结果2(b)、模拟结果3(c) Fig. 7 Three geostatistical simulations constrained by logging and 100 borehole seismic rays |
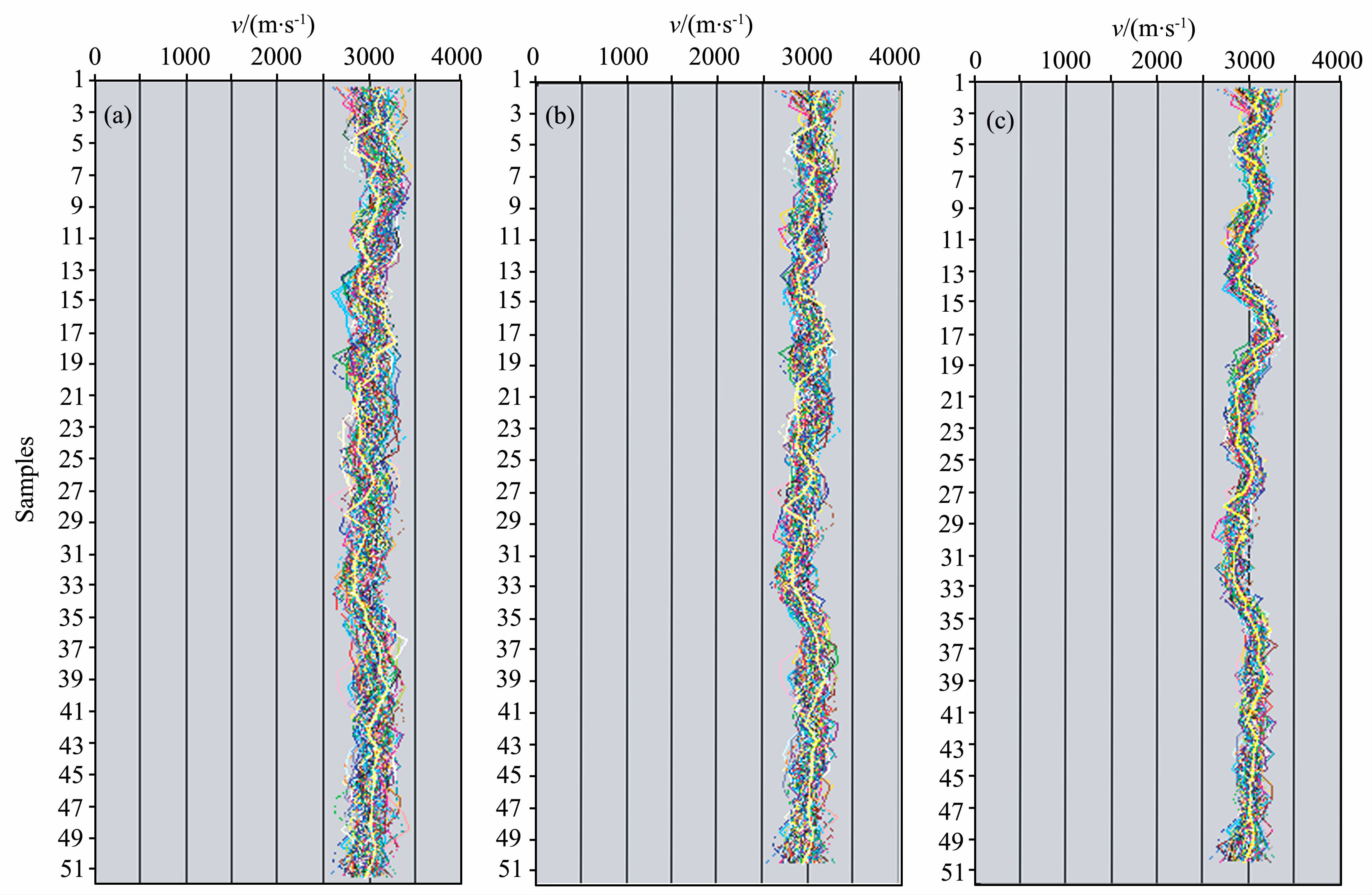
通过比较可以发现,两类数据同时约束下的模拟结果明显好于仅仅使用A 类数据约束下的反演结果、在两类数据同时约束下,射线根数越多,模拟结果越好.图 8(a-c)显示了两类数据联合约束时的三种射线配置情形下模型中第10 道的100 个拟合结果,其中浅黄色线代表了真实的速度分布;可以看出在没有体数据约束时,100 个模拟结果与真实速度分布差距较大;当使用了25根射线约束时,100个模拟结果与真实模型的分布差距明显缩小;当使用了100根射线约束时,100 个模拟结果与真实模型的分布差距变的非常接近.这充分证明了在射线信息越密集、对拟合模型的约束效果最好.
|
图 8 不同射线约束下的100个模拟结果第10道速度对比(a)0根射线;(b)25根射线;(c)100根射线。 Fig. 8 A velocity profile at trace No. 10 simulated from three geostatistical simulations constrained by logging and different borehole seismic rays |
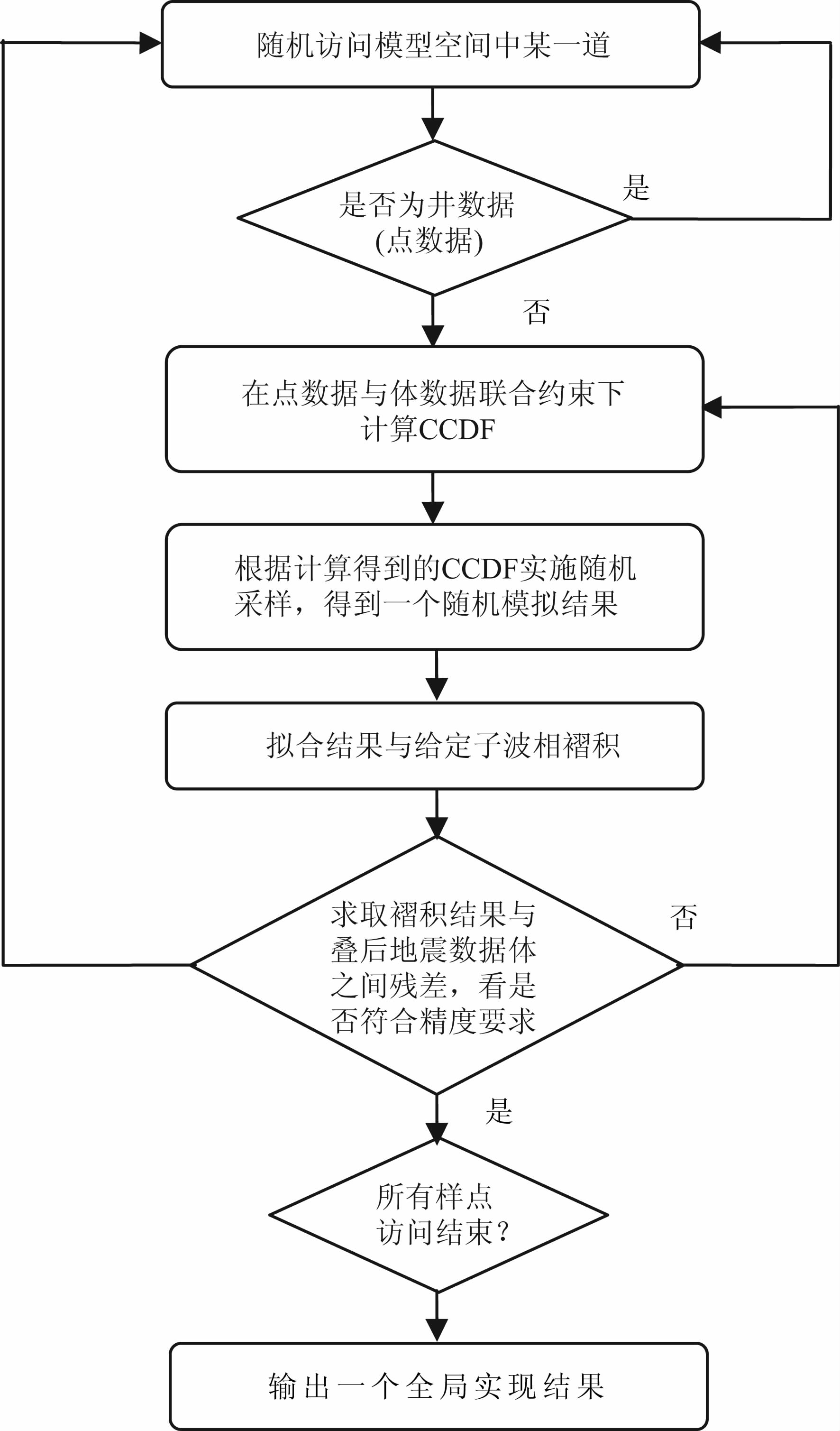
通过上一节对SGS随机模拟的实践可以发现,测井与井间地震数据联合约束下的序贯模拟结果确实优于仅用测井数据约束的序贯模拟结果,而且射线越密效果越好.如果能够利用测井、井间地震数据与地面地震数据联合约束实施地质统计学反演,这种新的地质统计学反演方法的建模精度应该优于传统地质统计学反演.基于上述考虑,设计了一种通过测井、井间地震与地面地震数据联合约束的地质统计学反演流程(如图 9所示).
|
图 9 基于测井、井间地震数据、地面地震数据联合约束下的地质统计学反演流程 Fig. 9 A work-flow for geostatistical inverseon constrained by logging,cross-hole seismic data and surface seismic data |
从图 9可以看出,这种新的反演(建模)流程将测井数据(点数据)与井间地震数据(体数据)作为随机模拟的条件数据计算CCDF,但是在选择是否接受模拟结果则比Hansen等[12]严格的多,因为在随机模拟之后还需要将其褶积结果与叠后地面地震数据之间进行比对,保留符合残差要求的模拟结果,这就是传统地质统计学反演的思路.但是由于在随机模拟过程中我们已经尊重了井间射线的信息,因此模拟的精度必然将比传统方法高出许多,此时再将地面地震数据纳入实施进一步约束无疑将获得比传统地质统计学反演更好的模拟精度和更低的不确定性.
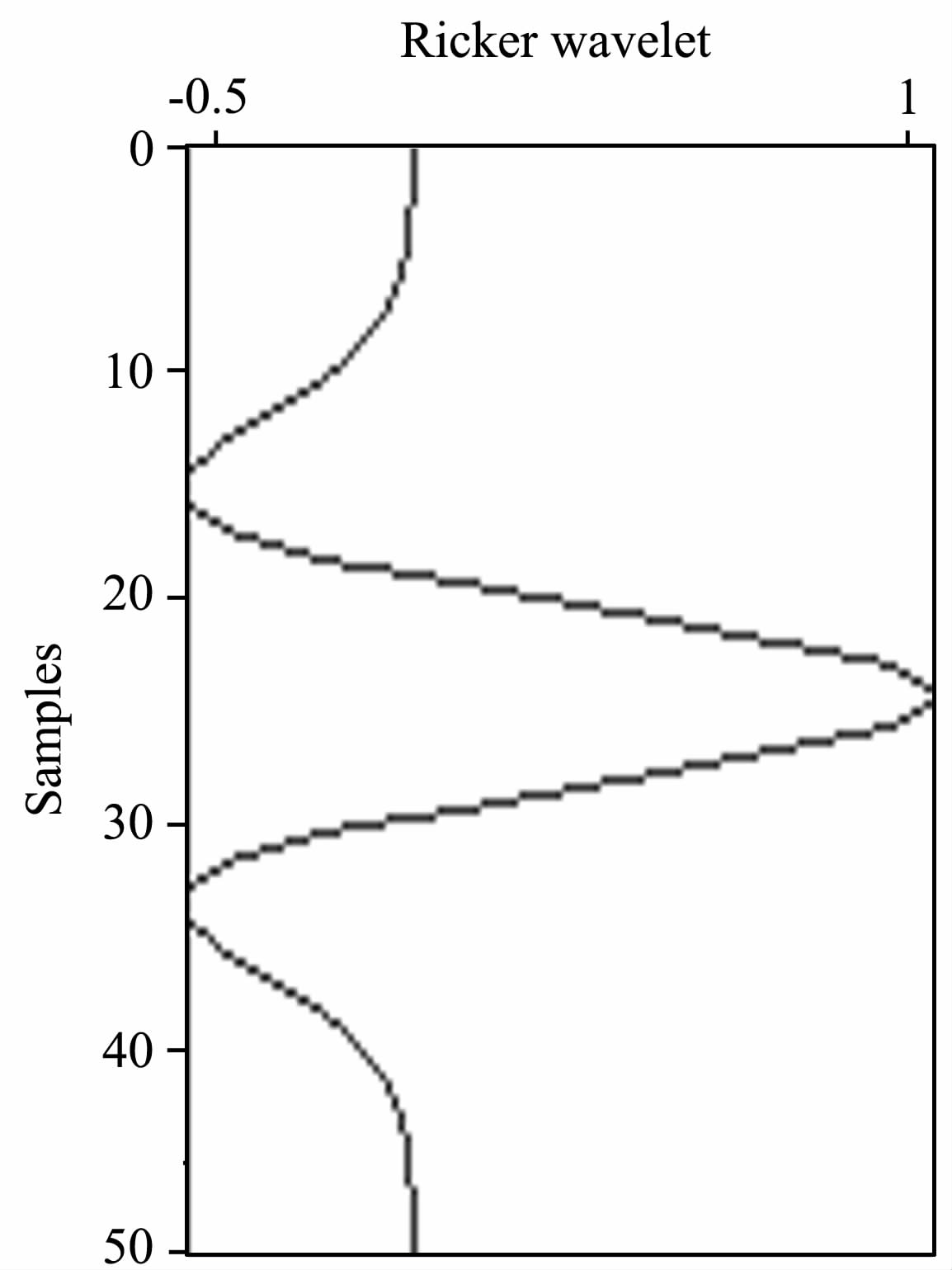
这里仍然使用与第2节同样的高斯分布速度场(如图 3c所示).图 10为进行褶积计算时使用的雷克子波,其主频为8Hz,纵向量纲依然为样点数,不妨认为它是一个深度域子波.使用的变差函数仍为球型变差函数模型,其参数与图 3c相同.
|
图 10 用于正演的雷克子波 Fig. 10 A Ricker wavelet used in forward modelin |
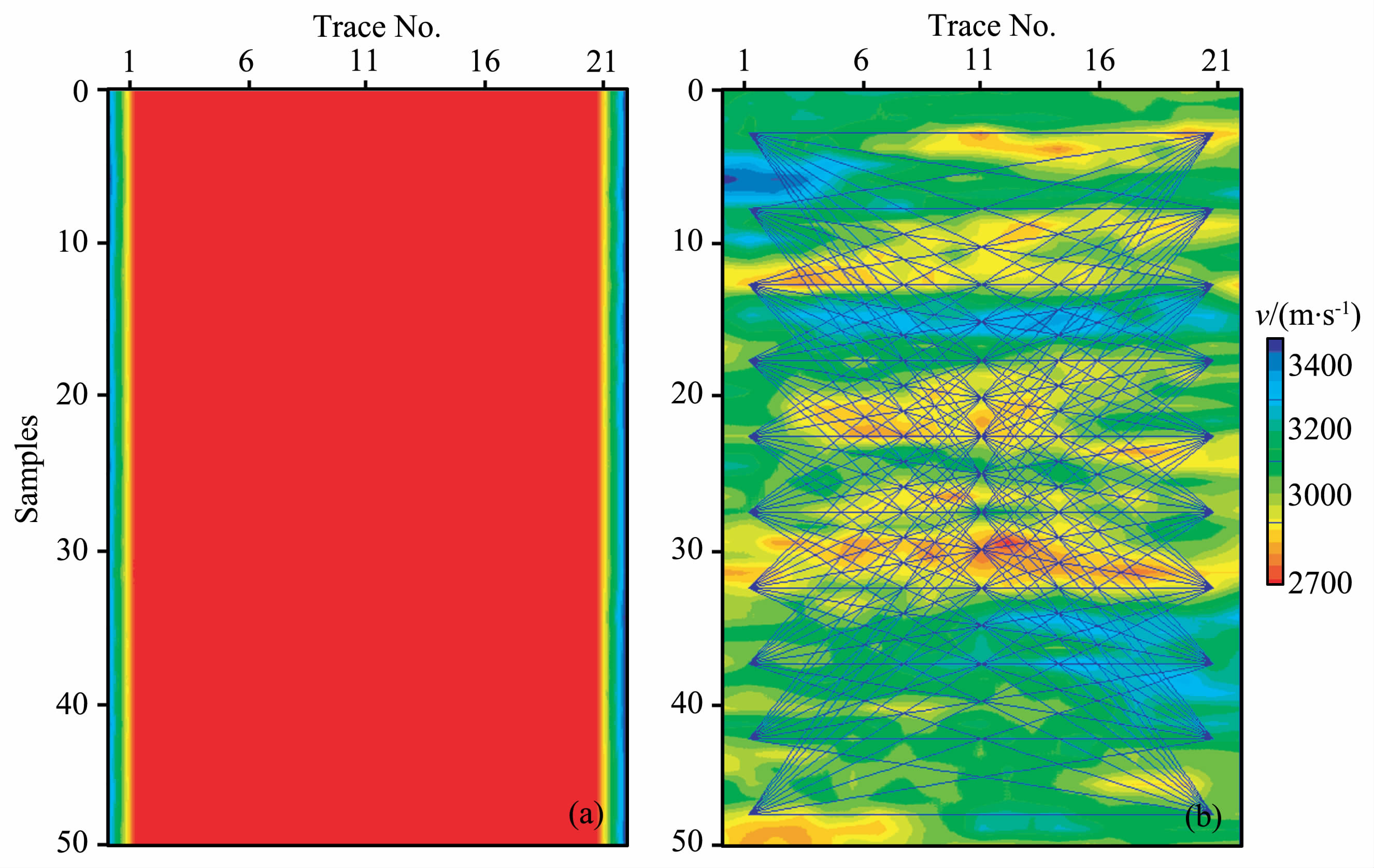
图 11a为使用的测井数据(点数据)的所在位置和速度分布情况,图 11b为使用井间射线数据(体数据)的射线路径示意图.这里仍然暂时只考虑假设射线直线传播的情况.其实在模型已知的情况下,无论换成弯曲射线还是菲涅尔体射线计算走时,对模拟的约束效果都是一样的[11].
|
图 11 使用的点数据(a)及体数据射线路径示意图(b) Fig. 11 Point data and volume data used in comparison RAW SIM1 SIM2 SIM3 SIM4 SIM5 SIM6 SIM7 SIM8 SIM9 SIM 10 |
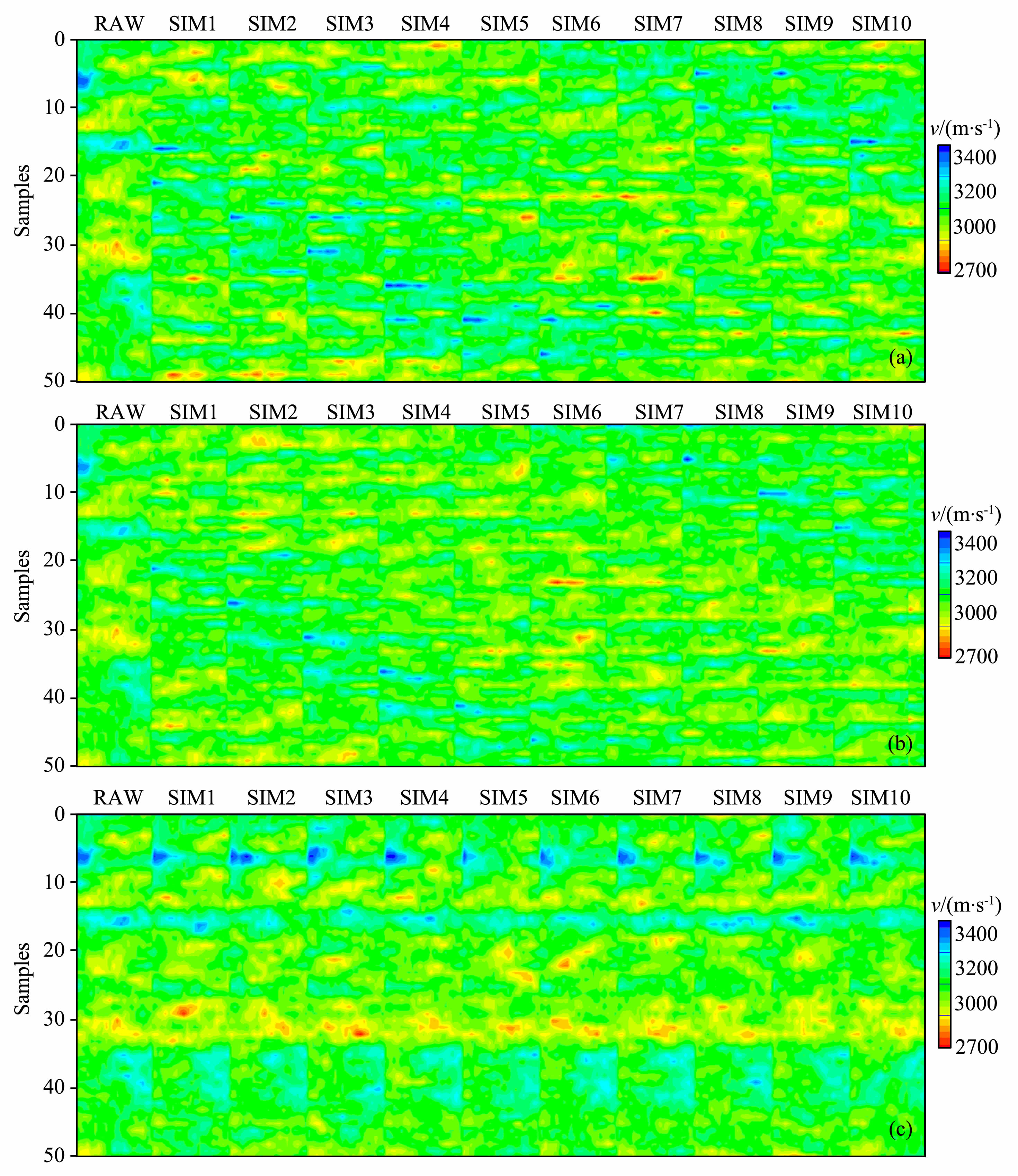
图 12a分别为传统地质统计学反演的10 个实现(即测井数据与地面地震数据两类数据联合约束的10个实现);图 12b为测井数据与井间地震数据(应用100根射线)两类数据联合约束下的10 个实现;图 12c为测井数据、井间地震(应用100根射线)和地面地震数据联合约束下的10个实现.每一张图的最左边都是原始模型,从左边第二张到最后一张为10个模拟结果.通过比较可以看出,在两种数据约束下的模拟结果其不确定性明显超过在三种数据约束下的模拟结果,因为图(c)中的10 个模拟结果与原始模型的相似程度很高,而图(a)和图(b)中的10个模拟结果与原始模型的相似程度就远远低于图(c).显然,这是由于图(c)中的10 个模拟结果同时忠于测井数据(点数据)、井间地震数据(体数据)与叠后零炮检距数据的结果,由于图(a)中没有加入井间地震数据约束而图(b)没有加入零炮检距数据的约束,因此测井与井间数据联合约束下实施序贯拟合、同时又在地面地震下约束下进一步挑选出的反演结果显然明显提高了地质统计学反演的准确度,降低了储层建模的不确定性.
|
图 12 不同数据约束下10个模拟结果(SIM1-10)与原始模型(RAW)对比的反演比较(a)测井、地面地震零炮检距两类数据;(b)测井、井间地震两类数据;(c)测井、井间地震数据、叠后地面地震数据 Fig. 12 A comparison between RAW velocity model and ten simulations generated by different type of data |
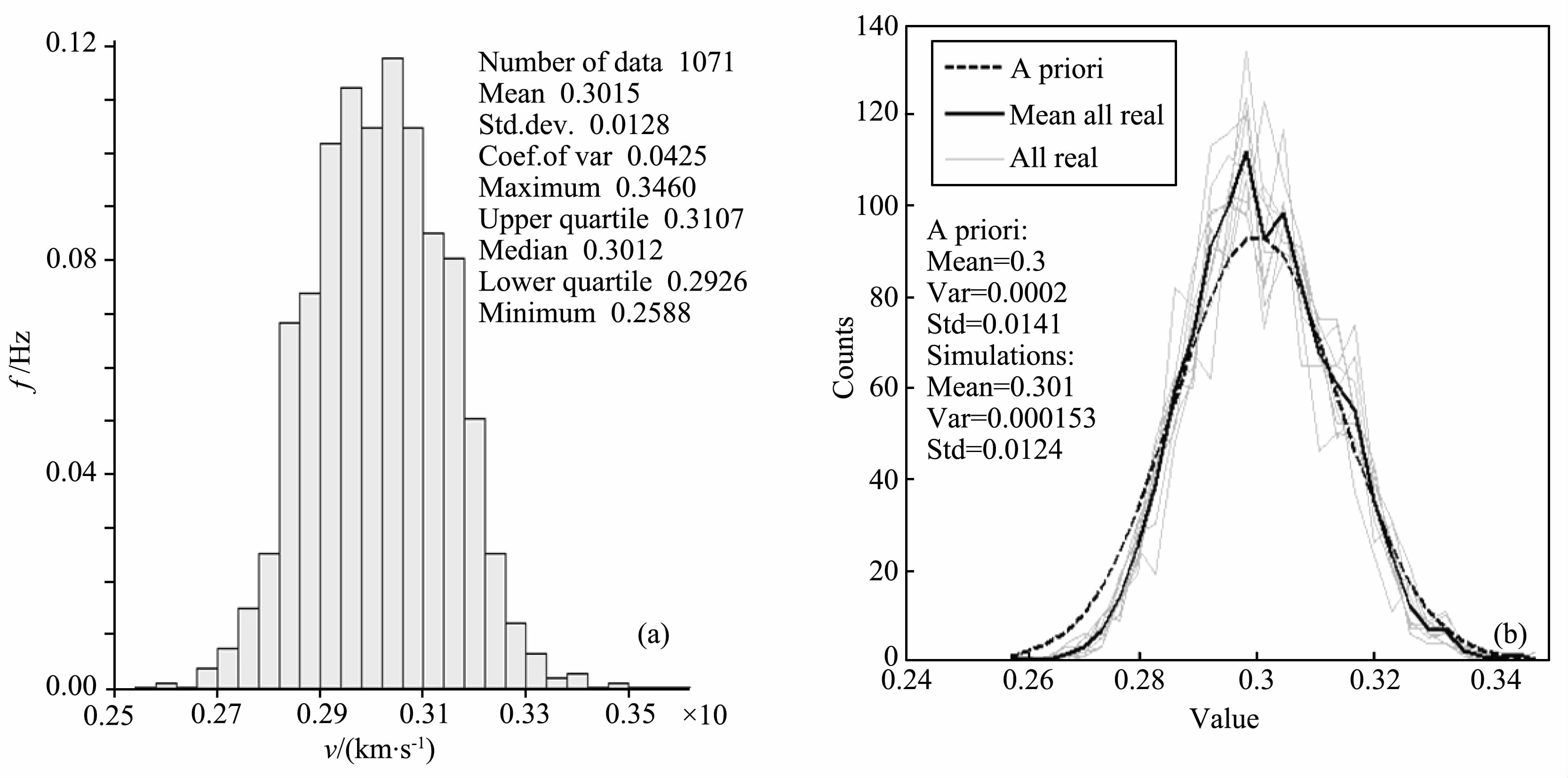
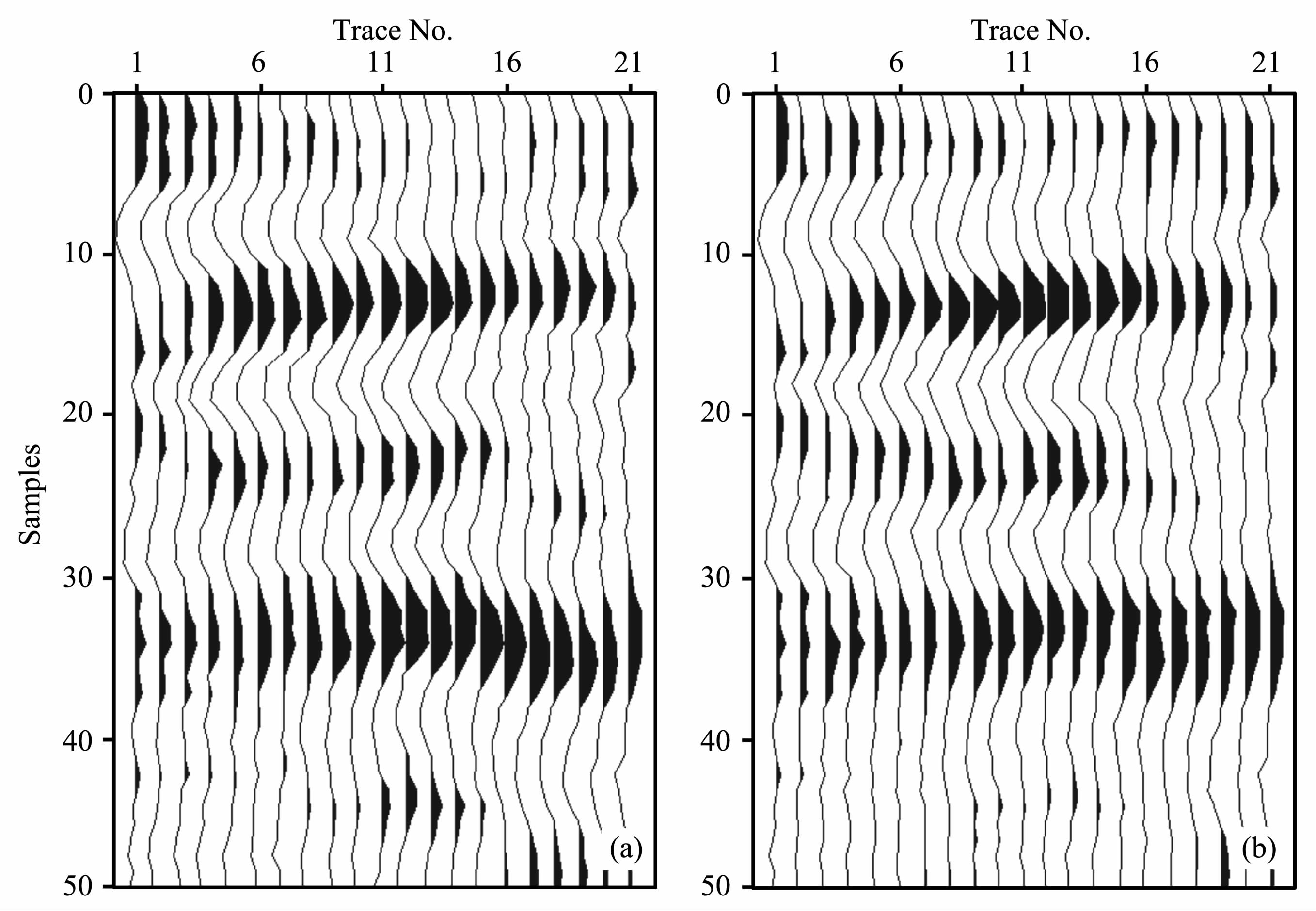
图 13a为原始模型的速度分布直方图.图 13b为图 12c中的10个实现的速度分布(灰色线)、它们的均值分布(黑色线)与原始速度分布(虚线)的对比.可以看出,三类数据联合约束下的模拟结果的速度分布的平均结果与原始模型的速度分布十分相似.图 14a为原始模型的褶积结果,图 14b与某个模拟结果的褶积结果的比较,相似性依然很高.
|
图 13 初始模型的速度分布直方图(a)及将图 12c中的10个实现的速度分布与初始速度分布比较(b) Fig. 13 The histogram of initial velocity distribution; (b) A comparison between initial velocity model and ten simulations generated in Fig 12c |
|
图 14 初始模型的褶积结果(a)及将图 12c中的10个实现中的一个进行褶积后的结果(b) Fig. 14 Acomparison between synthetic data and forward-modeling data based on one simulation of ten shown inFig 12 |
反演问题的多解性,即其确定性与随机性是求解反问题时需要深入讨论的问题.前人的研究表明,只有在贝叶斯框架下对反演问题的后验概率密度函数进行充分采样才能够对其进行正确的求解和合理的评估.可以说储层模型的建立实质上就是一个在不同类型观测数据约束下的随机建模过程.由于地质统计学反演(建模)可以方便地整合先验信息,实现对后验概率密度函数的等概率采样,使得它在储层建模中发挥着重要的作用.
本文首先实现了可以同时整合测井数据与井间地震数据的地质统计学随机模拟方法.然后加入地面地震数据就得到了一种新的地质统计学反演(建模)方法.不同与以往的地质统计学反演方法仅仅整合了测井数据与地面地震数据,这种方法将测井、井间地震与地面地震数据同时用于介质参数的随机反演.由于更多类型的先验信息被加入到随机反演的算法中,很多无用的模拟结果得到了排除,使得模拟出的介质参数的不确定性大为降低,反演精度则相应得到了提高.通过对典型的二维理论数据的计算,证实了上述观点.这个方法可以非常方便地推广到三维.
在处理实际资料的过程中,首先需要通过常规的走时层析反演对井间地震信息进行分析,提供这种新的地质统计学反演方法所需要的井间射线与走时信息.其次一个关键的工作就是变差函数的统计,对于实际数据而言,需要拟合的物理参数往往不一定符合高斯分布,因此对实际数据的大量采样和深入细致的统计学分析是必不可少的,而这个工作恰恰是地质统计学模拟与反演成败的关键.
虽然本文方法在实际应用中还有许多技术上的困难需要克服,但是综合尽可能多的先验信息,在随机模拟与反演的意义下进行讨论将是日后许多研究者在考虑储层反演与建模时必须重视的核心问题.随着地球物理勘探投入的不断加大,在同一个探区各种地球物理手段的综合应用成为趋势,一个综合测井、井间地震数据、VSP 地震数据、地面地震数据甚至重、磁、电观测数据的随机储层建模与反演方法在不远的将来就会出现.
| [1] | Journel A G, Huijbregts C J. Mining Geostatistics. New York: Academic Press, 1978 . |
| [2] | Deutsch C V, Journel A G. GSLIB: Geostatistical Software Library and User's Guide. Oxford: Oxford University Press, 1998 . |
| [3] | 印兴耀, 刘永社. 储层建模中地质统计学整合地震数据的方法及研究进展. 石油地球物理勘探 , 2002, 37(4): 423–430. Yin X Y, Liu Y S. Methods and development of integrating seismic data in reservoir model-building. Oil Geophysical Prospecting (in Chinese) , 2002, 37(4): 423-430. |
| [4] | 孙思敏, 彭仕宓. 基于模拟退火算法的地质统计学反演方法. 石油地球物理勘探 , 2007, 42(1): 38–43. Sun S M, Pen S B. A geostatistical inversion method based on simulated annealing algorithm. Oil Geophysical Prospecting (in Chinese) , 2007, 42(1): 38-43. |
| [5] | Bosch M, Carvajal C, Rodrigues J, et al. Petrophysical seismic inversion conditioned to well-log data: Methods and application to a gas reservoir. Geophysics , 2009, 74(2): 1-15. |
| [6] | Bosch M. Lithologic tomography: From plural geophysical data to lithology estimation. Journal of Geophysical Research , 1999, 104(B1): 749-766. DOI:10.1029/1998JB900014 |
| [7] | Mosegaard K, Sambridge M. Monte Carlo analysis of inverse problems. Inverse Problems , 2002, 18(3): R29-R54. DOI:10.1088/0266-5611/18/3/201 |
| [8] | Goovaerts P. Geostatistics for natural resources evaluation. Oxford: Oxford University Press, 1997 . |
| [9] | Haas A, Dubrule O. Geostatistical inversion—A sequential method for stochastic reservoir modeling constrained by seismic data. First Break , 1994, 12(11): 561-569. |
| [10] | Pendrel J, van Riel P. Using seismic inversion and geostatistics to estimate porosity—A Western Canadian reef example. CSEG Ann. Mtg. Abs, 1997. |
| [11] | Torres-verdin C, Victoria M, Merletti G, et al. Trace-based and geostatistical inversion of 3-D seismic data for thin-sand delineation: An application in San Jorge Basin, Argentina. The Leading Edge , 1999, 18: 1071-1077. |
| [12] | Hansen T M, Journel A G, Tarantola A, et al. Linear inverse Gaussian theory and geostatistics. Geophysics , 2006, 71(6): R101-R111. DOI:10.1190/1.2345195 |
| [13] | Tarantola A. Inverse problem theory and methods for model parameter estimation. Society for Industrial and Applied Mathematics, 2005. |
 2012, Vol. 55
2012, Vol. 55

