3D3C 采用纵波震源激发、三分量检波器接收[1]方法.其优势是可记录到不同方位不同炮检距的反射,尤其是可同时记录到反射P 波和PS波.相比常规纵波勘探,3D3C 勘探的采集费用并无明显提高,但记录的信息量却提高了三倍,是一种经济有效的陆地勘探技术[2-3].不仅如此,3D3C 也为发展岩性和裂隙探测提供了数据支持[4].发展3D3C 技术,并用它来综合解释P波和PS波的动力学特征,首先需要做好P 波和PS 波叠加成像[5].由于P 波为纯波反射,通常记录的信噪比也较高[6],所以目前三维P波成像技术已被广泛接受.相比之下,PS 波的处理要更加困难和复杂,其成像质量也一直不理想,甚至有时会出现三维和二维处理的构造形态存在较大差异[7]的情况.
目前,PS波叠加成像方法有很多种,如CMP、ACCP(近似共转换点)[8]、CCP(共转换点)[9]、倾角CCP[10]等方法.其中,PS 波CMP 叠加成像方法可视为P 波CMP 叠加成像方法的延伸.该方法存在以下优势:一、抽道集简单,与其它PS 波处理方法相比无需预知纵横波速度比等参数;二、软件实现上不需要在P 波CMP 方法的基础上做大的改动,经济实用.近年来,Tsvankin 和Grechka[11]对PS 波CMP方法理论上已有大量研究,通过分析该方法的有关特性为PS 波CMP 成像提供了理论基础.但是,经过对实际三维资料处理后发现,PS 波CMP叠加成像结果不甚理想,尤其倾斜界面的成像质量较差.对于CMP抽道集,虽然倾斜界面P 波反射点离散,但能够叠加成像;而PS波在倾斜界面上同样存在转换点离散问题,成像质量却很差甚至难以成像,其中原因一直未能给出解释.与PS波界面转换点离散相关的还有PS波的静校问题.近年来对PS波的静校问题有很多讨论,认为PS 波的静校比P波的静校更为困难[12].但关于PS波倾斜界面成像,三维静校相比二维静校将出现哪些新的问题至今没有明确提出和回答.三维地震PS 波成像是不同方位和不同炮检距叠加的结果,CMP道集动校叠加过程中涉及的问题对倾斜界面成像的影响也需要进一步讨论.PS波的界面转换点离散、三维静校和动校叠加复杂是影响CMP 叠加成像的三个相互关联的问题.
本文首先给定不同偏移距、纵横波速度比和界面倾角,对三维PS波CMP转换点的离散问题进行讨论;然后对比PS 波倾角CCP 方法,分析PS 波CMP方法如何引起新的静校问题;接下来结合蔡明刚等[13]给出的三维倾斜界面PS波CMP 道集近炮检距时距方程,对其时距特征进行分析;最后给出某煤区3D3C 实际资料处理的PS 波CMP 和倾角CCP叠加成像结果对比.
2 PS波CMP成像影响因素分析针对我国东部地区构造情况,对影响PS 波CMP成像质量的因素进行讨论.由于我国东部地区沉积层较厚,地下界面倾角不大、横波速度较低,所以在讨论过程中假设倾角δ在30°以内、纵横波速度比γ 在3.0以内.
2.1 转换点离散因素分析PS波由于下行为P 波、上行为S 波,其反射路径不对称[12],所以在进行CMP抽道集时,界面转换点会发生离散现象[9, 14],使得叠加后的成像质量降低.在水平二维界面反射时,转换点的离散现象为单个方向,当反射界面由二维转为三维时,这种离散现象就由单个方向扩展到圆周上的各个方向.在三维倾斜界面反射时,转换点在圆周上的离散程度较水平界面变大.此外,纵横波速度比γ 的变化也会引起转换点的离散程度变化.在实际资料采集过程中,地下反射界面往往带有一定倾角,因此,我们将对三维倾斜界面PS波CMP 方法,通过给定不同的倾角δ值和纵横波速度比γ 值,分析其转换点离散情况.
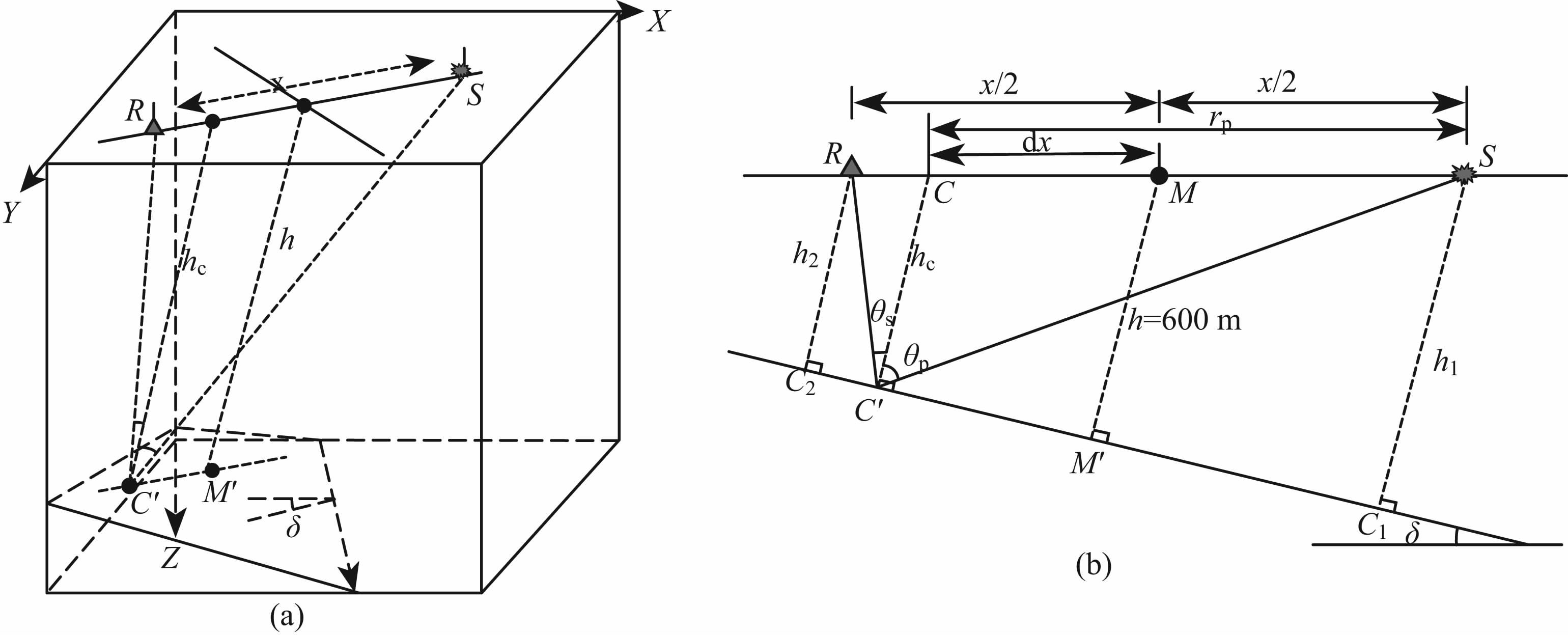
如图 1a所示,假设存在一个三维倾斜界面,界面倾角为δ.M为三维CMP 点,它到此界面的垂直距离为h,在界面上的投影点为M′.地表上以M点为中心点的炮点检波点对包含很多个方位,其中一条测线SR,S为炮点位置,R为检波点位置,SR长为x.此炮点检波点对在倾斜界面上的真正转换点为C′,CC′垂直于此界面与地表面相交于点C,长为hc.对路径面SRM′进行二维显示如图 1b.设SC长为rp,rp 与x/2之差的绝对值为dx,P 波入射角为θp,S波出射角为θs,界面视倾角为δ.为了便于分析,选取q来代表点M的离散度:
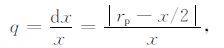
|
(1) |
|
图 1 三维倾斜界面PS波传播路径示意图 Fig. 1 The schematic of the spreading path for PS wave on three dimensional dipping interface |
点S、R在倾斜面的投影点为C1、C2,设SC1 =h2、SC2=h2.假设给定倾斜界面走向为λ=240°,界面倾角分别为δ=0°、10°、20°,h=600 m,炮检距分别为x=100、200、300、400、500、600m,纵横波速度比分别为γ=2.0、3.0,纵波速度α=2500m/s.观察式(1),若想得到q,则必须求得rp,也就是要找准hc的长度.PS波反射转换满足Snell定律:
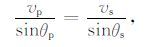
|
(2) |
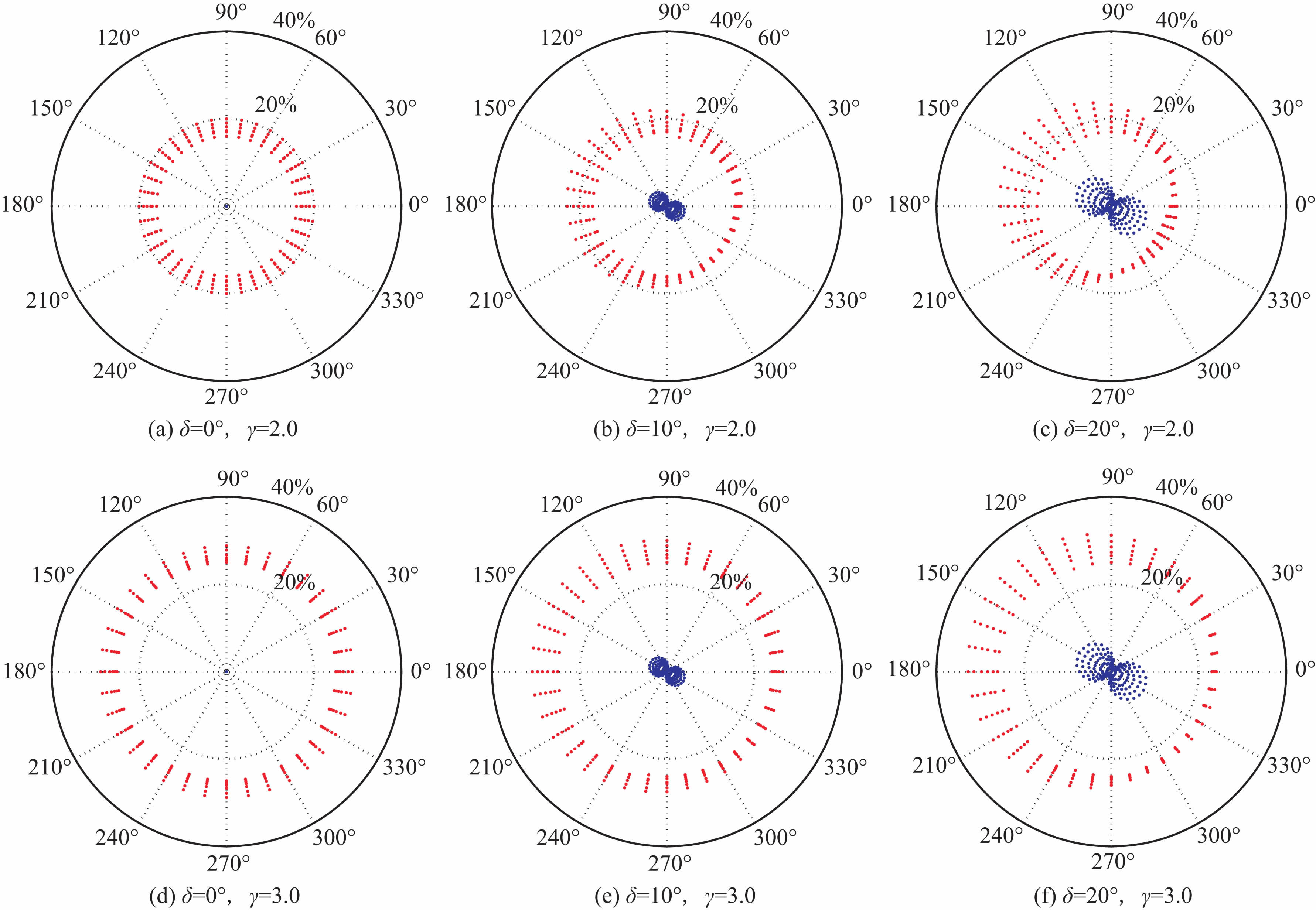
应用图中三角函数关系,采取迭代的方法,使hc 从h1 扫描到h2,找得一点C′满足式(2)的Snell定律,从而取定rp 的长度,求得离散度q.现以M为CMP点,10°为一个间隔,抽取圆周上36 个方位的CMP道集,每个方位上被抽出6 个记录道,按照上述方法,分别计算它们的q值.图 2为极坐标显示的计算结果,原点位置可看成CMP 点M,红色点代表转换点C的离散度q,为了便于与P波对比,同时计算了P波在不同界面倾角时的反射点离散度,即图 2 中蓝色点.
|
图 2 三维PS波CMP转换点、P波CMP反射点离散计算结果 Fig. 2 The discrete results of conversion-point using CMP method of three dimensional PS wave |
原点为CMP点;红色点为转换点C的离散程度q,蓝色点为P波反射点的离散度,道集分布在圆周上的36个方位,每个方位有6个记录道;PS波的dx最大分别为:(1)dxmax=120 m;(2)dxmax=139 m;(3)dxmax=157m;(4)dxmax=173m;(5)dxmax=187m;(6)dxmax=200 m;P 波的dx最大分别为:dxmax=0m、26m、51m.
由图 2可知,影响PS波CMP 转换点离散的因素有三个:偏移距x、纵横波速比γ 和界面倾角δ.观看图 2中的6个结果图可知,随着x值的增大,q值普遍增大.分别比较图 2 中a、b、c和d、e、f可知,δ值不变,γ 值由2.0增大到3.0后,各个方位上转换点离散程度明显增大.比较图 2 中a、b、c或d、e、f可知,γ 值不变,δ 值由0°增大到10°、20°后,q值随着δ 值的增大在圆周上的分布由中心对称变为以倾向方位为对称轴对称,但是沿走向方位成不对称现象,并且不对称性逐渐增强.这种不对称性也体现了q值具有不连续性:(1)在x不变的情况下,q值在测线方位为330°(与倾向方位一致)时最小,随着测线方位向150°(与倾向方位相反)方位移动,q值逐渐增大,直到150°方位时q值达到最大;(2)在x变化的情况下,图 2c显示q值在测线方位为330°时随着x的增大而减小,在测线方位为150°时,q值随着x的增大而增大,并且在x最大时q值也达到最大.与PS波相比,P 波CMP 反射点离散的因素只有界面倾角δ 和偏移距x,其离散现象整体明显降低.与PS波类似,P波的q值随着x的增大而增大.δ 等于0°时(图 2a、d),P 波无离散现象,CMP 道集为共反射点道集,δ 值由0°增大到10°、20°时,q值逐渐增大,但与PS波不同的是,q值在圆周上的分布始终成中心对称,且离散度也小很多.所以,P 波的离散现象对CMP 道集同相轴的连续性影响不大.在小倾角进行反射时,P波CMP叠加成像结果基本能反映地下构造信息.
通过上述三维PS 波CMP 转换点离散程度分析,可以总结出:γ 值影响的是PS波CMP转换点在不同方位上的整体离散程度,γ 越大,离散度越大,表现在CMP道集中为同相轴整体向下偏移;δ 值影响的是PS波CMP转换点在圆周上的对称性,δ 越大,不对称性越强,表现在CMP 道集中为同相轴不连续;x值的影响是对PS波CMP 转换点离散进行加强,表现在CMP道集中为同相轴向下偏移更大、不连续也更严重.三维PS 波CMP 叠加成像方法,由于存在上述三个因素造成转换点离散,使得实际资料处理中所抽取CMP 道集的同相轴不连续,动校速度很难确定,同时转换点离散又增强了道集中静校因素的影响,最终导致其成像质量下降.
2.2 静校因素分析三维PS波CMP 叠加成像不好,其中一个重要因素是我们所采集的实际资料中一般会存在静校影响[15-17],而PS波CMP抽道集会增强这种静校因素的影响.静校影响越大,PS 波CMP 叠加成像质量越不好.下面针对三维倾斜界面,对比PS 波CMP方法和PS波倾角CCP 方法[10],分析并讨论这两种方法对PS波静校正的影响.
图 3为当纵横波速比较小时,二维水平界面PS波CMP道集和CCP道集的传播路径示意图.由图可知,PS波CMP 道集比PS波CCP 道集的转换点更加离散,导致上行S波在横向上跨度比较大.S波入射到速度横向变化的近地表地层后,使得检波器接收到不同S波的走时差异增大,从而增加了道集内S波静校正量差异,破坏了PS 波同相轴的连续性,表现为静校影响突出.如图 4 所示,当纵横波速度比增大时,根据Snell定律,下行P 波的入射角与上行S波的出射角之差增大,导致PS波CCP 上行S波路径及对应接收点位置更加集中,而PS 波CMP接收点位置不变.这意味着相对PS波CCP方法,PS波CMP方法的接收点位置在横向上跨度增大,导致静校影响也增大.

|
图 3 二维水平界面PS波CMP(a)和CCP(b)传播路径示意图(纵横波速比较小) Fig. 3 The schematic of the spreading path for PS wave using CMP (a) and CCP (b) methods on |

|
图 4 二维水平界面PS波CMP(a)和CCP(b)传播路径图(纵横波速比较大) Fig. 4 The schematic of the spreading path for PS wave using CMP (a) and CCP (b) methods on two dimensional horizontal interface (greater P-S velocity ratio) |
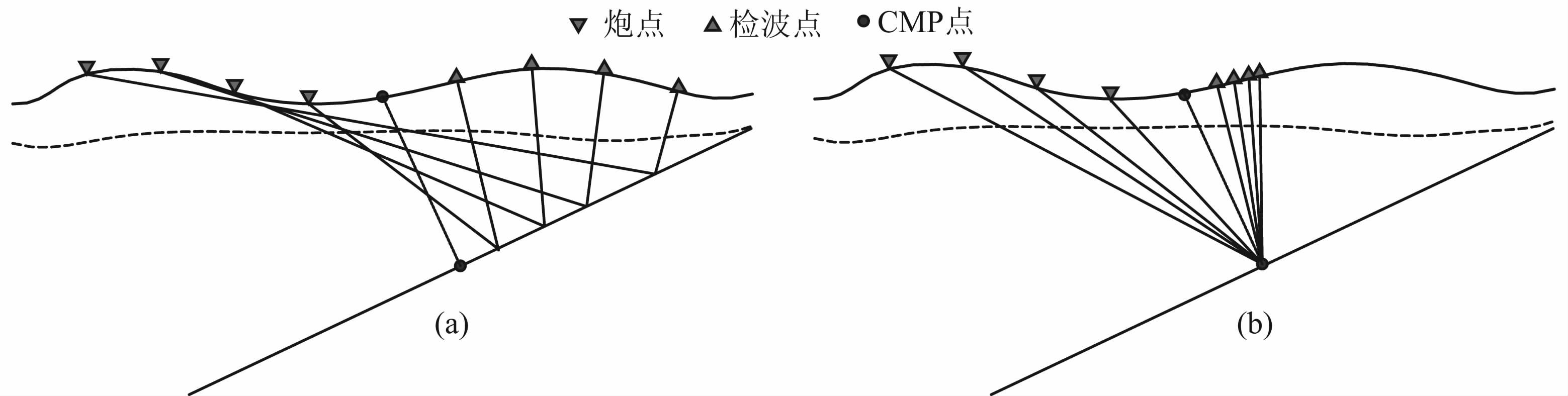
图 5中,当地下界面由水平变为倾斜时,将存在两个因素造成静校影响增大:一,转换点更加离散.由2.1分析可知,当界面存在倾角时,PS波CMP转换点的离散程度增大,相对转换点较集中的PS 波倾角CCP方法,其接收点位置横向跨度变大,导致道集中静校正量增大;二,上行S波在入射到近地表地层时角度差异增大.由图 5a可知,不同炮检距的上行S波入射到近地表地层时,其入射角度变化很大,而PS波倾角CCP 的S波入射到近地表地层的角度比较接近.这样就会导致S波在近地表地层内所经过的路程长短不一,对应走时差异增大,造成静校影响突出.当近地表地层速度更低时,上述两个因素导致的走时差更加明显.
|
图 5 二维倾斜界面PS波CMP(a)和倾角CCP(b)传播路径图 Fig. 5 The schematic of the spreading path for PS wave using CMP (a) and dipping CCP |
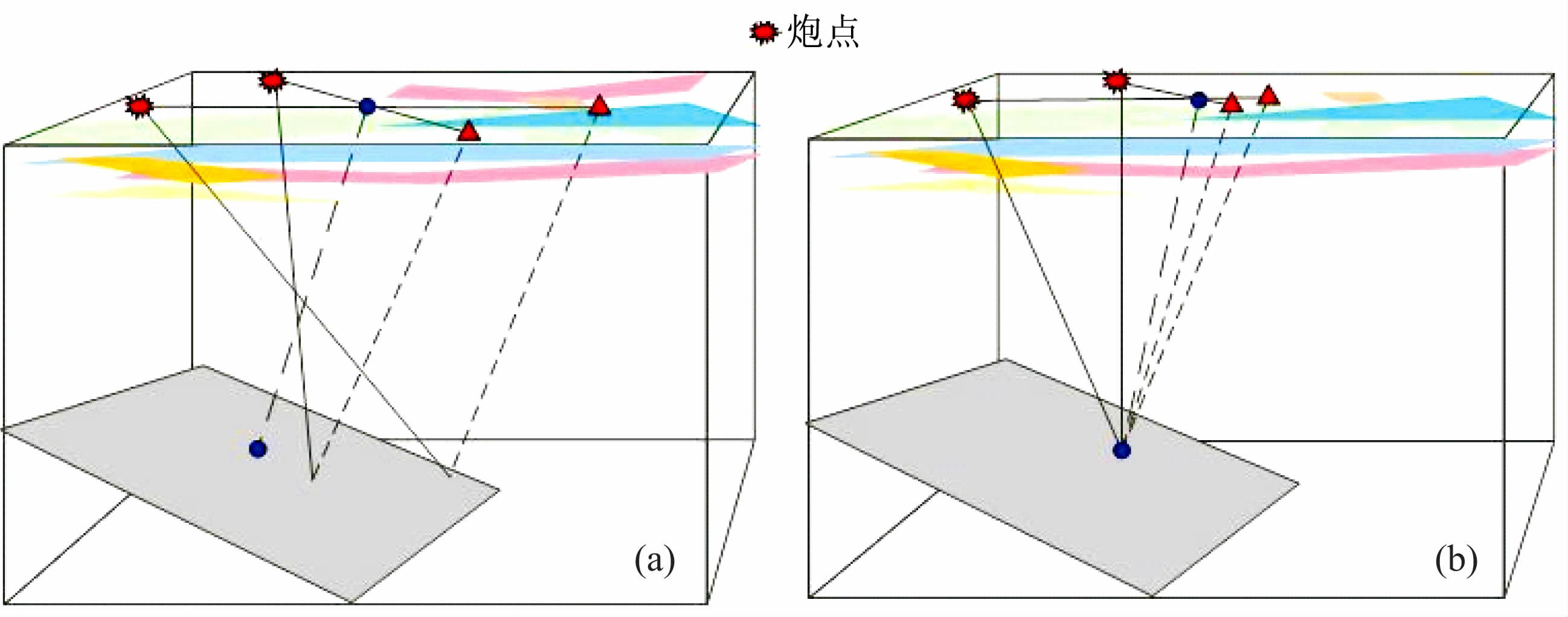
如图 6所示,当观测系统由二维转为三维时,PS波CMP的转换点在界面上的离散从单个方向扩展到圆周上的所有方向.由于三维近地表地层特点随不同方位一般会发生变化,加之PS波CMP 方法对应接收点在地表上的跨度较大、三维倾斜界面的出射S 波穿过近地表风化层时入射角变化也较大,从而导致不同方位组成的CMP 道集的同相轴连续性变差,叠加成像质量降低.而PS波倾角CCP方法相应接收点在地表上位置比较集中,使得从各个方向反射上来的S波经过相似的浅层静校影响,倾角CCP 道集同相轴的连续性相对较强,三维PS波倾角CCP成像质量也较好.
|
图 6 三维倾斜界面PS波CMP(a)和倾角CCP(b)传播路径示意图 Fig. 6 The schematic of the spreading path for PS wave using CMP (a) and dipping CCP (b) methods on three dimensional dipping interface |
无论是P波处理还是PS 波处理,速度分析无疑是地震勘探数据处理流程中一个至关重要的处理环节[18].动校速度的准确度直接关系到地震波叠后成像质量的好坏.2.1 节中讨论了影响PS 波CMP转换点离散的因素,得知反射界面倾角δ 值会引起CMP道集的同相轴不连续.2.2 节中讨论PS 波CMP方法会增大道集内静校正量差异,同相轴的连续性因此受到破坏.以上因素造成同相轴的连续性较差,将增加实际资料处理中速度分析的难度.
由于PS波反射路径不对称,即使是水平界面,其时距曲线也不符合双曲规律.但是在近炮检距情况下,PS波时距曲线方程可近似写成双曲线形式.Tsvankin和Grechka[11]通过射线参数给出偏移距x和时间t的关系式,没有直接给出二者的明确关系.其动校速度V也通过射线参数来表示,在三维倾斜界面条件下,无法直接分析动校速度V随倾角δ、倾向φ、测线方位φ 变化的情况.对于三维倾斜界面PS波CMP道集,蔡明刚等[13]给出如下近炮检距的时距方程:
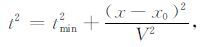
|
(3) |
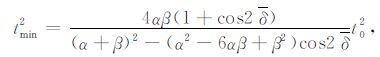
|
(4) |
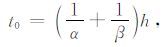
|
(5) |
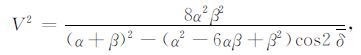
|
(6) |
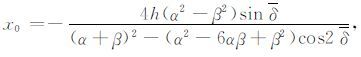
|
(7) |
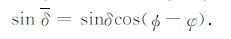
|
(8) |
其中t为PS波走时;t0 为PS波双程自激自收时间;tmin为PS 波到时最小值,它小于或等于t0;h为CMP 点到三维倾斜界面的垂直距离;α 为纵波速度,β 为横波速度;V为PS波动校速度,为包含纵波速度和横波速度的综合速度;x为炮点到接收点之间的距离;x0 为PS波时距曲线顶点的水平位置;δ 为界面的视倾角;δ、φ、φ 分别为界面倾角、倾向和测线方位.
当纵横波速度相等即α =β 时,由上式可得
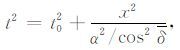
|
(9) |
其中V2 =α2/cos2δ,此为传统倾斜界面P波NMO速度[19].当倾角δ=0°时,反射界面为水平界面.由上式可得
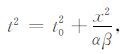
|
(10) |
此为大家所熟知的水平界面PS 波时距关系,其中V2 =αβ.观察式(3)可知,tmin并不一定等于t0,而是随测线方位φ 的变化而变化.由式(5)、(6)可知,V、x0 也与φ 有关.假设界面倾角δ=30°,界面走向φ=60°,纵波速度α=2500m/s,横波β=1250m/s,h=600m,则给定不同的测线方位φ,V、tmin、x0 的变化情况见表 1.
|
|
表 1 不同测线方位的V、tmin、x0 Table 1 V、tmin、x0of different azimuth |
同一个PS 波CMP 道集在不同测线方位所对应的V、tmin、x0 都有所不同,其最大、最小值之差分别为233m/s、15 ms、288 m,x0 变化最剧烈.由于三个变量都在随测线方位变化,所以在实际3D3C资料处理中很难确定其准确值,导致CMP 道集中同相轴很难校平.三个变量相互制约,使得PS 波CMP动校叠加过程非常复杂,导致三维倾斜界面PS波CMP 叠加成像不理想.而在水平界面反射时,由于动校速度V=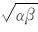
在某些实际资料处理中,由于观测系统的不同,面波也可造成三维PS 波CMP 叠加成像质量不理想.例如某三维勘探区观测系统针对P 波CMP 设计,因为横波速度较纵波速度低,所以面波对PS波的影响要比P波的影响大.对于某些特定反射点来说,由于PS波倾角CCP 方法在抽道集过程中炮距往往大于检波点距,它可以将受面波干扰较小的较大炮检距(对应炮距较大)记录道抽取出来,而CMP方法由于受炮距等于检波点距的约束,只能抽取受面波干扰较大的较小炮检距(对应炮距也较小)记录道.这样,PS波倾角CCP 道集由于存在较大炮检距记录,在叠加时提高了信噪比,从而使得成像质量也较好;而CMP却由于抽取记录的炮检距比较小,在叠加时降低了信噪比,从而导致最后的成像质量也降低.
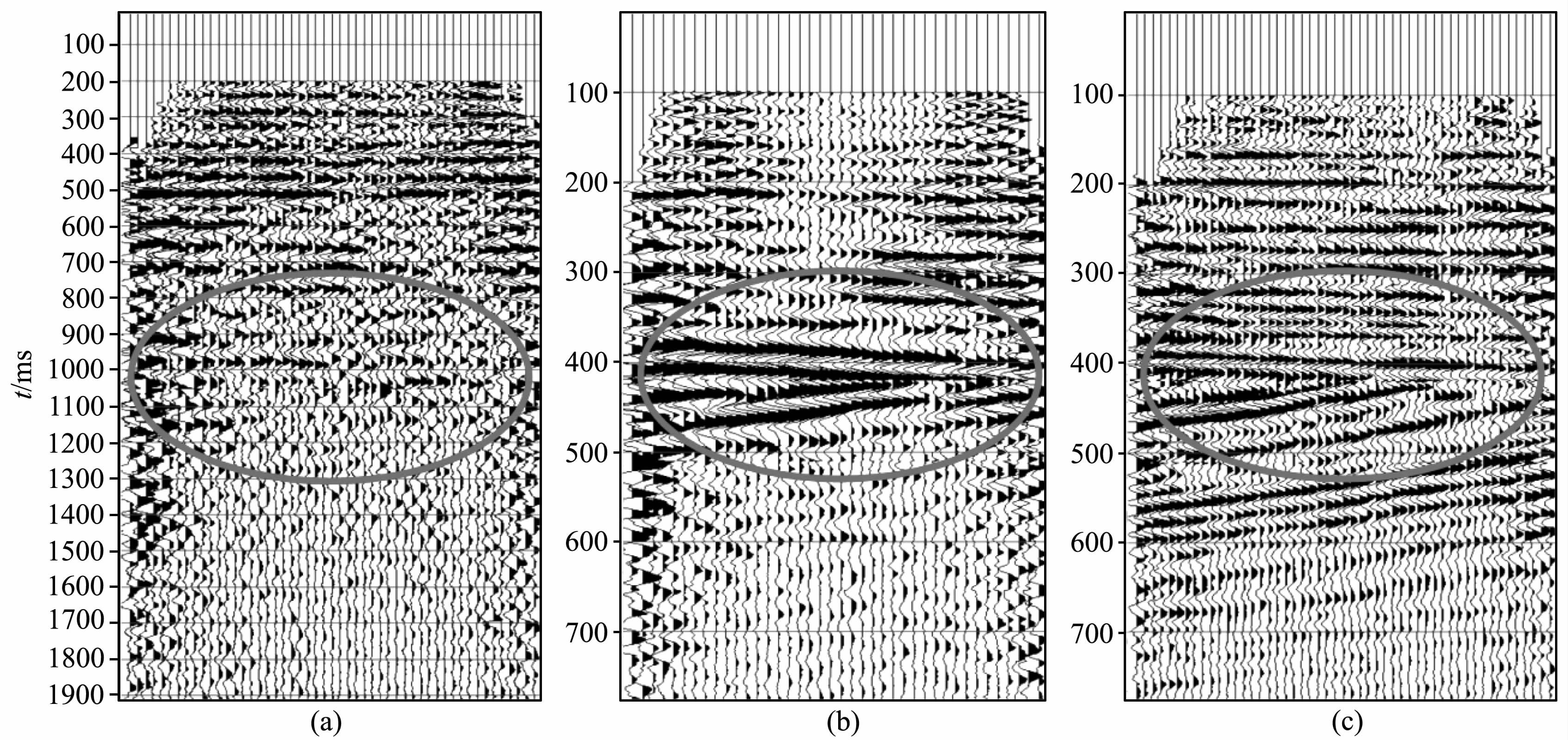
3 不同方法实际资料处理结果对比以某煤区3D3C 实际资料为例,其观测系统依据共中心点方法设计.对此区原始炮集R分量上的PS波分别进行CMP抽道集和倾角CCP抽道集,并对CMP道集采用常规速度分析方法得到叠加成像如图 7a.图 7b为PS波倾角CCP 的初步叠加结果,图 7c为对应的P波叠加剖面.观察可知,PS波倾角CCP的叠加剖面与P波的叠加剖面层位对应较好,反之,PS波CMP的叠加剖面的层位很难与P 波叠加剖面对应.并且PS波倾角CCP 叠加剖面在深部的倾斜层区域叠加成像信噪比很高,而PS波CMP的叠加剖面对应的位置基本没有叠加波组出现.之所以PS波CMP成像质量不好,是因为存在第二节中分析的转换点离散、静校正量较大、动校速度确定不准确和面波影响等四个重要因素的影响.
|
图 7 PS波CMP(a)、PS倾角CCP(b)、P波CMP叠加剖面对比(c) Fig. 7 A comparison of PS wave CMP stack section (a),dipping CCP stack section (b) and P wave CMP stack section (c) |
三维倾斜界面PS波CMP 叠加成像方法,虽然抽道集简单,无需预知纵横波速度比等参数,但实际资料处理结果往往不尽如人意.经过上述讨论得出其原因主要有三个:第一,转换点离散.同一倾斜界面不同方位转换点的离散度不一致,且离散度随着纵横波速度、偏移距和倾角的增大而增大;第二,静校影响突出.由于此方法接收点横向跨度较大,尤其当纵横波速度比增大、反射界面由水平转为倾斜或观测系统由二维扩展到三维时,检波器接收到的上行S波走时差异更大,表现为更为严重的静校问题,从而导致此方法在实际资料处理时叠加成像质量差;第三,动校叠加过程非常复杂.由于三维倾斜界面PS波CMP 叠加成像中涉及到的三个变量(即V、tmin、x0)同时随测线方位发生变化,并且变化程度不等,相互制约,动校叠加后很难给出优质的成像结果.而水平界面反射时,以上三个变量均不随测线方位变化,动校速度较容易确定,动校叠加过程相对容易,叠加成像质量一般也较好.除了上述原因,当实际资料来自于特定的观测系统时,面波对CMP 道集信噪比的影响也很大,从而使最后的叠加成像质量降低.
综上所述,若应用PS波CMP 方法对3D3C 资料进行叠加成像,则应尽量减少以上因素的影响.可以尽量选取近炮检距、低纵横波速度比、倾角较小的实际资料来处理,或者可以选择本文中提到的转换点相对集中的PS波倾角CCP 方法来处理,叠加效果较好.除此以外,各向异性介质的运动学和动力学特征[20-22]也会影响到三维PS 波CMP 转换点的离散,将在后续工作中讨论各向异性对离散的影响.
| [1] | 赵邦六. 多分量地震勘探技术理论与实践. 北京: 石油工业出版社, 2007 : 95 -101. Zhao B L. The Theory and Applications of Multi-Component Seismic Exploration Techniques (in Chinese). Beijing: Petroulem Industry Press, 2007 : 95 -101. |
| [2] | 程冰洁, 唐建明, 徐天吉. 转换波3D3C地震勘探技术的研究现状及发展趋势. 石油天然气学报 (江汉石油学院学报) , 2008, 30(2): 235–238. Cheng B J, Tang J M, Xu T J. The present research situation of P-S converted wave and 3D3C seismic exploration techniques. Journal of Oil and Gas Technology (in Chinese) , 2008, 30(2): 235-238. |
| [3] | 彭苏萍, 霍全明, 勾精为, 等. 基于模型的3D3C采集设计与评价. 中国煤田地质 , 2002, 30(5): 51–54. Peng S P, Huo Q M, Gou J W, et al. Model-based 3D3C acquisition design and evaluation. Coal Geology of China (in Chinese) , 2002, 30(5): 51-54. |
| [4] | 杨德义, 彭苏萍. 多分量地震勘探技术的现状及进展. 中国煤田地质 , 2003, 15(1): 51–57. Yang D Y, Peng S P. Status and progress on the multicomponent seismic prospecting technology. Coal Geology of China (in Chinese) , 2003, 15(1): 51-57. |
| [5] | 姚陈, 于光明, 蔡明刚等. 倾角CDP和倾角CCP叠加. 中国地球物理第二十一届年会论文集, 2005. Yao C, Yu G M, Cai M G, et al. Dip CDP and dip CCP stack. The 21th Annual Conference of Chinese Geophysical Society Proceedings (in Chinese), 2005. |
| [6] | 姚陈. 地震三维矢量反射波场. 地球物理学进展 , 2006, 21(2): 430–439. Yao C. Three dimensional vector seismic reflection field. Progress in Geophysics (in Chinese) , 2006, 21(2): 430-439. |
| [7] | 傅旦丹. 海上多分量地震资料处理技术研究. 中国海上油气 (地质) , 2003, 17(4): 259–263. Fu D D. The researches on processing techniques of offshore multicomponent seismic data. China Offshore Oil and Gas (Geology) (in Chinese) , 2003, 17(4): 259-263. |
| [8] | Schafer A W. A comparison of converted-wave binning methods using a synthetic model of the Highwood structure, Alberta. CREWES Research Report , 1992(4): 1-9. |
| [9] | Tessmer G, Behle A. Common reflection point data-stacking technique for converted waves. Geophysical Prospecting , 1988, 36(7): 661-688. |
| [10] | 于光明, 姚陈. 倾斜CCP道集抽取方法及影响因素分析. 煤田地质与勘探 , 2007, 35(4): 65–69. Yu G M, Yao C. The sorting method of CCP gathers and influencing factors in slanting interface. Coal Geology and Exploration (in Chinese) , 2007, 35(4): 65-69. |
| [11] | Tsvankin I, Grechka V. 3D description and inversion of reflection moveout of PS-waves in anisotropic media. Geophysical Prospecting , 2002, 50(3): 301-316. DOI:10.1046/j.1365-2478.2002.00319.x |
| [12] | 黄中玉, 曲寿利, 王于静, 等. 三维多分量地震资料处理技术研究. 石油物探 , 2010, 49(2): 140–14. Huang Z Y, Qu S L, Wang Y J, et al. 3-D multi-component data processing technologies. Geophysical Prospecting for Petroleum (in Chinese) , 2010, 49(2): 140-14. |
| [13] | 蔡明刚, 姚陈, 王海宁. 三维倾斜界面PS转换波CMP道集时距及参数估计. 地球物理学报 , 2012, 55(7): 2432–2440. Cai M G, Yao C, Wang H N. Moveout and parameter estimation of converted waves at CMP gathers from 3D dipping interface. Chinese J. Geophys. (in Chinese) , 2012, 55(7): 2432-2440. |
| [14] | Chung W Y, Corrigan D. Gathering mode-converted shear waves: A model study. 55th SEG Mtg, Expanded Abstracts , 1985: 602-604. |
| [15] | Cary P W, Eaton D W S. A simple method for resolving large converted-wave (P-SV) statics. Geophysics , 1993, 58(3): 429-433. DOI:10.1190/1.1443426 |
| [16] | 刘洋, 魏修成. 转换波地震勘探的若干问题与对策. 勘探地球物理进展 , 2003, 26(4): 247–267. Liu Y, Wei X C. Some problems and strategy on converted wave seismic exploration. Progress in Exploration Geophysics (in Chinese) , 2003, 26(4): 247-267. |
| [17] | 罗英伟, 段卫星, 徐维秀, 等. 几种静校正方法的研究与比较. 油气地球物理 , 2010, 8(1): 34–39. Luo Y W, Duan W X, Xu W X, et al. The study and comprision of several static corrections. Petroleum Geophysics (in Chinese) , 2010, 8(1): 34-39. |
| [18] | Boehm G, Carcione J, Vesnaver A. Reflection tomography versus stacking velocity analysis. Journal of Applied Geophysics , 1996, 35(1): 1-13. DOI:10.1016/0926-9851(95)00025-9 |
| [19] | Levin F K. Apparent velocity from dipping interface reflection. Geophysics , 1971, 36(3): 510-516. DOI:10.1190/1.1440188 |
| [20] | 蔡晓刚, 陈晓非. 倾斜裂隙介质反透射系数研究. 地球物理学报 , 2009, 52(5): 1253–1262. Cai X G, Chen X F. Study on the reflection-transmission coefficients of elastic waves in the media with dipping fractures. Chinese J. Geophys. (in Chinese) , 2009, 52(5): 1253-1262. |
| [21] | 蔡晓刚, 姚陈, 陈晓非. 各向异性ATI介质剪切位错源地震矩张量. 地球物理学报 , 2011, 54(7): 1772–1782. Cai X G, Yao C, Chen X F. Seismic moment tensor in anisotropic ATI media: shear faulting. Chinese J. Geophys. (in Chinese) , 2011, 54(7): 1772-1782. |
| [22] | 蔡晓刚. 裂隙参数对衰减各向异性影响的数值模拟. 地震地质 , 2011, 33(3): 694–705. Cai X G. The effect of crack parameters on attenuation anisotropy: numerical modeling. Seismology and Geology (in Chinese) , 2011, 33(3): 694-705. |
 2012, Vol. 55
2012, Vol. 55


