2. 武汉大学卫星导航定位技术研究中心,武汉 430079
2. GNSS Research Center, Wuhan University, Wuhan 430079, China
地表形变是一种地壳表层发生位移的环境地质现象,可由火山运动、冰川漂移、地震活动、山体滑坡等自然因素或采矿和地下水开采等人为因素所引发,是城市和大型线性工程(如高速铁路、大跨度桥梁等)规划与建设中必须考虑的关键问题之一,因此,对地表形变进行有效而精确监测十分重要.目前,形变监测一方面使用大地测量途径,如精密水准或GPS测量等,另一方面使用新近发展起来的卫星合成孔径雷达差分干涉(DInSAR)遥感手段.前者存在监测效率低、空间分辨率低、劳动强度大和监测成本高等技术劣势,无法满足大范围形变监测的需求.后者具有空间分辨率高、监测效率高等技术优势[1-3],但易受大气延迟和时空失相关的负面影响[4-6],降低了其形变探测结果的精度和可靠性.针对常规DInSAR 应用的局限性,目前的研究已转移到基于SAR 影像时间序列探测区域地表形变的时空变化上来,其中最为典型的两种思路是:Ferretti等[7-8]率先提出的永久散射体干涉(PS)和Berardino等[9]提出的短基线子集(SBAS)干涉,已被广泛应用于城市沉降和地壳位移监测.在PS 和SBAS 算法的基础上,国内外相关学者对永久散射体雷达干涉(PSI)的数学模型和解算方法进行了改进和扩展[10-13],提高了形变探测的精度和可靠性.然而,这些已有研究大多使用单一卫星SAR (如ERS-1/2、ENVISAT ASAR、ALOSPALSAR 和TerraSAR-X 等)影像数据,通过DInSAR 或PSI提取沿雷达视线(LOS)方向的一维形变信息,无法得到三维位移信息[14],使得该技术在工程和大范围形变监测中的应用受到制约.
如何通过雷达干涉数据提取地表三维位移是当前亟待解决的一个问题.基于空间后方交会的思想,本文提出了基于多卫星平台PSI提取三维地表形变速度场的模型与算法.考虑到不同传感器对同一地区成像的时间差异性,我们仅针对线性形变分量(形变速度)展开分析.其核心思想是:首先针对每一卫星平台的SAR 影像时间序列进行PSI分析,并计算各地面目标沿LOS方向的位移速度值,然后依据各平台SAR 传感器的成像几何,建立LOS 向位移速度与地表三维位移速度的函数关系,并使用最小二乘方法解算各地面目标的三维位移速度分量.因多平台数据的引入,无需引入任何外部形变参考信息,便可以实现形变场的偏差校准和三维位移速度场的恢复.
为验证该模型与算法的有效性和可靠性,我们选取天津市西北部的城乡结合处作为测试区域,以2007-2010年所获取的39 幅TerraSAR-X 影像、23幅ENVISAT ASAR影像和16幅ALOSPALSAR影像作为数据源,使用Liu 等[6, 12-13]提出的PSI算法分别求解各类SAR 影像的LOS 向位移速度场,然后通过最小二乘估算各形变场的整体偏差和水平位移分量,并获得地表垂直位移速度场.为验证解算结果的精度,我们结合同期水准数据和已有GPS观测成果进行对比论证.研究结果表明:该算法能够对LOS向位移速度场的整体偏差进行有效校正,并且能够准确估算出水平位移分量,最终得到的垂直位移速度场具有毫米级的精度.
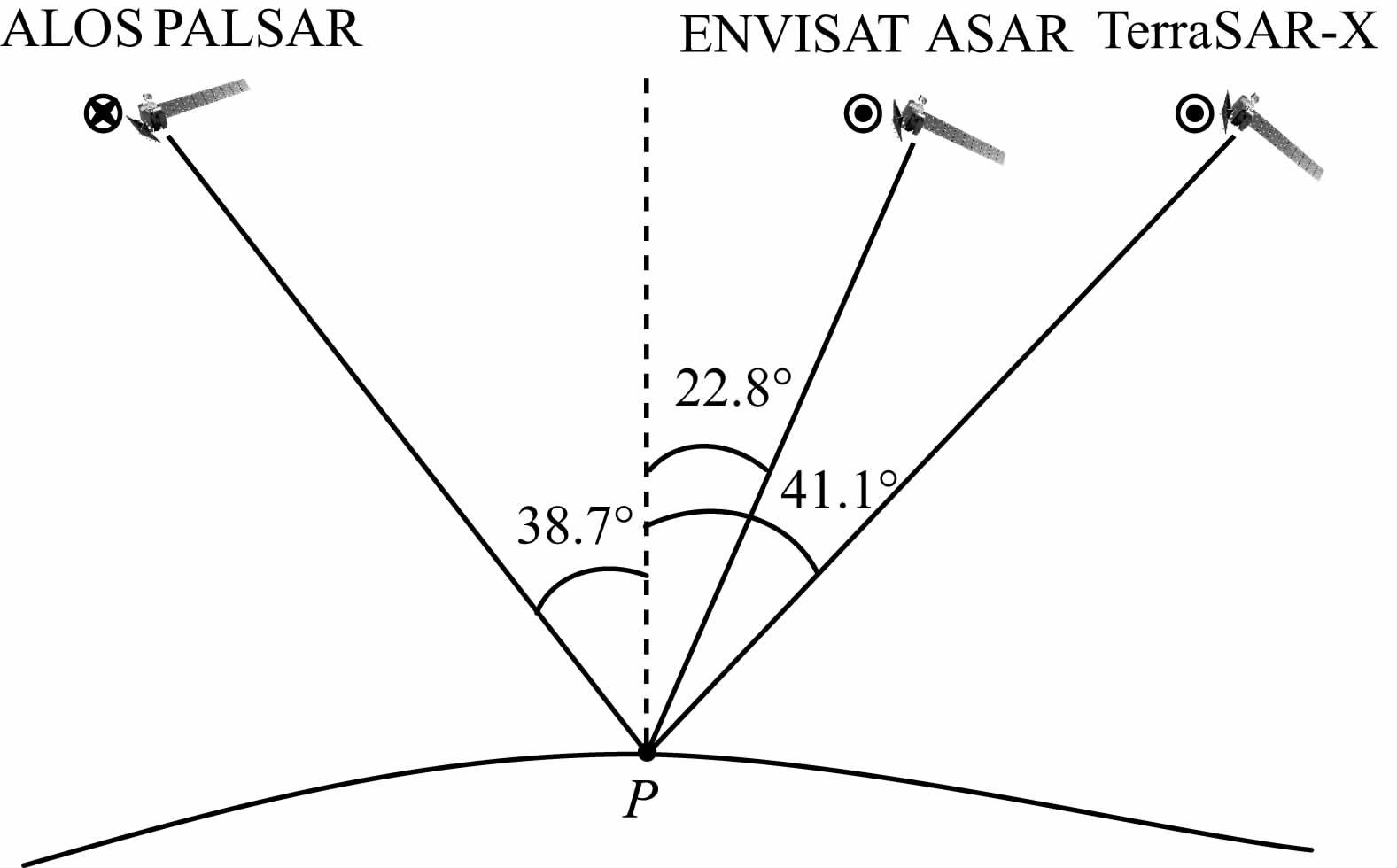
2 基于多平台PSI提取三维地表形变速度场合成孔径雷达采用侧视成像方式对地物的雷达后向散射信息进行记录,故DInSAR 探测结果为LOS向的一维形变量.为解决地表形变三维重建的问题,本文借鉴测量学中的空间后方交会思想,在传感器空间位置和侧视成像参数已知的条件下,使用多平台SAR 数据的LOS向PSI形变探测结果进行联合分析(如图 1所示),从而实现三维形变场的恢复与重建.需要说明的是,本文所提及的多平台数据源既可以是不同传感器所获取的SAR 影像,也可以是同一SAR 传感器沿升轨和降轨所获取的影像数据与其他传感器数据的组合.因不同SAR 传感器对同一地区成像的时间不一致,不同数据源所获得的LOS向形变时间序列不具可比性,因此,本文仅考虑形变速度场的重建与恢复问题.
|
图 1 多平台SAR成像的交会关系 Fig. 1 Imaging geometry of multi-platform SARs |
永久散射体(PS)雷达干涉分析主要基于两个出发点,一是使用由单一卫星平台SAR 传感器对监测区域所获取的影像时间序列进行形变信息提取,二是以监测区域内的所有PS 作为形变跟踪目标.PS目标一般为硬目标如混凝土建筑、裸露岩石、堤坝和铁路路基等,它们对入射雷达信号的反射特性不易随时间发生变化,故可以保证PS 目标的高信噪比相位观测,这有利于建模与形变信息的提取.关于使用单一卫星平台SAR 影像时间序列计算地表位移的问题,我们已提出永久散射体(PS)网络化时序差分雷达干涉的建模与解算方法,相应的详细描述可参见文献[12-15],为便于本文后续研究结果的理解,下面简要阐述其主要的数据处理策略.
实际上,我们可将地表形变过程理解为线性与非线性形变的叠加,因而可采取分级提取的策略.我们所提出的PS网络化时序差分雷达干涉的基本思想是:依据给定的时间基线和空基线阈值自由组合成多个短基线干涉对,并计算差分干涉图序列,筛选出监测区域内的天然PS目标,连接相邻的PS目标构成自由网络[12-13],据此可将PS 目标的线性与非线性形变时间序列提取出来.PS网络化时序差分雷达干涉的主要数据处理流程如图 2 所示,主要包括4个方面:(1)在获得监测区域多时相的SAR 影像后(设为N幅),首先要进行影像配准和PS 自动探测,并基于自由连接准则进行PS网络构建(参见文献[13]的图 1);(2)对符合干涉条件的所有干涉像对进行差分干涉处理,假设生成M幅干涉图,采用精密轨道数据和外部数字高程模型(DEM)去除参考椭球面和地形的相位贡献,从而获得M幅差分干涉图;(3)基于PS网络进行建模和模型参数估计,并进一步对网络进行最小二乘平差计算获得各PS点的LOS向线性形变速度和高程改正量;(4)在差分干涉图中扣除线性项得到残余差分干涉相位,然后利用非线性形变和大气相位在空间和时间尺度上具有不同频率结构的特点,对残余差分干涉相位进行信号分解并估计非线性形变.
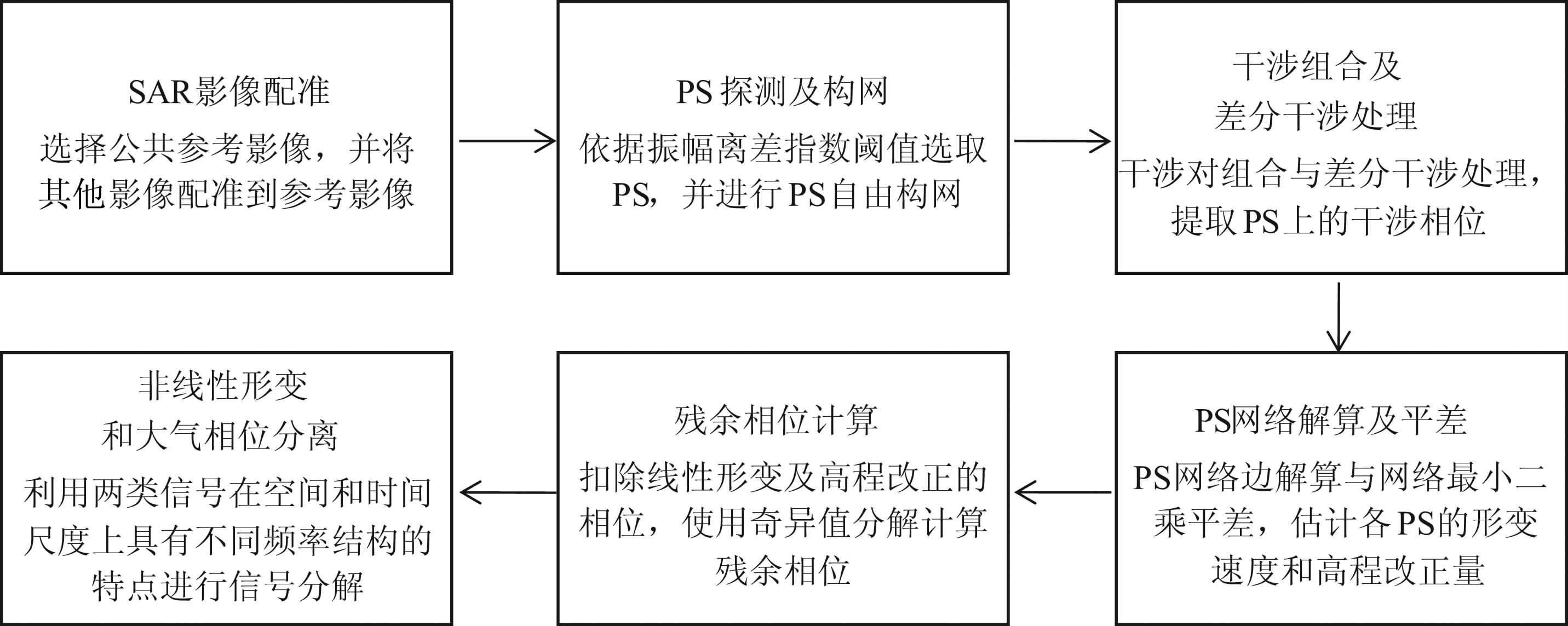
|
图 2 PS网络化时序差分雷达干涉数据处理流程 Fig. 2 Flowchart of data processing for PS-networking radar interferometry |
在LOS向线性形变速度估计方面,受大地测量网如三角网和差分GPS 的启示,我们针对各PS 网络边进行差分建模,并求解各网络边即相邻两PS目标间的LOS 向形变速度增量,然后以某一PS(一般假设其形变为0)为起算点进行带权最小二乘网平差,以求解所有PS目标的绝对形变速度.为了求解各网络边的形变速度增量,可将任一网络边相邻两PS的差分相位表达为形变速度增量、高程改正增量和雷达系统参数等的函数,这样可建立M个观测方程,然后依据Ferretti等[7]所提出的干涉相关系数最大化思想将这M个观测方程组合成一个目标函数,我们可在预先给定的解空间中搜索出一组解使得干涉相关系数达到最大值,此解即为所求的最佳形变速度增量和高程改正增量,此最大相关系数可作为随后网平差定权的依据[12-13].值得说明的是,这样的线性形变速度估计策略是出于两方面的考虑,一是通过构建PS观测网并引入邻域差分,可削弱具有空间自相关特性的大气延迟等因素对形变估计的影响,这类似于GPS 差分观点,二是通过目标函数优化途径直接确定线性形变速度增量,无须确定相位整周模糊度,从而可避免原始差分干涉图相位解缠的困难.本文不涉及非线性形变的分析,其关键模型与提取方法可参见文献[16-17].
依据上述流程可对不同卫星平台的SAR 影像时间序列分别进行差分干涉处理和PS 时序分析,这样可得到对应于不同平台的所有离散PS目标的LOS向年形变速度场.为便于联合不同LOS 向的多平台PSI形变速度观测结果进行三维重建,需保证PS目标的空间一致性,首先经投影计算将不同平台的形变速度场分别转换到相同的地图投影坐标系下,并且采用Kriging内插方法[18]计算规则格网化的形变速度.
2.2 三维形变速度的恢复与重建图 3显示了SAR 侧视成像几何(以升轨成像为例)及在三维坐标轴系下的角度参数,S为成像时刻卫星位置,P为PS目标,S和P的连线为雷达视线(LOS)方向,LOS向与垂直方向的夹角θ为雷达信号局部入射角,星下点轨迹是卫星轨道在水平面上的投影;φ 为卫星航向角;星下点O和目标点P的连线即为LOS向在水平面上的投影.
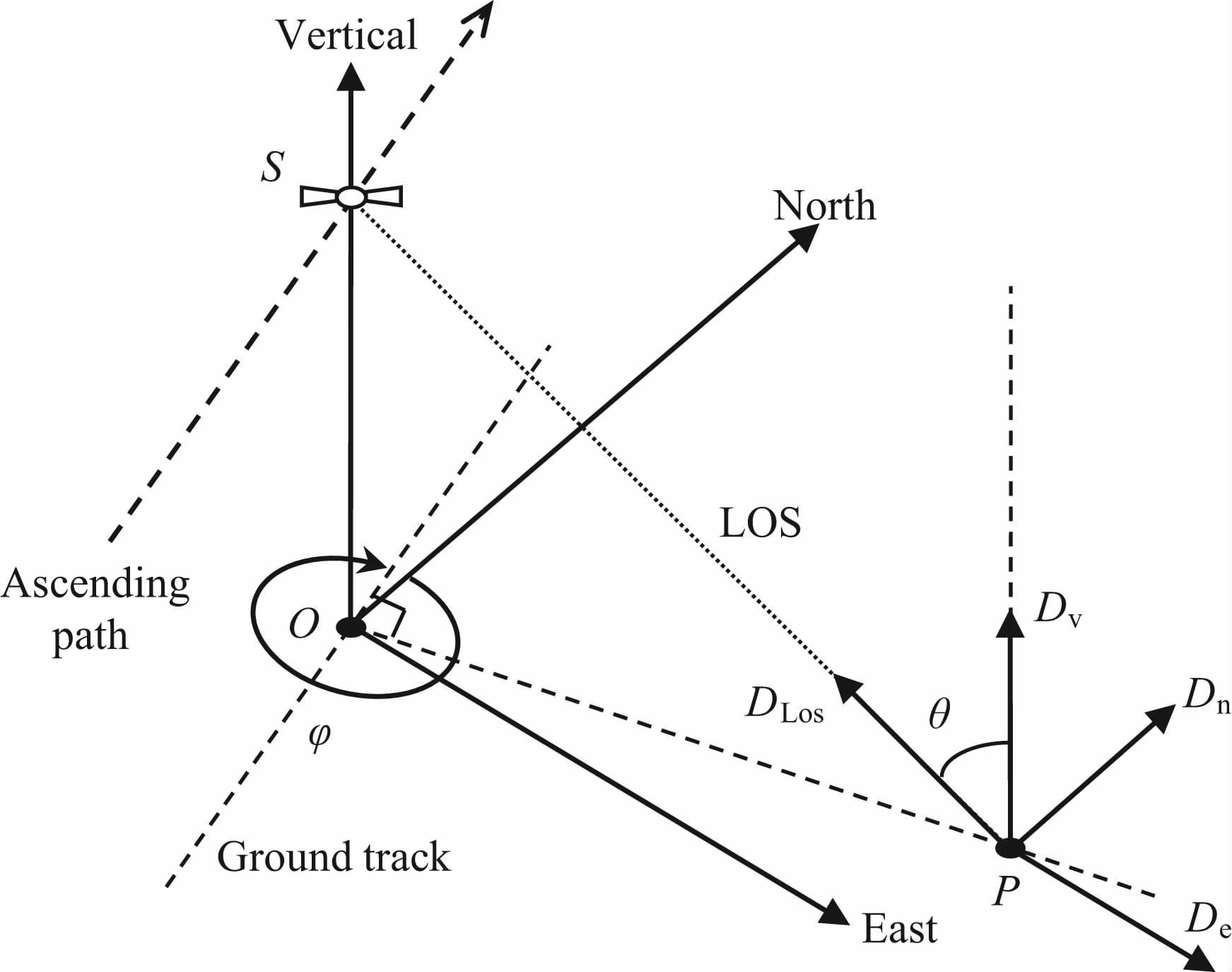
|
图 3 SAR 侧视成像几何及角度参数 Fig. 3 Side-looking geometry of a SAR sensor and angular parameters |
卫星平台的轨道参数是基于WGS84参考椭球框架下的球心地固坐标系,而SAR 影像成像范围内的地面目标可通过投影坐标转换至相同的坐标空间.据此,由传感器平台的侧视成像几何框架和目标点P的地面坐标可确立统一的参考坐标基准,在三维空间对观测目标的真实空间位移量进行量测.而在雷达干涉测量过程中,在LOS向获得的形变速度量测结果(以D表示)是地面目标点三维位移速度分量在LOS向上的投影之和,即:
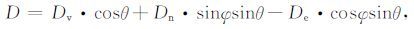
|
(1) |
式中,De
前已述及,通过PSI计算所得到的形变速度场是以一个选定的PS目标的形变速度作为起算数据的,在缺乏先验信息的情况下,一般假定此PS目标的形变速度为0,故整个监测区域的LOS向PSI形变速度R与真实的LOS向形变速度D存在系统偏差K,即D=R+K,式(1)可重写为
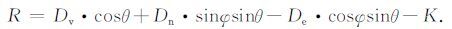
|
(2) |
对不同的卫星平台来说,雷达入射角θ 和卫星航向角φ 各不相同,对一种卫星平台来说,每一目标点的PSI形变速度R与真实的LOS向形变速度D之间的系统偏差K为常数.设有n个卫星平台的PSI数据可用于三维形变速度场的恢复,则可列出如下方程组:
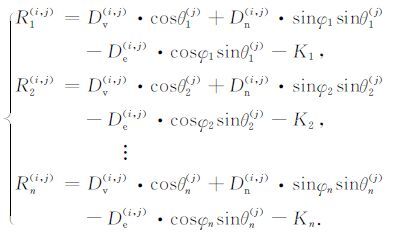
|
(3) |
式(3)中,(i,j)表示目标点在影像空间的行列号;Rn(i,j)表示第n种传感器在像元(i,j)处的LOS 向形变速度;θn(j)表示第n种传感器在像元(i,j)处的已知局部入射角,一般可以通过SAR 影像头文件参数内插得到(与所在列号j相关);φn表示第n种传感器的已知航向角,可当作常量处理.若选取监测区域内的m个目标进行分析,则如式(3)的观测方程总数为n×m,待求解的参数包括每一目标的三维位移速度分量(De(i,j) ,Dn(i,j) ,Dv(i,j) )和对应于各平台的系统偏差常数K1,K2,…,Kn,则待求解参数的总数为3m+n个.在使用足够多的监测目标的前提下,当且仅当平台数n≥4时,可保证这样的线性方程组完全可解.
如果监测区域相对较小(如10km×10km),且整个监测区域内的水平位移矢量较为一致(整体水平位移,相对变化较小),则不同地面目标之间的LOS向位移量差异主要由垂直向不均匀地表沉降所引起,在这种情况下,可将各地面目标的东西向位移速度分量De 和南北向位移速度分量Dn 作为常数来处理,则模型可简化为
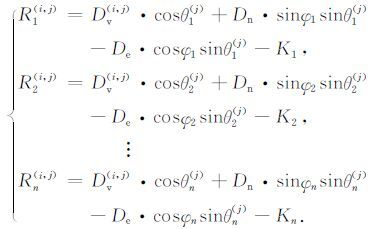
|
(4) |
若选取监测区域内的m个目标进行分析,则如式(3)的观测方程总数为n×m,待求解的参数包括常数项De 和Dn、各目标的Dv(i,j)以及对应于各平台的系统偏差常数K1,K2,…,Kn,则待求解参数的总数为m+n+2个,在n≥2的条件下,即可保证方程组有解.
为了确定地表三维位移速度及各平台PSI所对应的系统偏差常数,我们可以对监测区域内所有目标点如式(3)或式(4)所示的观测方程进行联合,采用最小二乘准则进行整体求解.以3 个卫星平台和式(4)简化模型为例,设地面目标行列总数分别为r和c(总数m=r×c),则所有观测方程的矩阵表达形式为
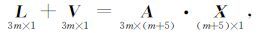
|
(5) |
其中,观测向量L、改正数向量V、未知向量X和系数矩阵A分别为
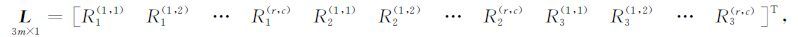
|
(6) |
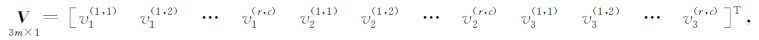
|
(7) |
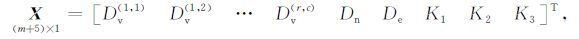
|
(8) |

|
(9) |
如果观测向量L服从正态分布,则未知向量的最优无偏估计可通过最小二乘方法解算得到,即:
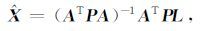
|
(10) |
式中,P为权矩阵(大小为3m×3m).设各观测量相互独立,则权矩阵非对角线元素均为0,对角线元素可由PSI网络平差解算过程所得到的LOS 向形变速度中误差确定[12-15],即每一观测值的权为相应形变速度中误差平方的倒数.
大量的模拟研究表明,如果不同卫星平台SAR传感器的侧视角和航向角较为接近时,法方程系数矩阵(ATPA)-1接近奇异,从而可导致最小二乘解算失败,故在选择平台数据时应尽量选择侧视角差异较大的不同平台SAR 数据,也应考虑升轨与降轨的组合,以增大航向角的差异.此外,卫星PSI对三维位移速度分量的敏感度存在差异,由式(2)求偏导并取绝对值可得到如下敏感度方程:
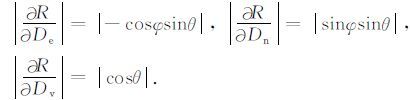
|
(11) |
因现有SAR 卫星的运行轨道一般为极地轨道,且与经线方向的夹角一般为10°左右,即卫星航向角φ约为170°(降轨)或350°(升轨),雷达侧视角θ 一般在20°至45°间变化(如图 1所示),将这些参数代入式(11)计算可知,卫星PSI对东西向、南北向和垂直向位移速度的敏感度区间分别为[0.34,0.70]、[0.06,0.12]和[0.71,0.94].显然,对垂直向位移速度的敏感度最高,对东西向位移速度的敏感度次之,对南北向位移速度的敏感度最低.我们可以看出,尽管联合多平台卫星PSI的观测量可以对三维位移速度进行重建与恢复,但因对南北向位移的敏感度最低,所恢复出的南北向位移速度的精度将会最低,而所恢复出的垂直向位移速度的精度将最高.
3 研究区域与卫星SAR 数据本研究的实验区域涉及天津市.作为华北平原的最大城市之一,天津市位于海河流域最下游,其所辖的94%范围为平原区域,因具有半干旱气候特征及其他自然条件的限制,天津地区的水资源较为缺乏,近年来,为了满足工农业发展的需要,地下水资源受到过量开采,致使许多地区出现了地表不均匀下沉的现象[19-21].为了控制市区的沉降速度,天津市政府已制定并实施了地下水控制开采的制度与措施,然而,城郊结合部及广大农村地区的地下水开采仍难以控制.已有常规研究表明[22],天津市区内的沉降速度呈逐渐降低的趋势,目前的沉降率为1~2cm/a,但郊区的沉降速度仍然偏大,已发现一些局部地区存在明显的沉降漏斗.此外,相关研究表明[23-27],华北平原相对于稳定的欧亚板块具有整体向南东东方向运动的趋势.因此,该研究区域存在水平和垂直方向的形变.
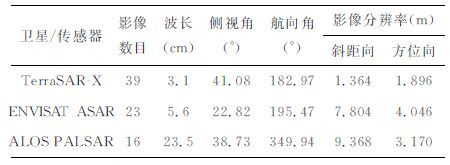
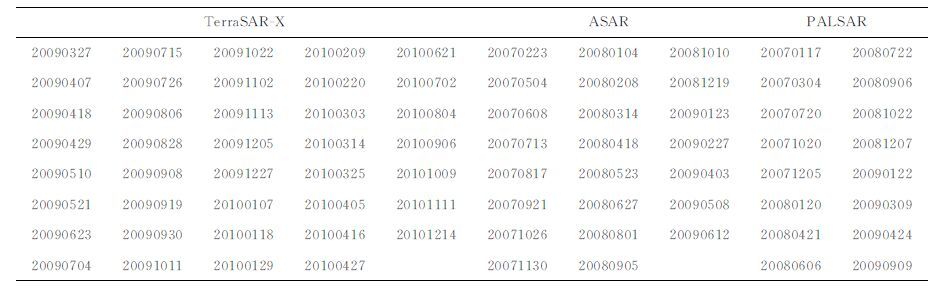
为验证本文所提出的基于多平台PSI提取三维地表形变速度场的模型与算法,我们选取天津市西北部的城乡结合处作为实验区域,使用2007-2010年所获取的39 幅X 波段TerraSAR-X (TSX)影像、23幅C 波段ENVISAT ASAR 影像和16 幅L波段ALOSPALSAR (PSAR)影像进行PSI分析,进而联合求解三维形变速度场,并使用地面水准实测数据与已有GPS分析结果[23]进行对比验证.表 1和表 2分别列出了这三种卫星平台SAR 传感器的成像基本参数和所有影像的获取时间,其中TSX 和ASAR 影像序列均为沿降轨获取,而PSAR 影像序列则为升轨获取,其构成的交会模式如图 1 所示,ASAR、TSX 和PSAR 的侧视角分别为22.82°、41.08°和38.73°,这些参数条件保证了足够大的侧视角差异和一定的航向角差异,为形变速度场的重建与恢复提供了有效的几何强度.此外,TSX 影像的空间分辨率优于2 m,重访周期在1 个月以内,ASAR 和PSAR 的空间分辨率相对较低,重访周期相对较长.
|
|
表 1 三种卫星平台SAR传感器的成像基本参数 Table 1 Basic imaging parameters of three types of spaceborne SAR sensors |
|
|
表 2 三类SAR影像的成像时间 Table 2 Generation dates of three types of SAR images |
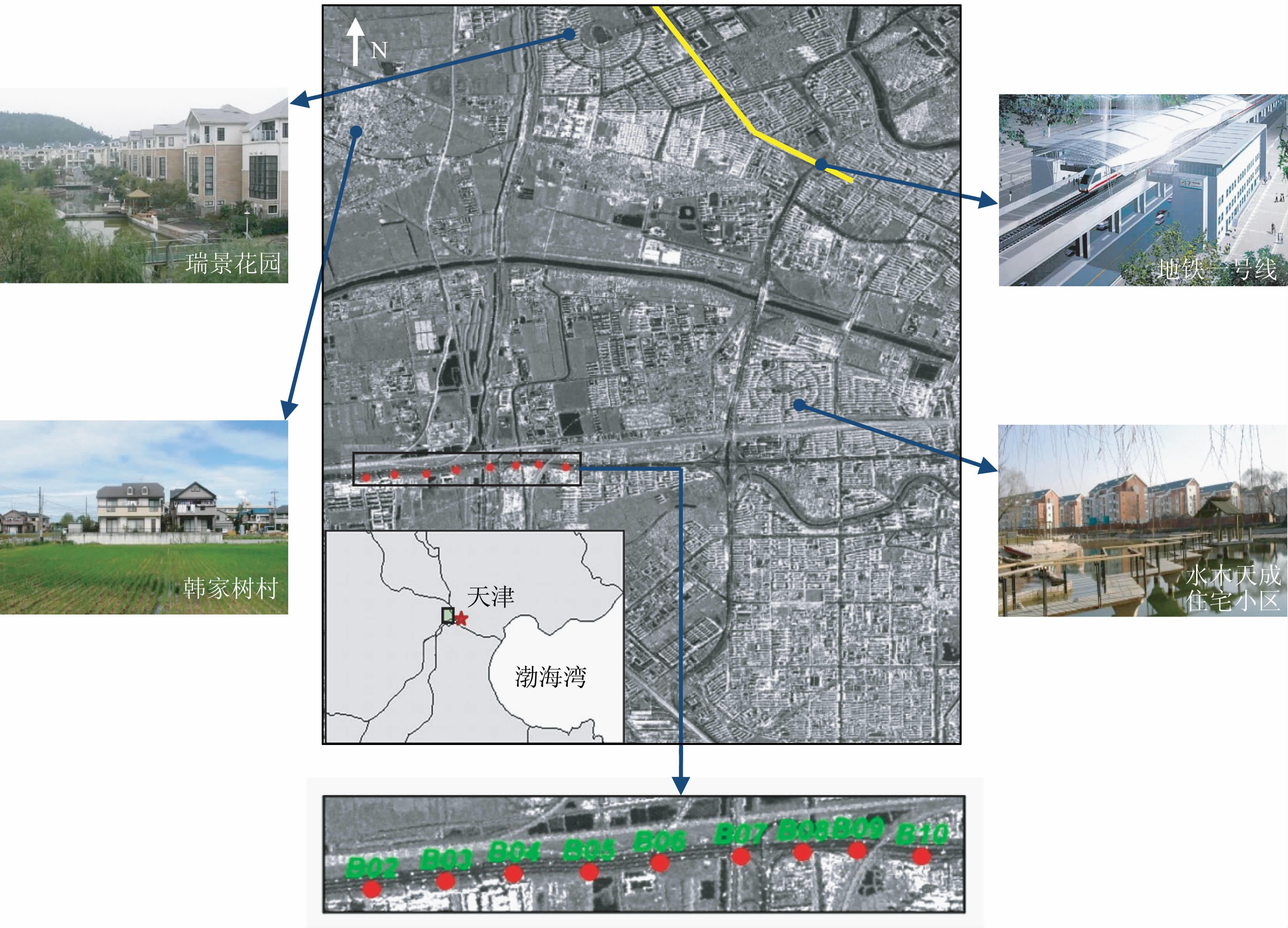
图 4显示了实验区域即天津市西北部城乡结合处的TSX 振幅影像及用于验证的水准点分布情况,该区域东西向跨度为7.8km,南北向跨度为9.1km.该研究区域靠近渤海湾,平均海拔高为2~3 m,属海河流域冲积平原,存在较厚的淤积层,地质水文条件较为复杂[20-21].该区域多为住宅社区和新兴工业园区,图 4中也给出了现场实拍的典型建筑和地铁站的图片,天津市的建筑物顶面一般为尖顶,采用陶制瓦或金属制瓦覆盖,这样的房顶可被认为是优良的永久散射体,能维持长时间稳定的雷达后向散射特性.此外,该研究区域内的房顶高度较为一致,可大大降低雷达成像几何畸变(如阴影、叠掩和透视收缩等)的机会,这样可维持较好的干涉空间相关性.尽管实验区域地势较为平坦,我们仍使用分辨率为3弧秒的SRTM 数字高程模型作为差分干涉处理所需的外部数据.为验证算法的可靠性,我们在2009年4月至2010年4月间对沿西青公路布设的9个水准点(编号为B02-B10,如图 4所示)进行了三期观测,这些观测数据将用于对比验证.
|
图 4 实验区域与水准点分布 Fig. 4 Testing area and distribution of leveling points |
依据第2 节所陈述的建模方法与数据处理策略,我们对表 2 所列出的三种卫星平台所获取的SAR 影像时间序列进行处理.首先依据2.1节所述的过程对39 幅TSX 影像、23 幅ASAR 影像和16幅PSAR 影像分别进行单平台PSI处理,这主要包括干涉组合与差分干涉处理、PS 探测与构网、各网络边LOS向形变速度增量估计、网络最小二乘平差、以及投影转换与Kriging内插等数据处理过程,这样可得到对应于三种卫星平台不同LOS 向的形变速度场;然后依据2.2 节所述的模型与算法对三种PSI形变速度场进行联合求解,从而完成各形变场的偏差校准与三维形变速度的重建与恢复;最后使用精密水准数据和已有GPS分析结果作为参照,分析与验证三维形变速度结果的精度.
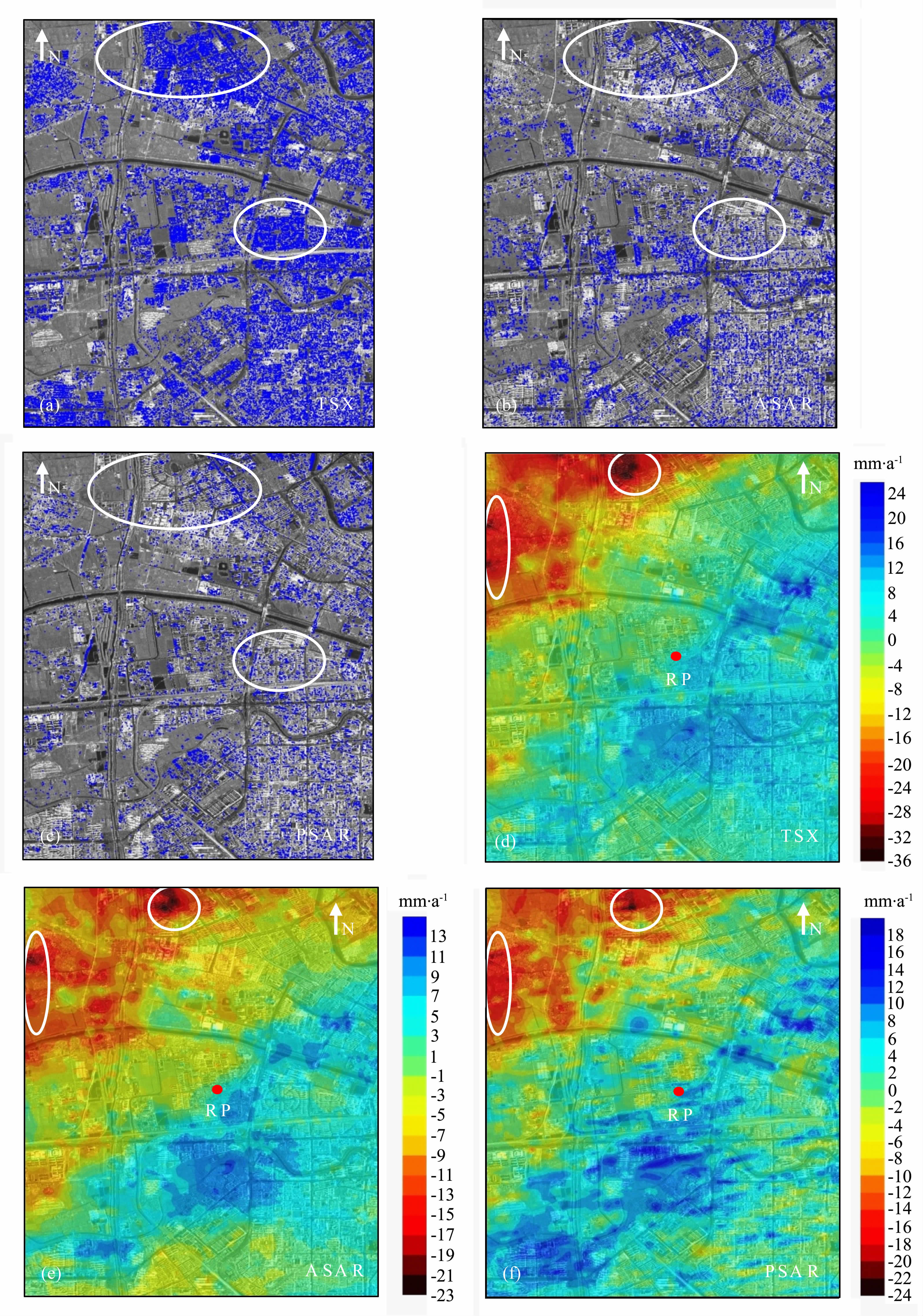
4.1 PS分布及PSI形变速度场图 5显示了基于不同卫星平台SAR 数据计算得到的研究区域内PS分布以及LOS向形变速度分布.图 5a-5c 显示了分别对应于TSX、ASAR 和PSAR 的PS分布情况.很明显,影像空间分辨率越高,PS目标密度越高,分布越均匀,基于高分辨率TSX 影像探测出的PS 点密度达到4500 个/km2,而基于ASAR 和PSAR 影像探测出的PS点密度约为500个/km2.通过PS 数目对比可知,基于TSX影像共探测出416182 个PS 点,而因ASAR 和PSAR 影像的空间分辨率相对较低,分别仅获得36427和35142 个PS 点.基于不同类别的SAR 影像探测出的PS 目标的空间分布也存在较大差异,例如,图 4中所标示的瑞景花园及水木天成住宅小区周边的PS 目标分布格局和密度存在明显的差异,这表明侧视角、航向角以及时空分辨率的不同对PS目标的分布格局会造成一定的影响.显然,建筑密集区域PS密度非常高,但是农田区域的PS目标相对稀少,水域没有任何PS点.这是因为城市区域含有高密度的天然和人工硬目标(主要为建筑物),在数月乃至数年内仍能维持较稳定的雷达后向散射特性;农田区域的表面存在明显的季节性变化,例如,农田的翻耕、土壤含水量的变化、农作物生长及其叶片随风摆动等均可能引起入射雷达信号的后向散射特性随时间发生变化,即引起相位测量的时间失相关;水域的入射雷达信号会发生镜面反射,因而无法检测出任何PS目标.值得说明的是,天津地铁1号线在图 4中标示出的部分为轻轨式铁路桥构筑形式,对雷达波具有稳定的后向散射特性,故在该段沿线探测出了呈线状分布的大量PS 点,这说明应用PSI可对公路、桥梁等大型线状地物目标进行形变探测.
|
图 5 三类SAR影像序列分别进行PSI分析得到的PS分布(a-c)及LOS向形变速度分布(d-f) Fig. 5 Distribution of PSs (a -c) and LOS deformation rates (d -f) derived by PSI analysis with the use of three types of SAR images |
为便于对比分析,三种平台的PSI计算采用了相同的参考点(即区域中心所标示出的RP 点),并给定该点的LOS形变速度为0.图 5d-5f显示了经PSI解算得到的分别对应于TSX、ASAR 和PSAR的三组LOS 向形变速度场,均已由投影转换和Kriging内插取样到相同的坐标格网上,格网间隔为15m,共有522×605个格网点.对比三组形变速度场可知,使用不同SAR 数据计算得到的LOS 向形变速度量级和空间分布存在较大的差异,TSX 形变速度场在-36~24mm/a间变化,最大相对形变差异为60mm/a;ASAR形变速度场在-23~13mm/a间变化,最大相对形变差异为36mm/a;PSAR 形变速度场在-24~18mm/a间变化,最大相对形变差异为42mm/a.然而,三个形变速度场所反映的地表位移总体趋势具有一致性,即西北部区域呈现沿LOS向远离卫星运动,而南部区域呈现朝向卫星运动.已有研究结果表明[20-21, 23],这种地表位移可归结为两类因素所引起,一是因构造运动主要导致地壳水平位移,二是因地下水的过量开采导致不均匀地面沉降.然而,不同卫星SAR 成像传感器的观测方向、侧视角和航向角存在明显差异,也就是LOS向的姿态各不相同,对同一地面目标来说,其三维位移投影到不同LOS向的一维位移量必然不一致,因此图 5d-5f所呈现的位移速度场在量级和空间分布上存在明显的差异.值得注意的是,三组形变速度场均显示:在北部瑞景花园和西北部韩家树村周边的形变速度在空间尺度上变化较快,且量级较大,而靠近东侧和东南部的天津主城区部分的形变速度呈低频趋势,且量级相对较小,这可以由郊区地下水开采量比城区更大来解释.
4.2 三维形变速度场及分析考虑到华北平原相对于稳定的欧亚板块具有整体向南东东方向运动的趋势[23-27],而且实验区域的覆盖范围相对较小,其内部地质结构相对稳定,因而可合理地假定整个研究区域的地壳水平位移表现为刚体运动,而垂直位移主要是因地下水过量抽取所导致的沉降所引发,因此我们将研究区域内的南北向水平位移分量Dn 和东西向水平位移分量De 作为待求解的常量来处理,在此基础上,根据式(5)-(10),我们利用研究区域内所有格网点的三类LOS向形变速度数据(如图 5所示)进行整体最小二乘解算,表 3 列出了计算所得到的对应于TSX、ASAR和PSAR 三类速度场的整体偏差常数,分别为-7.1、-15.8和-28.6mm/a,而得出的整体东向水平位移分量为16.5mm/a,南向水平位移分量为6.8mm/a.
|
|
表 3 三类LOS向形变速度场的整体偏差 Table 3 Global offsets of three LOS deformation-rate fields |
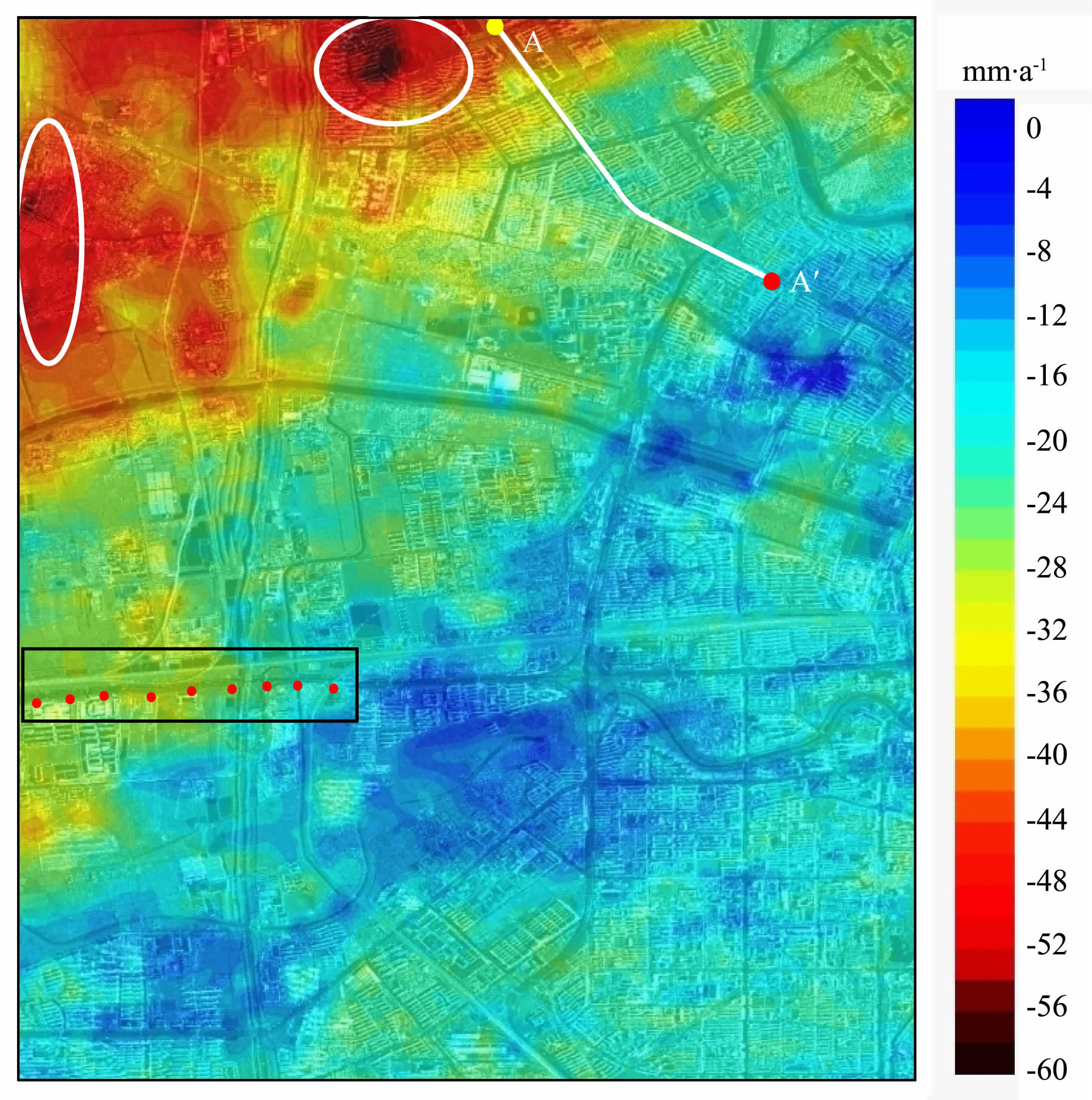
图 6显示了所有网格点的垂直位移速度,均表现为沉降,其速度在0~60 mm/a间变化.很明显,总体沉降趋势表现为:越远离天津主城区域,沉降速度较高,越靠近城市中心,沉降速度越低.以瑞景花园和韩家树村为中心的西北部城郊结合部表现出明显的不均匀沉降,且沉降速度较大,瑞景花园为58.6mm/a,韩家树村为55.7mm/a.而东侧及东南部的天津主城区相对稳定,沉降速度低于25mm/a.这充分表明,主城区的地下水开采控制较好,而城乡结合部的地下水开采仍没有得到有效控制.
|
图 6 实验区域沉降速度场 Fig. 6 Subsidence-rate field of the testing area |
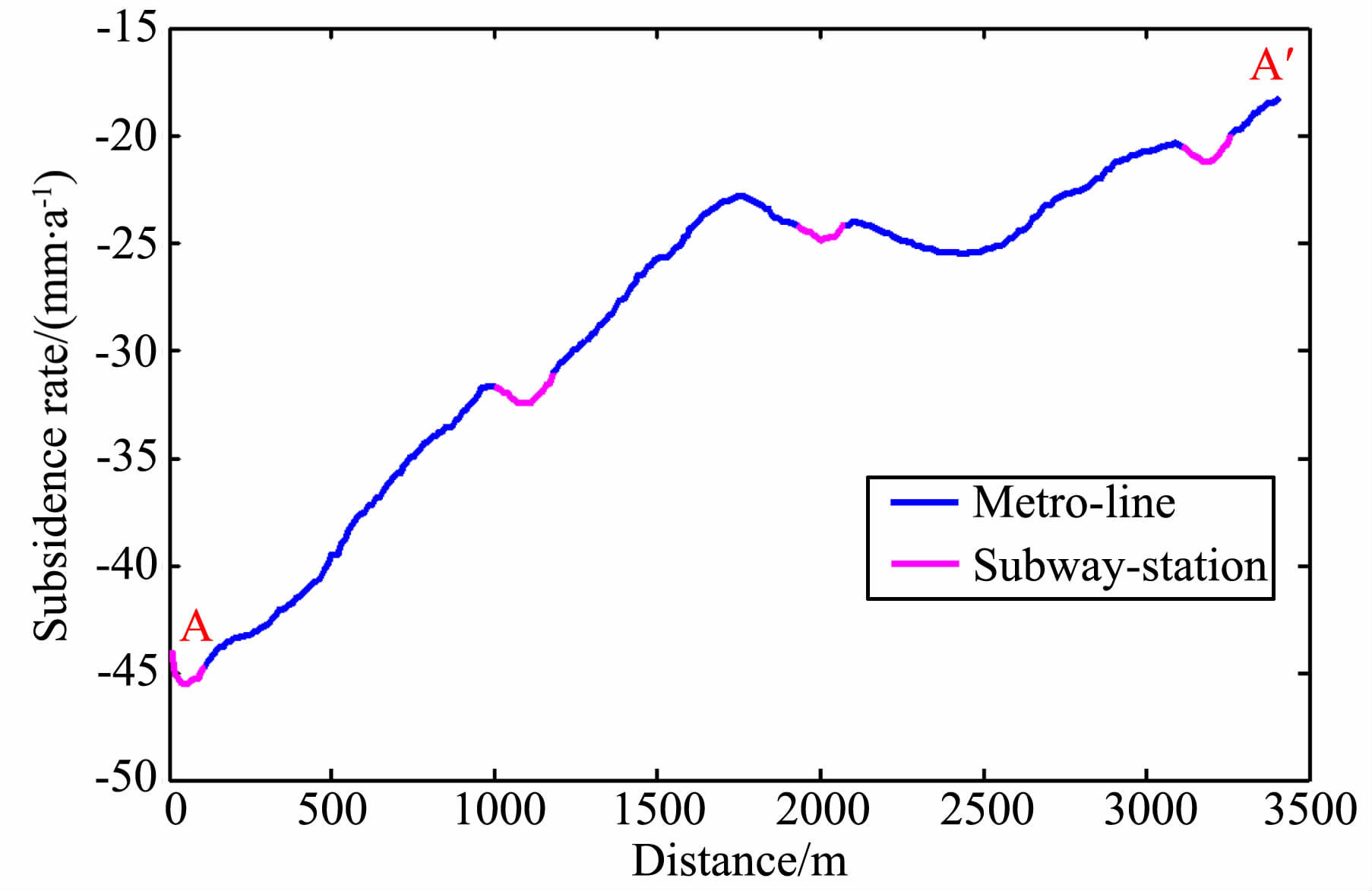
为便于理解图 6所示的沉降分布特征,我们提取并分析了地铁1号线部分区段(图 6 中所标示的折线AA′)的沉降速度.天津市地铁1 号线全长26.2km,在西北段的刘园站至西南角站区段为轻轨铁路桥建设形式,折线AA′全长约3.5km,包含刘园、西横堤、果酒厂和本溪路四个地铁站,均为高架桥车站.图 7 给出了AA′沿线沉降速度分布情况,从北端的刘园车站(A 点)到本溪路站以南(A′点),沉降速度呈抛物线渐变趋势,考虑到铁路桥以深埋桥墩作为支撑,所提取的沉降速度曲线能较好地反映沿线地表或结构的沉降特征.沉降速度曲线的前半段位于城郊结合部,该段沉降速度和梯度均较大,表明地表的不均匀沉降较为显著,靠近A 点的刘园车站附近,最大沉降速度达到45 mm/a,而曲线的后半段则渐趋稳定,沉降速度逐渐降低,在接近市区A′点的沉降速度约为20mm/a.值得注意的是,该区段的四个车站(间隔约为1km)位置(图 7中的红色标注部分)的局部沉降速度相对较大,现场调查表明,这四个车站均为二层高架设计,车站主体为框架结构,围绕铁路桥而建,上部架设顶棚,顶棚自重和列车的长期振动作用或许是导致车站位置的沉降速度相对较大的原因.
|
图 7 天津地铁1号线部分区段的沉降速度 Fig. 7 Subsidence rates along a section of No. 1 metro line in Tianjin |
相关研究表明[23-27],中国东部的华南和华北块体相对于稳定的欧亚板块(西欧和西伯利亚)具有整体向南东东方向运动的趋势.依据“中国地壳运动观测网络"1998年以来的GPS连续观测成果,中国东部沿海区域地块运动东南向的平面运动速度约为20mm/a[26-27].该结论与我们通过多平台PSI联合求解所得到的水平位移速度分量(东向水平位移速度为16.5mm/a,南向水平位移速度为6.8mm/a)基本吻合.此外,应用GPS 网进行地壳形变的相关研究还发现[23]:整个华北地块和燕山地块的垂直运动表现为缓慢隆升,但在北京和天津地区,因地下水过度抽取出现了明显的沉降漏斗,最大沉降速度达到60mm/a.这一GPS分析的结论也与图 6所显示的沉降速度结果一致.
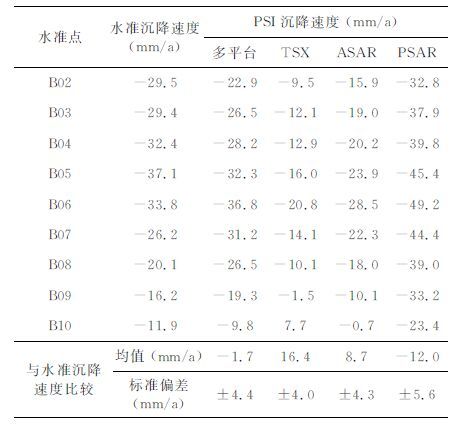
为了评估单平台及多平台PSI沉降速度的解算精度,我们沿西青公路约4km 线路范围内布设了9个水准点(B2-B10,见图 4和图 6),先后于2009年4月、2009年9月和2010年4月对这些水准点进行了三次二等水准测量,并联测至天津市区内的基岩水准点上.经详细分析可知,各水准点呈现明显的线性沉降,由这些观测数据可计算出每一水准点的沉降速度,以此作为PSI沉降速度的评价标准.表 4列出了9个水准点上由水准测量所得到的沉降速度与经PSI(单一卫星平台TSX、ASAR 及PSAR 和多平台)分析所得到的沉降速度的对比情况,表中所列出的单平台PSI的沉降速度是由图 5d-5f所示的LOS向形变速度投影到垂直方向所得到的,具体计算方法可参见文献[13].对比统计分析表明:单平台PSI的沉降速度与水准沉降速度存在显著的差异,而多平台PSI的沉降速度与水准沉降速度吻合最好.TSXPSI的沉降速度与水准沉降速度的差异均值为16.4 mm/a,标准偏差为±4.0 mm/a,ASARPSI与水准的差异均值为8.7 mm/a,标准偏差为±4.3mm/a,PSAR PSI 与水准的差异均值为-12.0mm/a,标准偏差为±5.6mm/a,多平台PSI与水准的差异均值为-1.7 mm/a,标准偏差为±4.4mm/a.很明显,使用本文提出的基于多平台PSI联合解算的沉降速度与水准沉降速度的偏差(统计差异均值)最小.值得指出的是:因不同波长对形变的敏感度存在差异,受数据获取时间的不一致和多源数据建模分析过程中引入的多平台间系统误差等方面的影响,多平台PSI沉降速度的精度未能得到显著提升,而是表现为三种平台PSI沉降观测精度的综合反映,这一点可由统计结果的差异标准偏差变化不大得到反映.
|
|
表 4 9个水准点上PSI沉降速度与水准沉降速度对比 Table 4 Comparison between the subsidence rates derived by multiple-platform PSI and leveling |
为便于进一步对比,图 8显示了西青公路沿线的9个水准点上各种沉降速度结果(见表 4).图中以红、绿、蓝三色实线分别表示使用TSX、ASAR 和PSARPSI计算得到的各水准点上LOS向形变速度,红、绿、蓝三色虚线分别表示相应平台PSI的沉降速度(由LOS向形变速度向垂直方向投影得到);黑色实线表示联合多平台PSI解算的沉降速度;粉色实线表示水准测量得到的沉降速度.综合考虑入射角、航向角和水平位移分量的贡献,使用不同平台PSI计算得到的各水准点上LOS 向形变速度必然存在较大差异,但各条曲线的变化趋势总体上是一致的,这说明单平台PSI观测能够对地表形变做出客观而真实的反映.从图中各曲线的位置关系可知,直接将LOS向形变速度投影到垂直方向所得到的沉降速度与水准沉降速度存在明显的差异,而顾及水平形变分量的多平台PSI联合解算与水准沉降速度最为接近,这说明通过本文所提出的模型和算法恢复与重建三维形变速度场是可行的.
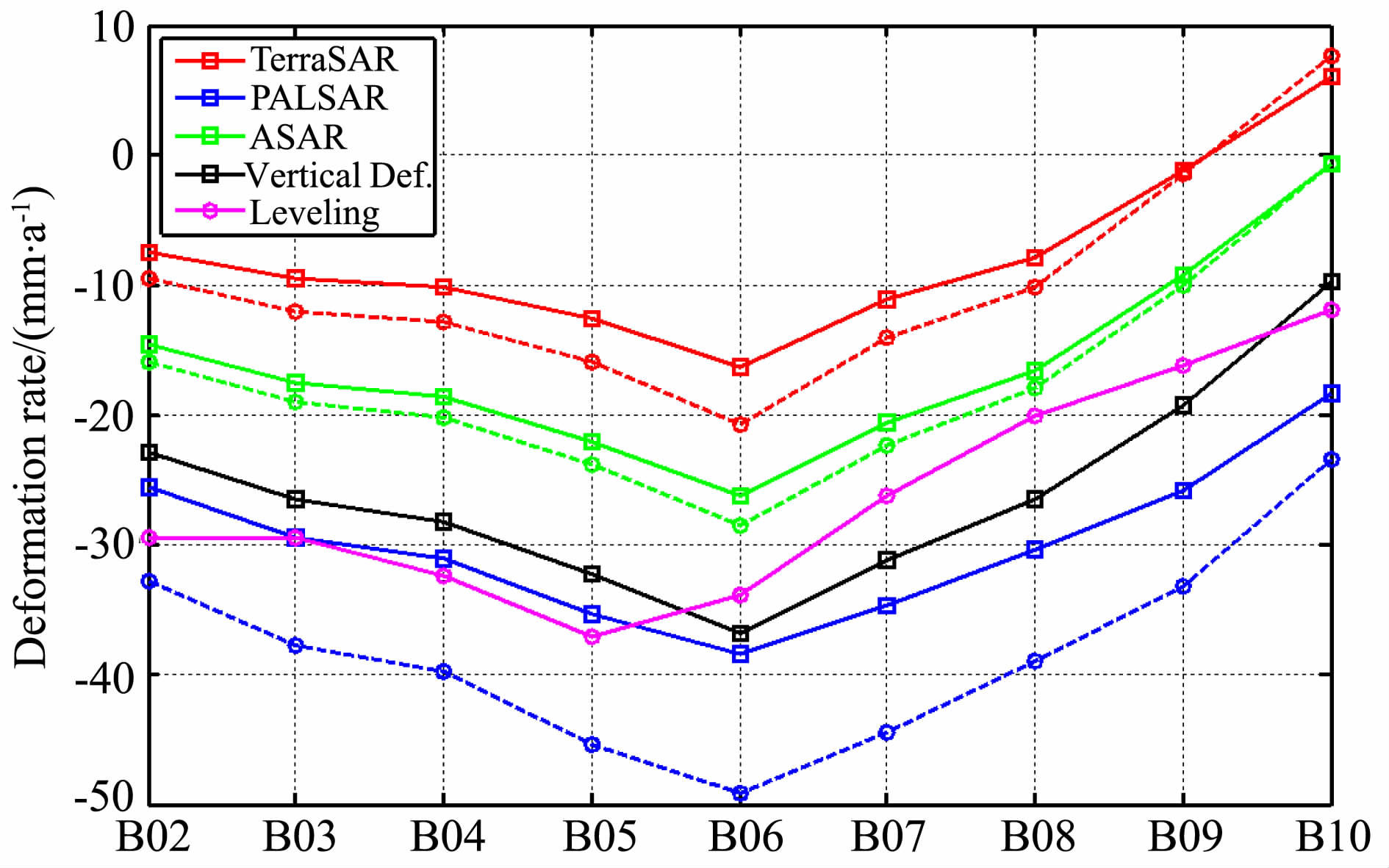
|
图 8 9个水准点上PSI形变速度与水准结果的对比 Fig. 8 Comparison between PSI deformation rates and leveling results at 9 leveling points |
本文提出了基于多平台永久散射体雷达干涉提取三维地表形变速度场的模型与算法,选取天津市西北部的城乡结合部作为实验区域(面积7.8km×9.1km),首先使用2007-2010年所获取的X 波段TerraSAR-X、C 波段ENVISAT ASAR 和L 波段ALOSPALSAR 影像时间序列分别进行单平台PSI形变速度计算与分析,得到了三种平台的LOS向形变速度场,然后联合三类LOS向形变速度结果进行三维形变速度的最小二乘解算,得到了该实验区域的沉降速度场以及南北向和东西向水平位移速度分量,并实现了对每一平台的LOS向形变速度场的整体偏差校准,最后以沿西青公路布设的9 个水准点沉降数据和已有GPS分析结果作为参考,验证了计算结果的精度与可靠性.
单平台PSI分析结果表明:使用不同类别SAR数据计算得到的LOS向形变速度场在量级和空间分布方面存在较大差异,TSX 形变速度场在-36~24mm/a 间变化,ASAR 形变速度场在-23~13mm/a间变化,PSAR 形变速度场在-24~18mm/a间变化;然而,三个形变速度场所反映的地表位移总体趋势具有一致性,这可归结为地壳水平位移与因地下水过量开采导致的不均匀地面沉降所引起;因不同卫星SAR 成像传感器的观测方向、侧视角和航向角存在明显差异,也就是LOS向的姿态各不相同,对同一地面目标来说,其三维位移投影到不同LOS向的一维位移量必然存在差异.
多平台PSI的联合解算结果表明:联合求解所得到的对应于TSX、ASAR 和PSAR 的三类形变速度场的整体偏差常数分别为-7.1、-15.8和-28.6mm/a,整体东向水平位移速度为16.5mm/a,南向水平位移速度为6.8 mm/a,与已有GPS分析所得到的该研究区域水平位移速度约为20 mm/a的结论基本吻合;联合求解所得到的沉降速度在0~60 mm/a间变化,越远离天津主城区,沉降速度较高,越靠近城市中心,沉降速度越低,这表明主城区的地下水开采控制较好,而城乡结合部的地下水开采仍没有得到有效控制;与9个水准点的地面沉降观测结果对比分析表明:单平台PSI的沉降速度与水准沉降速度存在显著差异,差异均值达到10~20 mm/a,标准偏差为±(4~6)mm/a,而顾及水平形变分量的多平台PSI联合解算与水准沉降速度最为接近,差异均值为-1.7mm/a,标准偏差为±4.4mm/a,这表明本文所提出的模型和算法是可靠的,具有无需引入任何外部形变参考信息便可以实现形变速度场的偏差校准和三维重建与恢复的优点.
致谢感谢Infoterra GmbH 公司和美国地质调查局为本研究分别提供了Terra SAR-X 影像数据和数字高程模型(SRTM DEM),同时也感谢欧洲空间局和日本遥感数据中心分别为本研究提供了ENVISAT ASAR 和ALOS PALSAR 影像数据.此外,感谢中国科学院遥感应用研究所与西南交通大学联合成立的“轨道交通工程遥感联合研究中心"的支持.
| [1] | Massonnet D, Rossi M, Carmona C, et al. The displacement field of the Landers earthquake mapped by radar interferometry. Nature , 1993, 364(6433): 138-142. DOI:10.1038/364138a0 |
| [2] | Liu G X, Ding X L, Li Z L, et al. Pre-and co-seismic ground deformations of the 1999 Chi-Chi, Taiwan earthquake, measured with SAR interferometry. Computers & Geosciences , 2004, 30(4): 333-343. |
| [3] | Liu G X, Li J, Xu Z, et al. Surface deformation associated with the 2008 Ms8. 0 Wenchuan earthquake from ALOS L-band SAR interferometry. International Journal of Applied Earth Observation and Geoinformation , 2010, 12(6): 496-505. DOI:10.1016/j.jag.2010.05.005 |
| [4] | Zebker H A, Villasenor J. Decorrelation in interferometric radar echoes. IEEE Transactions on Geoscience and Remote Sensing , 1992, 30(5): 950-959. DOI:10.1109/36.175330 |
| [5] | Zebker H A, Rosen P A, Goldstein R M, et al. On the derivation of coseismic displacement fields using differential radar interferometry: the Landers earthquake. J. Geophys. Res. , 1994, 99(B10): 19617-19634. DOI:10.1029/94JB01179 |
| [6] | Liu G X, Jia H G, Zhang R, et al. Exploration of subsidence estimation by persistent scatterer InSAR on time series of high resolution TerraSAR-X images. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2011, 4(1): 159-170. DOI:10.1109/JSTARS.2010.2067446 |
| [7] | Ferretti A, Prati C, Rocca F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing , 2000, 38(4): 2202-2212. |
| [8] | Ferretti A, Prati C, Rocca F. Permanent scatterers in SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing , 2001, 39(1): 8-20. DOI:10.1109/36.898661 |
| [9] | Berardino P, Fornaro G, Lanari R, et al. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Transactions on Geoscience and Remote Sensing , 2002, 40(11): 2375-2383. DOI:10.1109/TGRS.2002.803792 |
| [10] | Mora O, Mallorqui J J, Broquetas A. Linear and nonlinear terrain deformation maps from a reduced set of interferometric SAR images. IEEE Transactions on Geoscience and Remote Sensing , 2003, 41(10): 2243-2253. DOI:10.1109/TGRS.2003.814657 |
| [11] | Hooper A, Zebker H, Segall P, et al. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophysical Research Letters , 2004, 31(23): L23611. |
| [12] | Liu G X, Luo X J, Chen Q, et al. Detecting land subsidence in Shanghai by PS-networking SAR interferometry. Sensors , 2008, 8(8): 4725-4741. DOI:10.3390/s8084725 |
| [13] | Liu G X, Buckley S M, Ding X L, et al. Estimating spatiotemporal ground deformation with improved persistent-scatterer radar interferometry. IEEE Transactions on Geoscience and Remote Sensing , 2009, 47(9): 3209-3219. DOI:10.1109/TGRS.2009.2028797 |
| [14] | Chen Q, Liu G X, Ding X L, et al. Tight integration of GPS observations and persistent scatterer InSAR for detecting vertical ground motion in Hong Kong. International Journal of Applied Earth Observation and Geoinformation , 2010, 12(6): 477-486. DOI:10.1016/j.jag.2010.05.002 |
| [15] | 陈强, 刘国祥, 丁晓利, 等. 永久散射体雷达差分干涉应用于区域地表沉降探测. 地球物理学报 , 2007, 50(3): 737–743. Chen Q, Liu G X, Ding X L, et al. Radar differential interferometry based on permanent scatterers and its application to detecting regional ground subsidence. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 737-743. DOI:10.1002/cjg2.1088 |
| [16] | Ghiglia D C, Pritt M D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software. New York: John Wiley & Sons, Inc, 1998. |
| [17] | Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis. Proceedings of the Royal Society of London (Series A) , 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [18] | Krige D G. A statistical approach to some mine valuations and allied problems at the Witwatersrand. Witwatersrand: University of Witwatersrand, 1951 . |
| [19] | Hu R L, Yue Z Q, Wang L C, et al. Review on current status and challenging issues of land subsidence in China. Engineering Geology , 2004, 76(1-2): 65-77. DOI:10.1016/j.enggeo.2004.06.006 |
| [20] | Hu B B, Zhou J, Wang J, et al. Risk assessment of land subsidence at Tianjin coastal area in China. Environmental Earth Sciences , 2009, 59(2): 269-276. DOI:10.1007/s12665-009-0024-6 |
| [21] | Zhang S Y, Li T, Liu J N, et al. Urban subsidence observed by InSAR in Tianjin region. Proceedings of IGARSS2007 , 2007: 2078-2081. |
| [22] | Enviro-Library. Challenges and prospects of sustainable water management in Tianjin, 2008 . Available: http://enviroscope.iges.or.jp/modules/envirolib/upload/981/attach/07_chapter3-4tianjin.pdf. |
| [23] | 姚宜斌. 利用高精度复测GPS网进行中国大陆区域地壳运动特征分析. 地球物理学进展 , 2008, 23(4): 1030–1037. Yao Y B. Analysis of crustal movement characteristics in the China mainland by high precision repeated measurements of GPS network. Progress in Geophysics (in Chinese) , 2008, 23(4): 1030-1037. |
| [24] | Shen Z K, Zhao C, Yin A, et al. Contemporary crustal deformation in east Asia constrained by Global Positioning System measurements. J. Geophys. Res. , 2000, 105(B3): 5721-5734. DOI:10.1029/1999JB900391 |
| [25] | Wang Q, Zhang P Z, Jeffrey T F, et al. Present-day crustal deformation in China constrained by Global Position System measurements. Science China , 2001, 294(5542): 574-577. |
| [26] | Heki K, Miyazaki S, Takahashi H, et al. The Amurian Plate motion and current plate kinematics in eastern Asia. J. Geophys. Res. , 1999, 104(B12): 29147-29156. DOI:10.1029/1999JB900295 |
| [27] | 杨少敏, 王琪, 游新兆. 中国现今地壳运动GPS速度场的连续变形分析. 地震学报 , 2005, 27(2): 128–138. Yang S M, Wang Q, You X Z. Numerical analysis of contemporary horizontal tectonic deformation fields in China from GPS data. Acta Seismologica Sinica (in Chinese) , 2005, 27(2): 128-138. |
 2012, Vol. 55
2012, Vol. 55