土壤是地球系统的重要组成部分,它通过存储和释放热量改变地球物理系统能量与物质循环[1-2],对全球、区域乃至局地天气、气候过程产生重要的影响[3-7].土壤温度作为反映土壤热量存储的关键变量[4],决定了地表能量循环、水分等物质输送过程的强度、分布及变化[8-10],一直是陆面物理过程模式研究的重点[11-16].目前,土壤温度的模拟还存在较大的误差[17-19],这已成为制约陆面物理过程模式、天气预报模式、气候预测模式整体模拟结果提升的瓶颈[8, 20].
目前,国际上主流的第三代陆面物理过程模式常采用数值积分热扩散方程的方法预报土壤温度[4],该方法物理意义明确,方便与其他物理过程耦合,且适用于复杂下垫面[7].针对该方法,Mölders[21]分析了土壤热性质参数的不确定性对陆面物理过程模式和数值天气模式模拟结果的影响,指出土壤热扩散率是影响土壤温度模拟的关键因素.Best、Qu等人[22-23]通过敏感性实验,分析了边界条件对模拟土壤温度的影响.Best等[24]讨论了土壤温度模拟误差与格点设置的关系,解析地得到了四层土壤格点设置方案的最佳格距.但土壤温度模拟结果由热性质参数、初边界条件、差分方案、格点设置和时间步长等因素共同影响,以上的研究并没有能将某一因素独立出来进行分析和讨论.
利用土壤热扩散方程的von Neumann解析解,Bonan[25]排除热性质参数和边界条件的影响,分析了Crank-Nicolson差分格式的模拟能力,为进一步探讨误差成因指明了方向.但von Neumann解析解仅反映了土壤的自然冷却过程,并没有考虑对天气、气候变化更重要的土壤温度日变化过程,不切合实际.
本文采用Fourier解析解,进行理想实验,排除了热性质参数和边界条件不确定性所带来的误差.在此基础上,作者分析了显式、隐式和Crank-Nicolson三种差分格式对土壤温度日变化的模拟能力;讨论了模拟误差与格点设置、时间步长之间关系,指出了模拟误差的主要成因.基于常用的格点设置方案,作者还提出了一种优化的格点设置方案,通过理想实验和实测数据的检验,证明了该方案相较于常用方案,能较大地提高模拟精度.
2 土壤热扩散方程及差分方案 2.1 土壤热扩散方程土壤中热量的输送遵循热力学第一定律和梯度热扩散方程[24]:
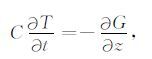
|
(1) |
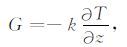
|
(2) |
其中,T为土壤温度(K),C为土壤体积热容量(J·m-3·K-1),G为土壤热通量(W·m-2);z为土壤深度(m, 地表为0,向上为正),k为土壤热传导系数(W·K-1·m-1).
在假设土壤热性质参数C和k不随深度z变化的情况下,土壤热扩散方程(1)还可以简化为[24]

|
(3) |
其中,λ =k/C为土壤热扩散率(m2·s-1).
2.2 理想个例及误差分析指标假设无穷深处土壤热通量为0,表层土壤热通量以及土壤温度初值如下:
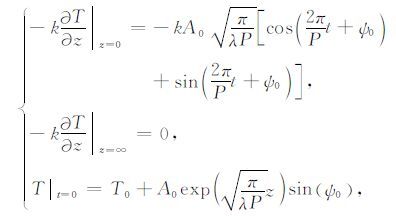
|
(4) |
此时,土壤热扩散方程(3)有解析解:
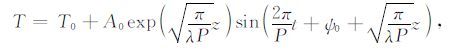
|
(5) |
式中,P为温度变化周期(s),T0 为初始温度(K),A0 为土壤温度变化的振幅(K),ψ0 为地表温度初始相位.
为了将数值积分结果与上述解析解进行比较,本文选择将西北干旱半干旱区典型土壤热力学参数和典型初始状态代入式(5):体积热容量C取1.28×106J·m-3·K-1,热传导系数k取值0.3 W·K-1·m-1,初始温度T0 设为298K,温度变化振幅A0 取值10K,温度的初始相位ψ0 设为-π/10.
由于土壤温度变化由地表热通量驱动,土壤温度振幅随着深度的增加而递减,可以定义z0 (式(6)),以反映地表热量强迫的影响深度:在z0 深度,土壤温度振幅为地表温度振幅的1%.在前述土壤参数设置下,z0 大小为-0.370m.下文对模拟结果的误差分析中,将不考虑z0 深度以下各层土壤.
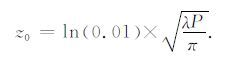
|
(6) |
此外,本文还引入了标准差(Standard ErrorofEstimate, SEE)η[26],以评估土壤温度的
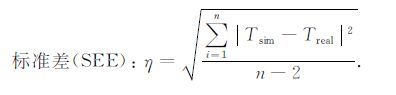
|
(7) |
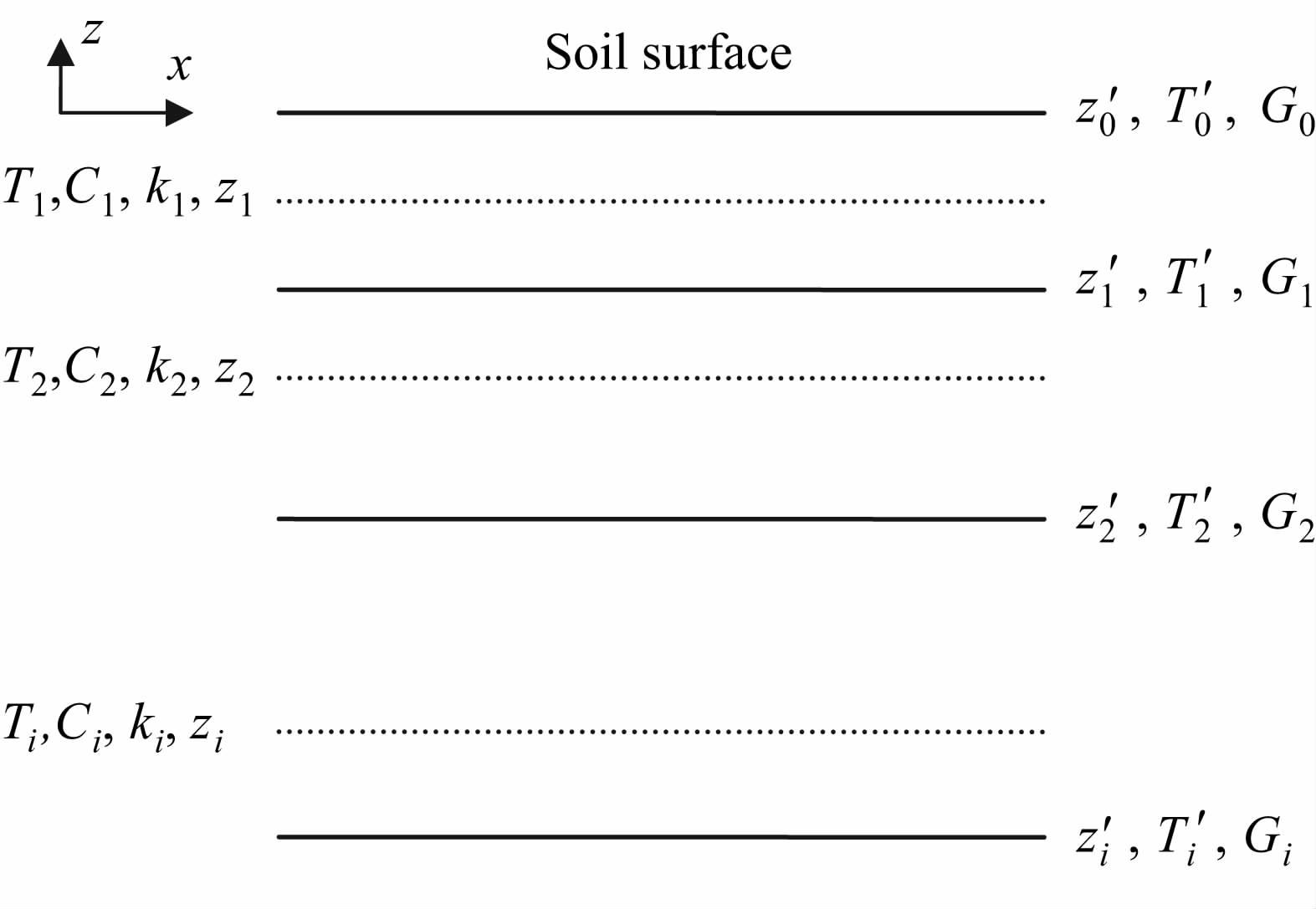
本文采用完全离散化的差分方案数值积分土壤热扩散方程,土壤从上到下、由密到疏垂直分为若干层,以脚标i表示土壤层数.格点设置如图 1 所示,第i层土壤温度Ti定义在该层土壤中心深度zi处,Ci、ki定义为该深度的土壤热性质参数.相邻两层土壤中心深度(zi与zi+1)的垂直平分面定义为土壤层间的界面zi′,土壤热通量Gi定义在该界面处,通量以向上输送为正.
|
图 1 土壤格点设置示意图 Fig. 1 Schematic diagram of soil grid |
在土壤层厚度较小的情况下,可以认为界面zi′处土壤热通量Gi,从zi到zi′的热通量、以及从zi′到zi+1的热通量三者相同,即:
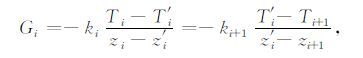
|
(8) |
其中,Ti′为界面zi′处的土壤温度.
通过消除式(8)中的Ti′,可得到Gi的计算式:
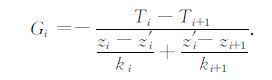
|
(9) |
本文分别使用显式差分方案、隐式差分方案和Crank-Nicolson(C-N)方案[27]计算土壤热扩散方程式(3).通过半步积分技术,还可以将上述三种方案进行组合使用[28],但这并不改变我们对差分方案计算误差的基本判断.
3.3.1 隐式方案隐式方案采用下一时刻的土壤温度,计算土壤热通量:
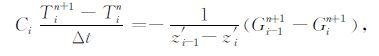
|
(10) |
变量上标n为时间步计数.
结合式(9),土壤热扩散方程的隐式差分方案可写为如下的计算形式:

|
(11) |
这是一个关于下一时间步上各层土壤温度的三对角线性方程,求解此方程即可得到要计算的各层土壤温度.
隐式方案是绝对稳定的,时间残项为一阶,空间上为二阶残项[27].
3.3.2 Crank-Nicolson方案土壤热扩散方程的C-N 差分方案为
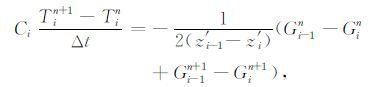
|
(12) |
类似于隐式方案,式(12)代入式(9),可写为如下的三对角线性方程:

|
(13) |
C-N 方案是绝对稳定的,时间和空间残项均是二阶的[27].
3.3.3 显式方案显式差分方案直接利用当前时刻的土壤温度计算土壤热通量;时间上采用前向差分:
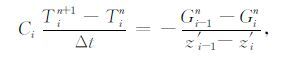
|
(14) |
结合式(9)与式(14),土壤温度的显式差分方案可写为如下的形式:
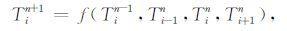
|
(15) |
显式方案条件稳定,稳定度判据为
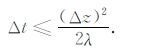
|
(16) |
显式差分格式的时间和空间残项均是二阶的[27].
4 数值差分方案对土壤温度模拟结果的影响本文分别利用三种差分方案,在边界条件式(4)下,模拟2m 厚土壤柱的温度变化,计算模拟结果的误差η.为方便结果比照,三次模拟实验均参考通用陆面过程模式(Community Land Model, CLM)的方案[16],统一按照指数分布放置计算格点:
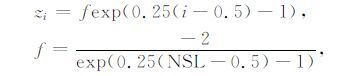
|
(17) |
式中,NSL 为土壤层数(Numberof Soil Layers).
三次实验均模拟7天,土壤层数NSL 从5层增加到20层,时间步长从2h缩减到1s, 前两天采用同化技术加速使模拟结果稳定.最后两天的模拟误差已经稳定,取其结果进行分析.
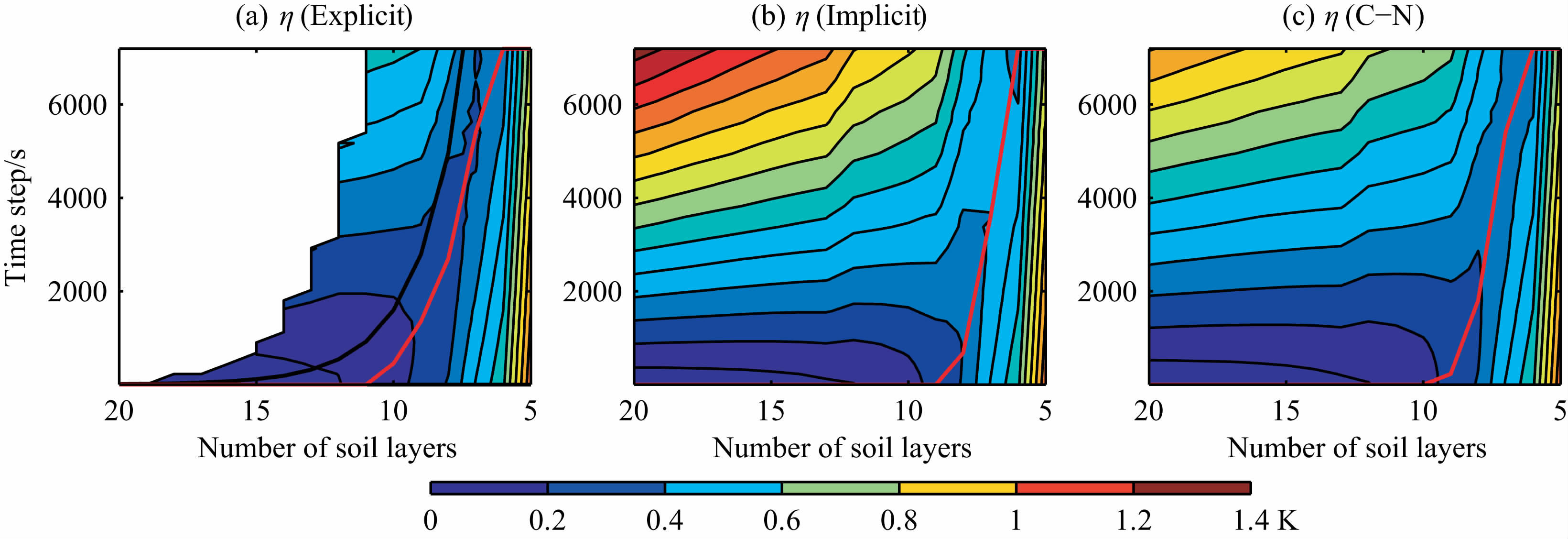
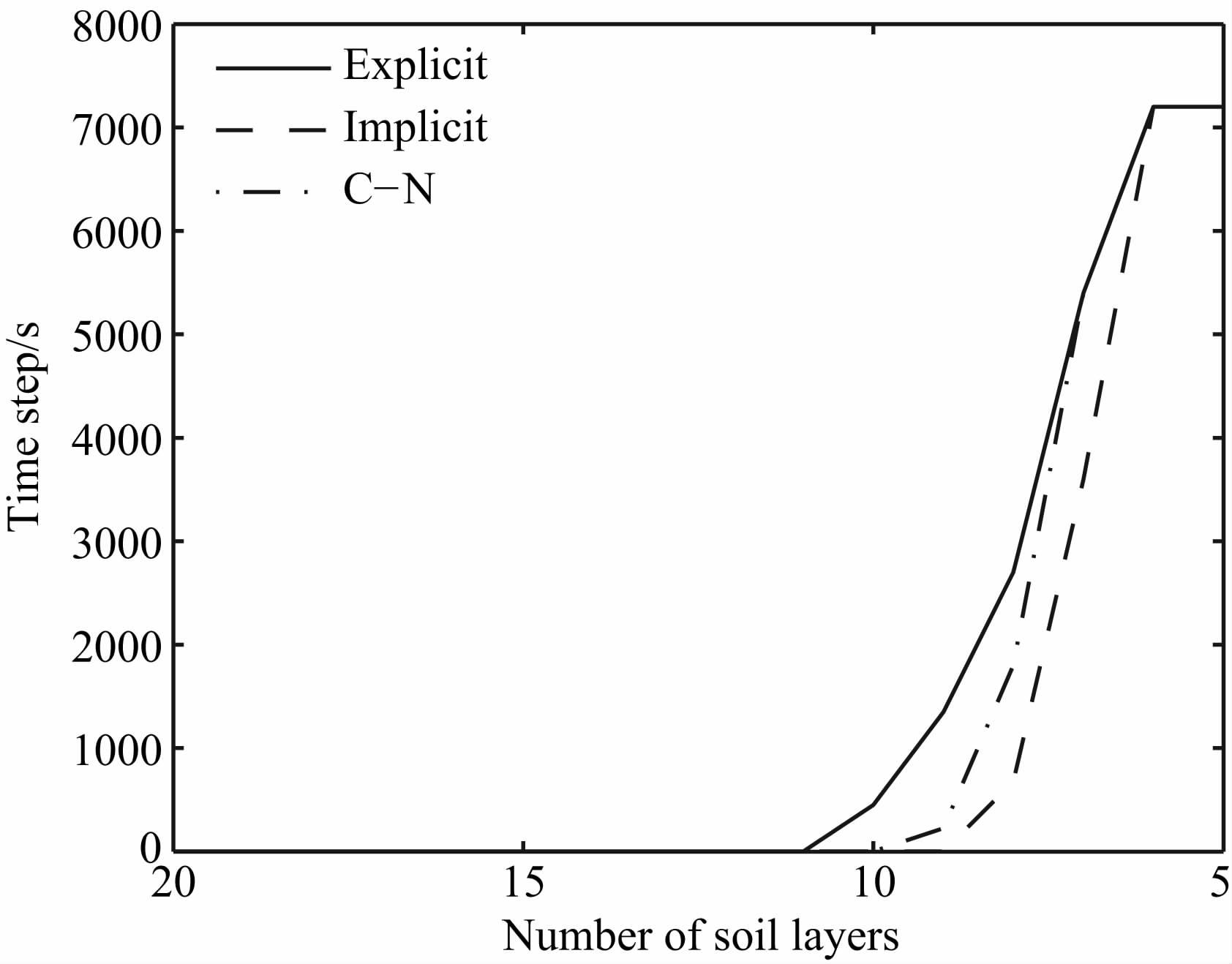
图 2为三种差分方案误差随时空分辨率的变化关系图.由图 2 可知,当时间步长趋于0,空间分辨率趋于无穷(NSL 无穷大)时,三种差分方案的标准差η 均趋近于零,说明三种差分方案与热扩散方程都是一致的.对于每一种空间分辨率,均存在一个最优化时间步长Δtopt(图 2中的红色曲线);在此时间步长下,计算误差取得最小值ηopt.当时间步长大于Δtopt时,模拟误差主要由时间步长过大造成,减小时间步长,模拟误差随之减小;当时间步长小于Δtopt时,误差主要由空间分辨率决定,提高时间步长并不能降低误差.图 3比较了三种方案的最优化时间步长的大小,结果表明,在相同的格点设置情况下,显式方案的最优化时间步长是三种方案中最小的,C-N 方案其次,隐式方案最大,但三者差别并不显著.
|
图 2 模拟结果误差随时空分辨率的变化关系 黑实线:显式方案的稳定度判据线;红实线:最优化时间步长线 Fig. 2 Standard deviation of three difference schemes Black solid line: stability criterion line of explicit scheme; red solid line: optimal time step line. |
|
图 3 三种差分方案的最优化时间步长 Fig. 3 Comparison of three difference schemes' optimal time step |
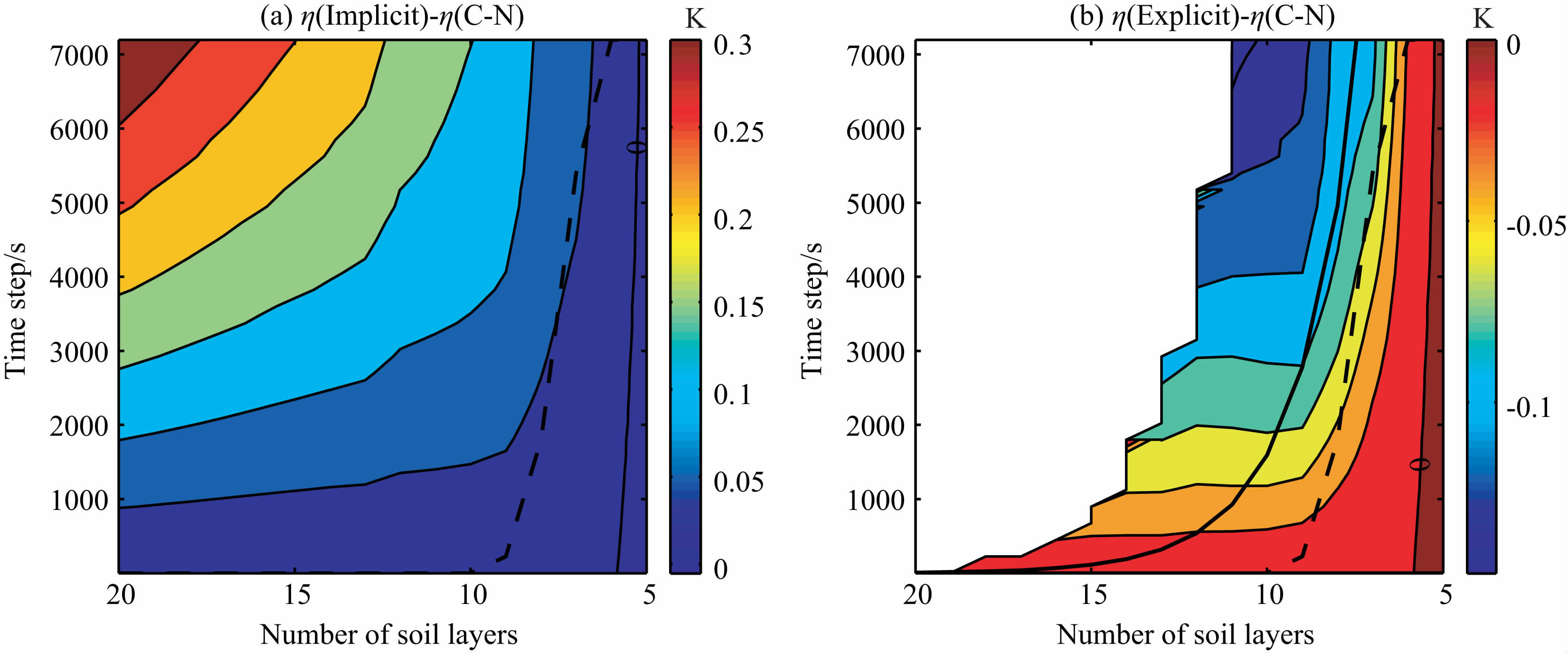
图 4为每两种差分方案模拟误差的比较,可以看出:在绝大多数情况下,显式方案的模拟误差比C-N 方案的模拟误差小,而C-N 方案又比隐式方案精确.在时间步长接近最优化时间步长(图中黑色虚线)时,三种方案的差别不大,显式方案比C-N 方案标准差约小0.02K,C-N 方案标准差约比隐式方案低0.05K,此时模拟结果主要受格点的控制.
|
图 4 三种方案标准差的比较图 Fig. 4 Difference of three difference schemes' standard deviations Black dashed line: optimal time step of C-N scheme; black solid line: stability criterion line of explicit scheme. |
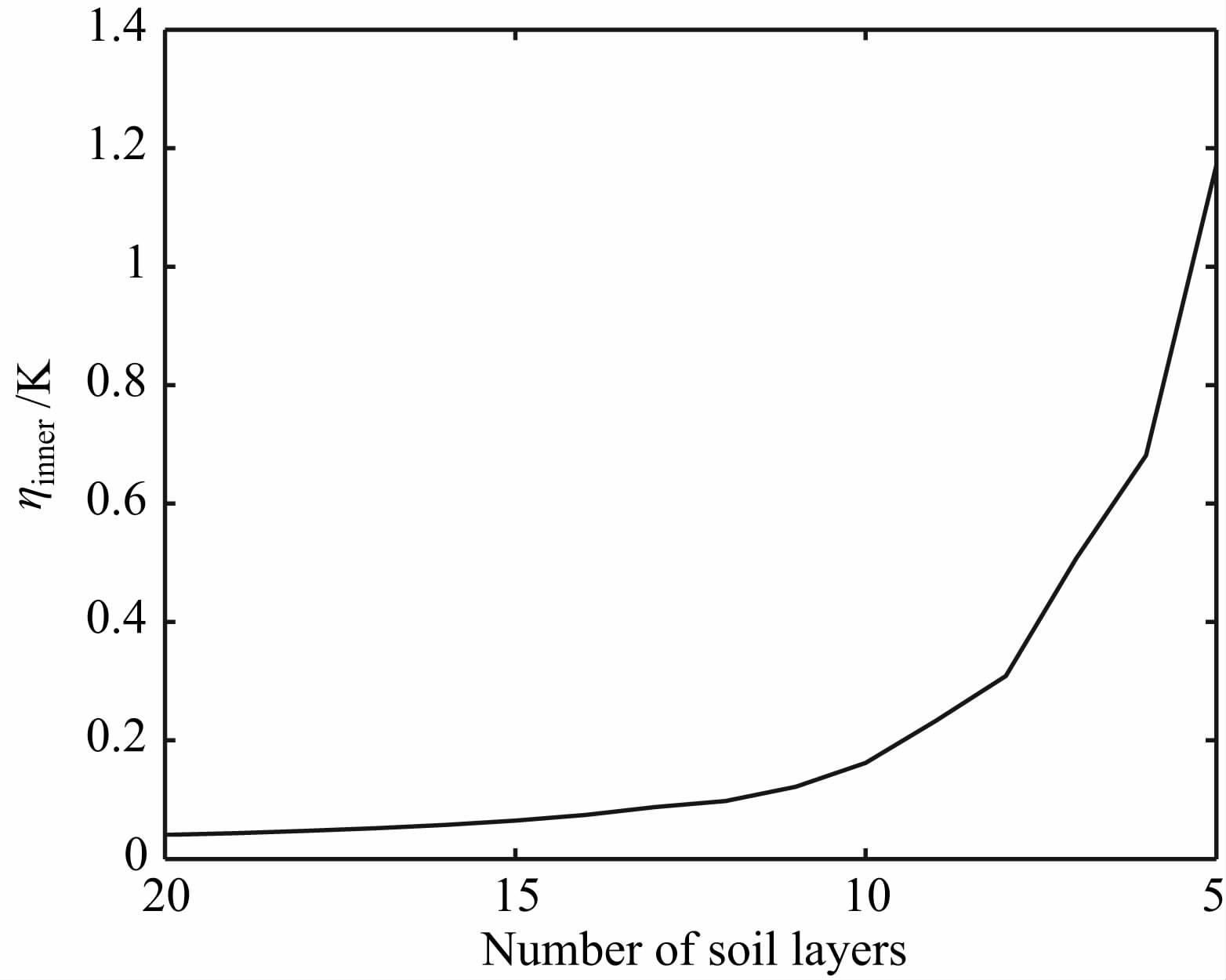
另外,当时间步长趋于0时,三种差分方案的模拟误差趋于一致,说明此时模拟误差仅由格点设置决定,与差分方案无关.本文定义该误差为格点固有误差,以ηinner表示.由图 5可知,格点的固有误差随着土壤层数的增加而减小,这和Best 等人的结论[24]相符合.
|
图 5 格点固有误差与土壤层数的关系图 Fig. 5 Relationship between grid intrinsic error and NSL |
显式差分方案计算量低,计算误差小,但它是一种条件稳定的差分格式,在常用的上疏下密的格点设置下,很容易导致表层土壤温度计算失稳.C-N 方案计算稳定、误差相对较小,近年来被陆面过程模式广泛使用[14-16].本文将以C-N 方案为例,讨论两种格点设置方案的模拟误差.
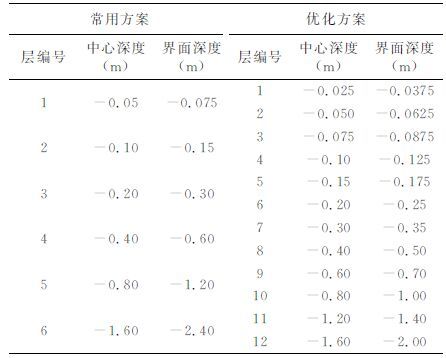
土壤温度的观测实验中,常把温度探头设置在如表 1(常用方案)中各深度的土层内.为了避免数据插值,方便结果与实测数据比较,土壤温度模拟也多采用相同的格点设置方案.在该格点设置方案的基础上,本文还提出了一种优化方案(表 1),经比较,该方案能较大地提高模拟计算的精度.
|
|
表 1 土壤格点设置方案 Table 1 Soil grid schemes |
本文分析了表 1中两种格点在不同时间步长下的计算误差.模拟时间跨度为8天,前两天采用同化技术,待计算稳定后,分析最后两天的模拟结果.
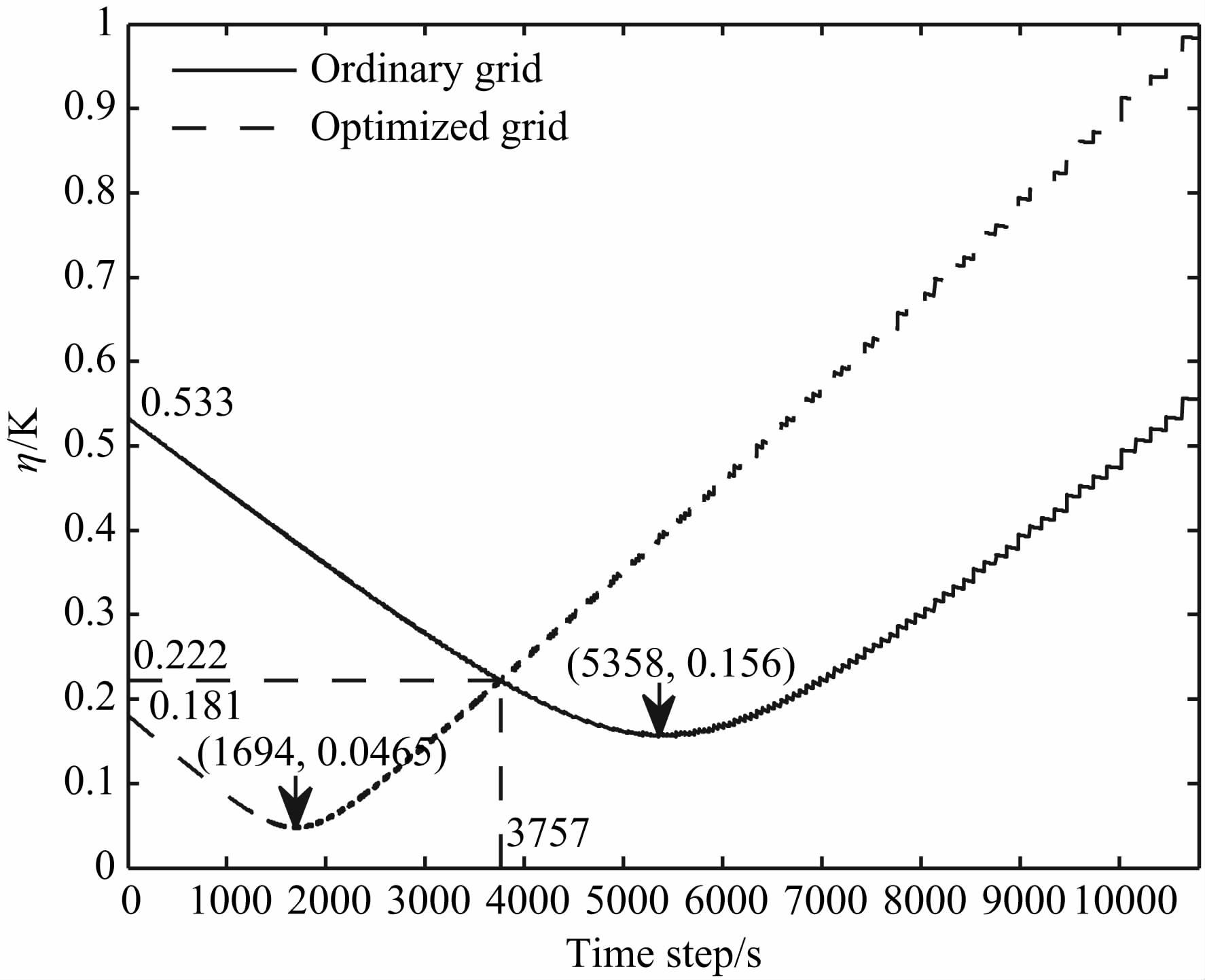
图 6比较了常用格点设置方案和优化格点设置方案的模拟误差.由图可知,随着时间步长的减小,两种方案的模拟误差先减小,到达最优化时间步长后增加.常用格点设置方案的最优化时间步长为5358s, 约1.5h(5400s),最小标准差为0.156K.当时间步长取1694s(约0.5h),优化方案结果误差取得最小值0.0465K,约为常用格点方案的1/3.两种方案适用于不同的时间步长;当时间步长较大时,常用方案的模拟误差小于优化方案的模拟误差;反之,优化方案的模拟误差较小.时间步长为3757s时,两种方案的计算误差相等,为0.222K.
|
图 6 两种格点设置方案模拟误差的比较 Fig. 6 Comparison of two grid scheme’s SEE |
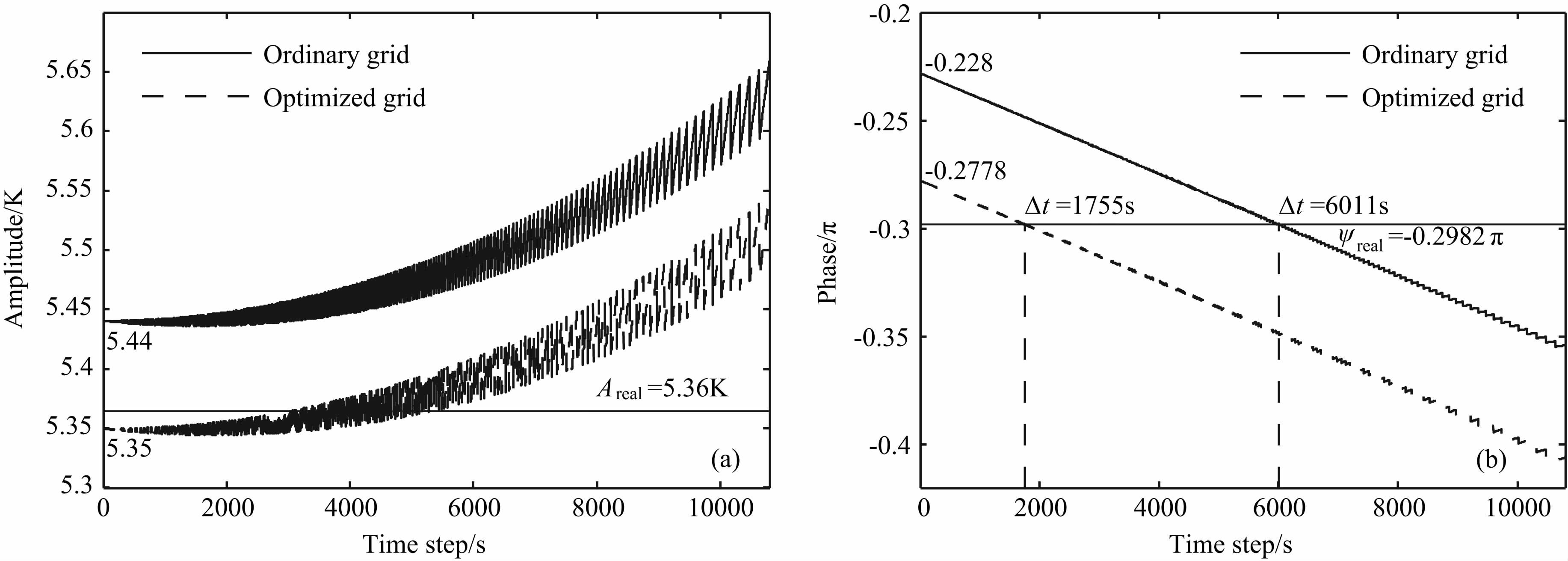
为了分析产生误差的原因,图 7比较了两种方案模拟的振幅和相位的误差.当时间步长趋于0时,两种格点方案模拟5cm 土壤温度变化的振幅分别趋近于各自的格点固有振幅.常用方案的固有振幅为5.44K,高出解析解(5.36K)1.5%;优化方案的为5.35K,略低于解析解0.2%.优化方案模拟的振幅始终优于常用方案;但其相位只有在时间步长较小时才更接近于解析解相位.两种方案模拟结果的相位均随着时间步长的增加而不断滞后,当时间步长接近各自格点方案的最优化时间步长时,即优化方案为1755s、常用方案取6011s时,相位偏差接近于0.在时间步长从1s变化到3h时,相位偏差变化了0.1π,相当于给结果造成了$\frac{\partial Asin(\psi )}{\partial \psi }d\psi ~=1.1K~$ 的误差;与此同时,两种格点设置方案的振幅只增加了约0.2K.因此,模拟误差主要是由模拟相位不准确造成的.
|
图 7 两种土壤格点方案模拟5cm 土壤温度变化的振幅(a)与相位(b) Fig. 7 Amplitude (a) and phase (b) of simulated soil temperature (z=5 cm) |
为了进一步分析和比较不同地表热强迫下数值模式对不同深度土壤温度的模拟能力,我们定义模拟结果的相对误差R=η/A(η 为一层温度模拟值和真实值间的标准差,A为该层土壤温度变化的振幅).当时间步长为1800s时,表 2比较了两种格点设置方案的模拟误差.可以看到,对5cm 土壤层,优化后方案的相对误差为0.21%,相比于常用方案的11.36%,改进幅度较大.采用优化方案,10cm 土层模拟结果的相对误差为5.56%,优于常用方案的1.66%.
|
|
表 2 土壤温度模拟误差比较表(Δt=1800s) Table 2 SEE of simulated soil temperature (Δt=1800 s) |
表 4 还比较了几位作者采用常用格点设置方案,实际模拟土壤温度的相对误差.可以看到,实际模拟的误差往往和理想个例的误差在同一量级上;这说明,在土壤温度模拟中忽略数值差分和格点设置带来的误差往往是不合理的.
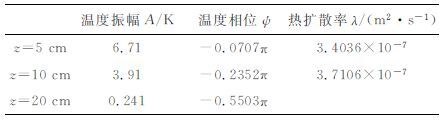
6 实例分析本文采用巴丹吉林沙漠(39.47°N,102.37°E)2009年加强期观测资料,观测站海拔高度1418 m, 地面平坦均一,地表为裸露沙土.土壤温度观测采用4个Campbell公司生产的109L传感器(误差±0.2℃),分别测量5cm、10cm、20cm 和40cm 深度土壤温度,采样频率为1800s.8月3日至17日,土壤温度观测资料完整、连续,且无显著天气系统影响,可认为期间土壤热扩散率近似保持不变.利用调和分析法[31],计算得到5cm 至10cm 深度与10cm 至20cm深度土壤热扩散率分别为3.4×10-7m2·s-1和3.7×10-7m2·s-1(见表 3)
|
|
表 3 土壤热扩散率 Table 3 Soil thermal diffusivity |
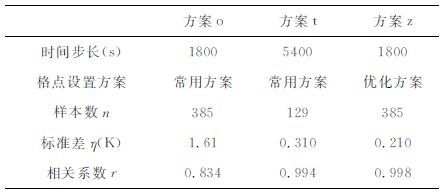
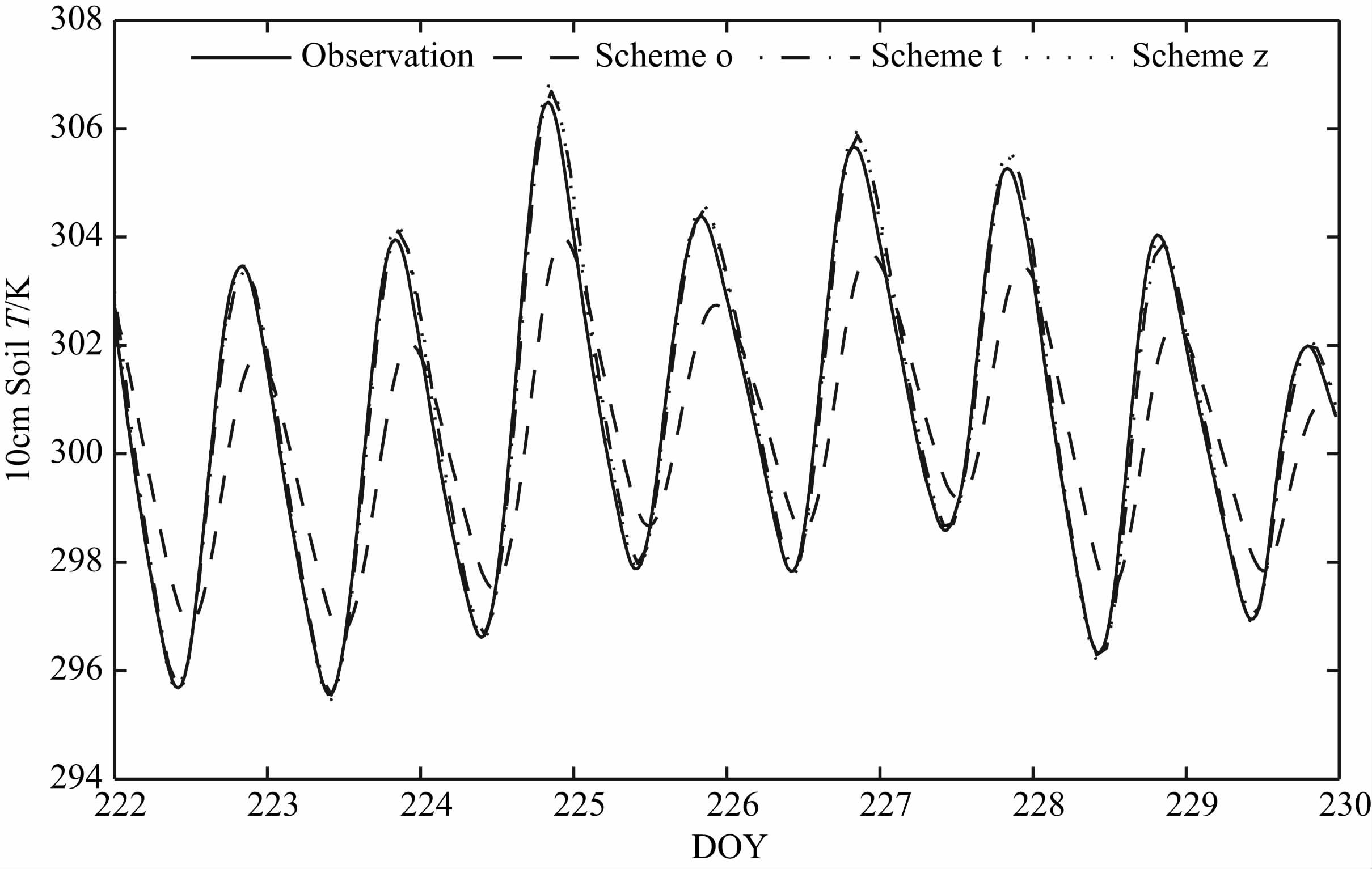
为了比较不同的时间步长和格点设置方案对模拟结果的影响,我们以5cm 和20cm 土壤温度观测值作为边界,使用C-N 差分格式,分别采用三种方案(依次命名为方案o、方案t和方案z, 每种方案的时间步长和格点设置列为表 4),模拟10cm 层土壤温度变化.模拟以8月3日10时的观测资料为初始值,8月9日24 时前共7 天作为模拟起转期(spinup).图 8为8月10日至17日的模拟结果.可以看到,采用常用格点设置,时间步长为1800s时,模拟的土壤温度振幅比观测振幅约小2 K,并且在相位上落后于观测值,模拟值与观测值之间的标准差(表 4)为1.61K.将时间步长由1800s增加为5400s, 模拟结果获得了明显的改善,模拟误差的标准差降至0.31 K.优化方案的模拟结果最优,标准差为0.21K.
|
|
表 4 模拟方案设置及结果 Table 4 Three simulating schemes and therr resulSs |
|
图 8 8月10日至8月17日巴丹吉林沙漠观测站10cm 土壤温度模拟值与观测值的对比 实线:观测值;虚线:方案o(常用格点,常用时间步长);点虚线:方案t(常用格点,优化时间步长);点线:方案z(优化格点,常用时间步长). Fig. 8 Comparisons between the simulated and observed soil temperature at the depth of 10 cm (Badanjaron Desert Station, from 10 Aug to 17 Aug) Solid line: observations; Dashed line: scheme o (ordinary grid, ordinary time step) ; Dashed dot line: scheme t (ordinary grid, optimal time step) ; Dot line: scheme z (optimal grid, ordinary time step). |
图 9为10cm 土壤温度模拟值与观测值之差的概率分布(Probability Distribution Function, PDF).可以看到,常用格点设置方案下,时间步长从1800s增加到5400s, 模拟结果与观测值的相关系数由0.834提高到0.994(表 4),模拟误差的PDF 向0附近集中.优化方案的模拟结果最优,模拟值与观测值的相关系数为0.998(表 4),且有70% 的模拟值分布在观测值±0.25K 的区间内.

|
图 9 10cm 土壤温度模拟值与观测值差的概率分布(PDF) Fig. 9 The PDF of the difference between the simulated and observed soil temperature at the depth of 10 cm |
土壤热扩散方程的数值积分误差受到初边条件、土壤热性质参数、差分格式、格点设置方案以及时间步长的影响.本文利用Fourier解析解,排除了边条件、热性质参数的影响;通过数据同化技术,将初始值的影响降到最低;在此基础上,比较了三种差分格式的计算精度,然后提出了优化的格点设置方案,分别模拟了一个理想个例和实测资料,分析研究了土壤温度数值模拟中差分格式、格点设置对结果不确定性的影响.主要结论如下:
(1) C-N 方案比隐式方案的计算误差小,且绝对稳定,适用于陆面过程模式.显式差分方案的计算误差是三者中最小的,且计算简单,计算量小;但它并不是一种绝对稳定的方案,不能满足模式使用的要求.
(2) 格点固有误差ηinner与差分方案、时间步长均无关,仅反映格点设置方案对模拟结果的影响,可作为衡量格点方案优劣的一个指标.随着土壤格点的加密,格点固有误差单调减小.
(3) 在保持格点不变的情况下,单独减小时间步长并不一定能降低模拟误差.每种格点方案存在一个最优化时间步长Δtopt, 在此步长下,模拟误差达到最低.当小于最优化时间步长时,时间步长越小,模拟误差越大,最终趋近于格点固有误差ηinner.
(4) 常用格点设置方案的固有误差为0.533K,时间步长取5358s时(约1.5h),得到最小误差为0.156K;优化方案的固有误差为0.181K,最优化时间步长为1694s(约0.5h),最小误差为0.0465K.优化方案的模拟精度较常用方案有较大提高.
(5) 采用优化格点方案,解析解的模拟误差不超过2%,模拟实测资料的误差为0.21K,与仪器的观测误差(0.2 K)接近,说明该方案能够很好地模拟土壤温度变化,可满足陆面过程模拟和计算土壤热性质参数的精度要求.
| [1] | 张强, 王盛, 卫国安. 西北地区戈壁局地陆面物理参数的研究. 地球物理学报 , 2003, 46(5): 616–623. Zhang Q, Wang S, Wei G A. A study on parameterization of local land surface physical processes on the Gobi of Northwest China. Chinese J. Geophys. (in Chinese) , 2003, 46(5): 616-623. |
| [2] | 刘树华. 环境物理学. 北京: 化学工业出版社, 2004 . Liu S H. Environmental Physics (in Chinese). Beijing: Chemical Industry Press, 2004 . |
| [3] | Pitman A J. The evolution of, and revolution in, land surface schemes designed for climate models. International Journal of Climatology , 2003, 23(5): 479-510. DOI:10.1002/(ISSN)1097-0088 |
| [4] | Sellers P J, Dickinson R E, Randall D A, et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science , 1997, 275(5299): 502-509. DOI:10.1126/science.275.5299.502 |
| [5] | Koster R D, Dirmeyer P A, Guo Z C, et al. Regions of strong coupling between soil moisture and precipitation. Science , 2004, 305(5687): 1138-1140. DOI:10.1126/science.1100217 |
| [6] | Clark P A, Hopwood W P. One-dimensional site-specific forecasting of radiation fog. Part 1: Model formulation and idealised sensitivity studies. Meteorological Applications , 2001, 8(3): 279-286. DOI:10.1017/S1350482701003036 |
| [7] | Wen L, Yu W, Lin C A, et al. The role of land surface schemes in short-range, high spatial resolution forecasts. Monthly Weather Review , 2000, 128(10): 3605-3617. DOI:10.1175/1520-0493(2001)129<3605:TROLSS>2.0.CO;2 |
| [8] | Schulz J P, Dümenil L, Polcher J, et al. Land surface energy and moisture fluxes: comparing three models. Journal of Applied Meteorology , 1998, 37(3): 288-307. DOI:10.1175/1520-0450(1998)037<0288:LSEAMF>2.0.CO;2 |
| [9] | Liu S H, Yue X, Hu F, et al. Using a modified soil-plant-atmosphere scheme (MSPAS) to simulate the interaction between land surface processes and atmospheric boundary layer in semi-arid regions. Advances in Atmospheric Sciences , 2004, 21(2): 245-259. DOI:10.1007/BF02915711 |
| [10] | Liu S H, Yue X, Liu H Z, et al. Using a modified soil-plant-atmosphere scheme (MSPAS) to study the sensitivity of land surface and boundary layer processes to soil and vegetation conditions. Advances in Atmospheric Sciences , 2004, 21(5): 717-729. DOI:10.1007/BF02916369 |
| [11] | Deardorff J W. Efficient prediction of ground surface temperature and moisture, with inclusion of a layer of vegetation. Journal of Geophysical Research , 1978, 83(C4): 1889-1903. DOI:10.1029/JC083iC04p01889 |
| [12] | Xue Y, Sellers P J, Kinter J L, et al. A simplified biosphere model for global climate studies. Journal of Climate , 1991, 4(3): 345-364. DOI:10.1175/1520-0442(1991)004<0345:ASBMFG>2.0.CO;2 |
| [13] | Sellers P J, Randal D A, Collatz G J, et al. A revised land surface parameterization (SiB2) for atmospheric GCMs. 1. Model formulation. Journal of Climate , 1996, 9(4): 676-705. |
| [14] | Bonan G B. A Land Surface Model (LSM Version 1. 0) for Ecological, Hydrological, and Atmospheric Studies: Technical Description and User's Guide. Boulder: NCAR, 1996. |
| [15] | Bonan G B, Oleson K W, Vertenstein M, et al. The land surface climatology of the community land model coupled to the NCAR community climate model. Journal of Climate , 2002, 15(22): 3123-3149. DOI:10.1175/1520-0442(2002)015<3123:TLSCOT>2.0.CO;2 |
| [16] | Oleson K W, Lawrence D M, Bonan G B, et al. Technical Description of version 4.0 of the Community Land Model (CLM). Boulder: NCAR, 2010. |
| [17] | IPCC. Climate Change 2007: the Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press, 2007. |
| [18] | 周锁铨, 张翠, 王小宁, 等. 多层土壤温度模拟及其检验. 南京气象学院学报 , 2004, 27(2): 200–209. Zhou S Q, Zhang C, Wang X N, et al. Simulation of soil temperature with a multi-layer model and its verification. Journal of Nanjing Institute of Meteorology (in Chinese) , 2004, 27(2): 200-209. |
| [19] | 房云龙, 孙菽芬, 李倩, 等. 干旱区陆面过程模式参数优化和地气相互作用特征的模拟研究. 大气科学 , 2010, 34(2): 290–306. Fang Y L, Sun S F, Li Q, et al. The optimization of parameters of land surface model in arid region and the simulation of land-atmosphere interaction. Chinese Journal of Atmospheric Sciences (in Chinese) , 2010, 34(2): 290-306. |
| [20] | Chen T H, Henderson-Sellers A, Milly P C D, et al. Cabauw experimental results from the Project for Intercomparison of Land-Surface Parameterization Schemes. Journal of Climate , 1997, 10(6): 1194-1215. DOI:10.1175/1520-0442(1997)010<1194:CERFTP>2.0.CO;2 |
| [21] | M?lders N. Plant- and soil-parameter-caused uncertainty of predicted surface fluxes. Monthly Weather Review , 2005, 133(12): 3498-3516. DOI:10.1175/MWR3046.1 |
| [22] | Best M J. A model to predict surface temperatures. Boundary-Layer Meteorology , 1998, 88(2): 279-306. DOI:10.1023/A:1001151927113 |
| [23] | Qu W Q, Henderson-Sellers A, Pitman A J, et al. Sensitivity of latent heat flux from PILPS land-surface schemes to perturbations of surface air temperature. Journal of the Atmospheric Sciences , 1998, 55(11): 1909-1927. DOI:10.1175/1520-0469(1998)055<1909:SOLHFF>2.0.CO;2 |
| [24] | Best M J, Cox P M, Warrilow D. Determining the optimal soil temperature scheme for atmospheric modelling applications. Boundary-Layer Meteorology , 2005, 114(1): 111-142. DOI:10.1007/s10546-004-5075-3 |
| [25] | Bonan G B. A biophysical surface-energy budget analysis of soil-temperature in the boreal forests of interior Alaska. Water Resources Research , 1991, 27(5): 767-781. DOI:10.1029/91WR00143 |
| [26] | Colello G D, Grivet C, Sellers P J, et al. Modeling of energy, water, and CO2 flux in a temperate grassland ecosystem with SiB2. Journal of the Atmospheric Sciences , 1998, 55(7): 1141-1169. DOI:10.1175/1520-0469(1998)055<1141:MOEWAC>2.0.CO;2 |
| [27] | Heath M T. Scientific Computing: An Introductory Survey. New York: McGraw-Hill, 2002 . |
| [28] | 周锁铨, 代刊, 陈涛, 等. 陆面过程模式的改进及其检验. 气象学报 , 2003, 61(3): 275–291. Zhou S Q, Dai K, Chen T, et al. The improvement and verification of land surface process model (BATS). Acta Meteorologica Sinica (in Chinese) , 2003, 61(3): 275-291. |
| [29] | 代成颖, 高志球, 王琳琳, 等. 两种土壤温度算法的对比分析. 大气科学 , 2009, 33(1): 135–144. Dai C Y, Gao Z Q, Wang L L, et al. Intercomparison between two soil temperature algorithms. Chinese Journal of Atmospheric Sciences (in Chinese) , 2009, 33(1): 135-144. |
| [30] | 梁晓, 戴永久. 陆面模式中土壤和植被经验参数随机误差的传播研究. 大气科学 , 2010, 34(2): 457–470. Liang X, Dai Y J. Soil and plant parameters related stochastic uncertainty propagation in the common land model. Chinese Journal of Atmospheric Sciences (in Chinese) , 2010, 34(2): 457-470. |
| [31] | 刘树华, 崔艳, 刘和平. 土壤热扩散系数的确定及其应用. 应用气象学报 , 1991, 2(4): 337–345. Liu S H, Cui Y, Liu H P. Determination of thermal diffusivity of soil land and its application. Quarterly Journal of Applied Meteorology (in Chinese) , 1991, 2(4): 337-345. |
 2012, Vol. 55
2012, Vol. 55