核磁共振作为一种直接探测地下水的地球物理方法,是通过测量地下水中的氢核受到激发产生的磁共振探测(MagneticResonanceSounding, MRS)信号来实现对地下水的探测[1-3].该方法的主要优点是直接测量地下水中氢核产生的MRS 信号,通过改变激发脉冲矩就可以完成对应不同深度的测量.在对仪器采集的MRS 信号进行数据预处理之后,通过反演解释软件,就可以确定出含水层的深度、厚度、含水量、含水层平均孔隙度等信息[4-6].
但是,由于地面核磁共振探水仪的灵敏度高,接收到的信号非常微弱(纳伏级),极易受到周围环境中噪声成分的干扰,并且噪声的形式是复杂多样的,很难获得全部噪声形式的先验知识.中国人口密集,电网发达,电力线和电力设备布满城镇和村庄,电磁干扰情况严重,而缺水地区大部分处于城市附近和村庄等这些强干扰地区.强噪声干扰的存在,将会影响反演解释的水文地质参数结果的精确度,使MRS方法的应用受到限制.
针对MRS信号中的噪声干扰问题,国内外的许多专家和学者进行了相应的研究.通过铺设特殊形状线圈[7]和增加信号叠加次数等方法普遍被采用[8-9];Legchenko等采用区块对消法,正弦对消法和陷波滤波器等方法用于电磁噪声的滤除[10-15];德国柏林技术大学Strehl等把电磁噪声分类采用不同策略进行处理[16-17],这些方法在一定的前提条件下获得了较好的效果.但当噪声强度大、干扰成分复杂,信号中心频率与工频干扰频差较小时,难以获得较好滤波效果.Walsh 研制一种多通道地面核磁共振找水系统,从多个通道上提取主通道探测信号与其他通道噪声信号构成新的数据序列,基于频域自适应消噪算法实现噪声滤除[18].国内,王应吉、蒋川东等从设计极微弱信号放大器、4N 倍Lamor频率采样等滤波手段进行磁共振FID(FreeInductionDecay)信号去噪方法研究[19-21],尚未见针对全波磁共振信号采用时域变步长自适应LMS算法进行去噪方法研究.
基于相关抵消原理的自适应滤波具有这样的特点:在信号和噪声统计特性未知的前提下,通过自适应算法调整权系数来跟踪学习噪声的统计特性,实现从噪声中提取信号.笔者针对MRS 信号与工频谐波干扰频率、强度均不固定的特点,借鉴自适应滤波在其他领域[22-23]的成功应用,基于参考线圈的方式,设计90°移相自适应噪声抵消系统,采用时域变步长自适应LMS算法,对MRS信号中强工频谐波噪声进行滤除,以实现MRS信号的可靠提取.
2 核磁共振探测噪声分析及对策 2.1 核磁共振地下水探测核磁共振是原子核的一种物理现象,指具有核子顺磁性的物质选择性地吸收电磁能量.氢核是地层中具有核子顺磁性物质中丰度最高、磁旋比最大的核子.MRS方法就是通过测量地下水中的氢核来直接探测地下水.
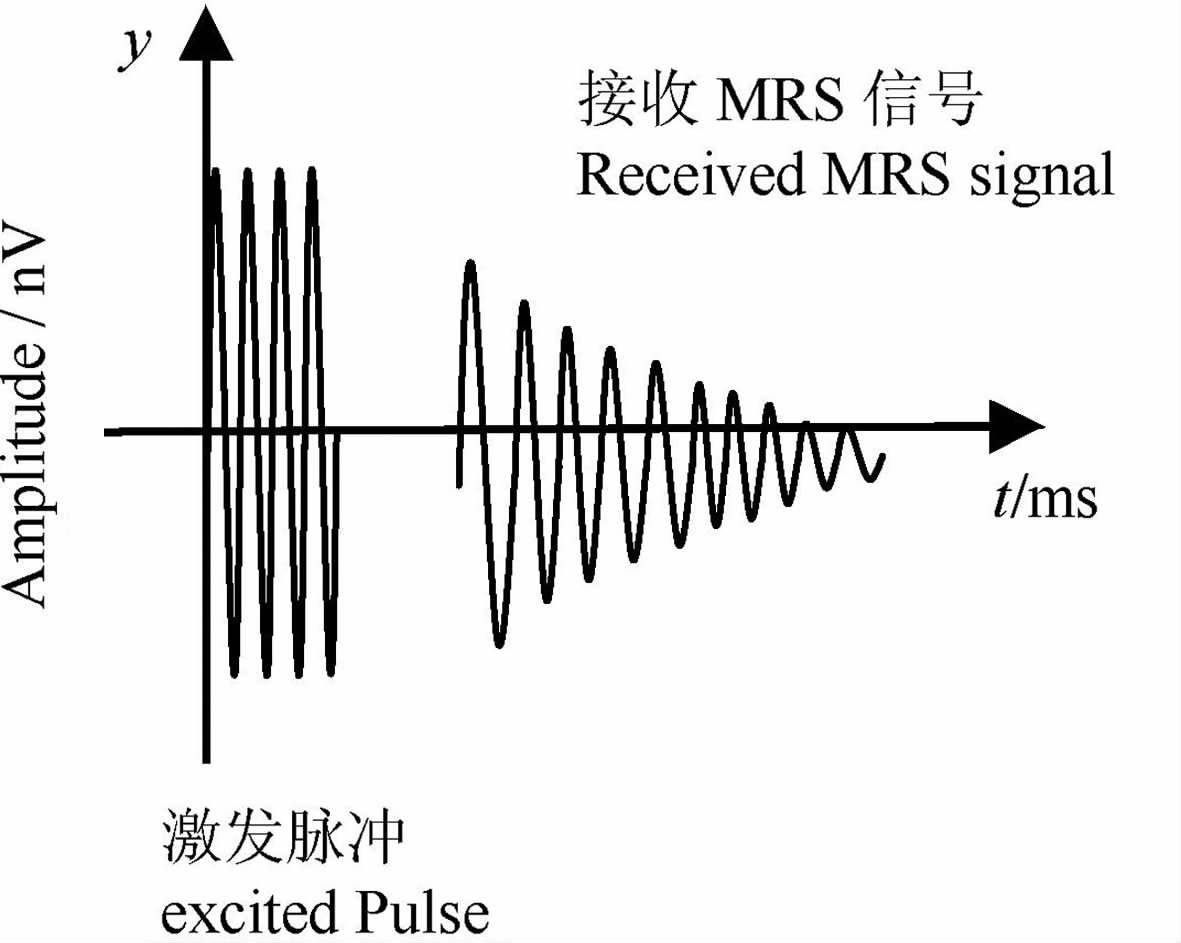
在MRS方法中,向铺在地面上的线圈中供入频率为拉摩尔频率的交变电流脉冲,在交变电流形成的交变磁场激发下,使地下水中氢核形成宏观磁矩.这一宏观磁矩在地磁场中产生旋进运动,其旋进频率为氢核所特有.在切断激发电流脉冲后,用同一线圈拾取由不同激发脉冲矩激发产生的MRS 信号,该信号的包络线(FID 信号)呈指数规律衰减.MRS信号强弱或衰减快慢与水中氢质子的数量有直接关系,即MRS 信号的幅值与所探测空间内自由水含量成正比,这就是核磁共振地下水探测方法的原理[24].图 1为核磁共振探水仪发射与接收的信号波形示意图.
|
图 1 核磁共振探水仪发射与接收信号波形示意图 Fig. 1 Transmitting and receiving signal waveforms of MRS instrument |
对MRS信号进行分析,通常包含如下几种噪声成分:工频谐波噪声和随机自然噪声,此外有时还包含尖峰噪声以及其他未知噪声.可见,噪声形式是极其复杂的.
MRS信号的频率(拉莫尔频率)与当地的地磁场成正比,在我国范围为1.7kHz到2.5kHz.在这个范围内,通常自然噪声是很低的,并不是影响MRS信号提取的主要因素.但是,在城市村庄附近,人为噪声远远强于自然噪声,并对MRS 信号造成复杂干扰,尤其高强度工频谐波噪声干扰会将MRS信号淹没.
强工频谐波噪声主要是50Hz电力线及其谐波干扰.其特点是频率基本固定,但是由于工频频率具有不稳定性,会导致谐波频率较小的偏差.
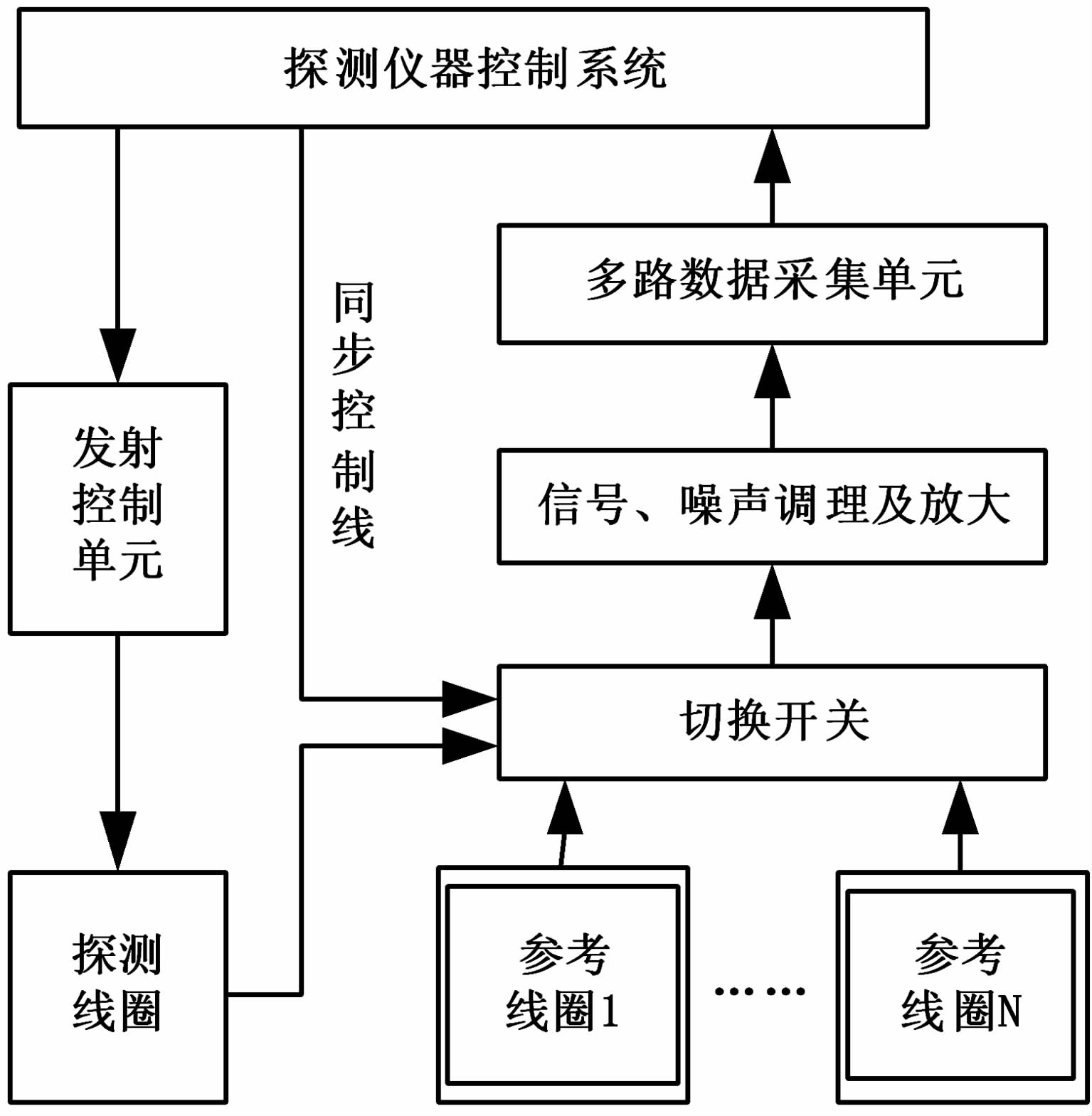
2.3 基于参考线圈的探测系统为了在城市周边和村庄附近进行地下水探测,如何在信噪比和地下水感应信号大小均未知的情况下,有效提取MRS信号变得至关重要.鉴于此,在现有JLMRS-I型地下水探测仪基础上[24],设计带有参考线圈的探测系统,如图 2所示,实现参考线圈与探测线圈全波数据的同步采集.根据探测线圈周围噪声源分布(移动基站、高压电)情况,可以考虑布设一个或多个参考线圈接收噪声干扰,参考线圈可以采用单匝或多匝线圈接收的方式,用参考线圈中的噪声来对消探测线圈采集数据中的噪声,实现噪声滤除.
|
图 2 参考线圈与探测线圈全波数据同步采集框图 Fig. 2 Block diagram of full-wave data synchronous acquisition with reference coil and detection coil |
为了采用基于参考线圈的方式来实现噪声与含噪MRS信号的同步采集,必须考虑参考线圈相对于主探测线圈布设时的相对位置,即保证探测线圈探测的地下水感应信号不能被参考线圈接收到.
MRS信号的初始振幅E0 的大小与地下含水层的水量大小成正比,可以用式(1)计算:
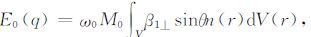
|
(1) |
其中ω0 为当地的拉莫尔角频率,M0 为磁化强度,β1⊥ =B1⊥/I0 =f(r,ρ(r),α)称为单位电流磁感应强度,是由位置矢量r,地下电阻率分布ρ(r)和地磁倾角α 决定的.n(r)表示含水量的大小.假定大地呈水平分布,电阻率的垂直分布ρ(z)已知,则初始振幅E0 可表示为
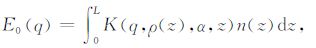
|
(2) |
式中K(q,ρ(z),α,z)称为核磁共振核函数,由脉冲矩q、电阻率的垂直分布ρ(z)、地磁倾角α 和深度z共同来决定.

|
(3) |
核磁共振核函数K(q,ρ(z),α,z)反映了地下不同深度含水层对核磁共振信号的贡献大小,与发射/接收线圈的匝数、大小,激发脉冲矩,地下电阻率等因素有关
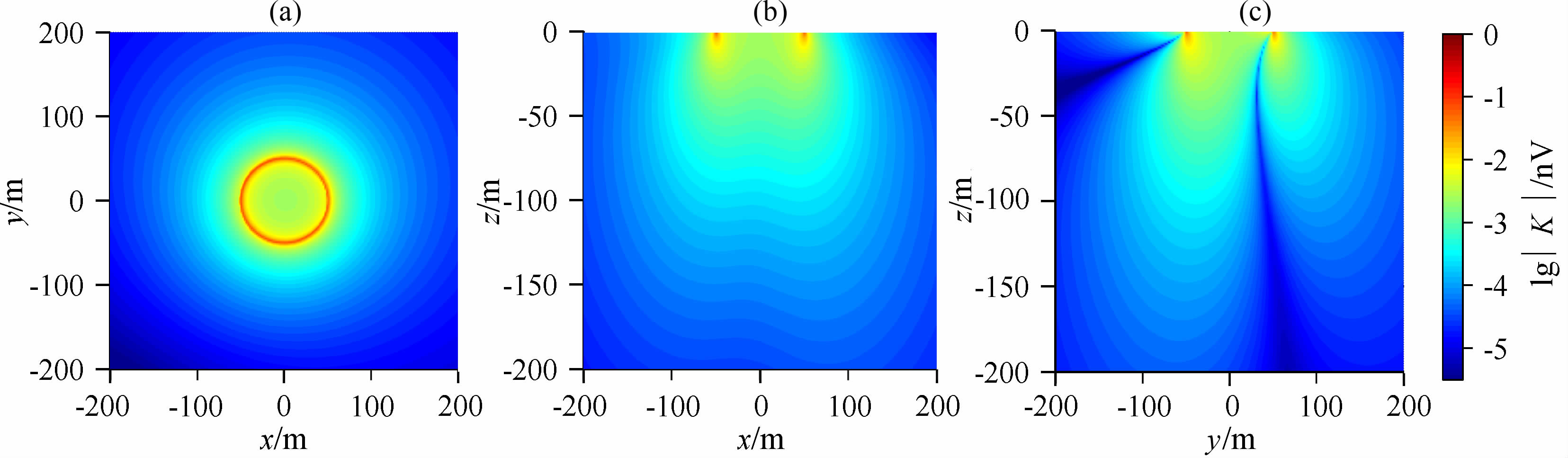
图 3给出了核磁共振核函数数值计算结果.假设整个地下空间电阻率为500Ωm, 地磁场强度为54000nT,地磁倾角为60°.发射线圈采用半径50m的单匝圆形线圈,采用收发共线方式
|
图 3 核磁共振核函数数值计算结果 (a)xy面;(b)xz面(东西方向);(c)yz面(南北方向) Fig. 3 Numerical results of MRS kernel function (a)xyprofile;(b)xzprofile(east west direction);(c)yzprofile(north south direction) |
颜色表示lg K,南北方向呈现的显著倾斜是由于地磁倾角影响的结果.可见,随着激发脉冲矩q的增加,核函数逐渐增大,由接收线圈处向周围扩散,甚至在发射线圈外100m 的区域均对核磁共振信号有贡献.由此可以认为:参考线圈必须铺设在距离主探测线圈100m以外的区域,才能够保证参考线圈没有接收到磁共振响应信号.
3 变步长自适应噪声抵消算法 3.1 自适应噪声抵消原理自适应噪声抵消系统原理如图 4所示,它以噪声干扰为处理对象,将噪声干扰进行抑制,以提高系统输出的信噪比[25]. 在图 4中,自适应噪声抵消系统有两路通道:主通道和参考通道.主通道接收信号源获得的信号s,但是信号s受到了噪声n0 的污染,因而主通道接收到的是信号s和噪声n0 的混合信号;参考通道接收噪声源信号n1,作用在于检测噪声干扰.噪声n1 与噪声n0 具有相关性,通过自适应滤波器调整其输出y,使y在最小均方误差意义下最接近主通道的噪声n0.这样,通过减法器,将主通道的噪声分量n0 尽量抵消掉,就得到系统输出ε.
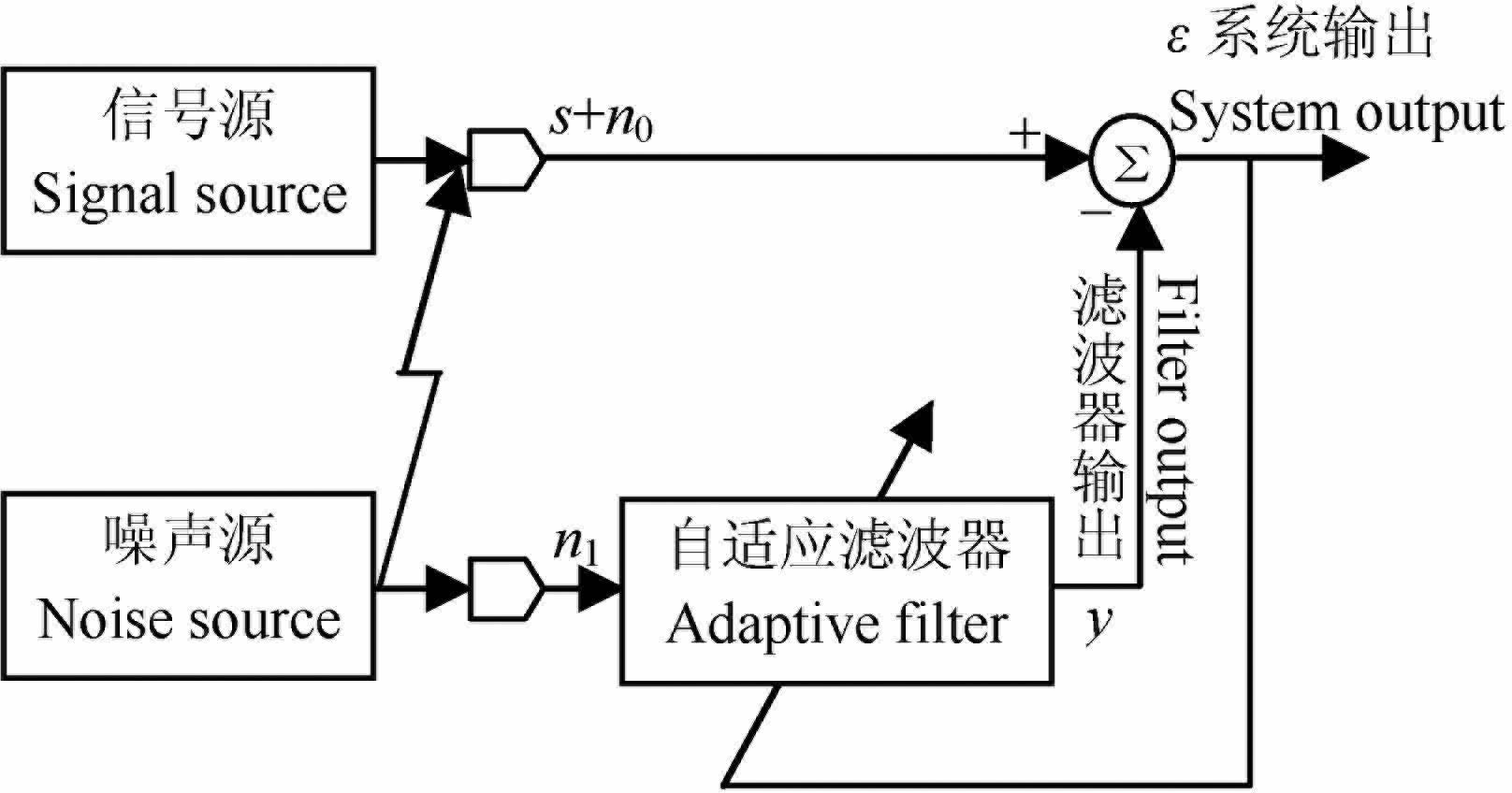
|
图 4 自适应噪声抵消系统原理图 Fig. 4 chematic diagram of adaptive noise cancellation system |
参考通道噪声信号n1(n)表示为
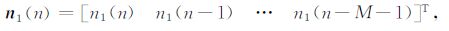
|
(4) |
用w(n)表示滤波器的权系数矢量,则有
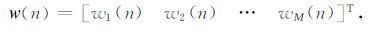
|
(5) |
M表示滤波器的阶数,μ 表示步长,权系数的迭代公式表示为
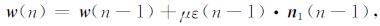
|
(6) |
显然,n时刻,自适应滤波器的输出信号y(n)可以用下式表示:
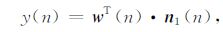
|
(7) |
系统输出ε(n)可以表示为
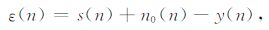
|
(8) |
系统通过适当的算法,调节参数wT(n)使性能函数E[ε2(n)]最小化,对式(8)两边平方后取数学期望,由于s(n)与n0(n),y(n)无关,可得
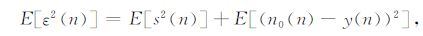
|
(9) |
从而得到
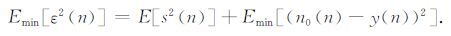
|
(10) |
当调节滤波器的参数使E[(n0(n)-y(n))2]达到最小时,E[(ε(n)-s(n))2]也是最小,因此得到
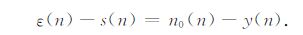
|
(11) |
由公式(11)可以看出:n时刻系统输出ε(n)为信号s(n)的最小方差估计
3.2 带有90°移相的自适应噪声抵消系统基于带有参考线圈探测系统,针对强工频谐波干扰,参考通道中设计了带有90°移相的自适应噪声抵消系统,其设计思想是根据工频谐波噪声模型可以表示成正余弦信号的特点,并源于自适应陷波器去噪原理.但其比自适应陷波器具有优势:相当于同时采用多个自适应陷波器一次滤除多个工频谐波干扰,避免了原始自适应陷波器在进行陷波之前必须进行频谱分析找到相对准确的工频谐波干扰频点作为参考以及进行多个工频干扰滤除时采用并联式或级联式进行算法处理.图 5给出了只带有一个参考通道的90°移相自适应噪声抵消系统框图.
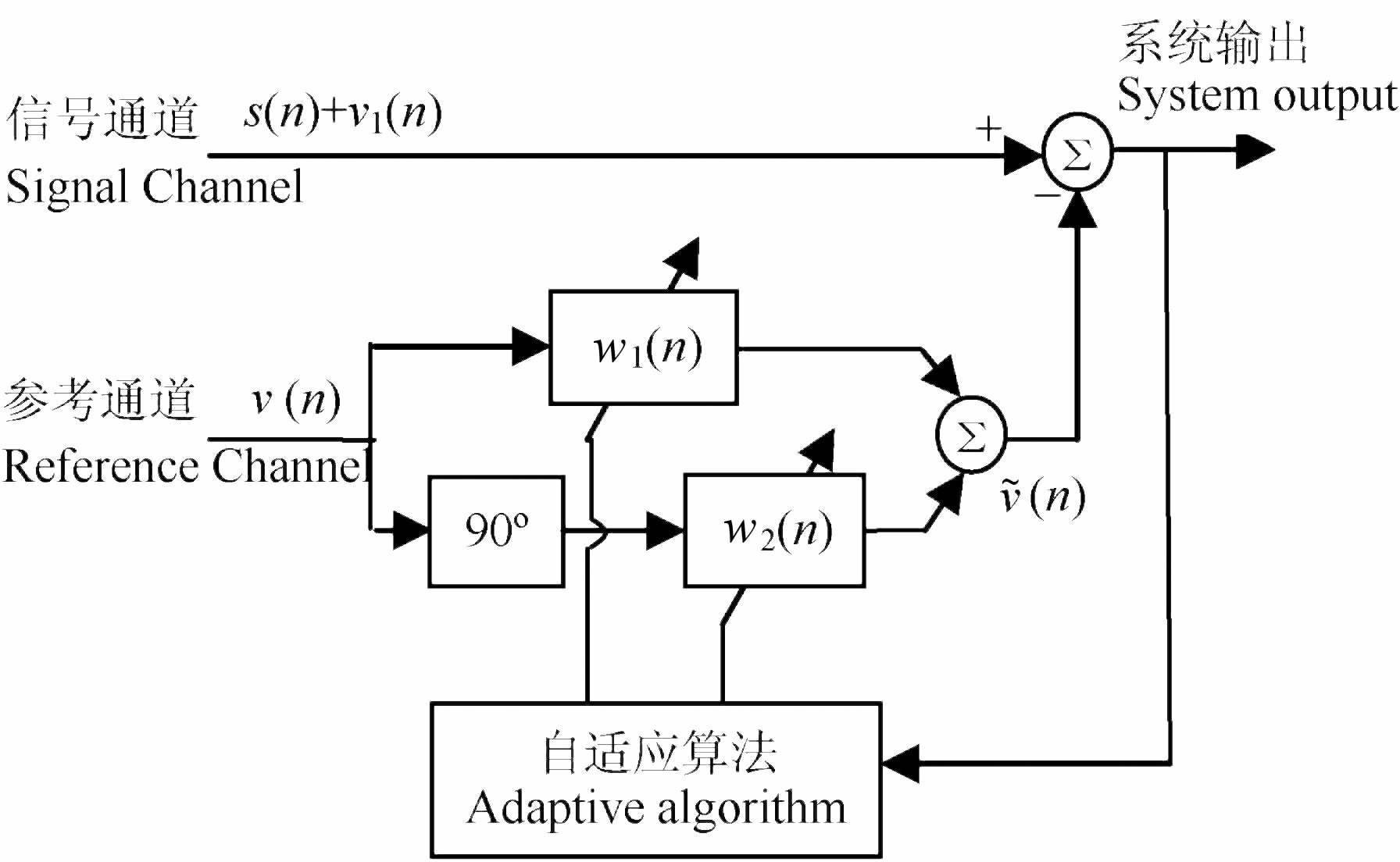
|
图 5 MRS信号自适应噪声抵消算法框图 Fig. 5 Diagram of adaptive noise cancellation algorithm for MRS signal |
以信号通道与参考通道中只含有某一个频率为ω0 的谐波分量为例,给出带有90°移相的自适应噪声抵消系统原理的理论论证.
假设信号通道的工频谐波噪声由如下公式表示:
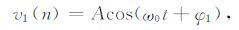
|
(12) |
虽然对信号通道与参考通道数据进行同步采集,但由于两个通道的布设距离等因素影响,致使参考通道采集噪声的幅值、相位与信号通道中噪声的幅值、相位不可能相同.所以,参考通道采集的工频谐波噪声表示为
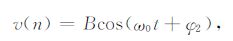
|
(13) |
那么,经90°移相自适应噪声抵消系统可以获得
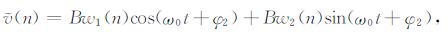
|
(14) |
把参考通道的相位φ2 表示为
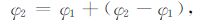
|
(15) |
根据三角函数的和差化积公式,可以得出:
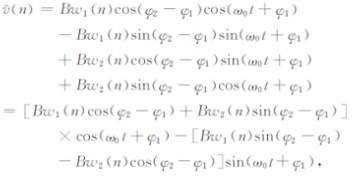
|
(16) |
为了使输出e(n)尽可能接近被测信号s(n),则应该使:
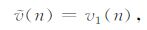
|
(17) |
若使公式(17)成立,需满足如下关系:
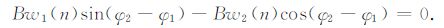
|
(18) |
对公式(18)两端分别平方,相加可得:
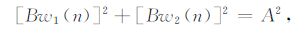
|
(19) |
整理得:
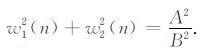
|
(20) |
可见,只需通过自适应算法,调整参考信号v(n)及其经过90°移相v⊥ (n)两个正交分量的权系数w1(n)和w2(n),使之满足公式(20),就可以使珘v(n)振幅和相角都与主通道信号中相应噪声分量的振幅、相角相同,最后使信号通道中干扰v1(n)被抵消,实现噪声的滤除
3.3 变步长LMS算法的提出传统的LMS 算法采用固定步长方式,存在收敛速度和稳态误差之间的矛盾,并且对于磁共振探测信号来说,对于不同的信噪比情况,需要反复调整步长参数才能够获得较好滤波效果,不具备解决不同环境条件下自适应输出信号的能力.
为了解决这一问题,结合带有90°移相的自适应噪声抵消系统,提出采用变步长LMS算法,使算法在不同MRS 信号强度以及不同信噪比下,能够自适应跟踪学习噪声成分,实现MRS 信号有效提取.迭代公式如公式(21)至公式(24)所示,其中,v⊥(n)代表v(n)移相90°后向量,μ 代表可变步长.
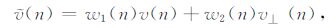
|
(21) |
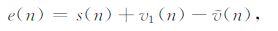
|
(22) |
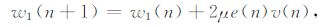
|
(23) |
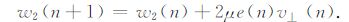
|
(24) |
由于自适应滤波变步长参数μ 与信噪比和信号强度均具有一定的关系,所以要建立μ 与信噪比和信号强度这两者之间的表达式.信噪比的定义为
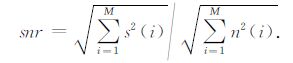
|
(25) |
公式(25)信噪比的定义没有采用dB 的表示方式,避免了求取步长μ 表达式时正负号的影响,后续采用SNR表示snr对应的dB 值.信号强度采用Σx2 来表征(x表示含噪MRS 信号),即噪声一定时,信号越强,其值越大.
本文通过实验方式来建立变步长μ 的表达式.给定一组初始值,振幅e0 ∈ [20~1000]nV,T2 ∈[110~1000]ms, snr∈ [0.3864,3.8640]范围内数值.当给定某一信噪比时,给定某一步长μ 时能够获得最佳输出信噪比,记录此步长值.令
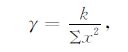
|
(26) |
γ 建立了与信号强度之间的关系.即使信号和环境(MRS信号强度、噪声大小未知)发生变化,如果能够使γ≈μ,就依然能够获得较好输出,基于这种考虑,定义补偿系数:
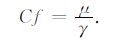
|
(27) |
图 6给出了补偿系数Cf以及Cf经过一系列变换与信噪比snr之间的关系曲线.
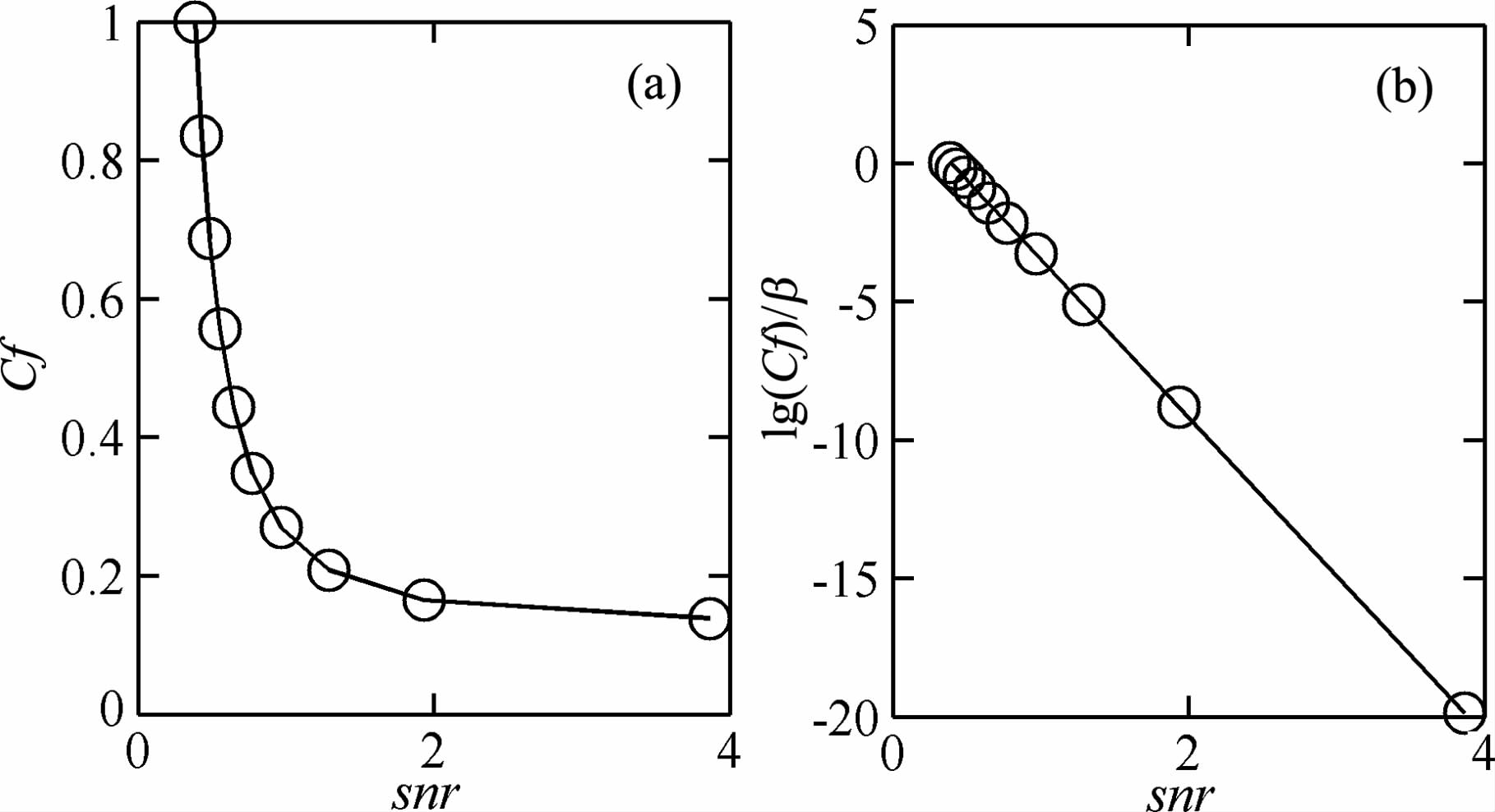
|
图 6 补偿系数Cf与snr关系曲线 Fig. 6 Relation curve between compensating coefficient Cf and snr |
从图 6a 中可以看出,补偿系数Cf与信噪比snr近似成e指数关系变化,将其取对数后,与衰减系数β 相除,获得与信噪比snr近似成线性关系.
经过上述分析,得出变步长表达式:

|
(28) |
其中:a=-5.70,b=2.25,是通过数据拟合获得的值.k=0.1,滤波器阶数M=300.β=[0—1]之间的数值,代表了探测线圈中噪声成分相对于参考线圈噪声成分的衰减,其值越大,表示探测线圈中的噪声成分越大,信噪比snr越低,则要采用较大的步长;反之亦然.Σx2 代表了含噪MRS信号的能量,这样就能够解决不同地下水含量时,步长μ 能够跟随其自适应改变,即当噪声一定时,地下水含量越大,Σx2 越大,γ 越小,相应的步长μ 也跟着减小(此时信噪比较高,所以采用较小的步长就可以跟踪噪声的变化,这与实际情况是相符合的);反之亦然.
4 模型建立及算法仿真分析 4.1 两种模型的建立及仿真为了对90°移相自适应噪声抵消系统去噪的效果进行验证,在MATLAB7.0 环境下,建立两种模型,对算法性能进行仿真实验.
实验满足如下条件:
(1) 含有工频谐波噪声和随机噪声两类典型噪声.
(2) 参考通道工频谐波噪声与主通道工频谐波噪声幅值和相位均不相同.
(3) 参考通道随机噪声与主通道随机噪声不完全相关.这三个条件,使得仿真的信号及噪声与实际信号及噪声情况尽可能相似,能够更好地验证去噪算法是否有效.
模型一:信号中心频率与工频谐波干扰不重叠.MRS信号中心频率f=2325 Hz, 工频谐波干扰频率f1=2350Hz, f2=2450Hz.
图 7至图 9 给出了e0=20nV,T2=150 ms, SNR=-6.3512dB 时的仿真结果.经过自适应滤波处理后,L_SNR=6.2500dB,可见信噪比提高了12.6012dB.经过数据拟合之后,初始振幅的拟合值F_e0 =20.0842nV,弛豫时间的拟合值F_T2 =147.1112 ms, 数据拟合误差分别为0.4212% 和1.9259%.
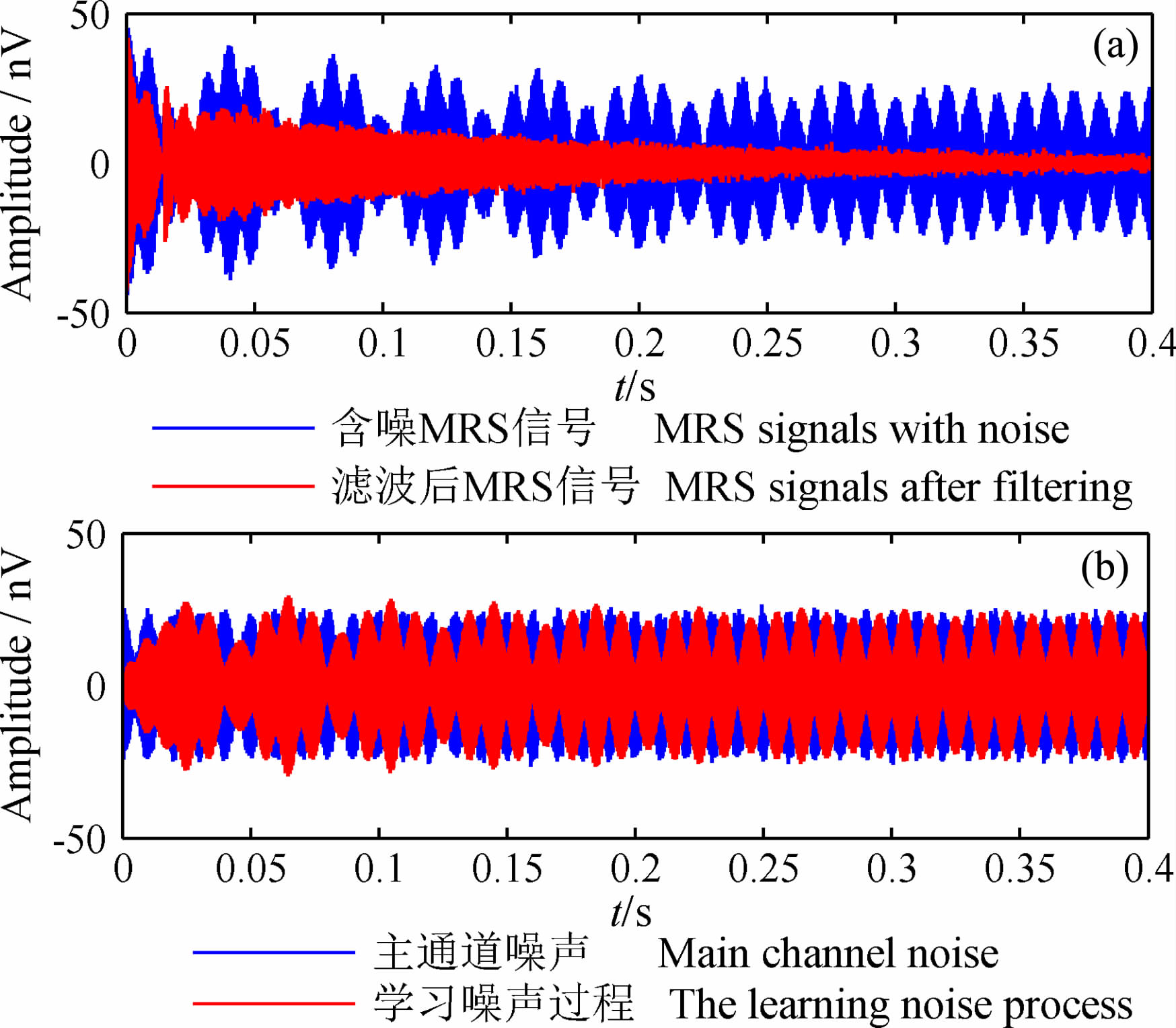
|
图 7 自适应滤波前后MRS信号及自适应学习过程 Fig. 7 MRS signal before and after adaptive filtering and adaptive learning process |
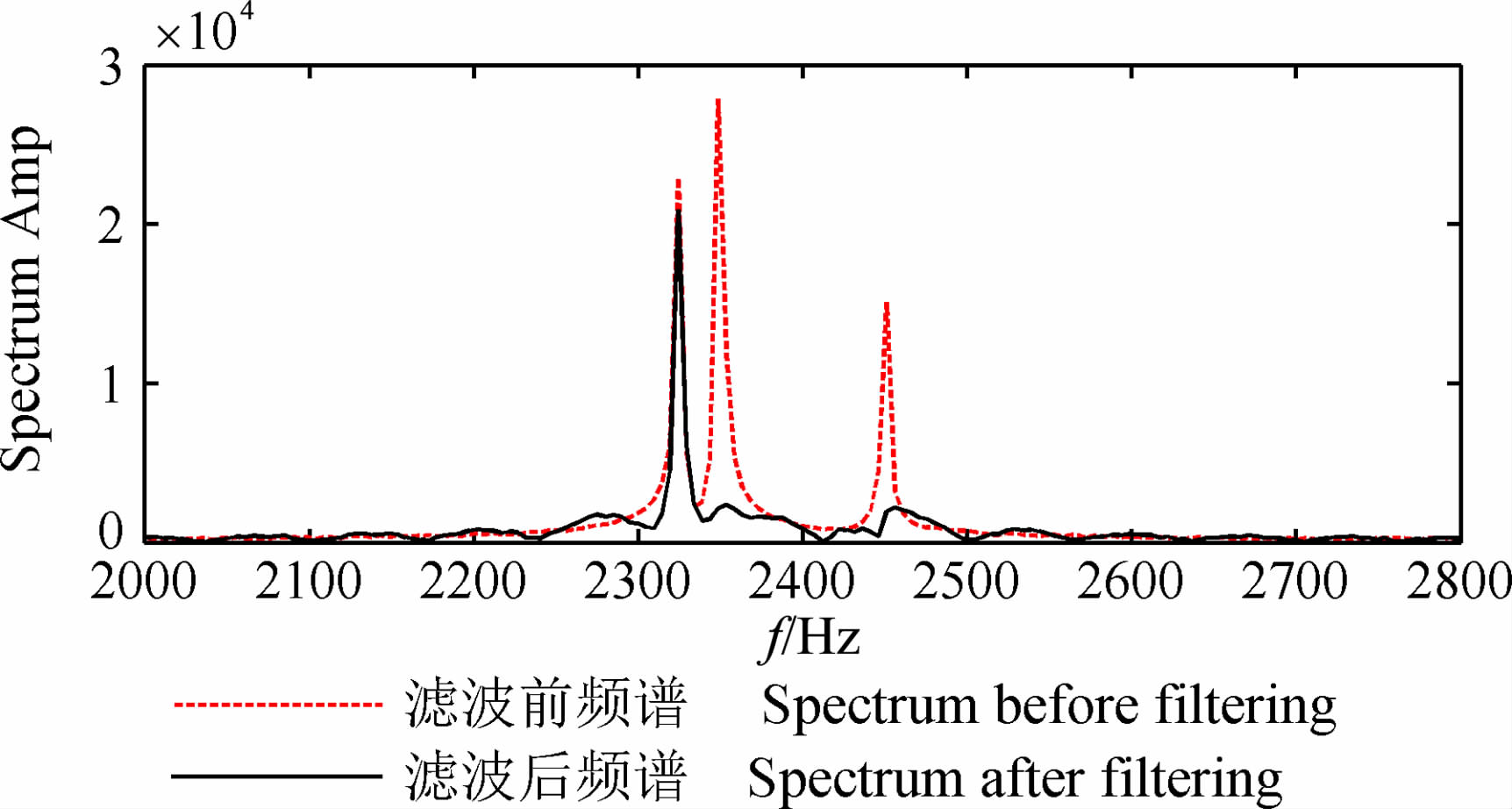
|
图 8 自适应滤波前后MRS信号频谱图 Fig. 8 Spectrum graphic of MRS signal before and after adaptive filtering |
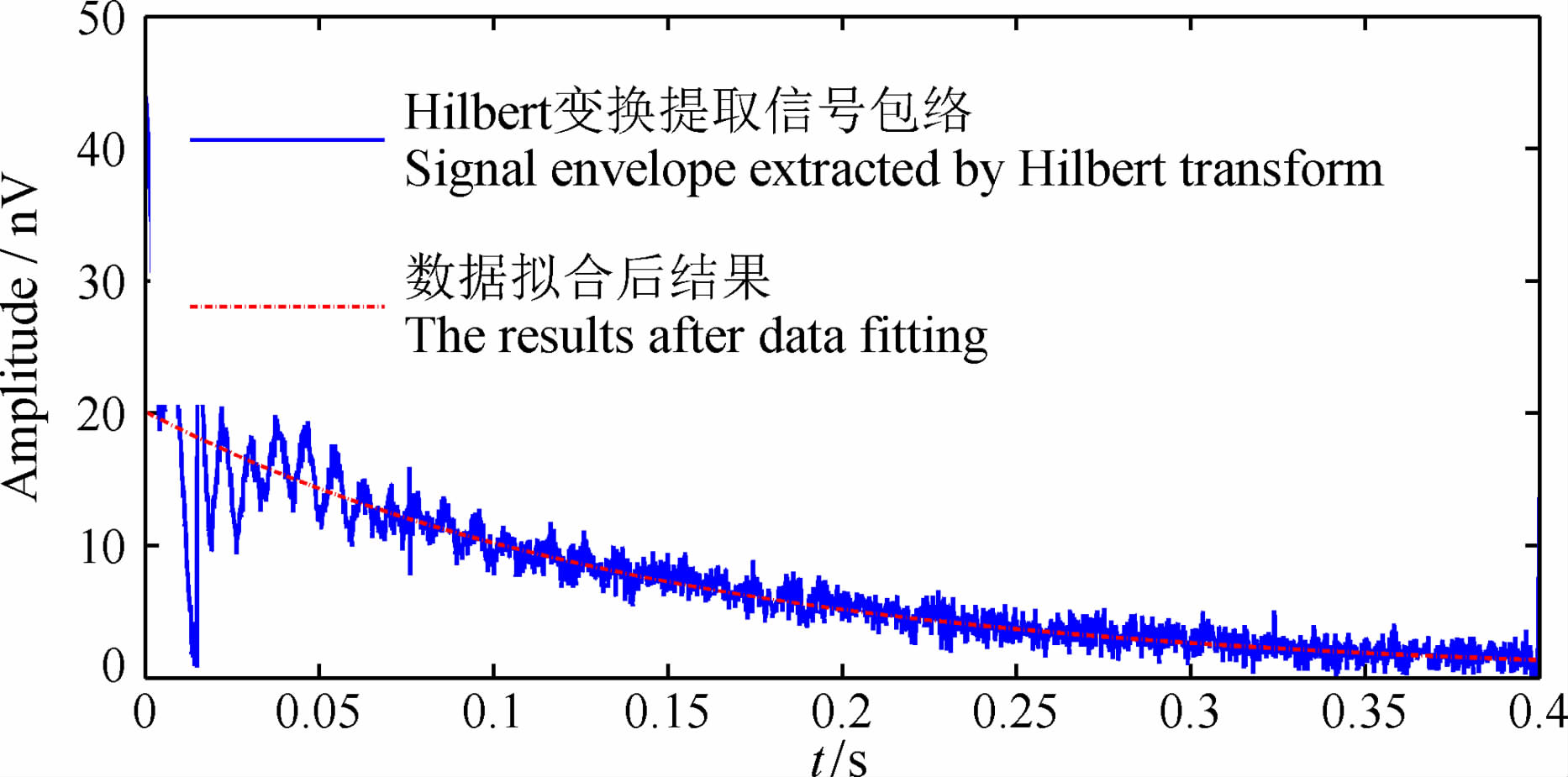
|
图 9 提取自适应滤波后MRS信号包络及拟合结果 Fig. 9 MRS signal envelope extracted after adaptive filtering and fitting |
模型二:信号中心频点与工频谐波干扰频点重合.MRS信号中心频率f=2350 Hz, 工频谐波干扰频率f1= 2350Hz.
对于信号中心频点与工频谐波干扰频点重合的情况,采用模型一提出的变步长自适应噪声抵消算法进行处理,部分结果如图 10所示.
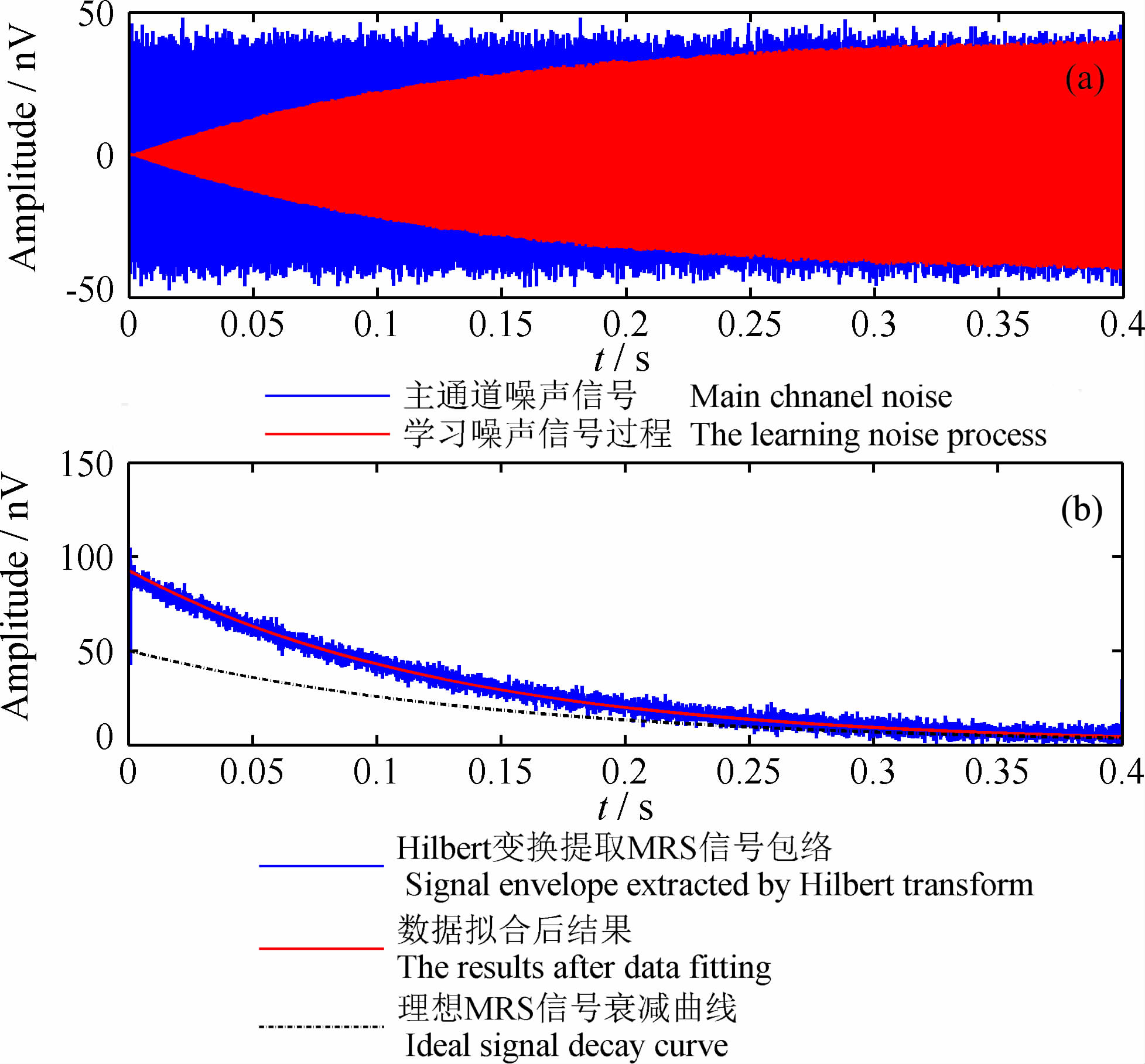
|
图 10 自适应学习噪声过程与数据拟合结果 Fig. 10 Adaptive learning noise process and data fitting |
由图 10可以看出存在的问题:采用模型一的算法只从一个方向进行自适应滤波处理时,起始阶段噪声的学习过程缓慢,这就使得自适应滤波后数据前端仍然含有大量噪声,输出信号的信噪比较低;进而也导致数据拟合结果与理想MRS衰减曲线的偏差非常大.
针对这一问题,当信号中心频点与工频谐波干扰频点重合时,为了使模型二在滤波后具有高信噪比和低数据拟合误差,在算法处理中提出采用双向自适应滤波方式.
所谓双向自适应滤波是指对除了对数据进行正常的自适应滤波处理(正向)之外,再把数据前后翻转进行自适应滤波(反向),然后选择一个连接点,将处理结果拼接.采用变步长表达式与公式(26)、(28)相同,但参数有所变化.其中:a= -6.5,b=3.k=0.1,滤波器的阶数M=10.连接点的选择如图 11所示.
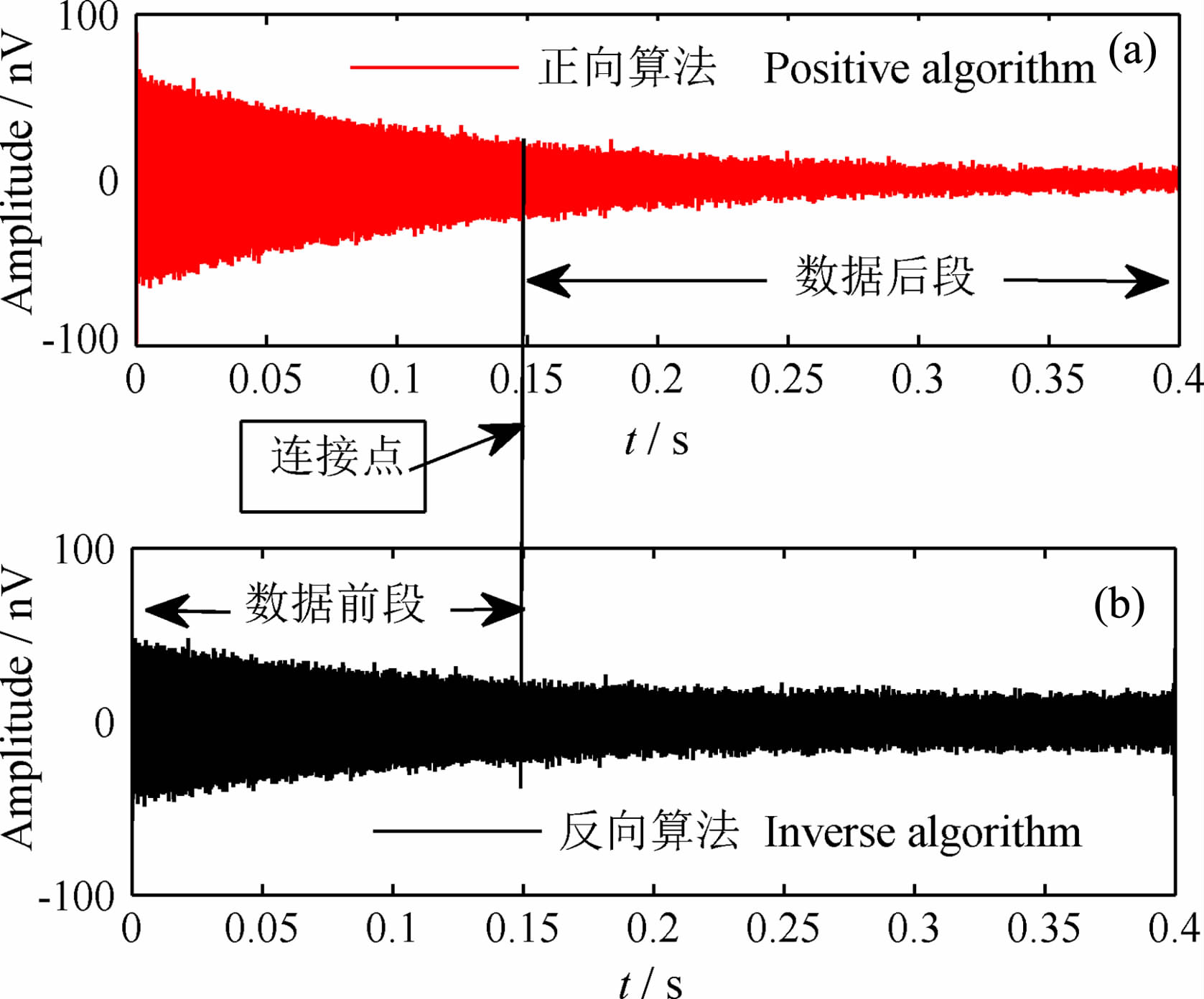
|
图 11 双向自适应滤波器连接点的选择 Fig. 11 Connection point selection of bi directional adaptive filte |
图 12至图 13给出了e0=50nV,T2=150ms, SNR=- 5.3929dB时模型二的仿真结果.经过数据拟合后,初始振幅的拟合值F_e0 =50.3159nV,弛豫时间的拟合值F_T2=147.2300ms, 数据拟合误差分别为0.6317%和1.8467%.
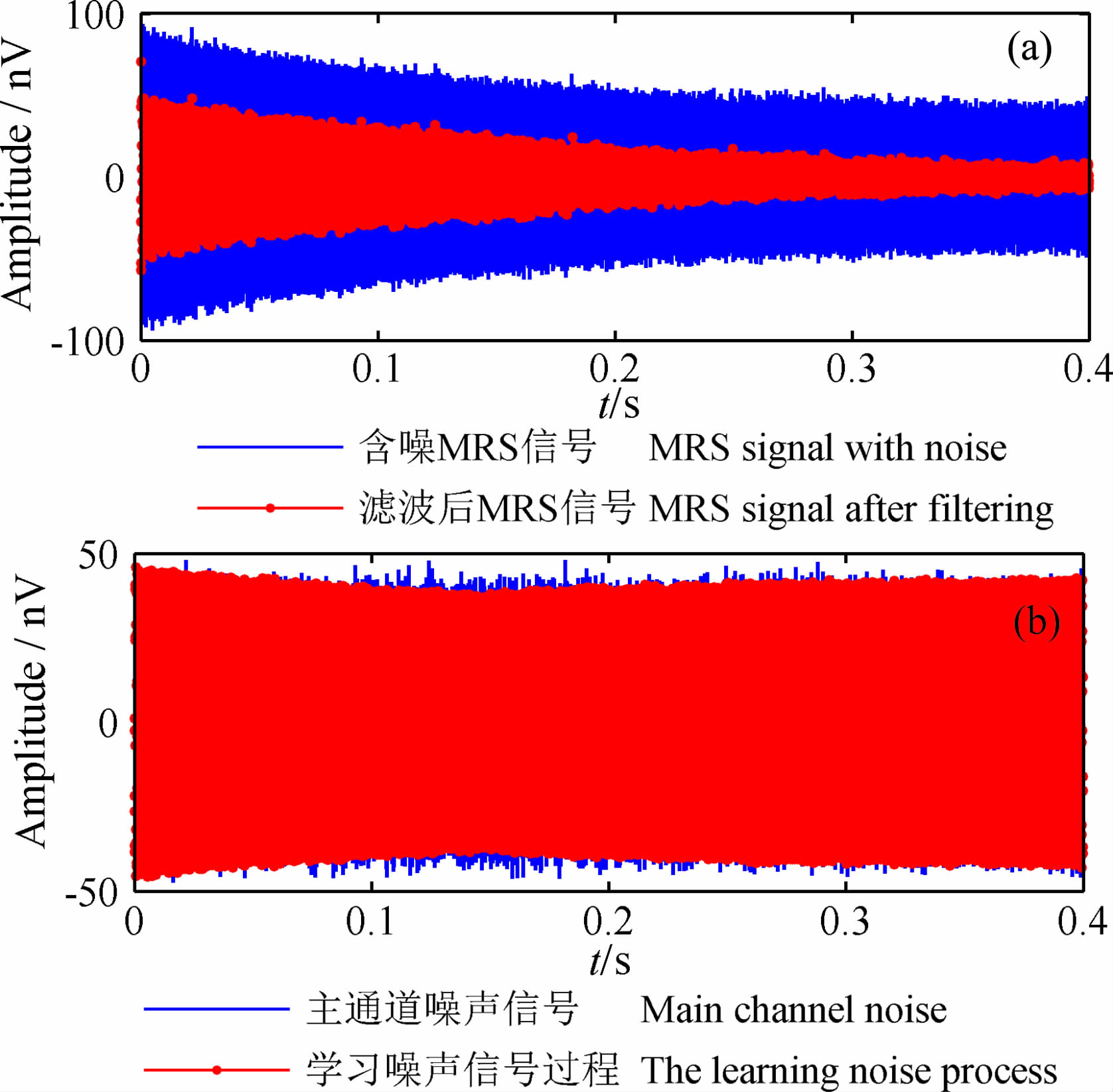
|
图 12 双向自适应滤波前后MRS信号及自适应学习过程 Fig. 12 MRS signal before and after bi-directional adaptive filtering and adaptive learning process |
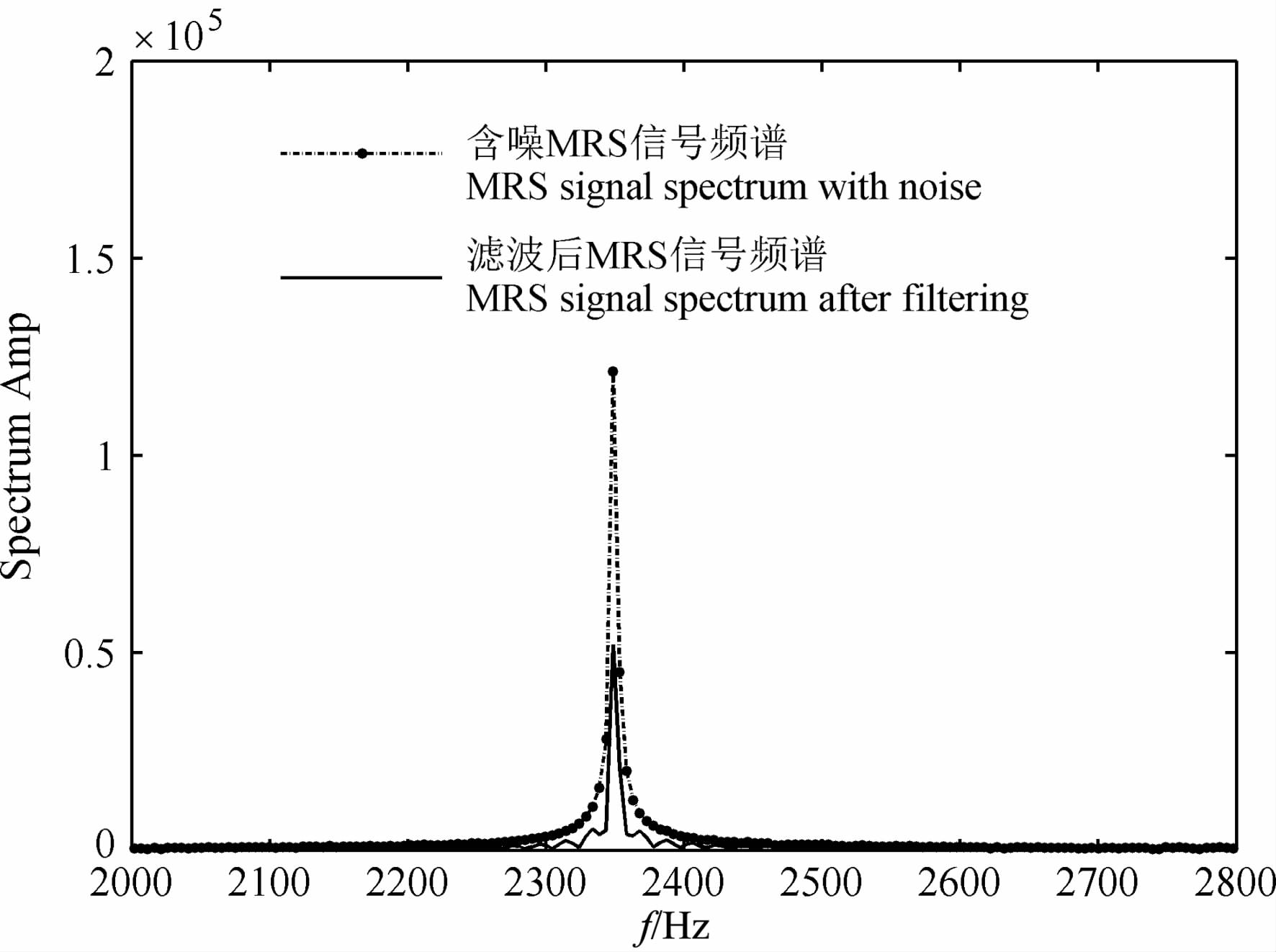
|
图 13 双向自适应滤波前后MRS信号频谱图 Fig. 13 Spectrum graphic of MRS signal before and after bi-directional adaptive filtering |
针对模型一,为比较带参考线圈的变步长自适应噪声抵消后信号与不带有参考的系统输出信号的质量,进行对比实验.
在不同e0下,含噪信号信噪比SNR=-8.2785dB时两种系统的对比结果如表 1所示.
|
|
表 1 不同e0 下,SNR=-8.2785dB两种系统对比结果 Table 1 The comparison results of two systems with differente0and SNR = -832785 dB |
从表 1中可以看出:在强噪声干扰下,经过系统(1)处理的信号信噪比较低,只有0.6298dB,而采用系统(2)处理后信号的信噪比可以达到5.94dB以上;并且系统(1)对于弛豫时间T2 数据拟合误差特别大,均在100% 以上,这是由于系统(1)没有经过噪声对消环节,强工频干扰严重影响了数据拟合结果.而系统(2)经过自适应噪声对消后,基本对消了强工频干扰的影响,初始振幅和弛豫时间的拟合误差均较小.
当e0=50nV一定时,在不同的SNR下,对于两种系统的性能比较如表 2所示.
|
|
表 2 不同 SNR 下,e0=50 nV 时两种系统对比结果 Table 2 The comparison results of two systems with different SNR and e0=50 nV |
从表 2中可以看出:在不同的噪声干扰环境下,系统(1)没经过噪声抵消信噪比提高的很低,弛豫时间T2 数据拟合误差特别大,不符合实际情况;而系统(2)经过自适应噪声对消后信噪比提高较大,初始振幅和弛豫时间的拟合误差均较小.
针对模型二,信号中心频点与工频谐波干扰频点重合时,分别采用双向自适应滤波与单向自适应滤波进行了算法仿真.
图 14给出了当地下水含量变化时(初始振幅e0在20~1000nV 之间),不同信噪比下SNR(-7~1dB范围内)分别采用单向与双向自适应滤波算法得到的信噪比SNR1 以及初始振幅和弛豫时间的数据拟合误差Δe0% 和ΔT2%.从图 14 中可以看出:采用双向自适应滤波算法处理的结果,信噪比均高于单向自适应算法的5dB,在数据拟合误差上,双向自适应算法一般控制在10%以内,优于单向自适应滤波算法的结果.
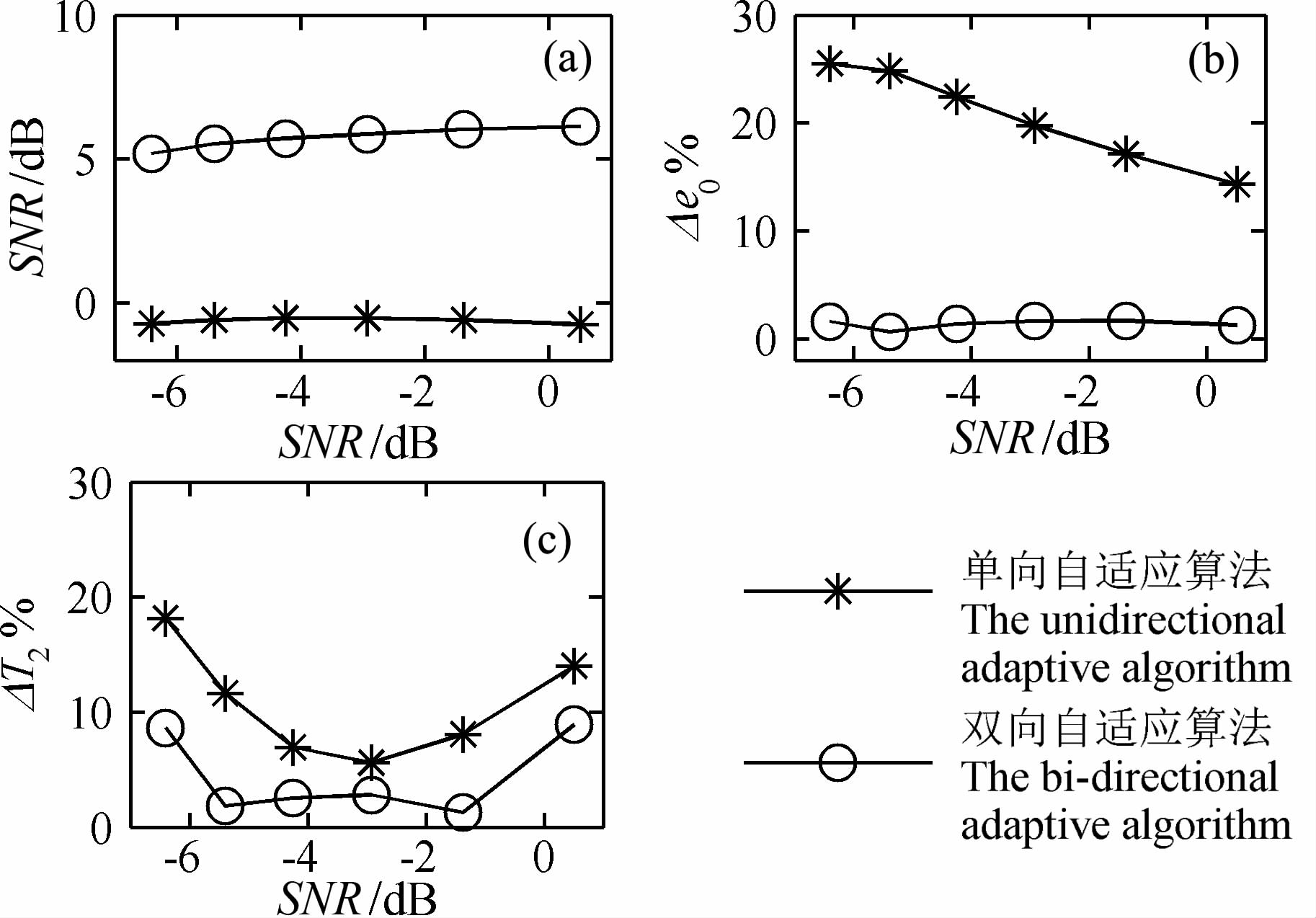
|
图 14 不同信噪比下单双向自适应滤波结果对比 Fig. 14 Result comparison of unidirectional and bi-directional adaptive filter with different SNR |
为了验证算法的性能,在长春市郊区烧锅镇进行了野外实验.实验场地附近有一砖场,是强电力线干扰区.实验采用带有一个参考通道的方式,在近邻砖场附近布设一个100 m×100 m 方形(相当于半径50m 的圆形线圈)参考线圈实现对噪声的采集,在远离砖场的区域布设一个100m×100m 探测线圈实现对含噪信号的采集,两个线圈之间相距100m 以上.当地的拉莫尔频率为2326 Hz, 图 15 给出了在某个测深点主(探测)通道和参考通道采集的含噪信号和噪声的时域波形以及相应的频谱图.
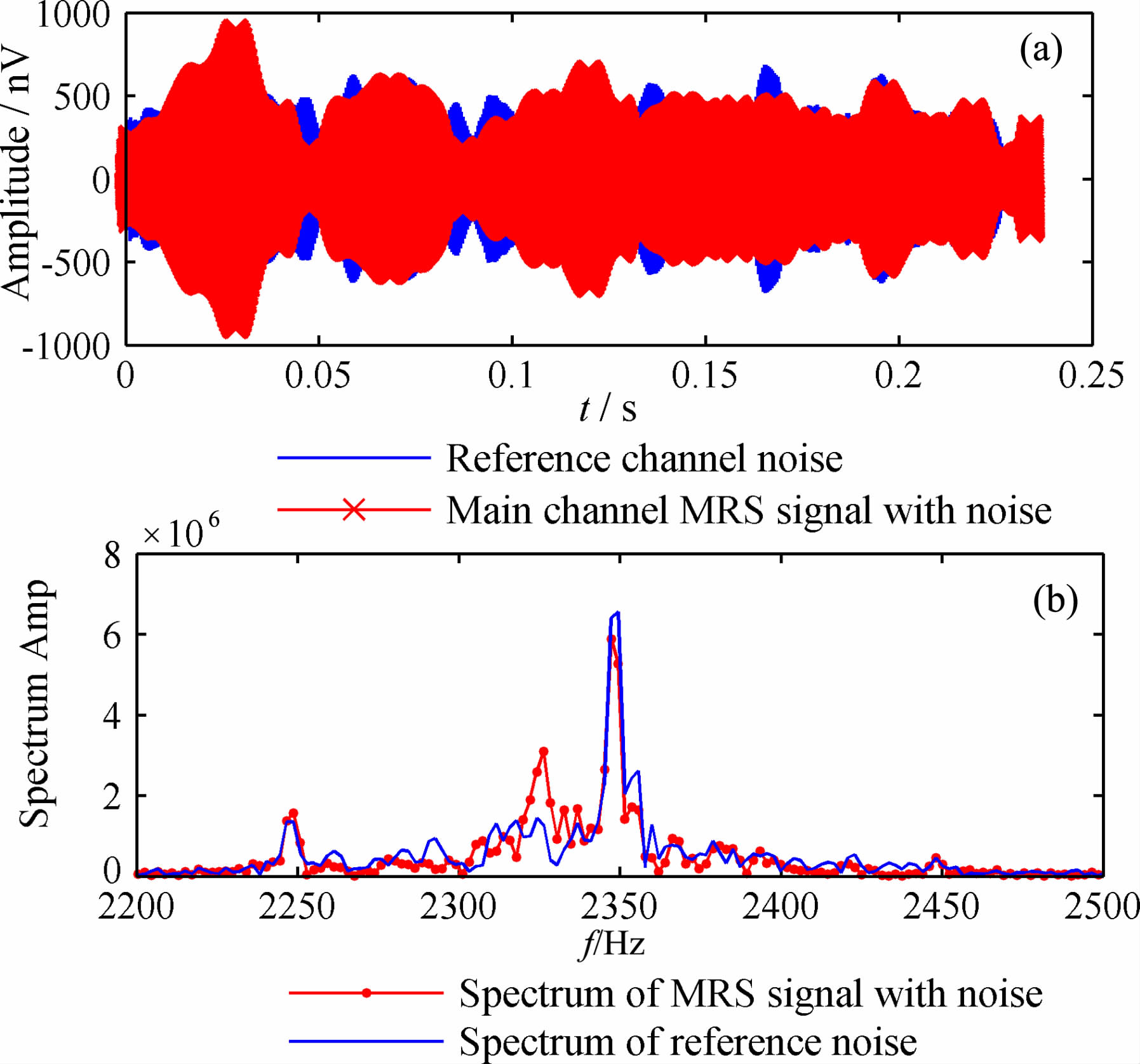
|
图 15 双通道采集的含噪信号与噪声及其频谱 Fig. 15 MRS signal and reference noise collected from double-channel and their spectrum |
图 15a给出了主通道采集的含噪MRS 信号(红色)以及参考通道采集的噪声信号(蓝色);结合图 15b频谱分析可以看出:主通道采集含噪MRS信号,其工频47 次谐波2350 Hz处的干扰最为严重,其幅值远远大于2326 Hz处有用的MRS 信号频谱幅值,信号被强工频干扰所淹没;同时分析参考通道采集的噪声信号频谱,并不含有有用的MRS信号频率成分,这也验证了参考线圈相对于探测线圈位置的理论计算的正确性.
图 16给出了采用变步长自适应噪声抵消算法对上述实测数据处理前后频谱对比的结果.从图 16中可以看出:2350 Hz和2250 Hz处的工频干扰被滤除.仪器系统所采用的采样频率为172kHz, 滤波器阶数设置为M=800,变步长算法中的参数分别为:a=-6,b=3,k=0.5.估算原始含噪MRS信号的信噪比为SNR0=-6.0666dB,滤波处理后信噪比为SNR1=5.2964dB.
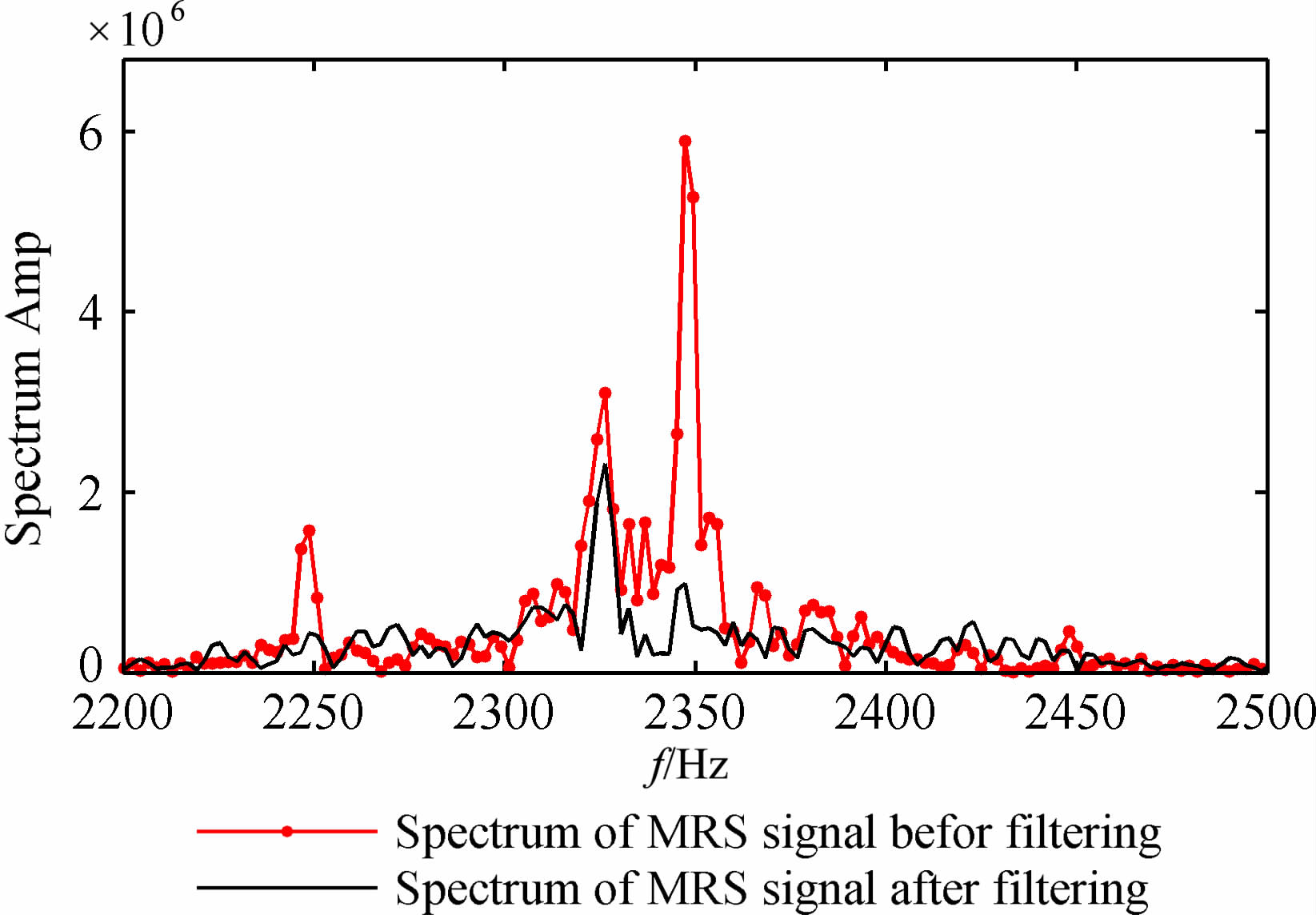
|
图 16 实测数据自适应滤波前后频谱图 Fig. 16 Spectrum of MRS signal before and after filtering |
为了进一步说明方法的有效性,分别对不同信噪比下的另外两个测试数据进行了处理,结果如图
17所示.
由图 17的频谱可以看出,对于不同信噪比实测数据,算法均可以获得较好的滤波效果.
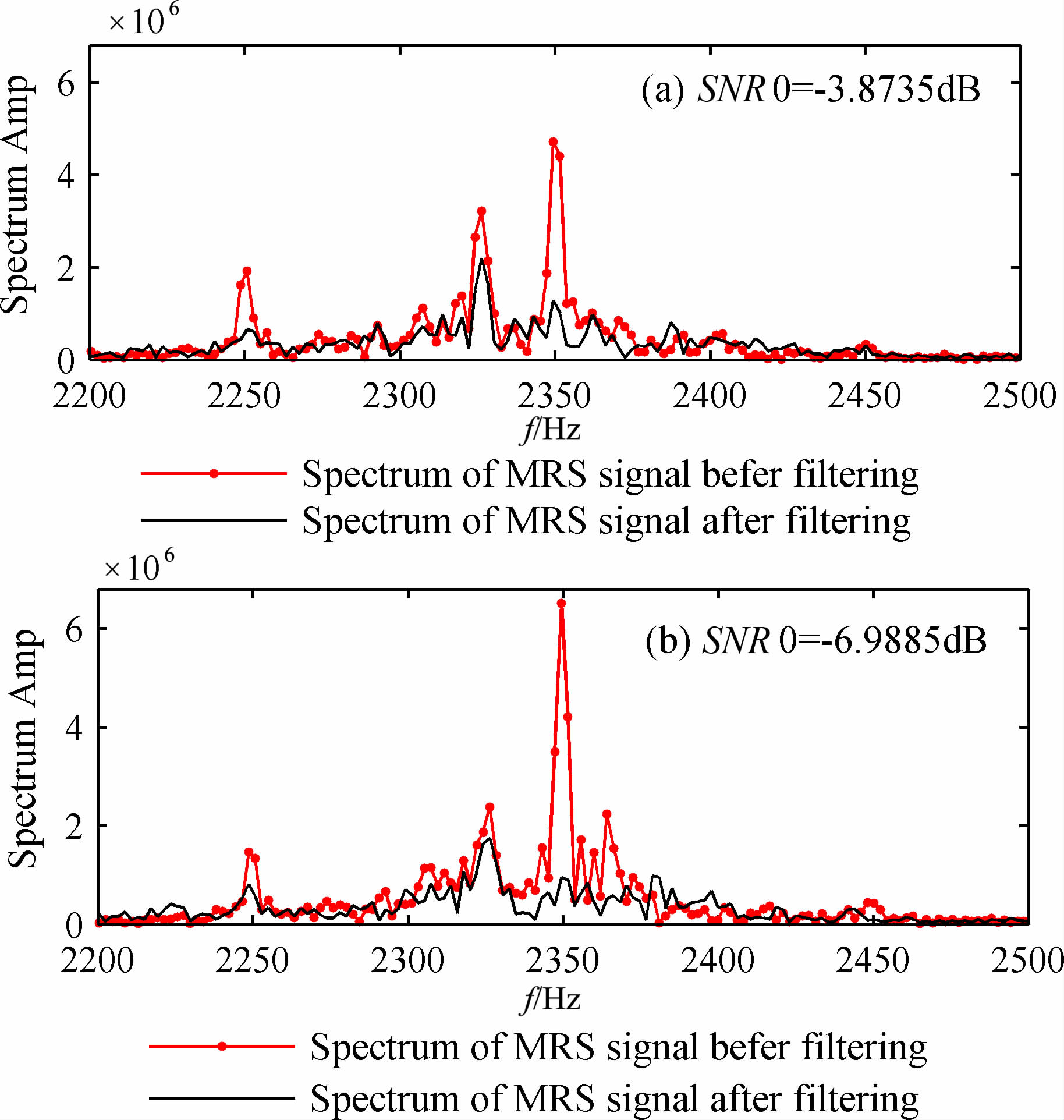
|
图 17 不同信噪比下实测信号处理结果 Fig. 17 Processing results of MRS signal on different SNRs |
在强电磁噪声干扰下如何更好地实现微弱MRS信号的提取是核磁共振地下水探测中的一个关键问题,它将影响到反演解释水文地质参数信息的精确度.自适应滤波可以在没有先验知识的情况下,直接利用观测数据不断递归更新处理参数,以逐步逼近某一最优值.本文根据自适应滤波的这一特点,针对强工频谐波干扰问题,设计带有参考线圈的自适应噪声抵消系统,采用变步长自适应LMS 算法,实现不同信噪比和信号强度下MRS 信号噪声的去除.通过数值计算、算法仿真和实测数据处理得出如下结论:
(1) 探测线圈采用收发共线方式时,对于半径50m 单匝圆形线圈,参考线圈距离探测线圈至少在100m 以外才能保证参考线圈仅接收噪声而不接收MRS信号.
(2) 当MRS信号与工频谐波频点不重合时,采用带有参考线圈的90°移相自适应噪声抵消系统能够实现淹没在强噪声背景中MRS 信号的有效提取,滤波后信噪比可以达到5.94dB以上,经数据拟合提取到初始振幅、弛豫时间特征参数的误差小于2.8%.
(3) 当MRS信号与工频谐波频点重合时,采用双向自适应滤波算法比单向自适应滤波算法能够获得更好的去噪效果,信噪比达到5dB 以上,初始振幅和弛豫时间的数据拟合误差能够控制在10% 以内,可以满足实际应用的要求.
(4) 实测数据处理表明,在地下水含量未知的条件下,对于不同强度的工频谐波干扰(信噪比不同),提出的变步长LMS算法均获得了较好去噪效果.在实际核磁共振地下水探测应用中,由于核磁共振测试数据还会受到除工频谐波之外,尖峰噪声、其他未知噪声等多种影响,噪声成分要复杂的多.因此,在运用本文算法对核磁共振野外实测信号进行噪声对消时,对滤波器阶数、变步长表达式等参数进行了相应修正.后续将进一步研究基于小波变换、经验模态分解等方法对其他噪声进行消除的问题.致 谢 在方法的研究过程中,得到吉林大学核磁共振研制与开发课题组成员的支持与帮助,在此一并表示衷心的感谢.
致 谢 在方法的研究过程中,得到吉林大学核磁共振研制与开发课题组成员的支持与帮助,在此一并表示衷心的感谢.
| [1] | Schirov M, Legchenko A, Creer G. New direct non-invasive ground water detection technology for Australia. Exploration Geophysics , 1991, 22(2): 333-338. DOI:10.1071/EG991333 |
| [2] | Lubczynski M, Roy J. Hydrogeological interpretation and potential of the new magnetic resonance sounding (MRS) method. Journal of Hydrology , 2003, 283(1-4): 19-40. DOI:10.1016/S0022-1694(03)00170-7 |
| [3] | Roy J, Lubczynski M. The magnetic resonance sounding technique and its use for groundwater investigations. Hydrogeology Journal , 2003, 11(4): 455-465. DOI:10.1007/s10040-003-0254-8 |
| [4] | 林君. 核磁共振找水技术的研究现状与发展趋势. 地球物理学进展 , 2010, 25(2): 681–691. Lin J. Situation and progress of nuclear magnetic resonance technique for groundwater investigations. Progress in Geophysics (in Chinese) (in Chinese) , 2010, 25(2): 681-691. |
| [5] | Yaramanci U, Lange G, Hertrich, M. Aquifer characterisation using Surface NMR jointly with other geophysical techniques at the Nauen/Berlin test site. Journal of Applied Geophysics , 2002, 50(1-2): 47-65. DOI:10.1016/S0926-9851(02)00129-5 |
| [6] | Perttu N, Wattanasen K, Phommasone K, et al. Characterization of aquifers in the Vientiane Basin, Laos, using magnetic resonance sounding and vertical electrical sounding. Journal of Applied Geophysics , 2011, 73(3): 207-220. DOI:10.1016/j.jappgeo.2011.01.003 |
| [7] | Chalikakis K, Nielsen M R, Legchenko A. MRS applicability for a study of glacial sedimentary aquifers in Central Jutland, Denmark. Journal of Applied Geophysics , 2008, 66(3-4): 176-187. DOI:10.1016/j.jappgeo.2007.11.005 |
| [8] | Plata J, Rubio F. MRS experiments in a noisy area of a detrital aquifer in the south of Spain. Journal of Applied Geophysics , 2002, 50(1-2): 83-94. DOI:10.1016/S0926-9851(02)00131-3 |
| [9] | Legchenko A, Valla P. Processing of proton magnetic resonance signals using non-linear fitting. Journal of Applied Geophysics , 1998, 37(2): 77-83. |
| [10] | Legchenko A, Valla P. A review of the basic principles for proton magnetic resonance sounding measurements. Journal of Applied Geophysics , 2002, 50(1-2): 3-19. DOI:10.1016/S0926-9851(02)00127-1 |
| [11] | Legcenko A, Valla P. Removal of power line harmonics from proton magnetic resonance measurements. Journal of Applied Geophysics , 2003, 53(2-3): 103-120. DOI:10.1016/S0926-9851(03)00041-7 |
| [12] | Legchenko A, Baltassat J M, Beauce A, et al. Nuclear magnetic resonance as a geophysical tool for hydrogeologists. Journal of Applied Geophysics , 2002, 50(1-2): 21-46. DOI:10.1016/S0926-9851(02)00128-3 |
| [13] | Butler K E. Comment on design of a hum filter for suppressing power-line noise in seismic data. Journal of Environmental and Engineering Geophysics , 2001, 6(2): 103-104. DOI:10.4133/JEEG6.2.103 |
| [14] | Legchenko A. MRS measurements and inversion in presence of EM noise. Boletín Geológicoy Minero , 2007, 118(3): 489-508. |
| [15] | Choi J W, Cho N I. Suppression of narrow-bandinterferenc DS-spreadspectrum systems using adaptive IIR notch filter. Signal Processing , 2002, 82(12): 2003-2013. DOI:10.1016/S0165-1684(02)00385-7 |
| [16] | Strehl S, Rommel I, Hertrich M, et al. New strategies for filtering and fitting of MRS signals. International MRS Workshop. Madrid, Spain , 2006: 65-68. |
| [17] | Strehl S. Development of Strategies for Improved Filtering and Fitting of SNMR-Signals. Germany: Technical University of Berlin, Institute of Applied Geosciences, Department of Applied Geophysics Diplomarbeit, 2006. http://www.oalib.com/references/18988468 |
| [18] | Walsh D O. Multi-channel surface NMR instrumentation and software for 1D/2D groundwater investigations. Journal of Applied Geophysics , 2008, 66(3-4): 140-150. DOI:10.1016/j.jappgeo.2008.03.006 |
| [19] | 王应吉, 林君, 荣亮亮, 等. 地面核磁共振找水仪放大器设计. 仪器仪表学报 , 2008, 29(8): 1627–1632. Wang Y J, Lin J, Rong L L, et al. Amplifier design of surface nuclear magnetic resonance instrument for underground water investigation. Chinese Journal of Scientific Instrument (in Chinese) (in Chinese) , 2008, 29(8): 1627-1632. |
| [20] | 王中兴, 荣亮亮, 林君, 等. 基于4 倍频采样的数字正交FID 信号检测技术. 数据采集与处理 , 2010, 25(5): 626–630. Wang Z X, Rong L L, Lin J, et al. FID signal detection based on DLIA sampled by quadruple Lamor frequency. Journal of Data Acquisition and Processing (in Chinese) (in Chinese) , 2010, 25(5): 626-630. |
| [21] | Jiang C D, Lin J, Duan Q M, et al. Statistical stacking and adaptive notch filter to remove high-level electromagnetic noise from MRS measurements. Near Surface Geophysics , 2011, 9(5): 459-468. |
| [22] | Nandi Z. Noninvasive fetal electrocardiogram extraction: Blind separation versus adaptive noise cancellation. IEEE Transactions on Biomedical Engineering , 2001, 48(1): 11-18. |
| [23] | Gnitecki J, Moussavi Z, Pasterkamp H. Recursive least squares adaptive noise cancellation filtering for heart sound reduction in lung sounds recordings. IEEE Engineering in Medicine and Biology Society , 2003, 3(17-21): 2416-2419. |
| [24] | 林君, 段清明, 王应吉, 等. 核磁共振找水仪原理与应用. 北京: 科学出版社, 2010 . Lin J, Duan Q M, Wang Y J, et al. Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and Its Applications (in Chinese). Beijing: Science Press (in Chinese), 2010 . |
| [25] | Haykin S. Adaptive Filter Theory. Upper Saddle River, New Jersey: Prentice Hall, 1996. http://www.oalib.com/references/17201481 |
 2012, Vol. 55
2012, Vol. 55