2. 油气资源与探测国家重点实验室, 北京 102249;
3. 海洋石油勘探国家工程实验室, 北京 102249
2. State Key Laboratory of Petroleum Resource and Prospecting, Beijing 102249, China;
3. National Engineering Laboratory for Offshore Oil Exploration, Beijing 102249, China
时移地震油藏监测技术测量由于油气生产造成的地震响应变化.由地震响应的变化(即反射系数的变化)可以得到纵横波阻抗和密度等弹性参数的变化,而这些弹性参数的变化可以进一步结合岩石物理模型转换为储层参数的变化,如流体饱和度和压力的变化等[1-5].不同时期的地震资料,通过时移地震资料匹配处理技术使其具有较好的重复性,能够通过其差异获得储层属性的变化.
时移地震反演有许多不同的方法,常见的有分别反演、同时反演和差异反演.分别反演是基础和监测资料各自反演,然后将反演结果求差;同时反演是将基础资料和监测资料同时进行联合反演,最终得到参数的差异结果;差异反演是直接在差异数据上进行反演,从而直接得到参数的变化.Sarkar等[4]的研究表明,不同年份时移地震数据间的反演有必要进行一些耦合,否则将引起最终模型的假象,从而导致不正确的解释结果,差异反演能够提供必要的耦合条件.所以如果基础测量和监测测量数据间的可重复性是合适的,差异反演是最合适的时移地震反演方法.
很多学者对时移地震反演方法进行了研究,Gluck等[6]研究了时移地震波阻抗反演,Abubakar等[7]探讨了时移地震非线性反演的可行性,Buland等[8]提出了基于贝叶斯理论的时移地震差异反演方法,李来林等[9]从最基本的地震波阻抗和地震反射系数关系式出发,推导出采用一次地震结果及测井资料计算近似时移波阻抗的方法.李景叶等[10-11]推导了时移地震AVO 反演计算方法,有效地分离油藏含油饱和度和有效压力的变化,实现对油藏的定量解释,并进一步研究了多波时移地震AVO 反演问题.陈小宏等[12]提出了基于岩石物理模型和混合优化算法的时移地震反演压力、饱和度变化方法.陈勇等[13]针对时移地震反演中待反演参数不连续的情况,构造了多尺度全变分法,提高了算法精度和计算效率.Eidsvik[14]研究了基于贝叶斯理论的时移地震AVO 块反演方法(Blockyinversion),对挪威海域时移地震数据进行了处理,结果显示该方法能更好地反映时移弹性参数的变化.Kato 等[15]研究了基于贝叶斯理论的时移地震AVO 同时反演方法.Hansteen等[16]提出了基于折射波的时移时间监测方法,得到比常规4D 地震成本更低的高分辨率储层时移平面图,进行时移地震监测.Suman 等[17]提出了时移地震数据和生产数据的联合反演方法.Zhao等[18]结合岩石物理模型和基于贝叶斯理论的叠前AVO 反演来预测碳酸盐岩含气储层,Li等[19]研究了时移地震弹性波阻抗差异反演及其应用,Zhu等[20]研究了利用叠前时移地震差异数据进行弹性波阻抗反演的方法,Asnaashari等[21]提出了通过时移地震差异波形反演进行时移地震成像的敏感性分析方法.
在时移地震反演过程中,十分突出的问题是注采过程导致的时移地震数据差异不大,同时采集和处理过程中存在一定的差异,不同年份地震资料在非注采过程影响区域也有一定的变化,导致最终的反演结果不理想.针对此问题,本文利用贝叶斯体系将纵横波阻抗和密度变化的先验信息和包含在时移地震数据中的信息结合起来.对于纵横波阻抗和密度变化,认为其概率密度函数为高斯分布函数,同时为了得到更好的差异反演结果,将时移地震分别反演结果作为其期望.对于弹性参数变化的导数,认为其服从改进的Cauchy分布[22],改进的Cauchy分布能够得到比常规Cauchy 分布更为稀疏的结果,从而突出真实的参数改变,更好地表征地下流体的变化,抑制非注采过程影响区域的弹性参数变化的假象.
2 贝叶斯AVO 反演方法 2.1 建立正演模型 2.1.1 Gidlow 近似方程

|
(1) |
其中,θ 表示入射角,ΔIp/2Ip 表示纵波阻抗反射系数,ΔIs/2Is 表示横波阻抗反射系数,Δρ/2ρ 表示密度反射系数,γ 表示横波速度与纵波速度的比值.将(1)式离散方程形式转换为时间连续的方程形式:
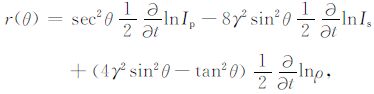
|
(2) |
其中,Ip, Is, ρ 分别为纵波阻抗、横波阻抗和密度.
2.1.2 叠前数据褶积模型令待求参数向量为
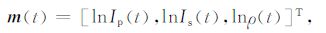
|
(3) |
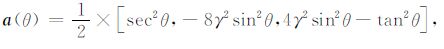
|
(4) |
则方程(2)所示的反射系数函数可以改写为
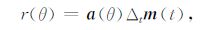
|
(5) |
Δt表示对时间求导.将待求参数向量m(t)离散化,同样用m表示,
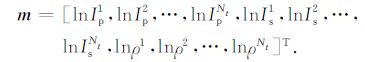
|
(6) |
令一阶差分算子为F,与角度有关的线性算子矩阵为A,则反射系数用矩阵形式表示为
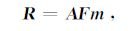
|
(7) |
假设子波矩阵为W,叠前道集为d,则
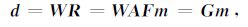
|
(8) |
其中,G= WAF,d= [d(θ1),d(θ2),…,d(θNθ)]T,θ1,θ2,…,θNθ为角度,Nθ 为参与计算角度个数,d(θ1),d(θ2),…,d(θN)表示不同角度观测到的地震记录,Nt为离散模型参数的个数,Nd为数据采样点数,则得到正演模型为
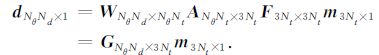
|
(9) |
在时移地震反演中,油藏的变化限定在特定的地层中,而在非油藏部分,时移地震基础测量资料和监测测量资料应该是相同的.差异反演从时移地震差异资料(监测测量资料-基础测量资料)中直接得到弹性参数的差值,进而表征油藏参数变化.
设时移地震基础测量资料为d1,监测测量资料为d2,δ 为监测测量资料与基础测量资料之差(δ=d2-d1),基础测量时油藏弹性参数的自然对数为m1,监测测量时油藏弹性参数的自然对数为m2,φ为弹性参数的自然对数的差值(φ=m2-m1),则
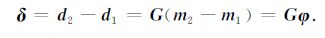
|
(10) |
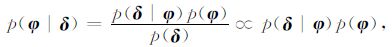
|
(11) |
待求参数向量φ 最可能的值对应PPDF 的最大值,参数估计不确定性的大小对应PPDF 的宽度.如果仅关心PPDF的形状,分母p(δ)是个可被忽略的常数.贝叶斯反演方法主要利用解估计的先验信息来克服反演问题求解的不适定性.p(δ狘φ)为似然函数,p(φ)为先验分布.
2.2.2 似然函数研究中认为地震噪声服从正态分布,则似然函数如下:
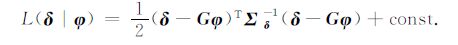
|
(13) |
由于信息量有限,反演问题往往是多解的,为了降低其多解性,可以根据已知信息增加约束条件.Todoeschuck等[24]通过对测井数据的样点值进行统计得到了这样的认识,从整口井的范围来看,测井数据不符合正态分布,但是如果只取其中一小段进行研究,则是正态分布的.而反演工作通常只是对目的层段进行反演,可以认为这一小段的弹性参数是服从正态分布的.Buland等[8]假设弹性参数的变化φ 服从正态分布,研究了基于贝叶斯理论的时移地震差异反演方法.本文根据Buland等所做的工作,假设先验模型服从正态分布:
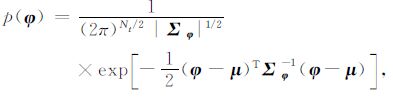
|
(14) |
同样,为计算方便,对上面的函数取负对数
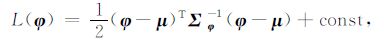
|
(15) |
式中,Σφ 为参数协方差矩阵,该矩阵约束了待求参数偏离均值(本文中为低频模型)的程度.通常生成协方差矩阵的方法是利用反演工区测井资料的弹性参数(如纵波阻抗、横波阻抗和密度)进行统计估计.因此,测井资料的好坏直接影响着反演结果的好坏,利用有代表性的测井资料或者对较多测井资料的统计情况进行综合考虑会得到较好的反演结果.
Walden[25]证明,反射系数服从长尾分布的假设是合理的,而反射系数服从长尾分布意味着反射系数是稀疏的.时移地震反演监测由于注采过程引起的储层流体变化情况,这种小范围的储层流体变化导致的参数变化应该是稀疏的.本文中,弹性参数变化的导数(R′=ADφ)可以理解为参数的反射系数,而改进的Cauchy分布为长尾分布中计算较为简便的一种.因此,为了突出油藏注采导致的储层流体变化,抑制非注采区域的假象,认为弹性参数变化的导数满足改进的Cauchy分布,其表达式为
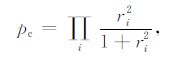
|
(16) |
其中R′ =ADφ,ri为矩阵R′ 中的元素,表示第i个采样点处的值.为计算方便,对上面的函数取对数,并进行归一化,得到
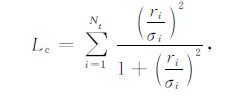
|
(17) |
其中,σi为相应的尺度常数.对(17)式求导得
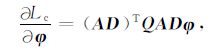
|
(18) |
其中Q为对角矩阵,其对角元素为

|
(19) |
用公式(11)将似然函数与先验分布结合起来,得到反演的目标函数为
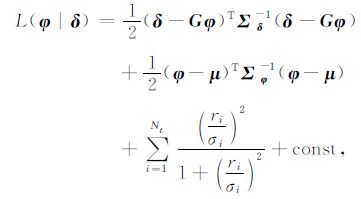
|
(20) |
为求极值,将方程(20)求导,并令其导数为0,得到
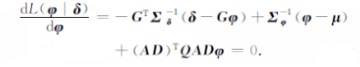
|
(21) |
将式(21)进行整理可以得到时移地震差异反演方程式:
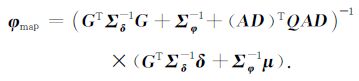
|
(22) |
利用公式(22)就可以反演出不同年份间纵波阻抗、横波阻抗和密度值的对数的差值,再利用常规反演得到的开发前(或开发后)的纵波阻抗、横波阻抗和密度值进行简单计算,就可以得到不同年份间纵波阻抗、横波阻抗和密度差值.
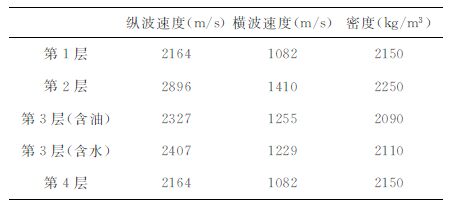
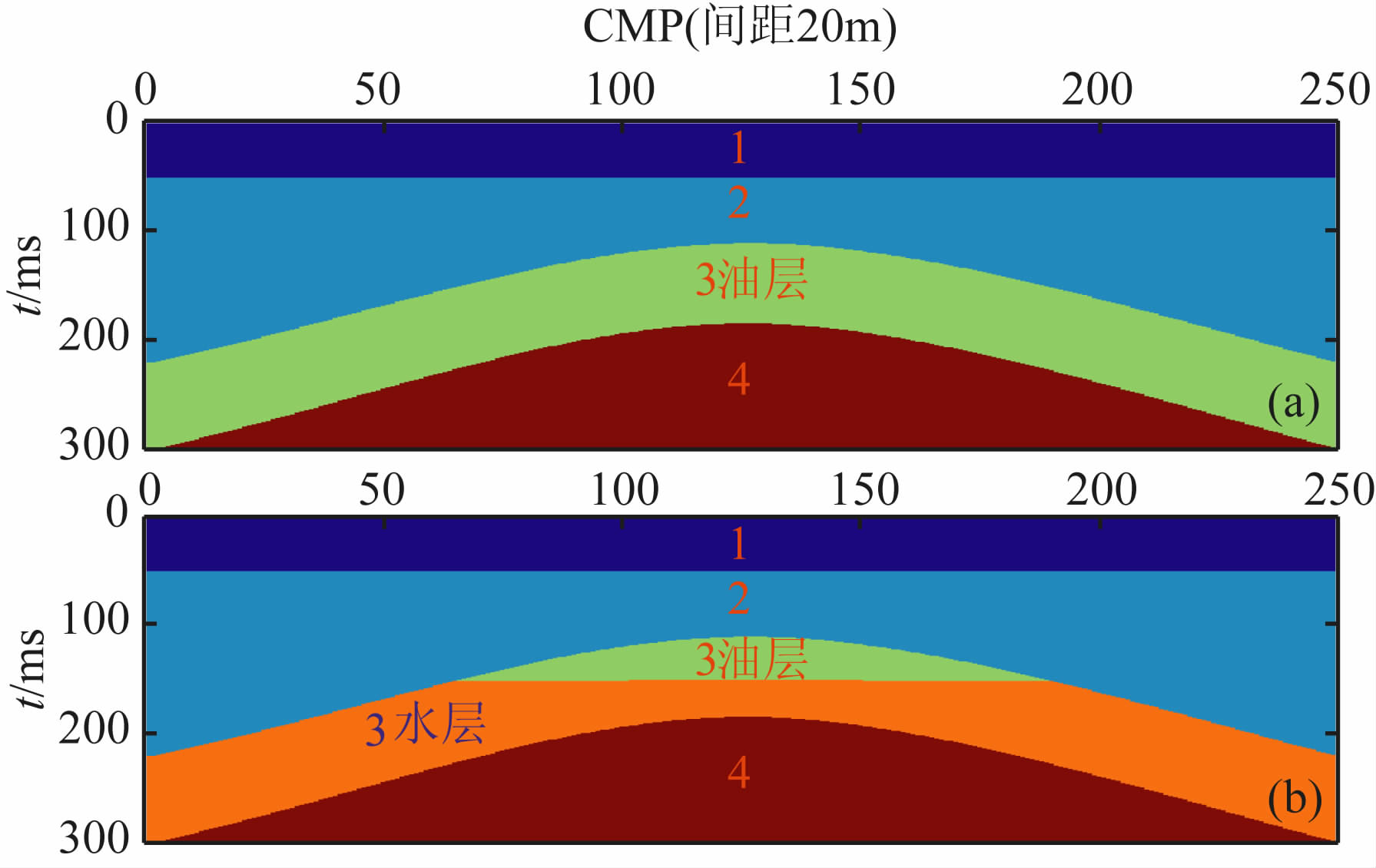
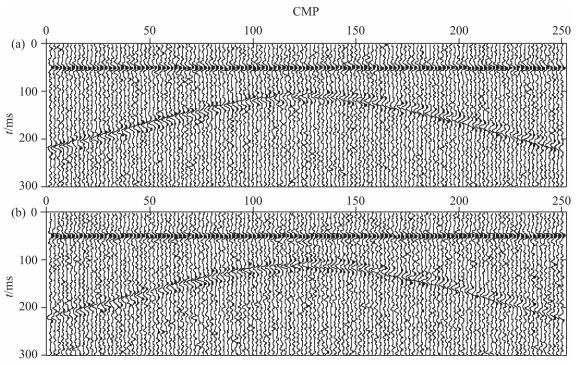
3 模型试算研究构建了如图 1所示的油藏地质模型,图 1a为油藏开发前地质模型,图 1b为开发后地质模型,CMP间距为20m, 模型参数见表 1.图 1a中第3层为含油层,为油藏开发区,其他区域为非油藏开发区.经过注采过程第3层变成如图 1b所示的油层和水层.采用精确Zoeppritz方程生成基础模型和监测模型的反射系数,用40 Hz雷克子波与其褶积生成基于基础模型和监测模型的合成叠前共角度地震记录剖面,角度分别为10°、20°、30°和40°,采样间隔为1ms, 对两个模型数据分别添加高斯噪声,加噪后地震数据的信噪比为1∶1.图 2a和图 2b分别是入射角为10°的基础模型和监测模型共角度地震记录剖面,20°、30°和40°的共角度地震记录剖面与此类似,这里不予显示.
|
|
表 1 时移地震地质模型弹性参数 Table 1 Elastic parameters of the time-lapse seismic geological model |
|
图 1 时移地震地质模型 (a)油藏开发前;(b)油藏开发后. Fig. 1 Time-lapse seismic geological model (a) Before production; (b) After production. |
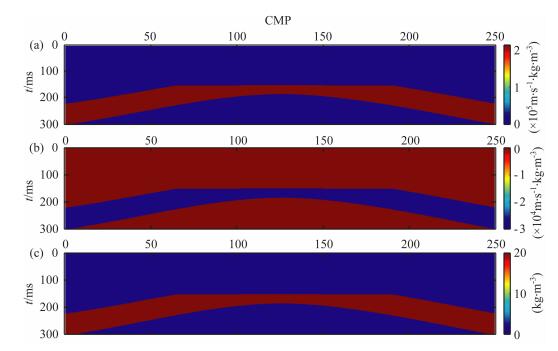
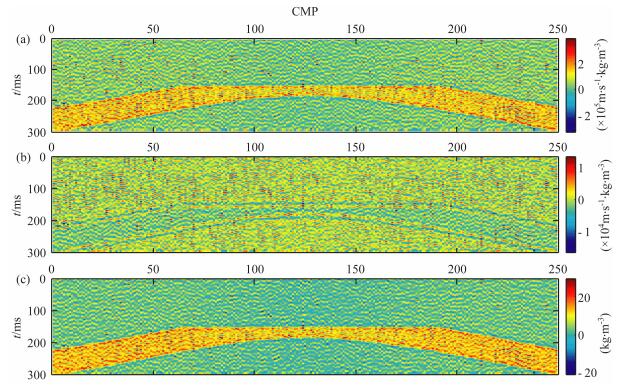
本文提出的时移地震反演就是要利用图 2所示的叠前地震资料求解弹性参数差值剖面.图 3 为模型真实参数差值剖面,首先对图 2 所示的合成地震记录分别进行反演,再将两次反演的结果求差得到参数差值剖面,如图 4所示.对比图 4和图 3可以看出,分别反演的结果噪声影响很大,有很多假象,弹性参数变化区域边界模糊,结果非常不理想.如果以此结果作为时移地震反演的最终结果不能令人满意,但该结果在一定程度上反映了弹性参数的变化情况,本文提出的方法以此结果为基础进一步进行差异反演,以期得到较为理想的反演结果.
|
图 2 入射角为10的合成时移地震记录(SNR=1:1) (a)基础地震记录;(b)监测地震记录. Fig. 2 Synthetic time-lapse seismogram with incident angle of 10 degrees (SNR=1:1) (a) Base seismic record; (b) Monitor seismic record. |
|
图 3 模型真实参数差值剖面 (a)纵波阻抗差值;(b)横波阻抗差值;(c)密度差值. Fig. 3 True results of the time-lapse seismic inversion model (a) P-wave impedance differences;(b) S-wave impedance differences;(c) Density differences. |
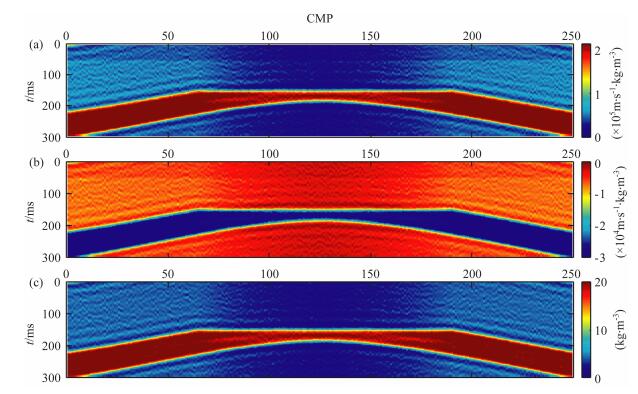
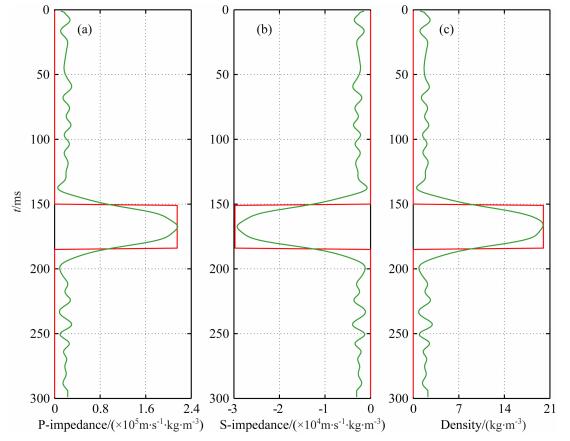
将图 4所示的分别反演结果进行低通滤波后的结果作为期望,利用本文研究的时移地震贝叶斯AVO 差异反演方法进行反演,得到了如图 5所示的反演结果.对比图 5和图 3可以看出,图 5所示的反演结果和图 3所示的实际差异非常接近,为了更好地进行比较,取模型中间的一地震道(CMP=125)的反演结果和实际油藏弹性参数差异绘制如图 6所示的曲线,可以明显看出,反演结果能够较好地反映由于开采而引起的油藏弹性参数的变化,验证了本文方法的有效性.从图 5中可以看出,反演结果受噪声影响较小,开采引起的弹性参数变化明显,边界清晰,参数变化值的大小接近真实值,而在非开采过程影响区域,基本上看不到假的弹性参数变化,可以在反演的差值剖面中分析出地下水替换油的区域,证明了本文方法能够有效地抑制假象,突出储层性质的变化,得到高分辨率的弹性参数变化信息.
|
图 4 移地震分别反演结果 (a)纵波阻抗差值;(b)横波阻抗差值;(c)密度差值. Fig. 4 Results of the time-lapse uncoupled inversion (a)P-wave impedance differences; (b) S-wave impedance differences; (c) Density differences. |
|
图 5 时移地震差异反演结果 (a)纵波阻抗差值;(b)横波阻抗差值;(c)密度差值. Fig. 5 Results of the time-lapse inversion of difference (a) P-wave impedance differences;(b) S-wave impedance differences; (c) Density differences. |
|
图 6 时移地震差异反演结果(绿色)和实际油藏弹性参数差异(红色)对比 (a)纵波阻抗差值;(b)横波阻抗差值;(c)密度差值. Fig. 6 Comparison of the results of the time-lapse inversion of difference (green) and the true results of the model (red) (a) P-wave impedance differences;(b) S-wave impedance differences;(c) Density differences. |
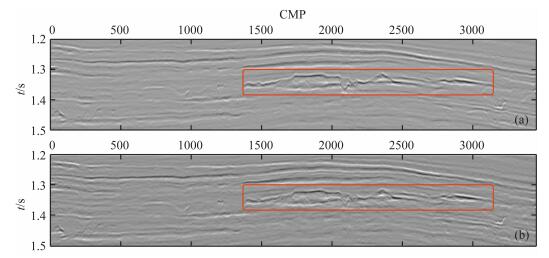
实际资料来自我国海上某气田的一条测线,该气田处的构造是深部泥岩在高温高压作用下塑性流体上拱,使上覆地层局部隆起变形形成的大型简单短轴背斜构造,具有圈闭面积大、闭合度大、埋藏浅的特点,圈闭面积50~254km2,闭合幅度99~271m, 埋深1205~1276m.这些条件对于时移地震油藏监测研究是有利的.图 7为该测线入射角为10°的叠前地震记录剖面,入射角为20°和30°的剖面与此类似,这里不予显示.图中红色矩形内为含气层,可以看到经过六年开采造成的地震记录的微弱变化.在地震记录的第1736道处,有一口井,有该井开发前的测井曲线,但没有开发后的测井曲线,因此只能通过岩石物理合成,这在一定程度上影响了井资料的准确性.通过对该井的开发前后的测井曲线进行统计,获得协方差矩阵.
|
图 7 入射角为10°的时移地震记录 (a)基础地震记录;(b)监测地震记录. Fig. 7 Time-lapse seismogram with incident angle of 10 degrees (a) Base seismcc record;(b) Monitor seismcc record. |
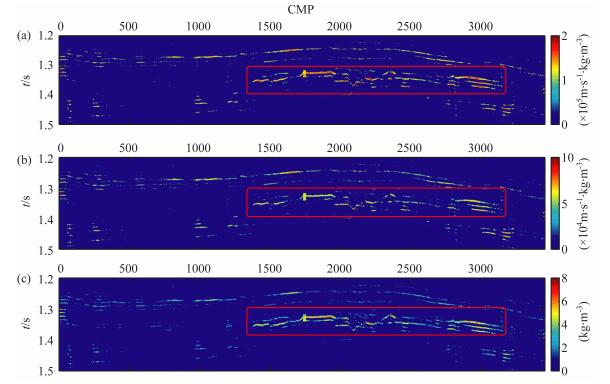
研究首先分别对基础测量资料和监测测量资料进行反演,然后对反演结果求差得到参数差值剖面,见图 8,图中也画出了由测井资料获得的弹性参数差异.从图中可以看出,由于受地震资料的影响,分别反演的结果虽然显示出了注采区域的参数变化(红色矩形区域),但在非注采区域,同样能够观察到明显的参数变化,这对反演结果的解释是不利的,可能导致错误的解释结果.
|
图 8 实际数据时移地震分别反演结果 (a)纵波阻抗差值;(b)横波阻抗差值;(c)密度差值. Fig. 8 Results of the time-lapse uncoupled inversion on real seismic data (a) P-wave impedance differences; (b) S-wave impedance differences; (c) Density differences. |
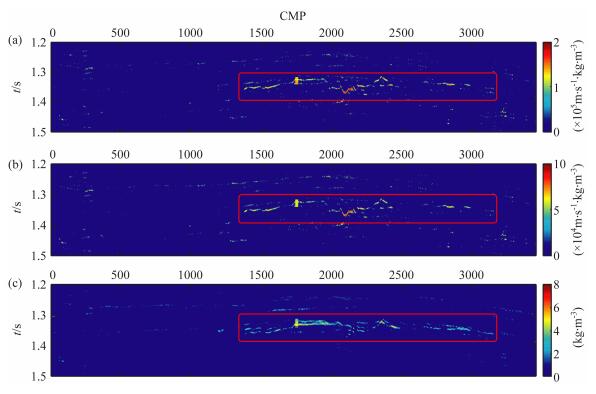
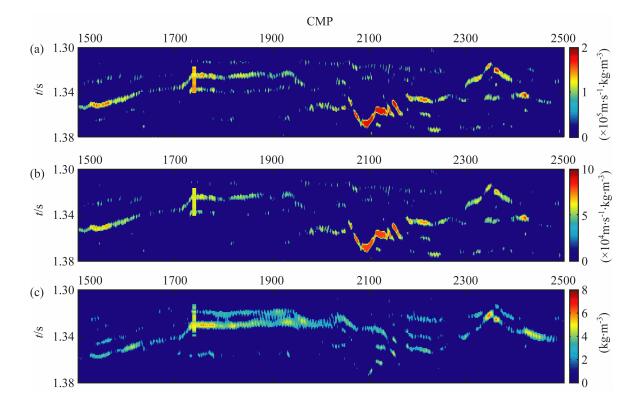
将分别反演的结果进行低通滤波后的数据作为期望,对测井曲线进行统计获得协方差矩阵,利用本文提出的时移地震贝叶斯AVO 差异反演方法进行反演,得到如图 9所示的结果.从图中可以看出,注采区域(红色矩形区域)显示出了明显的参数变化,非注采区域参数变化的假象得到有效抑制.为了更好地展示反演结果,将主要注采区域进行放大显示,如图 10.可以看出,反演结果和测井资料吻合得较好.图中弹性参数变化比较大的地方是气藏开采过程中天然气压力变化所导致的结果,而在其他非开采区域,弹性参数基本上没有变化.本文反演结果和实际情况是一致的,说明了本文提出的反演方法能够有效地抑制假象,突出储层性质的变化,从而较好地反映实际气藏的变化情况.
|
图 9 实际数据时移地震差异反演结果 (a)纵波阻抗差值;(b)横波阻抗差值;(c)密度差值. Fig. 9 Results of the time-lapse inversion of difference on real seismic data Results of the time-lapse inversion of difference on real seismic data |
|
图 10 差异反演结果放大图 (a)纵波阻抗差值;(b)横波阻抗差值;(c)密度差值. Fig. 10 The enlarged drawing of the results (a)P-wave impedance differences; (b)S-wave impedance differences; (c)Density differences. |
提出的时移地震资料AVO 波形反演方法能够利用时移地震差异数据同时反演出纵波阻抗、横波阻抗和密度的变化.针对时移地震反演中非注采过程影响区域易产生假象的问题,本文采用贝叶斯理论框架,基于Gidlow 三项近似方程,假设弹性参数变化的导数服从改进的Cauchy 分布,较好地抑制了非开采区域的虚假弹性参数变化信息,同时提高了反演结果的分辨率.本文反演方法假设纵横波阻抗和密度变化值服从高斯分布,并以时移地震分别反演结果作为其期望,提高了反演结果的精度,突出了储层弹性参数的变化.提出的方法基于贝叶斯统计理论,需要对测井数据进行统计以得到协方差矩阵和尺度常数等参数,这些参数统计的好坏直接影响着反演结果的好坏.因此,在井数目较多和测井数据较有代表性的情况下会得到更加理想的结果.
| [1] | Landr M. Discrimination between pressure and fluid saturation changes from time-lapse seismic data. Geophysics , 2001, 66(3): 836-844. DOI:10.1190/1.1444973 |
| [2] | Landr M, Veire H H, Duffaut K, et al. Discrimination between pressure and fluid saturation changes from marine multicomponent time-lapse seismic data. Geophysics , 2003, 68(5): 1592-1599. DOI:10.1190/1.1620633 |
| [3] | Batzle M, Wang Z. Seismic properties of pore fluid. Geophysics , 1992, 57(11): 1396-1408. DOI:10.1190/1.1443207 |
| [4] | Sarkar S, Gouveia W P, Johnston D H. On the inversion of time-lapse seismic data. 73th Annual International Meeting, SEG, Expanded Abstract, 2003:1489-1492. http://cseg.ca/assets/files/resources/abstracts/2005/044S0131-CSEG2005_abstract_mingyuzhang.pdf |
| [5] | Tura A, Lumley D E. Estimating pressure and saturation changes from time-lapse AVO data. 69th Annual International Meeting, SEG, Expanded Abstract, 1999:1655-1658. http://cn.bing.com/academic/profile?id=2051148376&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] | Gluck S, Deschizeaux B, Mignot A, et al. Time-lapse impedance inversion of post-stack seismic data. 70th Annual International Meeting, SEG, Expanded Abstract, 2000:1509-1512. http://cseg.ca/assets/files/resources/abstracts/2005/044S0131-CSEG2005_abstract_mingyuzhang.pdf |
| [7] | Abubakar A, Berg P M, Fokkema J T. A feasibility study on nonlinear inversion of time-lapse seismic data. 71th Annual International Meeting, SEG, Expanded Abstract, 2001:1664-1667. http://cseg.ca/assets/files/resources/abstracts/2005/044S0131-CSEG2005_abstract_mingyuzhang.pdf |
| [8] | Buland A, Ouair Y E. Bayesian time-lapse inversion. Geophysics , 2006, 71(3): 43-48. DOI:10.1190/1.2196874 |
| [9] | 李来林, 牟永光, 陈小宏. 计算时移波阻抗的新方法. 大庆石油地质与开发 , 2001, 20(6): 54–55. Li L L, Mou Y G, Chen X H. A new method for calculating time shift wave impedance. Petroleum Geology & Oil Field Development in Daqing (in Chinese) (in Chinese) , 2001, 20(6): 54-55. |
| [10] | 李景叶, 陈小宏, 金龙. 时移地震AVO反演在油藏定量解释中的应用. 石油学报 , 2005, 26(3): 68–73. Li J Y, Chen X H, Jin L. Application of time-lapse seismic AVO inversion to quantitative interpretation of reservoir. Acta Petrolei Sinica (in Chinese) (in Chinese) , 2005, 26(3): 68-73. |
| [11] | 李景叶, 陈小宏, 郝振江, 等. 多波时移地震AVO反演研究. 地球物理学报 , 2005, 48(4): 902–908. Li J Y, Chen X H, Hao Z J, et al. A study on multiple time-lapse seismic AVO inversion. Chinese J. Geophys. (in Chinese) (in Chinese) , 2005, 48(4): 902-908. |
| [12] | 陈小宏, 赵伟, 马继涛, 等. 时移地震非线性反演压力与饱和度变化研究. 地球物理学进展 , 2006, 21(3): 830–836. Chen X H, Zhao W, Ma J T, et al. Pressure and saturation change nonlinear inversion method using time-lapse seismic data. Progress in Geophysics (in Chinese) (in Chinese) , 2006, 21(3): 830-836. |
| [13] | 陈勇, 韩波, 肖龙, 等. 多尺度全变分法及其在时移地震中的应用. 地球物理学报 , 2010, 53(8): 1883–1892. Chen Y, Han B, Xiao L, et al. Multiscale total variation method and its application on time-lapse seismic. Chinese J. Geophys. (in Chinese (in Chinese) , 2010, 53(8): 1883-1892. |
| [14] | Eidsvik J. Blocky inversion of time-lapse seismic AVO data. 79th Annual International Meeting, SEG, Expanded Abstract, 2009:3820-3824. http://library.seg.org/doi/pdf/10.1190/1.9781560803126.refs |
| [15] | Kato A, Stewart R R. Joint AVO inversion for time-lapse elastic reservoir properties. Hangingstone heavy oilfield, Alberta. 80th Annual International Meeting, SEG, Expanded Abstract, 2010:4432-4437. http://cn.bing.com/academic/profile?id=1974730941&encoded=0&v=paper_preview&mkt=zh-cn |
| [16] | Hansteen F, Wills P B, Hornman K, et al. Time-lapse refraction seismic monitoring. 80th Annual International Meeting, SEG, 2010:4170-4174. http://cn.bing.com/academic/profile?id=2329822628&encoded=0&v=paper_preview&mkt=zh-cn |
| [17] | Suman A, Fernandes-Martinez J L, Mukerji T. Joint inversion of time-lapse seismic and production data for Norne field. 81th Annual International Meeting, SEG, 2011:4102-4108. http://cn.bing.com/academic/profile?id=1983770051&encoded=0&v=paper_preview&mkt=zh-cn |
| [18] | Zhao L X, Geng J H, Cheng J B, et al. Combined Bayesian AVO inversion with rock physics to predict gas carbonate reservoir. 81th Annual International Meeting, SEG, 2011:2747-2751. http://cn.bing.com/academic/profile?id=2117637295&encoded=0&v=paper_preview&mkt=zh-cn |
| [19] | Li J Y, Wang S D, Chen X H. Time-lapse seismic elastic impedance difference inversion and application. 81th Annual International Meeting, SEG, 2011:2492-2496. http://cn.bing.com/academic/profile?id=2328703484&encoded=0&v=paper_preview&mkt=zh-cn |
| [20] | Zhu Z Y, Jiang X D, Zhao W, et al. Time-lapse prestack elastic impedance inversion based on seismic difference data. 81th Annual International Meeting, SEG, 2011:2497-2501. http://cn.bing.com/academic/profile?id=649887298&encoded=0&v=paper_preview&mkt=zh-cn |
| [21] | Asnaashari A, Brossier R, Garambois S, et al. Sensitivity analysis of time-lapse images obtained by differential waveform inversion with respect to reference model. 81th Annual International Meeting, SEG, 2011:2482-2486. http://cn.bing.com/academic/profile?id=2326482631&encoded=0&v=paper_preview&mkt=zh-cn |
| [22] | 张繁昌, 刘杰, 印兴耀, 等. 修正柯西约束地震盲反褶积方法. 石油地球物理勘探 , 2008, 43(4): 391–396. Zhang F C, Liu J, Yin X Y, et al. Modified Cauchy-constrained seismic blind deconvolution. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 2008, 43(4): 391-396. |
| [23] | Gidlow P M, Smith G C, Vail P J. Hydrocarbon detection using fluid factor traces, a case study: How useful is AVO analysis? Joint SEG/EAEG Summer Research Workshop, Technical Program and Abstracts, 1992:78-89. http://cn.bing.com/academic/profile?id=2117655138&encoded=0&v=paper_preview&mkt=zh-cn |
| [24] | Todoeschuck J P, Jensen O G, Labonte S. Gaussian scaling noise model of seismic reflection sequences: Evidence from well logs. Geophysics , 1990, 55(4): 480-484. DOI:10.1190/1.1442857 |
| [25] | Walden A T, Hosken J W. The nature of the non-Gaussianity of primary reflection coefficients and its significance for deconvolution. Geophys. Prosp , 1986, 34(7): 1038-1066. DOI:10.1111/gpr.1986.34.issue-7 |
 2012, Vol. 55
2012, Vol. 55