2. 西安科技大学, 西安 710054
2. Xi'an university of science and technology, Xi'an 710054, China
逆时偏移成像技术早在20世纪80年代就被提出(Whitmore[1];Baysal等[2]),但由于该技术对硬件要求非常高,受计算机计算能力和存储能力的限制而发展非常缓慢.近年来,随着计算机技术的快速发展,特别是计算能力和存储能力的大幅提高,逆时偏移越来越受到人们的重视(张美根、王妙月[3];Yoon 等[4, 5];BednarJB 和BednarCJ[6],Zhang等[7],Liu等[8-9]).但这些工作在个人计算机上仍然仅限于二维逆时偏移,且工作效率非常低,往往需要好几天才能得到一张二维偏移剖面.使得程序调试周期过长,严重影响了逆时偏移的研究.最近几年,图形处理器(GraphicProcessing Unit)的浮点数据运算能力得到了大幅度提升(GTX480 的单精度浮点运算能力已经达到了1.35T,即每秒钟1.35万亿次浮点运算).Nvidia公司推出的CUDA(ComputerUnifiedDeviceArchitecture, 统一计算设备架构)平台可以使程序编写员非常容易地编写出可在GPU上运行的程序源代码.特别值得一提的是,2009 年中国科学院地质与地球物理研究所等科研人员成功地研制出基于GPU/CPU 协同并行计算的三维双程波波动方程叠前逆时偏移软件[10-14],使得逆时偏移的工作效率提高了1~2个数量级.
在逆时偏移存储问题上,近年来很多学者进行了卓有成效的研究:Symes[15]提出了使用checkpointing技术来降低逆时偏移的存储量;Dussaud等[16]比较了几种常用的存储策略,并认为checkpointing技术对存储量的需求最小,但是却较明显地增加了计算量;Clapp[17]提出的边界存储策略可在不增加计算量的情况下较大地降低逆时偏移的存储量,这种策略只要求存储边界网格层内的波场,在反传时作为边界条件来使用.Clapp[18]建议地震波传播算法中设置随机边界,可使逆时偏移不需要对波场进行任何额外的存储,缺点是在偏移剖面中会引入一些噪声,这种方法还有待于进一步的研究.尽管GPU 可以用来加速逆时偏移,解决计算效率问题,但是大存储问题仍然没有得到有效解决,甚至出现了新的问题:GPU 和CPU 之间的频繁的数据交换会严重影响逆时偏移的计算效率.本文将重点在逆时偏移的存储问题上展开研究.首先回顾了逆时偏移成像的原理,并引出了逆时偏移存储量问题;接着对常用的存储策略进行了详细论述,并重点研究了边界存储策略;然后在边界存储策略的技术上提出了有效边界存储策略,并使用checkpointing技术对有效边界存储策略进行了进一步的改进;最后使用Marmousi模型为例说明有效边界存储策略在降低存储量方面的效果.
2 逆时偏移的原理逆时偏移的基本思想是通过波动方程在时间上对采集到的地震数据进行反向传播来实现的.偏移过程中使用的是双程波波动方程,不受倾角限制,且能自动地使回转波、多次波等进行成像.逆时偏移的原理本文不再赘述.二维情况下,基于各向同性介质的一阶应力-速度声波波动方程为:
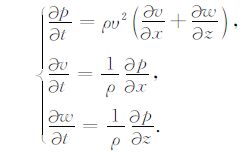
|
(1) |
上式中:ρ 为介质密度,υ 为介质纵波速度,v和w分别为x和z轴上的质点振动速度.本文将主要以基于二维声波波动方程的高阶交错网格有限差分方法来说明逆时偏移成像的具体实现过程.波场正演通常使用有限差分来对波动方程进行离散,本文对公式(1)采用交错网格技术[19-21]来构建波场传播算子.考虑到逆时偏移的计算量和为避免数值频散问题对逆时偏移结果的影响,在时间方向采用二阶而在空间方向采用高阶差分格式(≥8阶).
实际中地震波是在无限区域中传播的,而逆时偏移中地震波的传播是使用数值方法进行的,需要对无限区域进行截取,增加人工边界.地震波传播的数值模拟中引入的人工边界会产生很强的边界反射,影响逆时偏移的成像质量,因此在数值模拟过程中必须采用边界处理技术来消除这种影响.在已有的边界处理技术中,完全匹配层(PML)[22-25]技术被认为是对边界反射吸收较好的技术,因此本文使用PML 技术来对边界进行处理,消除人工边界反射造成的影响.
炮域实现逆时偏移主要包括以下三个步骤:
(1) 震源波场在时间方向从零时刻进行正向传播至最大时刻,并将所有时刻的波场值保存到存储空间(硬盘);
(2) 接收波场在时间方向从最大时刻进行反向传播至零时刻,并在每一时刻读取相应时刻的震源波场值;
(3) 利用互相关成像条件对两次传播得到的波场进行零延时互相关成像,成像条件公式为:
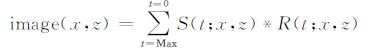
|
(2) |
其中S表示震源处震源信号正向传播的波场,R表示接收点处接收记录反向传播的波场.
3 常用存储策略回顾从上述步骤可以看出,在实现逆时偏移过程的第一步要求保存所有时刻的震源波场,这对计算机有较高的配置要求,特别是硬盘容量和带宽.以Marmousi模型为例,横向网格数2301(4m 网格),纵向网格数751(4 m 网格),PML 层为32,采样点数10000(时间采样间隔为0.3 ms),波场数据类型为4字节浮点型,则共需要约64G 左右的硬盘存储空间(只存储内部网格的波场).10000 个波场快照从内存写入硬盘需要耗时25min左右,再从硬盘读入内存又需要耗时9 min, 读写共需要耗时34 min(测试机型:Inter CoreTM 2 QuadCPU Q6600 @2.4GHz, 4GBDDR2 内存).正演一炮Marmousi模型记录(基于CPU,时间二阶,空间8 阶)耗时29min左右,而基于GPU 时耗时仅15s左右(测试GPU 型号:GTX480).由此可见,对于基于CPU 的一炮Marmousi记录的逆时偏移来说,除了需要64G 的存储空间外,还额外增加了约50% 的耗时(用于存取波场),而对基于GPU 的逆时偏移来说,由存储引起的耗时更多(增加了GPU 和CPU 之间的数据传递耗时),且存取耗时在整个逆时偏移耗时中的比重更大(计算波场只需30s, 而存取波场需34min, 还不包括GPU 和CPU 之间的数据传递耗时).所以逆时偏移的存储是一个亟待解决的问题.
3.1 常用存储策略逆时偏移提出以后,寻求如何降低逆时偏移对存储空间的需求就一直是研究者们探索的一个重要方向.目前常用的有以下几种存储策略:
(1) 首先从0时刻开始将震源正向传播到最大时刻Nt(正演时间点数,下同),并将所有时刻的震源波场存储在大容量硬盘中,进行偏移成像时再从硬盘读出.这种策略的计算量最小(为2Nt),易于实现,但是存储量巨大,导致存取非常耗时.
(2) 假设需要t时刻的震源波场,则从0时刻通过正演传播模块将震源正向传播到t时刻,即每时刻的震源波场都从0 时刻计算得到.这种策略的好处就是不需要存储任何波场,但是极大地增加了计算量(约为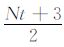
(3)先进行一次震源的正向传播,并每N步保存一次波场值pt0(二维情况下可保存到内存);在进行逆时偏移成像时,t′ 时刻的震源波场可以通过利用最近的波场值pt0(t′ >t)经过正向传播计算得到.这种策略降低了逆时偏移的存储需求,但是增加了正向传播的计算量,对计算量与存储量进行了折中.存储量降低为原来的1/N,而计算量为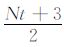
(4) 先进行一次震源正向传播,然后利用最后几个时刻的波场作为初始波场值(由正演时间阶数决定,如时间2阶情况时,是最后两个波场)使用伴随波动方程进行反向传播.这种策略中,震源波场反向传播能够与接收点波场反向传播同步,因此不需要额外的存储量,只增加了一次反向传播的计算量,且实现过程简单.但是该策略只适用于Dirichlet边界条件,而不适用于其他边界条件,比如边界吸收效果更好的完全匹配层(PML).该策略的存储量为0,计算量为3Nt.
(5) Clapp2008[17]年提出了边界存储策略:只存储人工边界层内的炮点正传波场,反传时将这些边界波场取出并作为边界条件来重构之前时刻的波场.该策略需要事先进行一次炮点正向传播,但较大地降低了逆时偏移的存储量(详见下文).
(6) Symes2007[15]年提出了一种checkpointing技术:首先确定Nb个波场存储点和Nc个checkpoint点(Nb\[\ll \]Nc);然后进行一次震源波场的正演传播,并记录规定时刻的波场值(Nb个);成像时利用checkpoint点中之前最近时刻的波场进行正演传播得到该成像时刻的震源波场(如果该checkpoint点中没有存储波场,则从波场存储点中之前最近的波场进行正演传播得到).当Nc=Nt时等同于策略1,而当Nc=0时等同于策略2.checkpointing技术将计算量和存储量之间的折中关系更加细化,有利于对计算量和存储量进行更好地折中.
(7) 2009年Clapp[18]提出在逆时偏移的震源波场传播过程中使用随机散射边界技术[5]:这种技术是将模型外面增加一定厚度的随机边界(速度、密度等参数从内边界到外边界按照下降趋势随机给定),地震波在传播到边界处时发生,而不至于形成反射,且能量也没有像其他边界条件一样被吸收,因此完全可以通过最后两个时刻的波场反向外推出之前任一时刻的波场值,且在此过程中不必考虑边界(边界内和边界外使用同一个方程),进而可以减少正演计算时间.随机散射边界技术的使用可以使逆时偏移不需要额外的存储空间,且计算量较小(为3Nt,等同于策略4),但是随机边界的设置仍然有待于研究(随机边界厚度参数、随机分布规律、以及随机边界对低频分量散射效果不佳等).
3.2 边界存储策略的实现原理在这些常用策略中,边界存储策略(策略5)具有存储量小,计算量相对较少,易于实现,且能适用于任何边界条件(包括PML)等优点.下面将详细地叙说这种策略.
以二维各向同性介质的一阶应力-速度声波波动方程的逆时偏移为例,采用常用的交错网格高阶有限差分方法对其(式1)进行时间二阶空间2N阶离散:
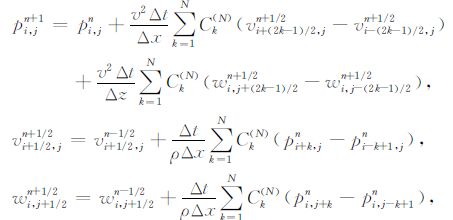
|
(3) |
式中Δt、Δx和Δz分别表示时间、空间x方向和空间z方向的采样步长,C(N)k表示高阶交错网格有限差分系数[19],下标i和j分别表示空间位置,上标n表示时间步.应力p、位移速度v和w被交错地置于空间网格和时间网格上.
策略4中通过利用最后两个时刻的波场值进行反向传播计算出之前任一时刻的波场值,这在传播顺序上和接收波场反向传播一致,因此不需要额外的存储量.但是其仅适用于Dirichlet边界条件,而不适用于吸收效果更好的PML.其原因在于PML边界条件在时间方向上是不可逆的,而如果事先将边界区域的波场存储下来,反向传播时作为边界条件来替换边界处的波场,就可完全正确地计算出之前任一时刻的波场.反向传播时所用离散差分格式如下两式:

|
(4) |
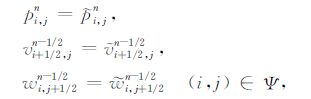
|
(5) |
其中,Ω 表示内部网格,Ψ 表示所有边界层网格.公式(4)用于计算内部网格波场,而在人工边界层内用公式(5)计算,(5)式在此作为边界条件.珟p、珘v和珦w表示炮点正向传播时所存储的波场.该策略的具体实现步骤(一阶应力速度声波方程交错网格有限差分)如图 1.从图 1 可以看出,反向传播是正向传播的反过程;同时,反向传播时不需要对边界区域进行额外处理,只需取出事先保存好的边界波场值进行替换,从而节省了边界处理所使用的计算时间.

|
图 1 波场正反向传播流程图 (a)震源波场正向传播流程图;(b)震源波场反向传播流程图. Fig. 1 The flowchart of forward propagating and backward propagating (a) The flowchart of source wavefield forward propagating;(b) The flowchart of receivewavefiefd backward propagating. |
由(5)式可计算出该策略的存储量为:
Memory=2L(Nx+Nz)Nt×4 bytes (6)其中,Nx,Nz分别为内部网格的横向和纵向网格数,L为边界层厚度.
4 有效边界存储策略 4.1 有效边界存储策略原理边界存储策略可以在不增加计算量的情况下有效地降低逆时偏移所需要的存储量.比如对上面提到的Marmousi模型来说,假设完全匹配层的厚度为32(网格数),那么采用该策略可将约71G 的存储量需求降低到约7.1G.目前的硬盘容量足以满足这一存储量,但计算机内存特别是普通PC 机的内存和显存仍然不能存储7.1G 左右的波场.因此下面对该策略进行一些改进,并在此基础上提出有效边界存储策略,进一步地减小逆时偏移的存储量.
如上节所述,边界存储策略要求利用最后两个时刻的波场值通过反传播技术得到之前任意时刻的正确的波场,所谓正确的波场除了要求模型内部网格的波场正确外还要求外部边界区域的波场值也正确,因此就需要保存所有边界区域的波场值.而实际上逆时偏移仅对内部网格进行偏移成像,因此仅需要保证内部网格的波场值正确即可.下面将对如何在保证内部网格波场值正确的情况下修改边界存储策略以进一步减小逆时偏移的内存需求量.
公式(4)中用应力分量p来计算位移速度水平分量v时的计算示意图如图 2.求vi+1/2,j(内部区域最外层的一点)时,需要用到PML 区域和内部区域各N(空间为2N阶差分)个应力分量p节点,比如空间4 阶差分时需要用PML 区域中的pi-1,j和pi-2,j和内部区域的pi,j和pi+1,j.如果在每步反向传播时PML 区域内N(对空间2N阶差分)个层的应力分量p是正确的,就可以保证位移速度分量v和w是正确的.同理,从公式(4)可以看出计算应力分量p时用到v的左右边界和w的上下边界,此时只需保证v分量在PML 区域中的左右边界和w分量在PML 区域的上下边界的波场值,就可以确保计算出的应力分量p的内部波场值的正确性.因此在反向传播时只要事先保存每个时间步进时的p、v和w在PML 区域内N个层的波场值(v的左右PML 层,w的上下PML 层和p的上下左右PML层),就可以保证得到的前一时刻的内部区域的波场值是正确的.据此可将(5)式修改为:

|
图 2 改进原理示意图 Fig. 2 Sketch map for improvement |

|
(7) |
其中,
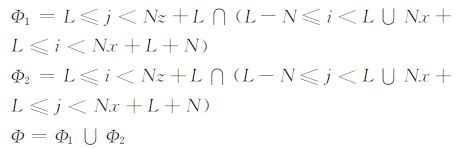
|
(7)式和(5)均可以保证每个时刻得到正确的的内部网格波场,但由于Φ 比Ω 小很多,因此使用(7)式存储量更小.上述方法中,需要分别保存p、v和w在PML 区域内N个层内所有时刻的波场值,实现比较繁琐.考虑到p、v和w相互之间的关系,如果事先保存p分量在PML 区域内2N个层内所有时刻的波场值,那么用p反向计算出的v和w除了内部波场正确外,它们的PML 区域中的内N层也是正确的,这样就可保证最后用v和w计算出的p的内部波场也是正确.这样在存取波场时只需考虑应力分量p,而不需要再考虑v和w,便于编写程序.据此又可将(7)式改写为:
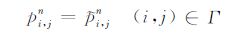
|
(8) |
其中,
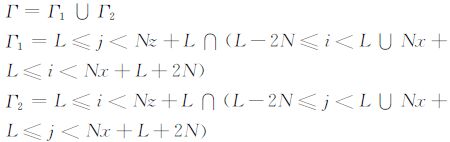
|
边界条件(8)式和(7)式是等效的,均能得到完全正确的内部网格处波场,同时两者所需的存储量也是相等的,即从区域大小上说满足,Г =Φ+Φ1+Φ2.但从公式上可以看出,(8)式只需对应力分量p进行边界处理,而不需考虑另外两个位移速度分量v和w,实现更加简单.⑻式中的Γ (图 3中蓝色区域)能有效保证内部网格Ω 中的波场完全正确,且Γ Ψ,因此便于叙述,本文将该区域称为有效边界,将这种存储策略称为有效边界存储策略.

|
图 3 有效边界存储策略(灰色为需要存储的区域r,黑色为节省的区域平一 r,白色为内部区域n) Fig. 3 Sketch map for efficient boundary storage strategies (blue is to be stored,red for saving and white for the interior) |
有效边界存储策略的存储量可通过下式计算:
Memory=2N(Nx+Nz)Nt×4 bytes (9)与总存储量比值为

|
(10) |
仍以上面的Marmousi模型为例,如果使用空间8阶的差风格式,则有效边界存储策略只需要2×8×(2301+751)×10000×4Bytes≈1.82G.与边界存储策略的7.1G 相比降低了很多(为改进前的N/L),通常N<L).普通PC 机的内存可以满足1.8G 的存储量,甚至一些用于科学计算的GPU 的显存也能满足.有效边界存储策略的需求量与PML 层的厚度无关,而与差分精度有关:精度越高存储量越大,精度越低存储量也越低,另外从(10)看出,模型越大(Nx,Nz越大),R就越小,表示该策略越有效.
4.2 基于checkpointing技术的有效边界存储策略对Marmousi模型来说.有效边界存储策略可将71G 的存储量(Marmousi模型)降为1.82G 左右,约为原来的2.5%.无论是普通PC 机的内存还是用于并行计算的GPU 的显存都可以满足1.8G的存储量需求.但是当逆时偏移的模型比较大,特别是进行三维逆时偏移时存储量需求仍然比较大,因此有必要进一步改进.
有效边界存储策略主要是从空间上对边界存储策略进行的改进,如果从时间上考虑还可以进一步降低存储需求.如上所述,有效边界需要进行一次正演计算,并保存每个时间步有效边界区域Γ 内的波场值,虽然一个时间步的存储量很小,但由于逆时偏移中的时间步数通常较大,因此总的存储量就比较大.借鉴策略6 的checkpointing 技术,可在时间方向设置Nb个checkpoint(等分总时间步),并配备Nb个缓冲区,用来保存每个checkpoint处的p,v和w的波场值.这样只需保存每两个checkpoint间的有效边界区域Г 内的波场值.具体实现步骤如下(以Nb=3为例,如图 4):
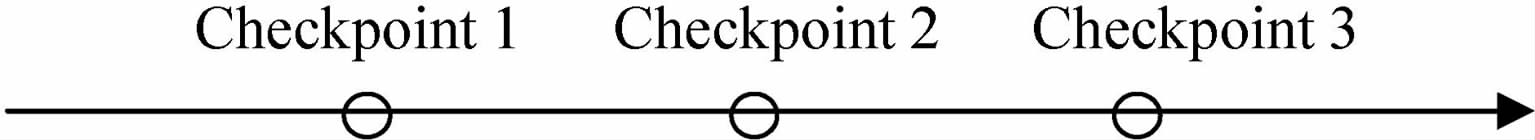
|
图 4 基于checkpointing技术的有效边界存储策略 Fig. 4 Sketch map for efficient boundary storage strategies based on checkpointing |
① 对震源进行正向传播,在checkpoint1 和checkpoint2处保存p,v和w的波场值,从checkpoint3开始保存每个时间步的有效边界区域Г 内的波场值;
②利用上一步最后得到的震源波场进行反向传播,每传播一步,利用事先保存好的该时刻有效边界区域Г 内的波场值替换应力分量p中相应位置的波场值,并与接收波场进行零延时互相关成像,直至checkpoint3.
③使用checkpoint2处事先保存好的p,v和w的波场值作为初值,进行正演传播,直至checkpoint3,并保存每个时间步的有效边界区域Г 内的波场值;
④利用上一步最后得到的震源波场进行反向传播,每传播一步,利用事先保存好的该时刻有效边界区域Г 内的波场值替换应力分量p的相应位置的波场值,并与接收波场进行零延时互相关成像,直至checkpoint2.
⑤使用checkpoint1处事先保存好的p,v和w的波场值作为初值,进行正演传播,直至checkpoint2,并保存每个时间步的有效边界区域Г 内的波场值;
⑥利用上一步最后得到的震源波场进行反向传播,每传播一步,利用事先保存好的该时刻有效边界区域Г 内的波场值替换应力分量p的相应位置的波场值,并与接收波场进行零延时互相关成像,直至checkpoin1.
⑦从零时刻进行正演传播,直至checkpoint1,并保存每个时间步的有效边界区域Г 内的波场值;
⑧利用上一步最后得到的震源波场进行反向传播,每传播一步,利用事先保存好的该时刻有效边界区域Г 内的波场值替换应力分量p的相应位置的波场值,并与接收波场进行零延时互相关成像,直至零时刻.
从上述步骤上可以看出:有效边界存储策略经改进后有效边界区域Г 内的波场值的存储量降低到为改进前1/(Nb+1),但增加了Nb个checkpoint处的p,v和w的波场值所需要的存储量;同时也增加了正演计算量,改进后的存储量的计算式如下:
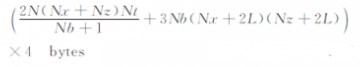
|
(11) |
改进后的计算量(正演次数)的计算式如下:

|
(12) |
为了显示Nb对存储量和计算量的具体影响,以前面提到的Marmousi模型为例进行绘图说明,如图 5.从图可以看出,随着checkpoint个数Nb的增大,逆时偏移中的计算量从3 迅速增大,但最大不超过4;而存储量则随着Nb的增大,呈现出先快速减小后缓慢增大的趋势(当存储量最小为383M 时,计算量为3.9).具体如何确定Nb的大小,还得视计算机的具体配置:如果内存足够大,能够满足1.8G 的存储量需求,可令Nb=0,此时计算量为最小;如果不能满足1.8G 的存储量需求,但能满足1G 的存储量需求,可令Nb=1,此时计算量为3.5,增加了半次正演的计算量.如果使用GPU进行逆时偏移,由于GPU 具有超级并行计算能力,可使正演模拟的计算效率提高好几十倍甚至上百倍,但其内存和显存之间频繁交换数据会严重影响逆时偏移效率,因此通过增大Nb,使数据直接存储在显存内,从而可避免显存与内存之间频繁的数据交换.

|
图 5 Nb对逆时偏移中存储量和计算量的影响(以Marmousi模型为例) Fig. 5 The influences of Nb on memory and computation i RTM (for example with Marmousi model) |
模型仍然使用上述的Marmousi模型,程序采用GPU 对逆时偏移进行并行加速,所使用的GPU规格参数和实验结果分别如下(表 1和表 2):
|
|
表 1 GPU规格参数 Table 1 GPU specifications |
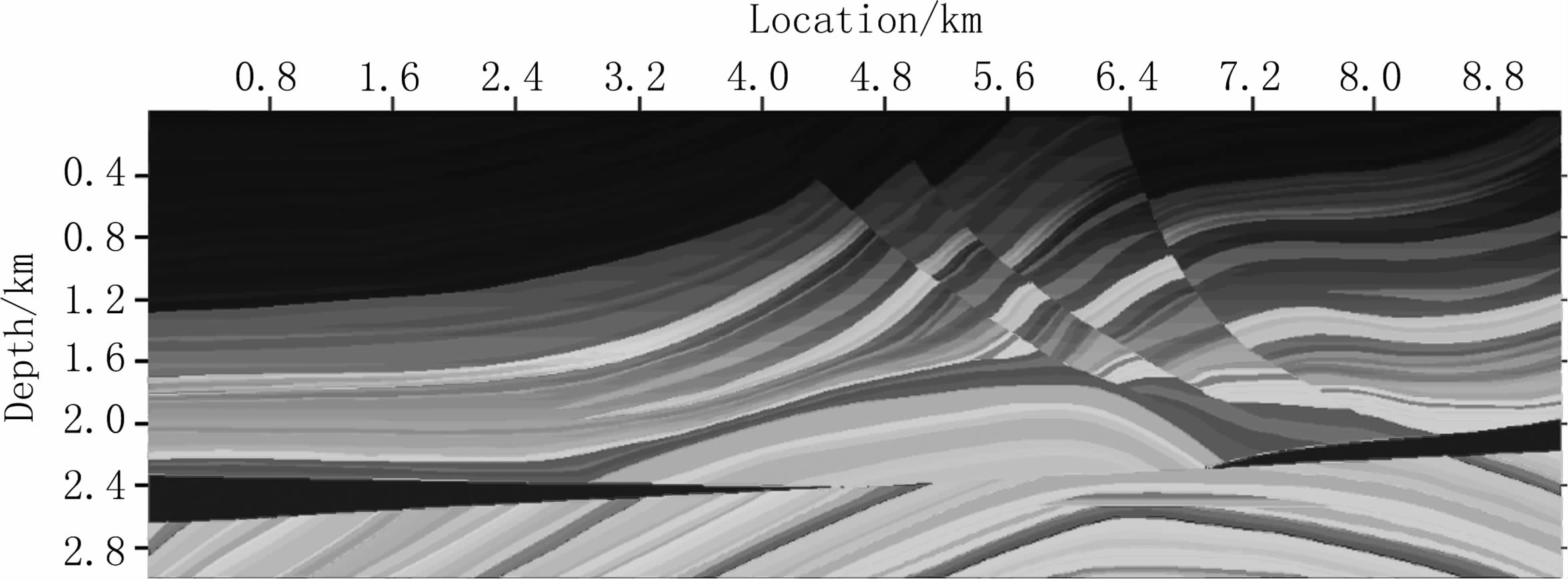
从表 2可以看出,有效边界存储策略在Nb=0时可使逆时偏移的存储量在不增加额外运算量的情况下减少为原来的4 倍左右.由于本次试验采用GPU 进行并行加速,所有的计算量均由GPU 承担,而GPU 的显存只有1.5G,不足以满足1.82G 的波场存储量,同时也为了避免GPU 的显存与内存之间的频繁数据交换,因此令Nb=1.此时,增加了0.5Nt(约16.7%)的计算量,但是却使存储量从1.82G降为0.91G,降低了50%,从而使得GPU 的显存能够满足偏移所需的存储量,减少了GPU 和CPU之间频繁数据传输所用的时间.Marmousi模型及逆时偏移成像结果见图 6和图 7.
|
|
表 2 Marmousi模型测试 Table 2 Marmousi model testing |
|
图 6 Marmousi速度模型 Fig. 6 Velocity of the Marmousi model |

|
图 7 逆时偏移剖面(有效边界存储策略) Fig. 7 Reverse time migration of the Marmousi model (efficient boundaries storage strategy) |
表 2 中,采用随机散射边界策略[12, 18],可以在计算量为3Nt的情况下,使计算量降低为0.从计算量和存储量来说都很理想.但随机散射边界会带来噪音,特别是频率较低的噪音.图 8即为用随机散射边界策略得到的Marmousi模型(100 炮记录)逆时偏移结果,与图 7相比有较大的噪音,特别是在浅部较为明显.

|
图 8 逆时偏移剖面(随机散射边界策略) Fig. 8 Reverse time migration of the Marmousi model (random scatter boundaries strategy) |
地震叠前逆时偏移的巨大存储量严重影响了逆时偏移的效率,本文研究分析了常用的存储策略,并着重对边界存储策略进行了详细的论述;在边界存储策略的基础上通过修改边界条件提出了有效边界存储策略,使逆时偏移在不增加任何计算量的情况下将存储量减低为原来的N/L;借鉴了checkpointing技术,对有效边界存储策略进行了改进:设置若干个checkpoint点,通过计算换存储的方法来进一步降低了存储量需求.使用有效边界存储策略在进行二维逆时偏移时,可只使用内存(使用GPU 加速时可只用显存)进行存储,最大限度地降低了存储量需求;另外,该策略的存储需求量不受边界厚度的影响,只与空间差分精度有关:差分精度越高需求量越大,精度越小,需求量也越小;同时该策略适用于所有边界条件,可直接应用于三维情况下的逆时偏移.最后使用Marmousi模型进行了试验,在不增加计算量的情况下可将71G 的存储量降低到约1.8G;基于checkpointing技术的有效边界存储策略则可在增加16.7% 的计算量的情况下降低到约0.9G,而增加25%计算量的情况下更可降低到0.3483G,能直接存储在显存或内存中,从而验证了有效边界存储策略的有效性和优越性.
| [1] | Whitmore N D. Iterative depth migration by backward time propagation. 53rd Annual International Meeting,SEG Expanded Abstracts, 1983, 827-830. http://www.oalib.com/references/18991983 |
| [2] | Edip Baysal, Dan D Kosloff, and John W C Sherwood. Reverse time migration. Geophysics , 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [3] | 张美根, 王妙月. 各向异性弹性波有限元叠前逆时偏移. 地球物理学报 , 2001, 44(5): 711–719. Zhang M G, Wang M Y. Prestack finte element reverse-time migration for anisotropic elastic waves. Chinese J. Geophys.(in Chinese) (in Chinese) , 2001, 44(5): 711-719. |
| [4] | |
| [5] | Kwangjin Yoon, Kurt J Marfurt and William Starr. Challenges in reverse-time migration. 74th Annual International Meeting, SEG Expanded Abstracts, 2003, 1057-1060. http://www.oalib.com/references/18988177 |
| [6] | J Bee Bednar, Chris J Bednar C J, and Changsoo Shin. Two-way versus one-way: A case study style comparison. 76th Annual International Meeting, SEG Expanded Abstracts, 2006, 2343-2347. http://cn.bing.com/academic/profile?id=1921123335&encoded=0&v=paper_preview&mkt=zh-cn |
| [7] | |
| [8] | Liu Faqi, Zhang Guanquan, Scott A Morton, et al. Reverse time migration using one way wavefield imaging condition. 77rd Annual International Meeting,SEG Expanded Abstracts , 2007, 26(1). |
| [9] | |
| [10] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese) (in Chinese) , 2010, 53(7): 1725-1733. |
| [11] | 刘红伟, 刘洪, 邹振, 等. 地震叠前逆时偏移中的去噪与存储. 地球物理学报 , 2010, V53(9): 2171–2180. Liu H W, Liu H, Zou Z, et al. The problems of denoise and storage in seismic reverse time migration. Chinese Journal Geophysics (in Chinese) , 2010, V53(9): 2171-2180. |
| [12] | 李博, 刘红伟, 刘国峰, 等. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报 , 2010, 53(12): 1938–2943. Li B, Liu H W, Liu G F, et al. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU. Chinese J. Geophys. (in Chinese) (in Chinese) , 2010, 53(12): 1938-2943. |
| [13] | 刘洪, 佟小龙, 刘钦, 等. 油气地震勘探数据处理GPU/CPU协同并行计算技术. 北京: 石油工业出版社, 2010 . Liu H, Tong X L, Liu Q, et al. GPU/CPU Coprocessing Parallel Computation for Seismic Uata Processing in Oil and Gas Exploration (in Chinese). Beijing: Petroleum Industry Press, 2010 . |
| [14] | 李博, 刘国峰, 刘洪. 地震叠前时间偏移的一种图形处理器提速实现方法. 地球物理学报 , 2009, 52(1): 245–252. Li B, Liu G F, Liu H. A method of using GPU to accelerate pre-stack time migration. Chinese J. Geophys. (in Chinese) (in Chinese) , 2009, 52(1): 245-252. |
| [15] | William W Symes. Reverse time migration with optimal checkpointing. Geophysics , 2007, 72(5): SM213-SM221. DOI:10.1190/1.2742686 |
| [16] | Eric Dussaud, William W Symes, Paul Williamson, et al. Computational strategies for reverse-time migration. 78rd Annual International Meeting,SEG Expanded Abstracts , 2008, 27: 2267-2271. |
| [17] | Robert G Clapp. Reverse time migration: Saving the boundaries. Saving the boundaries , 2008, 136: 136-144. |
| [18] | Robert G Clapp. Reverse time migration with random boundaries. 79rd Annual International Meeting,SEG Expanded Abstracts , 2009, 28: 2809-2813. |
| [19] | 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报 , 2000, 43(3): 411–419. Dong L G, Ma Z T, Cao J Z, et al. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J.Geophys. (in Chinese) (in Chinese) , 2000, 43(3): 411-419. |
| [20] | 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法稳定性研究. 地球物理学报 , 2000, 43(6): 856–864. Dong L G, Ma Z T, Cao J Z, et al. A study on stability of the staggered grid high order difference method of first order elastic wave equation. Chinese J.Geophys.(in Chinese) (in Chinese) , 2000, 43(6): 856-864. |
| [21] | 黄超, 董良国. 可变网格与局部时间步长的交错网格高阶差分弹性波模拟. 地球物理学报 , 2009, 52(11): 2870–2878. Huang C, Dong L G. Staggered-grid high-order finite-difference method in elastic wave simulation with variable grids and local time-steps. Chinese J.Geophys. (in Chinese) (in Chinese) , 2009, 52(11): 2870-2878. |
| [22] | Dimitri Komatitsch and Roland Martin. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics , 2007, 72(5): SM155-SM167. DOI:10.1190/1.2757586 |
| [23] | 孙林洁, 印兴耀. 基于PML边界条件的高倍可变网格有限差分数值模拟方法. 地球物理学报 , 2011, 54(6): 1614–1623. Sun L J, Yin X Y. A finite difference scheme based on PML boundary condition with high power grid step variation. Chinese J.Geophys. (in Chinese) (in Chinese) , 2011, 54(6): 1614-1623. |
| [24] | 陈可洋. 完全匹配层吸收边界条件研究. 石油物探 , 2010, 49(5): 472–477. Chen K Y. Study on perfectly matched layer absorbing boundary condition. Geophysical Prospecting for Petroleum (in Chinese) (in Chinese) , 2010, 49(5): 472-477. |
| [25] | 熊章强, 毛承英. 声波数值模拟中改进的非分裂式PML边界条件. 石油地球物理勘探 , 2011, 46(1): 35–39. Xiong Z Q, Mao C Y. An improved NPML absorbing boundary condition in acoustic wave modeling. Oil Geophysics Prospecting (in Chinese) (in Chinese) , 2011, 46(1): 35-39. |
 2012, Vol. 55
2012, Vol. 55



